CFRP吊索中承式铁路拱桥缆索的破断冲击效应分析

曾永平; 刘力维; 陶奇; 万幸; 张迅; 贾宏宇

doi:10.3969/j.issn.0258-2724.20240555

CFRP吊索中承式铁路拱桥缆索的破断冲击效应分析

doi: 10.3969/j.issn.0258-2724.20240555

曾永平^1,,
刘力维¹,
陶奇¹,
万幸²,
张迅²,
贾宏宇^2, ,

1.
中铁二院工程集团有限责任公司，四川成都 610031
2.
西南交通大学土木工程学院，四川成都 610031

基金项目: 国家重点研发计划（2021YFB3704404）；四川省重大专项（2023ZDZX0010）

详细信息

作者简介:
曾永平（1982—），男，教授级高级工程师，博士，研究方向为桥梁工程，E-mail：12543706@qq.com

通讯作者:
贾宏宇（1981—），男，副教授，博士研究生导师，研究方向为桥梁抗震，E-mail：Hongyu1016@swjtu.edu.cn

中图分类号: U24
计量
- 文章访问数: 74
- HTML全文浏览量: 41
- PDF下载量: 14
- 被引次数: 0
出版历程
- 收稿日期: 2024-10-29
- 修回日期: 2025-02-28
- 网络出版日期: 2025-07-10

Analysis of Impact Effect of Cable Breakage in Half-Through Railway Arch Bridges with CFRP Cables

1.
China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031, China
2.
School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
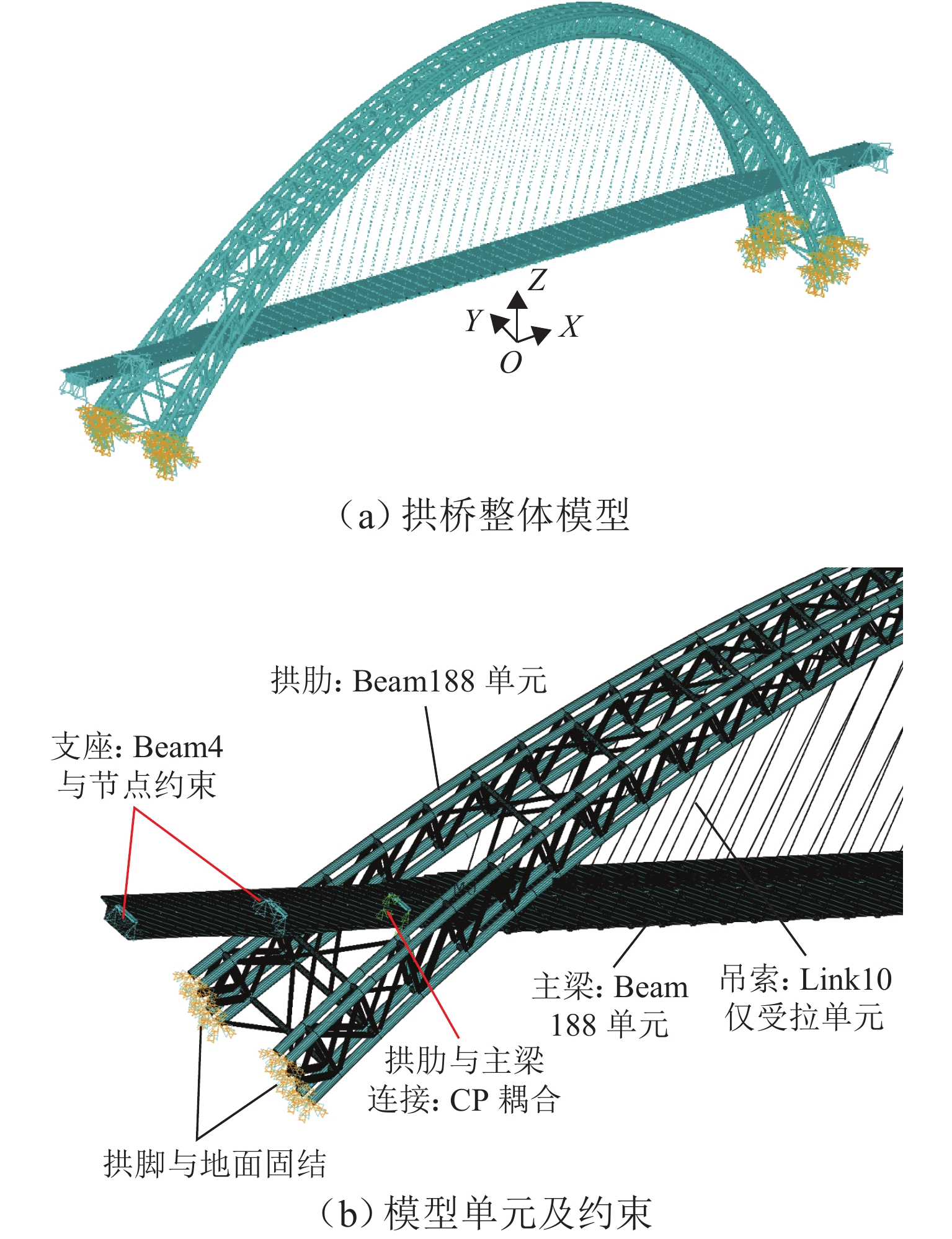
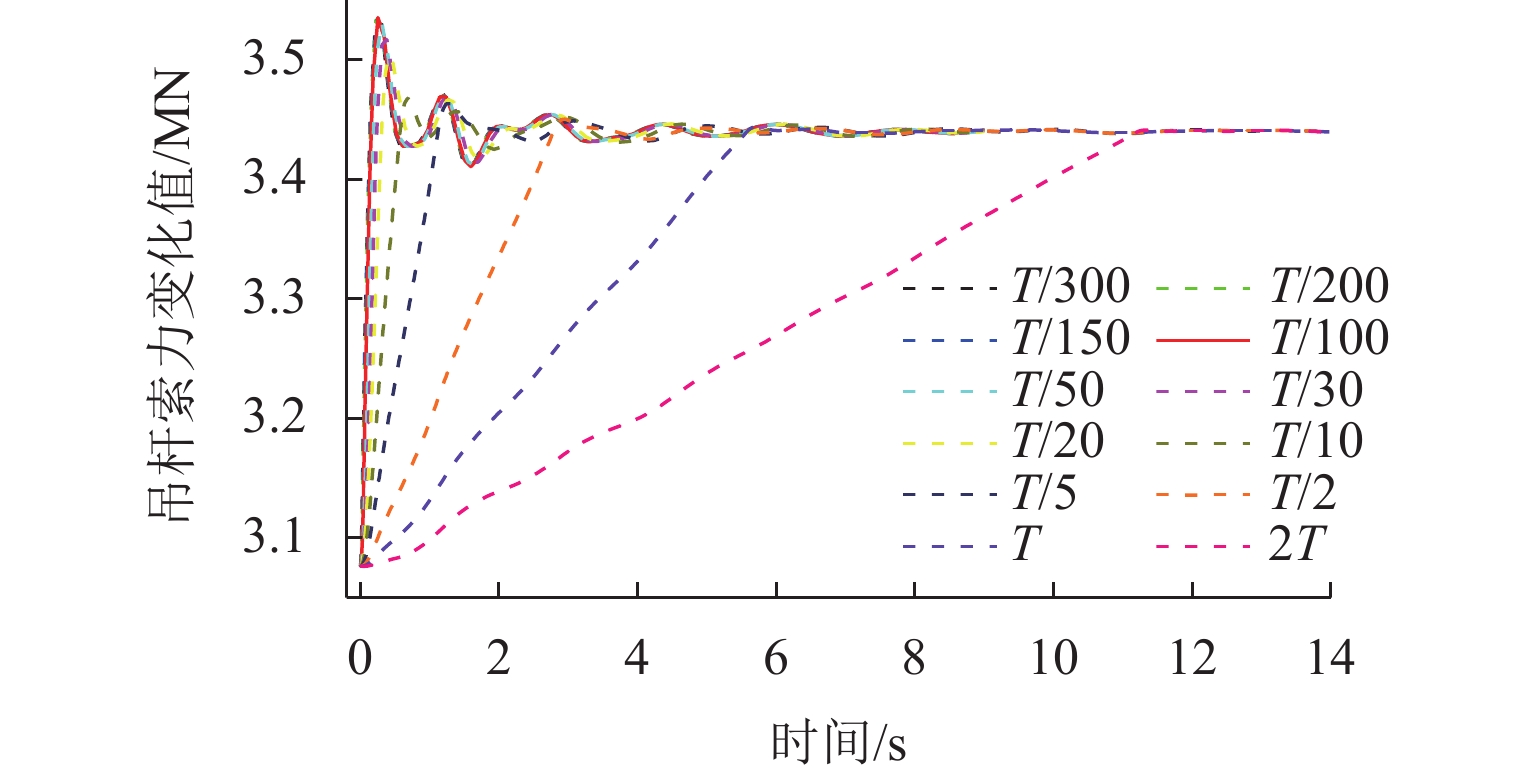
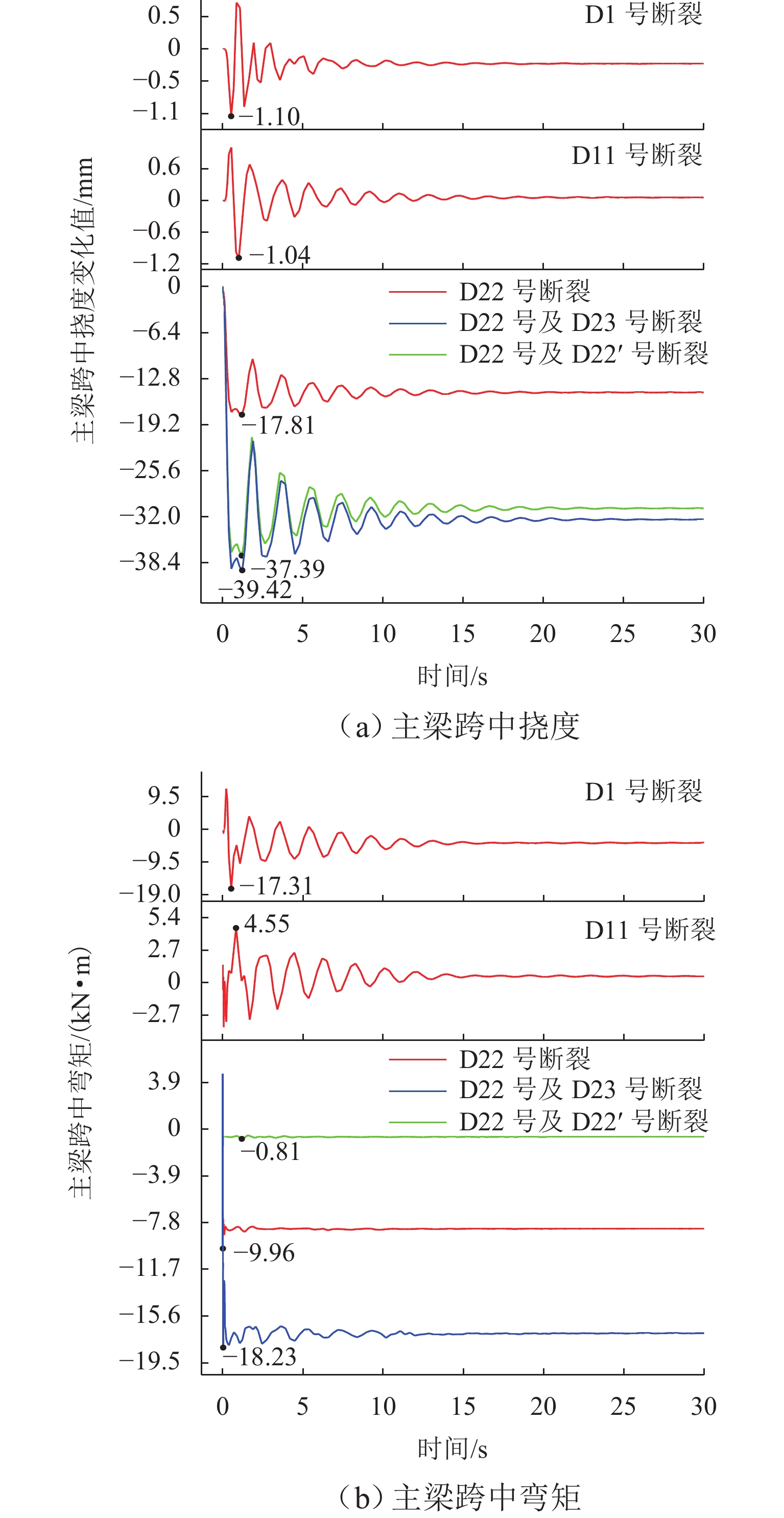
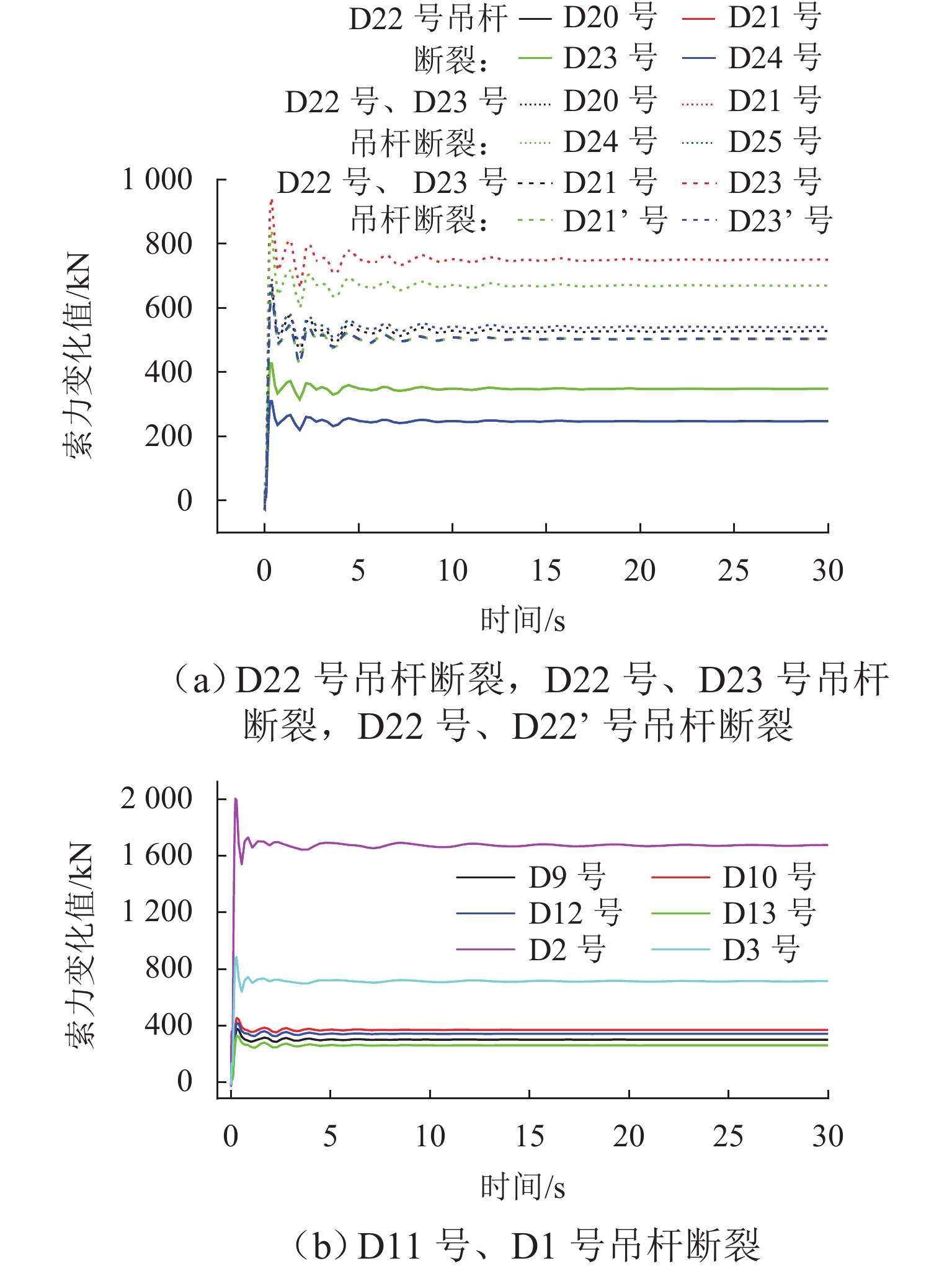
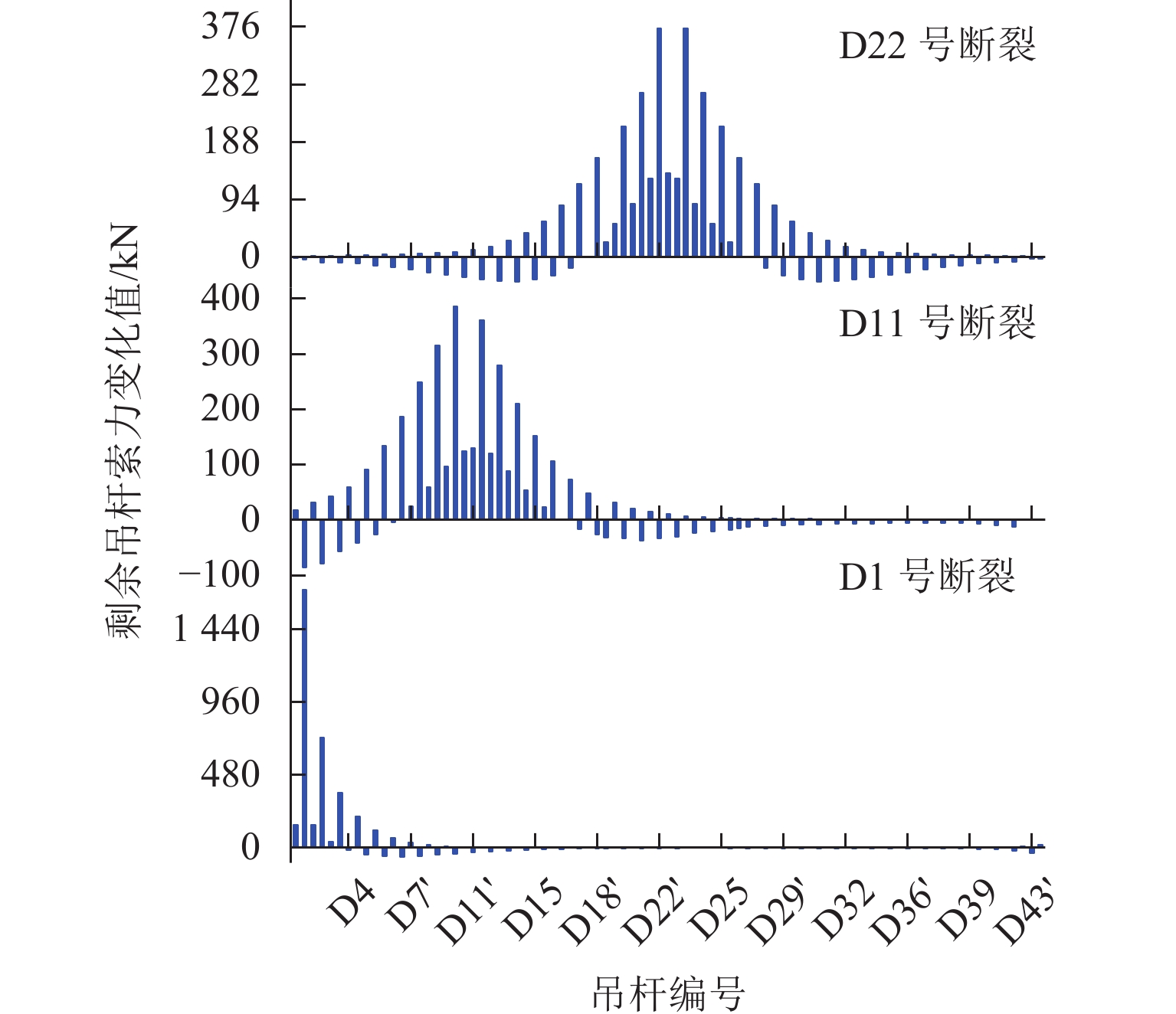
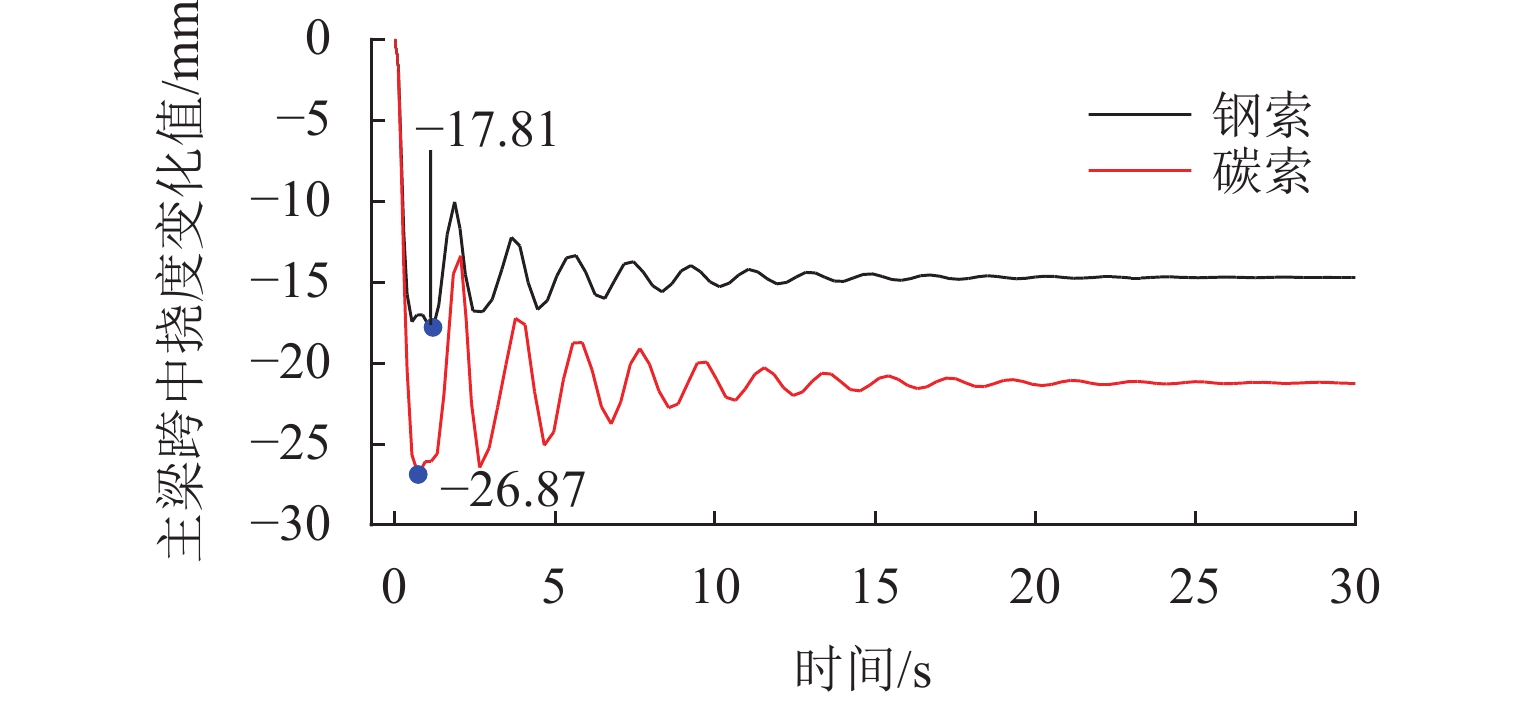
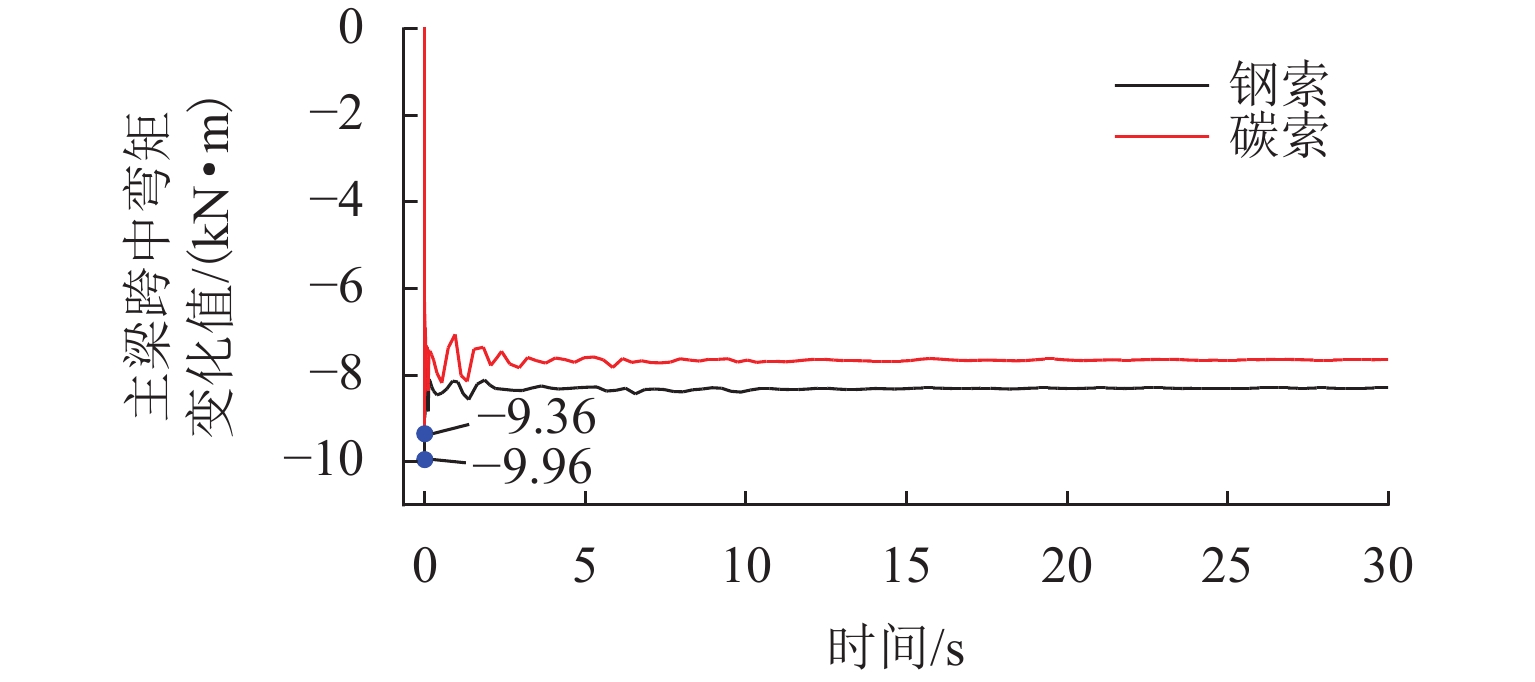
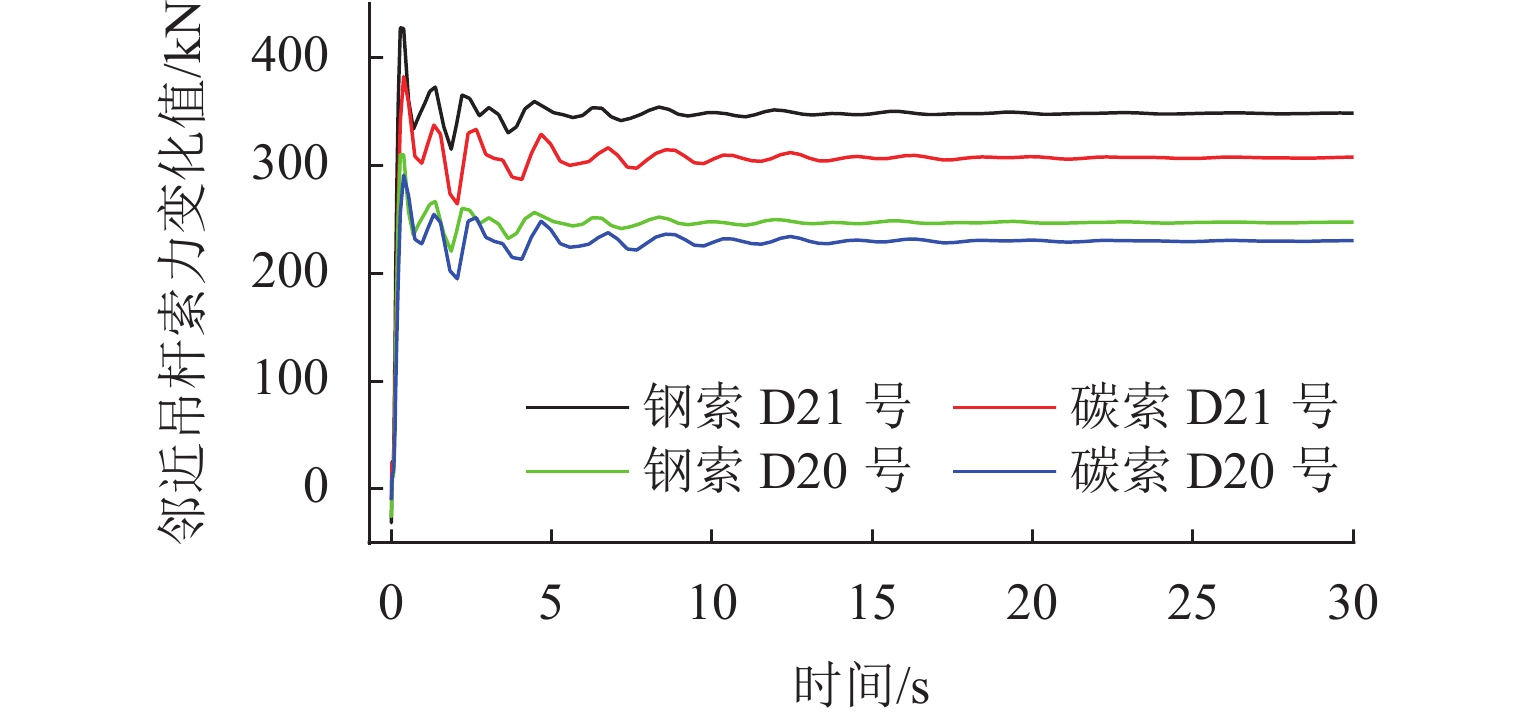
为研究吊杆断裂对钢管混凝土拱桥冲击响应的影响及对碳纤维复合材料索与钢索断索安全系数需求的差异，以某铁路特大桥为研究对象，分析偶然断索时全桥结构的动力响应. 采用ANSYS建立空间有限元模型，基于等效卸载法研究5种断索工况下拱桥剩余结构的受力特性变化规律；通过动力放大系数和能力需求比评估断索后结构的冲击敏感性；对比分析钢索与碳索不同缆索材料对桥梁断索动力响应的影响. 研究结果表明：断索位置和数量对主梁动力响应和拱肋应力影响显著；吊杆索力的重分配比例与距离断索区域的远近和索体长度成反比，与失效吊杆数量成正比；拱桥碳索对应的动力放大系数大于钢索的，均在1.19～1.43内变化；断索后剩余吊杆的应力需求比均未超过1，具有较大冗余；较钢索桥，拱桥碳索断索下的安全系数小，均在1.0～1.5内变化.
- 大跨度钢管混凝土拱桥 /
- 吊杆断裂 /
- CFRP索 /
- 动力响应 /
- 冲击影响 /
- 数值分析
Abstract:
To study the effect of cable breakage on the impact response of concrete-filled steel tube arch bridges and the difference in safety factor requirements between carbon fiber reinforced polymer (CFRP) cables and steel cables, the dynamic response of a railway bridge under accidental cable breakage was analyzed. A spatial finite element model was established by ANSYS. The force characteristic variations of the residual structure of the arch bridge under five cable breakage conditions were studied based on the equivalent unloading method. The impact sensitivity of the structure after cable breakage was evaluated by dynamic amplification factor (D_DAF) and demand capacity ratio (D_DCR). The effects of different cable materials, namely steel cables and carbon cables, on the dynamic response of the arch bridge were compared. The results show that the dynamic response of the main girder and the stress of the arch rib are greatly affected by the position and number of cable breakages. The redistribution ratio of the cable force is inversely proportional to the distance from the broken cable area and the cable length and directly proportional to the number of failed cables. The D_DAF of the arch bridge with carbon cables is higher than that of the arch bridge with steel cables, ranging from 1.19 to 1.43. The D_DCR of the remaining cable after cable breakage does not exceed 1, indicating large redundancy. Compared with bridges with steel cables, arch bridges with carbon cables require smaller safety factors under cable breakage conditions, ranging from 1.0 to 1.5.
- long-span concrete-filled steel tube arch bridge /
- cable breakage /
- CFRP cable /
- dynamic response /
- impact effect /
- numerical analysis

HTML全文

图 1 桥梁尺寸示意（单位：cm）

Figure 1. Bridge dimensions （unit: cm）

下载: 全尺寸图片幻灯片

图 2 拱桥有限元模型

Figure 2. Finite element model of arch bridge

下载: 全尺寸图片幻灯片

图 3 梁-索组合简化模型（单位：m）

Figure 3. Simplified model of beam and cable combination (unit: m)

下载: 全尺寸图片幻灯片

图 4 断索后节点5竖向振动时程曲线

Figure 4. Vertical vibration time history of Node 5 after cable breakage

下载: 全尺寸图片幻灯片

图 5 不同断索工况下节点5竖向振动时程曲线

Figure 5. Vertical vibration time history of node 5 under different cable breakage conditions

下载: 全尺寸图片幻灯片

图 6 D22号吊杆不同断索时间下D21号吊杆索力时程

Figure 6. Force time history of cable D21 under different breakage time of cable D22

下载: 全尺寸图片幻灯片

图 7 部分断索工况示意

Figure 7. Cable breakage conditions

下载: 全尺寸图片幻灯片

图 8 主梁跨中动力时程曲线

Figure 8. Time history of midspan of main girder

下载: 全尺寸图片幻灯片

图 9 断索后相邻吊杆索力增量的动力时程曲线

Figure 9. Time history of adjacent cables’ force increment after cable breakage

下载: 全尺寸图片幻灯片

图 10 单侧单根吊杆断裂后剩余吊杆索力变化值

Figure 10. Variation of cable force of remaining cables after unilateral single cable breakage

下载: 全尺寸图片幻灯片

图 11 断索处拱肋应力

Figure 11. Stress of arch rib at broken cable

下载: 全尺寸图片幻灯片

图 12 钢索与碳索主梁跨中挠度变化时程

Figure 12. Variation of main girder’s midspan deflection of steel cable and carbon cable

下载: 全尺寸图片幻灯片

图 13 钢索与碳索主梁跨中弯矩时程对比

Figure 13. Time history comparison of main girder’s midspan bending moment of steel cable and carbon cable

下载: 全尺寸图片幻灯片

图 14 钢索与碳索邻近吊杆索力变化时程对比

Figure 14. Time history comparison of adjacent cable force changes of steel cable and carbon cable

下载: 全尺寸图片幻灯片

图 15 钢索与碳索断索处拱肋应力时程对比

Figure 15. Time history comparison of arch rib’s stress at broken area of steel cable and carbon cable

下载: 全尺寸图片幻灯片

图 16 钢索与碳索索力动力放大系数对比

Figure 16. D_AF comparison of steel cable and carbon cable

下载: 全尺寸图片幻灯片

图 17 钢索与碳索断索后能力需求比对比

Figure 17. D_DCR comparison of steel cable and carbon cable after cable breakage

下载: 全尺寸图片幻灯片

表 1 索材料力学参数

Table 1. Mechanical parameters of cable materials

类型	弹性模量/GPa	强度/MPa	容重/（kN·m⁻³）
钢索	200	1860	78.5
CFRP索	160	3000	15.3

下载: 导出CSV

表 2 拱桥动力特性

Table 2. Dynamic characteristics of arch bridge

阶段	频率/Hz	振型特点
第 1 阶	0.179	主梁横向弯曲振动
第 2 阶	0.302	拱肋横向弯曲振动
第 3 阶	0.416	体系反对称竖向弯曲振动
第 4 阶	0.522	体系横向弯曲振动
第 5 阶	0.601	体系反对称横向弯曲振动
第 6 阶	0.606	体系正对称竖向弯曲振动
第 7 阶	0.826	体系正对称横向弯曲振动
第 8 阶	0.983	体系竖向弯曲振动
第 9 阶	1.043	体系正对称竖向弯曲振动
第 10 阶	1.077	体系正对称横向弯曲振动

下载: 导出CSV

表 3 断索工况模拟设置

Table 3. Cable breakage condition simulation

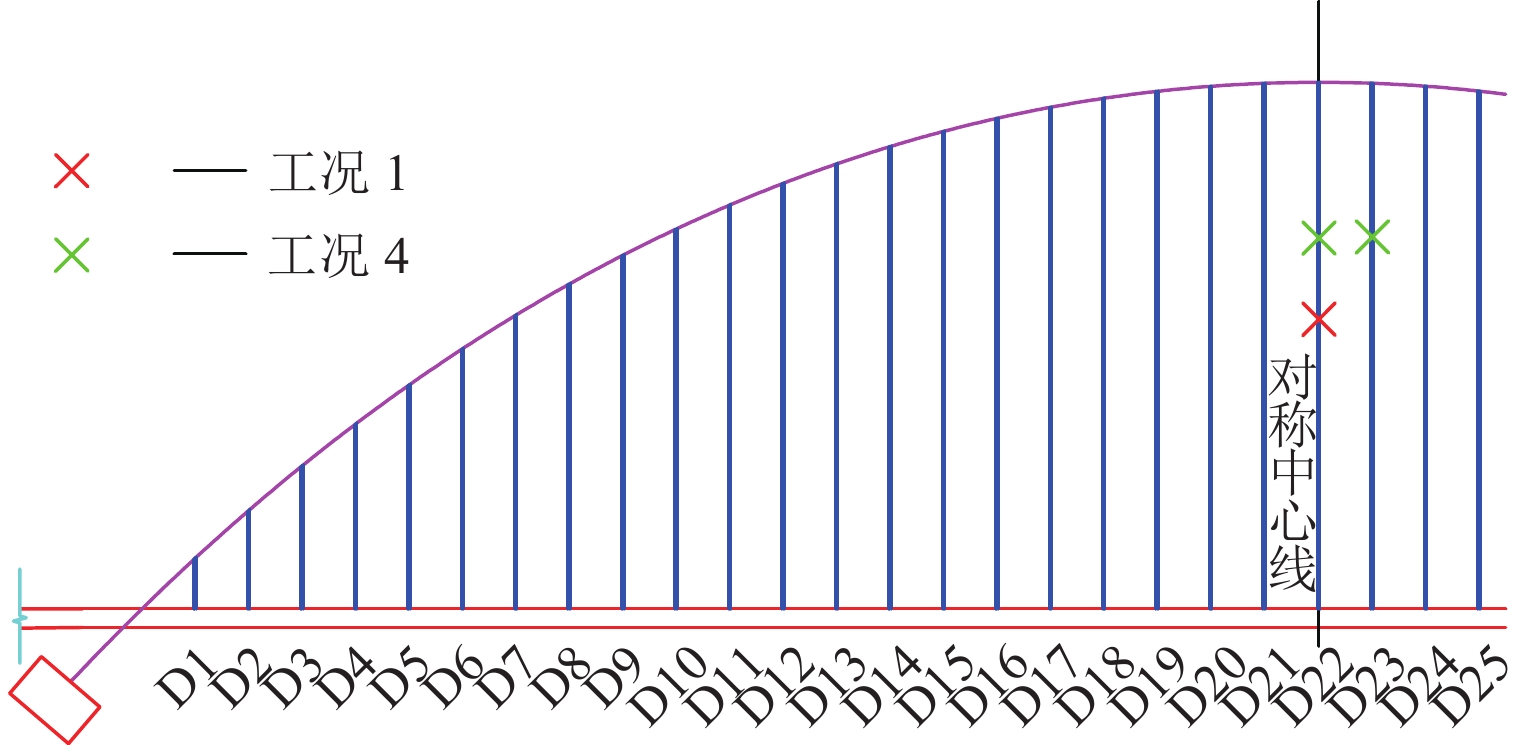
影响因素	断索工况	断索位置
断索位置	D22 号吊杆断裂（工况 1）	主梁跨中
	D11 号吊杆断裂（工况 2）	1/4 拱肋
	D1 号吊杆断裂（工况 3）	拱脚
断索数量	D22 号、D23 号吊杆断裂（工况 4）	主梁跨中
对称断裂	D22 号、D22’ 号吊杆断裂（工况 5）	主梁跨中

下载: 导出CSV

表 4 邻近吊杆索力冲击敏感性评估

Table 4. Impact sensitivity evaluation of adjacent cables’ force

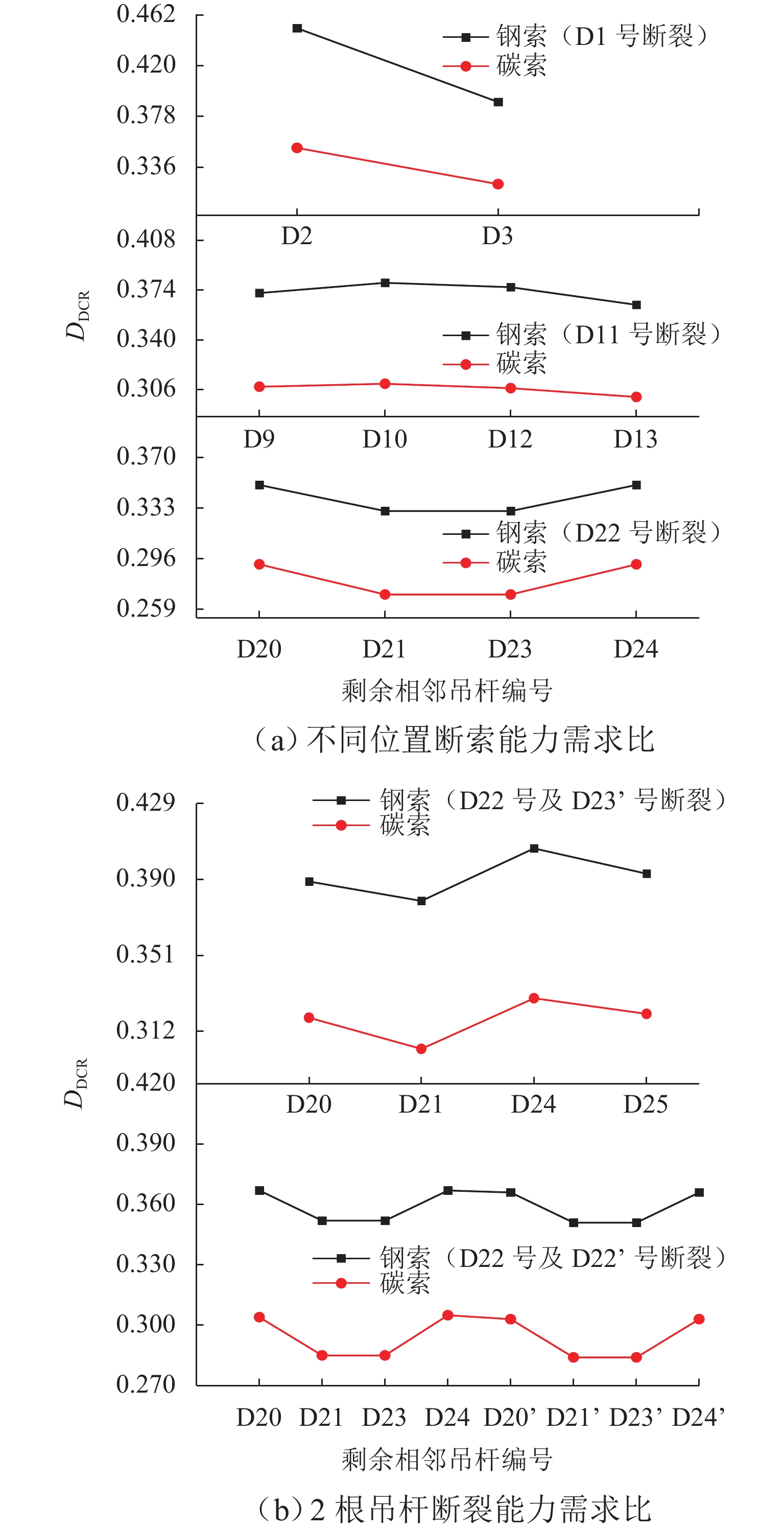
断索工况	邻近吊杆编号	吊杆应力最大值/Mpa		D_DCR		D_DAF		M
断索工况	邻近吊杆编号	钢索	碳索	钢索	碳索	钢索	碳索	钢索	碳索
D22 号断裂	D20 号	553.4	743.5	0.350	0.349	1.255	1.266	1.104	1.097
	D21 号	523.7	689.3	0.331	0.324	1.228	1.246	1.136	1.123
	D23 号	523.7	689.5	0.331	0.324	1.228	1.245	1.136	1.123
	D24 号	553.3	744.2	0.350	0.350	1.255	1.265	1.104	1.096
D11 号断裂	D9号	587.6	786.5	0.372	0.370	1.258	1.272	1.121	1.110
	D10 号	599.8	790.4	0.379	0.372	1.227	1.245	1.145	1.126
	D12 号	593.8	782.1	0.376	0.368	1.228	1.244	1.135	1.118
	D13 号	575.6	766.3	0.364	0.361	1.257	1.267	1.106	1.097
D1 号断裂	D2 号	713.7	898.0	0.451	0.423	1.198	1.236	1.490	1.388
D1 号断裂	D3 号	616.8	822.4	0.390	0.387	1.241	1.281	1.268	1.229
D22 号、D23 号断裂	D20 号	614.5	821.8	0.389	0.383	1.281	1.261	1.226	1.199
	D21 号	599.3	772.0	0.379	0.363	1.257	1.247	1.300	1.258
	D24 号	642.2	839.1	0.406	0.395	1.256	1.246	1.281	1.236
	D25 号	621.2	818.4	0.393	0.385	1.279	1.259	1.229	1.201
D22 号、D22’ 号断裂	D21 号	557.0	727.2	0.352	0.342	1.298	1.264	1.209	1.185
	D23 号	556.9	727.5	0.352	0.342	1.298	1.265	1.209	1.186
	D21’ 号	555.2	723.2	0.351	0.340	1.298	1.266	1.209	1.185
	D23’ 号	555.3	723.8	0.351	0.341	1.298	1.266	1.209	1.186

下载: 导出CSV

参考文献(27)

[1]	LIU Z X, GUO T, YU X M, et al. Corrosion fatigue and electrochemical behaviour of steel wires used in bridge cables[J]. Fatigue & Fracture of Engineering Materials & Structures, 2021, 44(1): 63-73.
[2]	ZHAO Y, GUO X L, SU B T, et al. Evaluation of flexible central buckles on short suspenders’ corrosion fatigue degradation on a suspension bridge under traffic load[J]. Materials, 2023, 16(1): 290.1-290.17.
[3]	WANG B T, JIA Y D, ZHAO H J, et al. Research on the dynamic response of a continuous steel box girder bridge based on the ANSYS platform[J]. Sustainability, 2022, 14(17): 10638.1-10638.22.
[4]	WANG S F, YU L, YANG F, et al. Effect of steel fiber distribution on the mechanical properties of UHPC caused by vehicle-bridge coupling vibration[J]. Composites Part B: Engineering, 2022, 245: 110201.1-110201.1.
[5]	SU J X, ZHANG J P, ZHOU J Y, et al. Fatigue life assessment of suspenders in tied-arch bridges under random traffic loads and environmental corrosion[J]. International Journal of Civil Engineering, 2023, 21(3): 523-540. doi: 10.1007/s40999-022-00792-3
[6]	ZHANG Y, FANG Z, JIANG R N, et al. Static performance of a long-span concrete cable-stayed bridge subjected to multiple-cable loss during construction[J]. Journal of Bridge Engineering, 2020, 25(3): 04020002.1-04020002.16.
[7]	LIU Z, NARASIMHAN H, KOTSOVINOS P, et al. Enhancing fire resilience of cable-supported bridges: current knowledge and research gaps[J]. Structural Engineering International, 2023, 33(4): 548-557. doi: 10.1080/10168664.2022.2164756
[8]	YIN T, SUN X S, WANG Y J, et al. Corrosion investigation of rock anchors served over 10 years in underground powerhouse of a hydropower station[J]. Advances in Materials Science and Engineering, 2022, 13: 4905010.1-4905010.14.
[9]	ZHANG L G, LIANG Z Z, LI S L. Effect of current density on the cathodic protection efficiency and mechanical properties of pre-stressed high-strength steel wires for stay cable[J]. Construction and Building Materials, 2022, 314: 125671.1-125671.11.
[10]	SCATTARREGGIA N, ORGNONI A, PINHO R, et al. Failure analysis of the impact of a falling object on a bridge deck[J]. Engineering Failure Analysis, 2023, 148: 107229.1-107229.21.
[11]	魏建东. 宜宾小南门大桥的抢修加固与恢复工程[J]. 公路, 2003, 48(4): 34-38. doi: 10.3969/j.issn.0451-0712.2003.04.010 WEI Jiandong. Urgent reinforcement and restoration of xiaonanmen bridge in Yibin City[J]. Highway, 2003, 48(4): 34-38. doi: 10.3969/j.issn.0451-0712.2003.04.010
[12]	邢丽丽, 常忠义. 国内近期桥梁垮塌案例分析与启示[J]. 福建建材, 2011(9): 27-28.
[13]	LIU P, LU H P, CHEN Y X, et al. Fatigue analysis of long-span steel truss arched bridge part II: fatigue life assessment of suspenders subjected to dynamic overloaded moving vehicles[J]. Metals, 2022, 12(6): 1035.1-1035.11.
[14]	NAKAMURA S, MIYACHI K. Ultimate strength and chain-reaction failure of hangers in tied-arch bridges[J]. Structural Engineering International, 2021, 31(1): 136-146. doi: 10.1080/10168664.2020.1775537
[15]	陈宝春, 范冰辉, 余印根, 等. 钢管混凝土拱桥强健性设计[J]. 桥梁建设, 2016, 46(6): 88-93. CHEN Baochun, FAN Binghui, YU Yingen, et al. Robustness design of concrete-filled steel tube arch bridges[J]. Bridge Construction, 2016, 46(6): 88-93.
[16]	FAN B H, SU J Z, CHEN B C. Condition evaluation for through and half-through arch bridges considering robustness of suspended deck systems[J]. Advances in Structural Engineering, 2021, 24(5): 962-976. doi: 10.1177/1369433220945835
[17]	曲兆乐, 石雪飞, 李小祥, 等. 斜拉桥拉索断裂损伤的动力过程模拟方法研究[J]. 结构工程师, 2009, 25(6): 89-92. doi: 10.3969/j.issn.1005-0159.2009.06.017 QU Zhaole, SHI Xuefei, LI Xiaoxiang, et al. Research on dynamic simulation methodology for cable loss of cable-stayed bridges[J]. Structural Engineers, 2009, 25(6): 89-92. doi: 10.3969/j.issn.1005-0159.2009.06.017
[18]	李岩, 崔石林, 陈逸民. 考虑模态更新的断索作用下斜拉桥动力响应分析方法[J]. 哈尔滨工业大学学报, 2024, 56(3): 1-8. doi: 10.11918/202205002 LI Yan, CUI Shilin, CHEN Yimin. Dynamic response analysis method of cable-stayed bridge under cable broken based on modal updating[J]. Journal of Harbin Institute of Technology, 2024, 56(3): 1-8. doi: 10.11918/202205002
[19]	陈康明, 吴庆雄, 罗健平, 等. 考虑吊杆断裂动力作用的钢管混凝土拱桥等效静力计算方法[J]. 土木工程学报, 2023, 56(6): 63-74. CHEN Kangming, WU Qingxiong, LUO Jianping, et al. Equivalent static calculation method for concrete filled steel tubular arch bridges considering dynamic effect of hanger fracture[J]. China Civil Engineering Journal, 2023, 56(6): 63-74.
[20]	邱文亮, 吴广润. 悬索桥吊索断裂动力响应分析的有限元模拟方法研究[J]. 湖南大学学报(自然科学版), 2021, 48(11): 22-30. QIU Wenliang, WU Guangrun. Research on simulation method of dynamic response analysis for suspension bridges subjected to hanger-breakage events[J]. Journal of Hunan University (Natural Sciences), 2021, 48(11): 22-30.
[21]	HUO J H, HUANG Y H, WANG J L, et al. Numerical analysis on the impact effect of cable breaking for a new type arch bridge[J]. Buildings, 2023, 13(3): 753.1-753.23.
[22]	吴庆雄, 罗健平, 陈康明, 等. 吊杆断裂破坏安全极限状态下中、下承式拱桥悬吊桥面系简化计算方法[J]. 土木工程学报, 2024, 57(10): 57-70. WU Qingxiong, LUO Jianping, CHEN Kangming, et al. Simplified calculation method for suspension bridge deck system of half-through and through arch bridge under safety limit condition of suspender fracture[J]. China Civil Engineering Journal, 2024, 57(10): 57-70.
[23]	ZHANG C, HAO H, BI K M, et al. Dynamic amplification factors for a system with multiple-degrees-of-freedom[J]. Earthquake Engineering and Engineering Vibration, 2020, 19(2): 363-375. doi: 10.1007/s11803-020-0567-9
[24]	刘永健, 刘江, 周绪红, 等. 桥梁长寿命设计理论综述[J]. 交通运输工程学报, 2024, 24(3): 1-24. LIU Yongjian, LIU Jiang, ZHOU Xuhong, et al. Review on long-life design theory for bridges[J]. Journal of Traffic and Transportation Engineering, 2024, 24(3): 1-24.
[25]	RUIZ-TERAN A M, APARICIO A C. Response of under-deck cable-stayed bridges to the accidental breakage of stay cables[J]. Engineering Structures, 2009, 31(7): 1425-1434. doi: 10.1016/j.engstruct.2009.02.027
[26]	霍建宏. 斜拱曲梁异型拱桥断索响应模型试验与有限元分析[D]. 广州: 广州大学, 2023.
[27]	黄永辉, 霍建宏, 傅继阳, 等. 拱桥断索冲击响应模型试验与有限元分析[J]. 中国公路学报, 2024, 37(5): 138-150. HUANG Yonghui, HUO Jianhong, FU Jiyang, et al. Model test and finite element analysis of arch bridge response to cable failure[J]. China Journal of Highway and Transport, 2024, 37(5): 138-150.