Optimized Design of High-Load Capacity Magnetic Bearings
-
摘要:
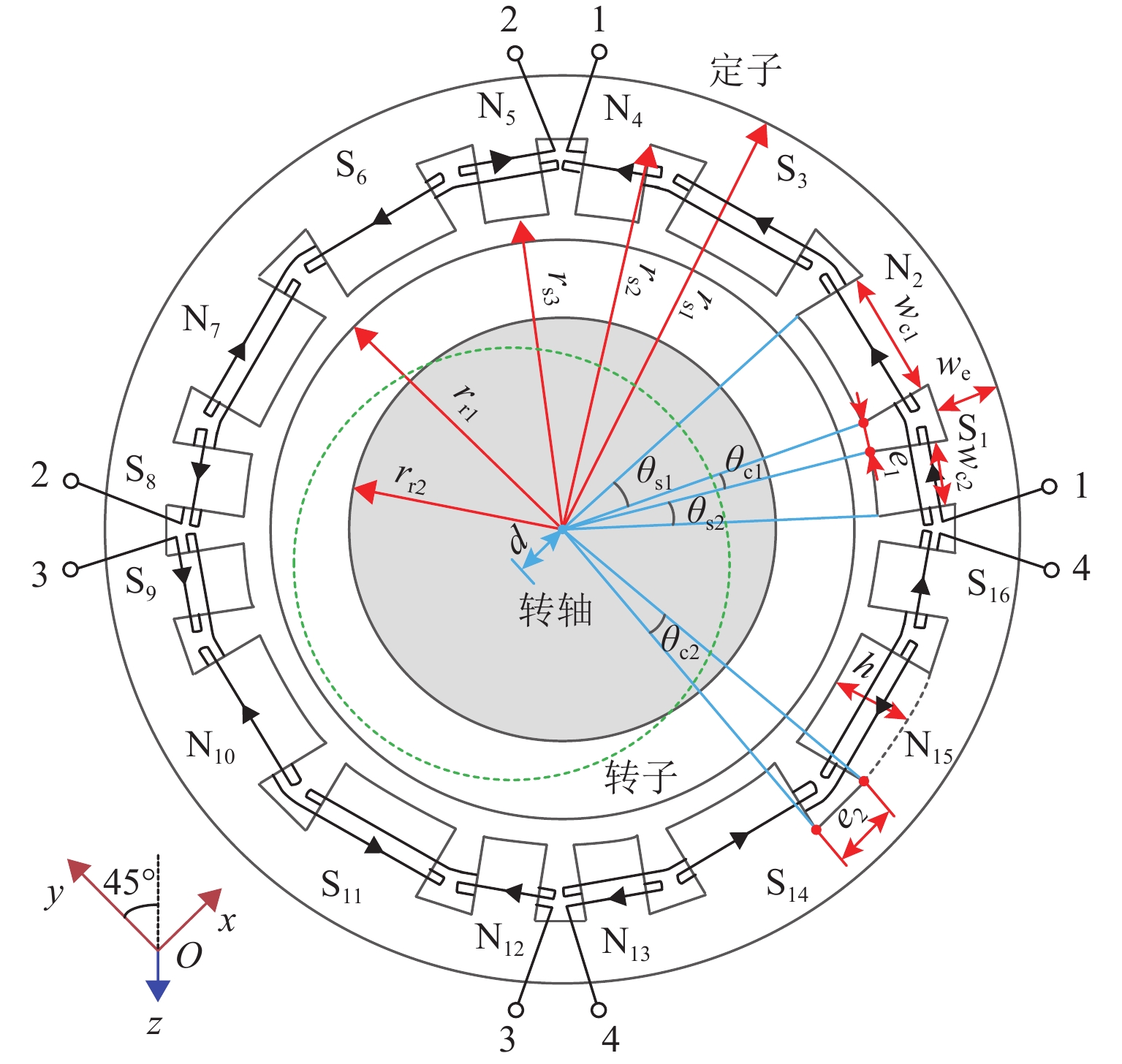
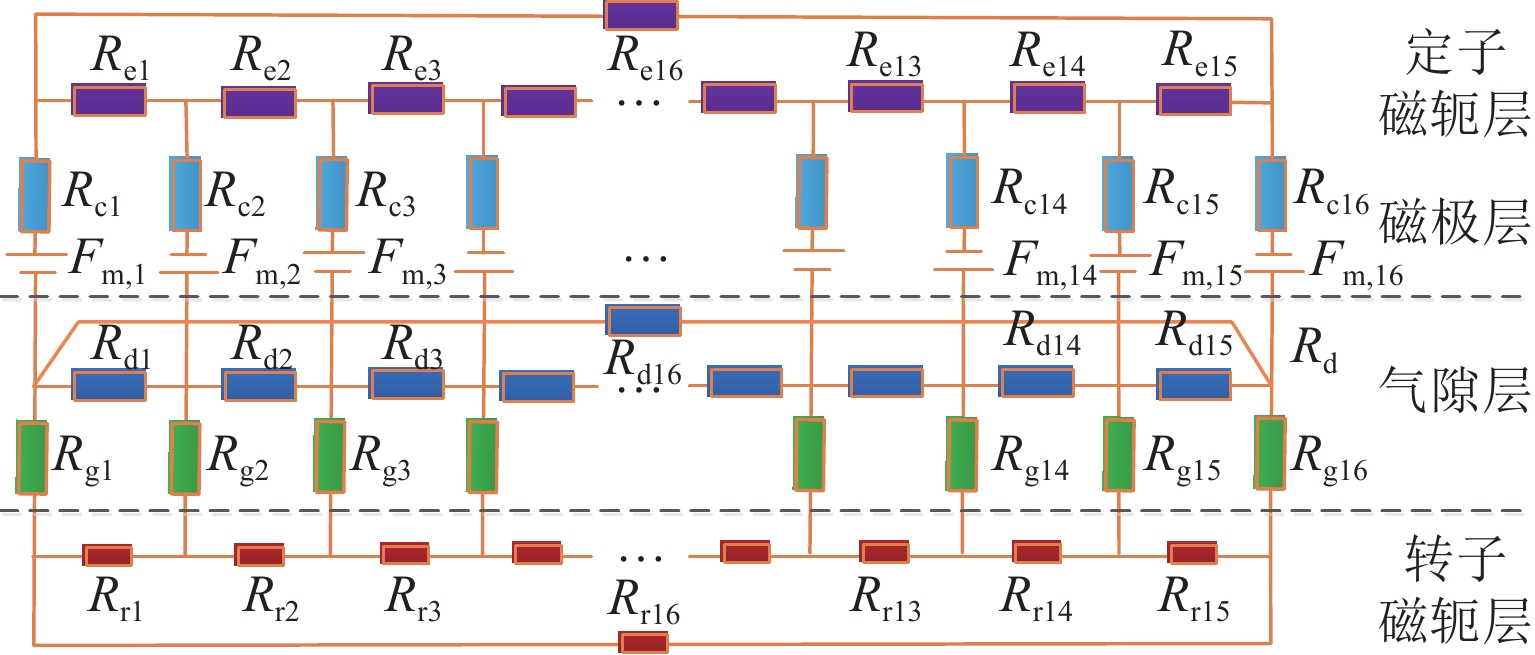
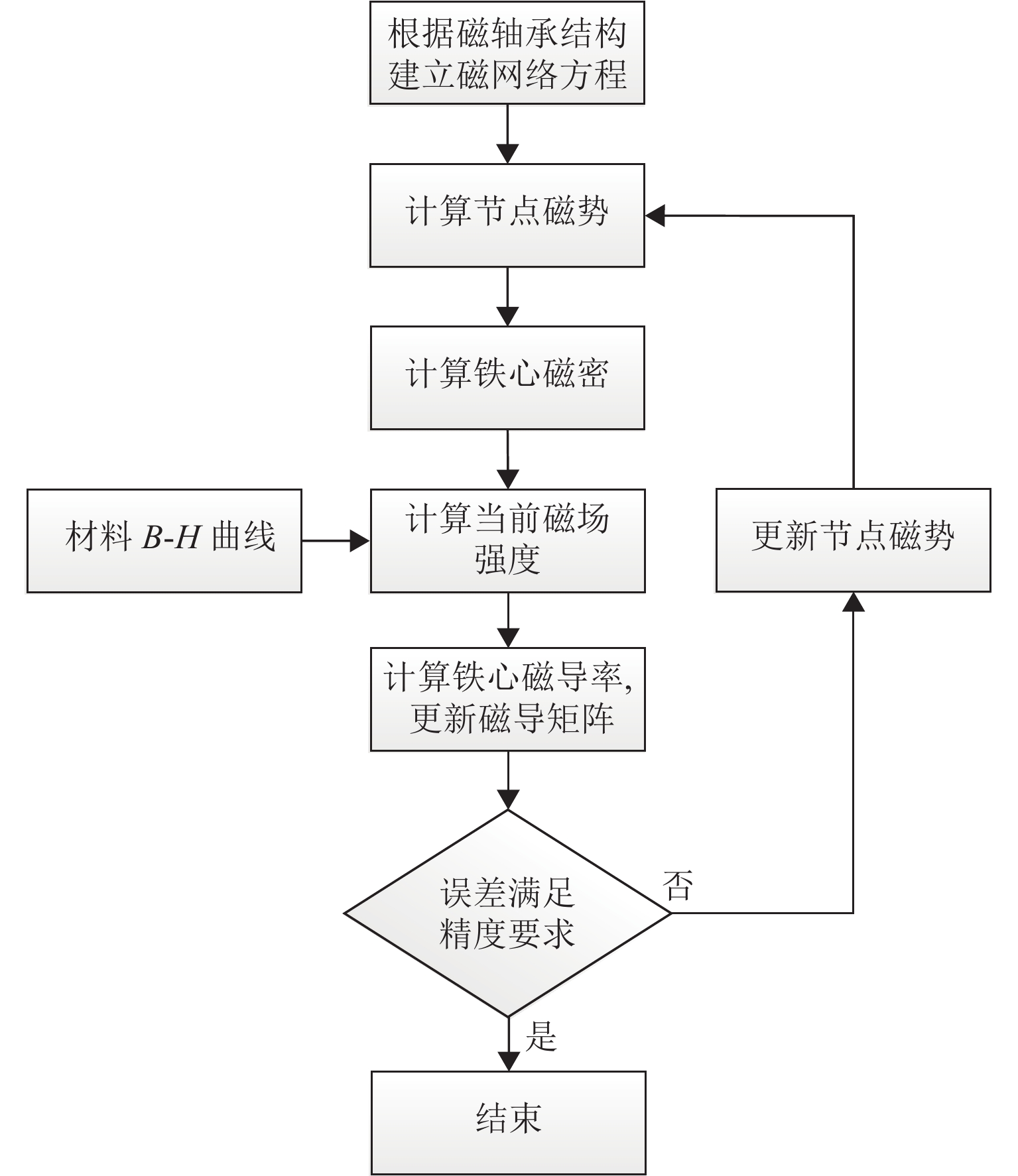
高速重载是磁轴承的重要应用趋势,针对传统磁轴承承载力密度低、电磁设计与控制器设计过程脱离等问题,本文提出通过增大磁轴承工作磁密到材料饱和区,用以提高磁轴承的承载力密度;在此基础上,考虑磁轴承饱和与强机电耦合特性,开展高承载力密度磁轴承结构-控制一体化设计. 首先,考虑饱和、转子偏心等因素,建立高承载力密度磁轴承的非线性磁路模型;其次,根据动力学模型构建磁轴承结构设计与控制系统的耦合关系,同时考虑磁轴承的承载力、功放电压和系统稳定性等约束,以最小轴向长度和最大力变化率作为优化目标,建立高承载力密度磁轴承的多目标优化模型,利用NSGA-Ⅱ算法求解得出高承载力密度磁轴承的设计方案;最后,利用有限元和实验验证设计方案的可行性. 结果表明:相较于传统磁轴承,高承载力密度磁轴承的承载力密度提高了21%,实测样机支承刚度与非线性磁路计算刚度的误差在4.6%以内,能够实现高转速下的稳定运行.
Abstract:High-speed and heavy-load applications are an important trend for magnetic bearings (MBs). To address issues such as low load capacity and disconnection between electromagnetic design and controller in traditional MBs, increasing the working magnetic flux density of the MBs to approach the material’s saturation region was proposed, which helps improve the load capacity. On this basis, an integrated structure-control design of high-load capacity MBs was carried out with the saturation and strong electromechanical coupling characteristics taken into consideration. Firstly, factors such as saturation and rotor eccentricity were considered to establish a nonlinear magnetic circuit model of the high-load capacity MBs. Then, based on the rotor dynamics model, the coupling relationship between the structural design and the control system was analyzed. Constraints such as load capacity, power amplifier voltage, and system stability of the MBs were considered, with optimization objectives set as minimizing the axial length and maximizing the rate of change of force. A multi-objective optimization model for high-load capacity MBs was established and solved using the NSGA-Ⅱ algorithm to obtain the design scheme. Finally, the proposed design scheme was validated through finite element analysis and experiments. The results show that compared to traditional MBs, high-load capacity MBs increase the load capacity by nearly 21%. The error between the measured support stiffness of the prototype and the calculated stiffness from the nonlinear magnetic circuit is within 4.6%, demonstrating stable operation at high rotational speed.
-
Key words:
- magnetic bearing /
- high-load capacity /
- saturation effect /
- coupling /
- multi-objective optimization
-
表 1 高承载力密度磁轴承的主要输入参数
Table 1. Main input parameters for high-load capacity MBs
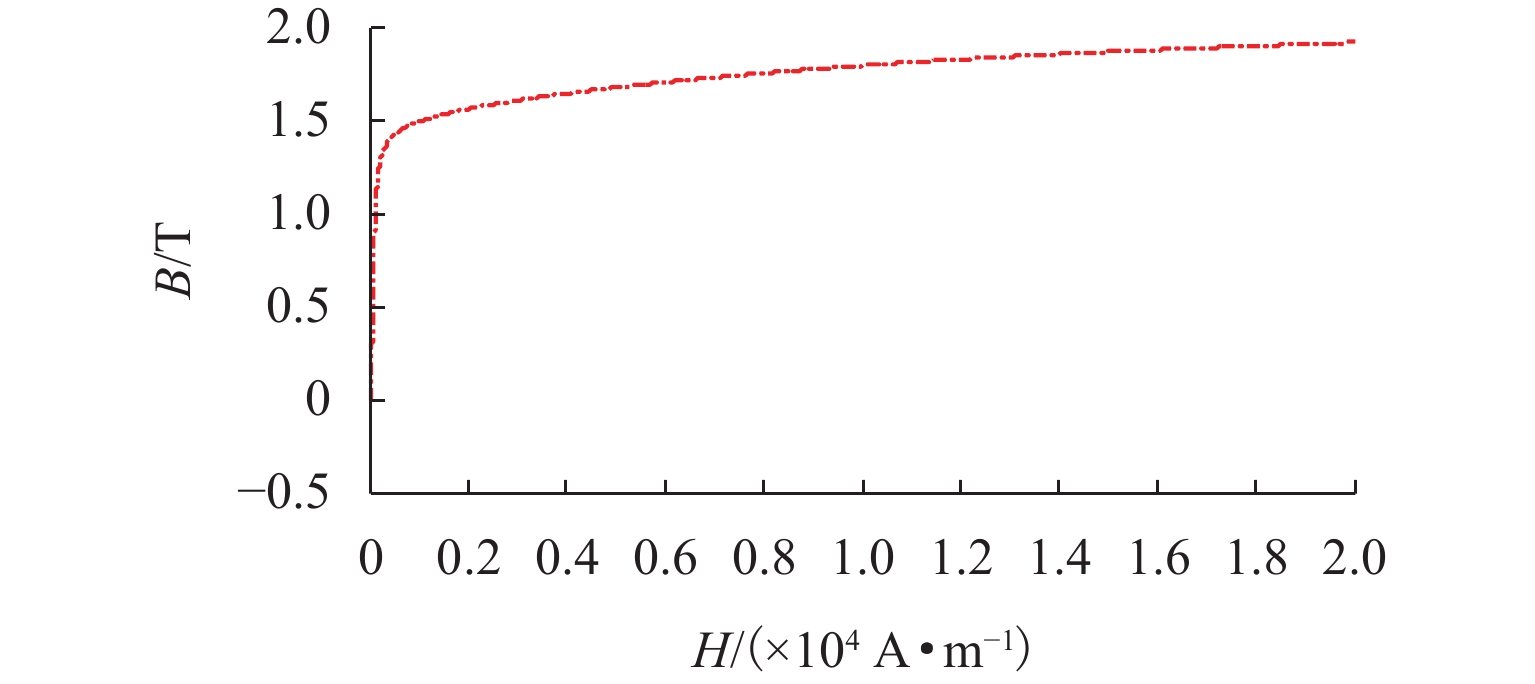
参数 值 转子重量/kg 490 深度饱和磁密点/T 1.8 气隙长度/mm 0.4 线径宽度/mm 2.5 线径高度/mm 1.4 最大定子外径/mm 330 最小转子内径/mm 120 转子角速度/(rad·s−1) 12000 π最大线速度/(m·s−1) 187 表 2 Pareto最优解集
Table 2. Pareto optimal solution set
最优解
序列磁极
宽度/
mm转子
外径/
mm轴向
长度/
mm磁极
高度/
mm比例
系数/
(A•mm−1)微分
系数/
(A•s•mm−1)1 22.0 125.0 77.6 18.1 46.52 0.047 2 22.8 124.1 60.5 18.6 47.98 0.046 3 22.0 125.0 69.1 18.1 46.52 0.047 4 22.0 125.0 70.4 18.1 46.51 0.047 5 22.0 125.0 71.4 18.1 46.52 0.047 6 22.0 125.0 73.7 18.1 46.51 0.047 7 22.9 123.5 59.7 18.7 48.19 0.046 8 23.4 121.5 59.3 20.7 48.57 0.045 9 23.5 119.0 62.2 22.0 46.58 0.047 10 22.9 124.0 59.7 18.7 48.17 0.046 表 3 高承载力密度磁轴承与传统磁轴承设计方案主要参数
Table 3. Main parameters of design scheme for high-load capacity MBs and traditional MBs
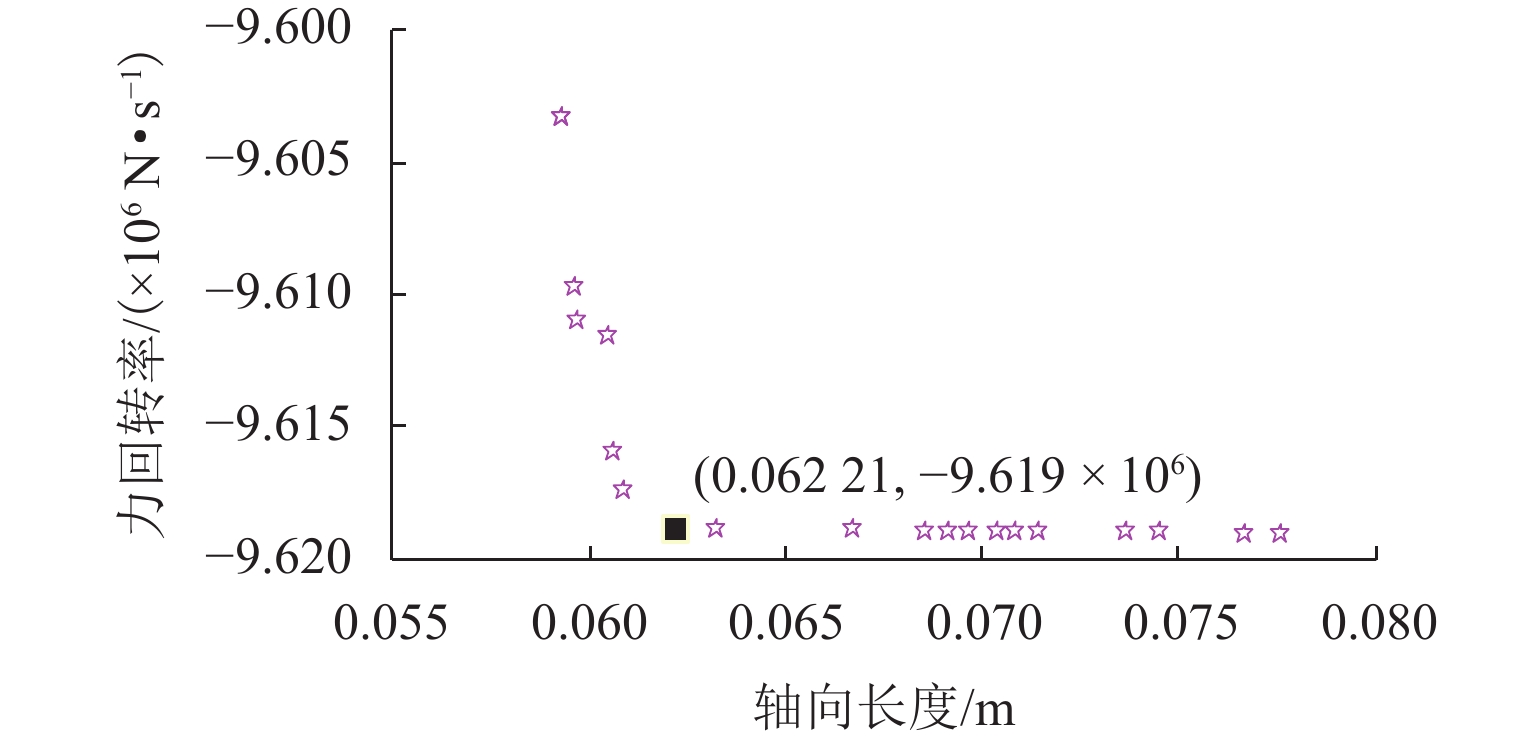
参数 高承载力密度磁轴承 传统磁轴承 实际最大承载力/N 7145 7145 偏置磁密/T 1.0 0.8 气隙/mm 0.4 0.4 定子外径/mm 165.0 165.0 转子内径/mm 60.0 60.0 轴向长度/mm 62.0 75.0 最大力回转率/(N·s−1) 9.62 × 106 6.86 × 106 承载力密度/MPa 0.484 0.40 表 4 刚度及其误差
Table 4. Stiffnesses and errors
参数 理论计算 实验辨识 相对误差/% 电流刚度/(N•A−1) 849 847.1 −0.22 位移刚度/(N•m−1) −3.11 × 107 −2.97 × 107 −4.52 -
[1] 张维煜,张林东,于焰均. 磁悬浮支承-飞轮系统稳定运行关键技术综述[J]. 西南交通大学学报,2022,57(3): 627-639. doi: 10.3969/j.issn.0258-2724.20210745ZHANG Weiyu, ZHANG Lindong, YU Yanjun. Review on key technologies of stable operation for magnetic suspension support-flywheel system[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 627-639. doi: 10.3969/j.issn.0258-2724.20210745 [2] 周扬,周瑾,张越,等. 基于RBF近似模型的磁悬浮轴承结构优化设计[J]. 西南交通大学学报,2022,57(3): 682-692. doi: 10.3969/j.issn.0258-2724.20210766ZHOU Yang, ZHOU Jin, ZHANG Yue, et al. Optimum structural design of active magnetic bearing based on RBF approximation model[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 682-692. doi: 10.3969/j.issn.0258-2724.20210766 [3] 胡余生,李立毅,郭伟林,等. 基于不等磁路面积设计方法的磁轴承刚度[J]. 西南交通大学学报,2022,57(3): 648-656.HU Yusheng, LI Liyi, GUO Weilin, et al. Support stiffness of magnetic bearing based on unequal magnetic circuit area design method[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 648-656. [4] 金超武,辛宇,周扬,等. 高温磁轴承-转子系统建模与动力学分析[J]. 西南交通大学学报,2024,59(4): 746-754.JIN Chaowu, XIN Yu, ZHOU Yang, et al. Modeling and dynamics analysis of high-temperature magnetic bearing-rotor system[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 746-754. [5] 王东,姜豪,苏振中,等. 船用磁悬浮轴承关键技术与发展综述[J]. 中国电机工程学报,2020,40(20): 6704-6715.WANG Dong, JIANG Hao, SU Zhenzhong, et al. A review on the key technologies and development of marine magnetic bearings[J]. Proceedings of the CSEE, 2020, 40(20): 6704-6715. [6] 禹春敏,邓智泉,梅磊,等. 基于精确磁路的新型混合型轴向-径向磁悬浮轴承研究[J]. 电工技术学报,2021,36(6): 1219-1228.YU Chunmin, DENG Zhiquan, MEI Lei, et al. Research of new hybrid axial-radial magnetic bearing based on accurate magnetic circuit[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1219-1228. [7] 赵旭升,邓智泉,汪波. 异极性永磁偏置径向磁轴承的参数设计与实现[J]. 电工技术学报,2012,27(7): 131-138,159.ZHAO Xusheng, DENG Zhiquan, WANG Bo. Parameter design and realization of permanent magnet biased heterploar radial magnetic bearing[J]. Transactions of China Electrotechnical Society, 2012, 27(7): 131-138,159. [8] 钟志贤,蔡忠侯,祁雁英,等. 新型径向混合磁轴承的解耦设计与分析[J]. 中国电机工程学报,2022,42(4): 1596-1606.ZHONG Zhixian, CAI Zhonghou, QI Yanying, et al. Decoupling design and analysis of a new radial Hybrid magnetic bearing[J]. Proceedings of the CSEE, 2022, 42(4): 1596-1606. [9] LIU X X, DONG J Y, DU Y, et al. Design and static performance analysis of a novel axial hybrid magnetic bearing[J]. IEEE Transactions on Magnetics, 2014, 50(11): 1-4. [10] 金俊杰,王岩峰,徐程程,等. 人工肾脏泵用磁悬浮轴承设计与磁力特性分析[J]. 西南交通大学学报,2024,59(4): 795-803. doi: 10.3969/j.issn.0258-2724.20230090JIN Junjie, WANG Yanfeng, XU Chengcheng, et al. Design and magnetic force characteristic analysis of magnetic levitation bearing for artificial kidney pumps[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 795-803. doi: 10.3969/j.issn.0258-2724.20230090 [11] SMIRNOV A, UZHEGOV N, SILLANPAA T, et al. High-speed electrical machine with active magnetic bearing system optimization[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9876-9885. doi: 10.1109/TIE.2017.2716875 [12] PINCKNEY F D, KEESEE J M. Magnetic bearing design and control optimization for a four-stage centrifugal compressor[J]. Tribology Transactions, 1992, 35(3): 561-565. doi: 10.1080/10402009208982157 [13] CHEN H C, CHANG S H. Genetic algorithms based optimization design of a PID controller for an active magnetic bearing[J]. International Journal of Computer Science and Network Security (IJCSNS), 2006, 6(12): 95-99. [14] ZHONG Y, WU L, HUANG X, et al. An improved magnetic circuit model of a 3-DOF magnetic bearing considering leakage and cross coupling effects[J]. IEEE Transactions on Magnetics, 2017, 53(11): 1-6. [15] SHAKIBAPOUR F, RAHIDEH A, MARDANEH M. 2D analytical model for heteropolar active magnetic bearings considering eccentricity[J]. IET Electric Power Applications, 2018, 12(5): 614-626. doi: 10.1049/iet-epa.2017.0669 [16] 王大朋,王凤翔. 利用场路结合方法分析磁轴承悬浮力[J]. 电机与控制学报,2011,15(11): 8-13.WANG Dapeng, WANG Fengxiang. Levitation force analysis of magnetic bearing by circuit-field combination method[J]. Electric Machines and Control, 2011, 15(11): 8-13. [17] JIANG H, SU Z Z, WANG D. Analytical calculation of active magnetic bearing based on distributed magnetic circuit method[J]. IEEE Transactions on Energy Conversion, 2021, 36(3): 1841-1851. doi: 10.1109/TEC.2020.3040975 [18] 叶品州,李红伟,于文涛,等. 考虑材料非线性及涡流影响的径向电磁轴承等效磁路建模[J]. 电工技术学报,2020,35(9): 1858-1867.YE Pinzhou, LI Hongwei, YU Wentao, et al. Equivalent magnetic circuit modeling of radial active magnetic bearing considering material nonlinearity and eddy current effects[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1858-1867. [19] 刘程子,邓智泉,梅磊,等. 基于漏磁与磁阻系数迭代的三自由度混合型磁悬浮轴承的设计[J]. 航空动力学报,2013,28(3): 603-612.LIU Chengzi, DENG Zhiquan, MEI Lei, et al. Design of 3-DOF hybrid magnetic bearing based on leakage coefficient and magnetoresistance coefficient iterative method[J]. Journal of Aerospace Power, 2013, 28(3): 603-612. [20] LE Y, WANG K. Design and optimization method of magnetic bearing for high-speed motor considering eddy current effects[J]. ASME Transactions on Mechatronics, 2016, 21(4): 2061-2072. doi: 10.1109/TMECH.2016.2569822 [21] ZHU R Z, XU W, YE C Y, et al. Design optimization of a novel heteropolar radial hybrid magnetic bearing using magnetic circuit model[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-5. doi: 10.1109/TMAG.2018.2800462 [22] JIN Z J, SUN X D, CAI Y F, et al. Comprehensive sensitivity and cross-factor variance analysis-based multi-objective design optimization of a 3-DOF hybrid magnetic bearing[J]. IEEE Transactions on Magnetics, 2021, 57(2): 1-4. [23] GERHARD S, ERIC H M. Magnetic bearing: theory, design, and application to rotating machinery[M]. Berlin: Springer, 2009. [24] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. doi: 10.1109/4235.996017 [25] JIANG H, SU Z Z, WANG D, et al. Multiparameter identification for active magnetic bearing with uncertainties based on a coupled nonlinear model[J]. IEEE Transactions on Industrial Electronics, 2023, 70(10): 10431-10441. doi: 10.1109/TIE.2022.3222595 -





 下载:
下载: