Theoretical Study on Non-Limit Active Earth Pressure of Sand under Rotational and Translational Coupling Mode Based on Particle Flow Simulation
-
摘要:
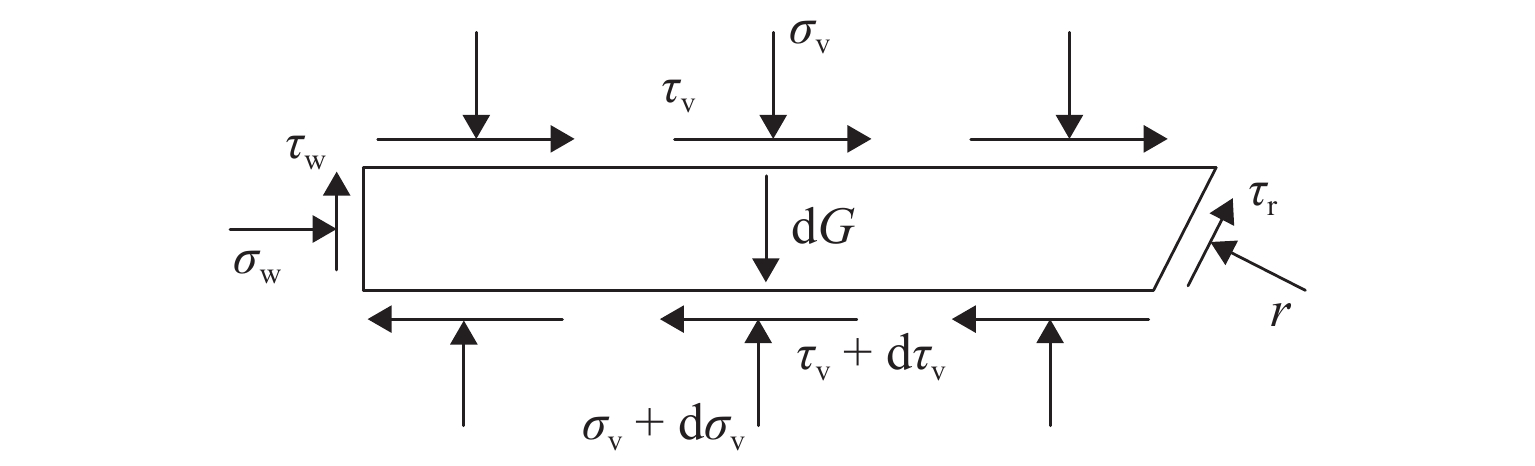
目的 支护结构在防止土体坍塌、维持土体稳定性方面起着重要作用. 准确确定作用在挡土墙上的土压力对基坑工程的安全性和经济性至关重要. 传统的土压力理论忽略了墙体的位移模式、位移大小、墙-土相互作用以及土拱效应等因素的影响. 因此,计算所得的土压力往往不准确,给工程设计和施工带来风险. 本文针对刚性挡墙绕墙顶转动与平动耦合(RTT)模式下砂土的主动土压力问题,考虑土楔体层间错动的影响,利用水平层分析法推导RTT模式下的非极限主动土压力计算公式.
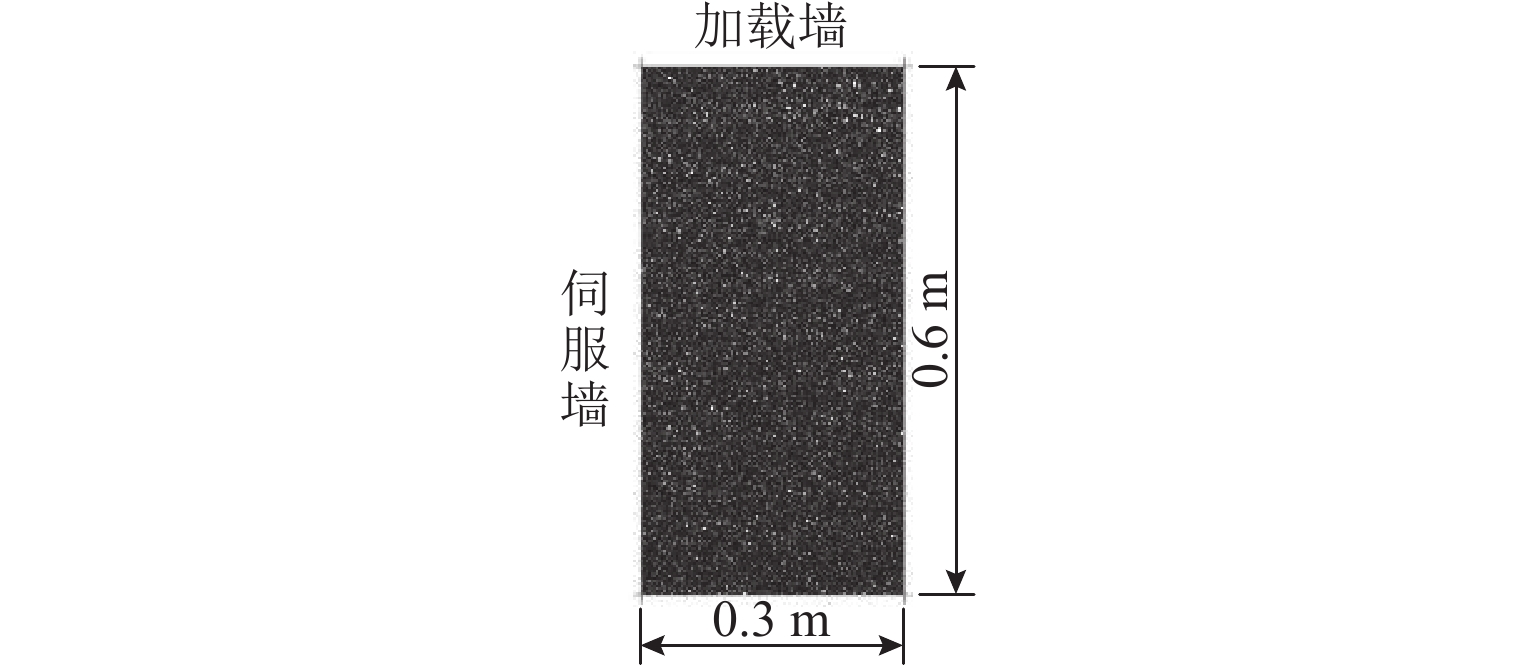
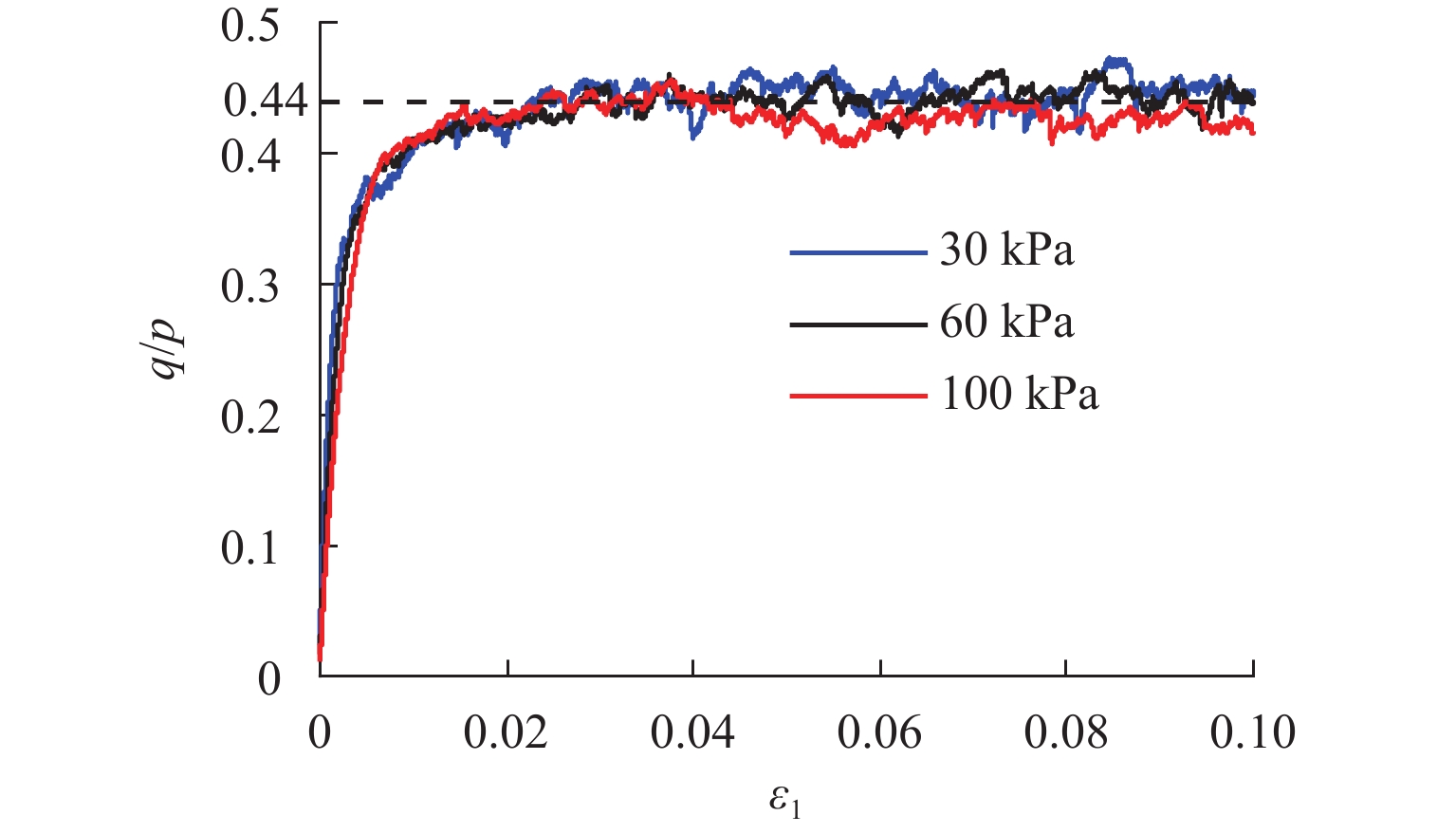
方法 本文将离散元模拟和理论推导相结合,研究RTT模式下的非极限主动土压力,以深入分析墙体位移、摩擦角、转动中心位置等因素对土压力的影响. 为准确模拟土颗粒的宏观物理性质,并减小抗转动弯矩的影响,选取三圆盘组成的椭圆颗粒簇作为基本颗粒. 基于学者研究确定模型参数,保证模拟结果的可靠性和相关性. 采用PFC2D软件建立土体模型,利用双轴试验(围压分别为30、60 kPa和100 kPa)获取土体的内摩擦角为26.1°. 采用重力沉积法分6层生成土体模型,并控制孔隙率为0.22. 设置测量圆以捕捉土体内部应力和旋转角度的变化情况. 试样成型后,控制位移墙体向外转动,保持墙体最大水平位移速度为6 × 10−4 m/s. 设置墙体最大水平位移为0.012
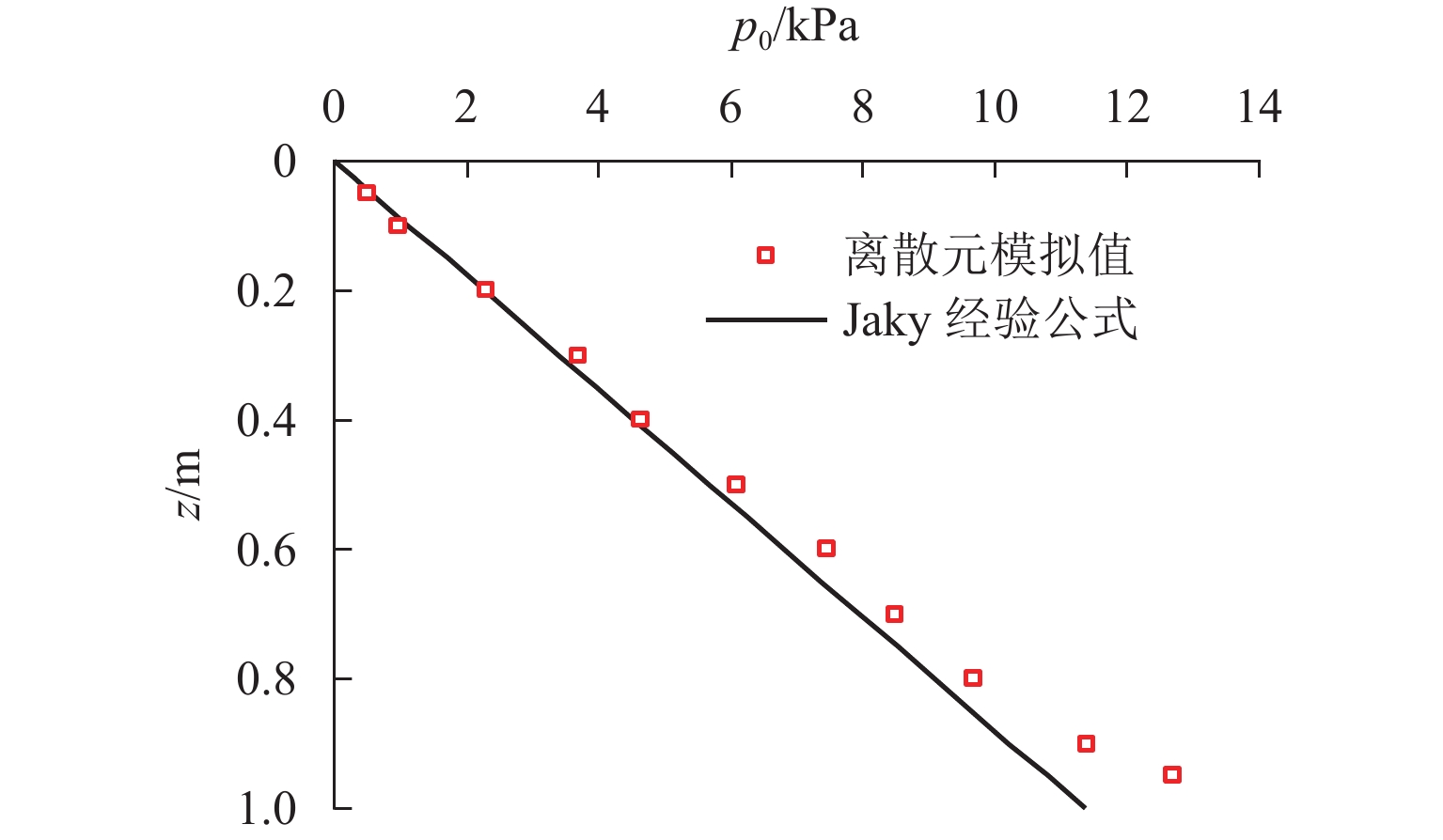
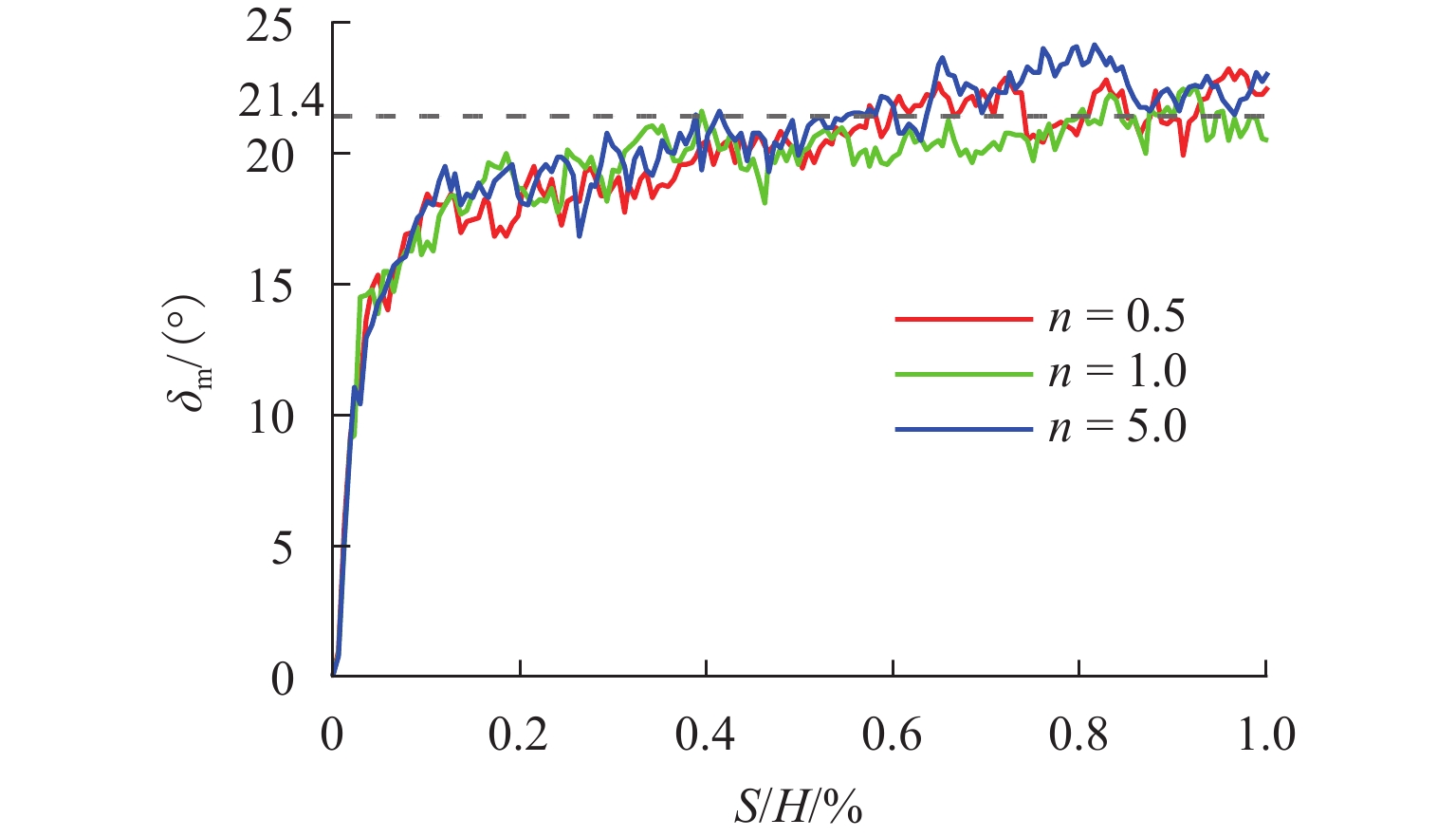
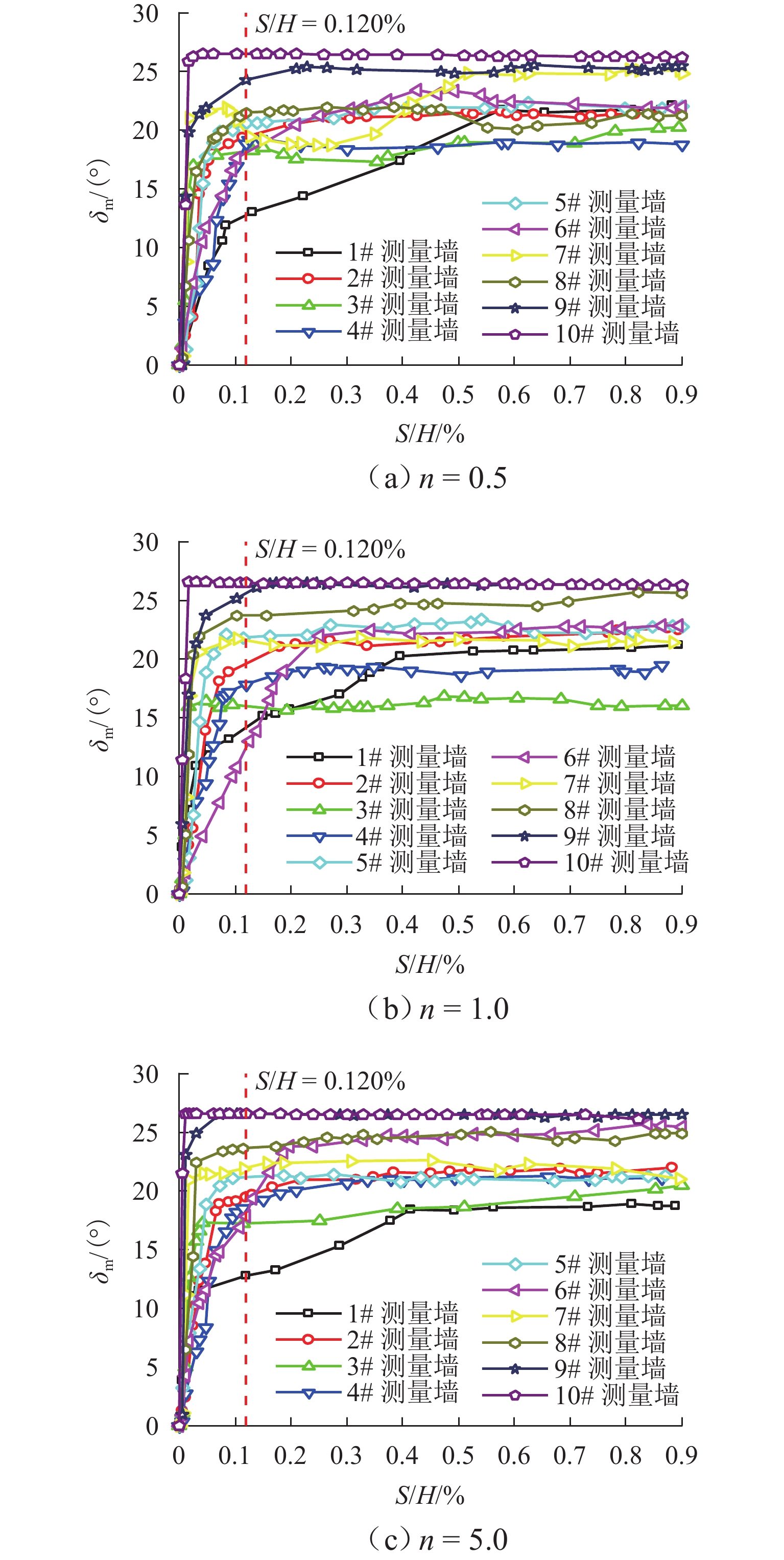
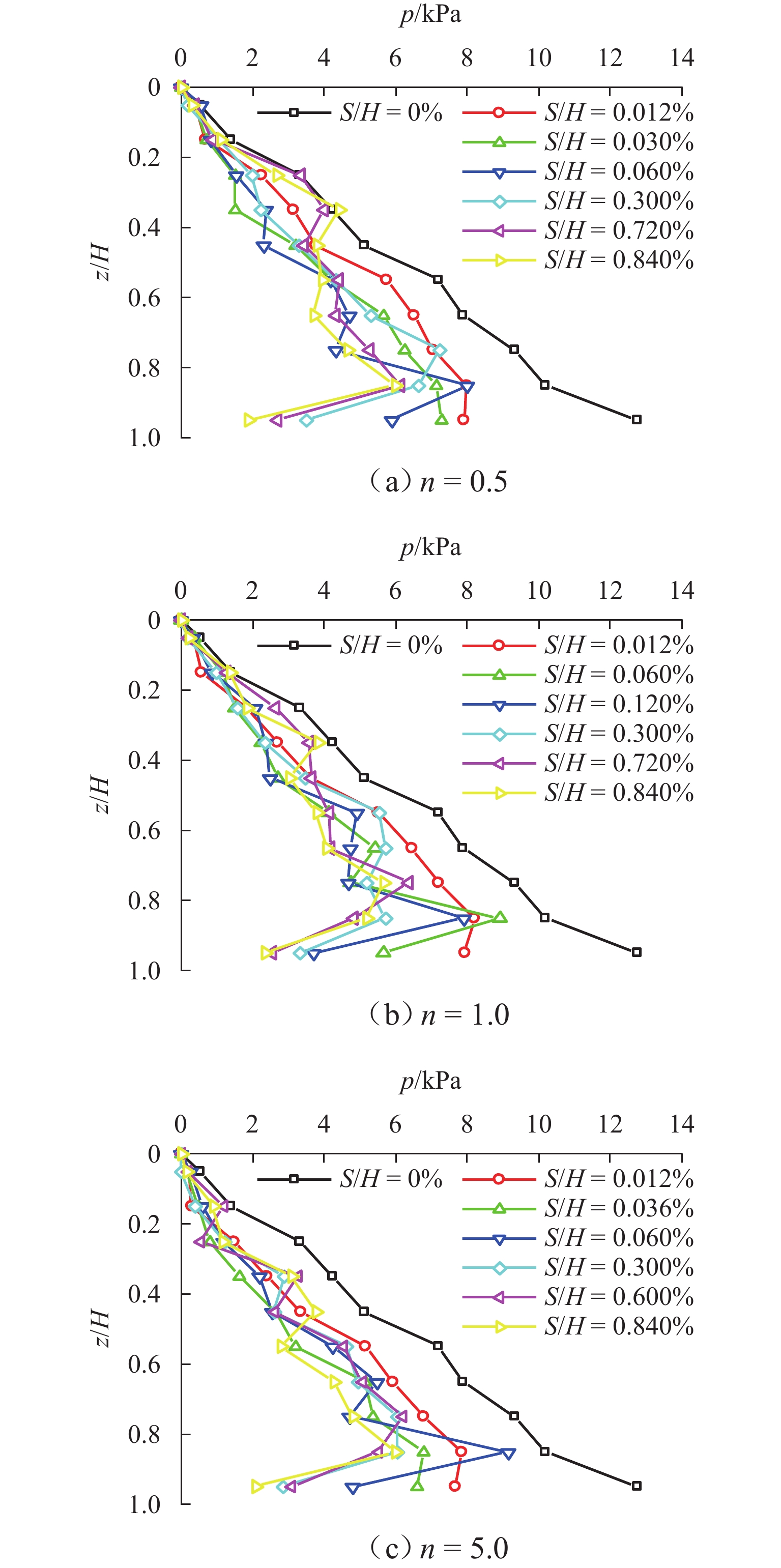
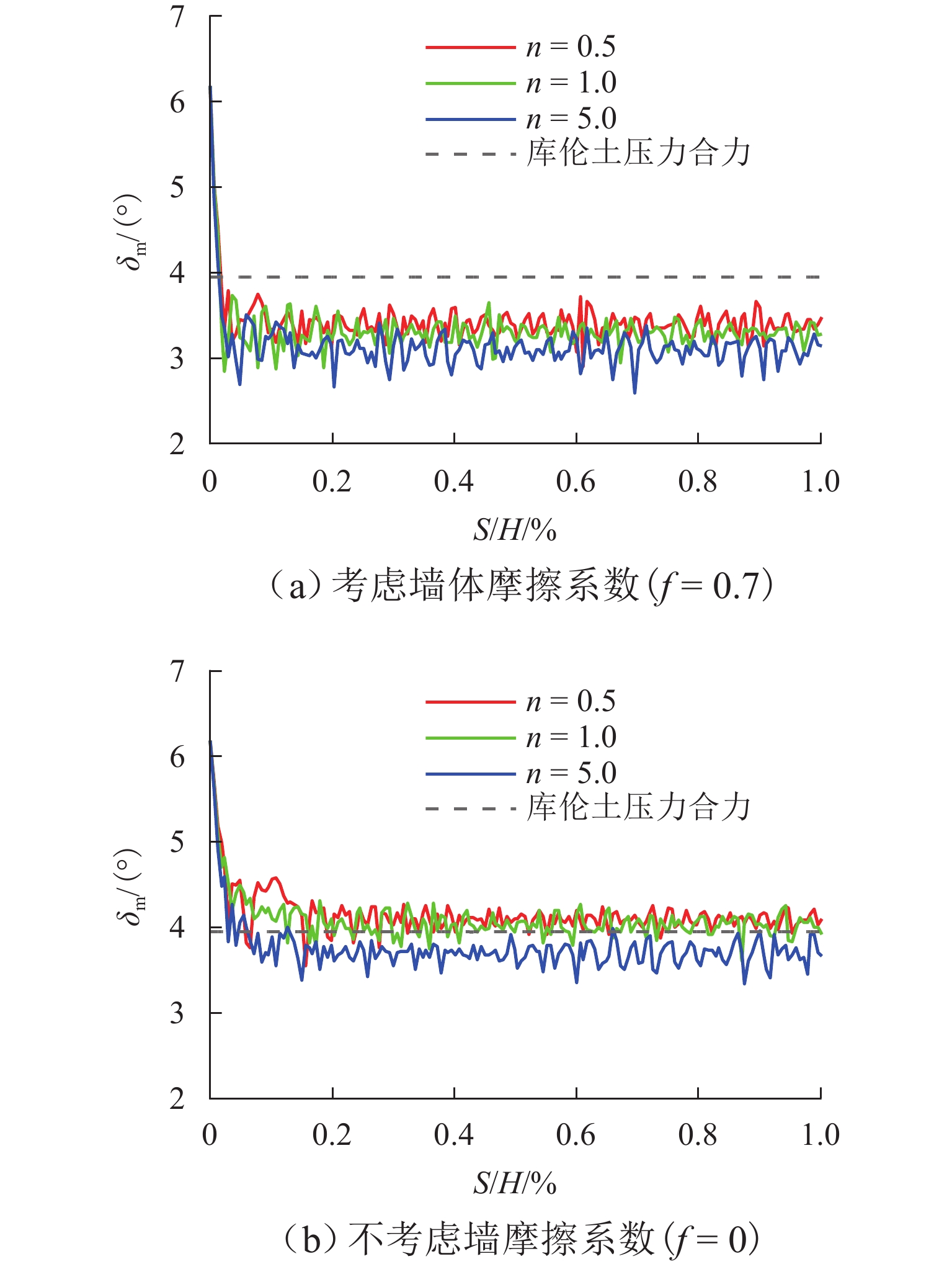
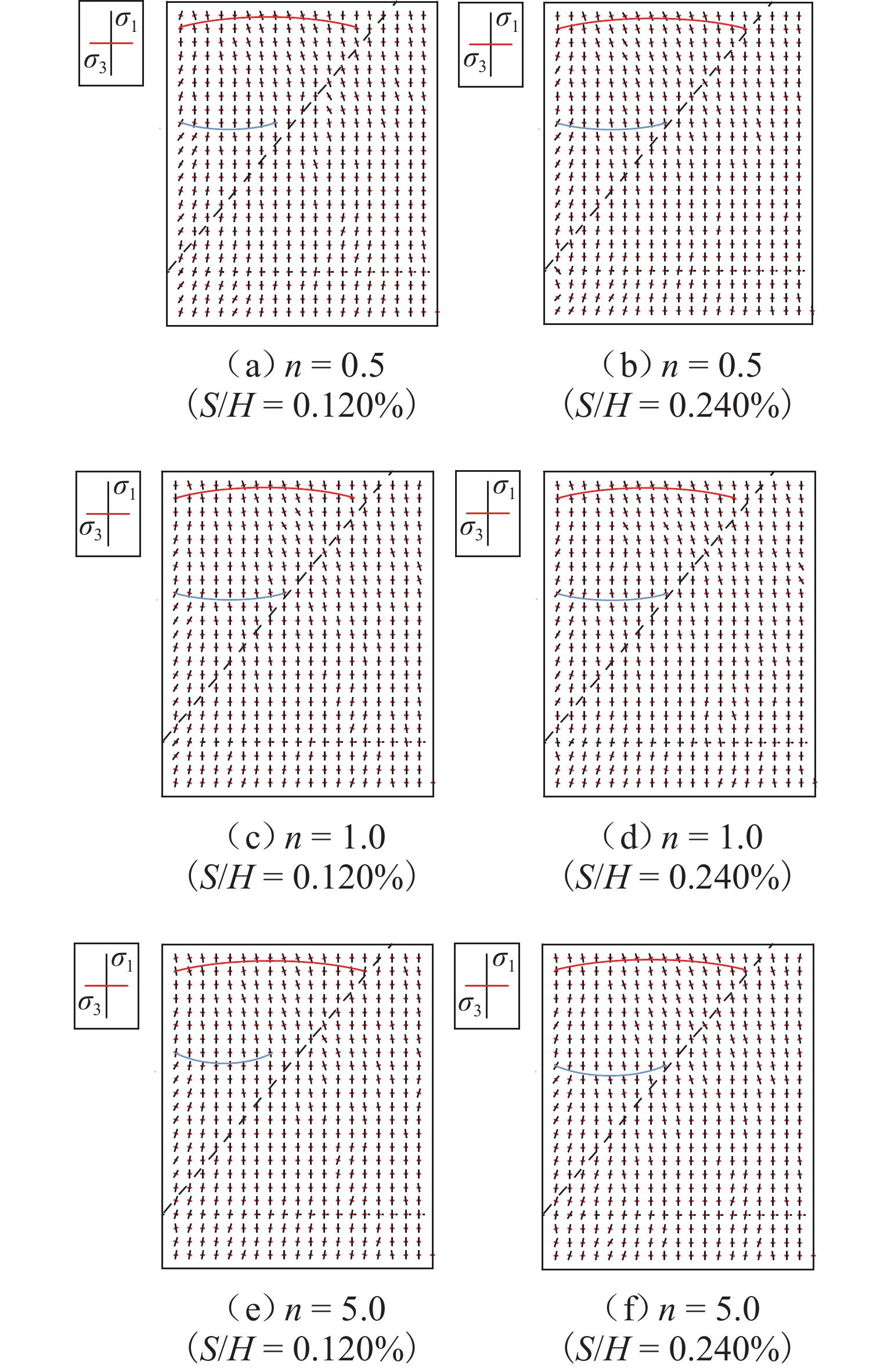
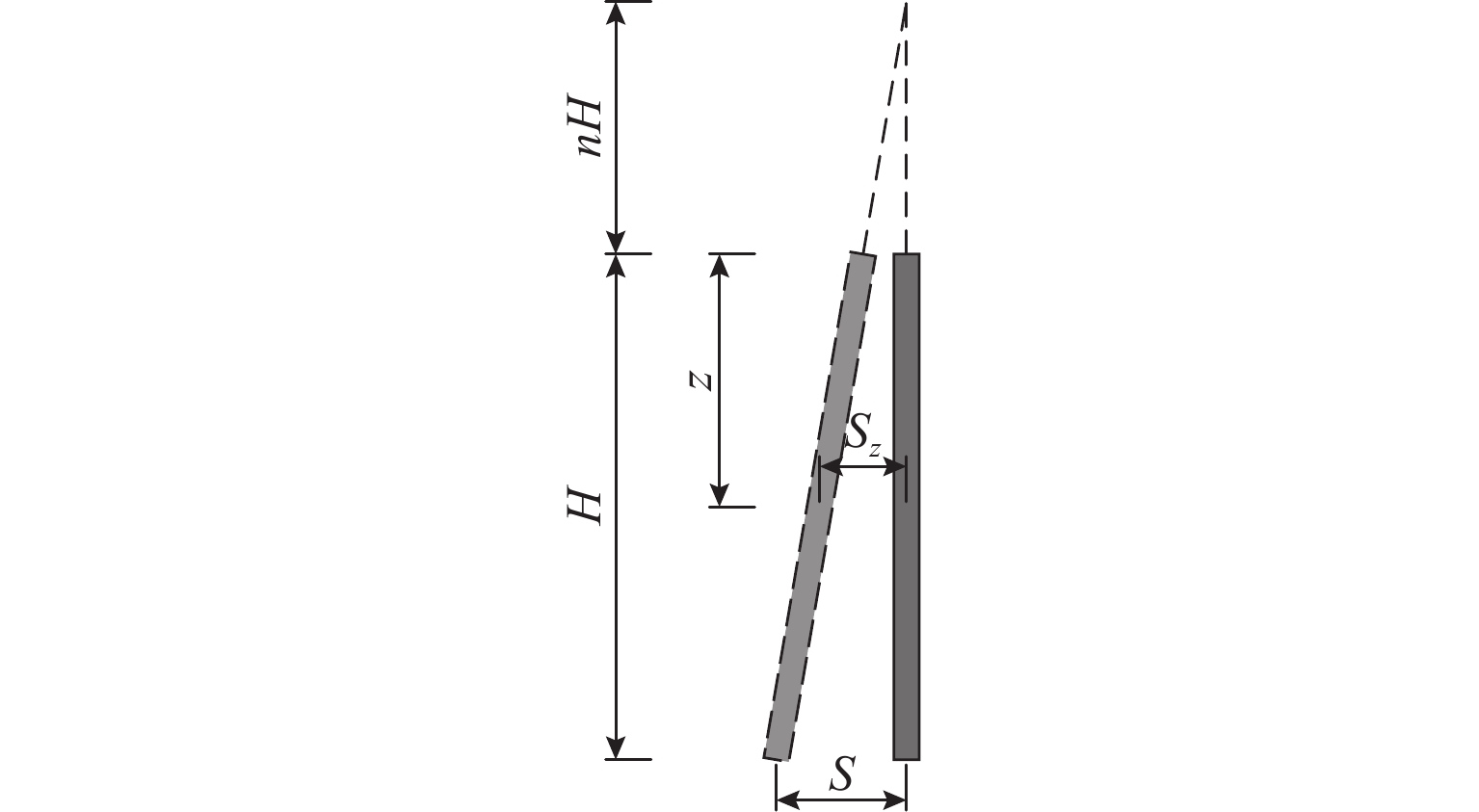
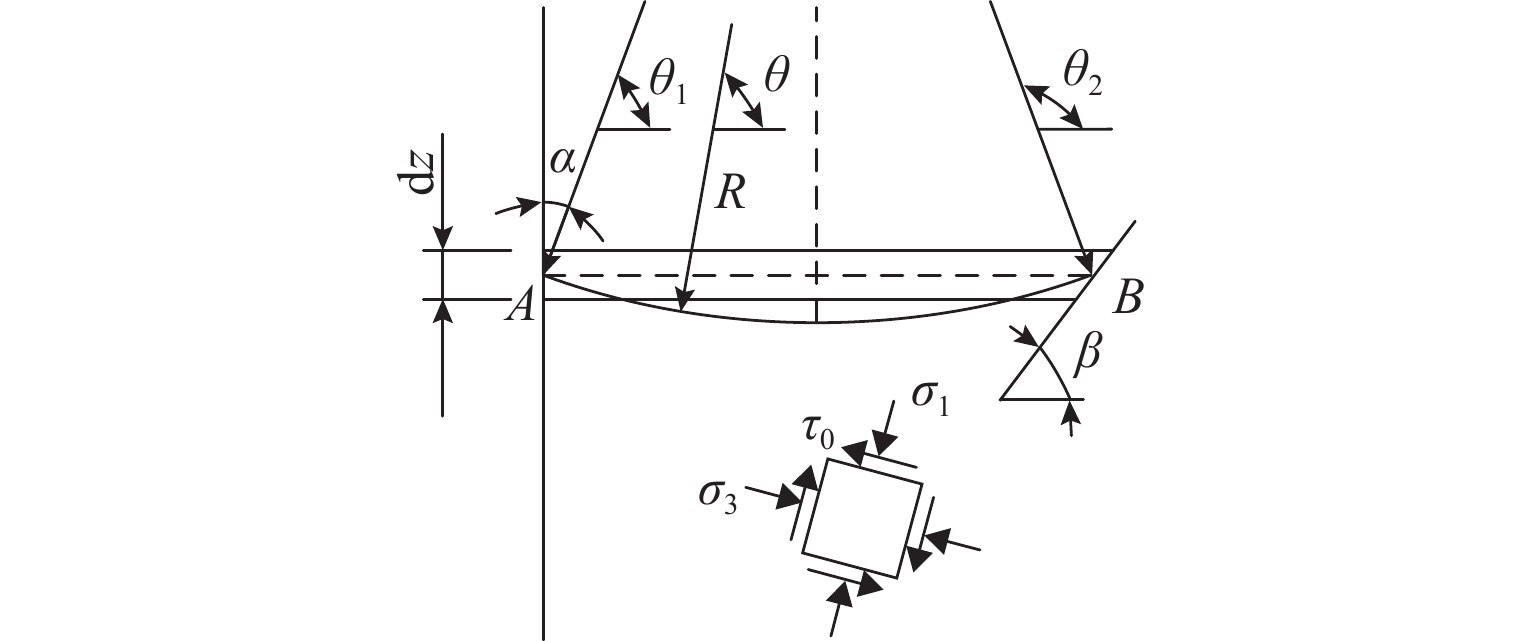
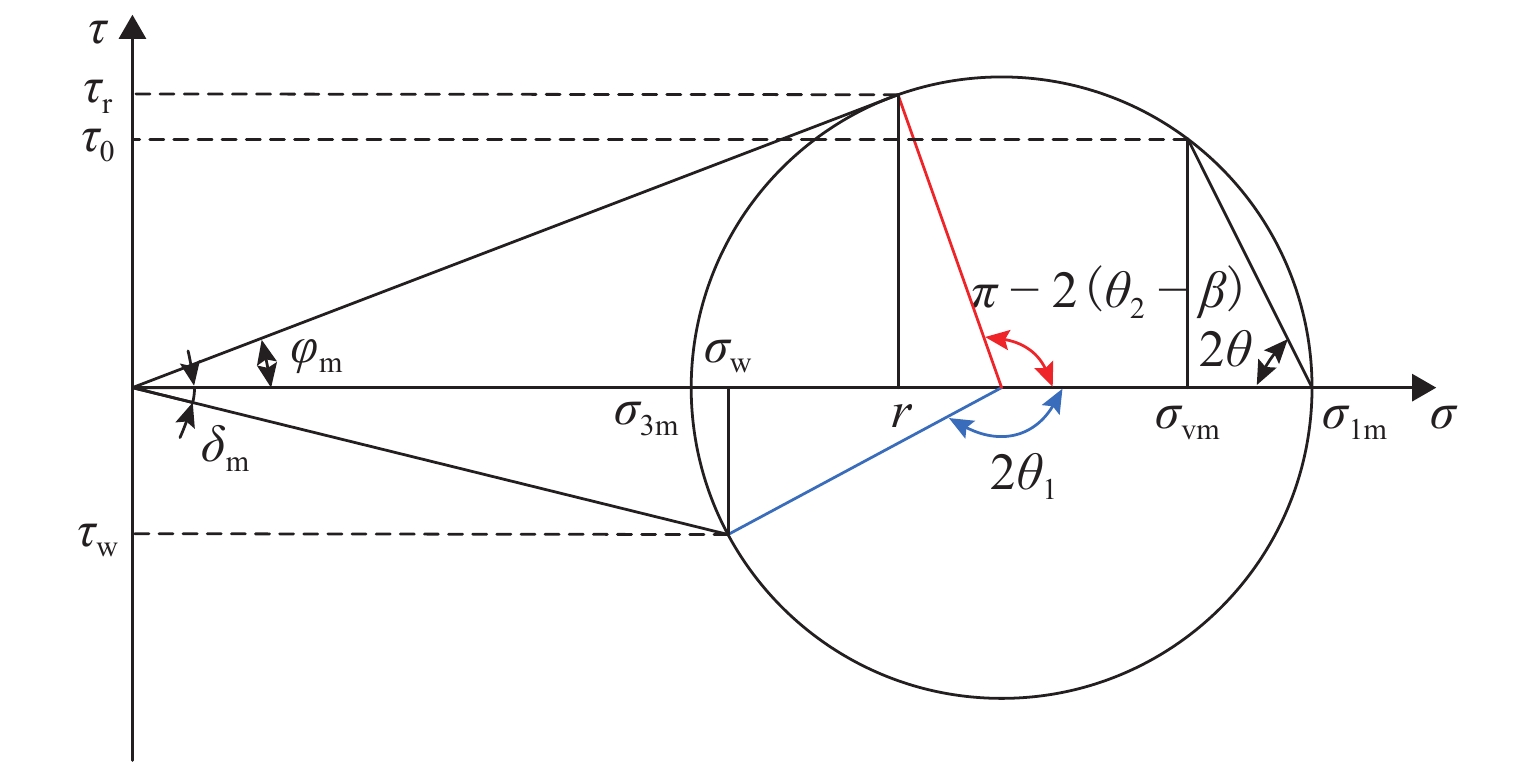
H (H 为位移墙的高度)以确保土体达到极限状态. 一共开展3种转动中心位置(中心参数n = 0.5, 1.0, 5.0)的离散元模拟,以探究不同转动中心位置对主动土压力、墙-土摩擦角、剪切破坏面发展以及土体内部应力状态的影响. 基于离散元模拟结果,假定土拱形状为中间对称圆弧,从而获得非极限滑动破裂面倾角. 考虑土楔体层间错动的影响,采用水平层分析法推导得到RTT模式下的主动土压力计算公式. 通过模型试验进一步验证了理论解,对比表明试验结果与理论预测吻合良好. 此外,还进行了全面的参数分析,研究RTT模式下墙体位移、内摩擦角、墙-土摩擦角以及转动中心位置对主动土压力大小和分布的影响.结果 本文总结了离散元模拟、模型验证和参数分析的结果如下所示: 模拟结果如下:1.不同转动中心位置的土样在RTT模式下的墙-土摩擦角表现基本一致;3组模型的平均墙-土摩擦角约为21.4°;随着墙体位移增加,墙-土摩擦角逐渐发挥并达到其极限值. 2. RTT模式下的主动土压力分布同时表现出平动模式和转动模式的特征;随着墙体位移增加,压力分布从线性向抛物线型过渡;转动中心参数
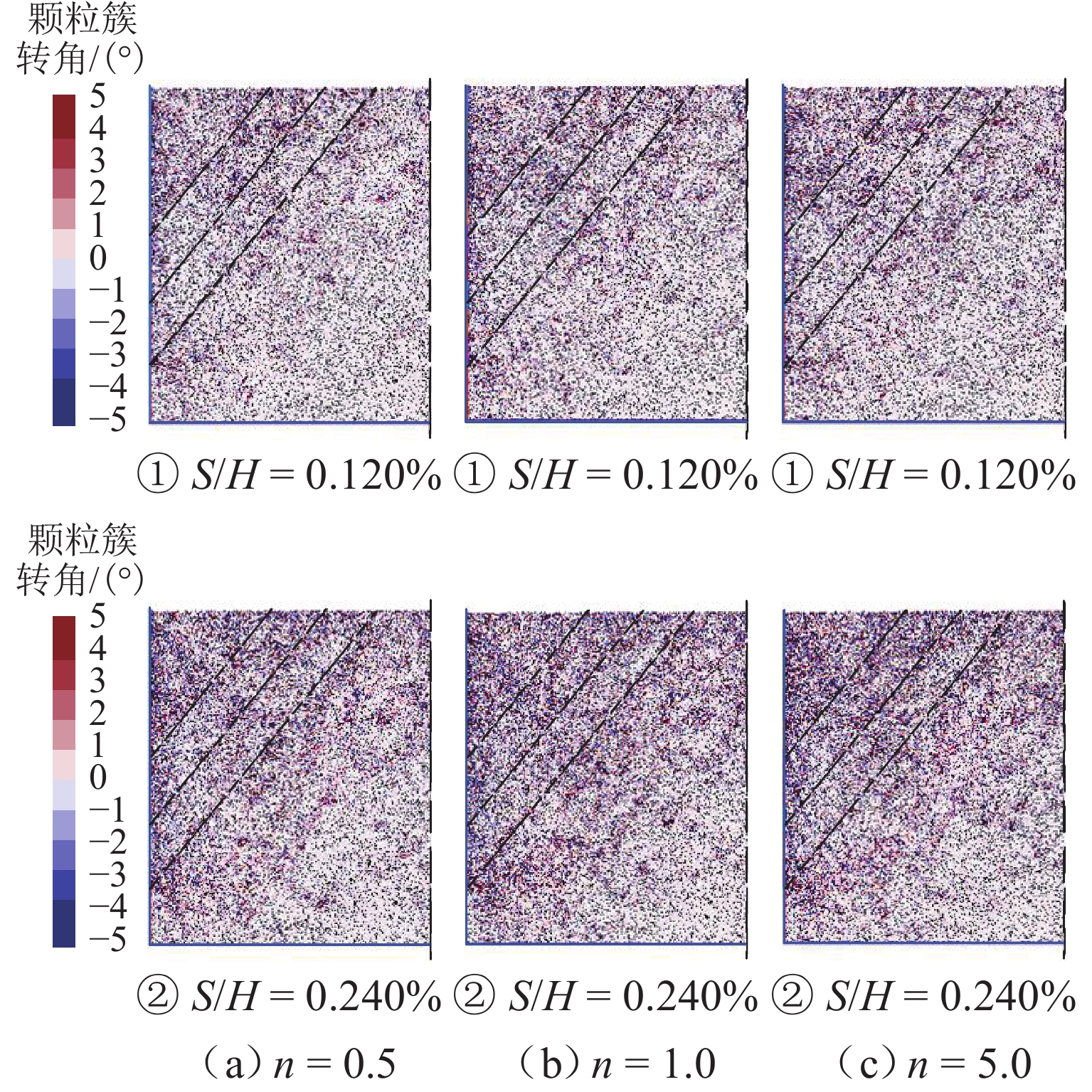
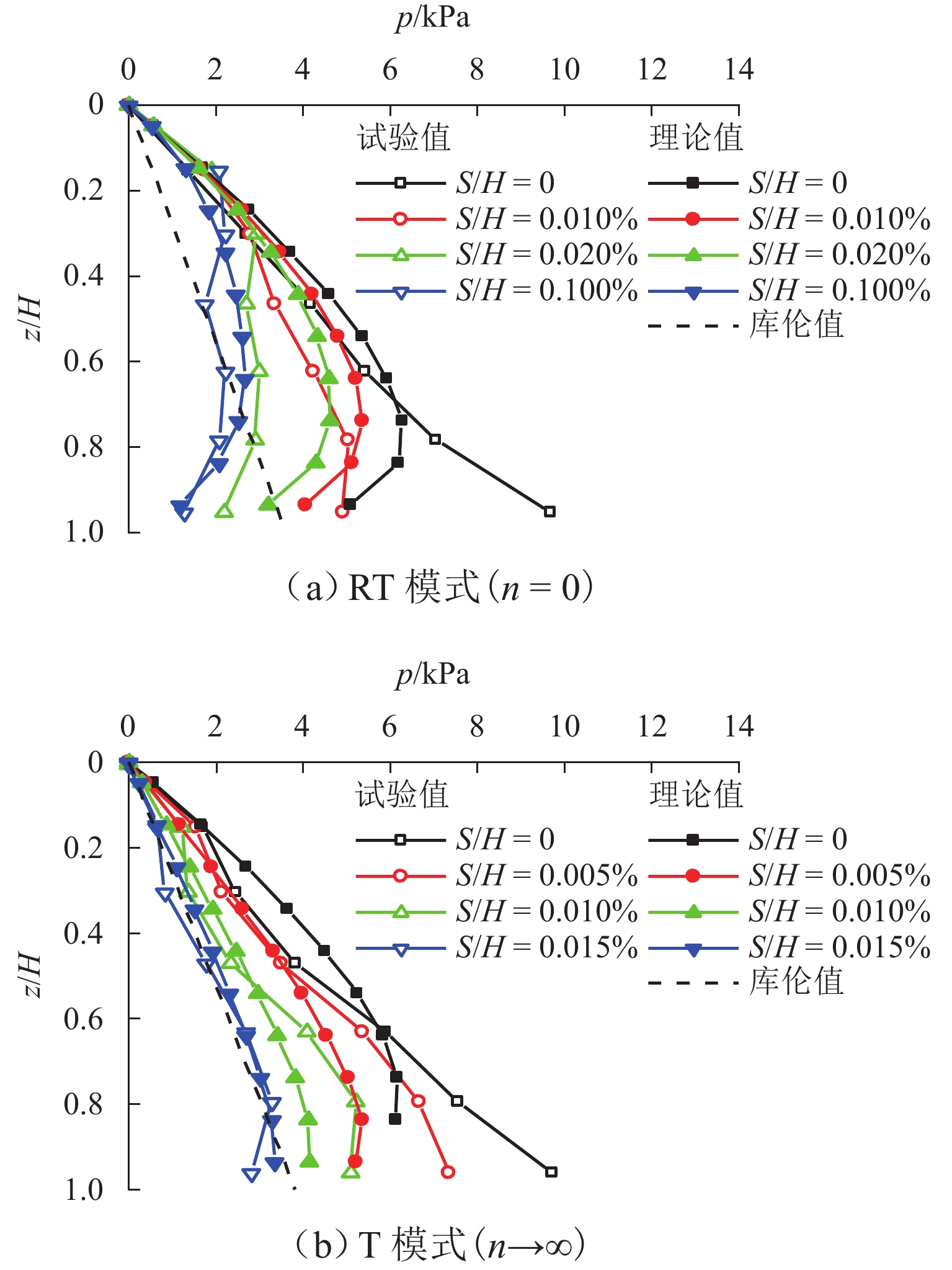
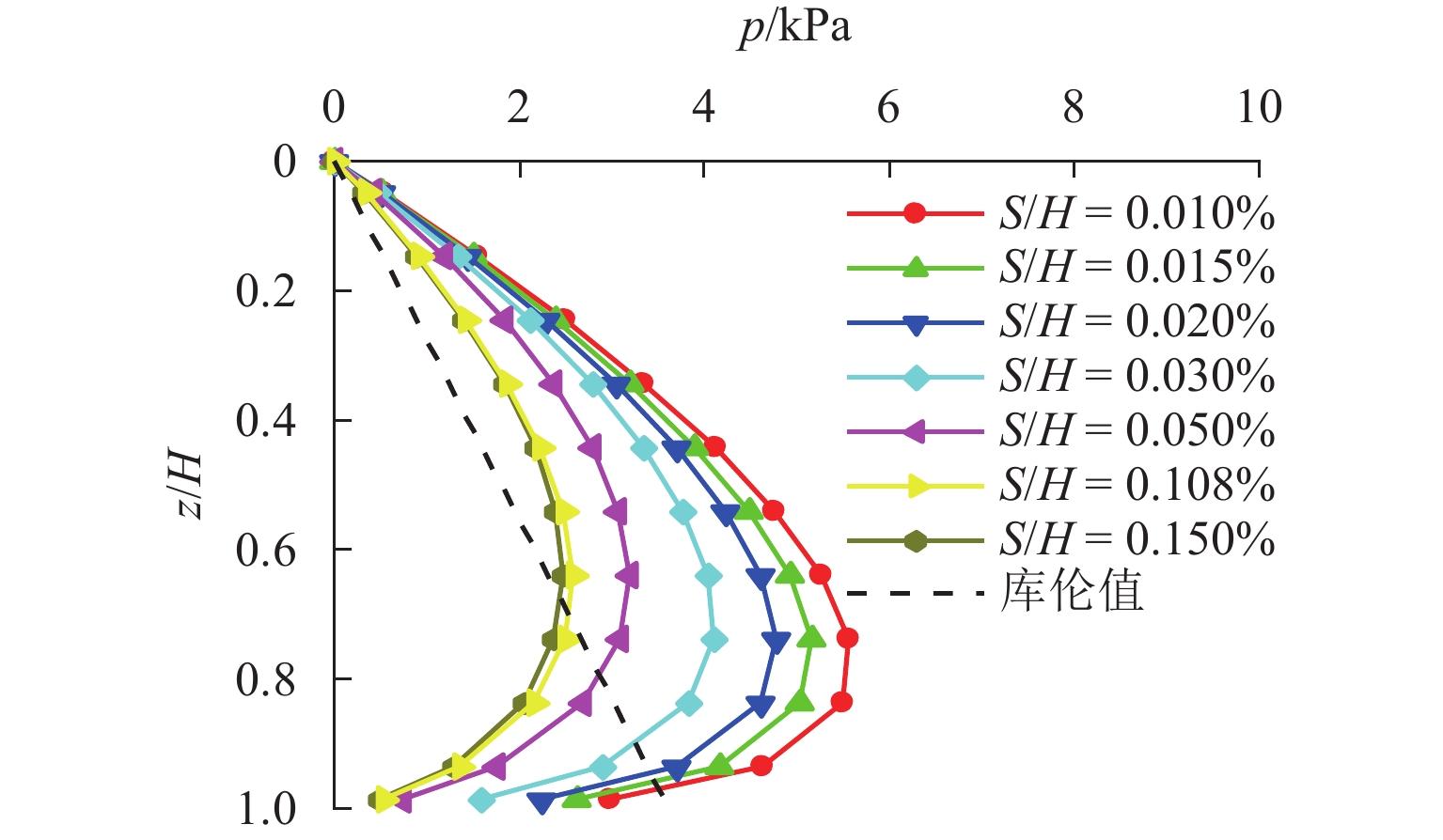
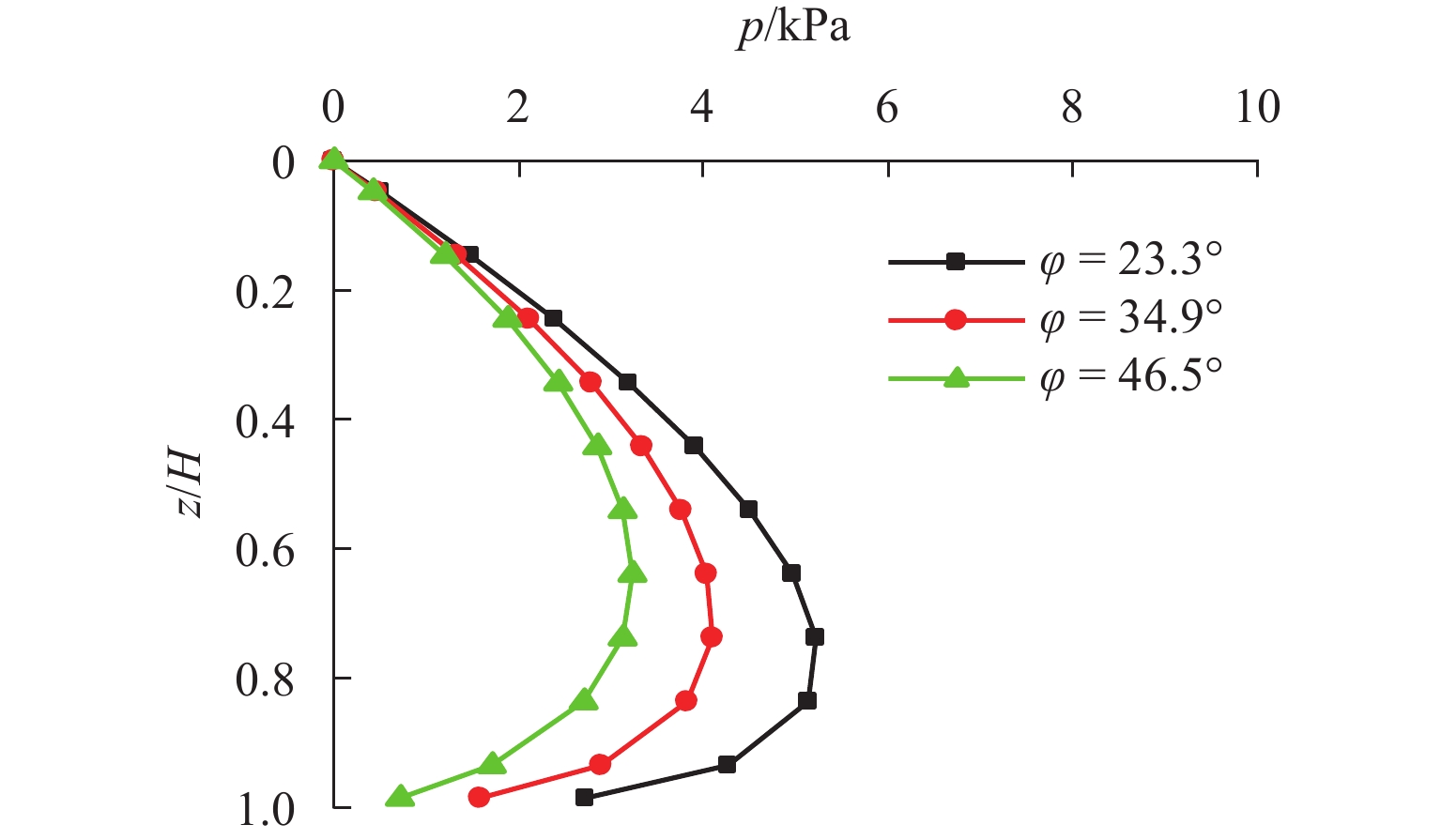
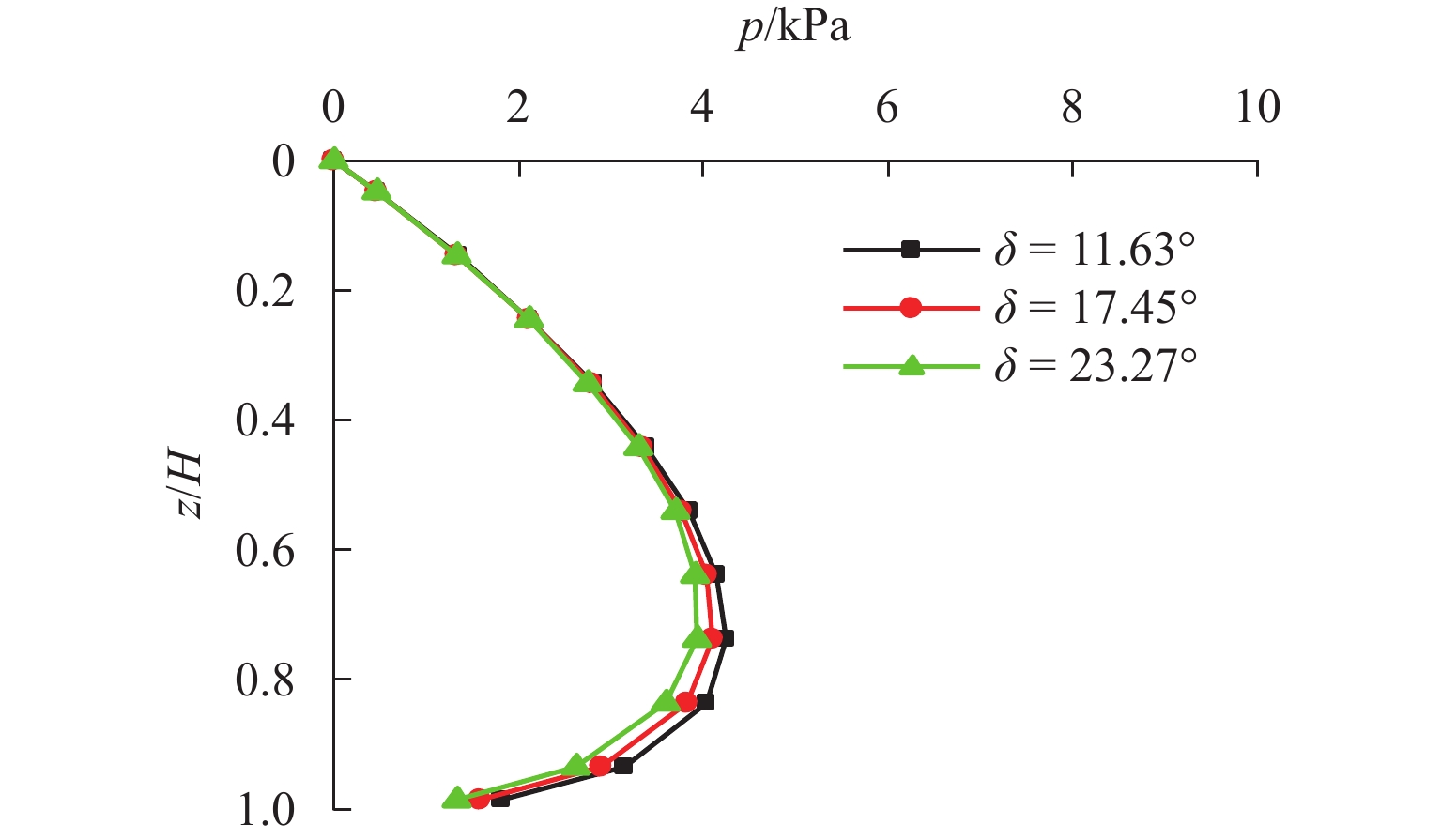
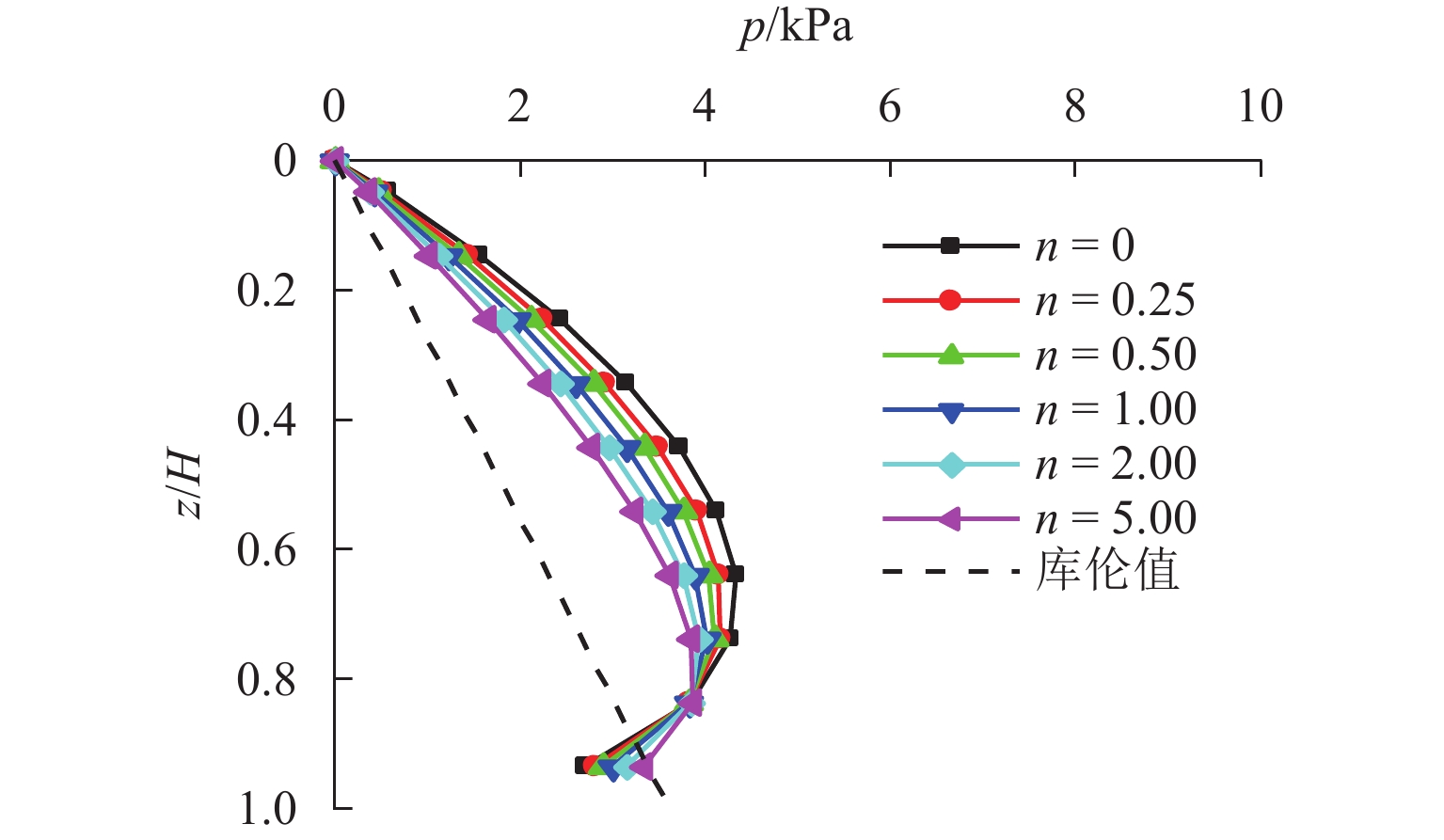
n 越大,压力分布越接近线性. 3. 随着墙体位移,内摩擦角φ 和墙-土摩擦角δ 逐渐发挥,土体从非极限状态过渡到极限状态;当位移比S /H 达到0.2%时(S 为某一时刻挡土墙上的最大水平位移),土压力合力基本稳定;在RTT模式下,砂土的墙-土摩擦角比内摩擦角更快达到极限值. 4.土体破坏过程显示,随着墙体位移,颗粒转动加剧,导致剪切破坏面逐渐发展;n 值越大,土颗粒转动越明显,破坏面也越清晰. 5.在RTT模式下,滑动面处的主应力方向发生偏转,在土体中上部区域,墙后及滑动破裂面处土颗粒的转动角度大致相同,中部区域的主应力偏转较小,土体内部发生土拱效应,形成近似对称的半圆形拱. 模型验证:理论计算结果与试验结果吻合良好. 当n =0时,RTT模式转变为特殊的绕墙顶转动模式,主动土压力呈上凸的抛物线分布. 当n →∞时,RTT模式转变为特殊的平动模式,主动土压力呈线性分布. 参数分析:1.在RTT模式下,主动土压力分布呈上凸的抛物线形;随着位移增加,主动土压力减小并逐渐趋近于库仑理论值. 2.内摩擦角对主动土压力大小和分布的影响大于墙-土摩擦角;内摩擦角和墙-土摩擦角越大,主动土压力越小. 3. 随着转动中心参数n 增大,RTT模式下的压力分布非线性程度减弱,趋近于线性分布;当n ≥5.0时,可近似按平动模式进行计算.结论 本研究不仅增强了对RTT位移下非极限主动土压力的认识,也为支护结构的设计和施工提供指导. 未来可进一步研究更复杂的挡墙系统、位移模式及土体条件下的土压力变化情况.
Abstract:Objective Retaining structures are crucial for preventing the collapse of soil and maintaining soil stability. The accurate determination of lateral earth pressure exerted by the soil is essential to the safety and economic feasibility of foundation pit engineering. Traditional earth pressure theories, however, overlook the displacement mode and displacement magnitude of the wall, wall-soil interaction, and soil arching effect. As a result, the calculated lateral earth pressure is often inaccurate, posing risks to engineering design and construction. To address the problem of active earth pressure in sandy soil under a rigid retaining wall in the rotational and translational coupling (RTT) mode, a more accurate and reliable calculation formula for non-limit active earth pressure in this scenario is developed, considering the interlayer sliding of soil wedges.
Method The non-limit active earth pressure was investigated under the RTT mode with a combination of discrete element simulations and theoretical derivation. The primary goal was to understand the impact of various factors such as wall displacement, friction angles, and rotation center position on earth pressure. To simulate the physical properties of soil particles accurately, and minimize the influence of resisting rotational moments, an elliptical particle cluster composed of three disks was chosen as the basic particle. The model parameters were selected based on previous research, ensuring the reliability and relevance of the simulation results. The PFC2D software was used to create a soil model, and three different confining pressures (30 kPa, 60 kPa, and 100 kPa) were applied in a biaxial test setup. The internal friction angle of the soil was found to be 26.1°. To generate the soil model, a gravity deposition method was employed, layering the soil into six distinct layers with a controlled porosity of 0.22. A series of measurement circles were set up to obtain the internal stress and rotation angle of the soil. After the sample was formed, the horizontal displacement speed of the wall was 6 × 10−4 m/s when the control displacement wall rotated outward. The maximum horizontal displacement of the wall was set to 0.012
H to ensure that the soil could reach the ultimate failure state under the RTT mode. Discrete element simulations were carried out for three rotation center positions (rotation centern = 0.5, 1.0, and 5.0) to explore the influence of rotation center position on the active earth pressure, wall-soil friction angle, the development of shear failure surfaces, and the internal stress state of the soil. Based on discrete element simulation analysis, the soil arch shape was assumed to be a middle-symmetric circular arc, and the non-limit slip fracture surface inclination was thus obtained. Taking into account the impact of interlayer staggering of soil wedges, the calculation formula for active soil pressure in the RTT mode was obtained using horizontal layer analysis method. The theoretical solution was further validated through model experiments, with a comparison showing good agreement between the experimental results and the theoretical predictions. Additionally, a comprehensive parameter analysis was conducted to investigate the effects of wall displacement, internal friction angle, wall-soil friction angle, and the rotation center position on the magnitude and distribution of active earth pressure under the RTT mode.Result The results of discrete element simulation, simulation verification, and parameter analysis are summarized. The simulation results are as follows: 1. The performance of the wall-earth friction angles of soil samples with different rotating center positions in the RTT mode is basically the same. The average wall-soil friction angle of the three groups of models is approximately 21.4°. As wall displacement increases, the wall-soil friction angle gradually mobilizes and reaches its limit value. 2. The distribution of active earth pressure in the RTT mode exhibits characteristics of both translational mode and rotational mode. As wall displacement increases, the pressure distribution transitions from linear to parabolic. A larger
n value results in a more linear pressure distribution. 3. With the displacement of the wall, both the internal friction angleφ and the wall-soil friction angleδ gradually mobilize. The soil transitions from a non-limit state to a limit state. The resultant earth pressure becomes essentially stable atS /H = 0.2%. In the RTT mode, the wall-soil friction angle of sand reaches its limiting value faster than the internal friction angle. 4. The soil failure process shows increasing particle rotation with wall displacement, leading to the development of a shear failure surface. The rotation of soil particles is more pronounced for highern , and the failure surface becomes more distinct. 5. In the RTT mode, the principal stress at the slip surface deflects. In the upper and middle zones of the soil mass, the rotation angle of soil particles behind the wall and at the slip fracture surface is approximately the same. The principal stress deflection in the middle area is small. The soil arching effect occurs inside the soil mass, forming approximately symmetrical semicircular arches. Model verification: The theoretical results match well with the experimental results. Whenn = 0, the RTT mode transforms into a special mode of rotation about the wall top, and the active earth pressure appears as a parabolic distribution with an upward convex shape. Whenn = ∞, the RTT mode becomes a special translational mode, and the active earth pressure shows a linear distribution. Parameter analysis: 1. In the RTT mode, the active earth pressure distribution is a parabolic shape with an upward convex curve. As displacement increases, the active earth pressure decreases and approaches the Coulomb value. 2. The influence of the internal friction angle on the magnitude and distribution of active earth pressure is greater than that of the wall-soil friction angle. The greater the internal friction angle and the wall-soil friction angle, the smaller the active earth pressure. 3. As then value increases, the pressure distribution becomes less nonlinear and approaches a linear form in the RTT mode. Whenn ≥ 5.0, calculations in the translational mode are acceptable.Conclusion The findings enhance the theoretical understanding of non-limit active earth pressure under RTT displacement and provide practical guidance for the design and construction of retaining structures. Future studies could explore the application of this model to scenarios of more complex retaining wall systems, displacement modes, and soil conditions.
-
表 1 DEM模型参数选取
Table 1. DEM parameters
粒径/ mm 颗粒重度/
(kN•m–3)初始孔隙率 颗粒摩擦系数 法向接触刚度/
( × 108 N•m–1)切向接触刚度/
( × 108 N•m–1)墙体摩擦系数 双轴试验 土压力试验 3~5 25.97 0.22 0.7 1.5 1.0 0 0.7 表 2 模型试验计算参数
Table 2. Calculation parameters of model experiment
位移
模式γ/
(kN•m–3)φ/(°) δ/(°) φ0/(°) δ0/(°) Sc/H H/m RT (n=0) 15.51 34.9 17.45 11.00 7.2 0.050% 1.015 T (n→∞) 15.40 34.0 17.00 10.10 7.2 0.150% 1.015 -
[1] PARK B S, LEE J, LEE S D. Experimental investigation of three-dimensional earth pressure according to aspect ratio of retaining wall[J]. Marine Georesources & Geotechnology, 2018, 36(2): 181-189. doi: 10.1080/1064119X.2017.1292334 [2] FANG Y S, ISHIBASHI I. Static earth pressures with various wall movements[J]. Journal of Geotechnical Engineering, 1986, 112(3): 317-333. doi: 10.1061/(ASCE)0733-9410(1986)112:3(317) [3] 芮瑞, 叶雨秋, 陈成, 等. 考虑墙壁摩擦影响的挡土墙主动土压力非线性分布研究[J]. 岩土力学, 2019, 40(5): 1797-1804. doi: 10.16285/j.rsm.2018.0261RUI Rui, YE Yuqiu, CHEN Cheng, et al. Nonlinear distribution of active earth pressure on retaining wall considering wall-soil friction[J]. Rock and Soil Mechanics, 2019, 40(5): 1797-1804. doi: 10.16285/j.rsm.2018.0261 [4] RUI R, YE Y Q, HAN J, et al. Experimental and theoretical investigations on active earth pressure distributions behind rigid retaining walls with narrow backfill under a translational mode[J]. International Journal of Geomechanics, 2020, 20(10): 4020178.1-4020178.12. doi: 10.1061/(asce)gm.1943-5622.0001832 [5] FAN X Z, XU C J, LIANG L J. Experimental and theoretical study for a displacement-controlled design method of embedded cantilever retaining walls (piles)[J]. Sustainability, 2023, 15(12): 9831.1-9831.17. doi: 10.3390/su15129831 [6] 崔兵兵. 不同位移模式下土拱效应及土压力分布规律研究[D]. 济南: 山东大学, 2018. [7] 范晓真. 非对称开挖内撑式支护受力变形机理及变形控制设计理论[D]. 杭州: 浙江大学, 2021. [8] 孙佳政. 不同位移模式下挡土墙 非极限主动土压力研究[D]. 杭州: 浙江大学, 2023. [9] ISKANDER M, CHEN Z B, OMIDVAR M, et al. Active static and seismic earth pressure for c–φ soils[J]. Soils and Foundations, 2013, 53(5): 639-652. doi: 10.1016/j.sandf.2013.08.003 [10] BANG S. Active earth pressure behind retaining walls[J]. Journal of Geotechnical Engineering, 1985, 111(3): 407-412. doi: 10.1061/(ASCE)0733-9410(1985)111:3(407) [11] NI P P, MANGALATHU S, SONG L H, et al. Displacement-dependent lateral earth pressure models[J]. Journal of Engineering Mechanics, 2018, 144(6): 4018032.1-4018032.12. doi: 10.1061/(asce)em.1943-7889.0001451 [12] MEI G X, CHEN Q M, SONG L H. Model for predicting displacement-dependent lateral earth pressure[J]. Canadian Geotechnical Journal, 2009, 46(8): 969-975. doi: 10.1139/T09-040 [13] 徐日庆, 龚慈, 魏纲, 等. 考虑平动位移效应的刚性挡土墙土压力理论[J]. 浙江大学学报(工学版), 2005, 39(1): 119-122.XU Riqing, GONG Ci, WEI Gang, et al. Theory of earth pressure against rigid retaining walls considering translational movement effect[J]. Journal of Zhejiang University (Engineering Science), 2005, 39(1): 119-122. [14] 卢坤林, 杨扬. 非极限主动土压力计算方法初探[J]. 岩土力学, 2010, 31(2): 615-619. doi: 10.3969/j.issn.1000-7598.2010.02.047LU Kunlin, YANG Yang. Preliminary study of active earth pressure under nonlimit state[J]. Rock and Soil Mechanics, 2010, 31(2): 615-619. doi: 10.3969/j.issn.1000-7598.2010.02.047 [15] MATSUZAWA H, HAZARIKA H. Analyses of active earth pressure against rigid retaining wall subjected to different modes of movement[J]. Soils and Foundations, 1996, 36(3): 51-65. doi: 10.3208/sandf.36.3_51 [16] 陈建旭, 钱波, 郭宁, 等. 组合位移模式下刚性挡土墙非极限主动土压力[J]. 公路, 2021, 66(6): 25-31.CHEN Jianxu, QIAN Bo, GUO Ning, et al. Non-limit active earth pressure for rigid retaining wall with combined displacement modes[J]. Highway, 2021, 66(6): 25-31. [17] DANG F N, WANG X, CAO X S, et al. Calculation method of earth pressure considering wall displacement and axial stress variations[J]. Applied Sciences, 2023, 13(16): 9352. doi: 10.3390/app13169352 [18] HE Z M, LIU Z F, LIU X H, et al. Improved method for determining active earth pressure considering arching effect and actual slip surface[J]. Journal of Central South University, 2020, 27(7): 2032-2042. doi: 10.1007/s11771-020-4428-5 [19] LIANG L J, XU C J, CHEN Q Z, et al. Experimental and theoretical investigations on evolution of soil-arching effect in 2D trapdoor problem[J]. International Journal of Geomechanics, 2020, 20(6): 1643.1-1643.8. doi: 10.1061/(asce)gm.1943-5622.0001643 [20] GEORGE T I, DASAKA S M. Numerical investigation of soil arching in dense sand[J]. International Journal of Geomechanics, 2021, 21(5): 4021051.1-4021051.16. doi: 10.1061/(asce)gm.1943-5622.0001971 [21] YANG B, SHI Q Y, ZHOU H X, et al. Study on distribution of sidewall earth pressure on open caissons considering soil arching effect[J]. Scientific Reports, 2023, 13(1): 10657.1-10657.12. doi: 10.1038/s41598-023-37865-9 [22] CHEN R P, LIU M C, MENG F Y, et al. Soil arching effect associated with ground movement and stress transfer adjacent to braced excavation in clayey ground[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2023, 149(12): 04023113.1-04023113.17. doi: 10.1061/jggefk.gteng-11236 [23] PAIK K H, SALGADO R. Estimation of active earth pressure against rigid retaining walls considering arching effects[J]. Géotechnique, 2003, 53(7): 643-653. doi: 10.1680/geot.53.7.643.37385 [24] GOEL S, PATRA N R. Effect of arching on active earth pressure for rigid retaining walls considering translation mode[J]. International Journal of Geomechanics, 2008, 8(2): 123-133. doi: 10.1061/(ASCE)1532-3641(2008)8:2(123) [25] XU M, GUO J W. DEM study on the development of the Earth pressure of granular materials subjected to lateral cyclic loading[J]. Computers and Geotechnics, 2021, 130: 103915.1-103915.12. doi: 10.1016/j.compgeo.2020.103915 [26] 张恒志, 徐长节, 何寨兵, 等. 基于离散元方法的不同挡墙变位模式下有限土体主动土压力研究[J]. 岩土力学, 2022, 43(1): 257-267. doi: 10.16285/j.rsm.2021.0708ZHANG Hengzhi, XU Changjie, HE Zhaibing, et al. Study of active earth pressure of finite soils under different retaining wall movement modes based on discrete element method[J]. Rock and Soil Mechanics, 2022, 43(1): 257-267. doi: 10.16285/j.rsm.2021.0708 [27] ZHANG R X, SU D, LIN X T, et al. DEM analysis of passive arching in a shallow trapdoor under eccentric loading[J]. Particuology, 2023, 77: 14-28. doi: 10.1016/j.partic.2022.08.004 [28] 孙佳政, 傅翼, 仇雅诗, 等. RB模式下砂土非极限主动土压力的离散元模拟与理论研究[J]. 岩土力学, 2023, 44(2): 603-614. doi: 10.16285/j.rsm.2022.0406SUN Jiazheng, FU Yi, QIU Yashi, et al. Discrete element simulation and theoretical study on non-limit active earth pressure of sand under RB mode[J]. Rock and Soil Mechanics, 2023, 44(2): 603-614. doi: 10.16285/j.rsm.2022.0406 [29] GOLDENBERG C, GOLDHIRSCH I. Friction enhances elasticity in granular solids[J]. Nature, 2005, 435: 188-191. doi: 10.1038/nature03497 [30] 申志福, 蒋明镜, 朱方园, 等. 离散元微观参数对砂土宏观参数的影响[J]. 西北地震学报, 2011, 33(增1): 160-165. doi: 10.3969/j.issn.1000-0844.2011.z1.034SHEN Zhifu, JIANG Mingjing, ZHU Fangyuan, et al. Influence of micro parameters of discrete element on macro parameters of sandy soil[J]. China Earthquake Engineering Journal, 2011, 33(S1): 160-165. doi: 10.3969/j.issn.1000-0844.2011.z1.034 [31] JIANG M J, KONRAD J M, LEROUEIL S. An efficient technique for generating homogeneous specimens for DEM studies[J]. Computers and Geotechnics, 2003, 30(7): 579-597. doi: 10.1016/S0266-352X(03)00064-8 [32] KHOSRAVI M H, PIPATPONGSA T, TAKEMURA J. Theoretical analysis of earth pressure against rigid retaining walls under translation mode[J]. Soils and Foundations, 2016, 56(4): 664-675. doi: 10.1016/j.sandf.2016.07.007 [33] LIU F Q. Lateral earth pressures acting on circular retaining walls[J]. International Journal of Geomechanics, 2014, 14(3): 4014002.1-4014002.12. doi: 10.1061/(asce)gm.1943-5622.0000291 [34] CHANG M F. Lateral earth pressures behind rotating walls[J]. Canadian Geotechnical Journal, 1997, 34(4): 498-509. doi: 10.1139/t97-016 [35] 胡俊强, 张永兴, 陈林, 等. 非极限状态挡土墙主动土压力研究[J]. 岩土工程学报, 2013, 35(2): 381-387. doi: 10.7666/d.D01008971HU Junqiang, ZHANG Yongxing, CHEN Lin, et al. Active earth pressure on retaining wall under non-limit state[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 381-387. doi: 10.7666/d.D01008971 [36] 江文放, 周亦涛, 俞缙, 等. 基于土拱效应的墙背非极限主动土压力[J]. 地下空间与工程学报, 2016, 12(6): 1676-1681. doi: 10.20174/j.juse.2016.06.036JIANG Wenfang, ZHOU Yitao, YU Jin, et al. Non-limit active earth pressure for rigid retaining wall based on soil arching effect[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(6): 1676-1681. doi: 10.20174/j.juse.2016.06.036 -




 下载:
下载: