Lateral Control of Permanent Magnet Electrodynamic Suspension Vehicle Based on Improved Nonlinear Model Predictive Controller
-
摘要:
针对横向力不足、模型不确定和时变扰动环境下永磁电动悬浮汽车横向运动控制问题，提出一种改进非线性模型预测横向跟踪控制方法（NMPC-ESO-EKF）以实现车辆横向精准控制. 首先，提出通过偏转磁轮来补偿系统横向力的横向运行模式，以此建立横向非线性动力学模型；然后，建立含有约束条件的非线性模型预测控制器（NMPC），并构造扩张状态观测器（ESO）来观测系统内外扰动以补偿控制输入，同时引入扩展卡尔曼滤波器（EKF）消除传感器测量噪声对ESO观扰的影响；最后，搭建联合仿真平台和实验平台进行仿真与实验验证. 研究结果表明：永磁电动悬浮汽车在横向运行模式下，能有效实现左右横移运动；相较于PID-EKF控制，在定常数参考信号下，NMPC-ESO-EKF超调量降低98.90%，系统调节时间缩短47.78%；在方波参考信号下，系统平均超调量和平均跟踪误差分别降低了93.77%和36.13%；施加扰动后，系统横向位移波动幅值减小34.51%，恢复时间缩短42.08%，横向控制精度与抗扰能力大幅提升，为永磁电动悬浮汽车横向控制研究提供一定参考.
Abstract:Objective The permanent magnet electrodynamic suspension (PMEDS) vehicle, with its integrated levitation and propulsion system, shows significant potential for applications in areas such as ultra-high-speed and heavy-load highways, as well as mountainous road transportation. However, the PMEDS vehicle is a lateral underdamped system, and its lateral open-loop system is extremely unstable. It is prone to instability when exposed to disturbances, such as lateral gusts, which seriously affect driving safety. Therefore, it is crucial to study lateral motion control under the conditions of insufficient lateral force, model uncertainty, and time-varying disturbances.
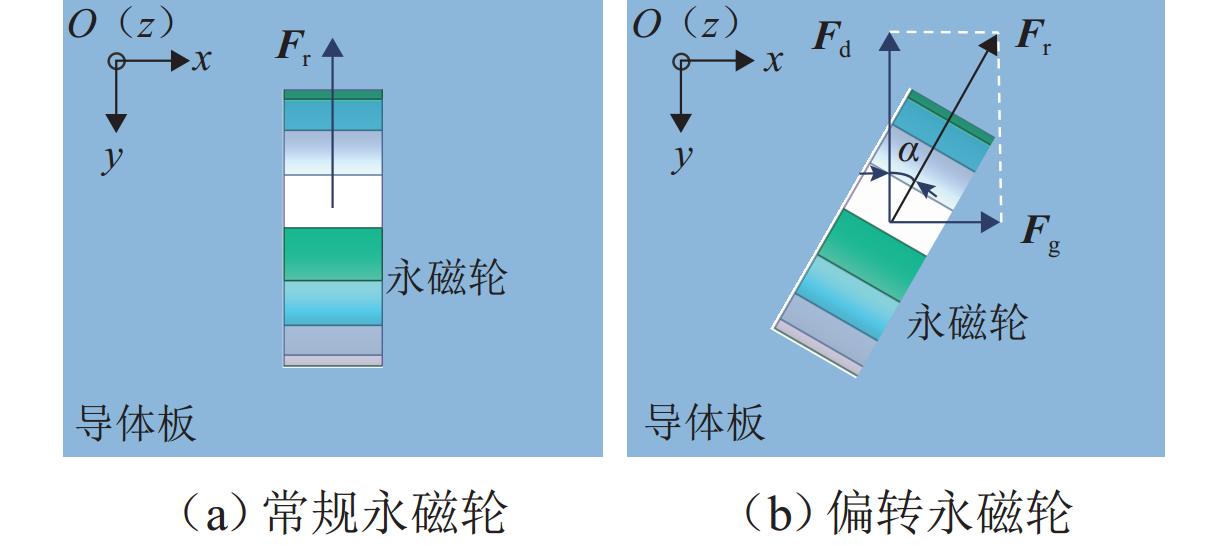
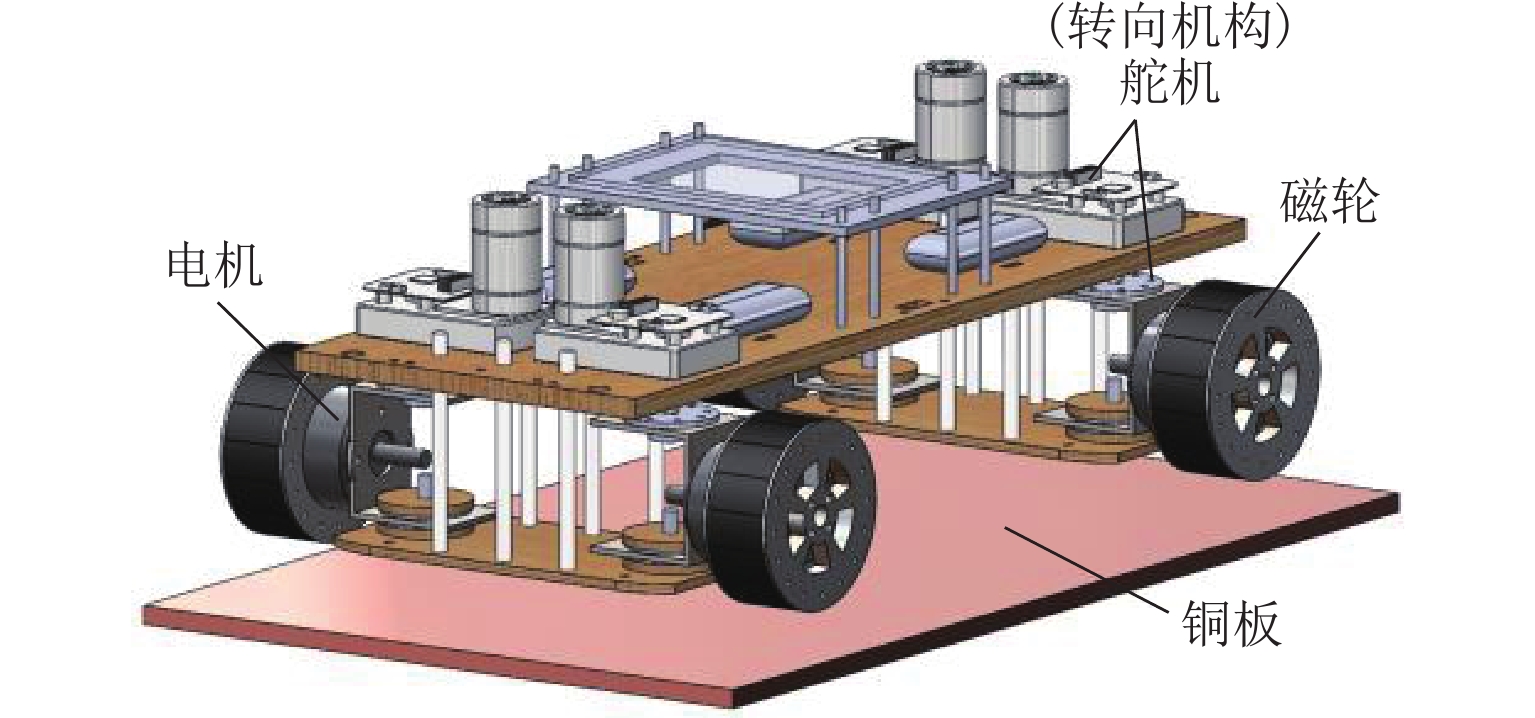
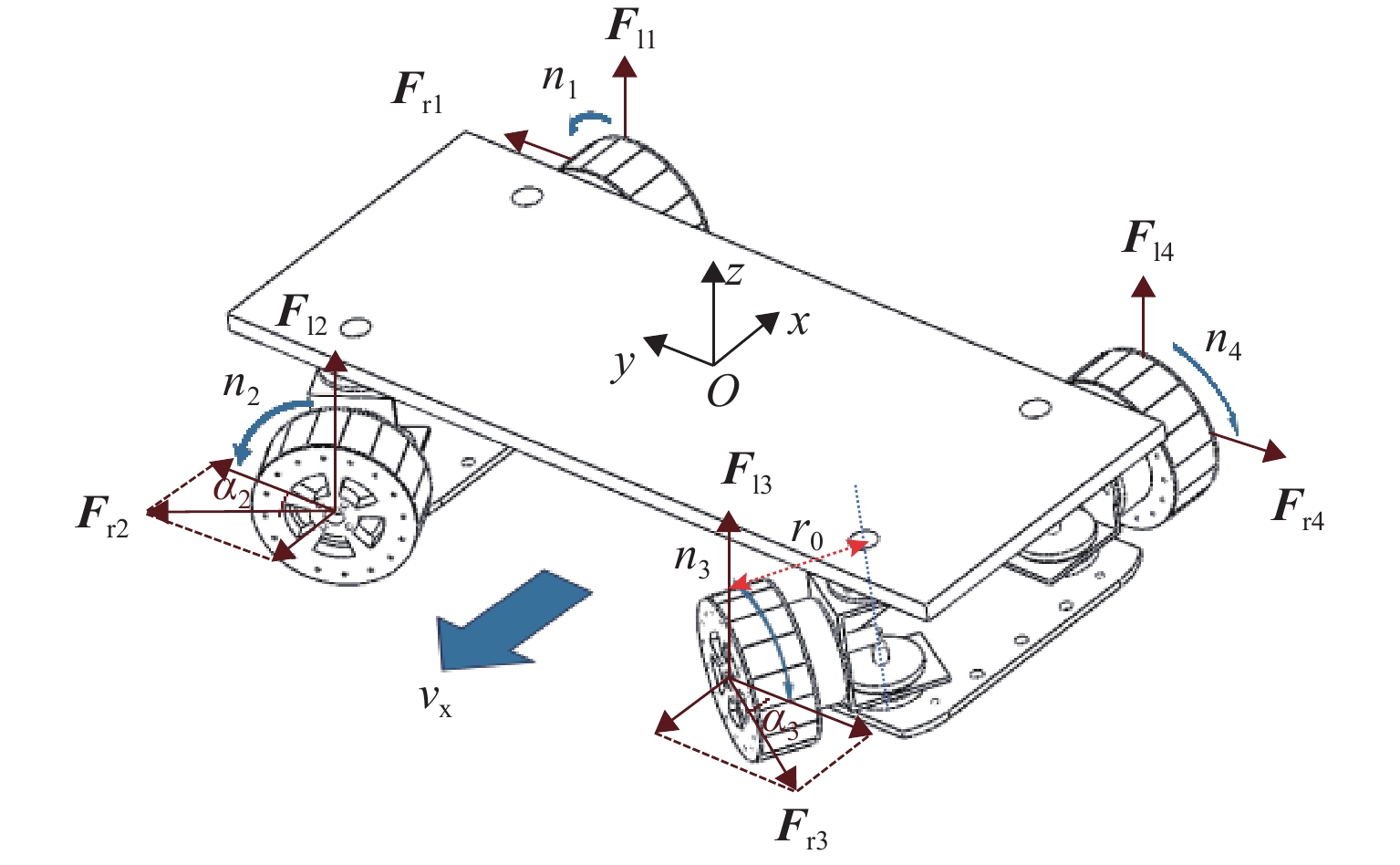
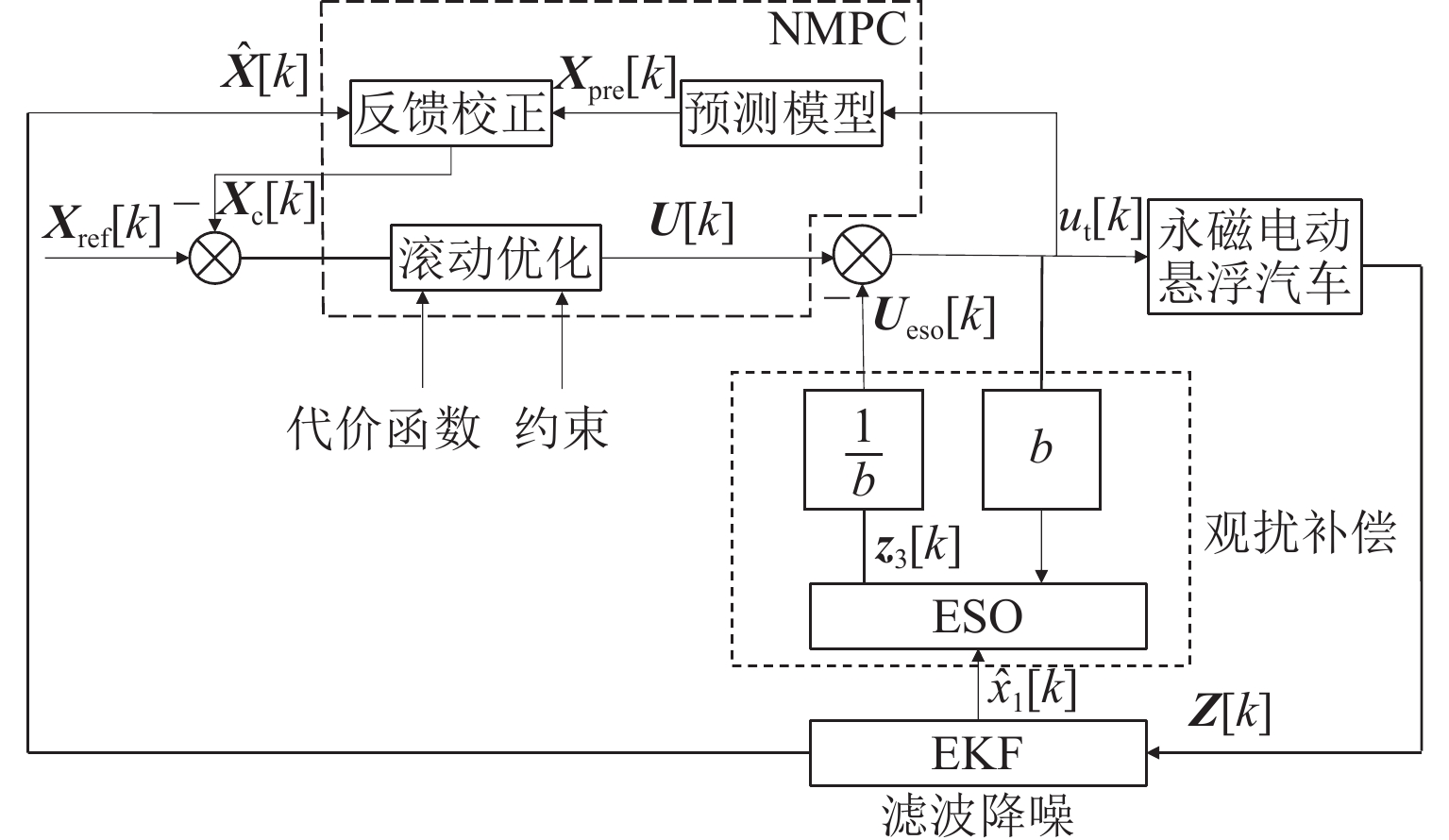
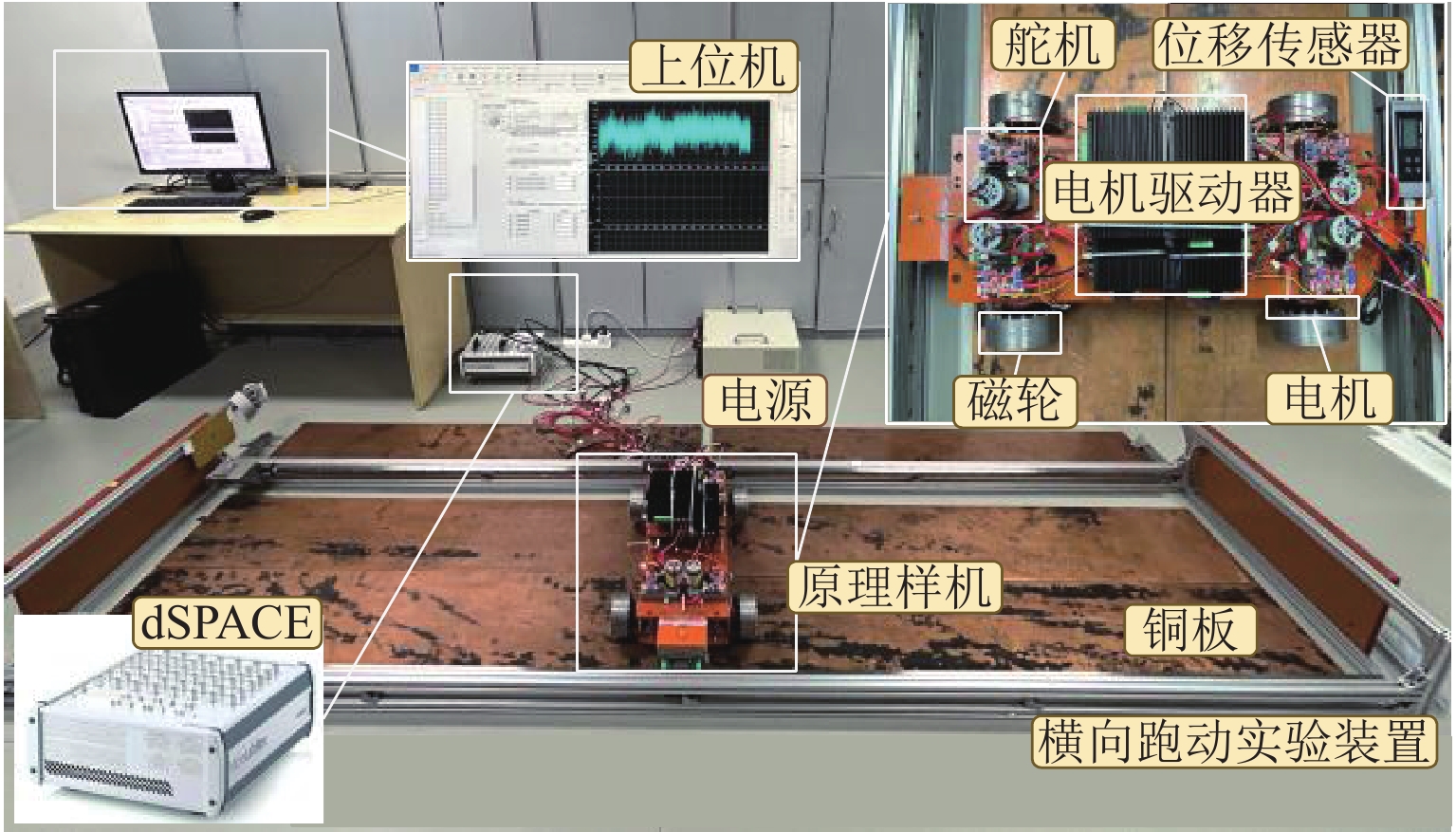
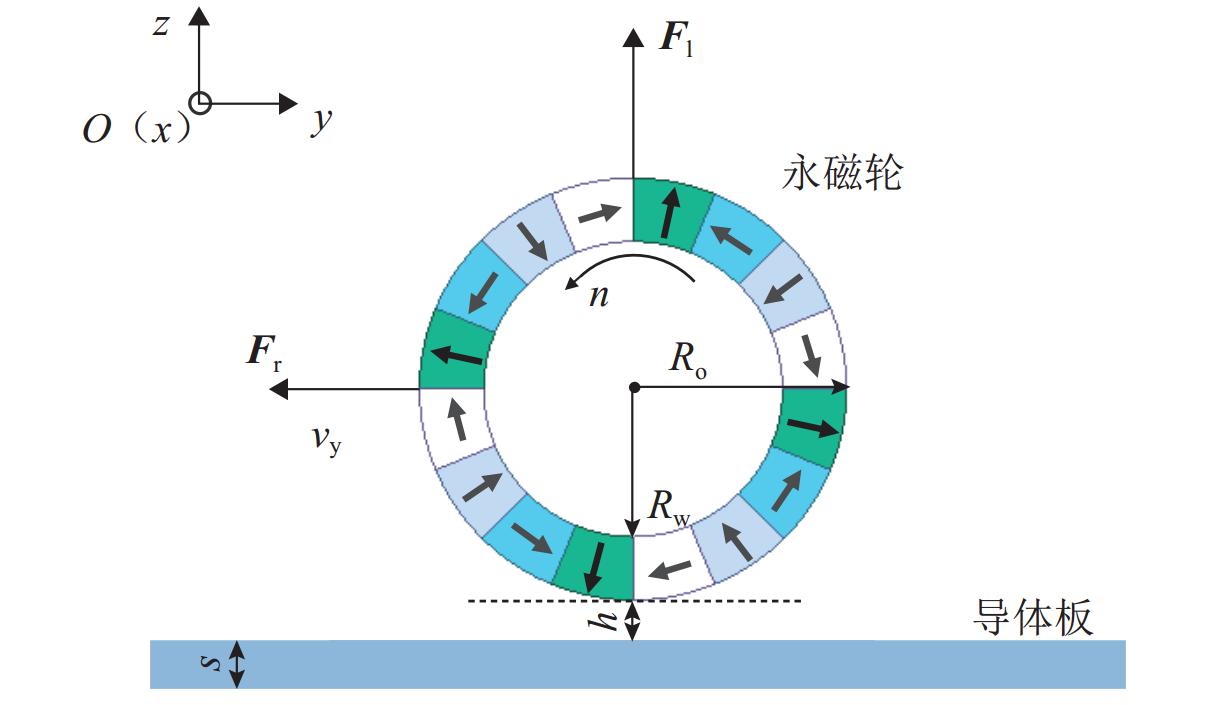
Method In order to achieve precise control of the lateral motion and enhance the lateral anti-disturbance ability of the PMEDS vehicle, a lateral operation mode was proposed, and a lateral nonlinear dynamic model was derived. Moreover, an improved nonlinear model predictive lateral tracking controller (NMPC-ESO-EKF) with constraints was established, and its effectiveness was verified by simulation and experiment. Firstly, the working principle of the radial annular Halbach permanent magnet wheel was introduced; the feasibility of compensating for the lateral force of the system by deflecting the magnetic wheels was analyzed, and the vehicle’s lateral operation mode via symmetrically deflecting the same-side magnetic wheels was proposed. Secondly, according to the principle of lateral operation, the lateral damping term was introduced to derive the lateral nonlinear dynamic model for the PMEDS vehicle. Then, based on the dynamic model, a nonlinear discrete state-space model was derived as the prediction model; a cost function and the amplitude constraint of the deflection angle were designed. According to the prediction model, cost function, and system constraints, the nonlinear model predictive controller (NMPC) was established; the control problem was transformed into a nonlinear programming problem in the finite time domain. Meanwhile, in order to improve the anti-disturbance ability of the NMPC, the extended state observer (ESO) was constructed to observe the internal and external disturbances of the system, compensating for the control input. In order to reduce the sensitivity of ESO to sensor measurement noise, an extended Kalman filter (EKF) was introduced to filter the raw signals. Moreover, the convergence of the overall control framework was demonstrated. Finally, the simulation and analysis of lateral constant trajectory tracking and lateral anti-disturbance under internal and external disturbances conditions were conducted using the Matlab/Simulink-Simscape joint simulation platform. Additionally, experiments were performed by using the lateral running experimental device and the principle prototype, covering short-distance constant trajectory tracking, square wave signal trajectory tracking, and the analysis of anti-disturbance ability under long-distance constant trajectory tracking.
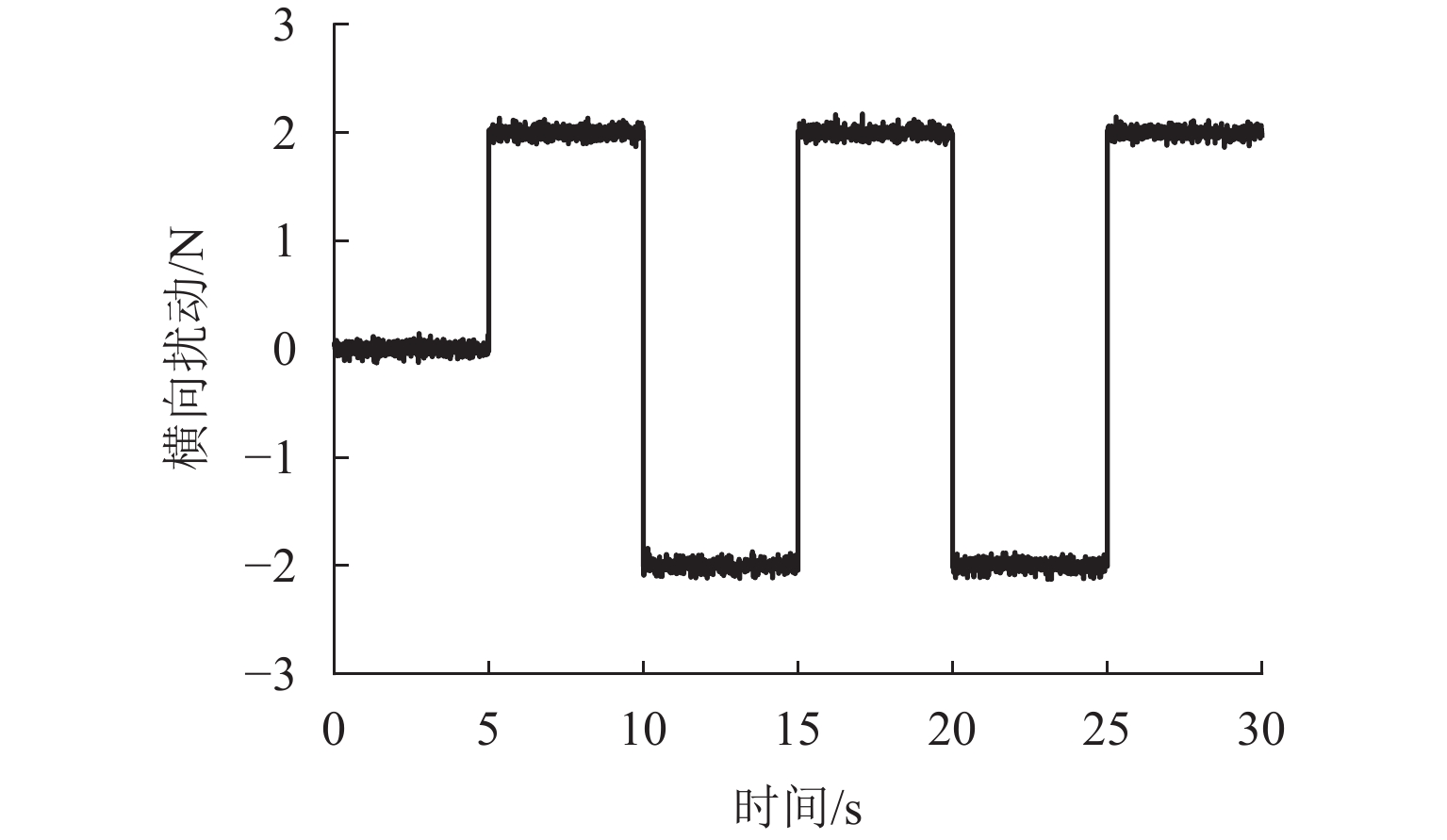
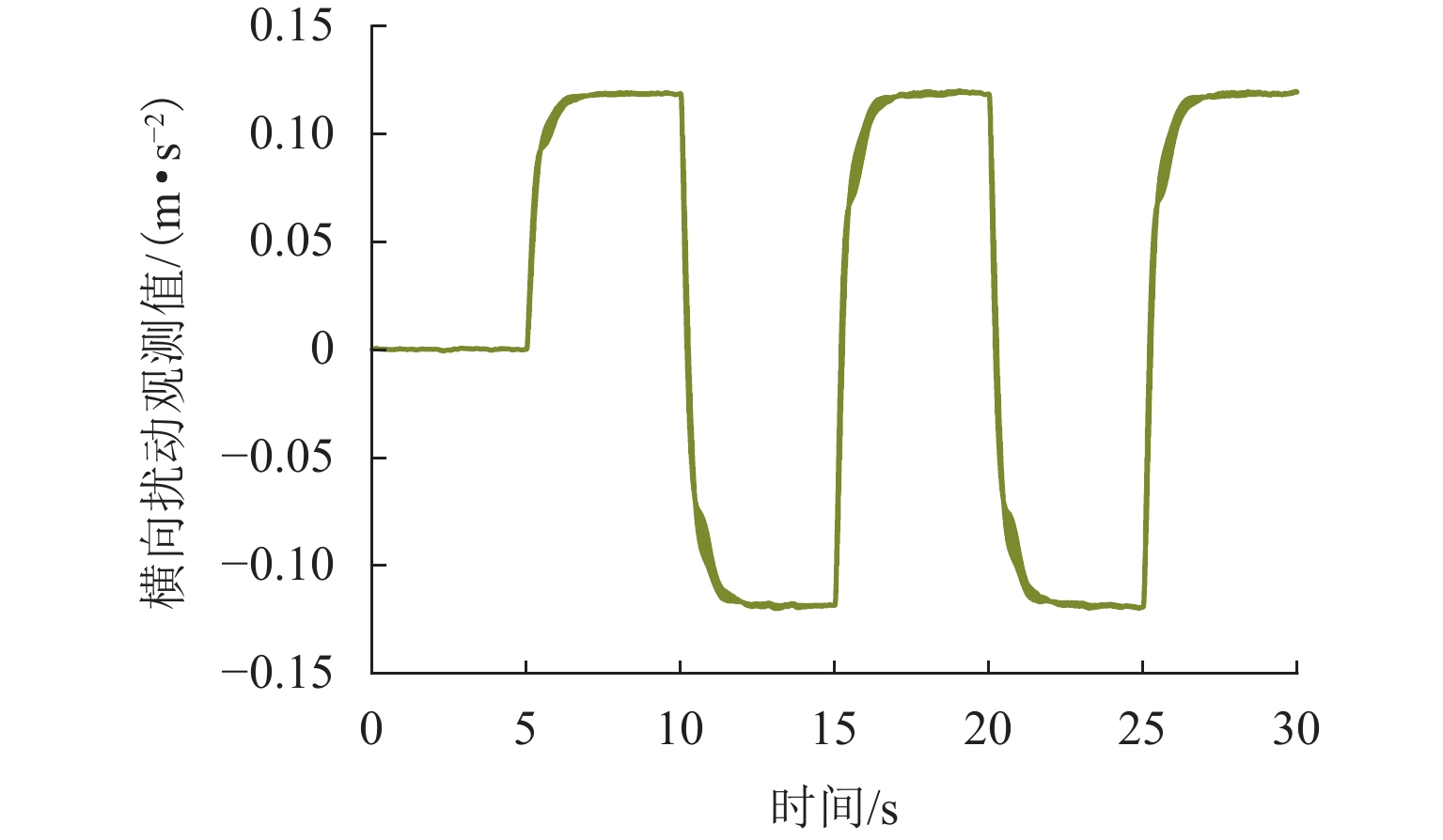
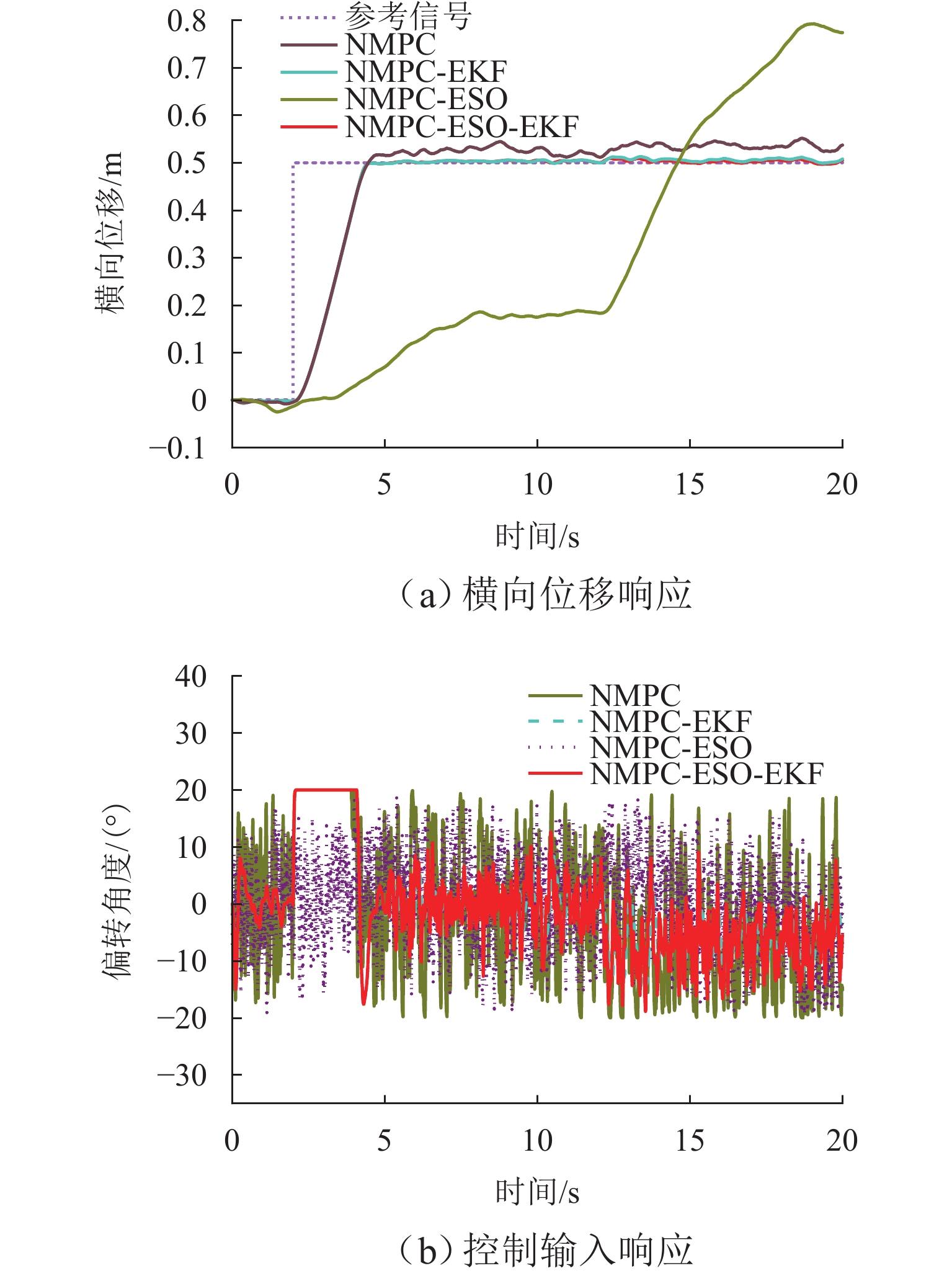
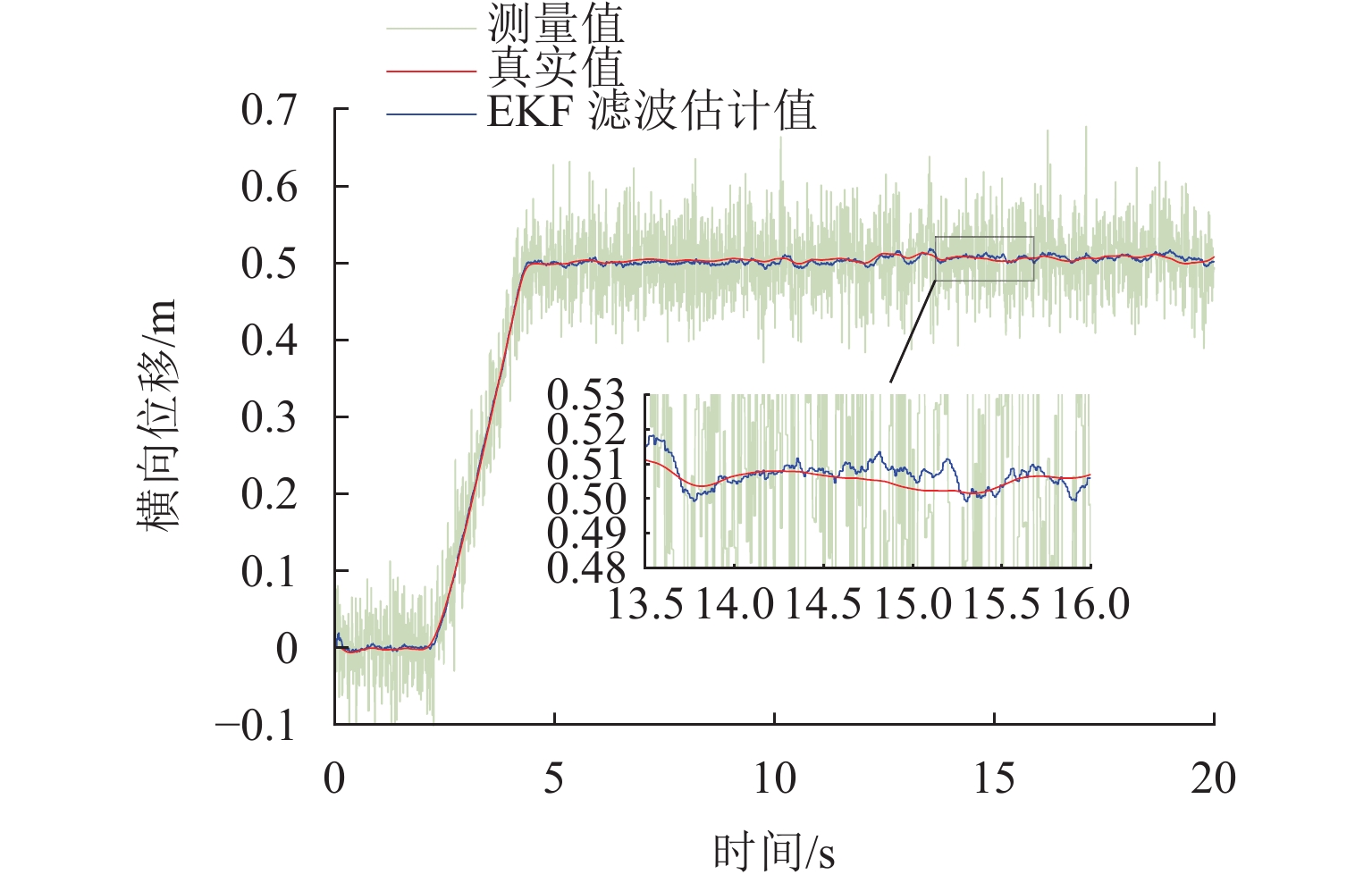
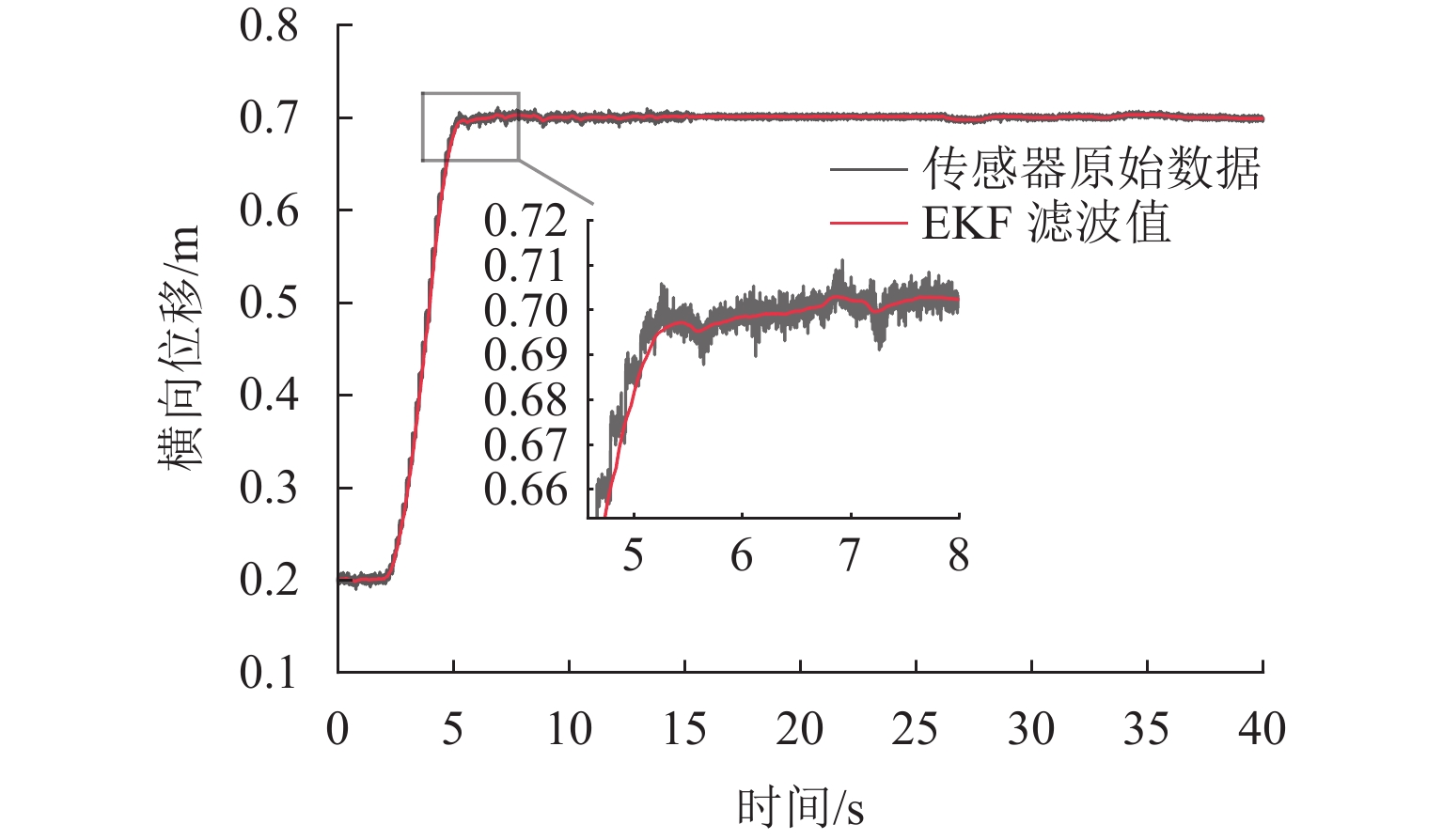
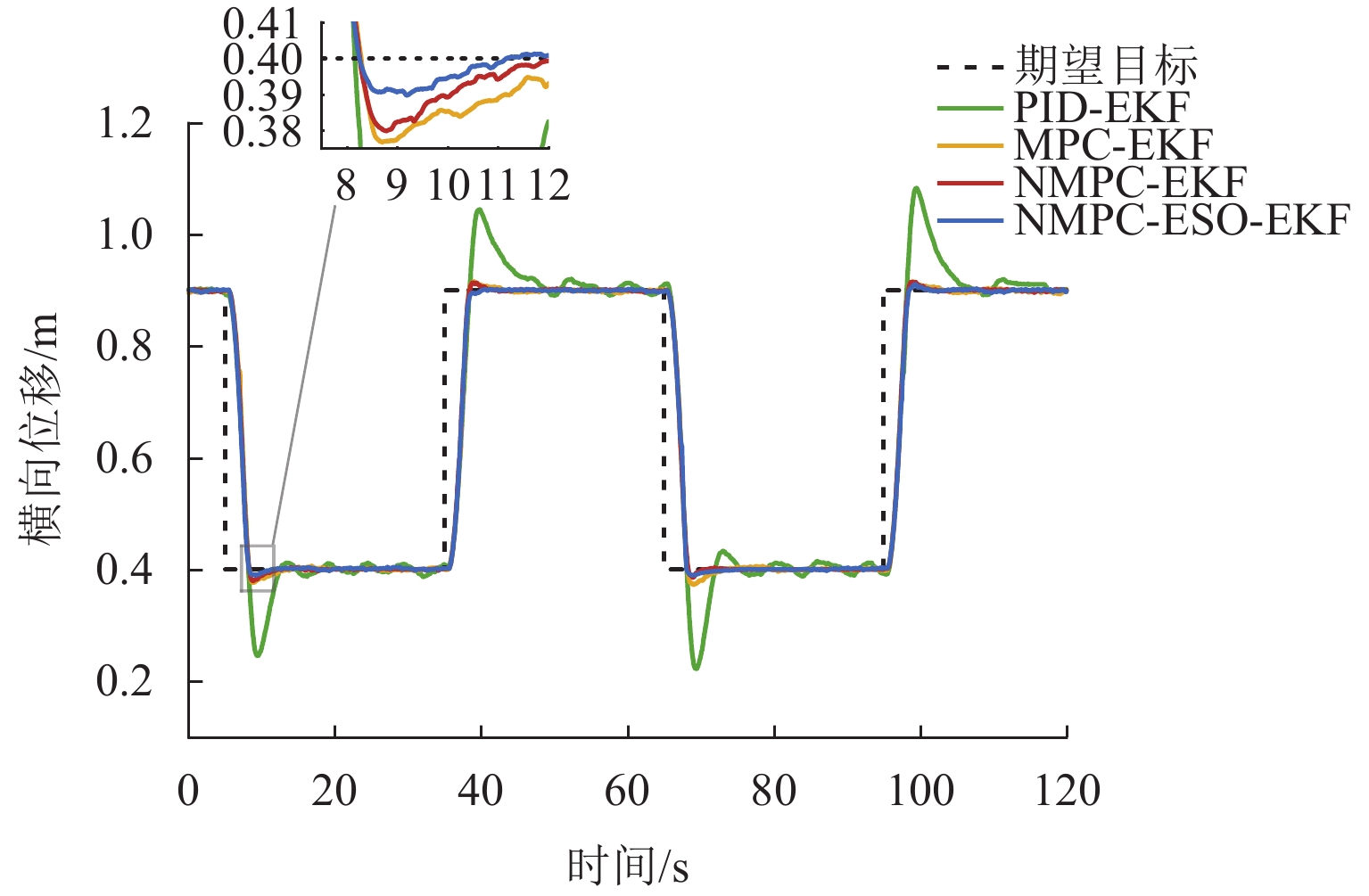
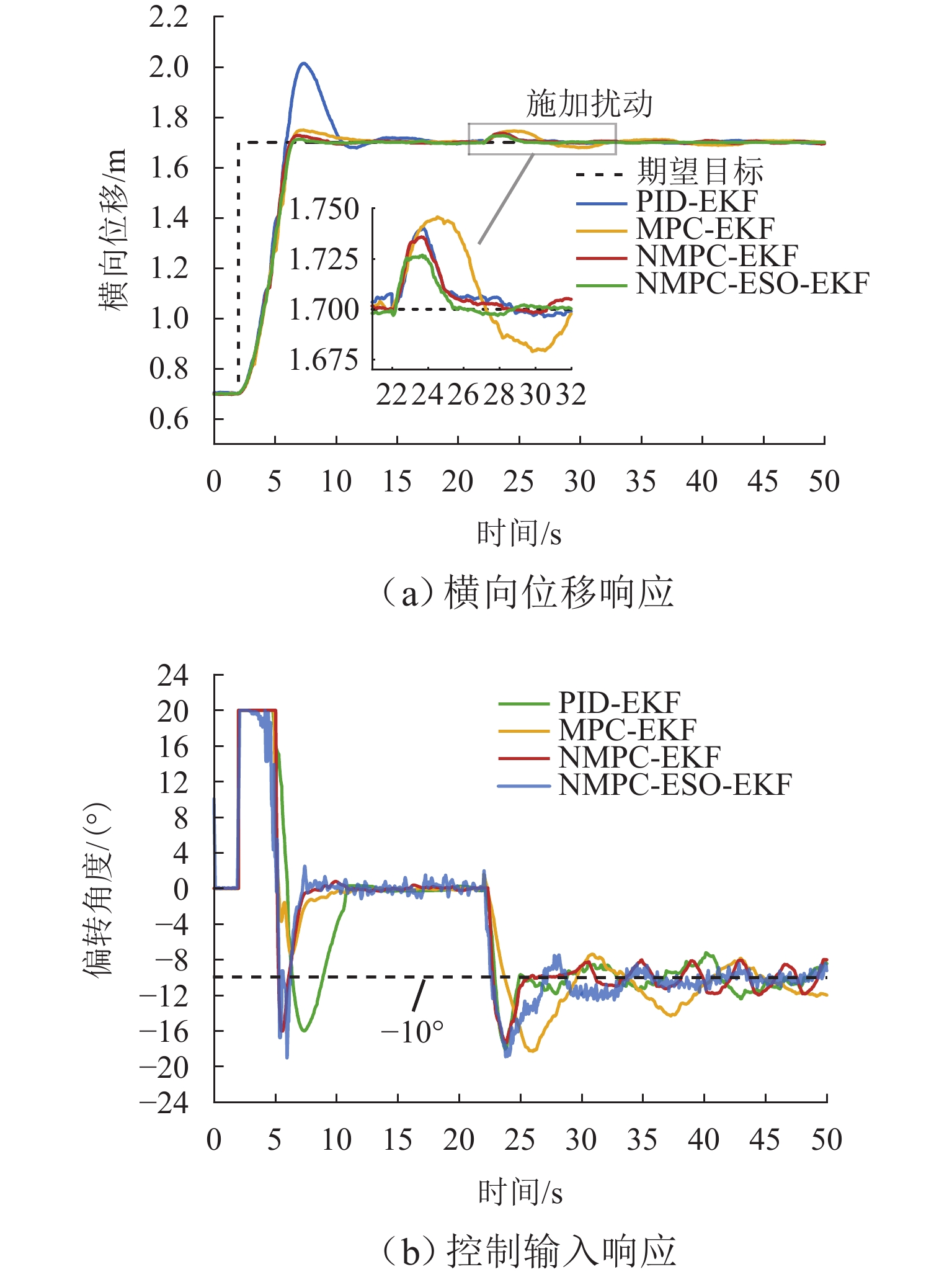
Result The simulation results show that under the disturbance-free condition, the system can effectively realize the lateral trajectory tracking control function under PID, MPC, NMPC, and NMPC-ESO control strategies. The response speeds of the various controllers are relatively similar. The PID controller exhibits the largest overshoot, while MPC experiences some overshoot, though significantly smaller than that of PID. Both NMPC and NMPC-ESO have minimal overshoot, with their response curves closely resembling each other, indicating that ESO has no noticeable effect. Under external disturbance conditions, the addition of ESO significantly improves the anti-disturbance ability of NMPC. The lateral displacement fluctuations are minimal for NMPC-ESO, and the system recovery time is the shortest. When sensor measurement noise is introduced, the system can stably control within a range close to the target position under NMPC control, but there is still an error compared to the target position. Due to the excessive sensitivity of ESO to the noise, it overcompensates the deflection angle, leading to instability in the NMPC-ESO control after ESO’s application. To address this issue, an EKF is introduced to suppress the impact of internal noise on ESO’s disturbance estimation. Under both internal and external disturbance conditions, NMPC-ESO-EKF significantly improves the lateral trajectory tracking accuracy by 89.77% and greatly enhances the anti-disturbance ability, demonstrating the necessity of incorporating EKF.The experimental results indicate that the error between the values filtered by EKF and the true values is very small. PID-EKF exhibits significant overshoot and oscillation under various operating conditions, which poses safety concerns in practical engineering applications. Under short-distance constant reference signals, compared to PID-EKF control, NMPC-ESO-EKF reduces the overshoot by 98.90% to 2.12 mm, with the shortest system settling time of 4.7 s, which is reduced by 47.78%. Under square wave reference signals, the trajectory tracking curves of MPC-EKF, NMPC-EKF, and NMPC-ESO-EKF are all relatively stable, with NMPC-ESO-EKF showing the smallest average overshoot and tracking error, improving performance by 93.77% and 36.13%, respectively, compared to PID-EKF. Under long-distance constant reference signals, larger overshoots are observed across all controllers. After applying continuous disturbances, each controller can make the system return to the stable target value. After stabilization, the input deflection angle fluctuates around −10° to continuously resist external disturbance; the displacement fluctuation amplitude of MPC-EKF is the largest, with the longest recovery time; the anti-disturbance ability of NMPC-ESO-EKF is optimal, with the fluctuation amplitude reduced by 34.51% and the recovery time shortened by 42.08% compared to PID-EKF.
Conclusion The PMEDS vehicle, under the improved nonlinear model predictive control method, has enhanced its lateral stability and possesses the basic functionality of flexible lateral movement. It is suitable for scenarios such as lateral anti-disturbance during normal driving, active lane change, lateral hill climbing, and parallel parking. Up to now, significant breakthroughs have been achieved in areas such as the optimization of electromagnetic forces of magnetic wheels, structural design of vehicles, and single-degree-of-freedom control research. However, it is still in the theoretical research stage. In order to realize engineering applications as soon as possible, future efforts will focus on intelligent system perception, path planning, and multi-degree-of-freedom coupling trajectory tracking control research.
-
图 2 常规永磁轮与偏转永磁轮示意
Figure 2. Conventional permanent magnet wheel and deflecting permanent magnet wheel
图 14 小距离定常数轨迹跟踪控制系统响应
Figure 14. System response of short-distance constant trajectory tracking control
图 15 方波信号轨迹跟踪控制系统响应
Figure 15. System response of square wave signal trajectory tracking control
图 16 大距离定常数轨迹跟踪控制系统响应
Figure 16. System response of long-distance constant trajectory tracking control
表 1 永磁电动悬浮汽车模型参数
Table 1. Model parameters of PMEDS vehicle
编号 参数 数值 整车
参数整车质量m/kg
悬浮间隙h/mm
横向阻尼系数c/（N·s·m−1）18.1
10
17.2磁轮
参数极对数P
外径Ro/mm
内径Ri/mm
宽度d/mm
磁化角q/°
磁轮转速n0/rpm
磁轮磁阻力Fr0/N4
50
32.5
35
90
2000
17.33磁轮偏转角度范围α/° −20～20 
下载: 导出CSV
表 2 系统响应结果对比
Table 2. Comparison of system response results
控制器 0～12 s 12 s 后 平均误差/mm 性能提升/% 平均误差/mm 性能提升/% NMPC 71.31 34.41 NMPC-ESO 319.54 −348.10 183.07 −432.03 NMPC-EKF 57.99 18.70 6.12 82.20 NMPC-ESO-EKF 57.93 18.76 3.52 89.77
下载: 导出CSV
表 3 方波信号轨迹跟踪控制系统响应结果对比
Table 3. Comparison of system response results of square wave signal trajectory tracking control
mm 控制器 平均跟踪误差 平均超调量 PID-EKF 57.60 164.96 MPC-EKF 38.48 20.48 NMPC-EKF 36.82 15.69 NMPC-ESO-EKF 36.79 10.27
下载: 导出CSV
表 4 大距离定常数轨迹跟踪控制系统响应结果对比
Table 4. Comparison of system response results of long-distance constant trajectory tracking control
控制器 位移波动幅值/mm 恢复时间/s PID-EKF 40.89 6.82 MPC-EKF 45.39 10.46 NMPC-EKF 35.73 6.80 NMPC-ESO-EKF 26.78 3.95
下载: 导出CSV
-
[1] LIU B, SUN C, WANG B, et al. Adaptive speed planning of connected and automated vehicles using multi-light trained deep reinforcement learning[J]. IEEE Transactions on Vehicular Technology, 2022, 71(4): 3533-3546. doi: 10.1109/TVT.2021.3134372 [2] 邓自刚,刘宗鑫,李海涛,等. 磁悬浮列车发展现状与展望[J]. 西南交通大学学报,2022,57(3): 455-474,530.DENG Zigang, LIU Zongxin, LI Haitao, et al. Development status and prospect of maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 455-474,530. [3] 林国斌,刘万明,徐俊起,等. 中国高速磁浮交通的发展机遇与挑战[J]. 前瞻科技,2023,2(4): 7-18.LIN Guobin, LIU Wanming, XU Junqi, et al. Opportunities and challenges for the development of high-speed maglev transportation in China[J]. Science and Technology Foresight, 2023, 2(4): 7-18. [4] 赵春发,刘浩东,冯洋,等. 五位姿参数下车载永磁体与永磁轨道之间的磁力特性研究[J]. 西南交通大学学报,2024,59(4): 804-811.ZHAO Chunfa, LIU Haodong, FENG Yang, et al. Magnetic force characteristics between on-board permanent magnet and permanent magnetic rail considering five pose parameters[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 804-811. [5] 胡永攀,曾杰伟,王志强,等. 超高速永磁电动悬浮系统性能优化[J]. 西南交通大学学报,2023,58(4): 773-782.HU Yongpan, ZENG Jiewei, WANG Zhiqiang, et al. Performance optimization of ultra-high speed permanent magnet electrodynamic suspension system[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 773-782. [6] QIN W, BIRD J Z. Electrodynamic wheel magnetic rolling resistance[J]. IEEE Transactions on Magnetics, 2017, 53(8): 8107407.1-8107407.7. [7] SHI H F, KE Z H, ZHENG J, et al. An effective optimization method and implementation of permanent magnet electrodynamic wheel for maglev car[J]. IEEE Transactions on Vehicular Technology, 2023, 72(7): 8369-8381. doi: 10.1109/TVT.2023.3245620 [8] WRIGHT J D. Modeling, analysis, and control of a radial electrodynamic wheel vehicle and analysis of an axial electrodynamic wheel[D]. Charlotte: The University of North Carolina at Charlotte, 2019. [9] FUJII N, NONAKA S, HAYASHI G. Design of magnet wheel integrated own drive[J]. IEEE Transactions on Magnetics, 1999, 35(5): 4013-4015. doi: 10.1109/20.800739 [10] FUJII N, HAYASHI G, SAKAMOTO Y. Characteristics of magnetic lift, propulsion and guidance by using magnet wheels with rotating permanent magnets[C]//Conference Record of the 2000 IEEE Industry Applications Conference. Rome: IEEE, 2002: 257-262. [11] JUNG K S. Parametric design of contact-free transportation system using the repulsive electrodynamic wheels[J]. Journal of the Korea Academia-Industrial Cooperation Society, 2016, 17(3): 310-316. doi: 10.5762/KAIS.2016.17.3.310 [12] JUNG K S. Transfer system using radial electrodynamic wheel over conductive track[J]. Journal of the Korea Academia-Industrial Cooperation Society, 2017, 18(11): 794-801. [13] 刘新,邓自刚,梁乐,等. 基于斜置环形Halbach永磁轮的磁浮列车“悬浮-导向-推进” 一体化方案设计[J]. 机车电传动,2023(2): 90-96.LIU Xin, DENG Zigang, LIANG Le, et al. Levitation-guidance-propulsion integrated design for maglev trains based on oblique ring Halbach permanent magnet wheels[J]. Electric Drive for Locomotives, 2023(2): 90-96. [14] ZHANG Z, DENG Z G, ZHANG S, et al. Design and operating mode study of a new concept maglev car employing permanent magnet electrodynamic suspension technology[J]. Sustainability, 2021, 13(11): 5827.1-5827.20. [15] 徐俊起,林国斌,荣立军,等. 中低速磁浮列车悬浮控制技术成果及应用[J]. 铁道技术标准(中英文),2022(10): 34-39.XU Junqi, LIN Guobin, RONG Lijun, et al. Research achievements and application of levitation control technology for medium-low speed maglev train[J]. Railway Technical Standard (Chinese & English), 2022(10): 34-39. [16] DE BOEIJ J, STEINBUCH M, GUTIERREZ H. Real-time control of the 3-DOF sled dynamics of a null-flux maglev system with a passive sled[C]//IEEE Transactions on Magnetics. Montreal: IEEE, 2006: 1604-1610. [17] ZHANG B J, KE Z H, LI Z Y, et al. Yawing stability and manipulative approach design for maglev car based on active disturbance rejection control[J]. Asian Journal of Control, 2024, 26(2): 1003-1016. doi: 10.1002/asjc.3246 [18] LI Z Y, KE Z H, SHI J H, et al. Investigation of RBF-SMC control strategy for vertical dynamics of maglev car considering temperature rise effects[J]. IEEE Transactions on Intelligent Vehicles, 2024, 99:1-14. [19] BIRD J, LIPO T A. Characteristics of an electrodynamic wheel using a 2-D steady-state model[J]. IEEE Transactions on Magnetics, 2007, 43(8): 3395-3405. doi: 10.1109/TMAG.2007.900572 [20] BIRD J, LIPO T A. Calculating the forces created by an electrodynamic wheel using a 2-D steady-state finite-element method[J]. IEEE Transactions on Magnetics, 2008, 44(3): 365-372. doi: 10.1109/TMAG.2007.913038 [21] PAUL S, BIRD J Z. A 3-D analytic eddy current model for a finite width conductive plate[J]. COMPEL: the International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2013, 33(1/2): 688-706. doi: 10.1108/COMPEL-03-2013-0083 [22] 闫玉盼,饶兵,刘砚菊,等. 基于非线性模型预测的四旋翼无人机轨迹跟踪控制[J]. 沈阳理工大学学报,2024,43(1): 36-43,49.YAN Yupan, RAO Bing, LIU Yanju, et al. Trajectory tracking control of quadrotor based on nonlinear model predictive control[J]. Journal of Shenyang Ligong University, 2024, 43(1): 36-43,49. [23] KAMEL M, ALEXIS K, ACHTELIK M, et al. Fast nonlinear model predictive control for multicopter attitude tracking on SO(3)[C]//2015 IEEE Conference on Control Applications (CCA). Sydney: IEEE, 2015: 1160-1166. [24] 许鹏,邢伯阳,刘宇飞,等. 基于扩张状态观测器和模型预测方法的四足机器人抗干扰复合控制[J]. 兵工学报,2023,44(增2): 12-21.XU Peng, XING Boyang, LIU Yufei, et al. Anti-disturbance composite controller design of quadruped robot based on extended state observer and model predictive control technique[J]. Acta Armamentarii, 2023, 44(S2): 12-21. [25] HAN J Q. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906. doi: 10.1109/TIE.2008.2011621 [26] 王天威,黄军魁. 控制之美(卷2): 最优化控制MPC与卡尔曼滤波器[M]. 北京:清华大学出版社,2023. [27] REIF K, UNBEHAUEN R. The extended Kalman filter as an exponential observer for nonlinear systems[J]. IEEE Transactions on Signal Processing, 1999, 47(8): 2324-2328. doi: 10.1109/78.774779 [28] LI J, XIA Y Q, QI X H, et al. On convergence of the discrete-time nonlinear extended state observer[J]. Journal of the Franklin Institute, 2018, 355(1): 501-519. doi: 10.1016/j.jfranklin.2017.11.019 [29] 陈松林,王鑫,何宗儒. 一种兼顾带宽拓展和噪声抑制的ESO参数整定方法[J]. 控制与决策,2018,33(10): 1908-1914.CHEN Songlin, WANG Xin, HE Zongru. A parameter tuning method for extended state observer with balance of bandwidth expansion and noise suppression[J]. Control and Decision, 2018, 33(10): 1908-1914. [30] 郭永飞,张荣彬,姚植元,等. 基于ESO-MPC的核电厂协调系统优化控制研究[J]. 核动力工程,2024,45(6): 178-184.GUO Yongfei, ZHANG Rongbin, YAO Zhiyuan, et al. Research on optimization control of nuclear power plant coordination system based on ESO-MPC[J]. Nuclear Power Engineering, 2024, 45(6): 178-184. [31] HUANG R, PATWARDHAN S C, BIEGLER L T. Robust stability of nonlinear model predictive control based on extended Kalman filter[J]. Journal of Process Control, 2012, 22(1): 82-89. doi: 10.1016/j.jprocont.2011.10.006 -
下载:
点击查看大图
计量
- 文章访问数: 120
- HTML全文浏览量: 43
- PDF下载量: 12
- 被引次数: 0