Study on Complex Mechanical Behavior of Coarse Granular Materials Based on Continuous-Discontinuous Deformation Analysis
-
摘要:
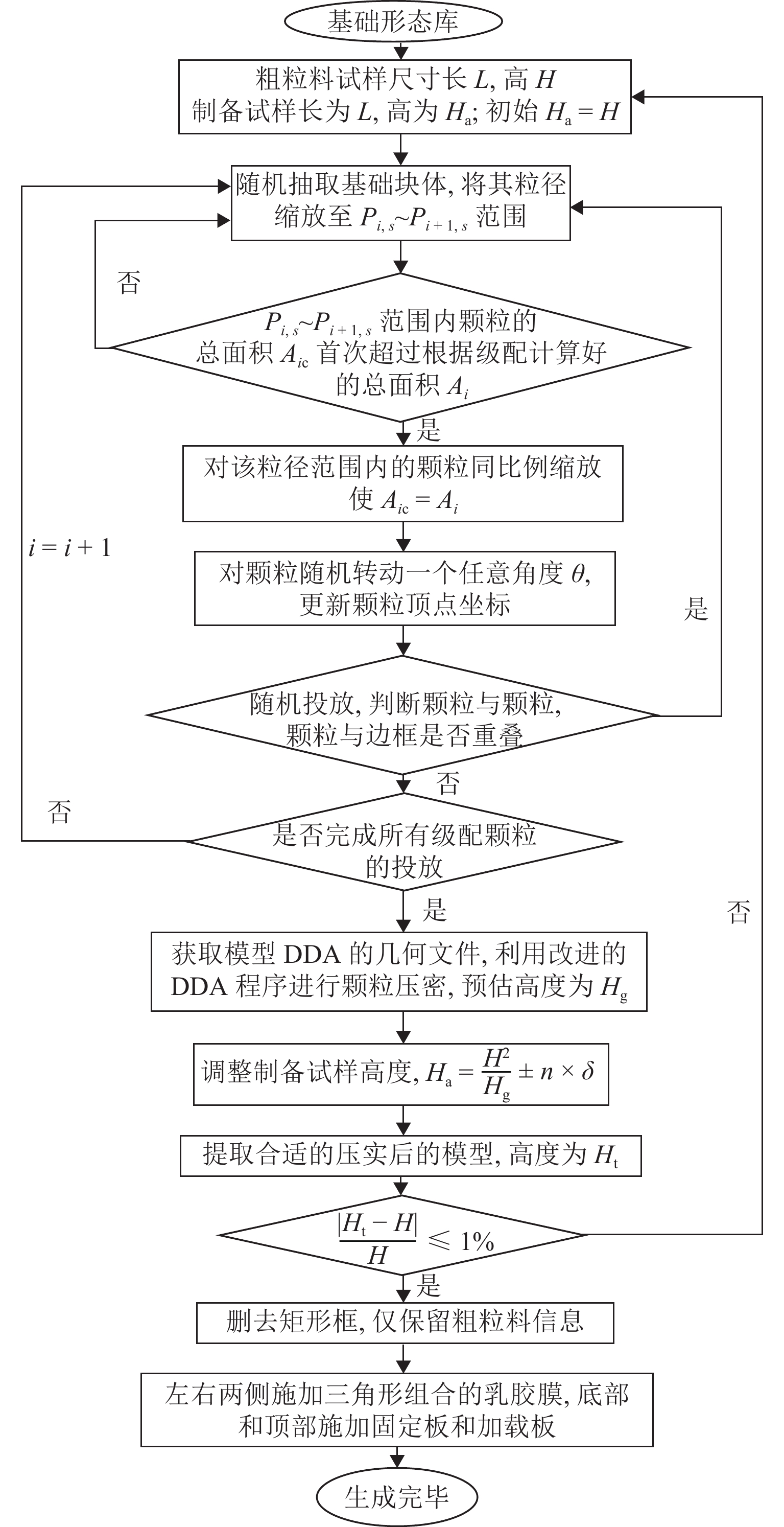
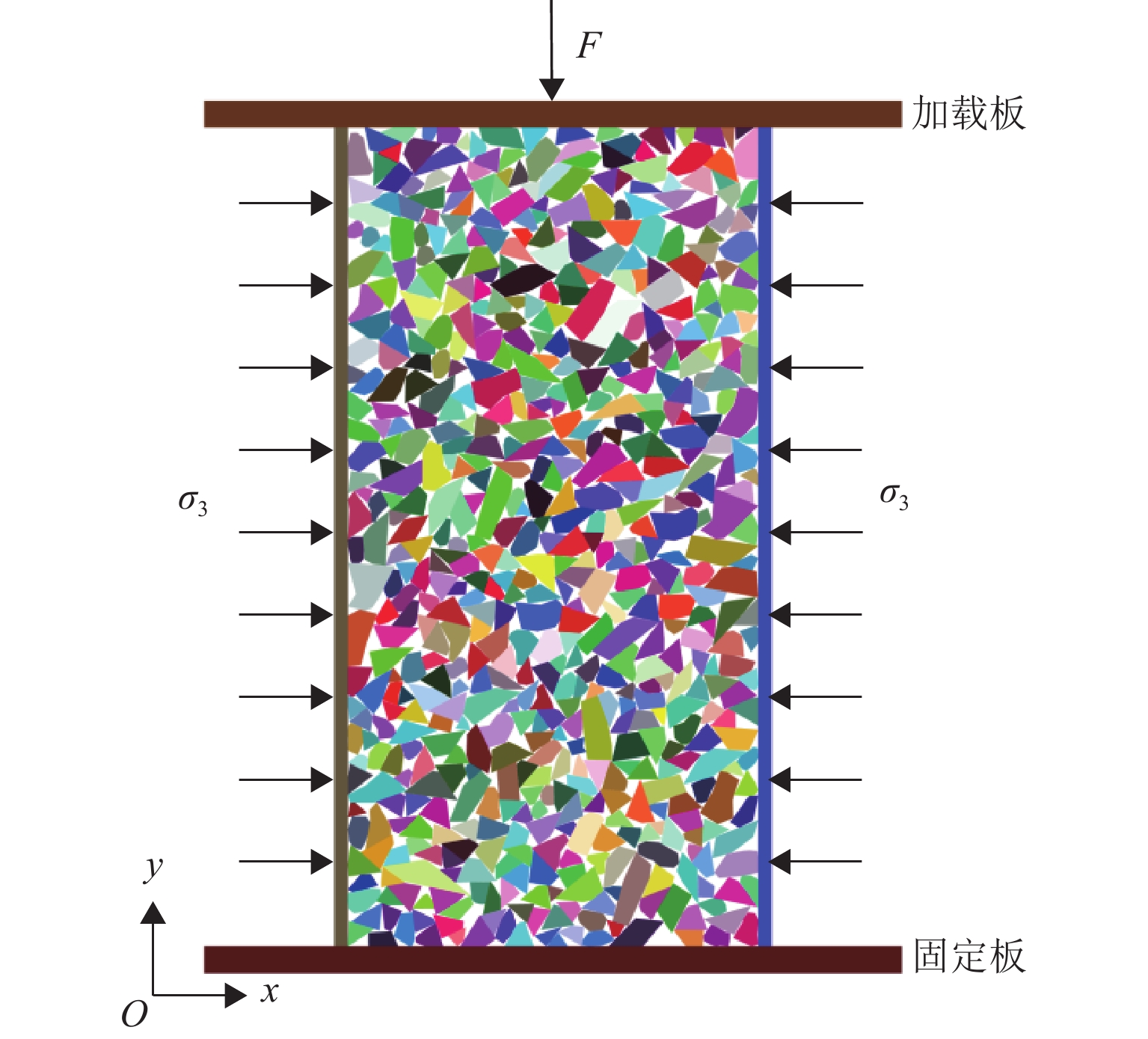
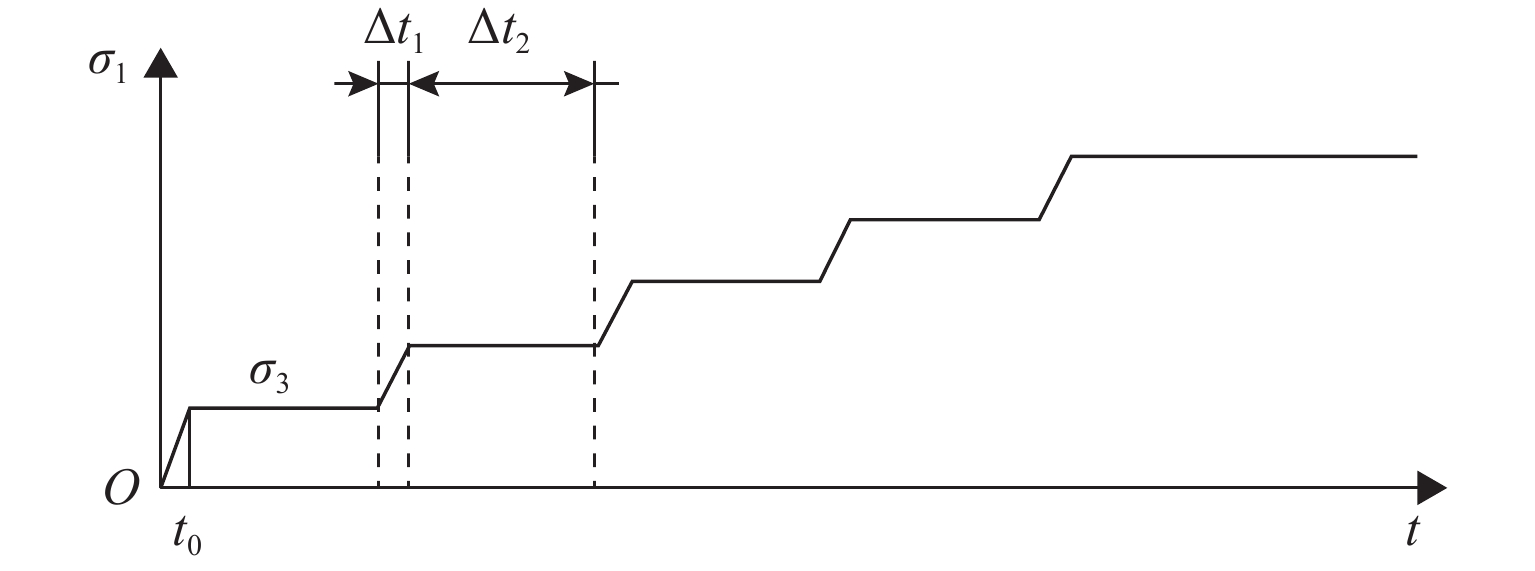
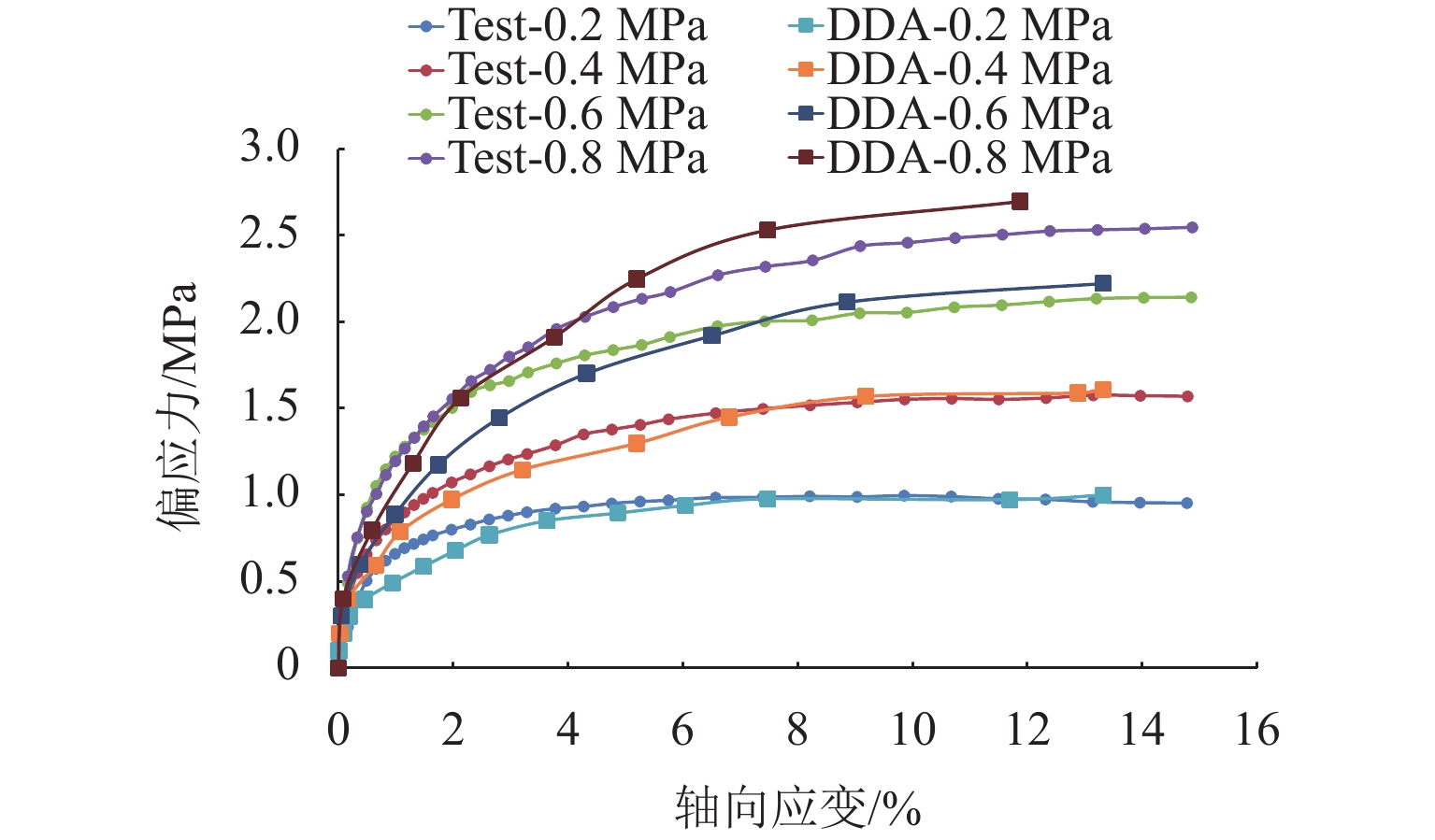
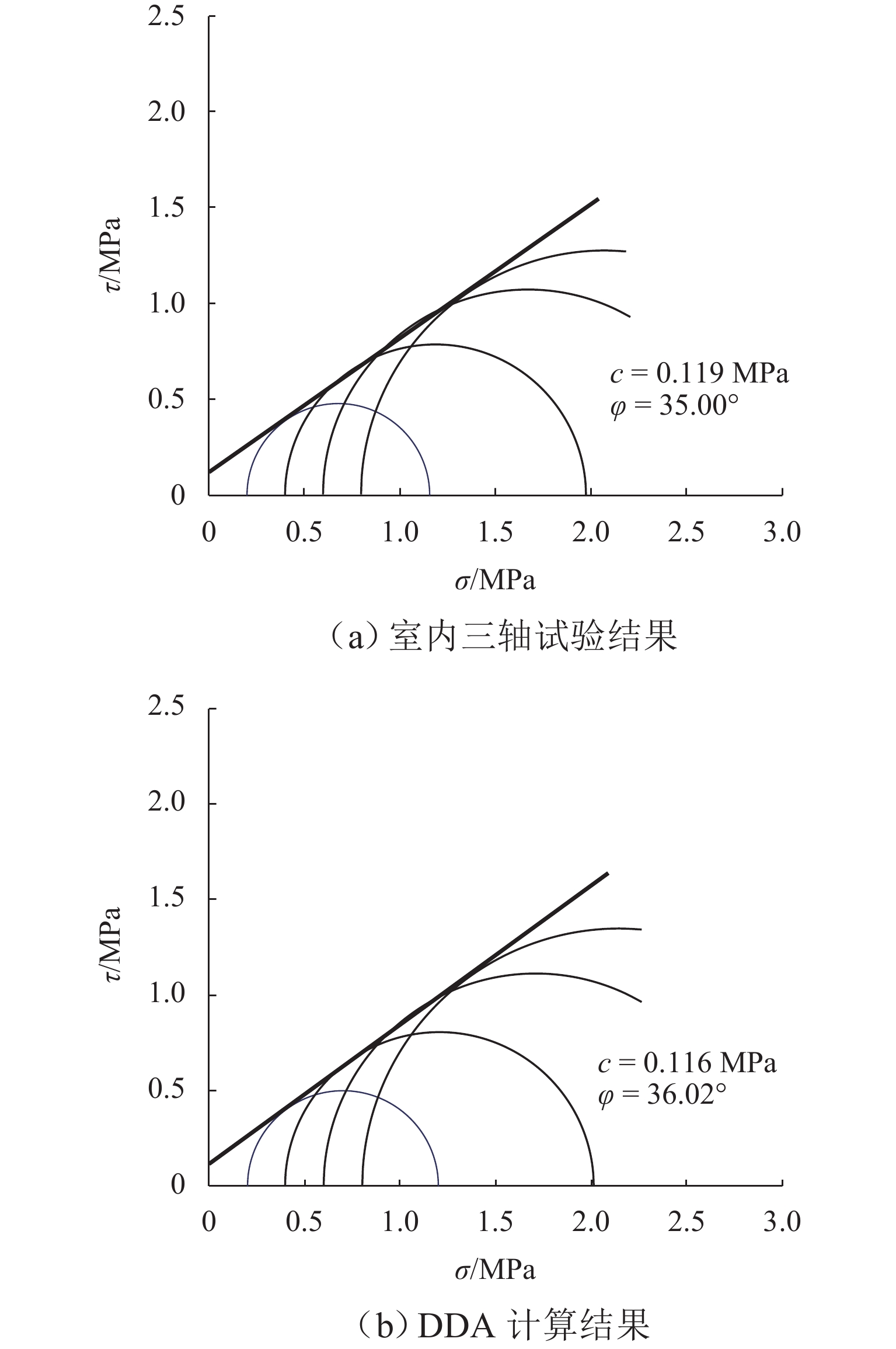
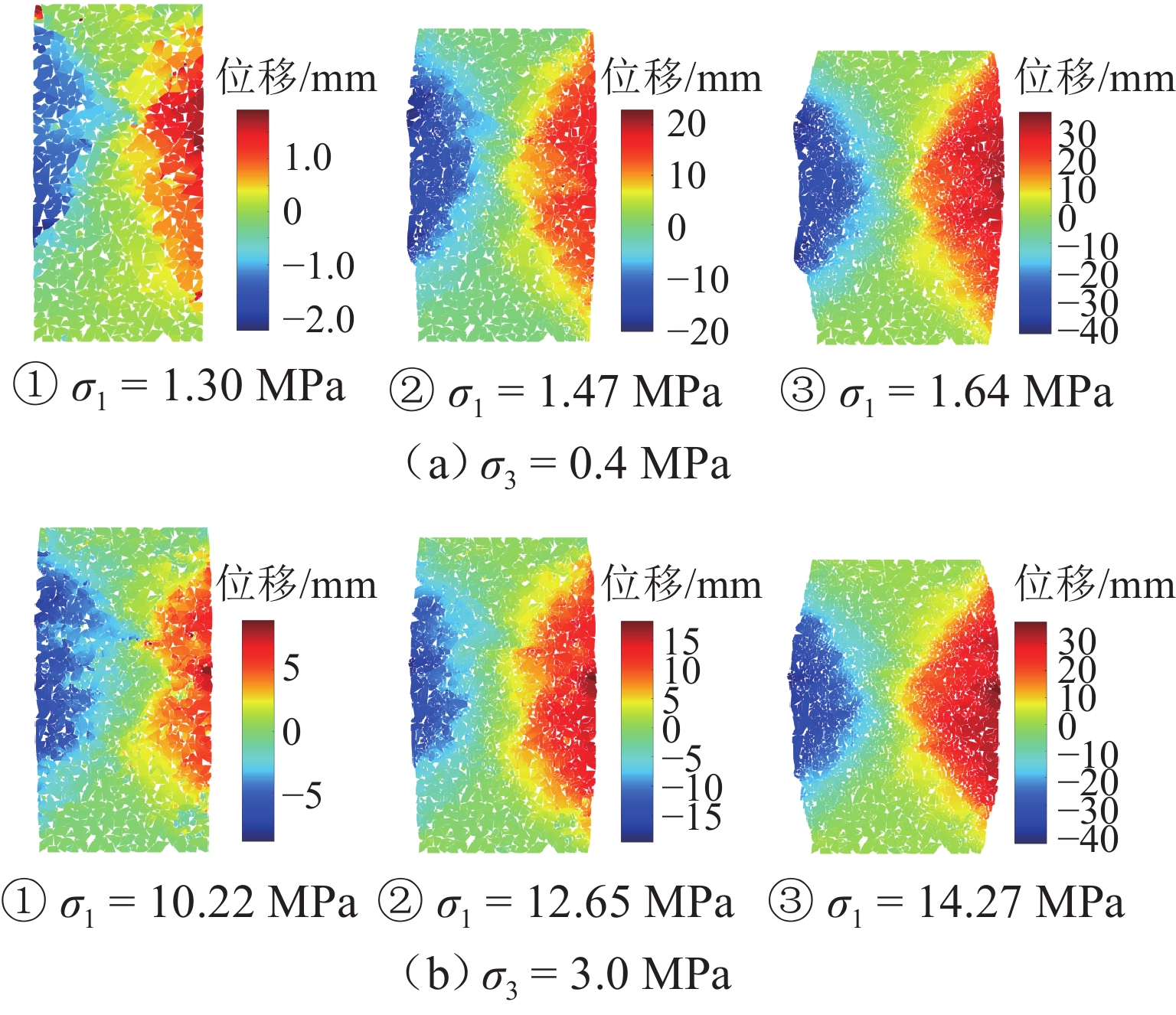
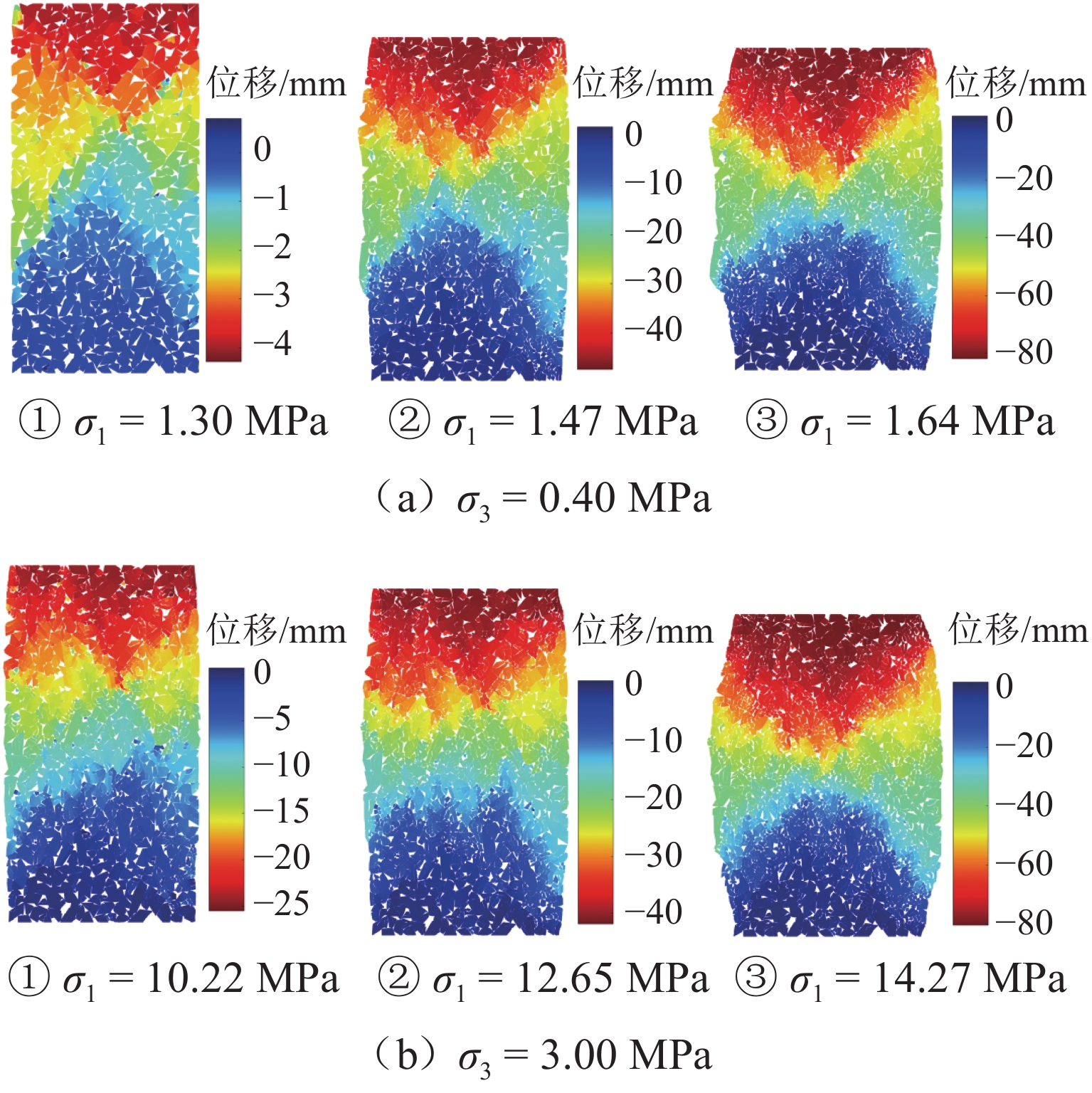
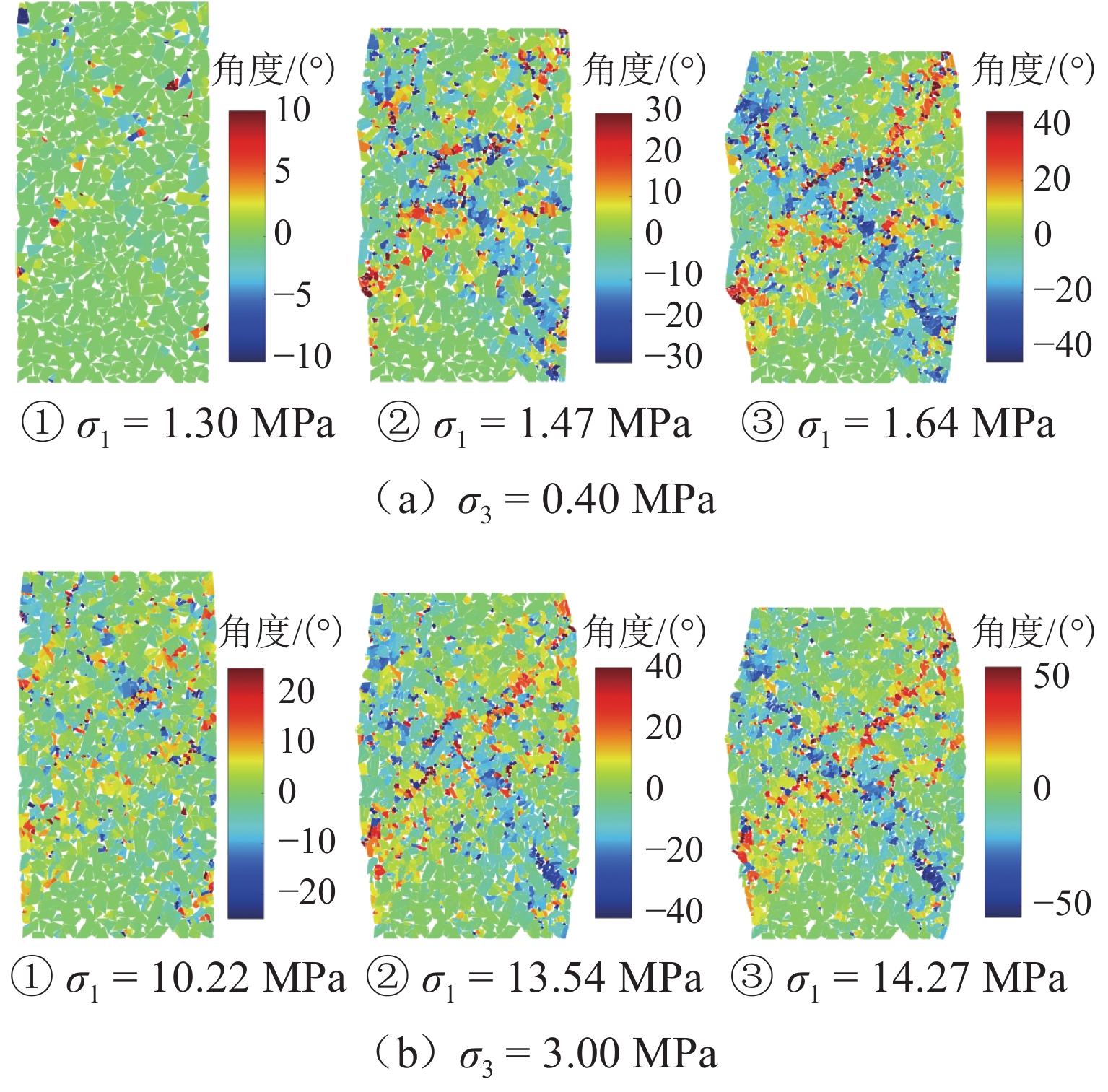
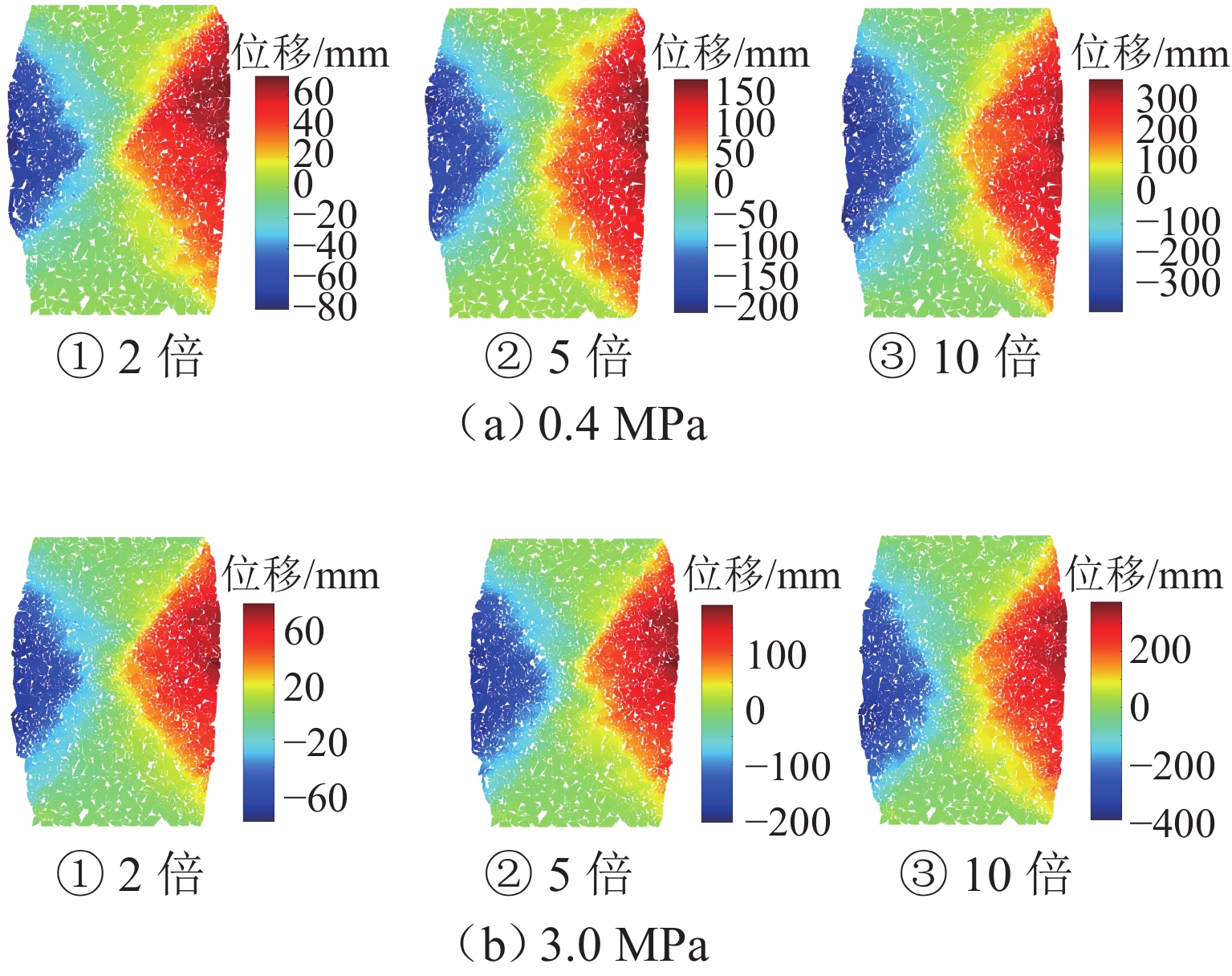
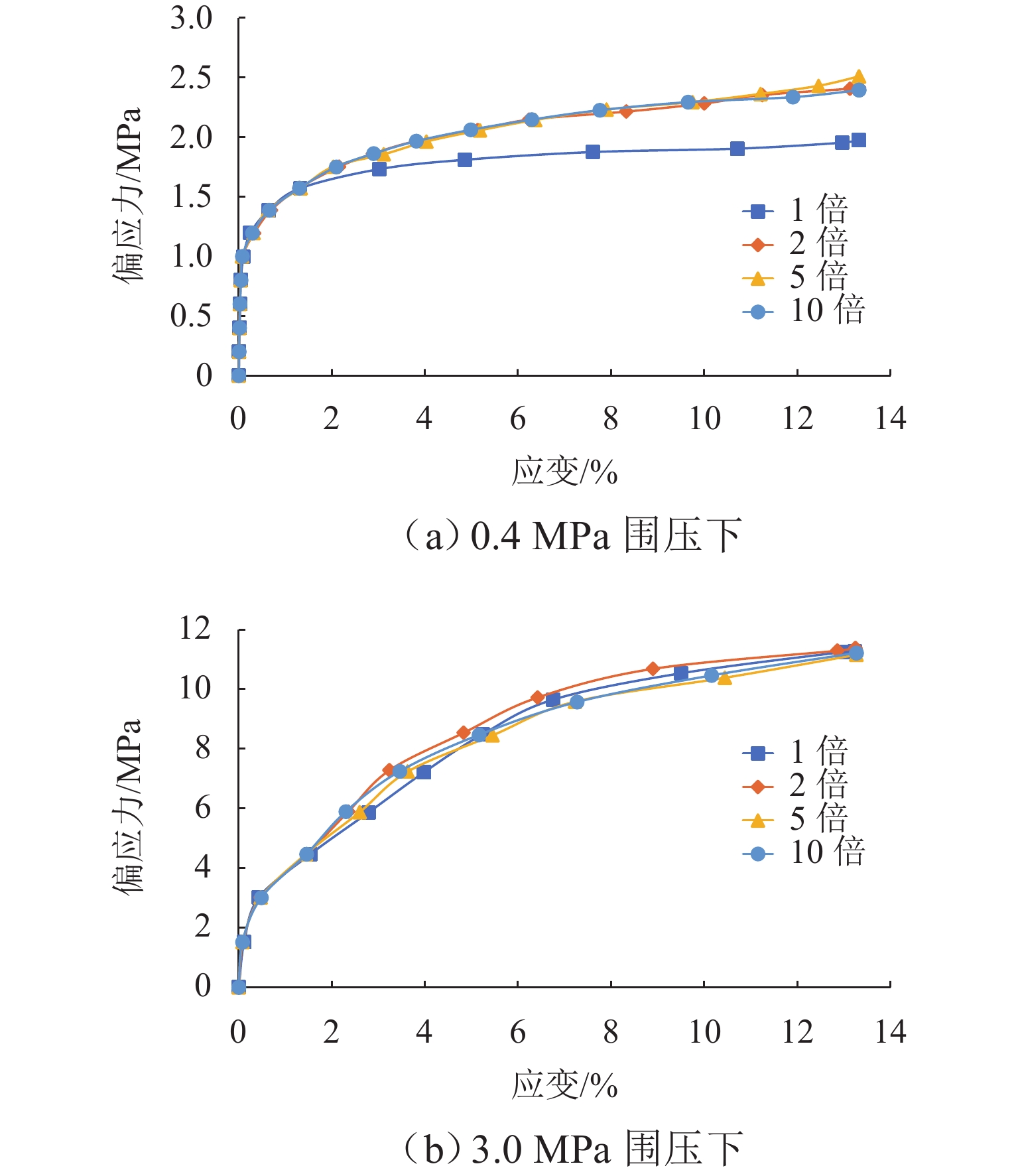
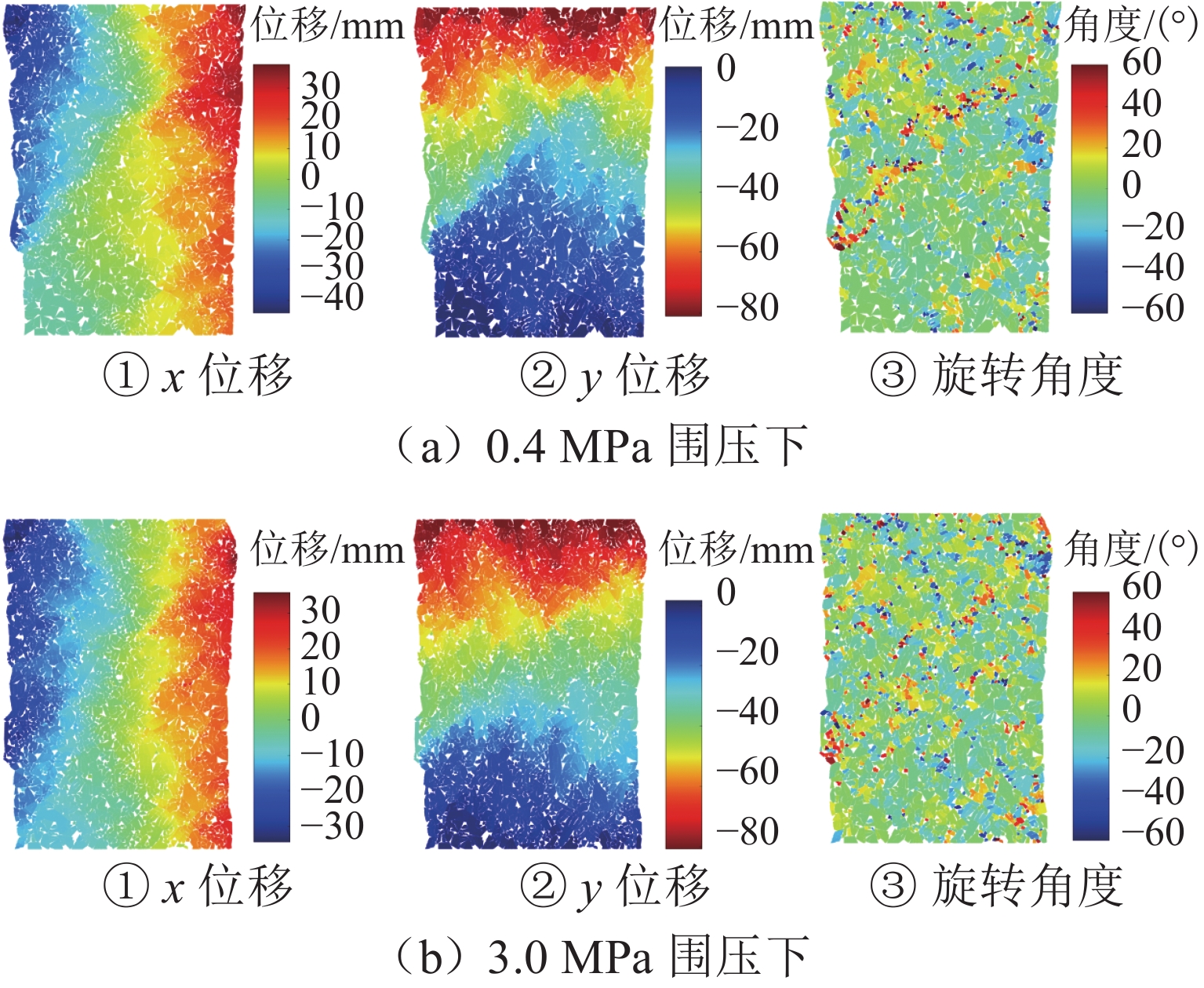
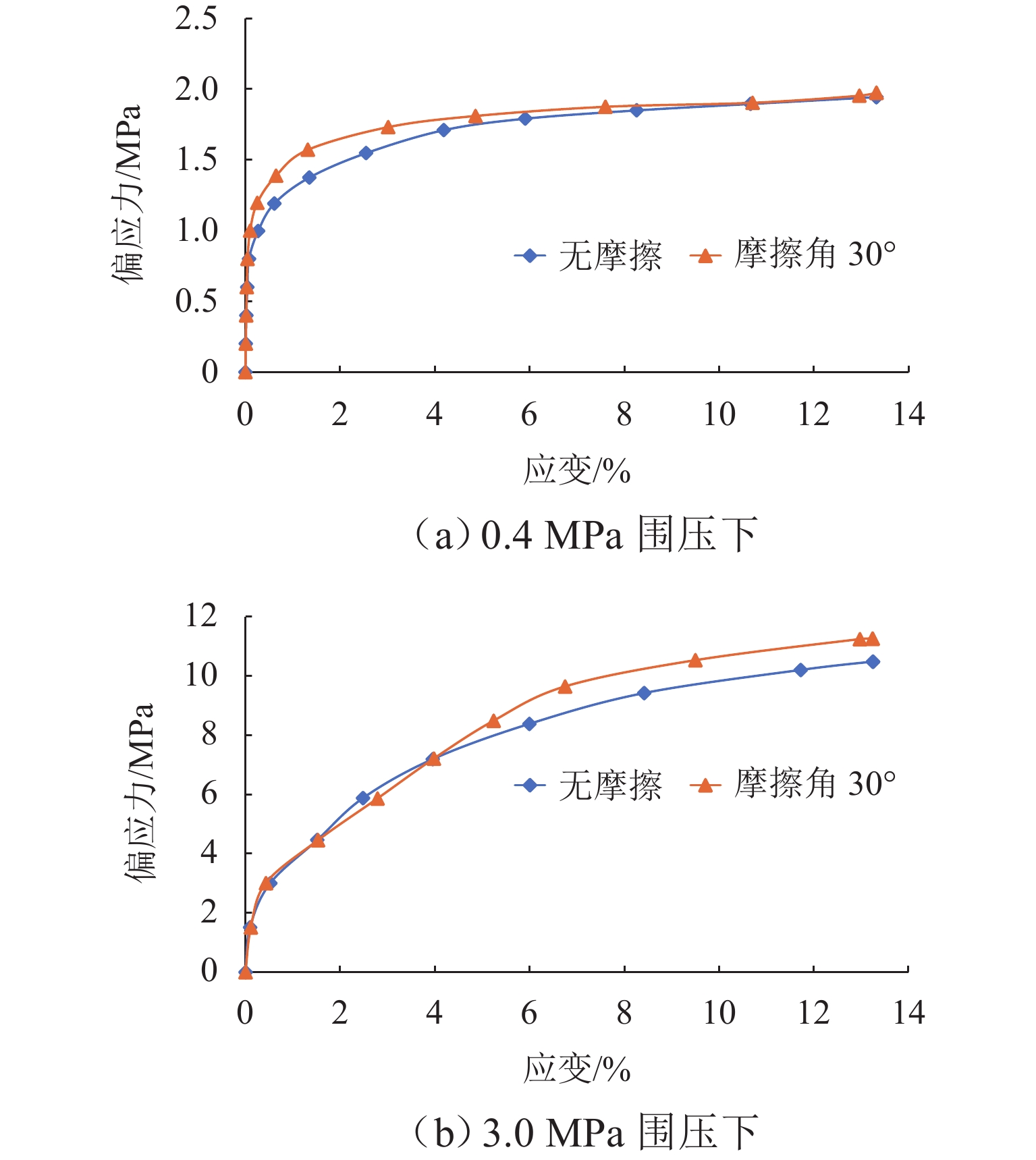
为系统揭示堆石坝粗粒料的细观力学机制和宏观力学响应机理，克服传统连续介质方法在力链演化与颗粒破碎模拟方面的局限性，发展了一种适用于粗粒料三轴试验的连续-非连续变形分析方法. 该方法在传统非连续变形分析方法（DDA）基础上，引入混合位移模式以区分不同块体的力学响应；采用临界阻尼加速计算收敛，并提出新的连续-非连续模拟技术以刻画颗粒破碎过程；通过常规三轴数值试验系统分析粗粒料在加载过程中的变形演化、力链发展、颗粒破碎及剪切带形成等力学行为，重点探讨尺寸效应与端部摩阻力的影响. 结果表明：该方法模拟结果与试验数据结果吻合良好，能够有效反映粗粒料的宏观力学响应与细观机制；围压0.4 MPa时，尺寸效应可使峰值应力提高21.3%，而在3.0 MPa高围压下对峰值应力影响不显著；端部摩阻力在3.0 MPa围压下可使峰值应力提升约7.4%. 研究成果为深入理解粗粒料力学特性提供了有效的数值分析手段.
Abstract:To investigate the mechanical meso-mechanism and macroscopic response of coarse granular materials in rockfill dams, and to overcome the limitations of traditional continuum-based methods in simulating force chain evolution and particle breakage, a continuous-discontinuous deformation analysis method suitable for triaxial tests on coarse granular materials was developed. This method, based on the traditional discontinuous deformation analysis (DDA) framework, introduced a hybrid displacement mode to differentiate the mechanical responses of various blocks. Critical damping was employed to accelerate computational convergence, and a continuous-discontinuous simulation technique was proposed to characterize particle breakage. Through conventional triaxial numerical simulations, the deformation evolution, force chain development, particle breakage, and shear band formation during loading were analyzed, with particular emphasis on the effects of size and end friction. The results indicate that the simulation outcomes agree well with experimental data, reflecting both the macroscopic mechanical response and meso-mechanisms of coarse granular materials. The size effect leads to a 21.3% increase in peak stress under 0.4 MPa confining pressure, whereas its influence becomes negligible at 3.0 MPa. Under 3.0 MPa confining pressure, end friction contributes to an approximately 7.4% increase in peak stress. This study provides an effective numerical tool for further understanding the mechanical properties of coarse granular materials.
-
图 5 DDA与室内三轴试验的偏应力-应变曲线对比
Figure 5. Comparison of deviatoric stress–strain curves between DDA and laboratory triaxial tests
图 9 粗粒料颗粒旋转角度演化过程
Figure 9. Evolution of particle rotation angles of coarse granular materials
图 10 不同围压下粗粒料力链演化过程
Figure 10. Evolution of force chains of coarse granular materials under varying confining pressure
图 12 不同围压下试样x方向位移云图
Figure 12. x-displacement of samples under varying confining pressure
-
[1] 程展林, 丁红顺. 堆石料蠕变特性试验研究[J]. 岩土工程学报, 2004, 26(4): 473-476. doi: 10.11988/ckyyb.20221305CHENG Zhanlin, DING Hongshun. Creep test for rockfill[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(4): 473-476. doi: 10.11988/ckyyb.20221305 [2] CUNDALL P A, HART R D. Numerical modeling of discontinua[M]//Analysis and Design Methods. Amsterdam: Elsevier, 1993: 231-243. [3] TAVAREZ F A, PLESHA M E. Discrete element method for modelling solid and particulate materials[J]. International Journal for Numerical Methods in Engineering, 2007, 70(4): 379-404. doi: 10.1002/nme.1881 [4] XU M, HONG J T, SONG E X. DEM study on the effect of particle breakage on the macro- and micro-behavior of rockfill sheared along different stress paths[J]. Computers and Geotechnics, 2017, 89: 113-127. doi: 10.1016/j.compgeo.2017.04.012 [5] MANSO J, MARCELINO J, CALDEIRA L. Crushing and oedometer compression of rockfill using DEM[J]. Computers and Geotechnics, 2018, 101: 11-22. doi: 10.1016/j.compgeo.2018.04.009 [6] ZHAO Z H, SONG E X. Particle mechanics modeling of creep behavior of rockfill materials under dry and wet conditions[J]. Computers and Geotechnics, 2015, 68: 137-146. doi: 10.1016/j.compgeo.2015.04.008 [7] SHAO X Q, CHI S C, TAO Y, et al. DEM simulation of the size effect on the wetting deformation of rockfill materials based on single-particle crushing tests[J]. Computers and Geotechnics, 2020, 123: 103429. doi: 10.1016/j.compgeo.2019.103429 [8] MA C H, YANG J, ZENZ G, et al. Calibration of the microparameters of the discrete element method using a relevance vector machine and its application to rockfill materials[J]. Advances in Engineering Software, 2020, 147: 102833. doi: 10.1016/j.advengsoft.2020.102833 [9] 杨冰, 杨军, 常在, 等. 土石混合体压缩性的三维颗粒力学研究[J]. 岩土力学, 2010, 31(5): 1645-1650.YANG Bing, YANG Jun, CHANG Zai, et al. 3-D granular simulation for compressibility of soil-aggregate mixture[J]. Rock and Soil Mechanics, 2010, 31(5): 1645-1650. [10] MUNJIZA A, JOHN N W M. Mesh size sensitivity of the combined FEM/DEM fracture and fragmentation algorithms[J]. Engineering Fracture Mechanics, 2002, 69(2): 281-295. doi: 10.1016/S0013-7944(01)00090-X [11] LISJAK A, TATONE B S A, GRASSELLI G, et al. Numerical modelling of the anisotropic mechanical behaviour of opalinus clay at the laboratory-scale using FEM/DEM[J]. Rock Mechanics and Rock Engineering, 2014, 47(1): 187-206. doi: 10.1007/s00603-012-0354-7 [12] MAHABADI O K, COTTRELL B E, GRASSELLI G. An example of realistic modelling of rock dynamics problems: FEM/DEM simulation of dynamic Brazilian test on barre granite[J]. Rock Mechanics and Rock Engineering, 2010, 43(6): 707-716. doi: 10.1007/s00603-010-0092-7 [13] ZHOU W, MA G, CHANG X L, et al. Discrete modeling of rockfill materials considering the irregular shaped particles and their crushability[J]. Engineering Computations, 2015, 32(4): 1104-1120. doi: 10.1108/EC-04-2014-0086 [14] MA G, ZHOU W, CHANG X L. Modeling the particle breakage of rockfill materials with the cohesive crack model[J]. Computers and Geotechnics, 2014, 61: 132-143. doi: 10.1016/j.compgeo.2014.05.006 [15] MA G, ZHOU W, CHANG X L, et al. Combined FEM/DEM modeling of triaxial compression tests for rockfills with polyhedral particles[J]. International Journal of Geomechanics, 2014, 14(4): 04014014. doi: 10.1061/(ASCE)GM.1943-5622.0000372 [16] 严成增, 郑宏, 孙冠华, 等. 粗粒料多边形表征及二维FEM/DEM分析[J]. 岩土力学, 2015, 36(增2): 95-103. doi: 10.16285/j.rsm.2015.S2.012YAN Chengzeng, ZHENG Hong, SUN Guanhua, et al. Polygon characterization of coarse aggregate and two-dimensional combined finite discrete element method analysis[J]. Rock and Soil Mechanics, 2015, 36(S2): 95-103. doi: 10.16285/j.rsm.2015.S2.012 [17] 郭培玺, 林绍忠. 粗粒料颗粒随机分布的数值模拟[J]. 长江科学院院报, 2007, 24(4): 50-52, 56.GUO Peixi, LIN Shaozhong. Numerical simulation on random distribution of coarse granular material particles[J]. Journal of Yangtze River Scientific Research Institute, 2007, 24(4): 50-52,56. [18] 郭培玺. 基于DDA的粗粒料力学特性研究[D]. 南京: 河海大学, 2016. [19] 苏明. 考虑颗粒破碎的粗粒料力学特性数值试验初步研究[D]. 武汉: 长江科学院, 2014. [20] SHI G H, GOODMAN R E. Two dimensional discontinuous deformation analysis[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1985, 9(6): 541-556. doi: 10.1002/nag.1610090604 [21] 美)石根华著, 裴觉民译. 数值流形方法与非连续变形分析[M]. 北京: 清华大学出版社, 1997. [22] LIN S Z, XIE Z Q. Performance of DDA time integration[J]. Science China Technological Sciences, 2015, 58(9): 1558-1566. doi: 10.1007/s11431-015-5893-1 [23] CHAGRA W. Accurate calculation of the settling time of a linear system using new expressions and iterative algorithms[J]. Circuits, Systems, and Signal Processing, 2018, 37(1): 408-431. doi: 10.1007/s00034-017-0560-3 -
下载:
点击查看大图
计量
- 文章访问数: 19
- HTML全文浏览量: 16
- PDF下载量: 3
- 被引次数: 0