考虑相移补偿的磁浮列车长定子高频信号注入无传感控制方法

张雯柏; 林国斌; 康劲松; 赵元哲; 廖志明

doi:10.3969/j.issn.0258-2724.20240310

考虑相移补偿的磁浮列车长定子高频信号注入无传感控制方法

doi: 10.3969/j.issn.0258-2724.20240310

张雯柏^{1, 2, 3,},
林国斌^{2, 3},
康劲松^{1, 3},
赵元哲^{1, 2, 3, ,},
廖志明^{2, 3}

1.
同济大学铁道与城市轨道交通研究院，上海 201804
2.
同济大学国家磁浮交通工程技术研究中心，上海 201804
3.
同济大学磁浮技术铁路行业重点实验室上海 201804

基金项目: 国家自然科学基金项目（52202449，52232013）；高速磁浮运载技术全国重点实验室开放基金（SKLM-SFCF-2023-010）

详细信息

作者简介:
张雯柏（1990—），男，博士研究生，研究方向为高速磁浮磁驱控制系统，E-mail：zhangwenbai@tongji.edu.cn

通讯作者:
赵元哲（1987—），男，讲师，博士，研究方向为高速磁浮磁驱控制系统与电能质量分析，E-mail：yuanzhezhao@tongji.edu.cn

中图分类号: TM359.4
计量
- 文章访问数: 52
- HTML全文浏览量: 21
- PDF下载量: 11
- 被引次数: 0
出版历程
- 收稿日期: 2024-06-27
- 修回日期: 2024-10-29
- 网络出版日期: 2025-03-08

Sensorless Control Method of High-Frequency Signal Injection for Long-Stator Synchronous Motor of Maglev Trains Considering Phase Shift Compensation

ZHANG Wenbai^{1, 2, 3
,},
LIN Guobin^{2, 3},
KANG Jinsong^{1, 3},
ZHAO Yuanzhe^{1, 2, 3
, ,},
LIAO Zhiming^{2, 3}

1.
Institute of Rail Transit, Tongji University, Shanghai 201804, China
2.
National Maglev Transportation Engineering R & D Center, Tongji University, Shanghai 201804, China
3.
Key Laboratory of Maglev Technology in Railway Industry, Shanghai 201804, China

摘要

摘要:
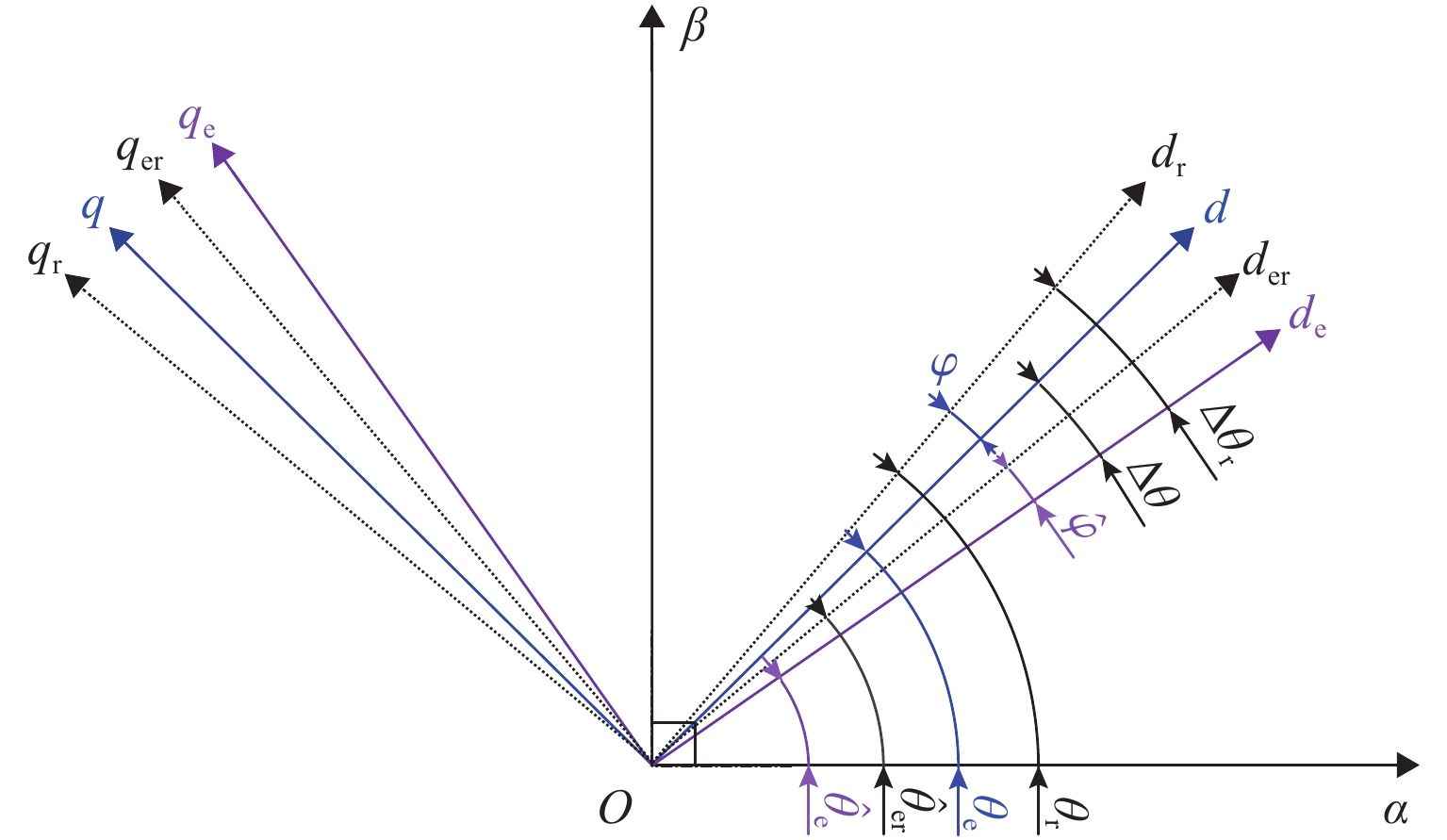
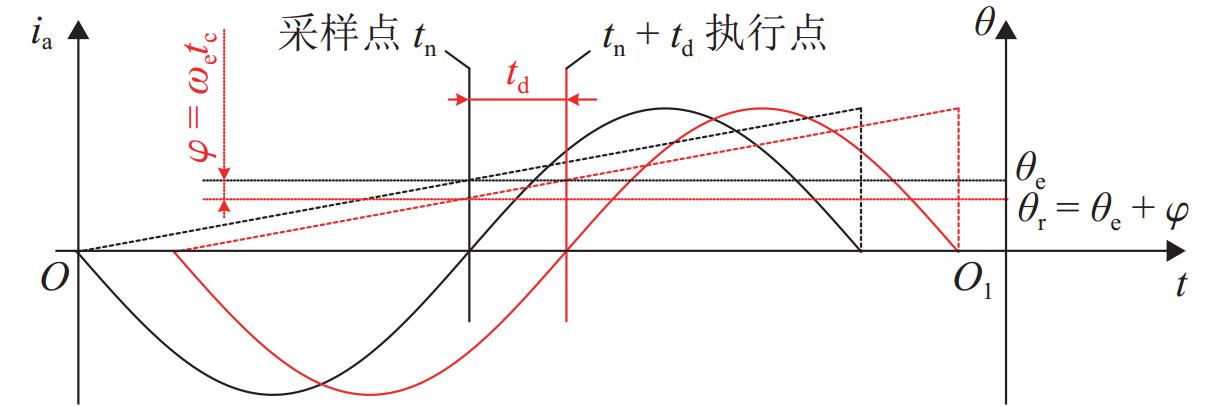
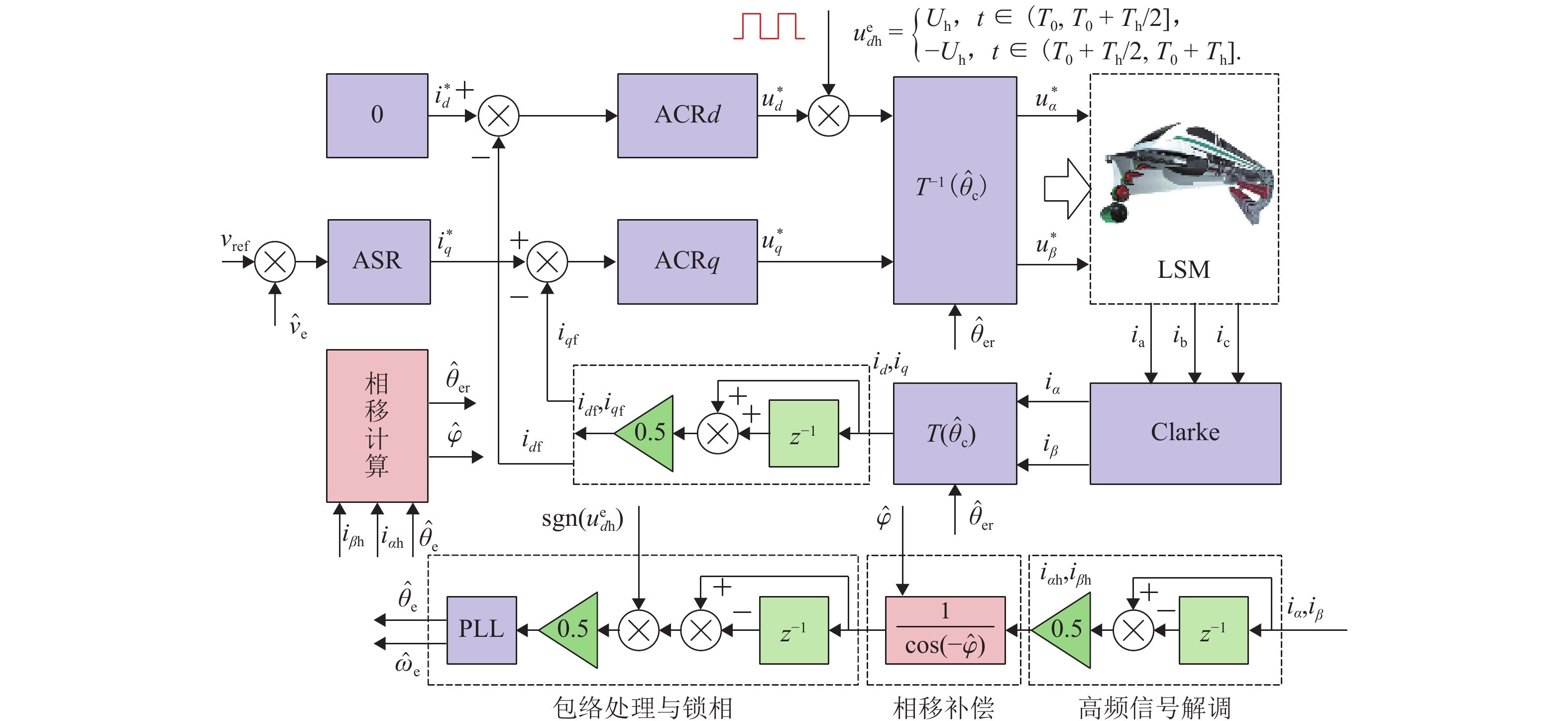
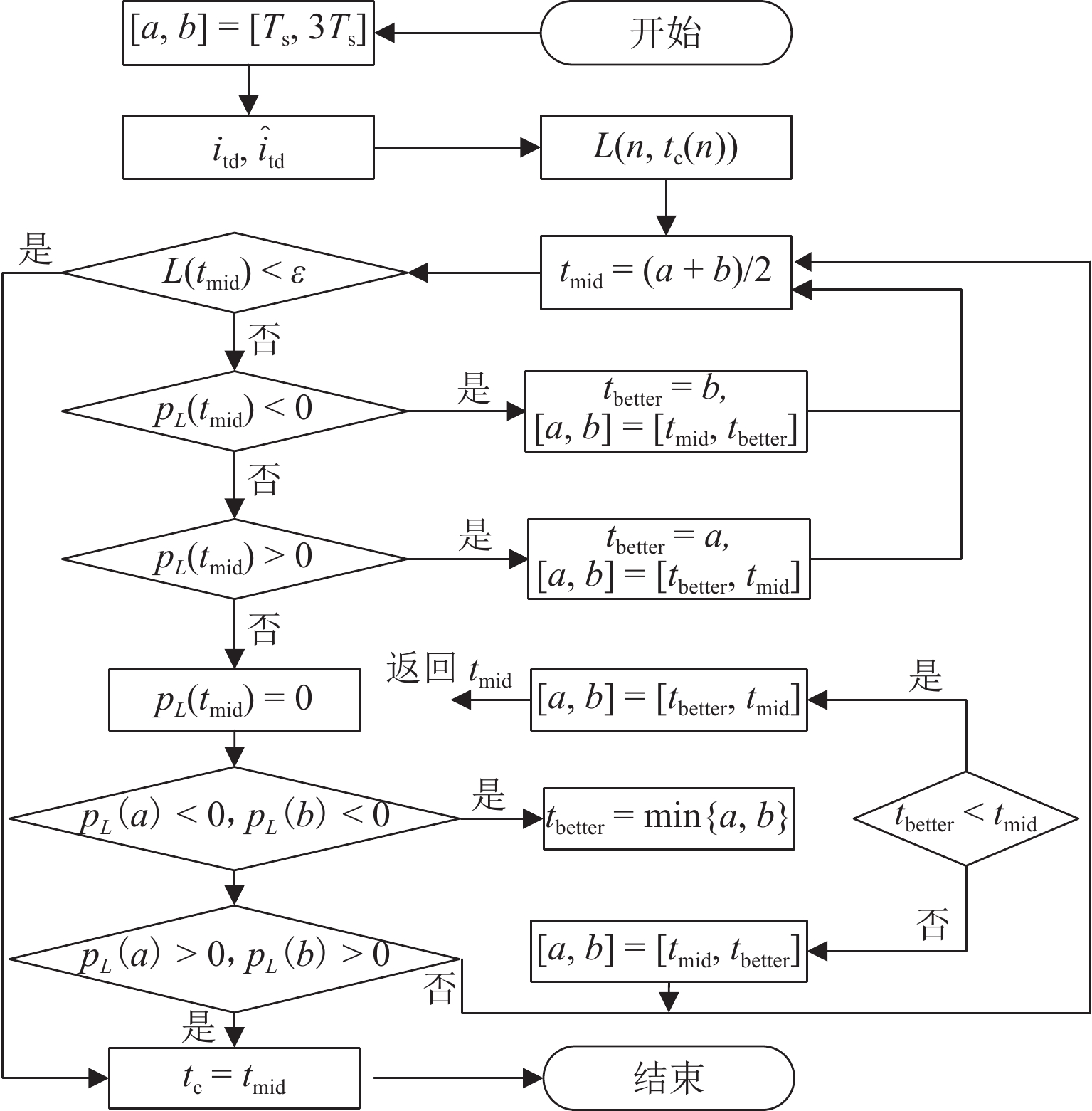
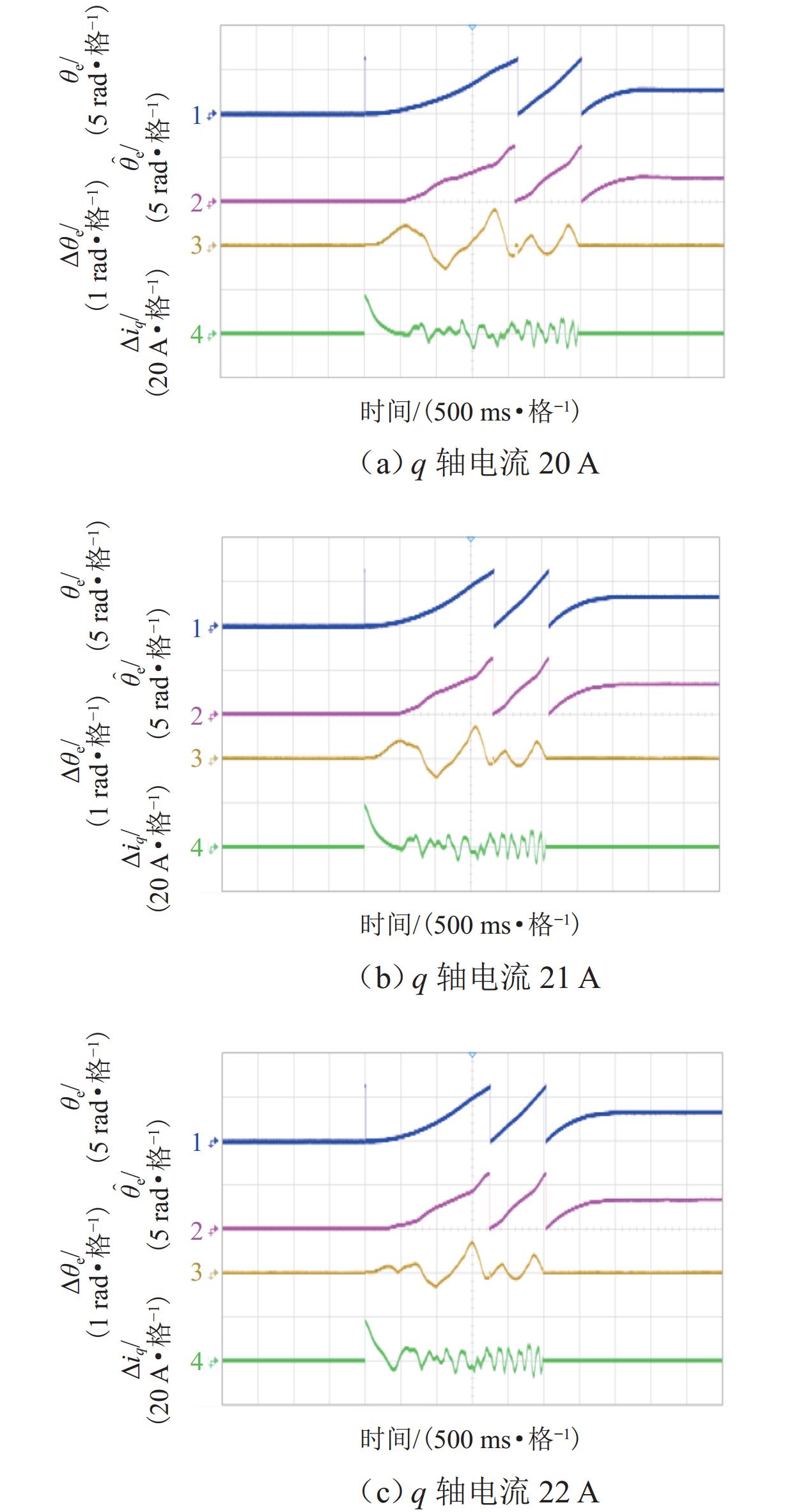
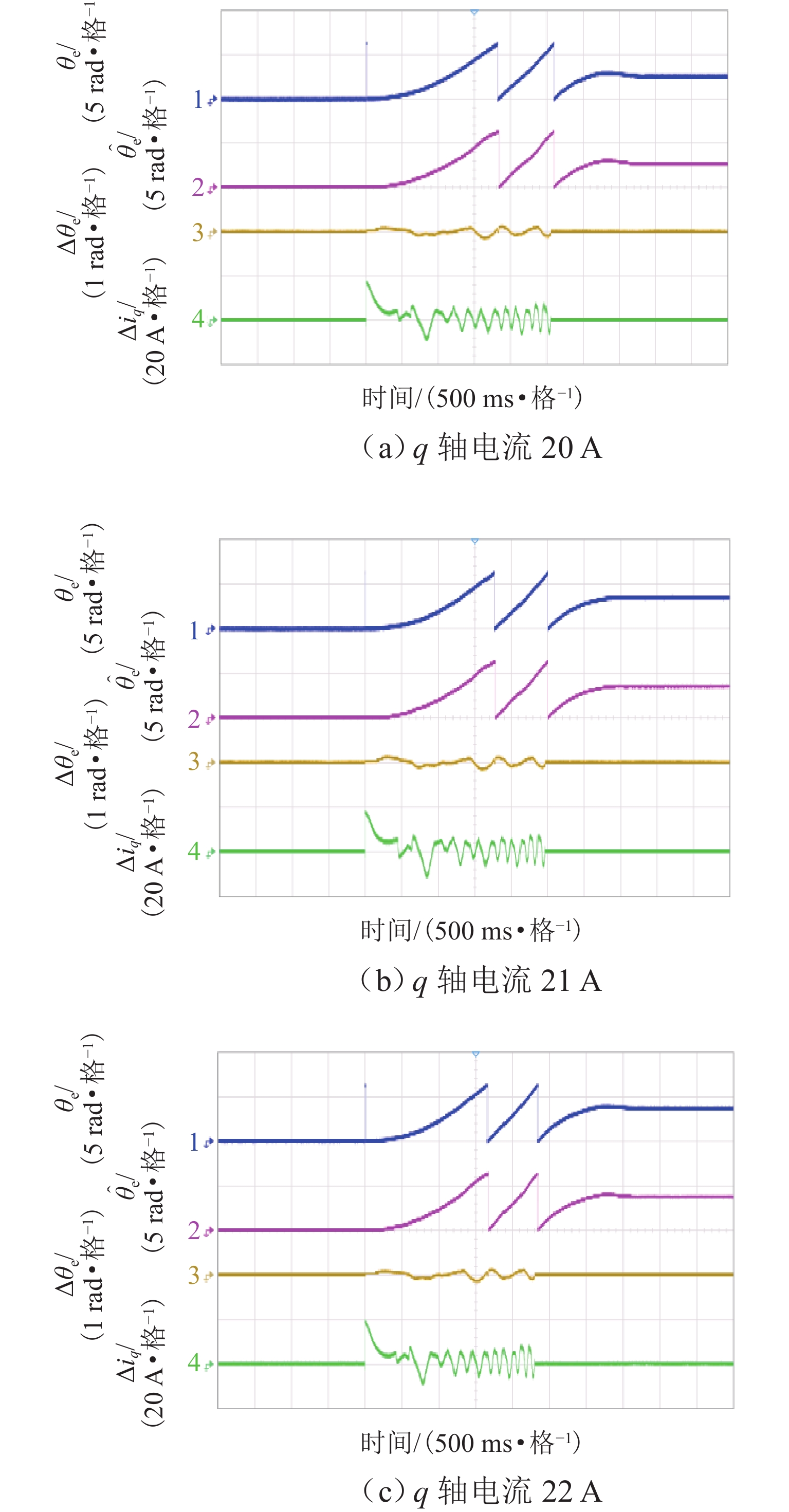
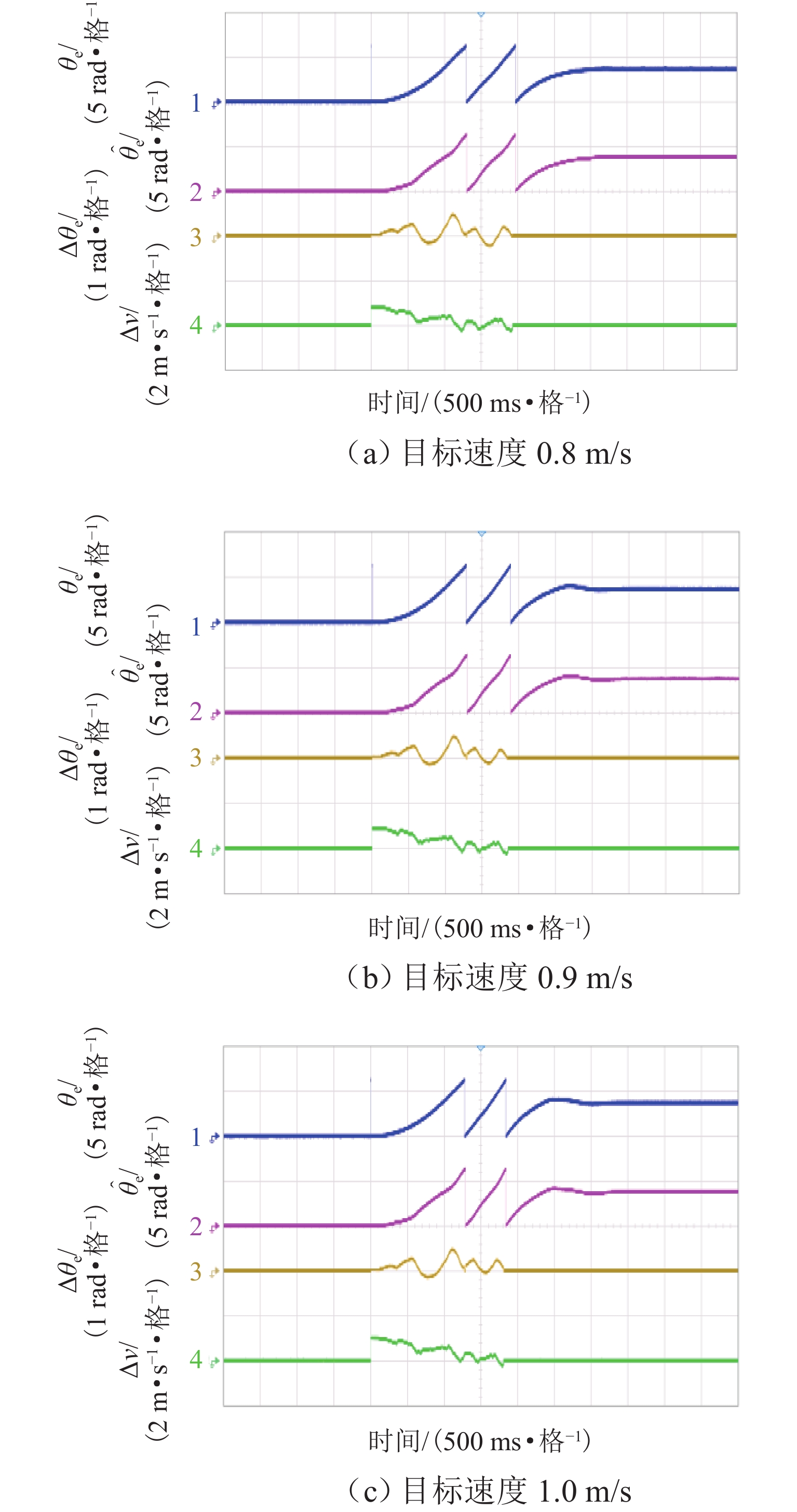
为研究高频注入响应电角度相移对磁浮列车低速控制精度的影响，考虑控制延时与采样延时对角度偏差滞后的约束关系，提出一种无传感估计角度偏差最小化寻优的补偿方法. 首先，建立高速磁浮长定子同步电机零低速高频方波信号注入模型，利用估计-实际-延时坐标系变换理论，构建高频响应电流模型；其次，通过分析大功率电传动系统中系统延时对角度偏差的影响，重构含估计角度相移偏差的高频响应电流模型；然后，设计离散化的估计角度偏差目标函数，提出采用考虑梯度变化的二分法在线计算系统延时与角度偏差；最后，通过磁浮电机低速试验平台验证算法. 试验结果表明：本文提出的考虑相移滞后补偿方法与未经补偿的无传感控制相比，当给定电流为20、21、22 A时，估计角度误差分别减小73.3%，70.4%和72.1%；当速度环给定速度为0.8、0.9、1 m/s时，估计角度误差分别减小67.9%、70.5%、75.5%，速度跟踪误差平均减小50%.
- 磁浮列车 /
- 长定子电机 /
- 高频注入 /
- 无感控制 /
- 角度补偿
Abstract:
In order to study the influence of high-frequency signal injection (HFSI) response to electrical angle phase shift on the low-speed control accuracy of maglev trains, the constraint relationship between the control delay and the sampling delay on the angular error lag was considered, and a compensation method for minimizing the angle error of sensorless estimation was proposed. Firstly, a zero-low-speed HFSI model for long-stator synchronous motor (LSM) of high-speed maglev trains was established, and a high-frequency response current model was constructed by using the estimation-real-delay coordinate transformation theory. Secondly, by analyzing the influence of system delay on angular error in a high-power electric drive system, the high-frequency response current model with estimated angular phase shift error was reconstructed. Then, the objective function for the discrete estimation of the angular error was designed, and the bisection method considering the gradient change was proposed to calculate system delay and angular error online. Finally, the algorithm was verified by the low-speed test platform of maglev motors. The experimental results show that compared with the uncompensated sensorless control, when the set current is 20 A, 21 A, and 22 A, the estimated angular error is decreased by 73.3%, 70.4%, and 72.1% by the proposed compensation method considering phase shift lag compensation. When the set speed is 0.8 m/s, 0.9 m/s, and 1 m/s, the estimated angular error is decreased by 67.9%, 70.5%, and 75.5%, and the speed tracking error is decreased by 50% on average.
- maglev train /
- long-stator motor /
- high-frequency signal injection (HFSI) /
- sensorless control /
- angle compensation

HTML全文

随着出行需求的不断增长和出行选择日渐向快捷、舒适方向发展，私家车或网约车使用率提高，造成交通拥堵^[1]，同时也导致公共交通特别是公交车的使用率逐渐下降. 因此，如何最大程度地发挥公共交通的优势，并满足各类灵活出行需求，是迫切需要深入研究的问题^[2-3].

公交车接驳大型轨道交通线路或站点不仅可以解决乘客的“最后一公里”问题，还能够维持公交车一定的运力. 在公交车接驳轨道交通时刻表编制方面，Wang等^[4]提出了一种公交接驳地铁发车时刻表和车辆调度一体化优化模型；窦雪萍等^[5]构建了公交接驳轨道交通时刻表并与车队规模联合的优化模型，以减少乘客排队等待出行成本与公交企业运营成本；Xiong等^[6]提出了关于社区班车与地铁服务协同优化的研究问题，使用遗传算法和Frank-Wolfe算法相结合的混合算法进行求解，得出最优同步调度方案；Liu等^[7]针对因轨道交通网络中断而导致大量乘客滞留的问题，构建了公交接驳轨道交通时刻表优化模型，并提出相关接运方案；Chen等^[8]为应对轨道交通中断问题，将快速和短途路线合并，提出时变需求下的公交桥接路线和时刻表综合优化框架.

由于地铁辐射范围越来越广，一些公交车线路因需求量变化导致改道或停运，还有少数公交车线路出于各方面原因与地铁线路保持较高程度的重合. 如果能够充分利用这部分公交车特性，在满足原有公交车出行需求的同时服务有短途出行需求的地铁乘客，无需开设新接驳线路，具有高效率低成本的特性. 可变线路公交（flex-route transit, FRT）^[9]的特点恰好可以满足上述需求，在与地铁重合的线路和站点中既能服务原有公交出行需求，又能在固定站点间改变线路，接送有短途出行需求的地铁乘客. 在可变线路公交时刻表编制方面，赵展轮^[10]结合可变线路式公交双重特性，构建车辆发车间隔模型和发车时间窗宽度确定方法；姚尹杰^[11]从发车时刻等方面对需求响应公交进行系统设计，综合考虑乘客上下车站点时空约束、车辆不可逆行约束等条件，构建了通道型需求响应公交时刻表与路径规划协同优化模型.

综上所述，由于可变线路公交基于乘客预约出行需求进行运行组织，因此运行方案设计需要与站点和线路同步调整. 目前针对可变线路公交运行周期、发车间隔和车辆配置与接驳站点、线路同步优化的研究相对较少，特别是考虑不同时空属性下的灵活出行特征（乘客类型及预约时空维度信息）和接驳站点处时间衔接的影响，因此有待进一步研究和探索. 乘客搭乘地铁和短途出行时会考虑地铁的到站、发车时间，以安排自己的出行计划. 为有效提供接驳服务，需要将可变线路公交与地铁的运营组织方案相配合. 目前，国内大部分城市的公交行车计划仍然依靠人工编制^[12]，因此需要在考虑运营需求的前提下，提出一种智能化公交行车计划编制方法.

1. 时刻表编制模型与方法

针对接驳地铁站点“最后一公里”出行需求，本研究建立了可变线路公交协同地铁运行时刻表编制模型，编制最优化的可变线路公交时刻表，以高效完成接驳服务，提高公交系统服务水平.

1.1 发车时间间隔

由于可变线路公交具有服务合乘的特点和车辆运行不确定性，既要考虑固定站点的发车间隔和发车时刻，也要考虑站点间灵活接送乘客时的松弛服务时间，因此，传统固定线路公交时刻表编制方式^[13-14]和发车频率计算方法^[15]并不完全适用于服务灵活出行需求的接驳可变线路公交. 本节提出了一种基于地铁时刻表、乘客预约需求和发车时间窗约束的可变线路公交车接驳地铁发车时间间隔计算方法.

在长（L）*宽（W）服务区域内存在I类乘客：地铁站出站（O）、站外/线外到达需求点（D）和II类乘客：站外/线外出发需求点（O）、地铁站进站（D），如图1所示，现存的常规公交转变成可变线路公交，完成乘客在站点和基准线外之间的需求的接驳服务.

图 1 可变线路公交接驳地铁短途出行乘客示意图

Figure 1. Schematic of FRT picking up/dropping off urban rail transit short-distance passengers

下载: 全尺寸图片幻灯片

地铁换乘接驳可变线路公交和接驳可变线路公交换乘地铁2种情况，最佳换乘的情况分别为：地铁换乘接驳可变线路公交的乘客抵达公交站台时，可变线路公交车辆恰好在站；接驳可变线路公交换乘地铁的乘客到达地铁站台时，地铁恰好在站，具体换乘过程用时空图表示，如图2所示. 图中：R_Ta、R_Td分别为地铁到站和发车时间；ε为乘客进出地铁站换乘所需时间，min；t_p、t_d分别为上、下可变线路公交时刻；t_a,k、t_b,k分别为可变线路公交班次k在固定站点的到达、发车时间；P_p,k、P_d,k分别为可变线路公交班次k理想时在固定站点接上、送达乘客时刻；K为接驳可变线路公交车辆发车次数集合，k∈K.

图 2 地铁与接驳可变线路公交换乘时空图

Figure 2. Transfer time-space of urban rail transit and feeder FRT

下载: 全尺寸图片幻灯片

左侧乘客从地铁换乘可变线路公交时，需要在R_Ta时刻完成下车，经过换乘时间ε在t_p时刻（t_b,k时刻前）到达接驳站公交点. 右侧乘客自可变线路公交换乘地铁需要在t_d时刻或之前到接驳站，经过换乘时间ε在R_Td时刻或之前到达地铁站点进行换乘.

乘客从地铁换乘可变线路公交时如果过早到达公交站，需要等待一定时间才能被服务；若乘客晚到公交站点，若上一班次被安排服务该乘客，车辆需等待乘客到达站点后接上乘客再发车，这一延误同样也记为等待时间成本. 乘客从可变线路公交换乘地铁时如果早到换乘地铁站则不记为延误；若实际到达时刻晚于预计到达时刻则乘客只能乘坐下一班次地铁，这一晚到延误记为晚到时间成本.

1.1.1 目标函数

接驳地铁可变线路公交时刻表编制模型的目标函数为系统成本U最小化，如式（1）所示.

$\text{min}U={\lambda }_{1}{U}_{{\mathrm{W}}} + {\lambda }_{2}{U}_{{\mathrm{L}}} + {\lambda }_{3}{U}_{{\mathrm{F}}} + {\lambda }_{4}{U}_{{\mathrm{O}}},$

(1)

式中：系统成本包括乘客/可变线路公交车辆等待时间成本U_W、乘客乘坐可变线路公交晚到时间成本U_L、换乘失败成本U_F和企业运营成本U_O，λ₁、λ₂、λ₃和λ₄为权重系数.

等待时间涉及车辆发车间隔和排班，故定义为式（2）；晚到时间成本根据上述规则定义为式（3）；换乘过程中换乘失败成本与换乘失败乘客人数有关，见式（4）；企业运营成本取决于车辆班次的运行时间成本，见式（5）.

${U}_{{\mathrm{W}}}={\theta }_{{\mathrm{W}}}{\sum }_{q\in {Q}_{\mathrm{I}}}{\sum }_{k\in K}{y}_{q,k}\left|{P}_{{\mathrm{p}},q,k}-{t}_{{\mathrm{p}},q}\right|,$

(2)

${U}_{{\mathrm{L}}}=\left\{\begin{array}{l}0,\quad{P}_{{\mathrm{d}},q,k}\leqslant {t}_{{\mathrm{d}},q},\\ {\theta }_{{\mathrm{L}}}{\displaystyle\sum }_{q\in {Q}_{\text{II}}}{\displaystyle\sum }_{k\in K}{y}_{q,k}({P}_{{\mathrm{d}},q,k}-{t}_{{\mathrm{d}},q}),\quad{P}_{{\mathrm{d}},q,k} > {t}_{{\mathrm{d}},q},\end{array}\right.$

(3)

${U}_{{\mathrm{F}}}={\theta }_{{\mathrm{F}}}({q}_{\mathrm{m}}-{\sum }_{k\in K}{q}_{k}),$

(4)

${U}_{{\mathrm{O}}}={\theta }_{{\mathrm{O}}}{\sum }_{\alpha \in S}{\sum }_{\beta \in S}{\sum }_{k\in K}{x}_{\alpha \beta ,k}{d}_{\alpha \beta ,k}/v ,$

(5)

式中：θ_W为地铁换乘可变线路公交的乘客或可变线路公交车辆在公交站的等待时间成本单位值，元/min；θ_L为可变线路公交换乘地铁的乘客乘坐车辆晚到公交站的时间成本单位值，元/min；θ_F为换乘失败（乘客未被服务）成本的单位转换值（人数转换为时间成本），元/min；θ_O为车辆/企业运营成本的单位值，元/min；Q_I、Q_II分别为I、II类乘客的集合；Q为所有乘客（需求）集合，Q=Q_I∪Q_II，q∈Q，q_m为服务区域内总乘客数量；q_k为实际乘坐可变线路公交班次k的乘客数量；R_C为研究区域内接驳站的集合，R_C={r₁, r₂,…, r_n}，r_n为研究区域内接驳站的数量；R_N为接驳可变线路公交车辆需要经过的临时站点（灵活需求点）集合；S为所有站点的集合，S = R_C∪R_N；P_p,q,k、P_d,q,k分别为可变线路公交班次k接上、送达乘客q的时间；t_p,q为地铁换乘可变线路公交的乘客q到达公交车站的时间；t_d,q为可变线路公交换乘地铁的乘客q预定到达公交车站的时间； d_αβ,k为可变线路公交班次k行驶自站点α至站点β的Manhattan距离，km；v为可变线路公交车辆行驶速度，千米/小时；x_αβ,k为0-1变量，可变线路公交班次k经过弧（α, β）时取1，否则取0；y_q,k为0-1变量，乘客q乘坐可变线路公交班次k时取1，否则取0.

1.1.2 约束条件

式（6）和式（7）表示班次k在运行过程中都必须从可变线路公交首站（第1个接驳站）出发，最后到达末站（最后1个接驳站），同时，站点最多只能被访问一次，即被访问的站点只能有一次到达和一次出发.

$\sum _{\alpha \in S}{x}_{\alpha \beta ,k}=1,\quad\forall \beta \in S\backslash \left\{{r}_{1}\right\},\; k\in K,$

(6)

$\sum _{\beta \in S}{x}_{\alpha \beta ,k}=1,\quad \forall \alpha \in S\backslash \left\{{r}_{\mathrm{n}}\right\},\; k\in K.$

(7)

式（8）表示当x_αβ,k= 1时，班次k车辆到达站点β的时间将不早于从站点α出发的时间加上两站之间的行驶时间，当x_αβ,k = 0时，此约束无效.

$\begin{split} &{t}_{{\mathrm{a}},\beta ,k}\geqslant {t}_{{\mathrm{b}},\alpha ,k} + {x}_{\alpha \beta ,k}{d}_{\alpha \beta ,k}/v-M(1-{x}_{\alpha \beta ,k}),\\ &\quad\forall (\alpha ,\beta )\in S,\;k\in K, \end{split}$

(8)

式中：t_a,β,k、t_b,α,k分别为可变线路公交班次k在站点β和α的到达、发车时间，M为一个足够大的数.

式（9）确保班次k在非接驳站的发车时间等于车辆到达非接驳站的时间加上停车服务时间. 类似地，式（10）确保班次k在接驳站的发车时间等于车辆在接驳站的到达时间加上服务时间.

${t}_{{\mathrm{b}},\alpha ,k}={t}_{{\mathrm{a}},\alpha ,k} + {t}_{{\mathrm{rn}}},\quad \forall \alpha \in R_{\mathrm{N}},\; k\in K,$

(9)

${t}_{{\mathrm{b}},\alpha ,k}={t}_{{\mathrm{a}},\alpha ,k} + {t}_{{\mathrm{r}}},\quad \forall \alpha \in RC\backslash \left\{{r}_{1},{r}_{\mathrm{n}}\right\},\; k\in K,$

(10)

式中：t_rn为可变线路公交在临时站点（灵活需求点）的服务时间，t_r为在接驳站的停靠时间.

式（11）表示消除使其他点不相交的所有循环，确保在最优解中不包含无意义的子循环

${\sum }_{\alpha \in \psi }{\sum }_{\alpha \in \psi }{x}_{\alpha \beta ,k}\leqslant \left|\psi \right|-1,\; \forall \psi \subseteq S,\; \psi \ne \varnothing ,\; k\in K,$

(11)

式中：ψ为集合S除空集外的真子集.

式（12）表示每个乘客最多被服务一次.

${\sum }_{k\in K}{y}_{q,k}\leqslant 1,\quad \forall q\in Q.$

(12)

式（13）和（14）用于判断换乘乘客能否顺利完成换乘，换乘成功（使用接驳可变线路公交）y_q,k则取1，反之为0.

$M\left({y}_{q,k}-1\right)\leqslant \left|{P}_{{\mathrm{p}},q,k}-{t}_{{\mathrm{p}},q}\right| < M{y}_{q,k},\quad \forall q\in {Q}_{\mathrm{I}},\;k\in K,$

(13)

$M\left({y}_{q,k}-1\right)\leqslant \left|{P}_{{\mathrm{d}},q,k}-{t}_{{\mathrm{d}},q}\right| < M{y}_{q,k},\quad \forall q\in {Q}_{\text{II}},\;k\in K.$

(14)

当换乘乘客q乘坐可变线路公交班次k的等待时间或晚到时间大于τ时为1，否则为0，如式（15）、（16）所示.

$M\left({{\textit{z}}}_{q,k}-1\right)\leqslant \left|{P}_{{\mathrm{p}},q,k}-{t}_{{\mathrm{p}},q}\right|-\tau < M{{\textit{z}}}_{q,k},\quad \forall q\in {Q}_{\mathrm{I}},\;k\in K,$

(15)

$M\left({{\textit{z}}}_{q,k}-1\right)\leqslant \left|{P}_{{\mathrm{d}},q,k}-{t}_{{\mathrm{d}},q}\right|-\tau < M{{\textit{z}}}_{q,k},\quad \forall q\in {Q}_{\text{II}},\;k\in K,$

(16)

式中：τ为乘客最大可容忍等待或晚到时间， min；z_q,k为0-1变量.

式（17）、（18）表示乘客下车时刻要大于上车时刻加上接驳站点或临时站点的服务时间.

${P}_{{\mathrm{p}},q,k} + {t}_{{\mathrm{r}}} < {P}_{{\mathrm{d}},q,k},\quad \forall q\in {Q}_{\mathrm{I}},\;k\in K,$

(17)

${P}_{{\mathrm{p}},q,k} + {t}_{{\mathrm{rn}}} < {P}_{{\mathrm{d}},q,k},\quad \forall q\in {Q}_{\text{II}},\;k\in K.$

(18)

式（19）表示可变线路公交运行中的发车间隔受时间区间约束.

${H}_{\mathrm{m}\mathrm{i}\mathrm{n}}\leqslant H\leqslant {H}_{\mathrm{m}\mathrm{a}\mathrm{x}},\quad \forall H\in {{N}}^{ + },$

(19)

式中：H_min、H_max分别为车辆发车间隔下、上限，min；H为可变线路公交运营周期内发车间隔，min.

运营周期内发车班次次数由下式（20）得到.

${k}_{m}=\frac{h}{H},\quad \forall h\in {{N}}^{ + },H|h$

(20)

式中：h为可变线路公交运营周期，分钟；k_m为运营周期内发车班次次数，次.

通过相关标准及经验确定发车间隔的上下限以及潜在的最优发车间隔（如：5 min、10 min），再根据上述提出的模型依次计算和对比不同发车间隔的各项系统成本，从而确定出最优发车间隔和发车班次.

1.2 站点发车时间

由于需求的不确定性和不均匀性，分配和制定站点之间的松弛时间（制定车辆运行时刻表时额外分配给服务灵活需求点的时间，其值等于系统所分配的运行周期时间减去车辆沿基准路线的直接行驶时间）和发车时间并不是简单的求平均值，要根据实际需求来进行合理的规划. 对于每个班次车辆来说，车辆到站和发车时间受各个接驳站之间的松弛时间影响，根据车辆行驶时间、车辆在每个临时站点和每个接驳站的服务时间可计算得到车辆每班次单程的运行周期时间，见式（21）.

$\begin{split} &{\varsigma }_{k}\geqslant {\sum }_{\alpha \in S}{\sum }_{\beta \in S}\frac{{x}_{\alpha \beta ,k}\times {d}_{\alpha \beta ,k}}{v} + {q}_{i,k}{t}_{{\mathrm{rn}}} + \left({r}_{\mathrm{m}}-2\right){t}_{{\mathrm{r}}},\\ &\quad\forall i\in RC\backslash \left\{{r}_{\mathrm{n}}\right\},k\in K, \end{split}$

(21)

式中：ς_k为可变线路公交班次k运行周期，min；q_i,k为可变线路公交班次k在接驳站r_i与r_{i + 1}之间的临时站点上、下车乘客的数量.

式（22）表示运行周期减去车辆沿基准线行驶的时间即为总松弛时间；式（23）表示各个接驳站区间的松弛时间之和，即各班次车辆完整运行的总松弛时间. 各个区间内的松弛时间主要由区间内车辆所需服务的临时站点数来分配和确定，不再受不同区间的服务区域大小的影响，如式（24）.

${L}_{k}={\varsigma }_{k}-\sum _{i\in RC\backslash \left\{{r}_{\mathrm{n}}\right\}}{d}_{r,i,k}/v,\quad \forall k\in K,$

(22)

${L}_{k}=\sum _{i\in RC\backslash \left\{{r}_{\mathrm{n}}\right\}}{L}_{i,k},\quad \forall k\in K,$

(23)

${L}_{i,k}=\frac{{q}_{i,k}}{\displaystyle\sum _{i\in RC\backslash \left\{{r}_{\mathrm{n}}\right\}}{q}_{i,k}}{L}_{k},\quad \forall i\in RC\backslash \left\{{r}_{\mathrm{n}}\right\},\;k\in K,$

(24)

式中：L_k为可变线路公交班次k运行周期内总的松弛时间，min；L_i,k为可变线路公交班次k在接驳站r_i与r_{i + 1}之间分配的松弛时间，min；d_r,i,k为班次k沿基准线路行驶时在接驳站r_i与r_{i + 1}之间的行驶距离，km.

各个接驳站的发车时间通常由前一个接驳站的发车时间和2个接驳站间的行程时间和松弛时间共同决定，见式（25）.

${\xi }_{i,k}={\xi }_{i-1,k} + {L}_{i-1,k} + \frac{{d}_{r,i-1,k}}{v},\quad \forall i\in RC\backslash \{{r}_{1},{r}_{\mathrm{n}}\},\;k\in K,$

(25)

式中：ξ_i,k为可变线路公交班次k在接驳站r_i的发车时间.

2. 算法设计

在编制接驳可变线路公交时刻表时，可以将问题细分为“发车间隔设置算法设计”“班次设置算法设计”和“发车时间设置算法设计”3个子问题.

2.1 发车间隔设置阶段

设置发车间隔时需要考虑公交时刻表的特性，制定合理高效的方案. 具体求解算法伪代码如表1所示.

表 1 发车间隔设置算法设计

Table 1. Algorithm design of departure interval setting

步骤	指令
输入	发车间隔下限H_min，发车间隔上限H_max，发车间隔H_ν，其中：H_ν = H_min, $\cdots$ , H_max，ν = 1, 2, $\cdots$ , n
步骤	取初始H₁ = H_min，令H* = H₁，计算当前U（H₁），令U（H） = U（H₁）
循环	当ν < n时，执行步骤1、2
步骤1	在上述基础上，获取新的H_{ν + 1}，判断是否满足约束，若H_{ν + 1}不满足约束，则重复步骤1
步骤2	计算H_{ν + 1}下的U（H_{ν + 1}），若U（H_{ν + 1}） < U（H），则接受H_{ν + 1}作为新的最优发车间隔，H* = H_{ν + 1}，否则保留原来的H*
步骤3	若满足终止条件H_n = H_max，则输出H和U（H*），结束程序，否则返回步骤1.
输出	最优发车间隔H，最优系统成本U（H*）

下载: 导出CSV

| 显示表格

2.2 班次设置阶段

每个不同的发车间隔对应了不同的乘客分配和可变线路公交车辆班次设置，通过对分配和设置后的具体接驳情况和班次安排计算得到系统成本，因此，这一部分也需要设计相应算法进行求解. 乘客分配和班次设置决定每个班次具体服务哪些乘客，可以运用遗传算法求解，在乘客分配和车辆班次设置的时候，尝试将被拒绝的乘客重新安排回运行班次，从而提高解的质量，具体求解算法伪代码如表2所示.

表 2 班次设置算法设计

Table 2. Algorithm design of shift setting

步骤	指令
输入	种群规模，交叉概率，变异概率，最大迭代数I_max
步骤0	输入运营参数，设置种群数量、交叉、变异概率，最大迭代次数I_max，初始化种群迭代次数I_n = 0
循环	当I_n < I_max时，执行步骤1～8
步骤1	编码：染色体采用由0-1变量构成的矩阵体现乘客分配和班次设置的二维关系，并假设存在一个新的虚拟班次存放被拒绝的乘客
步骤2	适应度函数：当完成运营周期内一次完整班次设置之后，计算染色体对应的适应度
步骤3	染色体更新：1）在每个乘客和班次完成分配和设置后，将被拒绝乘客的信息反馈给染色体，对相应的基因进行更改，实现染色体的更新；2）尝试将被拒绝的乘客重新安排回接驳可变线路公交中，提高染色体质量，跳出局部最优
步骤4	选择：精英保留策略和锦标赛法
步骤5	交叉：选用单点交叉方式
步骤6	变异：选用单点变异方式
步骤7	种群适应度更新并记录最优解
步骤8	迭代次数更新，I_n = I_n + 1
步骤9	算法终止条件：I_n ≥ I_max
输出	最优解u，最优系统成本U

下载: 导出CSV

| 显示表格

2.3 发车时间设置阶段

乘客分配和班次设置后需要对各班次的路径进行规划可求出系统成本U，同时路径规划后才能求解得到接驳可变线路公交系统的运行周期时间、松弛时间和站点发车时间. 站点发车时间主要指固定站点的发车时间，为避免过高的拒绝率或过长的延误时间，需要考虑整体运行周期，对每个运行区间分配合适的松弛时间. 具体求解算法如表3所示.

表 3 发车时间设置算法设计

Table 3. Algorithm design of departure time setting

步骤	指令
输入	初始运行站点、线路，出行需求信息，乘客分配情况，车辆班次情况，初始车辆状态
步骤0	输入出行需求行程时间分布和接驳可变线路公交线路运营各项参数
步骤1	将乘客起终点在各分配的车辆班次中依次插入
步骤2	判断约束，若乘客起点或终点的插入会导致可变线路公交违背接驳站的时间约束，则拒绝请求
步骤3	被拒绝乘客重新安排，明确班次的选择顺序，分别将乘客实际上、下车时间与预计/预约上、下车时间比较，时间成本越小，班次排序越靠前，乘客优先尝试插入到该班次中，不再尝试安排到其他班次；
步骤4	计算得到各班次的运行周期时间，松弛时间和固定站点发车时间；
步骤5	编制接驳地铁的可变线路公交时刻表.
输出	最优各班次车辆运行路径，运行周期时间，松弛时间，接驳站发车时间

下载: 导出CSV

| 显示表格

3. 案例研究

3.1 案例描述

本文选取南京市地铁2号线和公交5路作为研究对象，根据流量、线路、时刻表等运营数据验证模型及算法，布局走向如图3所示. 图中蓝色实线为南京市地铁2号线，红色实线为南京市公交5路，位于鼓楼区、秦淮区和栖霞区的交界处，承担着通勤、科研教育、旅游休闲等出行需求.

图 3 南京市地铁2号线和公交5路运行线路图

Figure 3. Operation route of metro line 2 and bus line 5 of Nanjing

下载: 全尺寸图片幻灯片

线路周围POI点非常多，如图4所示，图中紫色小点为各类型POI点，吸引着大量乘客出行往返，地铁和公交承担着高水平的出行需求服务. 乘客出行乘坐地铁后大概率要到达某个POI点，同样地，乘客乘坐地铁前会从某个POI点出发. 本文主要解决地铁乘客“最后一公里”出行问题，因此筛选得到线路和站点附近的POI点（潜在出行需求点），在图中显示，下述出行需求集合会在这部分POI点中随机生成，同时考虑线路和车辆可达性，形成可供可变线路公交接驳的潜在出行需求集合.

图 4 线路附近POI点

Figure 4. POI location around route

下载: 全尺寸图片幻灯片

公交车辆行驶速度和乘客出行需求水平在一天中是分时段变化的，具体随时间段变化情况如图5所示. 在高峰期时，出行需求水平较高，同时由于道路拥堵严重，公交车辆行驶速度较低；在平峰时段，出行需求较少，道路较为通畅，公交车辆行驶速度随之提高. 各时段出行需求从乘客出行需求集合中随机选取，用作系统仿真分析数据基础.

图 5 车辆行驶速度和乘客出行需求水平随时间段变化情况

Figure 5. Change trend of bus driving speed and passenger travel demand level with time period

下载: 全尺寸图片幻灯片

南京公交5路站点和线路与地铁2号线新街口-马群段高度重合，可将5路常规公交转换为可变线路公交，在保证原有公交定点定线乘客出行需求的同时接驳服务地铁乘客短途出行需求. 将重合度较高的地铁-公交站点作为接驳可变线路公交的固定站点，包括新街口-新街口东站、大行宫-大行宫东站、西安门•浦发银行-西安门站、明故宫-明故宫东站、下马坊-小卫街站、孝陵卫-孝陵卫站、钟灵街-钟灵街站、马群-马群站. 5路公交转变为可变线路公交后，无站外需求时按照原始线路（基准线）运行，如有站外需求点，包括站外到地铁乘车或地铁站下车到站外需求点，可变线路公交可以偏离基准线到站外需求点接、送乘客，方便各类型乘客的出行.

对系统进行仿真分析时，由于系统道路沿线路网较为复杂，因此根据前面章节的相关描述，将系统抽象为一个LW的服务区域，可变线路公交在服务区域内接驳乘客出行. L为接驳站两端间的路线长度，考虑到“最后一公里”短途出行的目的，将服务区域宽度W设为1公里. 接驳站相应位置信息如表4所示.

表 4 固定站点地铁运行时刻表

Table 4. Urban rail transit running timetable data of fixed stations

编号	接驳站（地铁-公交）	固定站点相对位置	始发时间	末班时间
r₁	新街口（东）	0	06：11	23：33
r₂	大行宫（东）	1.00	06：13	23：35
r₃	西安门•浦发银行	2.00	06：15	23：37
r₄	明故宫（东）	3.40	06：17	23：40
r₅	下马坊-小卫街	6.20	06：21	23：44
r₆	孝陵卫	7.20	06：23	23：46
r₇	钟灵街	8.30	06：25	23：48
r₈	马群	11.00	06：00	23：52

下载: 导出CSV

| 显示表格

接驳地铁的可变线路公交需要配合地铁运行时刻表才能更好地完成乘客接送服务，地铁到站/发车时刻表目前有始发时间和末班时间数据，如表4所示，具体运行周期（如1天）内的详细时刻表未被公布. 因此本文根据现有信息和相关运行规则，合理推算服务周期内的地铁到/发站时刻表，并依此仿真生成短途出行需求的时空信息，接驳可变线路公交根据出行需求时空信息合理编制运行时刻表，制定切实可行的发车和运行计划.

研究系统中相关参数参考^[6,13-15]. θ_W、θ_L和θ_O都设为1 元/min，考虑到公共交通的公益性，尽可能地满足出行需求，减少拒绝率，因此将θ_F设为15 元/min^[15]，H_min为3 min, H_max为30 min，ε为3 min，τ为5 min，t_r、t_rn分别为1 min和0.3 min. 与相关研究^[14,15]类似，应用直线运动来再现真实的道路网络.

本节基于Matlab R2021a平台，通过编程对模型进行求解. 对于每一次的仿真模拟实验，遗传算法的参数设置如下：染色体种群规模为80，发生交叉行为的概率为0.9，发生变异的概率为0.1，最大迭代次数为500次.

3.2 案例分析

根据系统相关参数值、车辆行程速度和乘客各时段需求时空数据，可得到不同需求水平下不同车速所对应的最优发车间隔，如表5所示. 这里的车辆发车间隔主要是针对转变后的可变线路公交车，并非原始5路公交车全部按照这一发车间隔和方案运营.

表 5 不同需求水平下不同车速所对应的最优发车间隔

Table 5. Optimal departure interval corresponding to different driving speeds under different demand levels

需求/（人·h⁻¹）	发车间隔H/（分钟）
需求/（人·h⁻¹）	v=20千米/ 小时	v=30千米/ 小时	v=40千米/ 小时
10	30	30	30
20	30	30	30
30	20	20	30
40	15	20	20
50	12	15	15
60	10	12	15

下载: 导出CSV

| 显示表格

根据系统中车辆行程时间和乘客需求随时间的变化情况，可得到运营周期内不同时段下接驳地铁可变线路公交发车时间间隔的变化情况，如表6所示.

表 6 不同时段下接驳地铁可变线路公交发车时间间隔

Table 6. Departure time interval of feeder FRT at different periods

时段	V/（km·h⁻¹）	需求/（人·h⁻¹）	H /min
7：00-8：59	20	60	10
9：00-10：59	40	40	20
11：00-12：59	30	50	15
13：00-14：59	30	50	15
15：00-16：59	40	30	30
17：00-18：59	20	60	10
19：00-20：59	30	20	30

下载: 导出CSV

| 显示表格

在计算系统成本时，默认各项时间成本的权重系数都为1，若重视乘客等待和晚到时间成本，增加其相应的权重，如设置等待时间成本、晚到时间成本、换乘失败成本和企业运营成本的权重系数比为2∶2∶1∶1，最优发车间隔随之发生变化，如图6所示.

图 6 发车间隔变化对比

Figure 6. Comparison of departure interval changes

下载: 全尺寸图片幻灯片

从图6可以看出，若重视乘客等待和晚到时间成本，相应权重系数增大后，最优发车间隔则发生改变，需要减小发车间隔，增加发车频率，降低乘客相关出行时间成本的同时得到最优系统运行成本.

根据表6，在早晚高峰时段（7：00-8：59、17：00-18：59），出行需求较大的同时车辆行驶速度缓慢，因此，发车时间间隔相应缩短；当出行需求较低车速较快时，发车间隔时间可以相应增大，也能满足乘客出行需求. 同时，计算得到各运行周期内的系统运行成本U、各运行周期内的平均车辆运行时间ς_k、各运行周期内的发车次数和所需车辆数，如表7所示. 其中，所需车辆数是根据每趟班车单程运行时间确定的，因本文主要对接驳系统和方法进行研究和验证，计算单程时刻表即可，假设回程所需时间与去程相等，从而计算各运行周期内所需总车辆数.

表 7 系统各运行时段的仿真结果

Table 7. Simulation results of each operating period of system

时段	H/min	U/元	平均ς_k/min	发车次数 /次	车辆数 /辆
7：00-8：59	10	801.22	53.71	12	11
9：00-10：59	20	279.18	33.73	6	4
11：00-12：59	15	430.76	42.17	8	6
13：00-14：59	15	493.44	43.48	8	6
15：00-16：59	30	192.75	35.12	4	3
17：00-18：59	10	895.30	57.99	12	11
19：00-20：59	30	210.46	41.27	4	3

下载: 导出CSV

| 显示表格

从表7中可以发现，车辆在早晚高峰时段运行因受制于行程速度限制以及高出行需求水平，其单程运行周期较长，导致在这2个时段内的运营费用相对较高. 为满足出行需求和发车时间间隔要求，需要在这2个时段内配置更多的车辆. 相比之下，在平峰时段，随着需求量减少和车辆行驶速度增加，较少车辆即可满足出行需求，系统总成本相应降低. 因此，在实际运营中，应根据不同时段行程速度和乘客需求的变化，设定不同的发车时间间隔，不仅有助于满足不同时段乘客出行需求，还能有效控制接驳地铁可变线路公交系统运营成本，从而实现更好的运营效果.

若重视乘客等待和晚到时间成本，运行周期内的平均车辆运行时间和系统运行成本也会随之发生变化，如图7、8所示.

图 7 运行周期内平均车辆运行时间变化

Figure 7. Changes of average vehicle running time during the operating cycle

下载: 全尺寸图片幻灯片

图 8 系统运行成本变化对比

Figure 8. Comparison of system operating cost changes

下载: 全尺寸图片幻灯片

从图7可以看出，重视乘客出行时间则系统发车间隔减小，运行周期内车辆数随之增加，使得各个班次车辆接送乘客平均数减少，对应的平均运行距离减少，因此，运行周期内平均车辆运行时间相应减少.

图8中常规系统运行成本指默认权重值情况下系统的总运行成本，与表7一致；常规发车间隔重视乘客系统运行成本指重视乘客时间成本情况下原发车间隔时的系统运行成本；重视乘客系统运行成本指发车间隔和平均车辆运行时间相应减少时的系统运行成本. 可以看出，当乘客权重系数增大时常规情况下的系统运行成本随之增大，此时降低发车间隔，增大发车频率，增加运行车辆数则可以更大程度上降低乘客等待和晚到时间，使系统总成本相应减少. 由于车辆数增加，相应的运营成本也随着增高，所以系统运行成本不会有大幅度的降低.

4. 结　论

1）分析了部分使用地铁出行乘客的“最后一公里”出行需求特征和换乘行为特征，分析了公交车和地铁的运行组织特征和衔接特征，提出一种将常规公交转变为可变线路公交接驳地铁的策略，在不需要开设新接驳线路的前提下可以同时服务原有公交车出行需求乘客和有短途出行需求的地铁乘客.

2）针对可变线路公交区别于常规定点定线公交的运行特征，以公共交通运行数据和服务范围内POI数据为基础，综合考虑了乘客出行成本和公交系统车辆运营成本，构建可变线路公交运行时刻表编制方法和接驳地铁的路径规划与运行时刻表编制协同优化模型与算法.

3）以实际路网中地铁和公交系统为例，分析研究了车辆运行速度与出行需求水平对系统各项指标的影响，并分析不同时间成本侧重情况下对系统发车间隔、车辆运行时间、运行成本等指标的影响，结果表明在运行周期内适当增加发车频率可以有效降低乘客出行时间成本同时不会过多增加系统运营成本，并编制车辆行车时刻表. 可为企业实际运营提供一定的参考，对具有短途出行需求的地铁乘客经济、便捷出行和公交系统低成本、高效性、公益性具有一定的促进意义.

4）在本文给出的时刻表构建方法和案例分析的基础上，进一步扩大协同服务网络规模、引入不同车辆车型组合是开展后续相关研究的重要方向.

致谢：合肥大学城市轨道交通安全与应急管理重点实验室开放课题（2024GD0007）.

图 1 常导高速磁浮直线长定子电机结构

Figure 1. Structure of EMS high-speed linear LSM

下载: 全尺寸图片幻灯片

图 2 考虑相移滞后影响的高频响应各坐标系

Figure 2. Coordinate system of high-frequency response considering effect of phase shift lag

下载: 全尺寸图片幻灯片

图 3 考虑延时的相移滞后示意

Figure 3. Phase shift lag considering delay

下载: 全尺寸图片幻灯片

图 4 考虑相位补偿的高频方波注入无传感控制框图

Figure 4. Sensorless control for HFSI considering phase shift lag compensation

下载: 全尺寸图片幻灯片

图 5 考虑梯度变化的二分法延时计算结构

Figure 5. Bisection delay computational structure considering gradient change

下载: 全尺寸图片幻灯片

图 6 基于二分法的延时与角度相移滞后计算流程

Figure 6. Flowchart of delay and angular phase shift lag based on bisection method

下载: 全尺寸图片幻灯片

图 7 试验平台与驱动控制平台

Figure 7. Test platform and drive control platform

下载: 全尺寸图片幻灯片

图 8 补偿前不同给定电流控制效果

Figure 8. Control effect of different set currents before compensation

下载: 全尺寸图片幻灯片

图 9 补偿后不同给定电流控制效果

Figure 9. Control effect of different set currents after compensation

下载: 全尺寸图片幻灯片

图 10 补偿前不同给定速度控制效果

Figure 10. Control effect of different set speeds before compensation

下载: 全尺寸图片幻灯片

图 11 补偿后不同给定速度控制效果

Figure 11. Control effect of different set speeds after compensation

下载: 全尺寸图片幻灯片

表 1 磁浮电机试验平台主要参数

Table 1. Main parameters of maglev motor test platform

参数	数值
直流侧电压/V	220
定子相电阻/Ω	0.12
d 轴电感/mH	1.8
q 轴电感/mH	1.4
定子极距/mm	2.58
动子极距/mm	266.5
励磁电流/A	20～23
动子励磁磁链/Wb	0.324 7

下载: 导出CSV

表 2 不同电流下补偿前、后误差最大波动

Table 2. Maximum fluctuation of error before and after compensation under different currents

电流/A	电角误差/rad		电流误差/A		电角波动变化/%	电流波动变化/%
电流/A	补偿前	补偿后	补偿前	补偿后	电角波动变化/%	电流波动变化/%
20	0.86	0.23	7.5	7.5	73.3	0
21	0.71	0.21	7.5	7.5	70.4	0
22	0.68	0.19	7.5	7.5	72.1	0

下载: 导出CSV

表 3 不同速度下补偿前、后误差最大波动

Table 3. Maximum fluctuation of error before and after compensation under different speeds

速度/（m·s⁻¹）	电角误差/rad		速度误差/（m·s⁻¹）		电角波动变化/%	电流波动变化/%
速度/（m·s⁻¹）	补偿前	补偿后	补偿前	补偿后	电角波动变化/%	电流波动变化/%
0.8	0.53	0.17	0.36	0.21	67.9	50
0.9	0.51	0.15	0.36	0.21	70.5	50
1.0	0.49	0.12	0.36	0.21	75.5	50

下载: 导出CSV

参考文献(24)

[1]	丁叁叁. 时速600公里高速磁浮交通系统[M]. 上海:上海科学技术出版社,2021.
[2]	林国斌,刘万明,徐俊起,等. 中国高速磁浮交通的发展机遇与挑战[J]. 前瞻科技,2023,2(4): 7-18. LING Guobin, LIU Wanming, XU Junqi, et al. Opportunities and challenges for the development of High-speed maglev transportation in China[J]. Science and Technology Foresight, 2023, 2(4): 7-18.
[3]	朱进权,葛琼璇,张波,等. 考虑悬浮系统影响的高速磁悬浮列车牵引控制策略[J]. 电工技术学报,2022,37(12): 3087-3096. ZHU Jinquan, GE Qiongxuan, ZHANG Bo, et al. Traction control strategy of high-speed maglev considering the influence of suspension system[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3087-3096.
[4]	康劲松,丁浩,倪菲,等. 计及悬浮系统影响的高速磁浮直线同步电机建模方法[J]. 西南交通大学学报,2024,59(4): 729-736. doi: 10.3969/j.issn.0258-2724.20230431 KANG Jinsong, DING Hao, NI Fei, et al. Modeling of high-speed maglev linear synchronous motors considering influence of suspension system[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 729-736. doi: 10.3969/j.issn.0258-2724.20230431
[5]	ZHU J Q, GE Q X, SUN P K. Extended state observer-based sensorless control for high-speed maglev application in single-feeding mode and double-feeding mode[J]. IEEE Transactions on Transportation Electrification, 2022, 8(1): 1350-1361. doi: 10.1109/TTE.2021.3093342
[6]	WANG G L, VALLA M, SOLSONA J. Position sensorless permanent magnet synchronous machine drives—a review[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 5830-5842. doi: 10.1109/TIE.2019.2955409
[7]	KIM H, JUNG H S, SUL S K. Stator winding temperature and magnet temperature estimation of IPMSM based on high-frequency voltage signal injection[J]. IEEE Transactions on Industrial Electronics, 2023, 70(3): 2296-2306. doi: 10.1109/TIE.2022.3174285
[8]	ORTOMBINA L, BERTO M, ALBERTI L. Sensorless drive for salient synchronous motors based on direct fitting of elliptical-shape high-frequency currents[J]. IEEE Transactions on Industrial Electronics, 2023, 70(4): 3394-3403. doi: 10.1109/TIE.2022.3177753
[9]	吴婷. 永磁同步电机全速范围无位置传感器控制策略研究[D]. 长沙:湖南大学,2022.
[10]	王涛,黄景春,杨天昊. 基于改进的Super-Twisting滑模观测器的永磁同步电机无传感器控制[J]. 西南交通大学学报,2025,60(3):445-453: . WANG Tao, HUANG Jinchun, YANG Tianhao. Sensorless control of permanent magnet synchronous motor based on improved Super-Twisting sliding mode observer [J]. Journal of Southwest Jiaotong University, 2025, 60(3):445-453.
[11]	沈泽微,蒋栋,陈嘉楠. 一种通用的PWM变流器开关脉冲延时补偿策略[J]. 中国电机工程学报,2021,41(9): 2990-2998. SHEN Zewei, JIANG Dong, CHEN Jianan. A general switch pulse delay compensation strategy for PWM converter[J]. Proceedings of the CSEE, 2021, 41(9): 2990-2998.
[12]	鄢永,黄文新. 基于闭环电流预测的永磁同步电机电流环延时补偿策略研究[J]. 中国电机工程学报,2022,42(10): 3786-3795. YAN Yong, HUANG Wenxin. Research on delay compensation strategy of permanent magnet synchronous motor based on closed-loop current prediction[J]. Proceedings of the CSEE, 2022, 42(10): 3786-3795.
[13]	王志强,郭伟鹏,桑孜良,等. 高速磁浮列车导向系统优化控制方法研究[J]. 西南交通大学学报,2025,60(4): . WANG Zhiqiang, GUO Weipeng, SANG Ziliang, et al. Optimization control for the guidance system of high-speed maglev train [J]. Journal of Southwest Jiaotong University, 2025, 60(4): .
[14]	WANG Y R, XU Y X, ZOU J B. Sliding-mode sensorless control of PMSM with inverter nonlinearity compensation[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 10206-10220. doi: 10.1109/TPEL.2018.2890564
[15]	WU X, LI C, ZHANG Y Y, et al. Sensorless control of IPMSM equipped with LC sinusoidal filter based on full-order sliding mode observer and feedforward QPLL[J]. IEEE Transactions on Power Electronics, 2024, 39(7): 8072-8085. doi: 10.1109/TPEL.2024.3390050
[16]	LIU Z H, NIE J, WEI H L, et al. A newly designed VSC-based current regulator for sensorless control of PMSM considering VSI nonlinearity[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(4): 4420-4431. doi: 10.1109/JESTPE.2020.3033037
[17]	WU S H, HU C X, ZHAO Z Y, et al. High-accuracy sensorless control of permanent magnet linear synchronous motors for variable speed trajectories[J]. IEEE Transactions on Industrial Electronics, 2024, 71(5): 4396-4406. doi: 10.1109/TIE.2023.3288145
[18]	ZHANG H, LIANG W R, GAO L Y, et al. Switching angle fitting-based delay compensation with IPLL for IPMSM sensorless drives under SHEPWM[J]. IEEE Transactions on Transportation Electrification, 2024, 10(1): 660-669. doi: 10.1109/TTE.2023.3276878
[19]	CAO X Q, GE Q X, ZHU J Q, et al. Periodic traction force fluctuations suppression strategy of maglev train based on flux linkage observation and harmonic current injection[J]. IEEE Transactions on Transportation Electrification, 2023, 9(2): 3434-3451. doi: 10.1109/TTE.2022.3221193
[20]	ZHANG H, LIU W G, CHEN Z, et al. An overall system delay compensation method for IPMSM sensorless drives in rail transit applications[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 1316-1329. doi: 10.1109/TPEL.2020.3015742
[21]	KANG J S, DING H, ZOU P R, et al. Model predictive thrust force control for 3L-NPC fed linear synchronous motor of maglev train[J]. IEEE Transactions on Transportation Electrification, 2024, 1: 3368071.1-3368071.9.
[22]	KANG J S, MU S Y, NI F. Improved EL model of long stator linear synchronous motor via analytical magnetic coenergy reconstruction method[J]. IEEE Transactions on Magnetics, 2020, 56(8): 3002964.1-3002964.13.
[23]	张昕,翟凌露,王舰深,等. 基于加权融合的常导高速磁浮列车UKF定位算法[J]. 西南交通大学学报,2024,59(4): 832-838. doi: 10.3969/j.issn.0258-2724.20230501 ZHANG Xin, ZHAI Linglu, WANG Jianshen, et al. Weighted fusion-based unscented Kalman filter positioning algorithm for normal-conducting high-speed maglev trains[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 832-838. doi: 10.3969/j.issn.0258-2724.20230501
[24]	WU T, LUO D R, WU X, et al. Square-wave voltage injection based PMSM sensorless control considering time delay at low switching frequency[J]. IEEE Transactions on Industrial Electronics, 2022, 69(6): 5525-5535. doi: 10.1109/TIE.2021.3094444

施引文献

附加材料(0)

访问统计

点击查看大图

图(11) / 表(3)

计量

文章访问数: 52
HTML全文浏览量: 21
PDF下载量: 11
被引次数: 0

1. 时刻表编制模型与方法
1.1 发车时间间隔
1.2 站点发车时间
2. 算法设计
2.1 发车间隔设置阶段
2.2 班次设置阶段
2.3 发车时间设置阶段
3. 案例研究
3.1 案例描述
3.2 案例分析
4. 结　论

考虑相移补偿的磁浮列车长定子高频信号注入无传感控制方法

doi: 10.3969/j.issn.0258-2724.20240310

作者简介: 张雯柏（1990—），男，博士研究生，研究方向为高速磁浮磁驱控制系统，E-mail：zhangwenbai@tongji.edu.cn

通讯作者: 赵元哲（1987—），男，讲师，博士，研究方向为高速磁浮磁驱控制系统与电能质量分析，E-mail：yuanzhezhao@tongji.edu.cn

计量

出版历程

Sensorless Control Method of High-Frequency Signal Injection for Long-Stator Synchronous Motor of Maglev Trains Considering Phase Shift Compensation

1. 时刻表编制模型与方法

1.1 发车时间间隔

1.1.1 目标函数

1.1.2 约束条件

1.2 站点发车时间

2. 算法设计

2.1 发车间隔设置阶段

2.2 班次设置阶段

2.3 发车时间设置阶段

3. 案例研究

3.1 案例描述

3.2 案例分析

4. 结 论

计量

出版历程

目录

1. 时刻表编制模型与方法

1.1 发车时间间隔

1.2 站点发车时间

2. 算法设计

2.1 发车间隔设置阶段

2.2 班次设置阶段

2.3 发车时间设置阶段

3. 案例研究

3.1 案例描述

3.2 案例分析

4. 结 论

作者简介:
张雯柏（1990—），男，博士研究生，研究方向为高速磁浮磁驱控制系统，E-mail：zhangwenbai@tongji.edu.cn

通讯作者:
赵元哲（1987—），男，讲师，博士，研究方向为高速磁浮磁驱控制系统与电能质量分析，E-mail：yuanzhezhao@tongji.edu.cn

4. 结　论

4. 结　论