Rotational Inertial Characteristics and Dynamic Response of Motorized Spindle Time-Varying Mass System for Magnetic Suspension Milling
-
摘要:
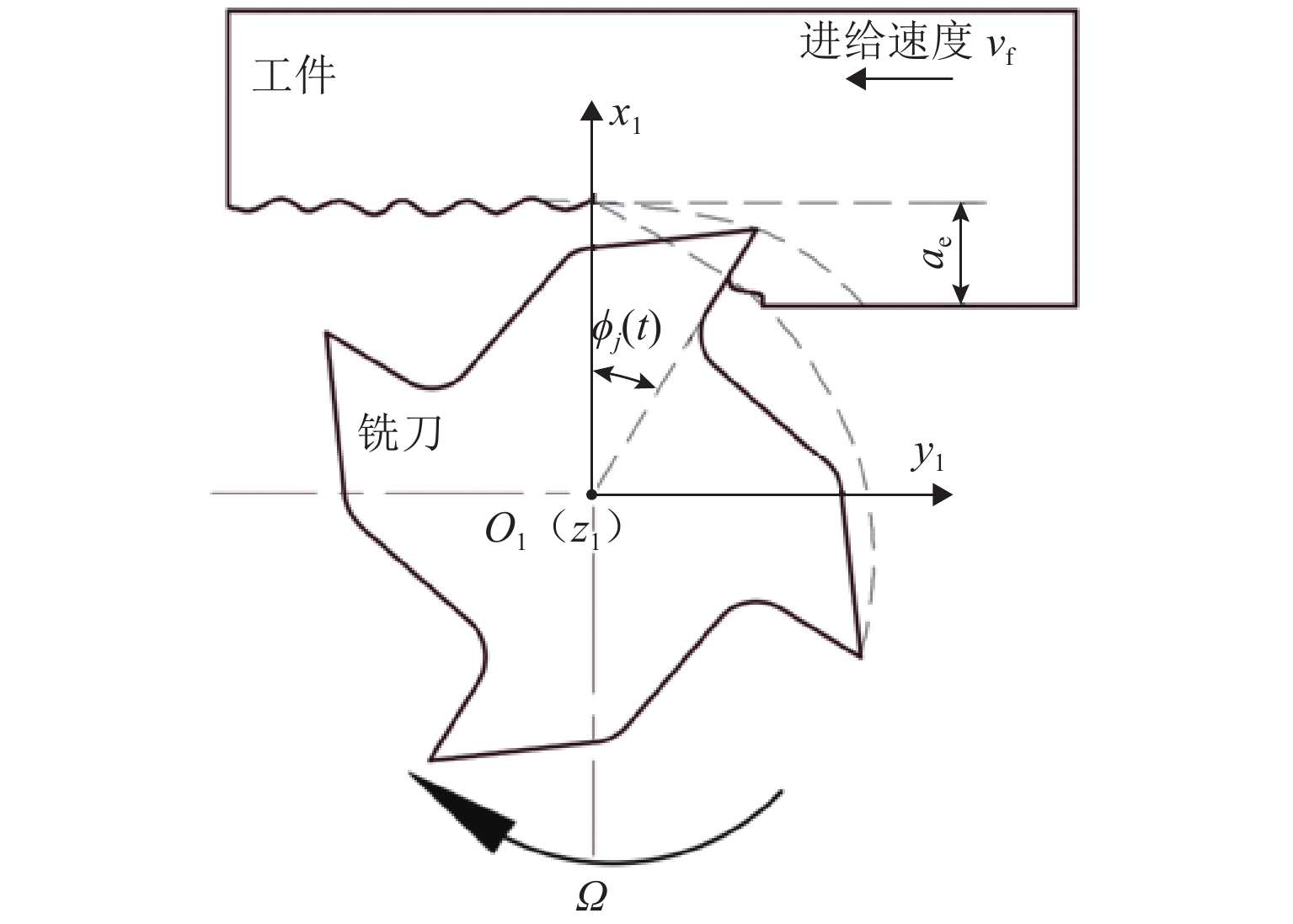
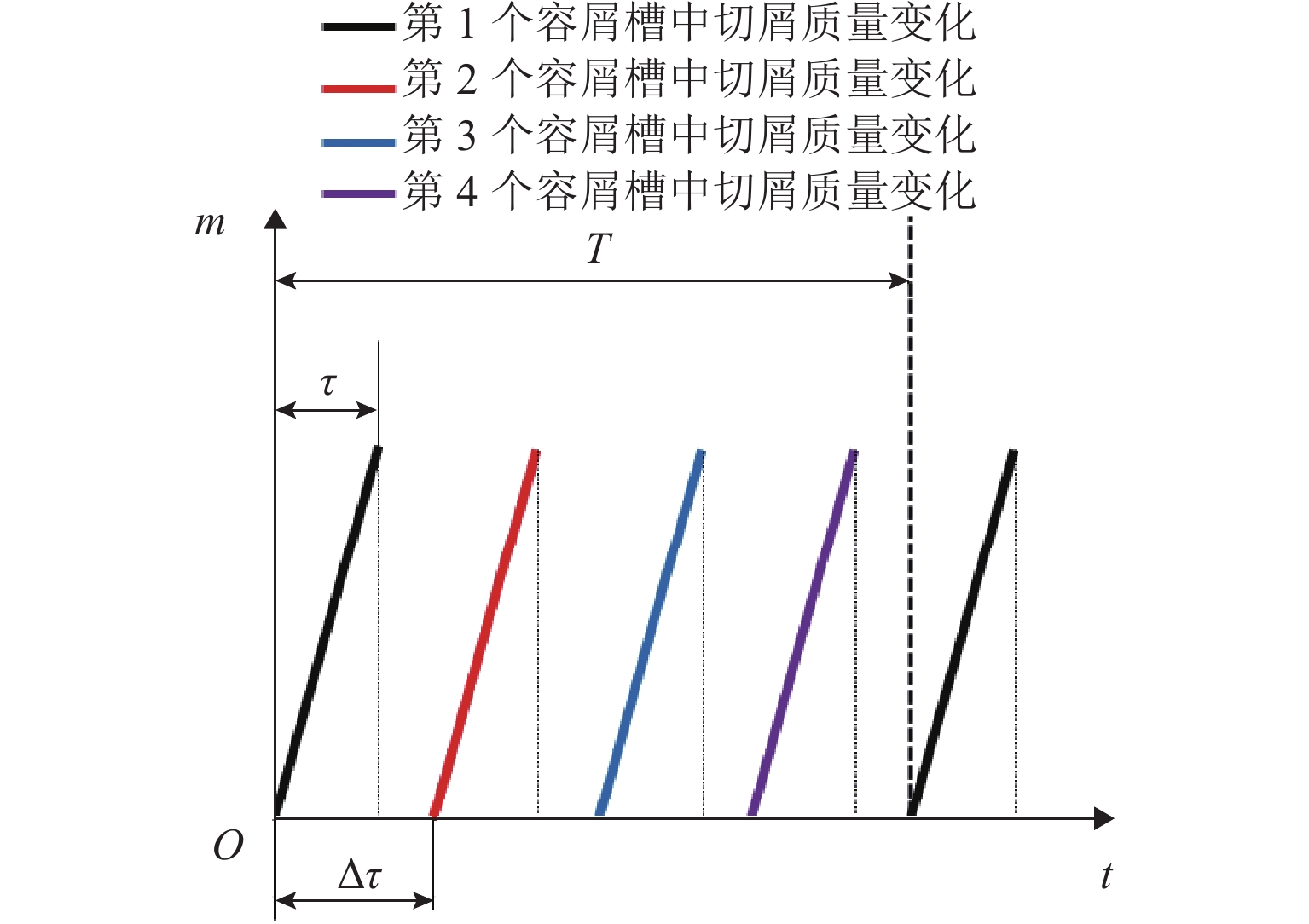
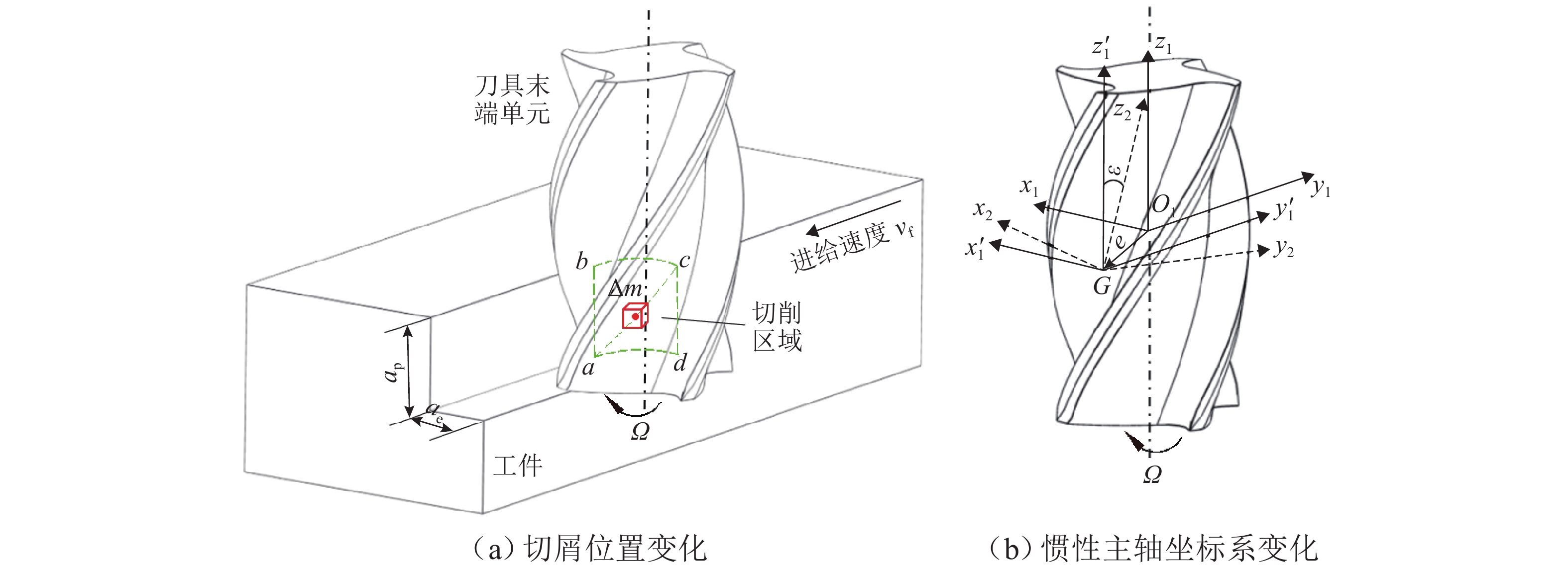
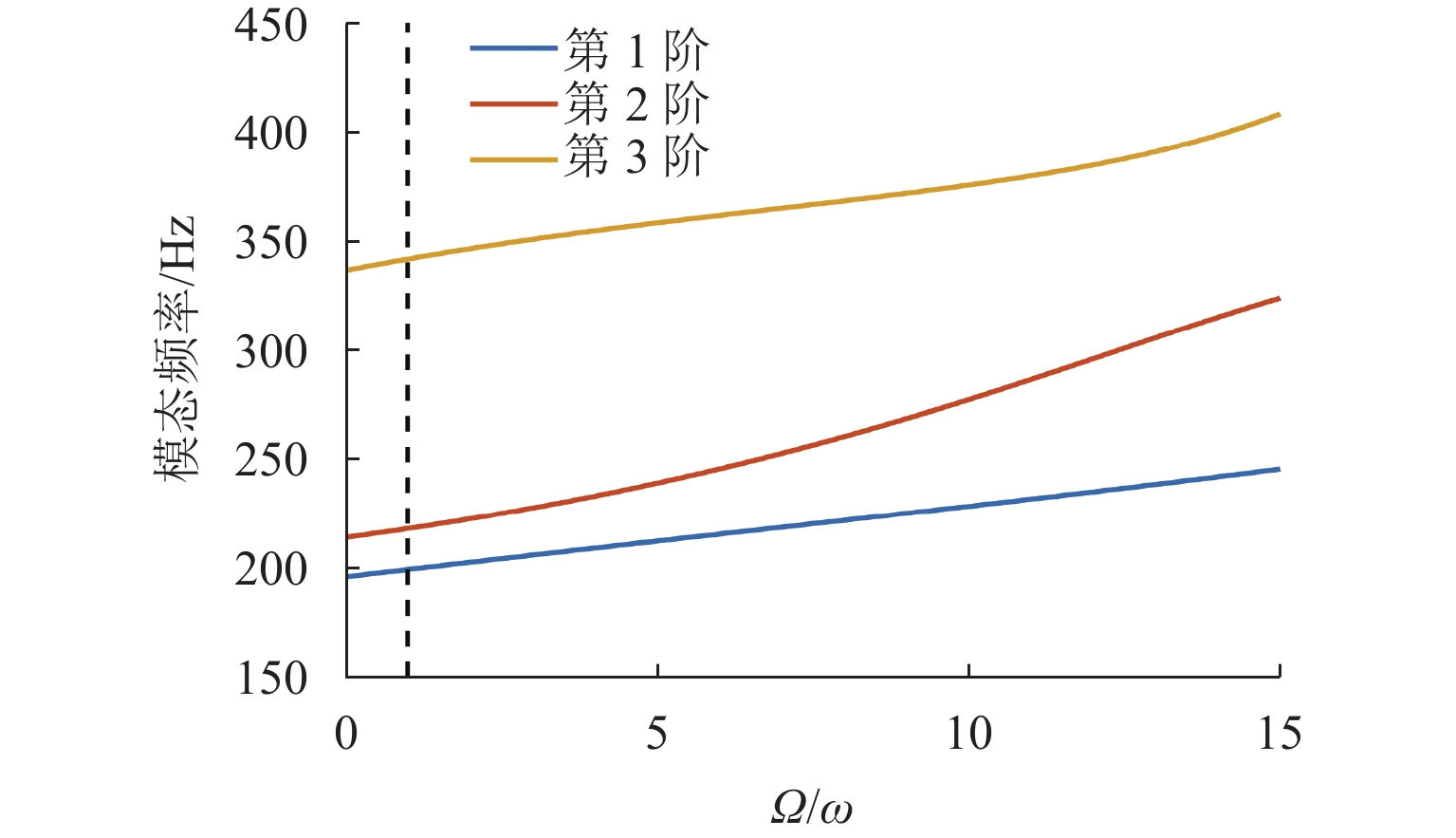
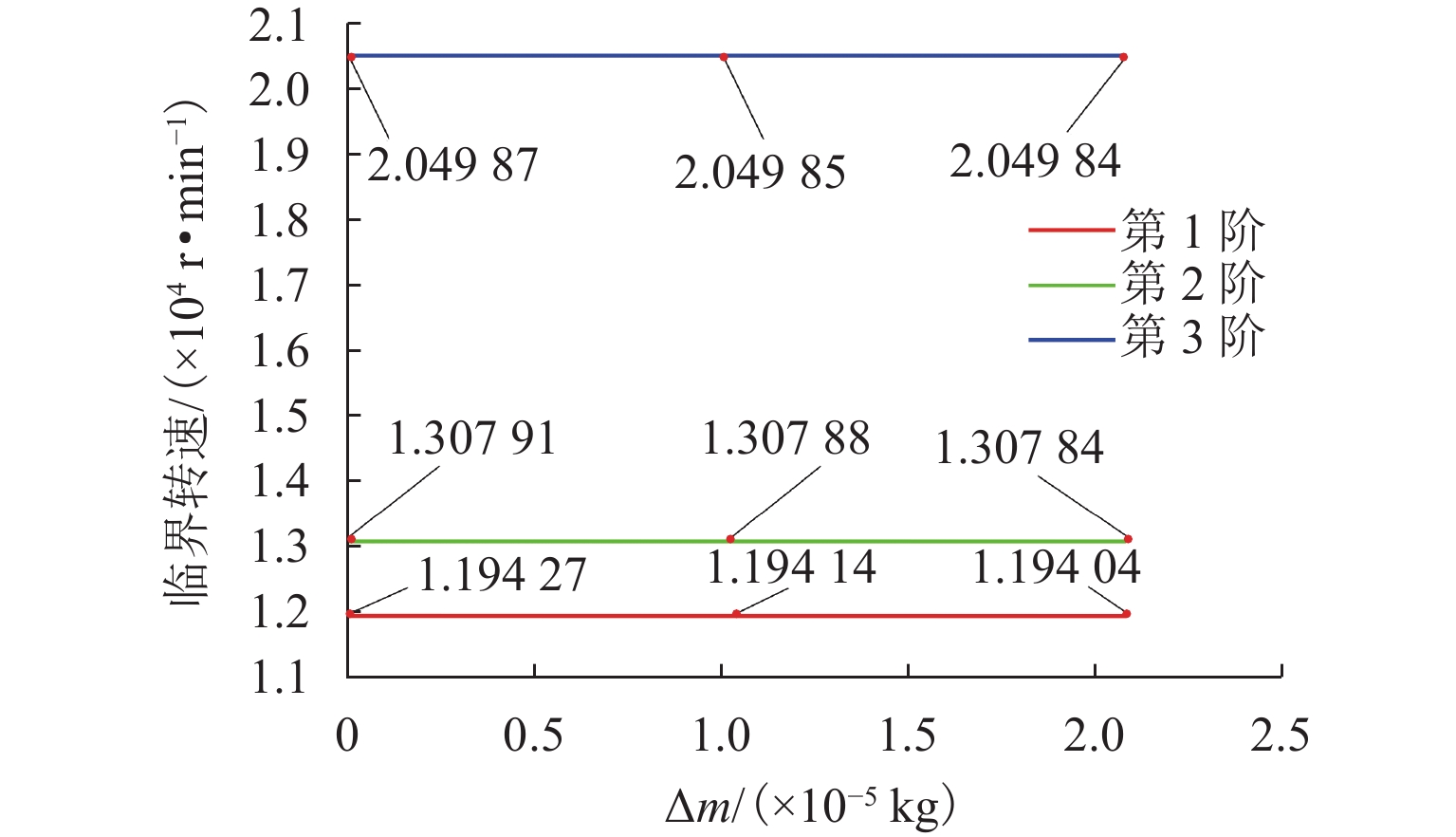
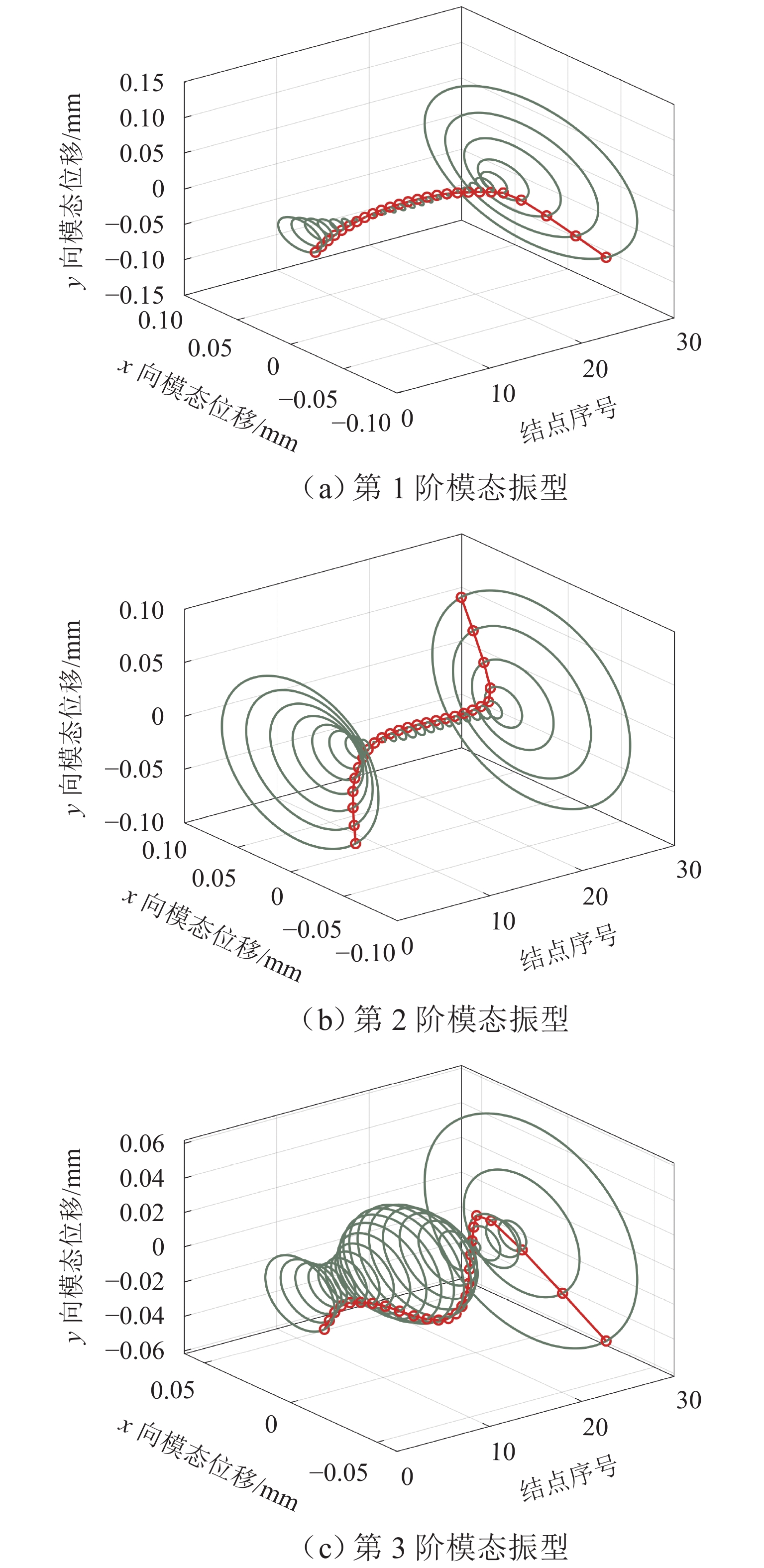
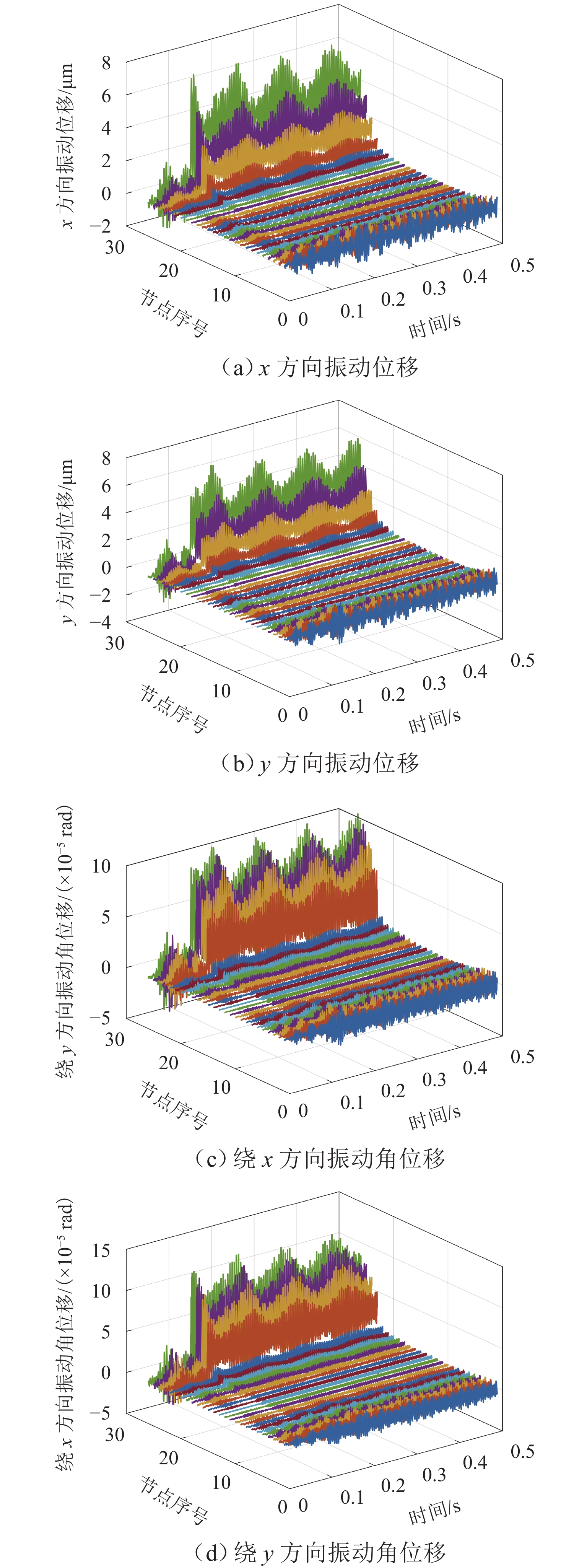
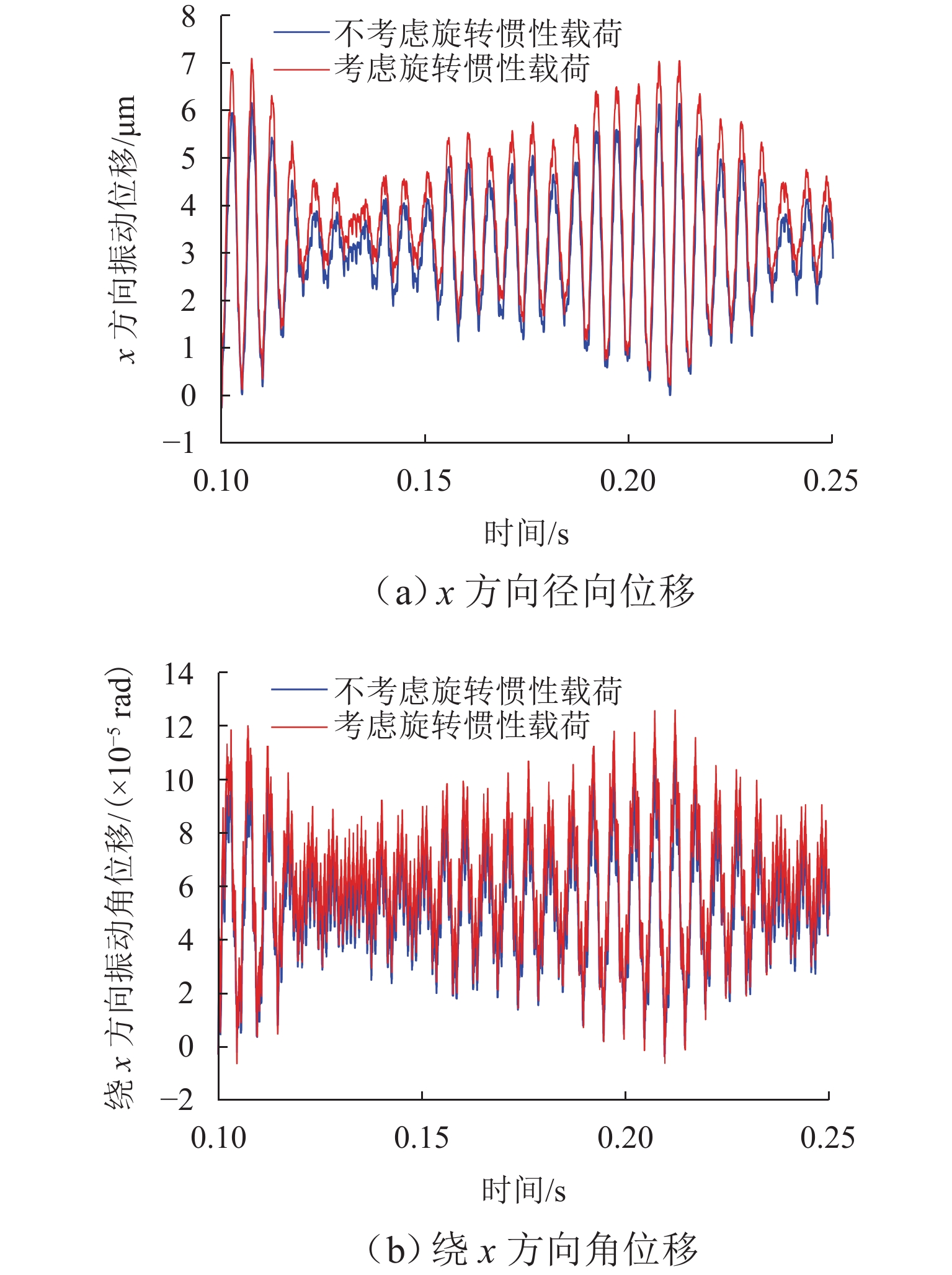
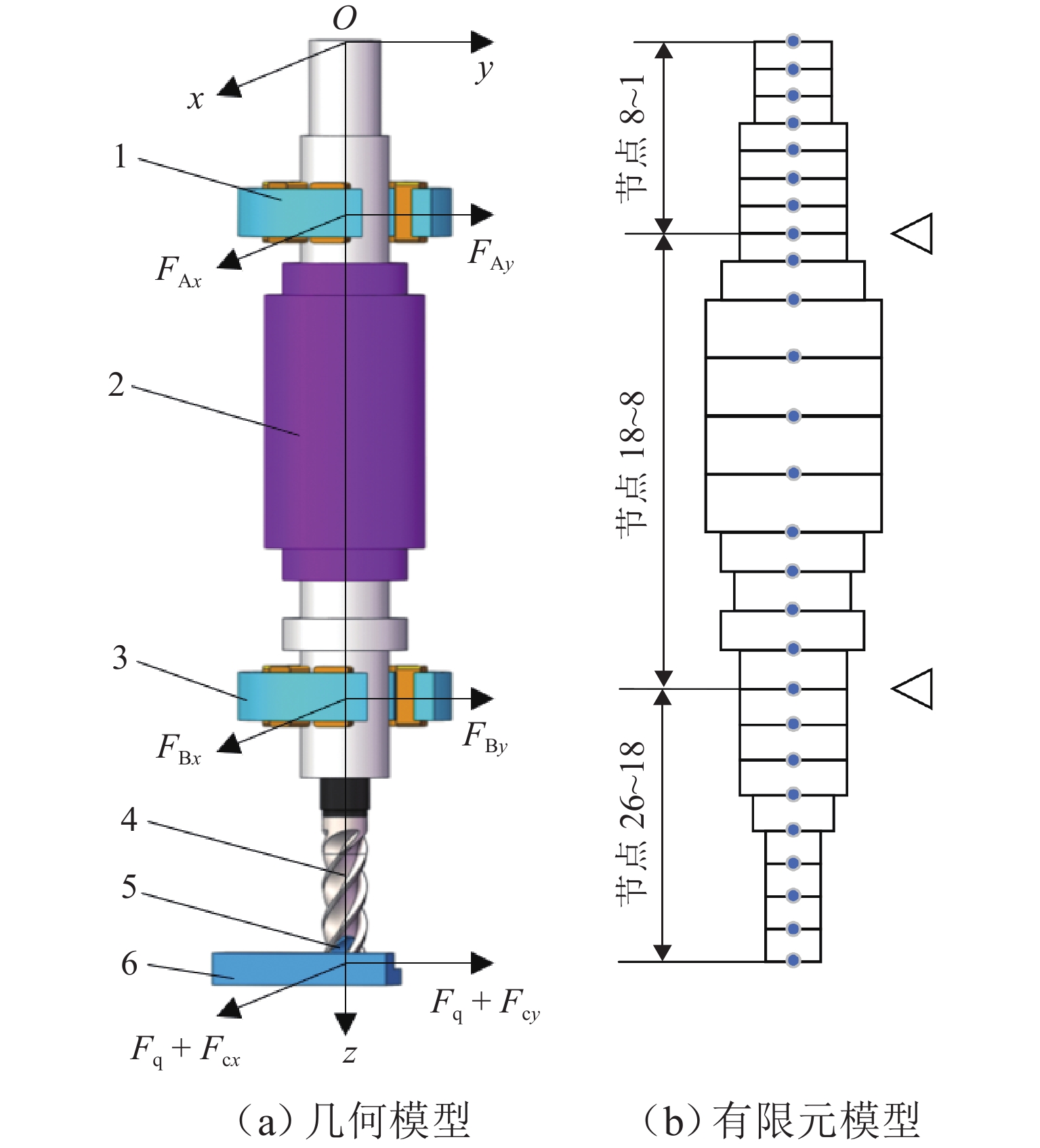
针对磁悬浮铣削电主轴在切削加工过程中，因切屑不断进入、离开刀具容屑槽导致系统质量大小和分布不断变化，进而引起系统动力学特性的非线性变化问题. 首先，依据金属连续切削原理求得单个切屑质量，并结合连续梁振动理论，应用有限单元法建立“磁悬浮轴承-电主轴-刀具-切屑”时变质量系统的动力学模型；然后，采用龙格库塔法对系统的运动微分方程进行求解，分析切屑从进入到离开容屑槽的整个过程，切屑质量变化对系统固有频率、振型的影响规律；进而探索由时变切屑质量所引起的旋转惯性载荷、陀螺力矩、切削力、磁悬浮轴承电磁力等激励下的系统振动响应规律；最后，利用MATLAB软件对系统进行仿真求解. 结果表明：切屑质量从0增大到2.08 × 10−5 kg时，系统前三阶临界转速分别下降约2.3、0.7、0.3 r/min，可知时变切屑质量对系统固有特性影响较小；旋转惯性载荷对系统的动态响应有较大影响，尤其是对切削加工点，使切削点的径向振动响应和角向振动响应的幅值出现0～9.7 × 10−7 m和0～2.5 × 10−5 rad不等的增大，还使加工点处径向振动和角向振动平衡位置的偏移距离分别增加约5.1 × 10−7 m和9.3 × 10−6 rad.
Abstract:As chips continuously enter and leave from the tool flute during the cutting process of the motorized spindle for magnetic suspension milling, the size and distribution of the system mass are constantly changing, leading to the nonlinear change of system dynamics characteristics. To address these issues, firstly, the mass of a single chip was calculated based on the principle of continuous metal cutting, and then combined with the theory of continuous beam vibration, the dynamics model of the “magnetic suspension bearing–motorized spindle–tool–chip” time-varying mass system was established by using the finite element method. Secondly, the Runge-Kutta method was used to solve the differential equation of motion of the system, and the influence of chip mass change on the natural frequency and mode shape of the system was analyzed during the entire process covering the chip’s entry into and leave from the tool flute. Then, the vibration response patterns of the system under the excitation of rotational inertial load, gyroscope torque, cutting force, and electromagnetic force of magnetic suspension bearings caused by time-varying chip mass were explored. Finally, the MATLAB software was used to simulate and solve the system. The results show that as the chip mass increases from 0 to 2.08 × 10−5 kg, the system’s first three critical speeds decrease by about 2.3, 0.7, and 0.3 r/min, respectively, indicating that the time-varying chip mass has a small effect on the system’s inherent characteristics. The rotational inertia load has a significant impact on the system’s dynamic response, especially at the cutting point, causing the radial vibration response and angular vibration response amplitudes at the cutting point to increase by 0–9.7 × 10−7 m and 0–2.5 × 10−5 rad, respectively, and it makes the radial vibration and angular vibration equilibrium positions at the cutting point to increase by about 5.1 × 10−7 m and 9.3 × 10−6 rad, respectively.
-
图 1 磁悬浮铣削电主轴系统模型示意
Figure 1. System model of motorized spindle for magnetic suspension milling
图 5 “主轴-刀具-切屑”变质量系统的坎贝尔图
Figure 5. Campbell diagram of “spindle–tool–chip” time-varying mass system
图 6 切屑质量对“主轴-刀具-切屑”变质量系统临界转速的影响
Figure 6. Influence of chip quality on critical speed of “spindle–tool–chip” time-varying mass system
图 8 磁悬浮电主轴-刀具-切屑系统振动响应
Figure 8. Vibration response of motorized spindle of magnetic suspension–tool–chip system
图 9 磁悬浮电主轴-刀具-切屑系统切削加工点的振动响应
Figure 9. Vibration response of motorized spindle of magnetic suspension–tool–chip system at cutting point
表 1 磁悬浮电主轴-刀具系统的物理几何参数
Table 1. Physical geometric parameters for motorized spindle of magnetic suspension–tool system
参数 数值 转子总长/mm 500 转子质量/kg 6.427 转子材料 30CrNiMo8 转子弹性模量/Pa 2 × 1011 刀具总长/mm 80 刀具直径/mm 16 刀具材料 W6Mo5Cr4V2Co8 工作转速/（r•min−1） 15000 磁轴承等效刚度/（N•m−1） −2 × 107 
下载: 导出CSV
-
[1] 熊万里,孙文彪,刘侃,等. 高速电主轴主动磁悬浮技术研究进展[J]. 机械工程学报,2021,57(13): 1-17.XIONG Wanli, SUN Wenbiao, LIU Kan, et al. Active magnetic bearing technology development in high-speed motorized spindles[J]. Journal of Mechanical Engineering, 2021, 57(13): 1-17. [2] 朱润生,杨作兴,赵雷,等. 主动磁轴承电主轴的磨削试验[J]. 机械工程学报,2002,38(6): 134-138.ZHU Runsheng, YANG Zuoxing, ZHAO Lei, et al. Grinding experiment using electrospindle levitated with active magnetic bearings[J]. Journal of Mechanical Engineering, 2002, 38(6): 134-138. [3] 钟志贤,祝长生. 主动磁轴承控制器对Jeffcott转子裂纹故障特征的影响[J]. 中国电机工程学报,2012,32(5): 105-110.ZHONG Zhixian, ZHU Changsheng. Effects of active magnetic bearing controller on fault characteristics of jeffcott cracked rotor[J]. Proceedings of the CSEE, 2012, 32(5): 105-110. [4] 吴超,苏振中,张贤彪,等. 磁悬浮汽轮机多盘转子动力学建模与参数辨识[J]. 中国电机工程学报,2021,41(2): 442-451.WU Chao, SU Zhenzhong, ZHANG Xianbiao, et al. Multi-disc rotordynamic modeling and parameter identification of magnetic levitation turbine[J]. Proceedings of the CSEE, 2021, 41(2): 442-451. [5] LEI S L, PALAZZOLO A. Control of flexible rotor systems with active magnetic bearings[J]. Journal of Sound and Vibration, 2008, 314(1/2): 19-38. [6] KUNG H K, HUANG B W. Vibration in a cracked machine tool spindle with magnetic bearings[J]. The Open Mechanical Engineering Journal, 2008, 2(1): 32-39. doi: 10.2174/1874155X00802010032 [7] BOUAZIZ A, BARKALLAH M, BOUAZIZ S, et al. Cutting parameters and vibrations analysis of magnetic bearing spindle in milling process[J]. Journal of Theoretical and Applied Mechanics, 2016, 54: 691-703. [8] ZHANG Y, ZHOU J, ZHANG Y B, et al. Modelling and vibration response of a magnetically suspended flexible rotor considering base motion[J]. Applied Mathematical Modelling, 2023, 118: 518-540. doi: 10.1016/j.apm.2023.01.020 [9] 陈小安,陈文曲,康辉民,等. 偏心电主轴动力学分析[J]. 重庆大学学报,2012,35(3): 26-32.CHEN Xiaoan, CHEN Wenqu, KANG Huimin, et al. Dynamic analysis of high speed motorized spindles with eccentrics[J]. Journal of Chongqing University, 2012, 35(3): 26-32. [10] 陈小安,张朋,陆永亚,等. 计电磁不平衡拉力的高速电主轴转子偏心特性研究[J]. 振动与冲击,2014,33(2): 37-40.CHEN Xiaoan, ZHANG Peng, LU Yongya, et al. Dynamic characteristics of high-speed motorized spindles affected by rotor’s eccentric mass[J]. Journal of Vibration and Shock, 2014, 33(2): 37-40. [11] 宋春生,尹睿,魏子航,等. 磁悬浮柔性转子系统解耦控制仿真[J]. 西南交通大学学报,2023,58(4): 761-772.SONG Chunsheng, YIN Rui, WEI Zihang, et al. Simulation on decoupling control of maglev flexible rotor system[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 761-772. [12] 王艺宇,周瑾,周扬,等. 考虑界面接触的磁悬浮转子高阶模态自激振动抑制研究[J]. 振动与冲击,2023,42(23): 29-40.WANG Yiyu, ZHOU Jin, ZHOU Yang, et al. Suppression of high order modal self-excited vibration of magnetic levitation rotor considering interface contact[J]. Journal of Vibration and Shock, 2023, 42(23): 29-40. [13] 彭超英,高燕青,朱均. 纺织机械变质量转子的振动机理分析[J]. 机械科学与技术,1996(1): 60-64. [14] 彭超英,陈瑞琪,朱均. 纺织机械变质量转子在不同支承下非线性自由振动研究[J]. 中国纺织大学学报,1993(3): 1-7.Peng Chaoying, CHEN Ruiqi, ZHU Jun. Study on nonlinear free vibration of variable mass rotor of textile machinery under different supports[J]. Journal of China Textile University, 1993(3): 1-7. [15] 袁龙翔. 柔性工件车削颤振分析及试验验证[D]. 沈阳:东北大学,2020. [16] CAO Z, KANG H M, LIU H C, et al. Modeling and dynamic response of variable mass system of maglev turning electric spindle[J]. Nonlinear Dynamics, 2023, 111(1): 255-274. doi: 10.1007/s11071-022-07868-8 [17] 欧阳智海,康辉民,刘厚才,等. 磁悬浮铣削电主轴转子-刀具变质量不平衡系统动态特性研究[J]. 机械工程学报,2022,58(23): 306-320.OUYANG Zhihai, KANG Huimin, LIU Houcai, et al. Study on dynamic characteristics of magnetic suspension milling motorized spindle rotor-tool variable mass unbalance system[J]. Journal of Mechanical Engineering, 2022, 58(23): 306-320. [18] 袁惠群. 转子动力学分析方法[M]. 北京:冶金工业出版社,2017. [19] MARTELLOTTI M E. An analysis of the milling process[J]. Journal of Fluids Engineering, 1941, 63(8): 677-695. [20] 杨中宝. 基于切削图形的动态铣削力建模[D]. 天津:天津理工大学,2011. [21] 洪杰,杨哲夫,孙博,等. 局部旋转惯性对转子系统动力特性的影响[J]. 航空动力学报,2022,37(4): 673-683.HONG Jie, YANG Zhefu, SUN Bo, et al. Influence of local rotary inertia on the dynamic properties of rotor systems[J]. Journal of Aerospace Power, 2022, 37(4): 673-683. [22] 王亚辉,王剑华,任亚杰. 理论力学[M]. 北京:科学出版社,2020. [23] 陈攀,康辉民,陈鹏,等. 主动磁悬浮电主轴最佳切削速度区间研究[J]. 机械科学与技术,2019,38(12): 1904-1909.CHEN Pan, KANG Huimin, CHEN Peng, et al. Research on optimal cutting speed range of active magnetic suspension electric spindle[J]. Mechanical Science and Technology for Aerospace Engineering, 2019, 38(12): 1904-1909. [24] 张耀宸. 机械加工工艺设计实用手册[M]. 北京: 航空工业出版社,1993. -
下载:
点击查看大图
计量
- 文章访问数: 30
- HTML全文浏览量: 11
- PDF下载量: 6
- 被引次数: 0