End Effect and Electromagnetic Force Characteristics of Two Adjacent Linear Induction Motors
-
摘要:
直线感应电机在中低速磁浮列车应用中两两相邻,磁场相互干涉. 为探究磁场干涉对相邻电机电磁力特性的影响,首先,基于麦克斯韦方程组建立相邻电机各区域矢量磁位方程,利用边界条件对各区域矢量磁位进行求解;然后,推导得到相邻电机气隙磁场、牵引力和法向力表达式,分析相邻电机磁场干涉对电机电磁力的影响,并利用有限元仿真对理论模型进行检验;最后,研究电机间距和滑差频率对相邻电机电磁力的影响. 研究结果表明:2台电机边端效应引起的行波相互影响,前一台电机(LIM1)受后一台电机(LIM2)影响较小,而LIM2则受LIM1影响较大;LIM2牵引力和法向力均随间距的变化产生波动,间距越小,滑差频率也越小,波动幅度越大,LIM2电磁力受间距影响波动幅度越大;当滑差频率为8 Hz、速度为160 km/h、电流为400 A时,LIM2牵引力相较LIM1最大可增加83%;LIM2法向力最大可减小6.6 kN,将大大减轻悬浮系统的负担. 研究结果可为直线电机在中低速磁浮列车中的应用提供理论指导和技术支撑.
Abstract:Objective The medium and low speed maglev is driven by linear induction motors (LIMs), which are composed of finite-length primary winding and infinite-length secondary induction rail. This configuration offers several advantages, including structural simplicity, low construction costs, and ease of maintenance. However, the structural characteristics of a discontinuous primary and a continuous secondary plate result in mutual interference of secondary eddy currents at adjacent positions. This interference alters the air-gap magnetic field of the motor, which directly impacts both the traction force and the normal force of the motor. To elucidate the influence characteristics and underlying mechanisms of adjacent motor configurations on electromagnetic forces, enhance motor traction performance, and address issues related to the normal force, this study focused on two adjacent and series-connected LIMs. Theoretical and simulation models were developed to investigate the effects of two key factors, including the motor spacing and slip frequency, on the traction and normal forces of the two motors.
Methods To investigate the influence of adjacent LIM arrangements on electromagnetic forces in medium and low speed maglev and gain a deeper understanding of the magnetic field interference between two LIMs, as well as its intrinsic effects on electromagnetic forces, firstly, vector magnetic potential equations were established for each region of the adjacent motors based on Maxwell’s equations, and the two-dimensional vector magnetic potential for each region was solved by using boundary conditions. Secondly, the expressions for the air-gap magnetic field, traction force, and normal force of the two LIMs were derived based on the air-gap vector magnetic potential and the distribution of primary currents. These expressions were used to analyze the characteristics and underlying mechanisms of how magnetic field interference between adjacent motors affects electromagnetic forces. Thirdly, a finite element analysis (FEA) model of two adjacent motors was developed by using Maxwell software to calculate the electromagnetic forces under different motor spacings. The simulation results were compared with theoretical predictions to validate the accuracy of the theoretical calculation method. Finally, the established theoretical model was utilized to explore the effects of two critical factors, including motor spacing and slip frequency, on the electromagnetic forces of the adjacent motors. By analyzing the air-gap magnetic field under various operating conditions, the study revealed the intrinsic mechanism by which the electromagnetic force of LIM2 was influenced by motor spacing.
Results The variation trends of the traction force between the two motors, as calculated through both theoretical and finite element simulation methods, exhibit a high degree of consistency, thereby validating the accuracy of the theoretical model. In the boundary conditions of the theoretical model, the magnetic permeability of the iron core and back iron is assumed to be infinite, and the primary current is approximated as a thin layer. Consequently, the theoretical calculations yield slightly larger fluctuations in the traction force of LIM2 with respect to motor spacing compared to the simulation results.From the expression of the air-gap magnetic field of the motor, the backward traveling wave caused by the end effect at the exit of LIM1 is influenced by factors such as the primary current, slip frequency, and motor spacing of LIM2. Similarly, the forward traveling wave caused by the end effect at the entry of LIM2 is affected by the parameters of LIM1 and the spacing between the two motors. Consequently, the air-gap magnetic field of the linear motor is altered due to the influence of the adjacent motor. The impact of adjacent motor arrangements on the longitudinal air-gap magnetic field is relatively minor, whereas the effect on the vertical air-gap magnetic field is more pronounced. This influence leads to corresponding variations in the motor’s traction force and normal force. As the motor is less affected by the backward traveling wave induced by the exit-end effect and more significantly affected by the forward traveling wave induced by the entry-end effect, LIM1 is less affected by LIM2, whereas LIM2 is more significantly influenced by LIM1.The computational results indicate that the traction force of LIM1 is nearly unaffected by motor spacing and exhibits minimal variation under different slip frequencies. For various slip frequencies, the operating speed and input current of LIM1 remain consistent, resulting in negligible differences. In contrast, for LIM2, as the slip frequency is smaller, its traction force is more significantly influenced by motor spacing. As the spacing increases, the amplitude of traction force fluctuations for LIM2 decreases across all slip frequencies. When the slip frequency is 8 Hz, and the spacing is 1.5 times the pole pitch, the traction force of LIM2 reaches 8.4 kN, which is 1.83 times that of LIM1 (4.6 kN), representing an 83% increase. Conversely, when the spacing is reduced to 0.6 times the pole pitch, the traction force of LIM2 drops to 0.6 kN, which is merely 13% of LIM1’s traction force, signifying an 87% reduction. These results underscore the importance of spacing design in optimizing the traction performance of LIM2.Furthermore, as the slip frequency decreases, the normal force of LIM1 increases. However, the normal force of LIM1 is almost unaffected by the motor spacing at different slip frequencies. In contrast, the normal force of LIM2 exhibits fluctuations with varying spacing under different slip frequencies. Smaller spacing and slip frequencies lead to a greater impact on the normal force of LIM2. A well-designed motor spacing can effectively reduce the normal force of LIM2, thereby enhancing the stability of maglev vehicles. When the slip frequency is 8 Hz, and the motor spacing is 2.1 times the pole pitch, the normal force of LIM2 is 1 kN, which is 6.6 kN lower than that of LIM1 measured at 7.6 kN. This reduction translates to a weight decrease of 660 kg per motor for the levitation system. However, when the motor spacing is reduced to 1.2 times the pole pitch, the normal force of LIM2 rises dramatically to 28.2 kN, which is 3.7 times greater than that of LIM1, representing a 270% increase. This additional force imposes approximately two tons of extra load on the levitation system per motor.
Conclusion The electromagnetic force of a rear-positioned LIM is significantly influenced by the presence of a front-positioned LIM, as well as the spacing between the motors. However, the optimal spacing for achieving the desired traction force and normal force varies under different operating conditions and system requirements. Therefore, in practical engineering applications, both the traction demands and levitation capabilities of the vehicle should be considered for the design of the motor spacing. The findings can provide theoretical guidance and technical support for the application of LIMs in medium and low speed maglev trains. However, due to the complexity of LIM theoretical derivations and the numerous parameters involved, certain idealized assumptions and simplifications are necessary during the mathematical analysis. The quantitative results presented should be interpreted as reference values, and the results of the study are based on two-dimensional electromagnetic field theory. Future research may explore the electromagnetic interaction between adjacent motors by using three-dimensional field models to achieve more precise findings.
-
Key words:
- medium and low speed maglev /
- linear induction motor /
- spacing /
- slip frequency /
- electromagnetic force
-
1. 前 言
中低速磁浮列车由于噪声低、转弯半径小、线路设计灵活、经济性好等优势越来越受到各国的青睐[1-3],通常应用于机场接驳线、景区旅游环线、市内通勤线和城际交通线等[4]. 直线感应电机(linear induction motor, LIM)结构简单、无需中间转换与传力装置、经济性好,常用于磁浮列车、地铁车辆以及电磁发射系统[5],因此中低速磁浮列车采用直线感应电机进行驱动.
在中低速磁浮列车中,LIM由有限长的初级绕组和无限长的次级感应轨组成,结构简单、造价低、便于维护. 然而,LIM存在一些不可避免的问题,例如法向吸力会增加悬浮系统的负担、效率低下使列车牵引耗能较大以及动态端部效应限制运行速度的提升[6,7]. 为提高LIM的牵引性能和运行效率,学者们在初级绕组参数优化、次级结构优化、控制策略优化等方面进行了大量的研究. Mishima等[8]通过优化初级绕组分布得到最佳气隙磁密分布,从而得到最优的推力效果. Lv等[9-11]展开了帽形、梯缝形、V形和双梯缝形次级结构对电机牵引性能和运行效率的影响研究,研究结果表明:梯缝次级结构可减小横向力和边缘效应,是实现轨道车辆横向稳定的一种较好方法;V形次级可减少谐波分量,提高电机性能;非对称梯缝比对称梯缝次级结构更能有效的减小横向边端效应.邓江明等[12,13]通过优化电机运行中的滑差频率得到较优的牵引力和法向力输出. Seo等[14]通过有限元分析获得较低法向力对应的滑差频率范围,然后反映到控制算法中,从而实现电机的低法向力控制. Wang等[15]通过动态调节d、q轴参考电流以及相应的闭环控制,将电机的输出推力移至峰值工作点附近,在不增加初级电流的情况下,提高LIM的牵引力. Han等[16]提出了一种实时修改滑差频率和转矩电流的矢量控制策略和弱磁场控制方法,该方法使LIM能够克服高速时的推力衰减. 为减小大气隙、边端效应和谐波等因素引起的损耗问题,Xiao等[17,18]建立了考虑电机损耗的控制模型,从而使电机的损耗为最小. Elmorshedy等[19,20]建立了不同的控制模型,用以提高LIM的效率,减小推力波动,提高电机的瞬态性能.
通过上述研究,LIM的牵引效能和法向力问题均得到一定程度的改善. 在中低速磁浮列车的运用中,LIM沿纵向排列,首尾相邻[21,22]. 在此运行环境下,LIM的纵向边端效应变化情况,及对电机电磁力的影响值得深入探讨. 在中低速磁浮列车中,电机初级开断,但次级板连续,次级感应涡流在电机相邻处必然相互干涉. 次级电流的相互干涉将改变电机的气隙磁场,而气隙磁场的改变将影响电机牵引力和法向力. 采用一维场理论对该问题进行研究表明,电机的边端效应等效系数会受到相邻电机的影响,从而影响电机的电压、电流和牵引力等指标[23,24]. 一维场理论中电机气隙磁场只考虑垂向分量,未考虑纵向分量,因此不能计算电机法向力. 为检验一维场分析结果的正确性,深入掌握相邻电机的相互影响,改善电机的牵引性能和法向力问题. 本文基于二维电磁场理论对相邻电机各区域的矢量磁位和电磁场进行求解,对相邻电机纵向动态边端效应等效系数进行表征. 二维场理论中磁场考虑了垂向分量和纵向分量,可同时计算电机牵引力和法向力,从而深入分析间距和滑差频率对2种力的影响,提出改善电机牵引性能和法向力问题的措施.
2. 基于二维场理论的相邻电机电磁场分析
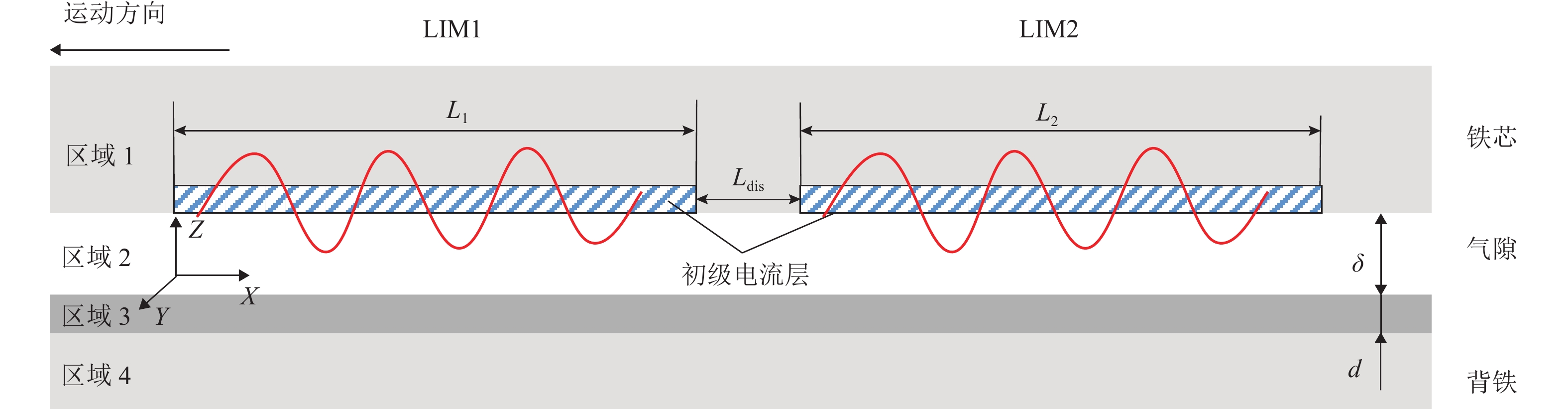
在中低速磁浮列车中,直线电机纵向排布,两两前后相邻,如图1所示. 为对实际应用中相邻两台电机电磁力特性进行分析,建立与之对应的二维场理论模型,如图2所示. 图中:Ldis为两段电流层的空间间距,L1、L2分别为电机LIM1、LIM2的长度,d为次级板厚度,δ为电机气隙
引入矢量磁位的麦克斯韦方程组,如式(1)所示.
\left\{ \begin{gathered} {\boldsymbol{B}} = \nabla {\boldsymbol{A}} , \\ {\boldsymbol{E}} = - \frac{{\partial {\boldsymbol{A}}}}{{\partial t}}, \\ \nabla \cdot {\boldsymbol{A}} = 0 , \\ {\nabla ^2}{\boldsymbol{{A}}} = {\mu _0}\sigma \left[ {\frac{{\partial {\boldsymbol{A}}}}{{\partial t}} - {{\boldsymbol{v}}_x} \nabla {\boldsymbol{A}}} \right] , \\ \end{gathered} \right. (1) 式中:B为磁通密度,A为矢量磁位,E为电场强度,μ0为真空磁导率,\sigma 为电导率,vx为速度,t为时间,\nabla 为微分算子,{\nabla ^2}为拉普拉斯算子.
为对理论模型进行求解,作如下假设:
假设1 气隙磁场只有x分量和z分量,即磁场不随横向(y方向)变化;
假设2 区域1为初级铁心,磁导率为 + ∞,电导率为0;
假设3 区域2为初级与次级之间的气隙,磁导率为 {\mu }_{0} ,电导率为0;
假设4 区域3为次级铝板,磁导率为 {\mu }_{0} ,电导率为 \sigma ;
假设5 区域4为次级背铁,磁导率为 + ∞,电导率为0.
边界条件:1) 区域1、2边界上有电流层 {j}_{1} ;2) 区域1、2边界上的磁感应强度法向分量相等;3)区域2、3边界上的磁场强度切向分量相等;4) 区域2、3边界上的磁感应强度法向分量相等;5) 区域3、4边界上的磁场强度切向分量相等;6)区域3、4边界上的磁感应强度法向分量相等.
初级电流层 {{{j}}}_{1} 由两部分组成,如式(2)所示.
{j_1} = \left\{ \begin{gathered} 0 , \quad {x < 0,} \\ {J_1}{e^{{\text{j}}(\omega t - kx)}}, \quad{0 \leqslant x \leqslant {L_1}}, \\ 0,\quad {{L_1} < x < {L_1} + {\mathrm{dis}},} \\ {J_2}{e^{{\text{j}}\left[ {\omega t - k\left( {x - {L_1} - {\mathrm{dis}}} \right) - \varphi } \right]}}, {{{L_1} +{\mathrm{ dis}} \leqslant x \leqslant {L_1} + {L_2} + {\mathrm{dis}}}}, \\ 0 ,\quad{ {x > {L_2} + {\mathrm{dis}}}}, \\ \end{gathered} \right. (2) 式中: {J}_{1}、{J}_{2} 分别为LIM1和LIM2电流密度幅值;{L_1}、{L_2}分别为电机LIM1和LIM2的长度;\omega 为角速度;\varphi 为相位差;x为纵向坐标 k=\text{π} /\tau , \tau 为电机极距.
基于式(1)中矢量磁位的一般电磁场方程可得二维场条件下各区域矢量磁位,如式(3)所示
\left\{ \begin{gathered} \dfrac{{{\partial ^2}{A_1}}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}{A_1}}}{{\partial {{\textit{z}}^2}}} = 0 , \\ \dfrac{{{\partial ^2}{A_2}}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}{A_2}}}{{\partial {{\textit{z}}^2}}} = 0, \\ \dfrac{{{\partial ^2}{A_3}}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}{A_3}}}{{\partial {{\textit{z}}^2}}} = {\mu _0}\sigma \left( {\dfrac{{\partial {A_3}}}{{\partial t}} + {v_x}\dfrac{{\partial {A_3}}}{{\partial x}}} \right) , \\ \dfrac{{{\partial ^2}{A_4}}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}{A_4}}}{{\partial {{\textit{z}}^2}}} = 0 , \\ \end{gathered} \right. (3) 式中:Ai为区域i的矢量磁位,i = 1,2,3,4;z为垂向坐标.
利用边界条件对各区域矢量磁位进行求解,可得各区域矢量磁位分布. 具体求解过程请参考文献[25],限于论文篇幅,此处不作详细介绍. 由气隙区域矢量磁位可得垂、纵向气隙磁场,如式(4)~(13)所示.
{B_{2{\textit{z}}}} = \left\{ \begin{gathered} \frac{{ - {\text{i}}{\xi _2}{\mu _0}({B_{A2}} - {B_{B2}} + {B_{C2}} - {B_{D2}})}}{{{\xi _2}\left( {k + {\xi _2}} \right)}}\frac{{{G_2}\left( {{\xi _2},{\textit{z}}} \right)}}{{{H^{'}}\left( {{\xi _2}} \right)}}\begin{array}{*{20}{c}} ,&{x < 0} \end{array}, \\ - \frac{{{\text{i}}{\xi _1}{\mu _0}{B_{A1}}}}{{{\xi _1}\left( {k + {\xi _1}} \right)}}\frac{{{G_2}\left( {{\xi _1},{\textit{z}}} \right)}}{{{H^{'}}\left( {{\xi _1}} \right)}} + \frac{{{\text{i}}k{\mu _0}{J_1}{{\text{e}}^{ - {\text{i}}kx}}}}{{ - k}}\frac{{{G_2}\left( { - k,{\textit{z}}} \right)}}{{H\left( { - k} \right)}} - \frac{{{\text{i}}{\xi _2}{\mu _0}( - {B_{B2}} + {B_{C2}} - {B_{D2}})}}{{{\xi _2}\left( {k + {\xi _2}} \right)}}\frac{{{G_2}\left( {{\xi _2},{\textit{z}}} \right)}}{{{H^{'}}\left( {{\xi _2}} \right)}}\begin{array}{*{20}{c}} ,&{0 < x < {L_1},} \end{array} \\ - \frac{{{\text{i}}{\xi _1}{\mu _0}({B_{A1}} - {B_{B1}})}}{{{\xi _1}\left( {k + {\xi _1}} \right)}}\frac{{{G_2}\left( {{\xi _1},{\textit{z}}} \right)}}{{{H^{'}}\left( {{\xi _1}} \right)}} - \frac{{{\text{i}}{\xi _2}{\mu _0}({B_{C2}} - {B_{D2}})}}{{{\xi _2}\left( {k + {\xi _2}} \right)}}\frac{{{G_2}\left( {{\xi _2},{\textit{z}}} \right)}}{{{H^{'}}\left( {{\xi _2}} \right)}}\begin{array}{*{20}{c}} ,&{{L_1} < x < {L_1} + {L_{dis}},} \end{array} \\ - \frac{{{\text{i}}{\xi _1}{\mu _0}({B_{A1}} - {B_{B1}} + {B_{C1}})}}{{{\xi _1}\left( {k + {\xi _1}} \right)}}\frac{{{G_2}\left( {{\xi _1},{\textit{z}}} \right)}}{{{H^{'}}\left( {{\xi _1}} \right)}} + \frac{{{\text{i}}k{\mu _0}{J_2}{{\text{e}}^{{\text{i}}k\left( {{L_{dis}} + {L_1}} \right) - {\text{i}}\varphi }}{{\text{e}}^{ - {\text{i}}kx}}}}{{ - k}}\frac{{{G_2}\left( { - k,{\textit{z}}} \right)}}{{H\left( { - k} \right)}} + \\ \quad \frac{{{\text{i}}{\xi _2}{\mu _0}{B_{D2}}}}{{{\xi _2}\left( {k + {\xi _2}} \right)}}\frac{{{G_2}\left( {{\xi _2},{\textit{z}}} \right)}}{{{H^{'}}\left( {{\xi _2}} \right)}}\begin{array}{*{20}{c}} ,&{{L_1} + {L_{dis}} < x < {L_1} + {L_2} + {L_{dis}},} \end{array} \\ - \frac{{{\text{i}}{\xi _1}{\mu _0}({B_{A1}} - {B_{B1}} + {B_{C1}} - {B_{D1}})}}{{{\xi _1}\left( {k + {\xi _1}} \right)}}\frac{{{G_2}\left( {{\xi _1},{\textit{z}}} \right)}}{{{H^{'}}\left( {{\xi _1}} \right)}}\begin{array}{*{20}{c}} ,&{x > {L_1} + {L_2} + {L_{dis}},} \end{array} \\ \end{gathered} \right. (4) {B}_{2x}=\left\{\begin{array}{l}\dfrac{{\mu }_{0}\left[{B}_{A2}-{B}_{B2} + {B}_{C2}-{B}_{F2}{\left(2x-{L}_{dis}-{L}_{1}-{L}_{2}\right)}^{-1}\right]}{{\xi }_{2}\left(k + {\xi }_{2}\right)}\dfrac{{G}_{2}{}^{\text{'}}\left({\xi }_{2},{\textit{z}}\right)}{{H}^{\text{'}}\left({\xi }_{2}\right)}\begin{array}{cc},& x < 0,\end{array}\\ \dfrac{{\mu }_{0}{B}_{A1}}{{\xi }_{1}\left(k + {\xi }_{1}\right)}\dfrac{{G}_{2}{}^{\text{'}}\left({\xi }_{1},{\textit{z}}\right)}{{H}^{\text{'}}\left({\xi }_{1}\right)} + \dfrac{{\mu }_{0}{J}_{1}{\text{e}}^{-\text{i}kx}}{-k}\dfrac{{G}_{2}{}^{\text{'}}\left(-k,{\textit{z}}\right)}{H\left(-k\right)} + \dfrac{{\mu }_{0}\left[-{B}_{B2} + {B}_{C2}-{B}_{D2}{\left(2x-{L}_{dis}-{L}_{1}-{L}_{2}\right)}^{-1}\right]}{{\xi }_{2}\left(k + {\xi }_{2}\right)}\\ \dfrac{{G}_{2}{}^{\text{'}}\left({\xi }_{2},{\textit{z}}\right)}{{H}^{\text{'}}\left({\xi }_{2}\right)}\begin{array}{cc},& 0 < x < {L}_{1}\end{array},\\ \quad \dfrac{{\mu }_{0}({B}_{A1}-{B}_{B1})}{{\xi }_{1}\left(k + {\xi }_{1}\right)}\dfrac{{G}_{2}{}^{\text{'}}\left({\xi }_{1},{\textit{z}}\right)}{{H}^{\text{'}}\left({\xi }_{1}\right)} + \dfrac{{\mu }_{0}\left[{B}_{C2}-{B}_{D2}{\left(2x-{L}_{dis}-{L}_{1}-{L}_{2}\right)}^{-1}\right]}{{\xi }_{2}\left(k + {\xi }_{2}\right)}\dfrac{{G}_{2}{}^{\text{'}}\left({\xi }_{2},{\textit{z}}\right)}{{H}^{\text{'}}\left({\xi }_{2}\right)}\begin{array}{cc},& {L}_{1} < x < {L}_{1} + {L}_{dis}\end{array},\\ \dfrac{{\mu }_{0}({B}_{A1}-{B}_{B1} + {B}_{C1})}{{\xi }_{1}\left(k + {\xi }_{1}\right)}\dfrac{{G}_{2}{}^{\text{'}}\left({\xi }_{1},{\textit{z}}\right)}{{H}^{\text{'}}\left({\xi }_{1}\right)} + \dfrac{{\mu }_{0}{J}_{2}{\text{e}}^{\text{i}k\left({L}_{dis} + {L}_{1}\right)-\text{i}\phi }{\text{e}}^{-\text{i}kx}}{-k}\dfrac{{G}_{2}{}^{\text{'}}\left(-k,{\textit{z}}\right){\left(2x-dis-{L}_{1}-{L}_{2}\right)}^{-1}}{H\left(-k\right)}-\\ \quad \dfrac{{\mu }_{0}{B}_{F2}}{{\xi }_{2}\left(k + {\xi }_{2}\right)}\dfrac{{G}_{2}{}^{\text{'}}\left({\xi }_{2},{\textit{z}}\right)}{{H}^{\text{'}}\left({\xi }_{2}\right)}\text{,}{L}_{1} + {L}_{dis} < x < {L}_{1} + {L}_{2} + {L}_{dis},\\ \dfrac{{\mu }_{0}\left[{B}_{A1}-{B}_{B1} + {B}_{C1}-{B}_{D1}{\left(2x-{L}_{dis}-{L}_{1}-{L}_{2}\right)}^{-1}\right]}{{\xi }_{1}\left(k + {\xi }_{1}\right)}\dfrac{{G}_{2}{}^{\text{'}}\left({\xi }_{1},{\textit{z}}\right)}{{H}^{\text{'}}\left({\xi }_{1}\right)}\begin{array}{cc},& x > {L}_{1} + {L}_{2} + {L}_{dis}\end{array},\end{array}\right. (5) {B_{Am}} = {J_1}{{\text{e}}^{{\text{i}}{\xi _m}x}}\begin{array}{*{20}{c}} ,&{m = 1,2} \end{array}, (6) {B_{Bm}} = {J_1}{{\text{e}}^{{\text{i}}{\xi _m}\left( {x - {L_1}} \right)}}{{\text{e}}^{ - {\text{i}}{L_1}k}}, (7) {B_{Cm}} = {J_2}{{\text{e}}^{{\text{i}}k\left( {{L_{dis}} + {L_1}} \right) - {\text{i}}\varphi }}{{\text{e}}^{ - {\text{i}}\left( {{L_{dis}} + {L_1}} \right)k}}{{\text{e}}^{{\text{i}}{\xi _m}\left( {x - {L_{dis}} - {L_1}} \right)}}, (8) \begin{split} & {B_{Dm}} = {J_2}\left( {2x - {L_{dis}} - {L_1} - {L_2}} \right){{\text{e}}^{{\text{i}}k\left( {{L_{dis}} + {L_1}} \right) - {\text{i}}\varphi }} \times \\& \quad {{\text{e}}^{ - {\text{i}}\left( {{L_{dis}} + {L_1} + {L_2}} \right)k}}{{\text{e}}^{{\text{i}}{\xi _m}x\left( {x - {L_{dis}} - {L_1} - {L_2}} \right)}}, \\ \end{split} (9) H\left( {{\xi _m}} \right) = \left( { - 1 + {{\text{e}}^{2\delta {\xi _m}}}} \right){\xi _m} + \left( {1 + {{\text{e}}^{2\delta {\xi _m}}}} \right){r_m}\tanh (d \cdot {r_m}) \text{,} (10) \begin{split} & {G_2}\left( {{\xi _m},{\textit{z}}} \right) = \left[ \left( {{{\text{e}}^{2d{\xi _m}}} + {{\text{e}}^{2{\textit{z}}{\xi _m}}}} \right){\xi _m} - \left( {{{\text{e}}^{2d{\xi _m}}} - {{\text{e}}^{2{\textit{z}}{\xi _m}}}} \right)\right. \\ & \left. \quad {r_m}\tanh (d{r_m}) \right] \times {{\text{e}}^{ - \left( {d + {\textit{z}} - \delta } \right){\xi _m}}}, \\ \end{split} (11) \begin{split} & {\xi _1} = \left( { - \sqrt { -4{\text{i}}d\left( {d + \delta } \right)\sigma \omega {\mu _0} - {d^2}{\sigma ^2}v_x^2\mu _0^2} - {\text{i}}d\sigma {v_x}{\mu _0}} \right) \times \\ &\quad \frac{1}{{2\left( {d + \delta } \right)}}, \end{split} (12) \begin{split} & {\xi _2} = \left( { - {\text{i}}d\sigma {v_x}{\mu _0} + \sqrt { - 4{\text{i}}d\left( {d + \delta } \right)\sigma \omega {\mu _0} - {d^2}{\sigma ^2}v_x^2\mu _0^2} } \right) \times \\& \quad \frac{1}{{2\left( {d + \delta } \right)}}, \end{split} (13) {r_m}^2 = {\xi _m}^2 + {\text{j}}{\mu _0}\sigma \omega + {\text{j}}{\mu _0}\sigma {v_x}{\xi _m} 式中:Bix为区域i纵向气隙磁场,Biz为区域i垂向气隙磁场;
由气隙磁场表达式可见,LIM2的初级电流幅值、相位以及2台电机间距等因素将影响LIM1出口端边端效应引起的逆向行波,LIM1的初级电流和电机间距等将影响LIM2入口端边端效应引起的正向行波. 由此可见,2台相邻电机气隙磁场相互影响,而气隙磁场的改变必将导致电机电磁力的变化.
基于两电机初级电流分布及二维场理论分析得到的气隙磁场分布,可得两相邻电机的牵引力表达式,如式(14)~(15)所示.法向力表达式,如式(16)~(17)所示.
{F_{Fx}} = 2a\int_0^{{L_1}} {{Re} \left[ {{j_1}\left( {x,t} \right)} \right]} {Re} \left[ {{B_{2{\textit{z}}}}\left( {x,\delta + d,t} \right)} \right]dx, (14) {F_{Bx}} = 2a\int_{{L_1} + {\mathrm{dis}}}^{{L_1} + {\mathrm{dis}} + {L_2}} {{Re} \left[ {{j_1}\left( {x,t} \right)} \right]} {Re} \left[ {{B_{2{\textit{z}}}}\left( {x,\delta + d,t} \right)} \right]dx , (15) \begin{split} & {F_{F{\textit{z}}}} = \frac{{2a}}{{{\mu _0}}}\int_0^{{L_1}} {{Re} {{\left[ {{B_{2{\textit{z}}}}\left( {x,\delta + d,t} \right)} \right]}^2}} dx + \\& \quad a\int_0^{{L_1}} {{Re} \left[ {{j_1}\left( {x,t} \right)} \right]} {Re} \left[ {{B_{2x}}\left( {x,\delta + d,t} \right)} \right]dx , \\[-1pt]\end{split} (16) \begin{split} & {F_{B{\text{{\textit{z}}}}}} = \frac{{2a}}{{{\mu _0}}}\int_{{L_1} + {\mathrm{dis}}}^{{L_1} + {\mathrm{dis}} + {L_2}} {{Re} {{\left[ {{B_{2{\textit{z}}}}\left( {x,\delta + d,t} \right)} \right]}^2}} dx + \\& \quad a\int_{{L_1} + {\mathrm{dis}}}^{{L_1} + {\mathrm{dis}} + {L_2}} {{Re} \left[ {{j_1}\left( {x,t} \right)} \right]} {Re} \left[ {{B_{2x}}\left( {x,\delta + d,t} \right)} \right]dx , \end{split} (17) 式中:2a为电机初级铁芯宽度; {F}_{Fx} 为前一台电机牵引力; {F}_{Bx} 为后一台电机牵引力; {F}_{F{\textit{z}}} 为前一台电机法向力; {F}_{B{\textit{z}}} 为后一台电机法向力.
3. 模型检验
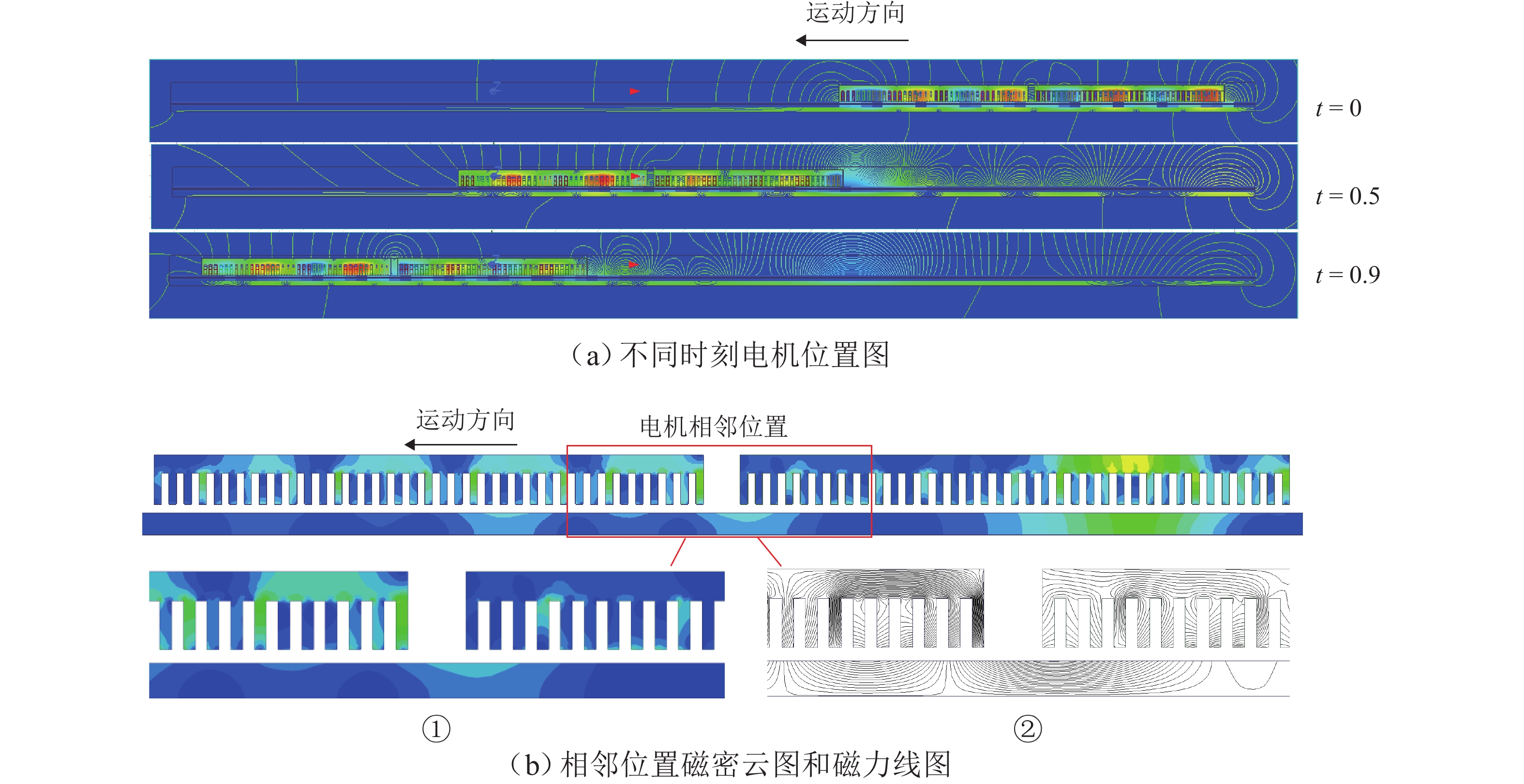
目前尚未搭建可进行2台直线电机运转的试验台,因此无法用试验结果对理论模型中LIM2电磁力变化进行直接检验. 但前期工作中搭建了单台电机试验台,并基于上述理论建立单台电机理论模型,该理论模型已在文献[13]中利用试验数据进行验证,证明了理论计算方法的正确性. 此外,本文建立了2台相邻电机有限元模型对理论模型进行检验. 由于计算工况较多,越大的有限元模型耗时越长,本节采用的电机极数为4极,即电机长度为表1电机的1/3,其余结构参数与表1一致. 模型仿真速度为100 km/h,相电流为400 A,滑差频率为12 Hz. 图3(a)所示为不同时刻模型的状态,当t=0时,电机在右端初始位置;随着时间的推移,2台电机运行到左端. 图3(b)所示为电机相邻位置的磁密云图(①)和磁力线图(②),可以看到,由于电机初级的断开,初级部分的磁场并不连续,而次级板上的磁场是连续的. 在相邻位置的次级感应板上,LIM1尾端磁场离开产生的涡流和LIM2前端磁场进入产生的涡流相互干涉,从而影响次级及气隙磁场的分布,这是导致2台电机电磁力不同的根本原因.
表 1 电机参数Table 1. Motor parameter名称 大小 名称 大小 电机长度/mm 2850 电机容量/(kV•A) 250 电机宽度/mm 220 额定相电压/V 212 极数/极 12 额定相电流/A 400 极距/mm 220 气隙/mm 10 相数 3 滑差频率/Hz 12 每极每相槽数 3 单相有效串联匝数/匝 72 次级板电阻率/
(Ω•m)2.83×10−8 次级板厚/mm 4 分别采用理论模型和仿真模型对采用不同间距的2台电机牵引力进行计算,图4为计算结果,可以发现牵引力随间距的变化趋势一致,只是幅值有所差异. 幅值的差异是因为理论计算中对铁芯和背铁的磁导率考虑为无穷大,且未考虑磁饱和,因此理论计算结果稍大于仿真值. 由于搭建的理论模型和仿真模型均沿X轴负向运动,所以得到的牵引力也为负值. 由图可见,LIM1牵引力受间距影响较小,LIM2牵引力随间距变化而波动,时而大于LIM1,时而小于LIM1;且间距越小,LIM2牵引力波动幅度越大. 合理的间距可有效提高LIM2的牵引力,而不合理的间距将大幅减小LIM2的牵引力.
4. 滑差频率与间距对LIM1和LIM2电磁力的影响
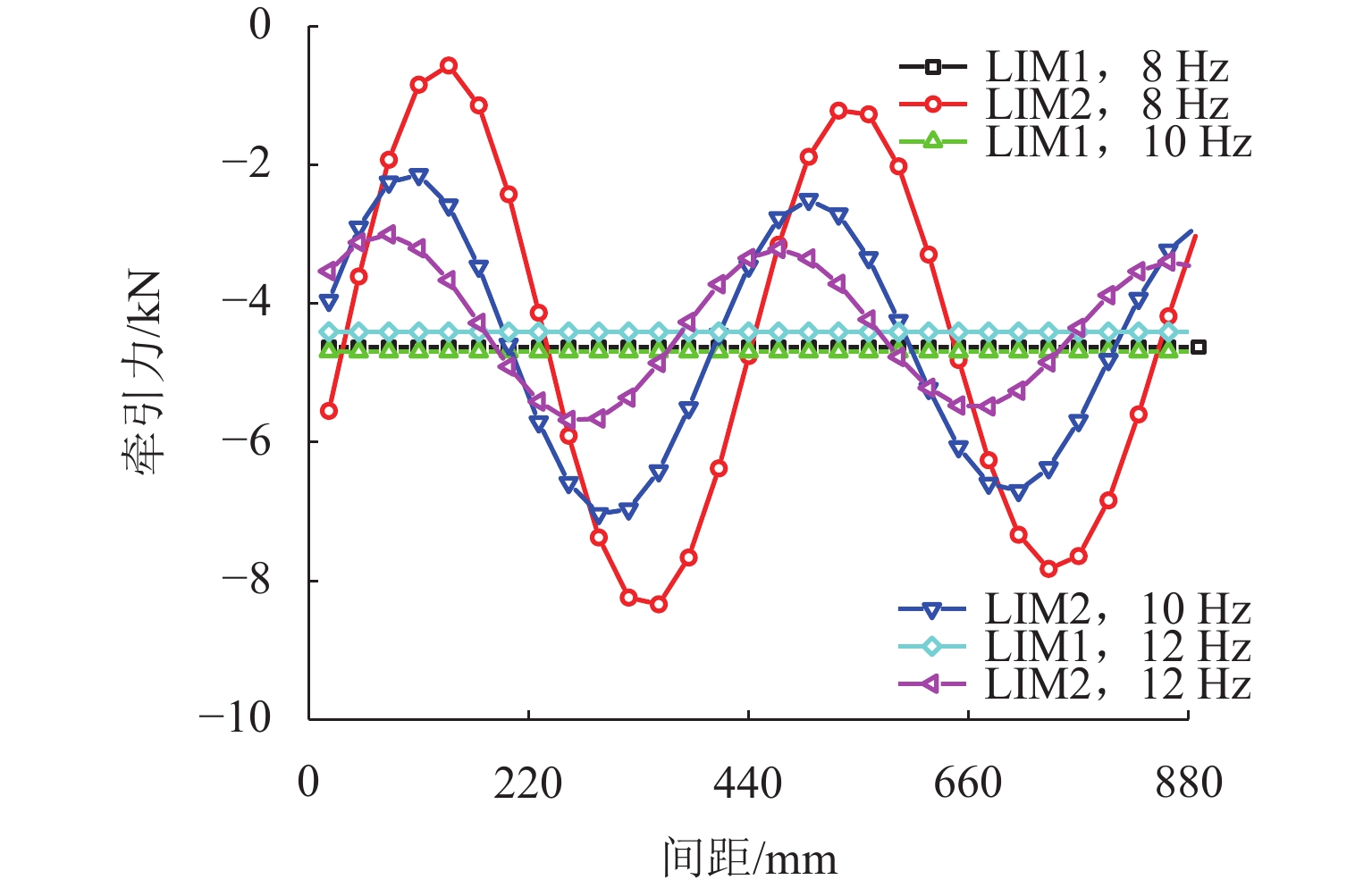
本节分析中电机结构参数如表1所示,图5为滑差频率分别为8、10和12 Hz时2台电机牵引力与间距的关系曲线. 由图可见,LIM1牵引力几乎不受间距的影响,不同滑差频率下变化也较小,这是因为3种滑差频率下电机的运行速度和输入电流相同,所以差异较小. 而对于LIM2,滑差频率越小,其牵引力受间距影响越大. 随着间距的增大,不同滑差频率下LIM2牵引力波动幅度均减小. 当滑差频率为8 Hz,间距为1.5倍极距时,LIM2的牵引力为8.4 kN,是LIM1牵引力4.6 kN的1.83倍,增加了83%;当间距为0.6倍极距时,LIM2的牵引力为0.6 kN,是LIM1牵引力的13%,削弱了87%. 由此可见,间距的设计对LIM2牵引性能的发挥至关重要.
图6为不同滑差频率下2台电机法向力随间距的变化曲线. 由图可见,滑差频率越小,LIM1法向力越大,但不同滑差频率下LIM1法向力几乎不受间距的影响. 然而,LIM2法向力在不同滑差频率下随间距的变化波动,间距和滑差频率越小,LIM2法向力受影响越大. 合理的间距设计可使LIM2法向力得到有效降低,更利于磁浮车辆的稳定运行. 当滑差频率为8 Hz、间距为2.1倍极距时,LIM2法向力为1 kN,比LIM1法向力7.6 kN减小了6.6 kN,即单台电机为悬浮系统减轻了660 kg的重量;当间距为1.2倍极距时,LIM2法向力为28.2 kN,是LIM1法向力的3.7倍,增大了270%,即一台电机给悬浮系统额外增加了约2吨的负担. 此外,LIM2法向力和牵引力在不同滑差频率下随间距的变化步调并不一致,即不同工况、不同需求下电机的较佳间距并不相同,所以电机间距和滑差频率的选择应综合考虑车辆的悬浮能力和牵引力需求.
5. 气隙磁场分析
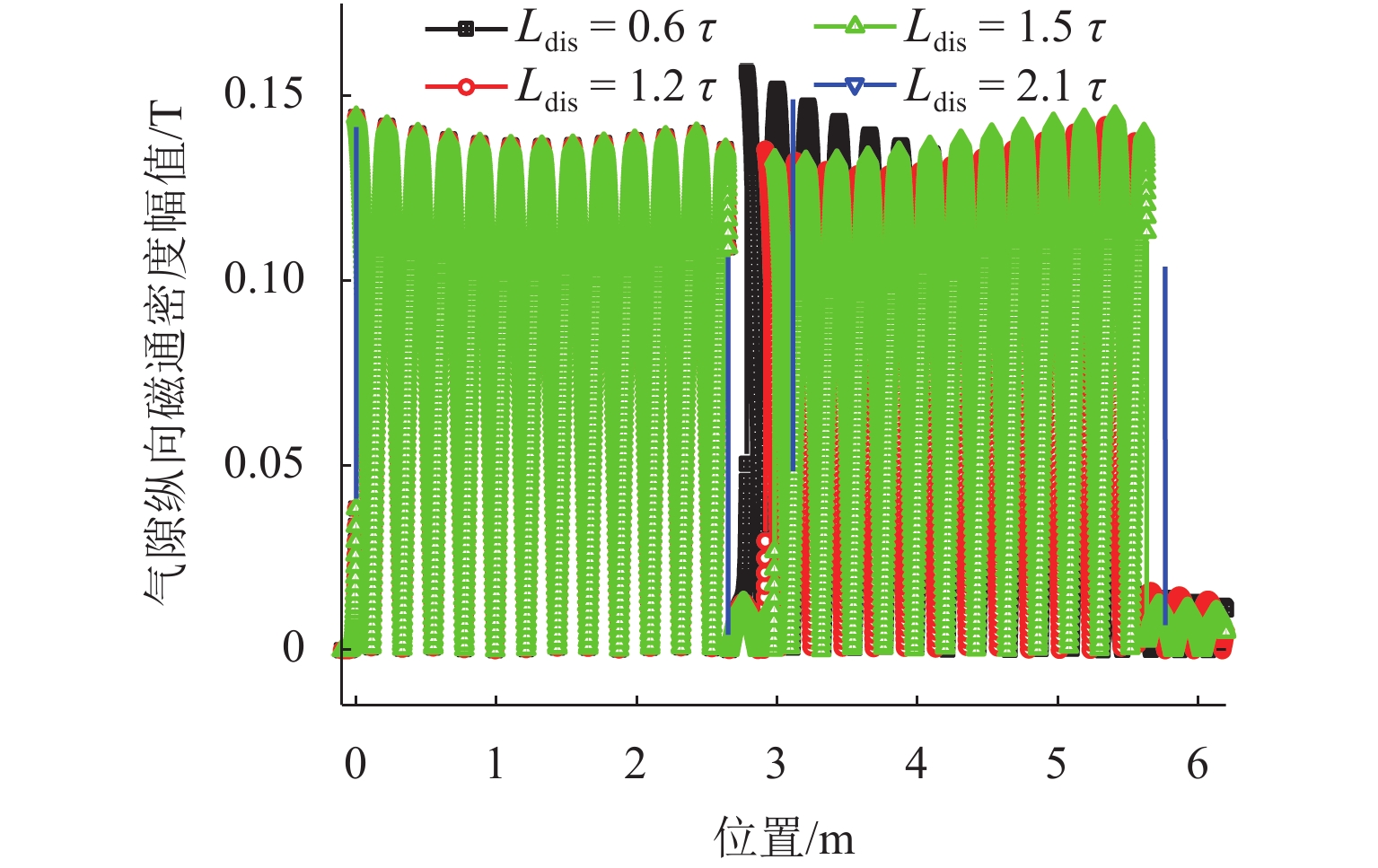
从上述分析可得,当滑差频率为8 Hz、间距为0.6倍极距时,LIM2牵引力取得最小值;间距为1.5倍极距时,LIM2牵引力取得最大值. LIM2法向力在间距为2.1倍极距时取得最小值,在间距为1.2倍极距时取得最大值. 为探清LIM2电磁力受间距影响的内因,对不同工况下的气隙磁场进行分析.
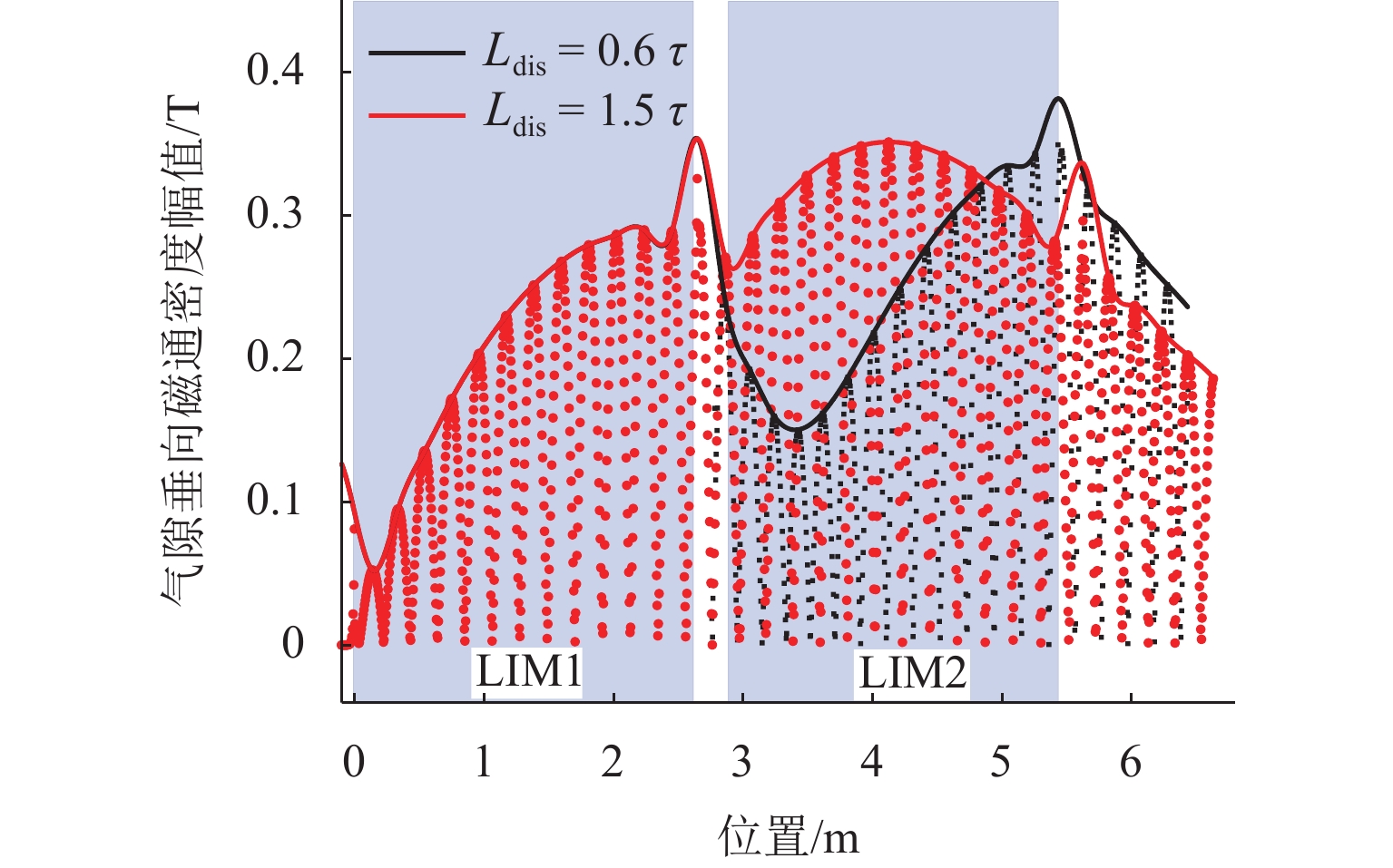
图7所示为上述4种间距条件下相邻2台电机的气隙磁场分布. 由图可见,不同间距下LIM1的气隙磁场基本不变,LIM2的气隙磁场有微小变化,所以间距对相邻电机纵向气隙磁场的影响较小.
间距分别为0.6和1.5倍极距下2台电机的垂向气隙磁密如图8所示. 由图可见,2种间距条件下LIM1的垂向气隙磁密无显著变化,且其前端垂向气隙磁密受边端效应影响被大幅削弱. 当间距为0.6倍极距时,LIM2的前端垂向气隙磁密也被大幅削弱;而间距为1.5倍极距时,LIM2前端垂向气隙磁密几乎不受边端效应的影响. 间距为1.5倍极距时,LIM2垂向气隙磁密明显强于间距为0.6倍极距时,而电机牵引力由垂向气隙磁密与初级电流相互作用产生,所以间距为1.5倍极距时的牵引力大于间距为0.6倍极距时.
电机的法向力由两部分组成,一部分为初级铁芯与次级背铁的吸力,另一部分为电机运行过程中形成的斥力. 吸力主要取决于垂向气隙磁场,斥力主要取决于纵向气隙磁场. 而纵向气隙磁场在不同间距下的分布差异较小,所以引起电机法向力变化的主要部分是吸力,即主要受垂向气隙磁场的影响. 电机法向力在间距为1.2和2.1倍极距时分别取得最大值和最小值,图9所示为2种间距条件下2台电机的垂向气隙磁密分布. 由图可见,间距为1.2倍极距时,LIM2垂向气隙磁密远大于间距为2.1倍极距时的垂向气隙磁密,且远大于LIM1的垂向气隙磁密,这使得该间距下LIM2的法向力远大于LIM1和2.1倍极距下的LIM2.
6. 结 论
基于二维电磁场理论,本文对短定子直线感应电机在中低速磁浮应用中出现的相邻电机磁场干涉问题进行了深入研究,主要结论如下:
1) LIM1出口端边端效应引起的逆向行波受LIM2初级电流、滑差频率、电机间距等因素的影响,LIM2入口端边端效应引起的正向行波受LIM1参数及间距的影响,所以直线电机气隙磁场会受到相邻电机的影响而发生改变.
2) 由于出口端引起的逆向行波对电机影响较小,而入口端引起的正向行波对电机影响较大,所以LIM1电磁力受LIM2影响较小,而LIM2电磁力受LIM1影响显著. LIM2牵引力和法向力均随间距的变化而波动;间距越小,波动幅度越大.
3) 合理的间距设计可显著提高LIM2牵引性能,减小其法向力;当滑差频率为8 Hz、速度为160 km/h、电流为400 A时,LIM2牵引力最大可增加83%,法向力最大可减小6.6 kN. 但是,牵引力和法向力对应的较优间距并不一致,实际工程中,电机间距的设计需综合考虑车辆的牵引需求和悬浮能力.
4) 由于直线电机理论推导过程复杂、涉及参数众多,在进行数学求解时不得不作必要的理想假设和条件简化,所以上述量化结果仅供参考. 本文结果基于二维电磁场理论获得,读者可继续探讨基于三维场理论的相邻电机电磁力变化特性,获得更为精确的结果.
-
表 1 电机参数
Table 1. Motor parameter
名称 大小 名称 大小 电机长度/mm 2850 电机容量/(kV•A) 250 电机宽度/mm 220 额定相电压/V 212 极数/极 12 额定相电流/A 400 极距/mm 220 气隙/mm 10 相数 3 滑差频率/Hz 12 每极每相槽数 3 单相有效串联匝数/匝 72 次级板电阻率/
(Ω•m)2.83×10−8 次级板厚/mm 4 -
[1] 邓自刚,刘宗鑫,李海涛,等. 磁悬浮列车发展现状与展望[J]. 西南交通大学学报,2022,57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001DENG Zigang, LIU Zongxin, LI Haitao, et al. Development status and prospect of maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001 [2] 马卫华,胡俊雄,李铁,等. EMS型中低速磁浮列车悬浮架技术研究综述[J]. 西南交通大学学报,2023,58(4): 720-733. doi: 10.3969/j.issn.0258-2724.20210971MA Weihua, HU Junxiong, LI Tie, et al. Summary of suspension frame technology of EMS medium and low speed maglev train[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 720-733. doi: 10.3969/j.issn.0258-2724.20210971 [3] 吴会超,罗建利,周文,等. 中低速磁浮车岔耦合振动研究[J]. 西南交通大学学报,2022,57(3): 483-489. doi: 10.3969/j.issn.0258-2724.20210829WU Huichao, LUO Jianli, ZHOU Wen, et al. Coupled vibration between low-medium speed maglev vehicle and turnout[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 483-489. doi: 10.3969/j.issn.0258-2724.20210829 [4] FRITZ E, WITT M. Maglev train development-history and today’s marketing chances[J]. Elektrische Bahnen, 2012, 110(3): 102-111. [5] BOLDEA I, TUTELEA L N, XU W, et al. Linear electric machines, drives, and MAGLEVs: an overview[J]. IEEE Transactions on Industrial Electronics, 65(9): 7504-7515. [6] LV G, ZENG D H, ZHOU T, et al. Investigation of forces and secondary losses in linear induction motor with the solid and laminated back iron secondary for metro[J]. IEEE Transactions on Industrial Electronics, 64(6): 4382-4390. [7] 徐伟,孙广生. 单边直线感应电机纵向边缘效应的研究[J]. 中国工程科学,2007,9(3): 21-27. doi: 10.3969/j.issn.1009-1742.2007.03.004XU Wei, SUN Guangsheng. Research on the longitudinal end effect of single linear induction motor[J]. Engineering Science, 2007, 9(3): 21-27. doi: 10.3969/j.issn.1009-1742.2007.03.004 [8] MISHIMA T, HIRAOKA M, NOMURA T. A study of the optimum stator winding arrangement of LIM in maglev systems[C]//IEEE International Conference on Electric Machines and Drives, 2005. San Antonio, TX, USA. IEEE, 2005: 1238-1242. [9] ZHAN J W, LU Q F. Design optimization and performance investigation of novel linear induction motors with V-shaped ladder-slit secondary[J]. International Journal of Applied Electromagnetics and Mechanics, 2018, 58(2): 157-174. doi: 10.3233/JAE-180036 [10] LV G, ZHOU T, ZENG D H, et al. Design of ladder-slit secondaries and performance improvement of linear induction motors for urban rail transit[J]. IEEE Transactions on Industrial Electronics, 65(2): 1187-1195. [11] LU Q F, LI L X, ZHAN J W, et al. Design optimization and performance investigation of novel linear induction motors with two kinds of secondaries[J]. IEEE Transactions on Industry Applications, 55(6): 5830-5842. [12] 邓江明,陈特放,唐建湘,等. 单边直线感应电机动态最大推力输出的滑差频率优化控制[J]. 中国电机工程学报,2013,33(12): 123-130,194.DENG Jiangming,CHEN Tefang,TANG Jianxiang,et al. Optimum slip frequency control of maglev single-sided linear induction motors to maximum dynamic thrust[J]. Proceedings of the CSEE,2013,33(12): 123-130,194. [13] 张敏,范屹立,马卫华,等. 滑差频率对磁浮车辆运行性能的影响[J]. 交通运输工程学报,2019,19(5): 64-73. doi: 10.3969/j.issn.1671-1637.2019.05.008ZHANG Min, FAN Yili, MA Weihua, et al. Influence of slip frequency on running performance of maglev vehicle[J]. Journal of Traffic and Transportation Engineering, 2019, 19(5): 64-73. doi: 10.3969/j.issn.1671-1637.2019.05.008 [14] SEO H, LIM J, CHOE G H, et al. Algorithm of linear induction motor control for low normal force of magnetic levitation train propulsion system[J]. IEEE Transactions on Magnetics, 54(11): 1-4. [15] WANG K, LI Y H, GE Q X, et al. An improved indirect field-oriented control scheme for linear induction motor traction drives[J]. IEEE Transactions on Industrial Electronics, 65(12): 9928-9937. [16] HAN Y, NIE Z L, XU J, et al. Control strategy for optimising the thrust of a high-speed six-phase linear induction motor[J]. IET Power Electronics, 2020, 13(11): 2260-2268. doi: 10.1049/iet-pel.2019.1334 [17] XIAO X Y, XU W, TANG Y R, et al. Improved loss minimization control based on time-harmonic equivalent circuit for linear induction motors adopted to linear metro[J]. IEEE Transactions on Vehicular Technology, 72(7): 8601-8612. [18] HU D, XU W, DIAN R J, et al. Loss minimization control of linear induction motor drive for linear metros[J]. IEEE Transactions on Industrial Electronics, 65(9): 6870-6880. [19] ELMORSHEDY M F, XU W, ALLAM S M, et al. MTPA-based finite-set model predictive control without weighting factors for linear induction machine[J]. IEEE Transactions on Industrial Electronics, 68(3): 2034-2047. [20] SUN X F, XU J, ZHU J J, et al. Thrust ripple suppression based on negative current control for short-primary low-speed large LIM under transient operation[J]. IEEE Transactions on Energy Conversion, 38(3): 1566-1575. [21] Zhang M, Luo SH, Gao C, et al. Research on the mechanism of a newly developed levitation frame with mid-set air spring[J]. Vehicle System Dynamics, 2018, 56(12): 1797-1816. doi: 10.1080/00423114.2018.1435892 [22] ZHANG M, HAN Y P, MA W H, et al. Optimal selection of the linear induction motor spacing for the medium-low speed maglev vehicle[J]. International Journal of Rail Transportation, 2021, 9(2): 157-185. doi: 10.1080/23248378.2020.1742209 [23] 张敏,罗世辉,马卫华. 接线相位差对直线电机牵引性能的影响[J]. 中国科学(技术科学),2019,49(8): 971-980. doi: 10.1360/N092018-00443ZHANG Min, LUO Shihui, MA Weihua. Influence of connection phase difference on the traction performance of linear induction motor[J]. Scientia Sinica (Technologica), 2019, 49(8): 971-980. doi: 10.1360/N092018-00443 [24] ZHANG M, LUO S H, GAO C, et al. Research on the mechanism of a newly developed levitation frame with mid-set air spring[J]. Vehicle System Dynamics, 2018, 56(12): 1797-1816. doi: 10.1080/00423114.2018.1435892 [25] ZHANG M, HAN Y P, MA W H, et al. Optimal selection of the linear induction motor spacing for the medium-low speed maglev vehicle[J]. International Journal of Rail Transportation, 2021, 9(2): 157-185. doi: 10.1080/23248378.2020.1742209 [26] 龙遐令. 直线感应电动机的理论和电磁设计方法[M]. 北京:科学出版社,2006. -






 下载:
下载:









 下载:
下载: