中低速磁浮列车悬浮系统模糊综合评价与改进设计

曹毅; 张敏; 刘静; 刘清辉; 马卫华; 单磊; 李铁

doi:10.3969/j.issn.0258-2724.20240190

中低速磁浮列车悬浮系统模糊综合评价与改进设计

doi: 10.3969/j.issn.0258-2724.20240190

曹毅^1,,
张敏¹,
刘静¹,
刘清辉¹,
马卫华^1, ,,
单磊²,
李铁³

1.
西南交通大学轨道交通运载系统全国重点实验室，四川成都 611752
2.
山东和顺电气有限公司，山东泰安 271600
3.
中车大连机车车辆有限公司，辽宁大连 116022

基金项目: 国家自然科学基金项目（52102442，52402480）；国家资助博士后研究人员计划（GZC20231937）

详细信息

作者简介:
曹毅（1996—），男，博士研究生，研究方向为悬浮冗余和悬浮控制，E-mail：caoyi@swjtu.edu.cn

通讯作者:
马卫华（1979—），男，研究员，博士，研究方向为车辆系统动力学，E-mail： mwh@swjtu.edu.cn

中图分类号: U237
计量
- 文章访问数: 37
- HTML全文浏览量: 12
- PDF下载量: 1
- 被引次数: 0
出版历程
- 收稿日期: 2024-04-20
- 修回日期: 2024-09-17
- 网络出版日期: 2025-05-22

Fuzzy Comprehensive Evaluation and Improved Design of Levitation System for Medium- and Low-Speed Maglev Trains

CAO Yi^1
,,
ZHANG Min¹,
LIU Jing¹,
LIU Qinghui¹,
MA Weihua^{1
, ,},
SHAN Lei²,
LI Tie³

1.
State Key Laboratory of Rail Transit Vehicle System, Southwest Jiaotong University, Chengdu 611752, China
2.
Shandong Heshun Electric Co., Ltd., Tai’an 271600, China
3.
CRRC Dalian Co., Ltd., Dalian 116022, China

摘要

摘要:
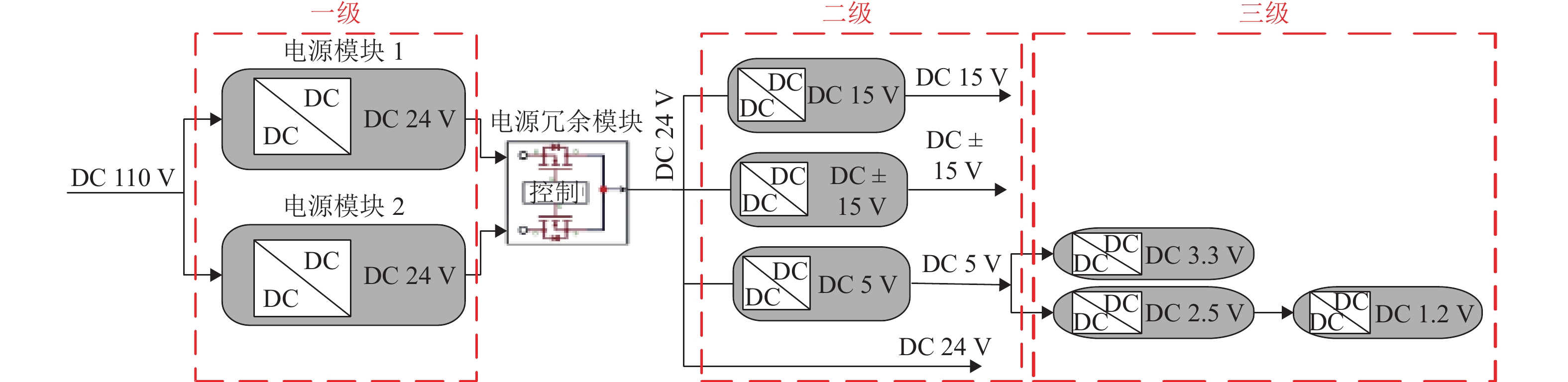
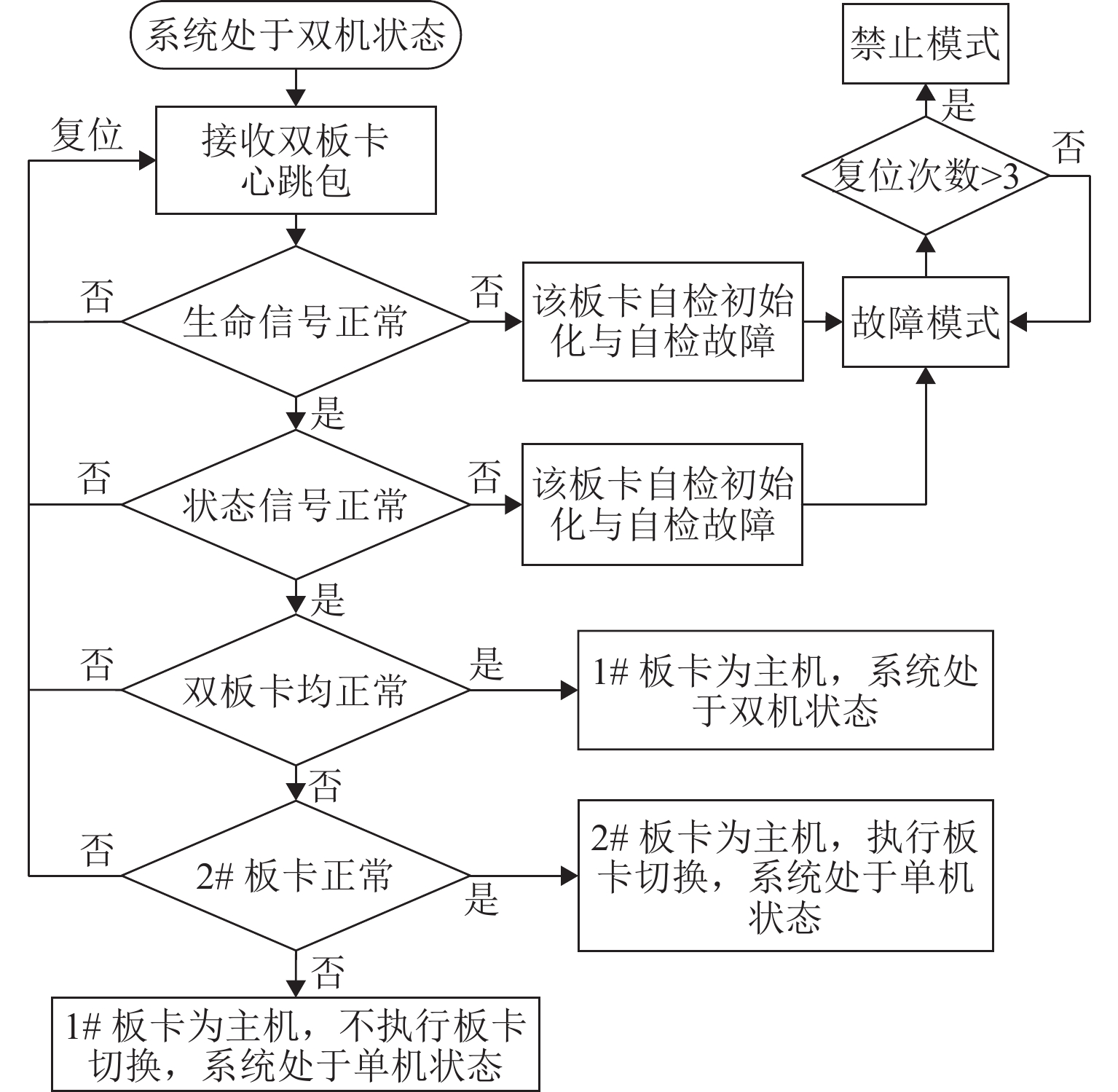
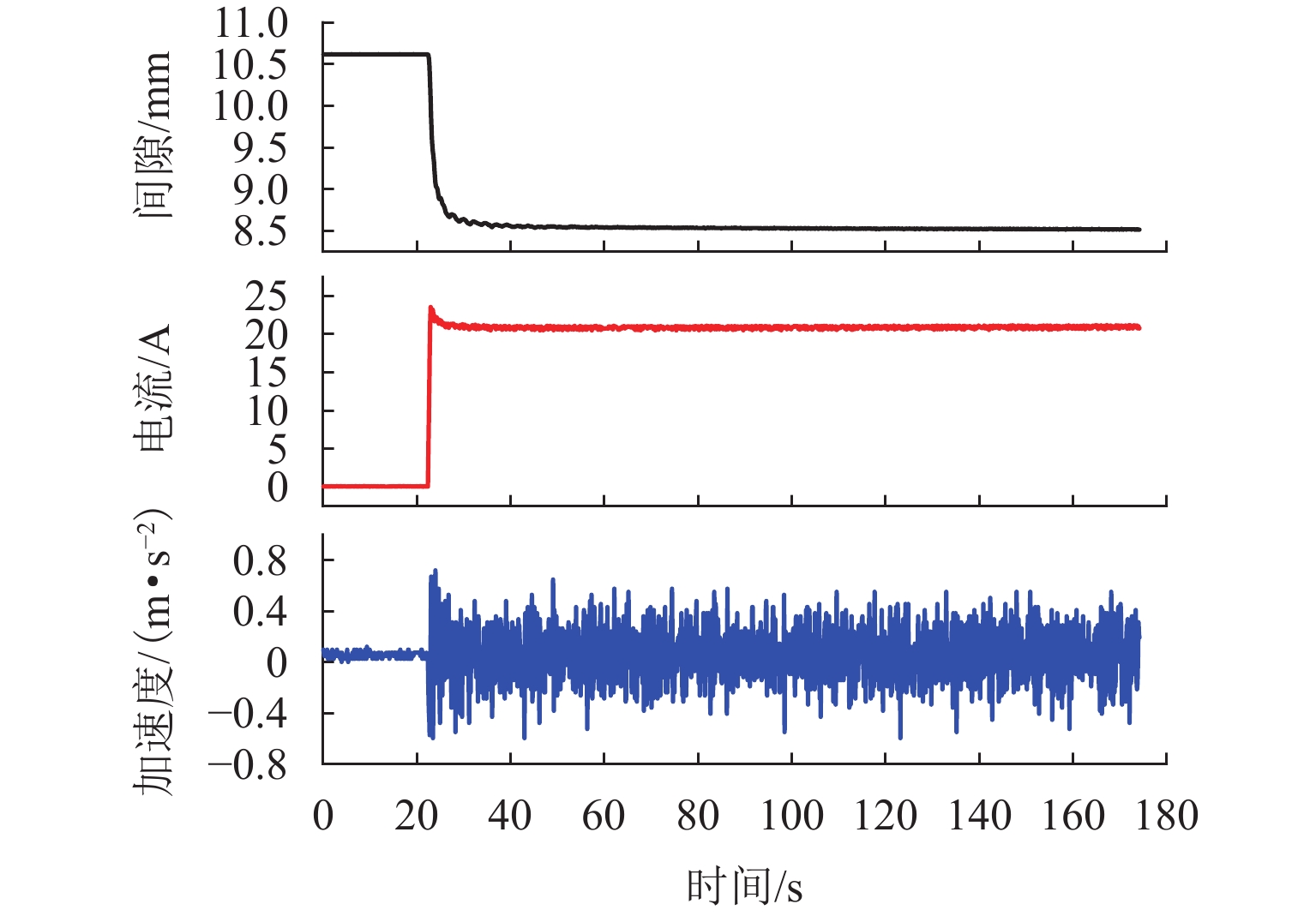
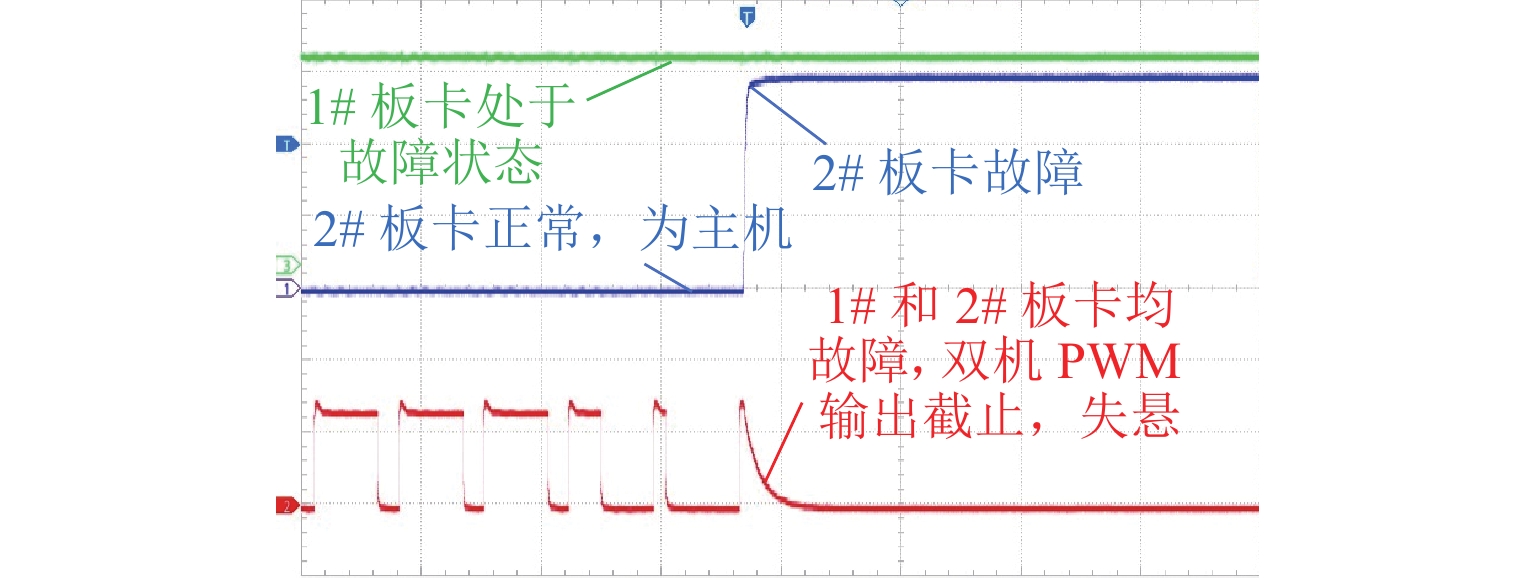
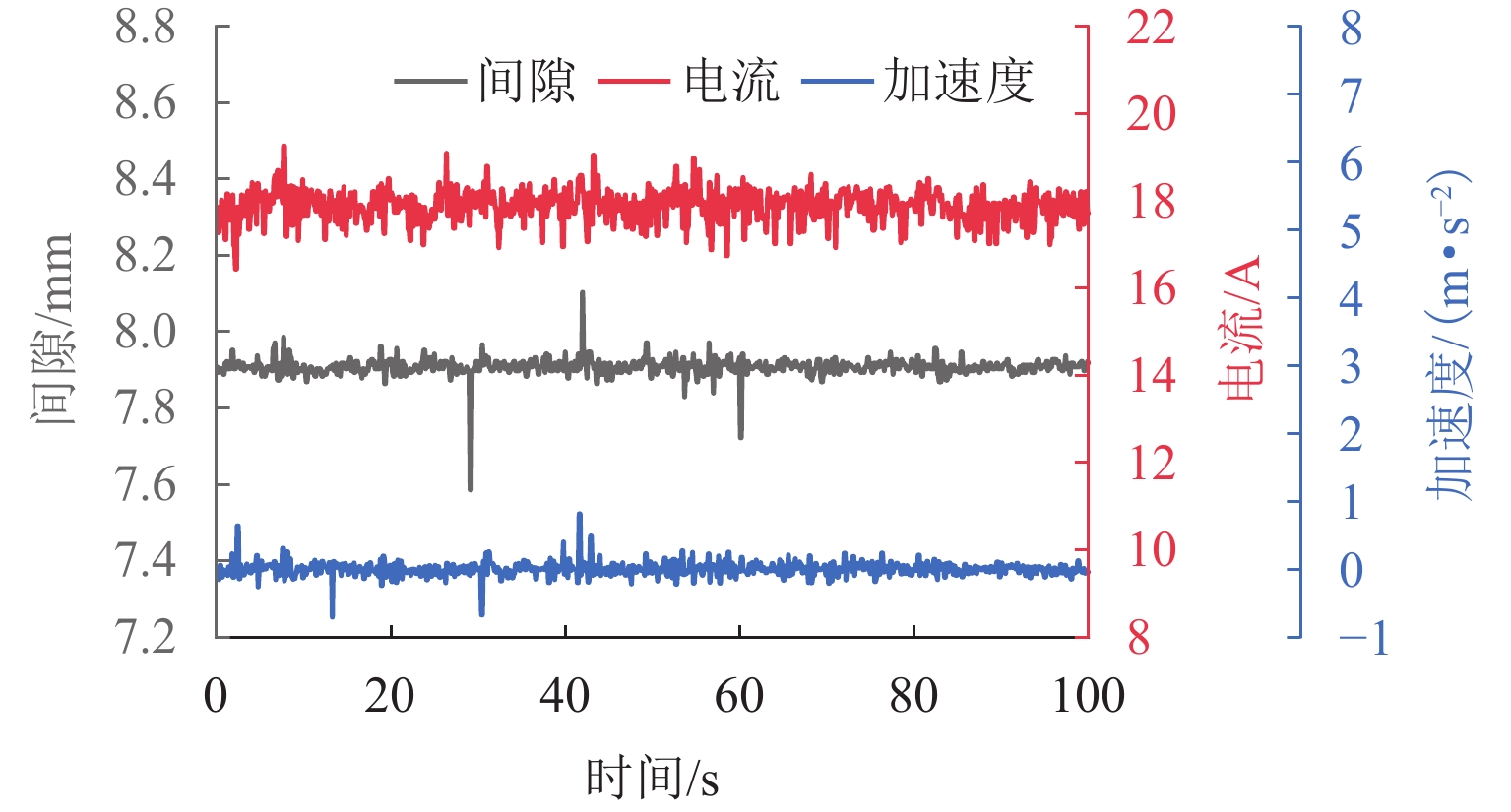
为提高某型中低速磁浮列车悬浮系统的容错能力，运用故障模式、影响及危害度分析（FMECA）方法对系统进行可靠性分析评估，识别出典型失效模式；通过专家模糊综合评价量化指标，以降低主观偏差，避免危害性取值重复的问题；利用层次分析法（AHP）对不同影响因素进行权值分配，使计算得到的各故障模式的综合危害性等级更符合实际工程需求；进一步，基于马尔可夫理论，针对综合危害性等级较高的故障模式提出改进措施；最后，研制样机并在单悬浮架试验台上开展悬浮试验与故障模拟试验. 研究结果表明：控制板、接口板和电源模块的综合危害等级最高，分别为6.3147、5.4841和5.6534；故障发生后，主从机切换时间小于100 us，悬浮间隙均方根误差小于0.1 mm，加速度波动在0.6 m/s²内.
- 磁浮列车 /
- 悬浮系统 /
- 容错 /
- 模糊规则
Abstract:
To enhance the fault tolerance capability of the levitation system of a medium- and low-speed maglev train, a reliability analysis was conducted using failure mode, effects, and criticality analysis (FMECA), identifying typical failure modes. A fuzzy comprehensive evaluation based on expert judgment was employed to quantify the indicators, reducing subjective bias, and avoiding duplication of hazard values. The analytic hierarchy process (AHP) was used to assign weights to different influencing factors, ensuring that the calculated comprehensive hazard levels of failure modes better reflect practical engineering needs. Furthermore, based on Markov theory, improvement measures were proposed for failure modes with high comprehensive hazard levels. A prototype was developed, and levitation and fault simulation tests were conducted on a single levitation test bench. The results indicate that the control board, interface board, and power module exhibit the highest comprehensive hazard levels, which are 6.314 7, 5.484 1, and 5.653 4, respectively. After a fault occurs, the master–slave switching time is less than 100 μs, with the levitation gap root-mean-square error remaining below 0.1 mm and acceleration fluctuations within 0.6 m/s².
- maglev train /
- levitation system /
- fault tolerance /
- fuzzy rule

HTML全文

当前，世界范围内投入运营的中低速磁浮列车均采用电磁悬浮技术. 该技术具有振动噪声小、运营维护成本低、运行平稳、舒适性高等优势^[1-2]，是一种战略性前沿性的新型轨道交通制式^[3-5]. 悬浮系统作为关键子系统，在工程实践中因故障导致列车无法正常运行的情况时有发生. 如何提高悬浮系统的可靠性和容错能力，仍是制约中低速磁浮应用的关键问题^[6].

分析悬浮系统失效原因是提升可靠性和容错能力的必要环节. 运用故障模式、影响及危害度分析（failure mode effects and criticality analysis，FMECA）方法是通过分析系统所有可能的故障模式和可能产生的影响，按每个故障模式产生的后果和可能性等多个因素予以归类排序的方法^[7]. 但传统FMECA方法存在一些典型问题，如不同故障模式的危害性评价相同、仅用少量整数表示危害性，以及较强的主观性等. 因此，许多学者对此方法进行了优化研究：Catelani等^[8]提出一种单元风险优先数（FMECA-RPN）优先级排序方法，在成本和阈值水平之间达到较好权衡；Ben Brahim等^[9]构建基于FMECA信息的贝叶斯网络，并进行案例验证；Lin等^[10]将故障扩散概率和故障数据结合，以评估机电系统的安全性；Catelani等^[11]提出一种基于统计分析的新方法，并将其与文献中仅有的3种定量排序技术进行比较；Aswin等^[12]通过案例研究发现，模糊FMECA和灰色理论FMECA比传统RPN （risk priority number）方法更准确；Renjith等^[13]证明了在复杂过程系统中模糊FMECA比传统FMECA对故障排序更准确；Giardina等^[14]设计一种FMECA和HAZOP （hazard and operability analysis）集成方法，用于分析液化天然气储存系统的风险；于涵等^[15]针对动车组牵引传动系统，利用模糊综合评价对传统FMECA进行改进.

针对中低速磁浮列车悬浮系统故障，Sun等^[16] 开发一种自适应非线性控制策略以优化执行器故障时的控制性能；Zhai等^[17]设计状态观测器来有效估计故障传感器的间隙数据. 硬件冗余方面，佘龙华等^[18]通过双机数字信号处理器（DSP），搭建冗余的磁悬浮控制器试验平台；Sung等^[19-20]提出控制器双机热备设计方案，确保在主控制器故障时自动切换到从控制器；Zhai等^[21]针对高速磁浮悬架控制单元失效，设计一种容错控制器，实现悬浮失效下的故障容错；Jang等^[22]提出一种主从切换电路，当主控制电路发生故障时将主控制电路隔离，系统切换到从控制电路；Liang等^[23]对悬浮控制单元进行双机热备方案的容错设计，并通过实验证明其可靠性；Jin等^[24]设计一种悬浮架搭接结构和电磁铁线包间隔排列结构，通过仿真验证该方法具有一定的容错效果.

本文聚焦于逐步推广的中低速磁浮列车悬浮系统，旨在识别系统薄弱环节并增强其容错能力. 研究盖悬浮系统的结构组成、故障模式及其优化措施，并最终在单悬浮架试验平台上验证改进后的悬浮系统性能和容错能力.

1. 悬浮系统故障分析

中低速磁浮列车常规悬浮系统主要由悬浮传感器、悬浮控制器和悬浮电磁铁组成，如图1所示. 悬浮传感器安装在电磁铁模块端部，检测悬浮间隙. 悬浮控制器是悬浮系统的核心部件，由控制单元、斩波器及其他周围部件组成^[25]，其中，控制单元一般为嵌入式电路，其功能是接收各传感器信号，进行滤波、模数转换，悬浮控制算法计算并生成作用于功率单元的驱动信号. 悬浮电磁铁是悬浮系统执行部件，磁浮列车通过悬浮电磁铁与F轨之间的电磁吸力实现悬浮与导向功能.

图 1 悬浮控制系统结构

Figure 1. Levitation control system structure

下载: 全尺寸图片幻灯片

首先，对悬浮系统进行拆分，如图2所示. 图中， IGBT为绝缘栅双极晶体管.

图 2 悬浮控制系统结构树

Figure 2. Structure tree of levitation control system

下载: 全尺寸图片幻灯片

悬浮控制器、悬浮传感器和悬浮电磁铁是系统的一级部件. 在此基础上，以最小可更换单元为单位进一步拆分，悬浮控制器可拆分到三级部件，悬浮电磁铁及悬浮传感器可拆分到二级部件. 根据划分的层次结构，通过深入分析各种故障器件的故障原因、故障模式及其影响，得到FMEA分析结果，由于结果所包含的部件和故障模式较多，因此，将典型的高综合危害性等级的部件列出，如表1所示. 表中：PWM为脉冲宽度调制.

表 1 悬浮系统典型故障模式FMEA分析结果

Table 1. FMEA results of typical failure modes in levitation system

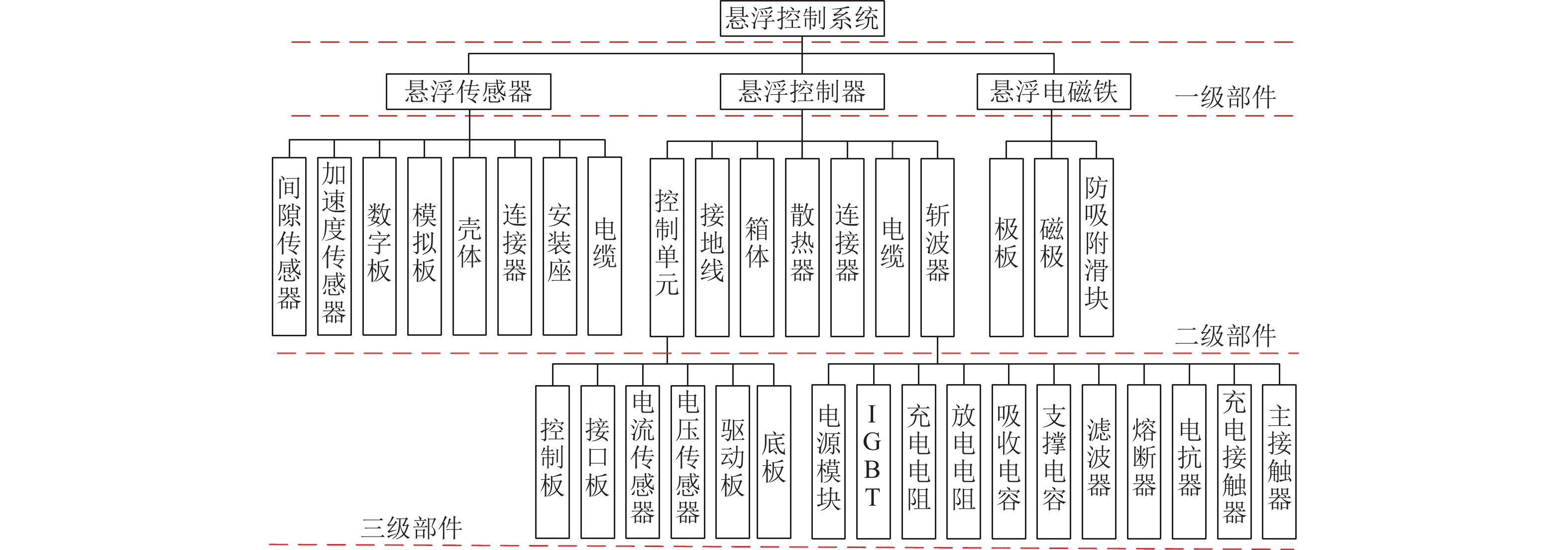
最低约定层次	故障模式	故障原因	系统影响	整车影响
控制板	无 PWM 输出/输出错误	源端电压不稳；过温虚焊，断路；抗振动冲击过大；内部短路；程序运行错误	驱动板无法接收到PWM，单点无法悬浮	车辆单点失悬或掉点砸轨，双点故障进入救援模式
接口板	悬浮控制故障	过温虚焊，断路；抗振动冲击能力差；抗干扰能力差；内部短路；源端电压不稳	控制板无法接收悬浮传感器信号，无法悬浮；控制板接收错误电流信号，悬浮失稳	车辆单点失悬，双点故障进入救援模式；车辆单点连续打轨，车辆降速运营
110 V 转 24 V 电源模块	DC 24 V断路	耐压能不足；温度过高；抗干扰能力不足	悬浮传感器及悬浮控制电路无法得电，悬浮控制缺少输入	车辆单点失悬，双点故障进入救援模式
电流传感器	信号输出不稳定；无输出信号	过流；接触不良；温度过高	无法监测悬浮电流，实际电流与预期存在误差，悬浮失稳	车辆单点连续打轨，车辆降速运营
电压传感器	信号输出不稳定	过压；接触不良	主接触器无法闭合	车辆单点失悬，双点故障进入救援模式
驱动板	无法启动	IGBT击穿导致的过流；抗振动冲击能力差；抗干扰能力差；高温虚焊	无法控制IGBT开断	车辆单点失悬，双点故障进入救援模式
IGBT	击穿	电磁铁短路；温度过高	无悬浮电流输出	车辆单点失悬，双点故障进入救援模式
支撑电容	损坏	老化；电容质量问题；温度过高	单支撑电容损坏无影响
支撑电容	击穿	过压	主电路短路，悬浮控制器停机	车辆单点失悬，双点故障进入救援模式

下载: 导出CSV

| 显示表格

2. 基于模糊评价的危害性分析

2.1 建立因素集 ${\boldsymbol{U}}$

结合悬浮控制系统的典型故障模式，建立因素集U，包含影响概率、故障严重度和综合检修难度共3类影响因素，分别用u₁、u₂、u₃表示，如式（1）所示.

${{\boldsymbol{U}}^{(k)}} = \left[ {\begin{array}{*{20}{c}} {u_1^{(k)}}&{u_2^{(k)}}&{u_3^{(k)}} \end{array}} \right],$

(1)

式中：上标(k)表示第 $k$ 项故障模式.

影响概率指在故障模式发生后，导致故障后果出现的额定条件概率，并结合实际行车试验记录进行综合评估. 故障严重度反映故障模式对悬浮系统约定层次造成的潜在影响的严重程度，是否会发生受到影响概率的影响. 综合检修难度包括诊断和修复故障的难度程度，以及维修或更换器件的成本等.

2.2 建立评价集 ${\boldsymbol{V}}$

评价集 ${\boldsymbol{V}}$ 是专家所反馈的评价结果的集合，由v₁～v₅共5个等级所组成，分别量化为1、3、5、7、9，如式（2）所示. 3种因素对应的等级划分如表2所示.

表 2 影响因素的评价等级划分

Table 2. Evaluation level classification for influencing factors

影响因素	等级
影响因素	1	3	5	7	9
影响概率	几乎没有	极少	偶尔	可能	经常
严重程度	可忽略	轻微的	临界的	危急的	灾难的
综合检修难度	极低	较低	中等	较难	很难

下载: 导出CSV

| 显示表格

${\boldsymbol{V}} = \left[ {\begin{array}{*{20}{c}} {{v_1}}&{{v_2}} &{{v_3}} &{{v_4}} &{{v_5}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&3 &5 &7 &9 \end{array}} \right].$

(2)

2.3 建立各故障模式评价矩阵

n位专家（本文中n=10）组成的专家团对悬浮控制系统典型故障模式进行打分评价. 专家团成员由车辆设计者、悬浮系统设计者和实际参与行车试验人员组成. 每位专家在对3类影响因素的评价中选出一个唯一的等级. 在对第k项故障模式进行评价时，设评价集为 ${\boldsymbol{R}}_i^{(k)}$ ，表示专家团对第k项故障模式的第i类影响因素的隶属度分布，i=1，2，3. 具体地，专家团队成员对影响因素 $u_i^{(k)}$ 评出一个且仅一个等级 ${v_j}$ ，j=1, 2, …, 5. 若n位成员中评定 $u_i^{(k)}$ 隶属于 ${v_j}$ 的有 $n_{ij}^{(k)}$ 人，得到评价集 ${\boldsymbol{R}}_i^{(k)}$ 为

$\begin{split} & {\boldsymbol{R}}_i^{(k)} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{n_{i1}^{(k)}}}{n}}&{\dfrac{{n_{i2}^{(k)}}}{n}} &\cdots &{\dfrac{{n_{i5}^{(k)}}}{n}} \end{array}} \right] = \\ &\quad \left[ {\begin{array}{*{20}{c}} {r_{i1}^{(k)}}&{r_{i2}^{(k)}}& \cdots &{r_{i5}^{(k)}} \end{array}} \right], \end{split}$

(3)

式中： $\displaystyle\sum _{j=1}^{5}\dfrac{{n}_{ij}^{(k)}}{n}=1$ .

将第 $k$ 项故障模式的评价集表达成故障模式 $k$ 的评价矩阵 ${{\boldsymbol{R}}^{(k)}}$ ，如式（4）所示.

${{\boldsymbol{R}}^{(k)}} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{R}}_1^{(k)}} \\ {{\boldsymbol{R}}_2^{(k)}} \\ \cdots \\ {{\boldsymbol{R}}_3^{(k)}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {r_{11}^k}&{r_{12}^k}& \cdots &{r_{15}^k} \\ {r_{21}^k}&{r_{22}^k}& \cdots &{r_{25}^k} \\ {r_{31}^k}&{r_{32}^k}& \cdots &{r_{35}^k} \end{array}} \right].$

(4)

以悬浮控制板PWM输出错误故障模式为例，k=1. 经综合评估，故障影响概率集为 ${\boldsymbol{R}}_1^{(1)} = \left[ {\begin{array}{*{20}{c}} 0&{0.1} &{0.4}&{0.5}&0 \end{array}} \right]$ ，故障严重度集为 ${\boldsymbol{R}}_2^{(1)} = \left[ {\begin{array}{*{20}{c}} 0&0 &{0.2}&{0.4}&{0.4} \end{array}} \right]$ ，综合检修难度为 ${\boldsymbol{R}}_3^{(1)} = \left[ {\begin{array}{*{20}{c}} 0&{0.2} &{0.4}&{0.4}&0 \end{array}} \right]$ . 因此，评价矩阵为

${{\boldsymbol{R}}^{(1)}} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{R}}_1^{(1)}} \\ {{\boldsymbol{R}}_2^{(1)}} \\ {{\boldsymbol{R}}_3^{(1)}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&{0.1}&{0.4}&{0.5}&0 \\ 0&0&{0.2}&{0.4}&{0.4} \\ 0&{0.2}&{0.4}&{0.4}&0 \end{array}} \right].$

(5)

2.4 建立基于AHP的因素权重集

建立权重集目的是更准确反映各因素重要程度对危害等级的影响，设权重集 ${{\boldsymbol{w}}^{(k)}}$ 中元素 ${w_i}^{(k)}$ 为第 $i$ 类影响因素对失效模式 $k$ 的权重，如式（6）所示.

$\left\{\begin{array}{*{20}{l}} {{\boldsymbol{w}}^{(k)}} = [\begin{array}{*{20}{l}} {w_1^{(k)}}&{w_2^{(k)}}&{w_3^{(k)}} \end{array}] ,\\ \displaystyle\sum\limits_{i = 1}^3 {w_i^{(k)}} = 1. \end{array}\right.$

(6)

采用层次分析法（AHP），10位专家和从业者基于自身的知识，采用两两比较和1～9标度法对2种不同因素进行比较，对3种因素的重要度进行打分，重要度定义如表3所示.

表 3 因素重要度判断值表

Table 3. Judgment values for factor importance

相对评价值	极重要	很重要	重要	略重要	同等
评分	9	7	5	3	1
注：8、6、4、2为评价价值的中间值.

下载: 导出CSV

| 显示表格

${a_{fg}}$ 为影响因素 ${u_f}$ 对影响因素 ${u_g}$ 相对重要性的数值大小，且存在 ${a_{ff}} = 1$ ， ${a_{fg}} = \dfrac{1}{{{a_{gf}}}}$ ，1≤f,g≤3. 专家的打分由判断矩阵 ${\boldsymbol{A}}$ 表示， ${\boldsymbol{A}}=({a_{fg}})$ . 以悬浮控制板PWM输出错误失效模式为例，其判断矩阵为

${\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 1&{1.25}&{1.667} \\ {0.8}&1&2 \\ {0.6}&{0.5}&1 \end{array}} \right].$

(7)

对每个判断矩阵计算最大特征值 ${\lambda _{\max }}$ 和对应的特征向量，之后计算一致性比率 ${R_{\mathrm{C}}}$ 为

$\left\{\begin{array}{l} {R_{\mathrm{C}}} = \dfrac{{{I_{\mathrm{C}}}}}{{{I_{\mathrm{R}}}}},\\ {I_{\mathrm{C}}} = \dfrac{{{\lambda _{\max }} - n}}{{n - 1}}, \end{array}\right.$

(8)

式中： ${I_{\mathrm{R}}}$ 为平均随机一致性指标，根据判断矩阵的阶数对照确定 ${I_{\mathrm{R}}}$ 取值； ${I_{\mathrm{C}}}$ 为一致性指标.

表 4 1～9阶判断矩阵

${I_{\mathrm{R}}}$ 值

Table 4. Judgment matrices

${I_{\mathrm{R}}}$ for orders 1–9

阶数	1	2	3	4	5	6	7	8	9
${I_{\mathrm{R}}}$	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45

下载: 导出CSV

| 显示表格

进行一致性检验，当随机一致性比率 ${R_{\mathrm{C}}} \leqslant 0.1$ 时，则判断矩阵的一致性是可以接受的，从而可以确定相对权重有效；否则，则需要对判断矩阵进行调整.

以悬浮控制板PWM输出错误失效模式为例，计算其一致性比率 ${R_{\mathrm{C}}} = 0.017$ ，通过一致性要求. 之后，对特征向量 $\xi$ 进行归一化计算，得到加权系数为 ${{\boldsymbol{w}}^{(1)}} = \left[ {\begin{array}{*{20}{c}} {0.409\;5}&{0.375\;2}&{0.215\;4} \end{array}} \right]$ .

2.5 一级模糊综合评价

将第 $k$ 项故障模式的因素权重向量 ${{\boldsymbol{w}}^{(k)}}$ 与其评价矩阵 ${{\boldsymbol{R}}^{(k)}}$ 相乘，得到模糊评价向量 ${{\boldsymbol{B}}^{(k)}}$ 为

${{\boldsymbol{B}}}^{(k)}={{\boldsymbol{w}}}^{(k)}{{\boldsymbol{R}}}^{(k)}.$

(9)

悬浮控制板PWM输出错误故障模式的模糊评价向量为

$\begin{split} & {{\boldsymbol{B}}^{(1)}} = {{\boldsymbol{w}}^{(1)}}{{\boldsymbol{R}}^{(1)}} = \\ &\quad \left[{\begin{array}{*{20}{c}}0.409\;5\\ 0.375\;2\\ 0.215\;4 \end{array}}\right]^{\mathrm{T}}\left[ {\begin{array}{*{20}{c}} 0&{0.1}&{0.4}&{0.5}&0 \\ 0&0&{0.2}&{0.4}&{0.4} \\ 0&{0.2}&{0.4}&{0.4}&0 \end{array}} \right] = \\ &\quad {{ [ 0\quad 0.084\;0\quad 0.325\;0\quad 0.441\;0\quad 0.150\;1]}} . \end{split}$

(10)

2.6 综合危害等级计算

将 ${{\boldsymbol{B}}^{(k)}}$ 与评价集 ${\boldsymbol{V}}$ 相乘，可得综合危害等级C^(k). 悬浮控制板PWM输出错误失效模式的综合危害性等级为 ${{\boldsymbol{C}}^{(1)}} = {{\boldsymbol{B}}^{(1)}}{{\boldsymbol{V}}^{\mathrm{T}}} = 6.314\;7$ .

各故障模式的综合危害等级如表5所示.

表 5 各故障模式的综合危害等级

Table 5. Comprehensive hazard levels for each failure mode

部件	综合危害性等级	部件	综合危害性等级
控制板	6.3147	驱动板	3.8714
接口板	5.4841	充电电阻	3.7696
110/24 V 电源	5.6534	吸收电容	2.9501
IGBT	4.5688	支撑电容	2.9932
电流传感器	4.1590	电压传感器	3.7798
主接触器	4.2963	熔断器	3.4600

下载: 导出CSV

| 显示表格

由表5可知，悬浮系统中控制板、接口板、110 V转24 V电源模块和IGBT综合危害性等级较高.

3. 悬浮系统改进方案设计

结合设计难度、改进必要性、经济性和可扩展性等因素，对控制板、接口板、电源模块和IGBT进行改进设计.

3.1 控制板

冗余设计是提升控制系统可靠性和容错能力的有效途径. 因此，本文采用控制单元冗余的方式进行设计. 常见的冗余方法包括双机热备冗余、三取二冗余以及二乘二取二冗余等.

本文将接口板与控制板合并，以提升连接可靠性并缩减空间占用，后文统称为控制板，且采用双机热备结构. 该结构的核心是在一台热备单元故障时，能够及时检测并隔离故障，另一正常单元则承担全部功能. 仅依靠两个热备单元互相检测不足以保障系统可靠性，因此结合悬浮控制器的成本和空间考虑，采用“双机热备 + 仲裁”方案，增加仲裁模块. 该模块通过监测双热备控制板的心跳信号（包括生命信号和状态数据），实现主从切换和控制输出. 当检测到其中一台单元故障时，仲裁模块会使悬浮控制系统降级，切换至备用单元，其结构如图3所示.

图 3 悬浮冗余控制器设计架构

Figure 3. Architecture of levitation redundant controller

下载: 全尺寸图片幻灯片

3.1.1 可靠性分析

首先，建立双机热备悬浮控制系统的可靠性模型. 系统中的双机热备模块完全相同，设其失效率为 $\lambda$ . 仲裁模块的失效率为 $\gamma$ . 同时，考虑单元故障检测的成功与否，分为可测失效和不可测失效，检测覆盖率用 $c$ 表示. 为考虑共因失效的影响，设共因失效因子为 $u$ . 将系统失效划分为以下4类：

可测常规失效率： ${\lambda _{{\text{dn}}}} = c(1 - u)\lambda$ ；

不可测常规失效率： ${\lambda _{{\text{un}}}} = (1 - c)(1 - u)\lambda$ ；

可测共因失效率： ${\lambda _{{\text{dc}}}} = cu\lambda$ ；

不可测共因失效率： ${\lambda _{{\text{uc}}}} = (1 - c)u\lambda$ .

基于马尔可夫过程，为简化分析，作出以下假设：

假设1　系统和模块仅有正常或故障两种状态，切换开关完全可靠；

假设2　元件的故障率和修复率为常数，状态转移服从指数分布，且在微小时间内不会同时发生2个及以上的状态转移.

定义系统5种工作状态：

状态0　主、从模块和仲裁模块均正常；

状态1　主模块或从模块之一发生常规可测失效，系统处于降级工作状态；

状态2　从模块发生不可测失效，系统处于降级状态；

状态3　仲裁模块发生可测或不可测故障，系统处于故障-安全状态；

状态4　系统处于故障危险状态.

建立双机热备悬浮控制系统的马尔可夫状态转移图（见图4），圈中数字表示工作状态，变量下标d、u分别表示可测故障和不可测故障.

图 4 马尔可夫状态转移

Figure 4. Markov state transition

下载: 全尺寸图片幻灯片

随后，根据马尔可夫状态转移图，构建相应的马尔可夫方程组（式（10）），其中， ${P_0}(t)$ ～ ${P_4}(t)$ 分别为系统处于状态0～4的瞬时概率，t为时间， $\Delta t$ 为微小时间间隔.

$\left\{ \begin{array}{l} {P_0}(t + \Delta t) = [1 - (2\lambda + \gamma )\Delta t]{P_0}(t), \\ {P_1}(t + \Delta t) = 2c(1 - u)\lambda \Delta t{P_0}(t) + \\ \quad [1 - (\lambda + \gamma )\Delta t]{P_1}(t), \\ {P_2}(t + \Delta t) = (1 - c)(1 - u)\lambda \Delta t{P_0}(t) + \\ \quad [1 - (\lambda + \gamma )\Delta t]{P_2}(t), \\ {P_3}(t + \Delta t) = \gamma \Delta t{P_0}(t) + \gamma \Delta t{P_1}(t) +\\ \quad \gamma \Delta t{P_2}(t) + {P_3}(t), \\ {P_4}(t + \Delta t) = [2u\lambda + (1 - c)(1 - u)\lambda ]\Delta t{P_0}(t) + \\ \quad \lambda [{P_1}(t) + {P_2}(t)] + {P_4}(t). \\ \end{array} \right.$

(11)

马尔可夫微分方程组为

$\left\{ \begin{gathered} P_0^{'}(t) = - (2\lambda + \gamma ){P_0}(t), \\ P_1^{'}(t) = 2c(1 - u)\lambda {P_0}(t) - (\lambda + \gamma ){P_1}(t), \\ P_2^{'}(t) = (1 - c)(1 - u)\lambda {P_0}(t) - (\lambda + \gamma ){P_2}(t), \\ P_3^{'}(t) = \gamma {P_0}(t) + \gamma {P_1}(t) + \gamma {P_2}(t), \\ P_4^{'}(t) = [2u\lambda + (1 - c)(1 - u)\lambda ]{P_0}(t) + \\ \quad \lambda [{P_1}(t) + {P_2}(t)]. \\ \end{gathered} \right.$

(12)

根据悬浮控制系统的实际工作过程可知初始条件为

$\left\{\begin{array}{l} {P_0}(0) = 1,\\ {P_1}(0) = {P_2}(0) = {P_3}(0) = {P_4}(0) = 0. \end{array}\right.$

(13)

求式（11）可得系统在各个状态下的瞬时概率，进而得到悬浮冗余控制系统的可靠度 ${P_{\text{a}}}(t)$ （式（14）），即系统的瞬时可靠性.

${P_{\text{a}}}(t) = {P_0}(t) + {P_1}(t) + {P_2}(t) + {P_3}(t).$

(14)

采用相同的计算方法，对单机系统、二乘二取二系统及三取二系统3种结构的可靠性进行分析. 仿真时间参考中低速磁浮列车悬浮控制器的寿命要求（8年，即70000 h），各结构在寿命期间的可靠性曲线如图5所示. 其中，仲裁双机热备系统在整个寿命之内的可靠性始终保持在29%以上，而其余3种结构在经过约35000 h后，可靠性降至10%以下，特别是单机系统，其可靠性下降最快，在30000 h时几乎接近于0.

图 5 不同冗余结构可靠性曲线

Figure 5. Reliability curves of different redundant structures

下载: 全尺寸图片幻灯片

3.1.2 冗余控制策略设计

1# 控制板卡和2# 控制板卡每隔固定的多个时钟周期向仲裁板卡发送一次心跳信号，若仲裁板卡在多个心跳环节中未接收到对应控制板卡的生命信号帧或收到错误的状态帧，则将该板卡判定为故障，逻辑如图6所示. 为确保数据实时性并减小通信通道对心跳信号的影响，采用双通道传输方案.

图 6 双机切换控制策略

Figure 6. Dual-machine switching control strategy

下载: 全尺寸图片幻灯片

3.2 IGBT改进设计

IGBT故障多由耐压不足和过高温度引发. 结合设计难度和器件特点，采用增加主动散热和选用更高规格IGBT的方法，确保系统具有充分的安全与功能冗余.

3.3 电源模块冗余设计

在优化器件选择基础上，110 V转24 V电源模块采用双热备结构，示意如图7所示. 两路110 V转24 V电源共同组成一级电源，通过电源冗余模块，确保在至少一路正常的条件下，输出持续不间断的24 V.

图 7 电源电路结构

Figure 7. Power circuit structure

下载: 全尺寸图片幻灯片

4. 试验验证

根据改进方案，设计、制造悬浮控制器，并进行故障模拟试验，验证其容错能力及悬浮控制的稳定性.

4.1 电源故障模拟试验

将两路24 V电源通过冗余模块持续供电，验证在单路故障时输出仍连续稳定. 如图8所示. 图中：1和2为两路110 V转24 V电源的输出截止控制端，施加低电平可封锁其输出，以模拟单路电源模块故障；3和4为正常工作指示灯，控制端1为低电平，第1路电源关闭，其电源指示灯3熄灭，经过冗余后，24 V输出未受影响.

图 8 电源模块故障模拟测试

Figure 8. Failure simulation test of power module

下载: 全尺寸图片幻灯片

4.2 试验台悬浮实验

在单悬浮架试验台上进行静态悬浮、电源故障及板卡故障模拟. 试验台由轨道梁、悬浮架、悬浮控制系统和车体平台组成，控制器吊挂于底部（见图9）.

图 9 单悬浮架试验台

Figure 9. Single levitation test bench

下载: 全尺寸图片幻灯片

悬浮架在落车状态下升起，悬浮稳定后，1# 板卡和2# 板卡的状态和输出信号如图10所示. 1# 板卡和2# 板卡均处于正常工作状态，此时，1# 板卡为主板，其主从状态为低电平，PWM信号作为系统输出；2# 板卡为从板，主从状态为高电平，PWM无输出.

图 10 无故障主从状态信号和PWM输出信号

Figure 10. Master–slave status signal and PWM output signal under fault-free condition

下载: 全尺寸图片幻灯片

在第80 s，模拟1# 板卡故障（图11）：断开其生命信号通道后，1# 板卡在40 us内由低电平变为高电平，转为从机，2# 板卡由高电平变为低电平，成为主机，系统PWM输出成功切换. 如图12所示，PWM控制信号由1# 板卡切换到2# 板卡，悬浮间隙、悬浮电流未出现变化，加速度在合理范围内，切换时间小于100 us，无信号丢失.

图 11 1# 板卡故障状态信号和PWM信号

Figure 11. Status signal and PWM signal under board #1 failure

下载: 全尺寸图片幻灯片

图 12 切换过程间隙、电流和加速度变化

Figure 12. Changes in levitation gap, current, and acceleration during switching process

下载: 全尺寸图片幻灯片

在板卡故障模拟中，1# 板卡发生故障后，2# 板卡升为主板，主从状态如图13左侧所示：此时，1# 板卡的主从状态为高电平（故障状态），2# 板卡正常，主从状态为低电平. 当将2# 板卡的生命信号通道断开后，仲裁板卡立即识别到故障并将其隔离，此时2块板卡均处于故障状态，系统无输出，悬浮失效，波形如图13右侧所示.

图 13 双板卡故障状态信号和PWM信号

Figure 13. Status signal and PWM signal under dual-board failure

下载: 全尺寸图片幻灯片

在2块板卡均正常时，1# 板卡的PWM信号作为系统输出，2# 板卡为热备，故障不影响系统输出. 断开2# 板卡生命信号后，状态信号和PWM信号如图14所示：1# 板卡仍为主板卡，2# 板卡故障后保持高电平，其控制信号未作为系统输出.

图 14 2#板卡故障后状态信号和PWM信号

Figure 14. Status signal and PWM signal after board 2# failure

下载: 全尺寸图片幻灯片

在悬浮架稳定悬浮状态下，模拟在第40 s发生的110 V/24 V单电源故障，间隙、电流和加速度的变化如图15所示. 单电源故障未对悬浮状态产生明显影响，间隙、电流和加速度稳定. 悬浮间隙的均方根误差为0.096 mm；加速度在0.6 m/s²以内波动，其均方根误差为0.11 m/s².

图 15 电源故障时刻间隙、电流和加速度变化

Figure 15. Changes in levitation gap, current, and acceleration during power failure

下载: 全尺寸图片幻灯片

所有板卡故障模拟均采用断开生命信号通道的方式，试验证明通过断电模拟的故障现象与断开生命信号通道的方式一致.

5. 结　论

1）本文对某中低速磁浮列车悬浮系统，运用模糊综合评价和AHP层次分析法，优化了传统FMECA分析，更贴合实际工程需求，识别出悬浮系统的高危害性部分.

2）采用马尔可夫理论，提出系统改进方案，并研制了悬浮冗余系统样机，在单悬浮架试验台上开展试验，切换时间小于100 us，悬浮间隙的均方根误差小于0.1 mm，加速度在0.6 m/s²内波动，加速度均方根误差为0.11 m/s².

3）通过系列故障模拟试验验证了改进后悬浮系统的故障识别与容错能力，提升了悬浮控制系统的整体容错性能.

致谢：高速磁浮运载技术全国重点实验室开放基金（SKLM-SFCF-2023-011）的支持.

图 1 悬浮控制系统结构

Figure 1. Levitation control system structure

下载: 全尺寸图片幻灯片

图 2 悬浮控制系统结构树

Figure 2. Structure tree of levitation control system

下载: 全尺寸图片幻灯片

图 3 悬浮冗余控制器设计架构

Figure 3. Architecture of levitation redundant controller

下载: 全尺寸图片幻灯片

图 4 马尔可夫状态转移

Figure 4. Markov state transition

下载: 全尺寸图片幻灯片

图 5 不同冗余结构可靠性曲线

Figure 5. Reliability curves of different redundant structures

下载: 全尺寸图片幻灯片

图 6 双机切换控制策略

Figure 6. Dual-machine switching control strategy

下载: 全尺寸图片幻灯片

图 7 电源电路结构

Figure 7. Power circuit structure

下载: 全尺寸图片幻灯片

图 8 电源模块故障模拟测试

Figure 8. Failure simulation test of power module

下载: 全尺寸图片幻灯片

图 9 单悬浮架试验台

Figure 9. Single levitation test bench

下载: 全尺寸图片幻灯片

图 10 无故障主从状态信号和PWM输出信号

Figure 10. Master–slave status signal and PWM output signal under fault-free condition

下载: 全尺寸图片幻灯片

图 11 1# 板卡故障状态信号和PWM信号

Figure 11. Status signal and PWM signal under board #1 failure

下载: 全尺寸图片幻灯片

图 12 切换过程间隙、电流和加速度变化

Figure 12. Changes in levitation gap, current, and acceleration during switching process

下载: 全尺寸图片幻灯片

图 13 双板卡故障状态信号和PWM信号

Figure 13. Status signal and PWM signal under dual-board failure

下载: 全尺寸图片幻灯片

图 14 2#板卡故障后状态信号和PWM信号

Figure 14. Status signal and PWM signal after board 2# failure

下载: 全尺寸图片幻灯片

图 15 电源故障时刻间隙、电流和加速度变化

Figure 15. Changes in levitation gap, current, and acceleration during power failure

下载: 全尺寸图片幻灯片

表 1 悬浮系统典型故障模式FMEA分析结果

Table 1. FMEA results of typical failure modes in levitation system

最低约定层次	故障模式	故障原因	系统影响	整车影响
控制板	无 PWM 输出/输出错误	源端电压不稳；过温虚焊，断路；抗振动冲击过大；内部短路；程序运行错误	驱动板无法接收到PWM，单点无法悬浮	车辆单点失悬或掉点砸轨，双点故障进入救援模式
接口板	悬浮控制故障	过温虚焊，断路；抗振动冲击能力差；抗干扰能力差；内部短路；源端电压不稳	控制板无法接收悬浮传感器信号，无法悬浮；控制板接收错误电流信号，悬浮失稳	车辆单点失悬，双点故障进入救援模式；车辆单点连续打轨，车辆降速运营
110 V 转 24 V 电源模块	DC 24 V断路	耐压能不足；温度过高；抗干扰能力不足	悬浮传感器及悬浮控制电路无法得电，悬浮控制缺少输入	车辆单点失悬，双点故障进入救援模式
电流传感器	信号输出不稳定；无输出信号	过流；接触不良；温度过高	无法监测悬浮电流，实际电流与预期存在误差，悬浮失稳	车辆单点连续打轨，车辆降速运营
电压传感器	信号输出不稳定	过压；接触不良	主接触器无法闭合	车辆单点失悬，双点故障进入救援模式
驱动板	无法启动	IGBT击穿导致的过流；抗振动冲击能力差；抗干扰能力差；高温虚焊	无法控制IGBT开断	车辆单点失悬，双点故障进入救援模式
IGBT	击穿	电磁铁短路；温度过高	无悬浮电流输出	车辆单点失悬，双点故障进入救援模式
支撑电容	损坏	老化；电容质量问题；温度过高	单支撑电容损坏无影响
支撑电容	击穿	过压	主电路短路，悬浮控制器停机	车辆单点失悬，双点故障进入救援模式

下载: 导出CSV

表 2 影响因素的评价等级划分

Table 2. Evaluation level classification for influencing factors

影响因素	等级
影响因素	1	3	5	7	9
影响概率	几乎没有	极少	偶尔	可能	经常
严重程度	可忽略	轻微的	临界的	危急的	灾难的
综合检修难度	极低	较低	中等	较难	很难

下载: 导出CSV

表 3 因素重要度判断值表

Table 3. Judgment values for factor importance

相对评价值	极重要	很重要	重要	略重要	同等
评分	9	7	5	3	1
注：8、6、4、2为评价价值的中间值.

下载: 导出CSV

1～9阶判断矩阵 ${I_{\mathrm{R}}}$ 值

Judgment matrices ${I_{\mathrm{R}}}$ for orders 1–9

阶数	1	2	3	4	5	6	7	8	9
${I_{\mathrm{R}}}$	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45

下载: 导出CSV

表 5 各故障模式的综合危害等级

Table 5. Comprehensive hazard levels for each failure mode

部件	综合危害性等级	部件	综合危害性等级
控制板	6.3147	驱动板	3.8714
接口板	5.4841	充电电阻	3.7696
110/24 V 电源	5.6534	吸收电容	2.9501
IGBT	4.5688	支撑电容	2.9932
电流传感器	4.1590	电压传感器	3.7798
主接触器	4.2963	熔断器	3.4600

下载: 导出CSV

参考文献(25)

[1]	LEE H W, KIM K C, LEE J. Review of maglev train technologies[J]. IEEE Transactions on Magnetics, 2006, 42(7): 1917-1925. doi: 10.1109/TMAG.2006.875842
[2]	徐飞,罗世辉,邓自刚. 磁悬浮轨道交通关键技术及全速度域应用研究[J]. 铁道学报,2019,41(3): 40-49. doi: 10.3969/j.issn.1001-8360.2019.03.006 XU Fei, LUO Shihui, DENG Zigang. Study on key technologies and whole speed range application of maglev rail transport[J]. Journal of the China Railway Society, 2019, 41(3): 40-49. doi: 10.3969/j.issn.1001-8360.2019.03.006
[3]	THORNTON R D. Efficient and affordable maglev opportunities in the United States[J]. Proceedings of the IEEE, 2009, 97(11): 1901-1921. doi: 10.1109/JPROC.2009.2030251
[4]	翟婉明,赵春发. 现代轨道交通工程科技前沿与挑战[J]. 西南交通大学学报,2016,51(2): 209-226. doi: 10.3969/j.issn.0258-2724.2016.02.001 ZHAI Wanming, ZHAO Chunfa. Frontiers and challenges of sciences and technologies in modern railway engineering[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 209-226. doi: 10.3969/j.issn.0258-2724.2016.02.001
[5]	马卫华,胡俊雄,李铁,等. EMS型中低速磁浮列车悬浮架技术研究综述[J]. 西南交通大学学报,2023,58(4): 720-733. doi: 10.3969/j.issn.0258-2724.20210971 MA Weihua, HU Junxiong, LI Tie, et al. Technologies research review of electro-magnetic suspension medium-low-speed maglev train levitation frame[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 720-733. doi: 10.3969/j.issn.0258-2724.20210971
[6]	马卫华,罗世辉,张敏,等. 中低速磁浮车辆研究综述[J]. 交通运输工程学报,2021,21(1): 199-216. MA Weihua, LUO Shihui, ZHANG Min, et al. Research review on medium and low speed maglev vehicle[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 199-216.
[7]	陈文彬,李晓阳,童邦安,等. 谐波减速器的传动效率确信可靠性建模与分析[J]. 振动工程学报,2022,35(1): 237-245. CHEN Wenbin, LI Xiaoyang, TONG Bang’an, et al. Belief reliability modeling and analysis for transmission efficiency of harmonic gear[J]. Journal of Vibration Engineering, 2022, 35(1): 237-245.
[8]	CATELANI M, CIANI L, GALAR D, et al. FMECA assessment for railway safety-critical systems investigating a new risk threshold method[J]. IEEE Access, 2021, 9: 86243-86253. doi: 10.1109/ACCESS.2021.3088948
[9]	BEN BRAHIM I, ADDOUCHE S A, EL MHAMEDI A, et al. Build a Bayesian network from FMECA in the production of automotive parts: diagnosis and prediction[J]. IFAC-PapersOnLine, 2019, 52(13): 2572-2577. doi: 10.1016/j.ifacol.2019.11.594
[10]	LIN S, JIA L M, WANG Y H. Safety assessment of complex electromechanical systems based on hesitant interval-valued intuitionistic fuzzy theory[J]. International Journal of Fuzzy Systems, 2019, 21(8): 2405-2420. doi: 10.1007/s40815-019-00729-4
[11]	CATELANI M, CIANI L, GALAR D, et al. Risk assessment of a wind turbine: a new FMECA-based tool with RPN threshold estimation[J]. IEEE Access, 2020, 8: 20181-20190. doi: 10.1109/ACCESS.2020.2968812
[12]	ASWIN K R, RENJITH V R, AKSHAY K R. FMECA using fuzzy logic and grey theory: a comparitve case study applied to ammonia storage facility[J]. International Journal of System Assurance Engineering and Management, 2022, 13(4): 2084-2103.
[13]	RENJITH V R, JOSE KALATHIL M, KUMAR P H, et al. Fuzzy FMECA (failure mode effect and criticality analysis) of LNG storage facility[J]. Journal of Loss Prevention in the Process Industries, 2018, 56: 537-547. doi: 10.1016/j.jlp.2018.01.002
[14]	GIARDINA M, MORALE M. Safety study of an LNG regasification plant using an FMECA and HAZOP integrated methodology[J]. Journal of Loss Prevention in the Process Industries, 2015, 35: 35-45. doi: 10.1016/j.jlp.2015.03.013
[15]	于涵,张和生. 基于模糊综合评价的动车组牵引传动系统改进FMECA[J]. 铁道学报,2022,44(9): 33-41. doi: 10.3969/j.issn.100-8360.2022.09.05 YU Han, ZHANG Hesheng. Improved FMECA for traction transmission system of EMU based on fuzzy comprehensive evaluation[J]. Journal of the China Railway Society, 2022, 44(9): 33-41. doi: 10.3969/j.issn.100-8360.2022.09.05
[16]	SUN Y G, LI F X, LIN G B, et al. Adaptive fault-tolerant control of high-speed maglev train suspension system with partial actuator failure: design and experiments[J]. Journal of Zhejiang University: Science A, 2023, 24(3): 272-283. doi: 10.1631/jzus.A2200189
[17]	ZHAI M D, LONG Z Q, LI X L. Fault-tolerant control of magnetic levitation system based on state observer in high speed maglev train[J]. IEEE Access, 2019, 7: 31624-31633. doi: 10.1109/ACCESS.2019.2898108
[18]	佘龙华,邹东升,李建泉,等. 磁悬浮控制器DSP的容错设计[J]. 机车电传动,2006(1): 33-35. doi: 10.3969/j.issn.1000-128X.2006.01.010 SHE Longhua, ZOU Dongsheng, LI Jianquan, et al. Design of error tolerance for maglev controller DSP[J]. Electric Drive for Locomotives, 2006(1): 33-35. doi: 10.3969/j.issn.1000-128X.2006.01.010
[19]	SUNG H K, KIM D, CHO H, et al. Fault tolerant control of electromagnetic levitation system[J]. Advances in Industrial Control, 2004, 57(10): 676-689.
[20]	KIM H J, KIM C K, KWON S. Design of a fault-tolerant levitation controller for magnetic levitation vehicle[C]//2007 International Conference on Electrical Machines and Systems (ICEMS). Seoul: IEEE, 2007: 1977-1980.
[21]	ZHAI M D, LI X L, LONG Z Q. Research on redundancy and fault-tolerant control technology of levitation join-structure in high speed maglev train[M]//Proceedings of the 3rd International Conference on Electrical and Information Technologies for Rail Transportation (EITRT) 2017. Singapore: Springer, 2018: 671-678.
[22]	JANG K H, KOOK Y S, SHIN B C, et al. Redundancy performance of levitation controller for maglev vehicle EcoBee[C]//2018 21st International Conference on Electrical Machines and Systems (ICEMS). Jeju: IEEE, 2018: 898-902.
[23]	LIANG S, ZENG J W, JIN L, et al. Computer design and test of suspension control based on two-machine hot standby for speed maglev train[C]//2020 39th Chinese Control Conference (CCC). Shenyang: IEEE, 2020: 4147-4152.
[24]	JIN L, LONG Z Q, ZENG J W. Research on fault-tolerant control problem for suspension system of medium speed maglev train[C]//2017 29th Chinese Control and Decision Conference (CCDC). Chongqing: IEEE, 2017: 2993-2998.
[25]	徐俊起,佟来生,荣立军,等. 磁浮列车悬浮控制系统工程化应用中的关键技术[J]. 城市轨道交通研究,2018,21(12): 14-17. XU Junqi, TONG Laisheng, RONG Lijun, et al. Key technologies of levitation control system applied to maglev train in practical engineering[J]. Urban Mass Transit, 2018, 21(12): 14-17.

施引文献

附加材料(0)

访问统计

点击查看大图

图(15) / 表(5)

计量

文章访问数: 37
HTML全文浏览量: 12
PDF下载量: 1
被引次数: 0

1. 悬浮系统故障分析
2. 基于模糊评价的危害性分析
2.1 建立因素集 ${\boldsymbol{U}}$
2.2 建立评价集 ${\boldsymbol{V}}$
2.3 建立各故障模式评价矩阵
2.4 建立基于AHP的因素权重集
2.5 一级模糊综合评价
2.6 综合危害等级计算
3. 悬浮系统改进方案设计
3.1 控制板
3.2 IGBT改进设计
3.3 电源模块冗余设计
4. 试验验证
4.1 电源故障模拟试验
4.2 试验台悬浮实验
5. 结　论

1. 悬浮系统故障分析
2. 基于模糊评价的危害性分析
2.1 建立因素集 ${\boldsymbol{U}}$
2.2 建立评价集 ${\boldsymbol{V}}$
2.3 建立各故障模式评价矩阵
2.4 建立基于AHP的因素权重集
2.5 一级模糊综合评价
2.6 综合危害等级计算
3. 悬浮系统改进方案设计
3.1 控制板
3.2 IGBT改进设计
3.3 电源模块冗余设计
4. 试验验证
4.1 电源故障模拟试验
4.2 试验台悬浮实验
5. 结　论

参考文献(25)

施引文献

附加材料(0)

访问统计

中低速磁浮列车悬浮系统模糊综合评价与改进设计

doi: 10.3969/j.issn.0258-2724.20240190

作者简介: 曹毅（1996—），男，博士研究生，研究方向为悬浮冗余和悬浮控制，E-mail：caoyi@swjtu.edu.cn

通讯作者: 马卫华（1979—），男，研究员，博士，研究方向为车辆系统动力学，E-mail： mwh@swjtu.edu.cn

计量

出版历程

Fuzzy Comprehensive Evaluation and Improved Design of Levitation System for Medium- and Low-Speed Maglev Trains

1. 悬浮系统故障分析

2. 基于模糊评价的危害性分析

2.1 建立因素集U {\boldsymbol{U}}

2.2 建立评价集V {\boldsymbol{V}}

2.3 建立各故障模式评价矩阵

2.4 建立基于AHP的因素权重集

2.5 一级模糊综合评价

2.6 综合危害等级计算

3. 悬浮系统改进方案设计

3.1 控制板

3.1.1 可靠性分析

3.1.2 冗余控制策略设计

3.2 IGBT改进设计

3.3 电源模块冗余设计

4. 试验验证

4.1 电源故障模拟试验

4.2 试验台悬浮实验

5. 结 论

计量

出版历程

目录

1. 悬浮系统故障分析

2. 基于模糊评价的危害性分析

2.1 建立因素集 {\boldsymbol{U}} {\boldsymbol{U}}

2.2 建立评价集 {\boldsymbol{V}} {\boldsymbol{V}}

2.3 建立各故障模式评价矩阵

2.4 建立基于AHP的因素权重集

2.5 一级模糊综合评价

2.6 综合危害等级计算

3. 悬浮系统改进方案设计

3.1 控制板

3.2 IGBT改进设计

3.3 电源模块冗余设计

4. 试验验证

4.1 电源故障模拟试验

4.2 试验台悬浮实验

5. 结 论

作者简介:
曹毅（1996—），男，博士研究生，研究方向为悬浮冗余和悬浮控制，E-mail：caoyi@swjtu.edu.cn

通讯作者:
马卫华（1979—），男，研究员，博士，研究方向为车辆系统动力学，E-mail： mwh@swjtu.edu.cn

2.1 建立因素集 ${\boldsymbol{U}}$

2.2 建立评价集 ${\boldsymbol{V}}$

5. 结　论

2.1 建立因素集 ${\boldsymbol{U}}$

2.2 建立评价集 ${\boldsymbol{V}}$

5. 结　论