Train Rescheduling Model Based on Combination Strategy for Urban Rail Transit Operation Interruption
-
摘要:
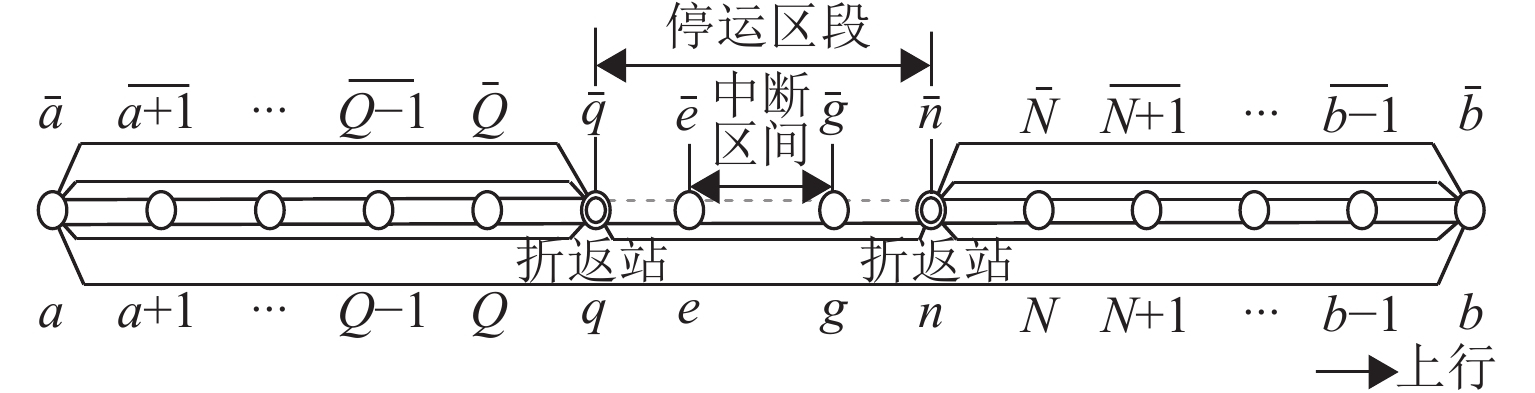
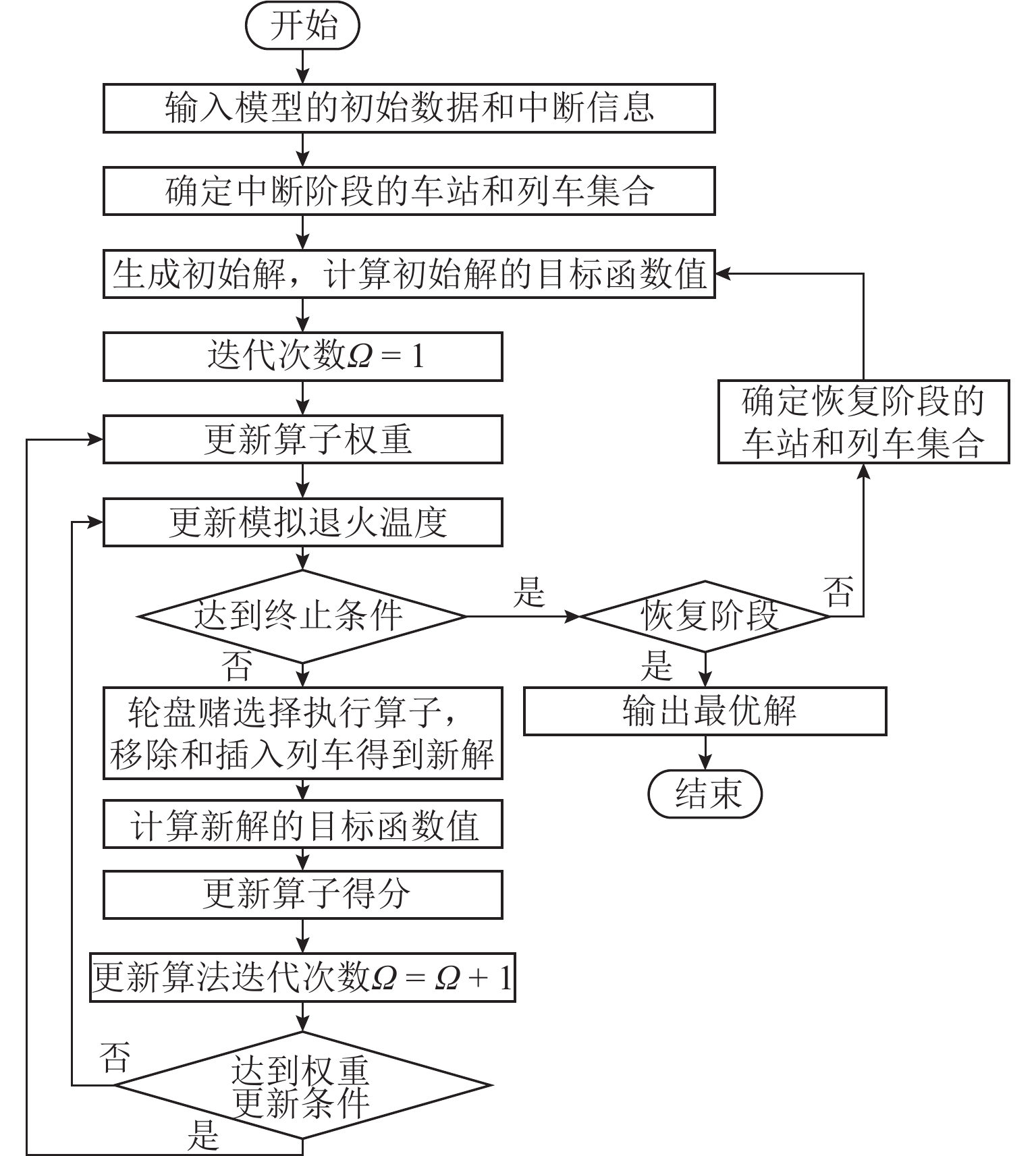
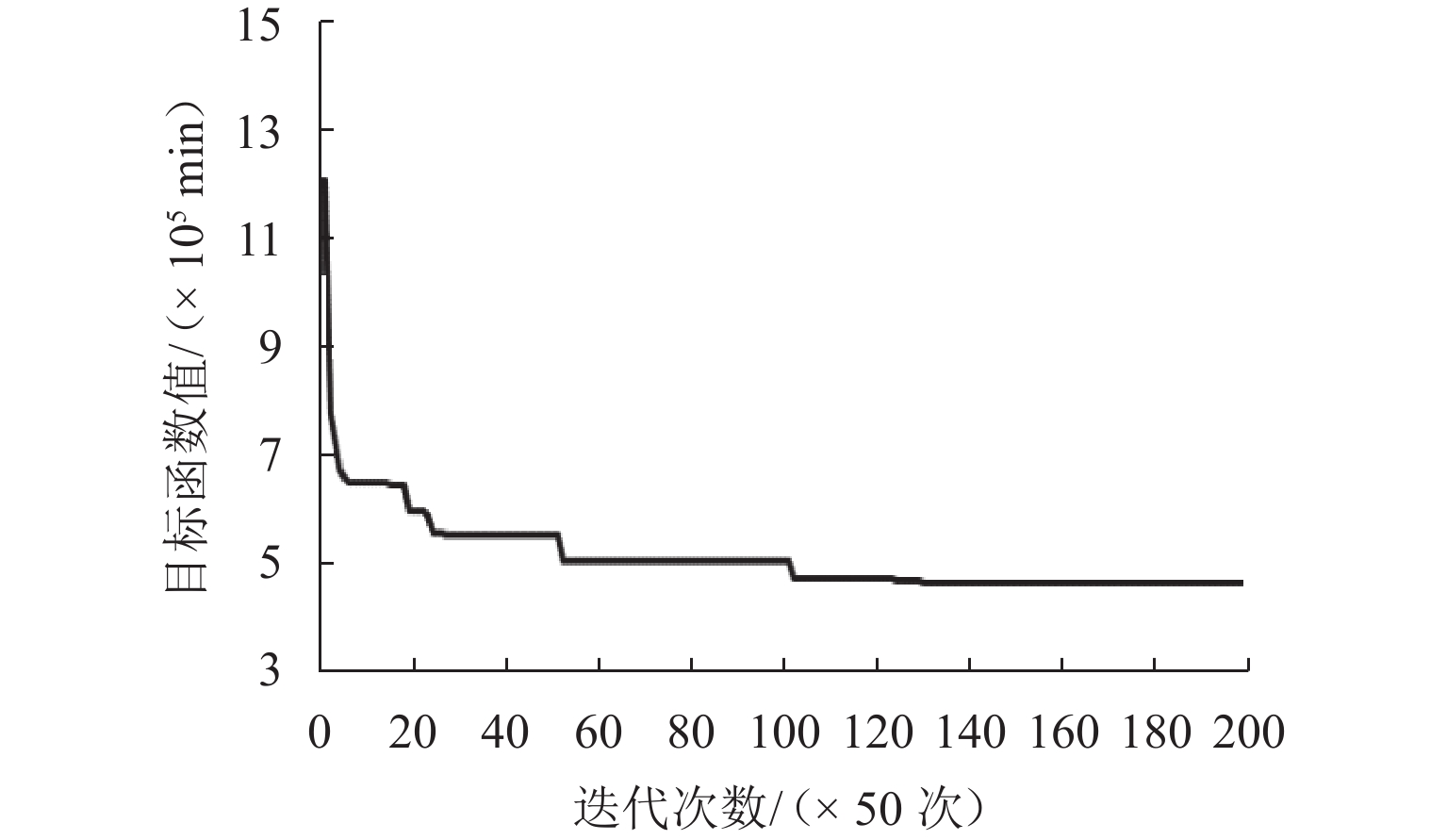
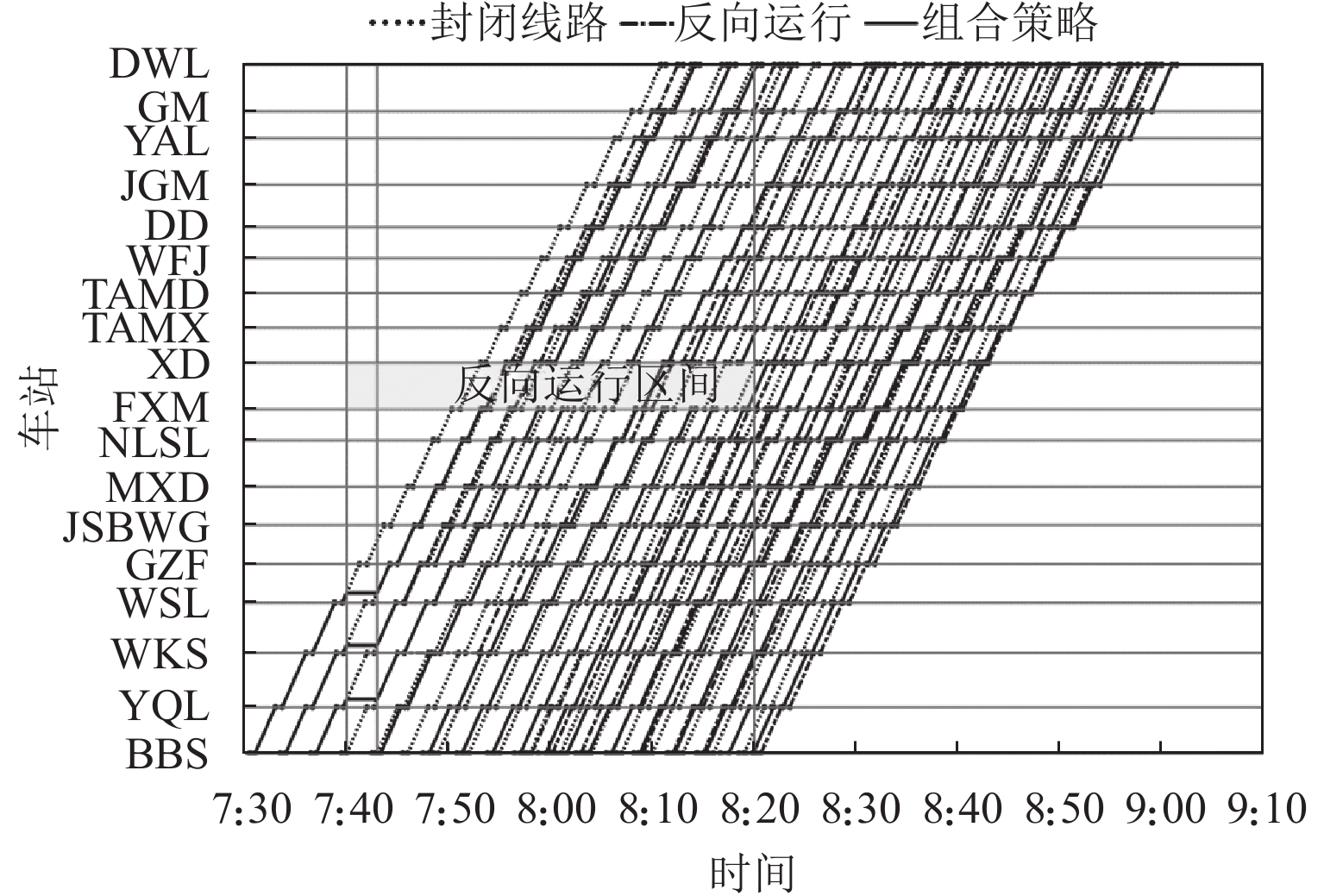
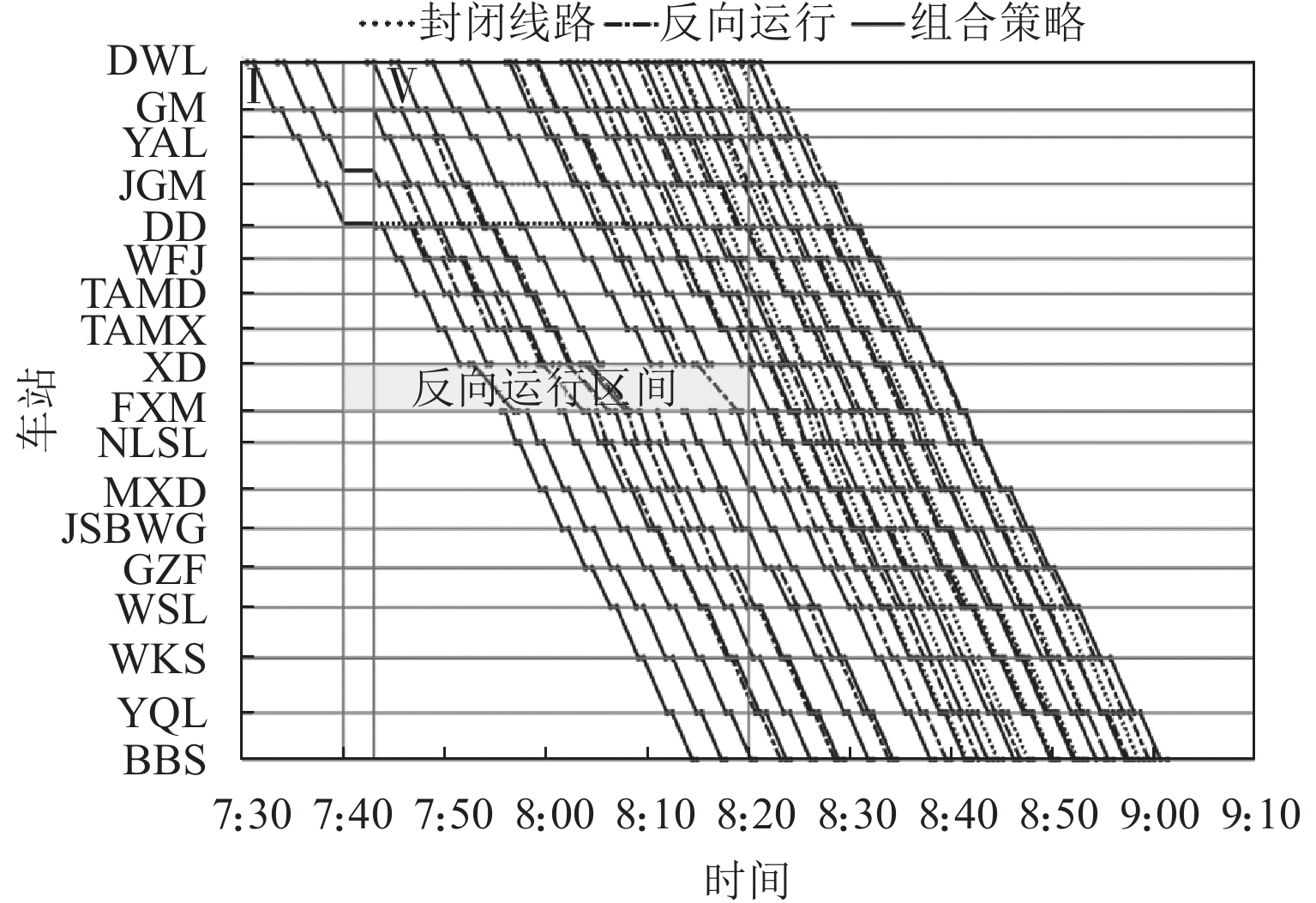
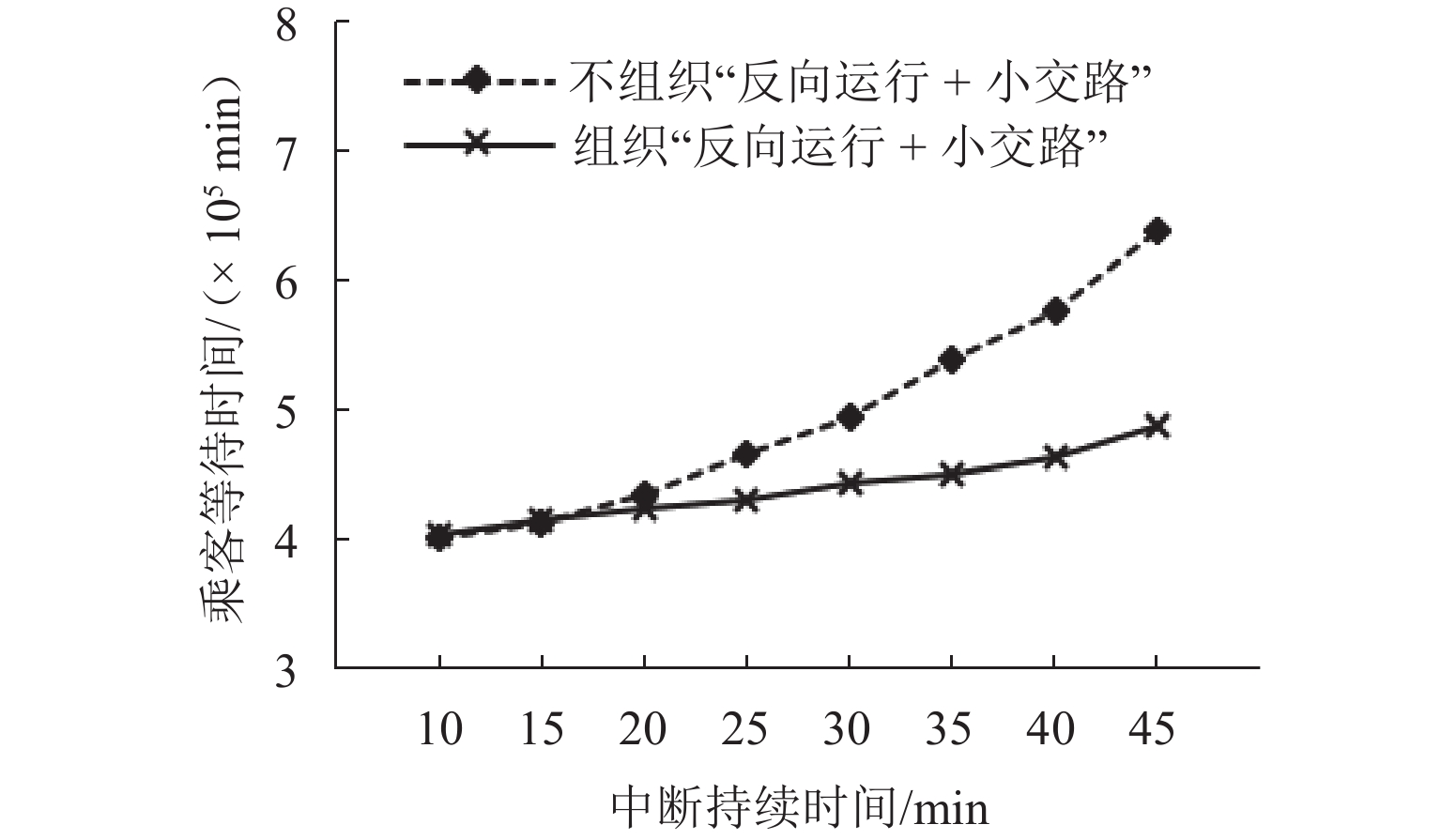
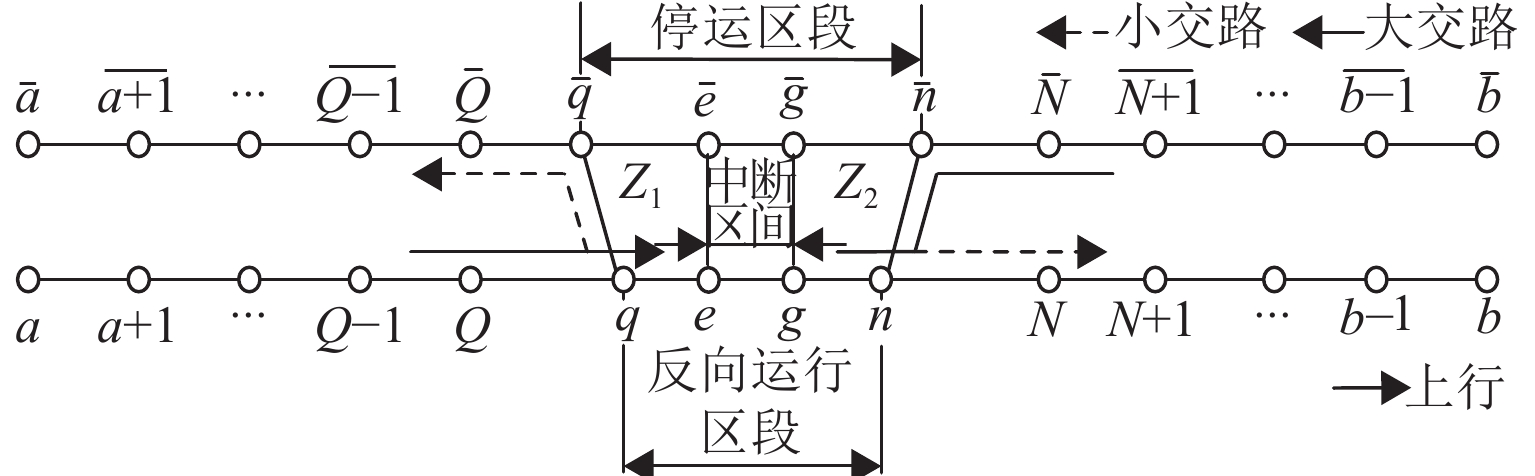
运营中断是城市轨道交通实际运营过程中不可忽略的安全因素. 针对城市轨道交通单向运营中断下的列车运行调整问题,本文提出“反向运行 + 小交路”组合调整策略. 从乘客时间价值的角度出发,以乘客在站等待时间最小为优化目标,分中断阶段和恢复阶段建立单向运营中断下城市轨道交通列车运行调整两阶段模型;考虑到模型复杂度以及调整问题对求解效率的需求,设计适用于所构建模型的不同交路选择自适应大规模邻域搜索算法,实现对大规模算例的有效求解. 案例研究表明:单向运营中断条件下基于“反向运行 + 小交路”策略组织列车运行调整,比采用反向运行策略的乘客等待时间减少5.19%;相较于封闭中断方向线路,可使全线乘客的在站等待时间减少19.80%,且上下行方向的运输服务更加均衡;此外,当中断持续时长超15 min时,与封闭中断方向线路相比,采用“反向运行 + 小交路”策略组织列车运行调整可以取得更好的效果.
Abstract:Operation interruption is a safety factor that cannot be ignored in the actual operation of urban rail transit. To address train operation adjustment under unidirectional operation interruption in urban rail transit, a combined adjustment strategy of “reverse operation + short turning” was proposed. From the perspective of passenger time value, taking the minimum waiting time of passengers at the station as the optimization objective, a two-stage model of urban rail transit train operation adjustment under unidirectional operation interruption was established for the interruption stage and the recovery stage. Considering the complexity of the model and the requirements of the adjustment problem for solution efficiency, an adaptive large-scale neighborhood search algorithm based on different service patterns was specifically designed for the proposed model, so as to achieve effective solutions for large-scale instances. The case study shows that, under unidirectional operation interruption, the “reverse operation + short turning” strategy reduces passenger waiting time by 5.19% compared with the reverse operation strategy. Compared with closing the interrupted direction line, it can reduce the waiting time of passengers on the whole line by 19.80%, and the transportation services in both directions are more balanced. In addition, when the interruption duration is more than 15 minutes, adopting the strategy of “reverse operation + short turning” to organize train operation adjustment can achieve better results than closing the interrupted direction line.
-
表 1 停站时间参数
Table 1. Train operation parameters
车站 停站时间/s 运行时间/s 上行 下行 上行 下行 BBS 30 30 120 120 YQL 40 30 140 140 WKS 40 40 130 130 WSL 45 40 100 110 GZF 45 40 100 100 JSBWG 40 40 100 100 MXD 30 30 120 120 NLSL 30 30 80 60 FXM 50 45 120 240 XD 30 40 90 90 TAMX 30 30 90 90 TAMD 30 30 90 90 WFJ 30 30 80 80 DD 45 45 110 110 JGM 45 45 120 120 YAL 30 30 70 70 GM 50 45 120 120 表 2 运行区间参数
运行区间 运行时间/s 上行 下行 BBS→YQL 120 120 YQL→WKS 140 140 ~ ~ ~ ⋮ GM→DWL 120 120 表 3 模型其他参数
Table 3. Other model parameters
参数 取值 参数 取值 上行列车数/列 17 研究时间长度/min 90 下行列车数/列 17 最小运行间隔/min 2 时间粒度/min 1 最小折返时间/s 120 最小停站时间/s 25 通过渡线时间/s 20 最大停站时间/s 90 道岔转换时间/s 10 表 4 单向运营中断下不同策略的列车运行调整结果对比
Table 4. Comparison of train operation adjustment results under unidirectional interruption
列车运行策略 目标函数/min 上行乘客等待时间/min 下行乘客等待时间/min 封闭线路 576997 222946 354051 反向运行 488086 279796 208290 “反向运行 + 小交路”组合策略 462750 271222 191528 效果对比(封闭线路)/% −19.80 +21.65 −45.90 效果对比(反向运行)/% −5.19 −3.06 −8.05 -
[1] WANG X H, JIN J G, SUN L J. Real-time dispatching of operating buses during unplanned disruptions to urban rail transit system[J]. Transportation Research Part C: Emerging Technologies, 2022, 139: 103696. doi: 10.1016/j.trc.2022.103696 [2] GHAEMI N, CATS O, GOVERDE R M P. A microscopic model for optimal train short-turnings during complete blockages[J]. Transportation Research Part B: Methodological, 2017, 105: 423-437. doi: 10.1016/j.trb.2017.10.002 [3] CANCA D, BARRENA E, ZARZO A, et al. Optimal train reallocation strategies under service disruptions[J]. Procedia-Social and Behavioral Sciences, 2012, 54: 402-413. doi: 10.1016/j.sbspro.2012.09.759 [4] CANCA D, BARRENA E, LAPORTE G, et al. A short-turning policy for the management of demand disruptions in rapid transit systems[J]. Annals of Operations Research, 2016, 246(1): 145-166. doi: 10.1007/s10479-014-1663-x [5] 王丹丹. 城市轨道交通运营中断下面向乘客的列车运行调整研究[D]. 北京: 北京交通大学, 2020. [6] 周玮腾, 钱蕾, 韩宝明, 等. 运营区间双向中断下城市轨道交通列车运行调整[J]. 东南大学学报(自然科学版), 2022, 52(4): 770-779.ZHOU Weiteng, QIAN Lei, HAN Baoming, et al. Train rescheduling of urban rail transit under bi-directional interruption in operation section[J]. Journal of Southeast University (Natural Science Edition), 2022, 52(4): 770-779. [7] YIN H D, HAN B M, LI D W, et al. Modeling and simulating passenger behavior for a station closure in a rail transit network[J]. PLoS One, 2016, 11(12): e0167126. doi: 10.1371/journal.pone.0167126 [8] 刘峰博, 周庭梁, 王小敏. 城市轨道交通故障下客流分布计算及评估方法[J]. 西南交通大学学报, 2021, 56(5): 921-927, 966.LIU Fengbo, ZHOU Tingliang, WANG Xiaomin. Calculation and evaluation method of passenger flow distribution under urban rail transit failure[J]. Journal of Southwest Jiaotong University, 2021, 56(5): 921-927,966. [9] XU X M, LI K P, YANG L X. Rescheduling subway trains by a discrete event model considering service balance performance[J]. Applied Mathematical Modelling, 2016, 40(2): 1446-1466. doi: 10.1016/j.apm.2015.06.031 [10] 刘浩江. 单线双向运行在地铁行车组织中的应用[J]. 都市快轨交通, 2008, 21(3): 17-19, 23. doi: 10.3969/j.issn.1672-6073.2008.03.005LIU Haojiang. Application of bidirectional operation on single track in subway train operation organization[J]. Urban Rapid Rail Transit, 2008, 21(3): 17-19,23. doi: 10.3969/j.issn.1672-6073.2008.03.005 [11] XU Y, JIA B, GHIASI A, et al. Train routing and timetabling problem for heterogeneous train traffic with switchable scheduling rules[J]. Transportation Research Part C: Emerging Technologies, 2017, 84: 196-218. doi: 10.1016/j.trc.2017.08.010 [12] HUANG Y R, MANNINO C, YANG L X, et al. Coupling time-indexed and big-M formulations for real-time train scheduling during metro service disruptions[J]. Transportation Research Part B: Methodological, 2020, 133: 38-61. doi: 10.1016/j.trb.2019.12.005 [13] VEELENTURF L P, KIDD M P, CACCHIANI V, et al. A railway timetable rescheduling approach for handling large-scale disruptions[J]. Transportation Science, 2015, 50(3): 841-862. doi: 10.2139/ssrn.2472934 [14] 户佐安, 夏一鸣, 蔡佳, 等. 延误条件下综合多种策略的城轨列车运行调整优化[J]. 吉林大学学报(工学版), 2021, 51(5): 1664-1672.HU Zuoan, XIA Yiming, CAI Jia, et al. Optimization of urban rail transit operation adjustment based on multiple strategies under delay[J]. Journal of Jilin University (Engineering and Technology Edition), 2021, 51(5): 1664-1672. [15] HUANG Y R, MANNINO C, YANG L X, et al. Coupling time-indexed and big-M formulations for real-time train scheduling during metro service disruptions[J]. Transportation Research Part B: Methodological, 2020, 133: 38-61. doi: 10.1016/j.trb.2019.12.005 [16] GHAEMI N, CATS O, GOVERDE R M P. Railway disruption management challenges and possible solution directions[J]. Public Transport, 2017, 9(1): 343-364. doi: 10.1007/s12469-017-0157-z [17] 孙晴, 张生瑞, 陈恒瑞. 城市轨道交通区间中断下列车运行调整[C]//2019世界交通运输大会论文集(上). 北京: 中国科学技术协会, 2019: 1642-1652. [18] LI S K, ZHOU X S, YANG L X, et al. Automatic train regulation of complex metro networks with transfer coordination constraints: a distributed optimal control framework[J]. Transportation Research Part B: Methodological, 2018, 117: 228-253. doi: 10.1016/j.trb.2018.09.001 [19] PENG S R, YANG X, WANG H W, et al. Dispatching high-speed rail trains via utilizing the reverse direction track: adaptive rescheduling strategies and application[J]. Sustainability, 2019, 11(8): 2351. doi: 10.3390/su11082351 [20] ROPKE S, PISINGER D. An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows[J]. Transportation Science, 2006, 40(4): 455-472. doi: 10.1287/trsc.1050.0135 [21] 徐长安, 李晟东, 李斯涵, 等. 高铁夕发朝至列车开行与天窗设置协同优化[J]. 西南交通大学学报, 2021, 56(4): 744-754.XU Chang’an, LI Shengdong, LI Sihan, et al. Collaborative optimization for overnight train operation and maintenance window setting of high-speed railways[J]. Journal of Southwest Jiaotong University, 2021, 56(4): 744-754. -




 下载:
下载: