基于尾流振子模型的桥梁涡振半主动控制

刘汉云; 任欣怡; 韩艳; 彭文林

doi:10.3969/j.issn.0258-2724.20240152

基于尾流振子模型的桥梁涡振半主动控制

doi: 10.3969/j.issn.0258-2724.20240152

长沙理工大学土木工程学院，湖南长沙 410114

基金项目: 国家自然科学基金项目（52108433，52178452）；湖南省领军人才项目（2021RC4031）；湖南省科技创新计划（2024RC3170）；湖南省自然科学基金项目（2024JJ40587）

详细信息

作者简介:
刘汉云（1989—），男，副教授，博士生导师，研究方向为桥梁结构抗震抗风与智能控制，E-mail：lhy_27@csust.edu.cn

通讯作者:
韩艳（1979—），女，教授，博士生导师，研究方向为大跨度桥梁风致振动与智能控制，E-mail：ce_hanyan@163.com

中图分类号: U441.3
计量
- 文章访问数: 44
- HTML全文浏览量: 23
- PDF下载量: 12
- 被引次数: 0
出版历程
- 收稿日期: 2024-03-24
- 修回日期: 2024-09-26
- 网络出版日期: 2025-08-08

Semi-active Control of Vortex-Induced Vibration of Bridge Based on Wake Oscillator Model

School of Civil Engineering, Changsha University of Science & Technology, Changsha 410114, China

摘要

摘要:
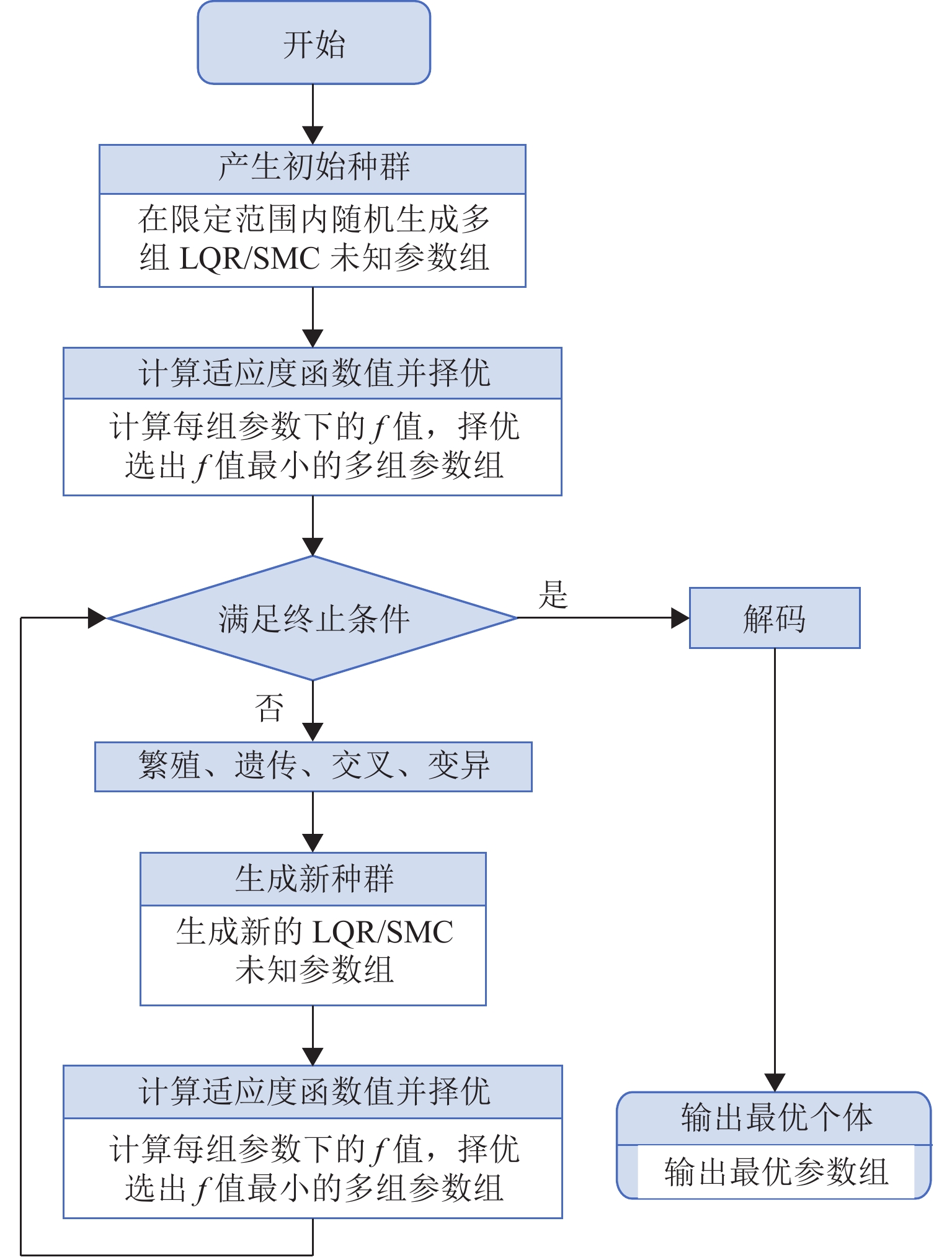
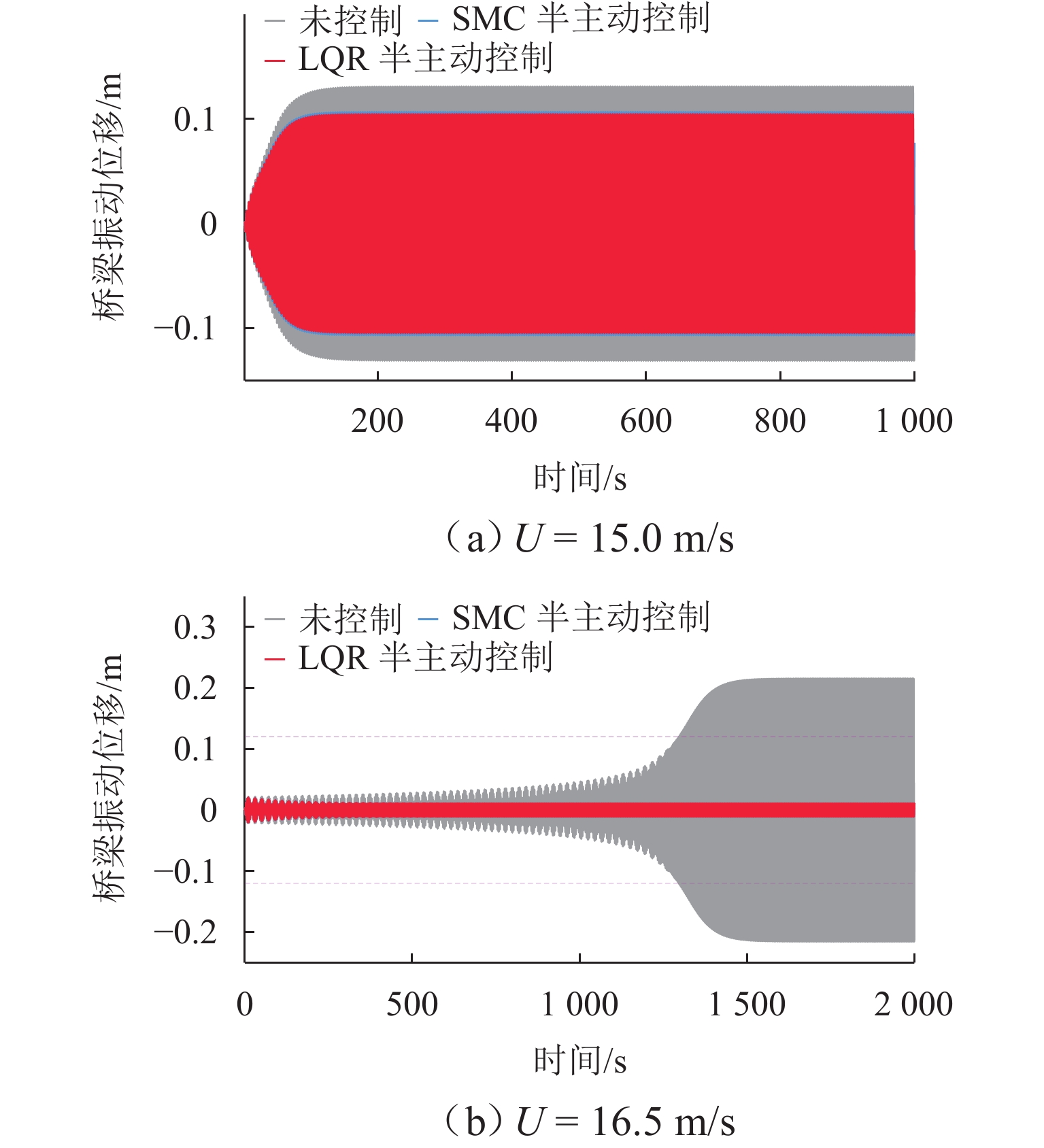
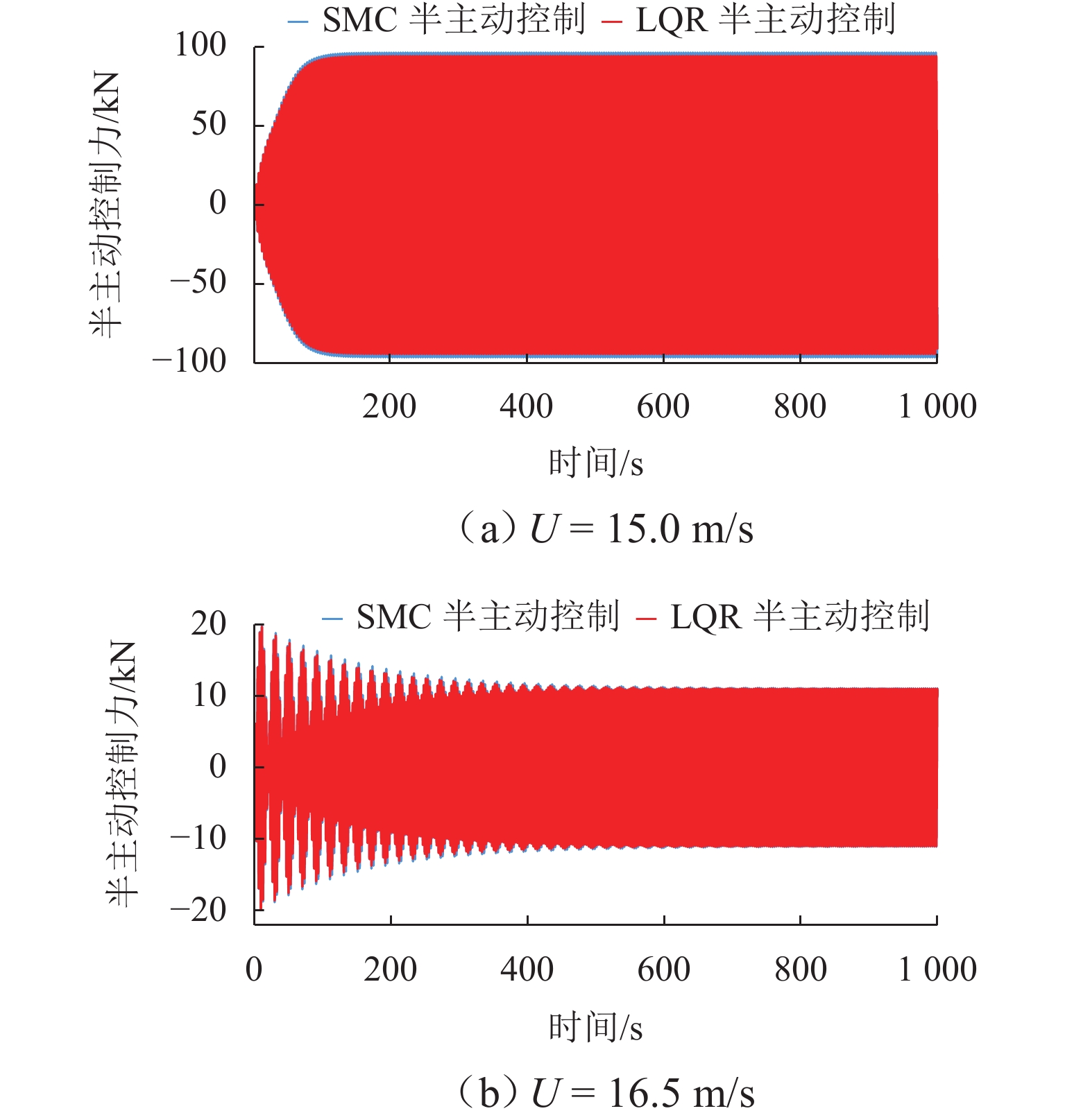
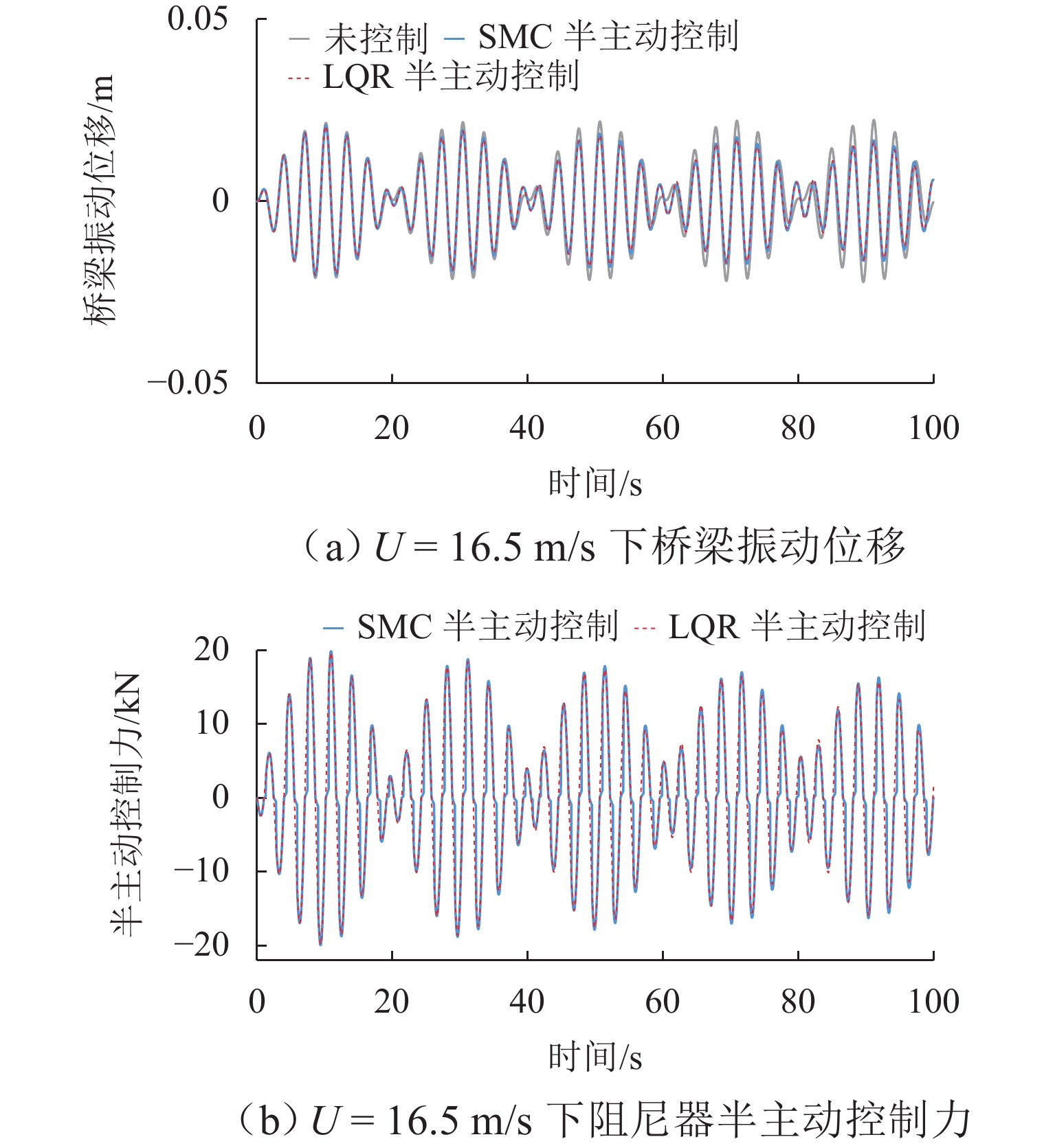
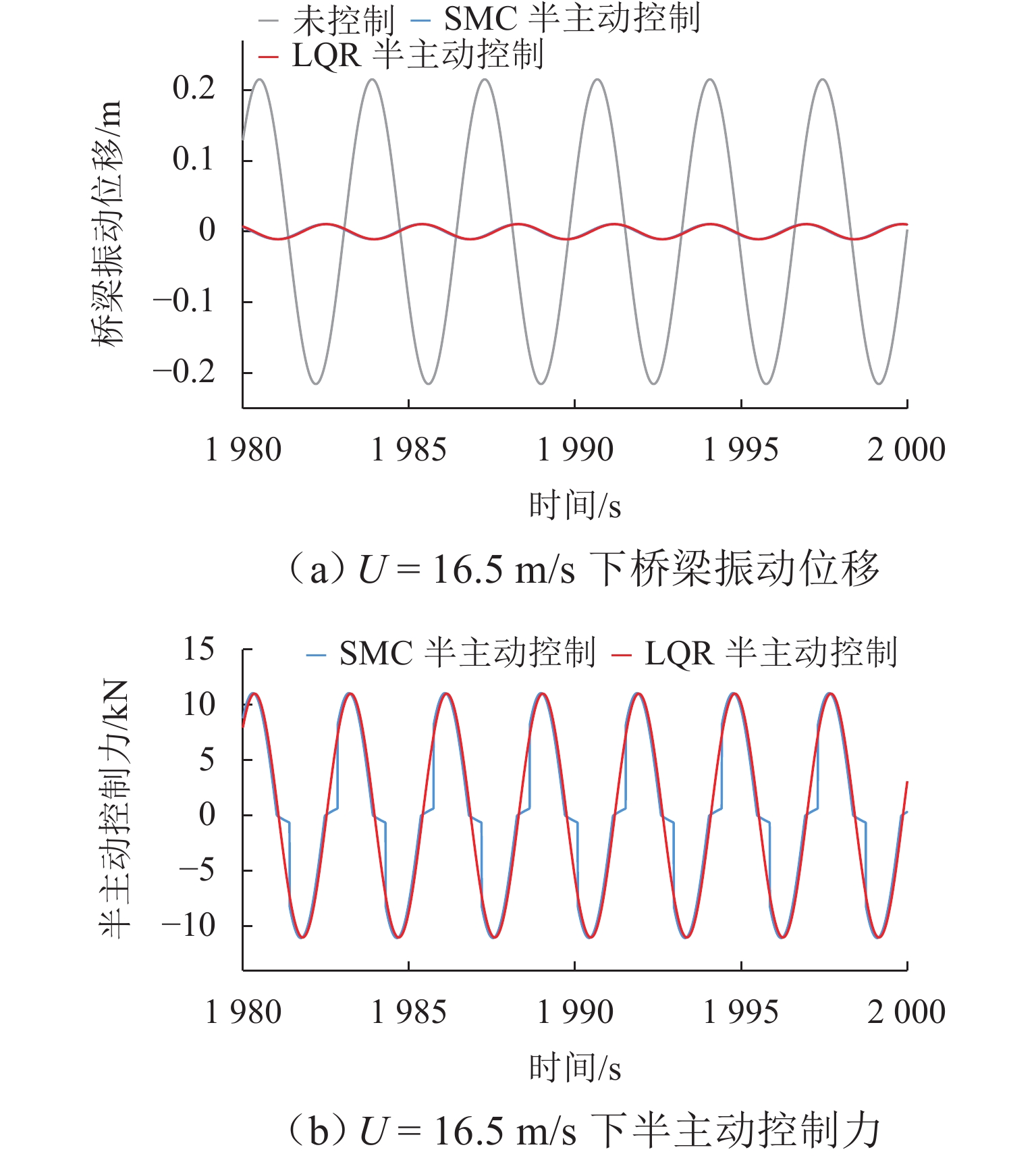
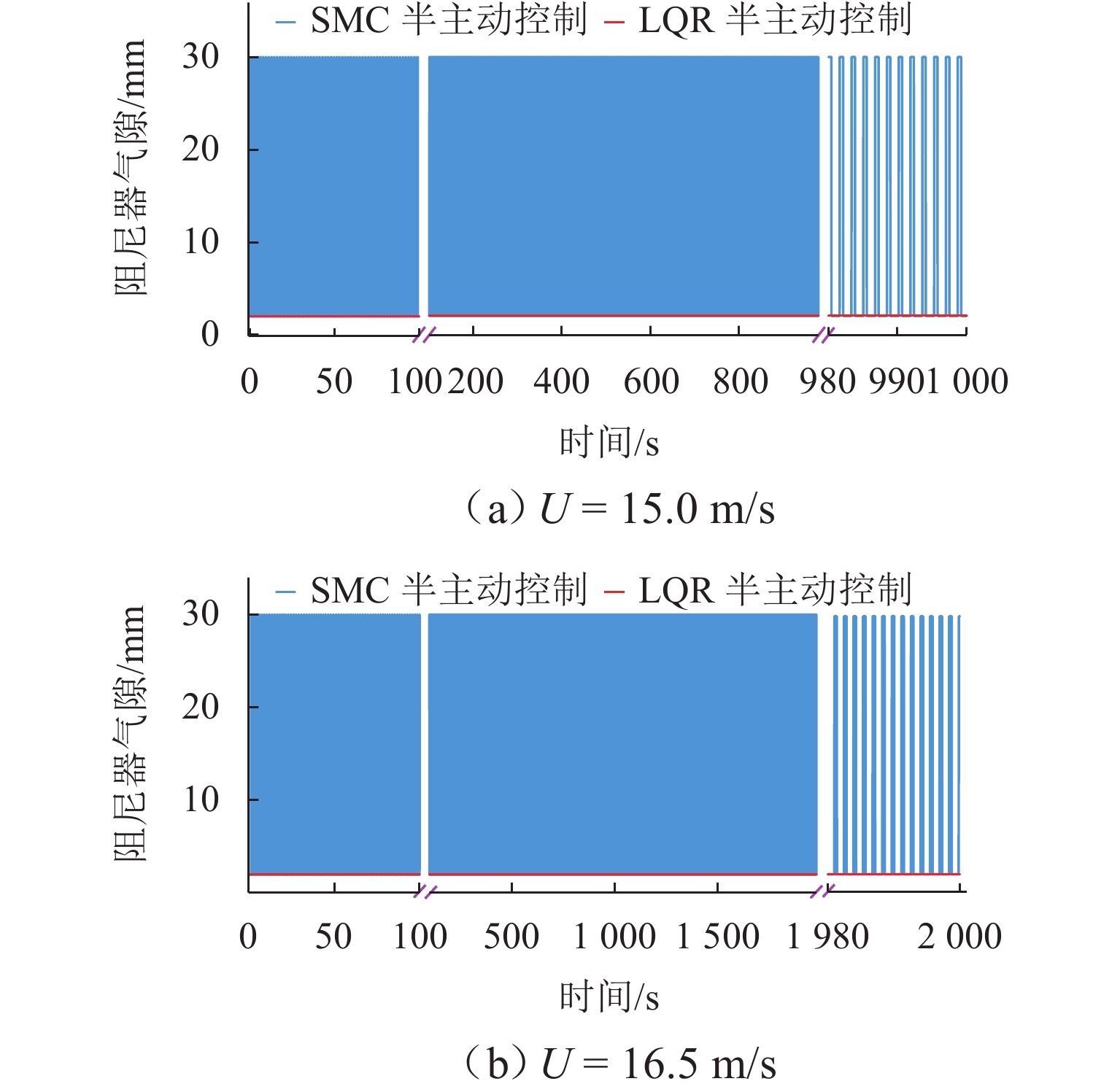
大跨度桥梁易发生低风速涡激振动，会导致桥梁结构疲劳和影响行车舒适性，基于尾流振子模型和变阻尼系数电涡流阻尼器开展桥梁涡激振动半主动控制研究. 首先，建立桥梁尾流振子无量纲涡激力模型，并基于遗传算法采用试验数据拟合获得模型参数；接着，设计可变间距滚珠丝杠电涡流阻尼器装置，并通过COMSOL模拟获得装置阻尼系数、阻尼力与轴向速度-气隙的对应关系；然后，应用遗传算法优化所选的线性二次型控制算法（LQR）和滑动模态控制算法（SMC）半主动控制参数；最后，以黑白水河大桥为研究背景，对比研究无控、LQR和SMC半主动控制的抑涡效果. 研究结果表明：桥梁尾流振子涡激力模型能很好地描述桥梁涡振特性；在最大涡振风速16.5 m/s，LQR与SMC半主动控制能将桥梁振幅控制在无控振幅的4.95%，远小于规范限值；整体上，LQR和SMC控制减振效果差别不大，但LQR控制策略下阻尼器气隙不变，而SMC控制策略下阻尼器气隙会周期性改变，气隙不变更有利于工程实现.
- 大跨度桥梁 /
- 半主动控制 /
- 尾流振子 /
- LQR控制 /
- 滑模控制
Abstract:
This study aims to address the issue of vortex-induced vibrations (VIV) in long-span bridges under low wind speeds, which can lead to structural fatigue of the bridge and affect driving comfort. Based on the wake oscillator model and a variable-damping coefficient eddy current damper, a semi-active control strategy was developed. Firstly, a dimensionless VIV force model of the bridge wake oscillator was established, and its parameters were fitted using experimental data via a genetic algorithm. Then, a variable-spacing ball screw eddy current damper was designed, and the corresponding relationships between the damping coefficient and the axial velocity–air gap, as well as the damping force and the axial velocity–air gap, were determined through COMSOL simulations. Next, a genetic algorithm was applied to optimize the semi-active control parameters for the selected linear quadratic regulator (LQR) and sliding mode control (SMC) algorithms. Finally, a comparative study was conducted on the VIV suppression effects of an uncontrolled system, LQR, and SMC semi-active control by using the Hei-Bai-Shui River Bridge as the engineering case. The results show that the wake oscillator model accurately describes the VIV characteristics of the bridge. At the maximum VIV wind speed of 16.5 m/s, LQR and SMC semi-active controls can reduce the bridge amplitude to 4.95% of the uncontrolled amplitude, which is well below the regulated limit. Overall, the damping effects of LQR and SMC control are similar, but under the LQR control, the air gap of the damper remains unchanged, while under the SMC control, the air gap varies periodically. The former offers more favorable conditions for engineering implementation.
- long-span bridge /
- semi-active control /
- wake oscillator /
- LQR control /
- sliding mode control

HTML全文

图 1 桥梁涡激振动结构与尾流振子耦合模型

Figure 1. Coupling model of structure and wake oscillator for bridge vortex-induced vibration

下载: 全尺寸图片幻灯片

图 2 主梁标准横断面（单位：cm）

Figure 2. Standard cross-section of main girder （unit: cm）

下载: 全尺寸图片幻灯片

图 3 1∶50节段模型风洞试验布置

Figure 3. Wind tunnel test layout for 1:50 sectional model

下载: 全尺寸图片幻灯片

图 4 涡激振动无量纲拟合结果

Figure 4. Non-dimensional fitting results of vortex-induced vibration

下载: 全尺寸图片幻灯片

图 5 电涡流阻尼器有限元模型

Figure 5. Finite element model of eddy current damper

下载: 全尺寸图片幻灯片

图 6 电涡流参数随轴向速度和气隙的变化图

Figure 6. Variation of eddy current parameters with axial velocity and air gap

下载: 全尺寸图片幻灯片

图 7 遗传算法优化流程

Figure 7. Genetic algorithm optimization flow chart

下载: 全尺寸图片幻灯片

图 8 半主动控制减振效果

Figure 8. Semi-active control damping effect

下载: 全尺寸图片幻灯片

图 9 半主动控制力

Figure 9. Semi-active control force

下载: 全尺寸图片幻灯片

图 10 前100 s半主动控制减振效果

Figure 10. Damping effect of semi-active control in first 100 s

下载: 全尺寸图片幻灯片

图 11 最后20 s半主动控制减振效果

Figure 11. Damping effect of semi-active control in last 20 s

下载: 全尺寸图片幻灯片

图 12 半主动策略下阻尼器气隙变化

Figure 12. Variation of damper air gap under semi-active control

下载: 全尺寸图片幻灯片

表 1 成桥状态主要参数

Table 1. Main parameters of bridge state

类别	参数名称	实桥值	模型值
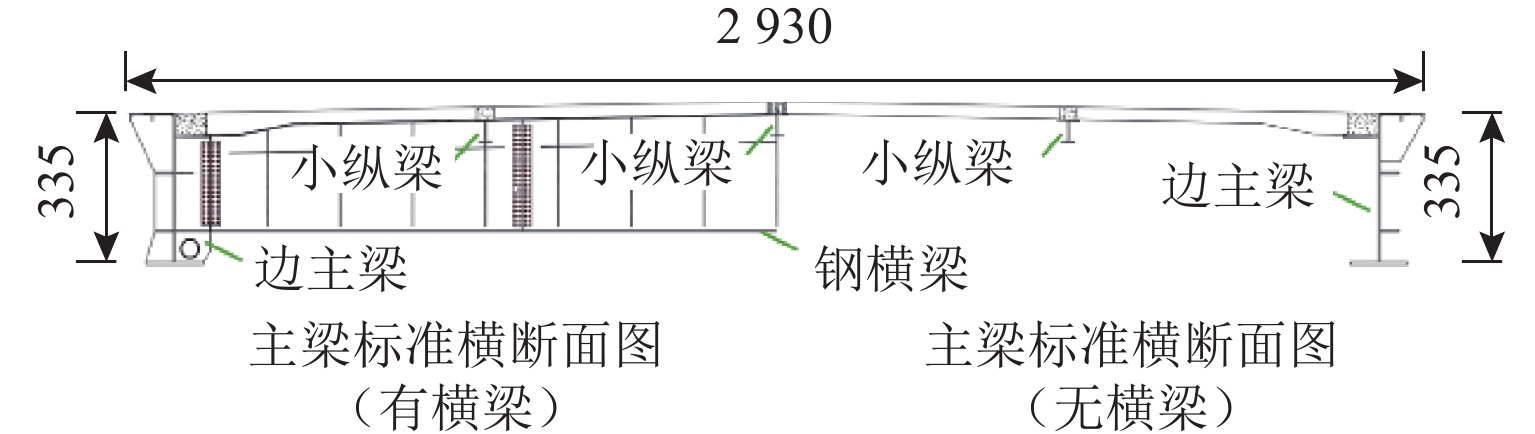
几何尺度	长度 L/m	77.00	1.54
	宽度 B/m	29.300	0.586
	高度 H/m	3.350	0.067
等效质量	m/（kg•m⁻¹）	54 450.5	21.8
等效质量	惯性矩 J_m/（kg•m²•m⁻¹）	4 313 880	0.690
频率	正对称竖弯 f_h/Hz	0.297	4.279
频率	正对称扭转 f_t/Hz	0.495	7.132
阻尼比	竖弯 ξ_h/%	0.7	0.7
阻尼比	扭转 ξ_t/%	0.7	0.7

下载: 导出CSV

表 2 模型参数识别结果

Table 2. Parameter identification results

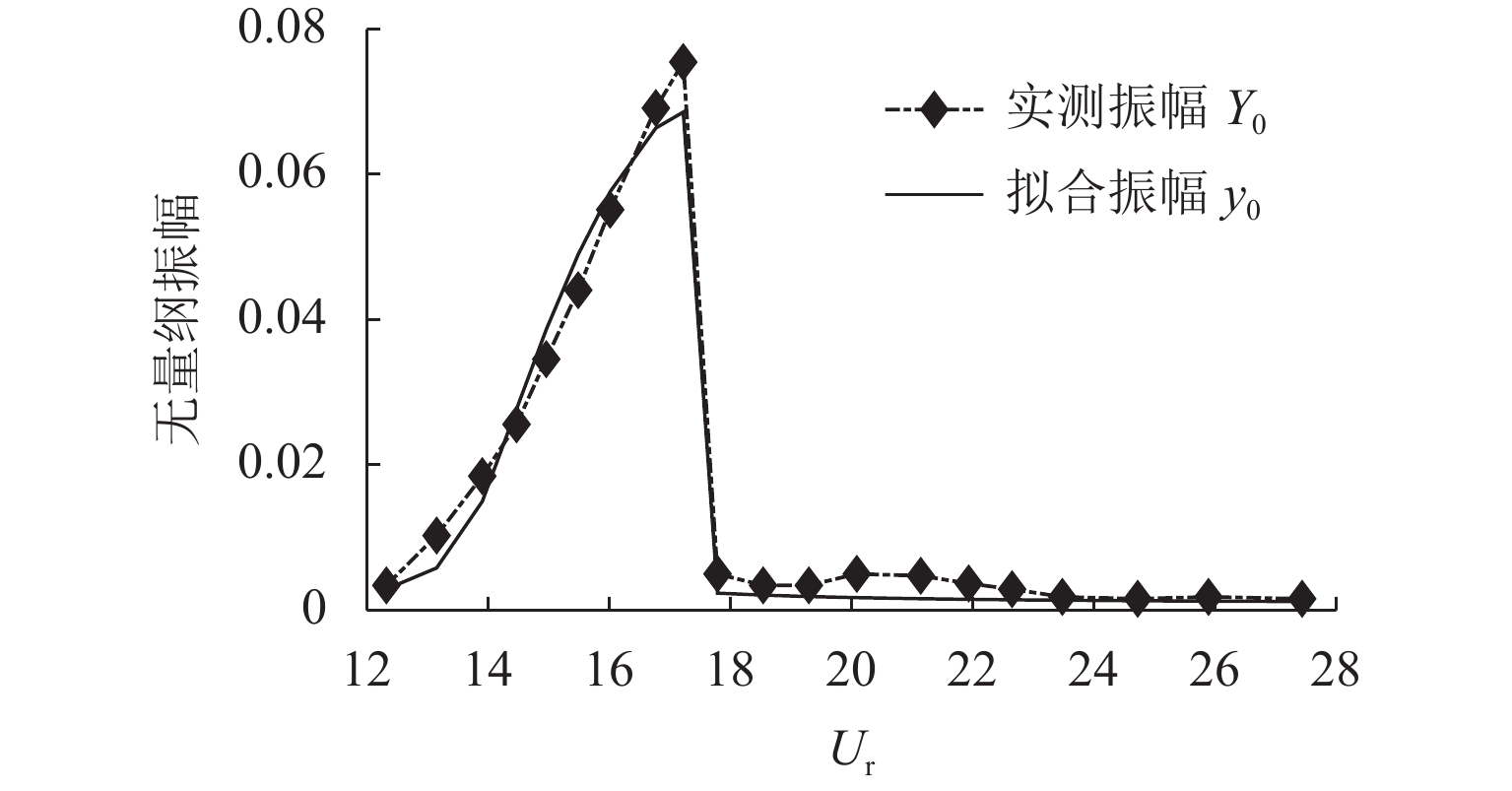
参数	St	$ \xi $	$ \varepsilon $	$ \eta $/×10⁻²	M/×10⁻⁴	A
取值	0.07	0.007 0	0.171 8	8.608	4.546	15.765 4

下载: 导出CSV

参考文献(26)

[1]	许福友, 丁威, 姜峰, 等. 大跨度桥梁涡激振动研究进展与展望[J]. 振动与冲击, 2010, 29(10): 40-49, 249. doi: 10.3969/j.issn.1000-3835.2010.10.009 XU Fuyou, DING Wei, JIANG Feng, et al. Development and prospect of study on vortex-induced vibration of long-span bridges[J]. Journal of Vibration and Shock, 2010, 29(10): 40-49, 249. doi: 10.3969/j.issn.1000-3835.2010.10.009
[2]	李琦, 齐东春, 杨虎, 等. 基于联合静动力修正的混凝土斜拉桥主梁挠度变化规律研究[J]. 中外公路, 2024, 44(1): 111-118. LI Qi, QI Dongchun, YANG Hu, et al. Deflection variation rule of main girder for a concrete cable‑stayed bridge based on combined static and dynamic modification[J]. Journal of China & Foreign Highway, 2024, 44(1): 111-118.
[3]	秦浩, 廖海黎, 李明水. 变截面连续钢箱梁桥典型施工阶段涡激振动[J]. 西南交通大学学报, 2014, 49(5): 760-765, 786. doi: 10.3969/j.issn.0258-2724.2014.05.003 QIN Hao, LIAO Haili, LI Mingshui. Vortex-induced vibration of continuous steel box-girder bridge with variable cross-sections at typical erection stages[J]. Journal of Southwest Jiaotong University, 2014, 49(5): 760-765, 786. doi: 10.3969/j.issn.0258-2724.2014.05.003
[4]	曾旻, 刘汉云, 毛娜, 等. 山区Π形梁斜拉桥涡振气动优化试验研究[J/OL]. 中外公路. [2024-03-20]. https://link.cnki.net/urlid/43.1363.U.20240125.1443.006.
[5]	郭增伟, 葛耀君, 卢安平. 竖弯涡振控制的调谐质量阻尼器TMD参数优化设计[J]. 浙江大学学报(工学版), 2012, 46(1): 8-13. GUO Zengwei, GE Yaojun, LU Anping. Parameter optimization of TMD for vortex-induced vibration control[J]. Journal of Zhejiang University (Engineering Science), 2012, 46(1): 8-13.
[6]	陈银伟, 王旋, 马行川, 等. 某上跨铁路桥梁涡振特性及气动优化试验研究[J]. 交通科学与工程, 2023, 39(6): 83-92. CHEN Yinwei, WANG Xuan, MA Xingchuan, et al. Study on vortex-induced vibration performance and aerodynamic optimization test of an overpass railway bridge[J]. Journal of Transport Science and Engineering, 2023, 39(6): 83-92.
[7]	杨猛, 王云飞, 赵家斌, 等. 考虑气动力跨向振幅依存性和相关性的桥梁涡振响应分析[J]. 西南交通大学学报, 2025, 60(1): 45-52. doi: 10.3969/j.issn.0258-2724.20220714 YANG Meng, WANG Yunfei, ZHAO Jiabin, et al. Vortex-induced vibration response of bridges considering both spanwise variation of vibration amplitude and correlation of aerodynamic forces[J]. Journal of Southwest Jiaotong University, 2025, 60(1): 45-52. doi: 10.3969/j.issn.0258-2724.20220714
[8]	黄林, 董佳慧, 廖海黎, 等. 基于CFD与风洞试验的边主梁涡振气动措施[J]. 西南交通大学学报, 2024, 59(2): 343-352. doi: 10.3969/j.issn.0258-2724.20220208 HUANG Lin, DONG Jiahui, LIAO Haili, et al. Vortex-induced vibration (VIV) aerodynamic measures of girder with side beam based on computation fluid dynamics (CFD) and wind tunnel test[J]. Journal of Southwest Jiaotong University, 2024, 59(2): 343-352. doi: 10.3969/j.issn.0258-2724.20220208
[9]	BISHOP R E D, HASSAN A Y. The lift and drag forces on a circular cylinder in a flowing fluid[J]. Proceedings of the Royal Society of London Series A, 1964, 277(1368): 32-50.
[10]	FACCHINETTI M L, DE LANGRE E, BIOLLEY F. Coupling of structure and wake oscillators in vortex-induced vibrations[J]. Journal of Fluids and Structures, 2004, 19(2): 123-140. doi: 10.1016/j.jfluidstructs.2003.12.004
[11]	高云, 张壮壮, 杨斌, 等. 圆柱体横流与顺流方向涡激振动耦合模型研究[J]. 振动与冲击, 2020, 39(11): 22-30. GAO Yun, ZHANG Zhuangzhuang, YANG Bin, et al. The study on cross-flow and in-line vortex-induced vibration coupled model of a circular cylinder[J]. Journal of Vibration and Shock, 2020, 39(11): 22-30.
[12]	SONG J X, DU J J, YAO Y. Applying LQR to control cross vortex-induced vibration of cylinders based on wake oscillators[J]. Ocean Engineering, 2023, 286: 115631.1-115631.9.
[13]	陈平, 陈强草, 华旭刚, 等. 结构-尾流振子耦合模型参数识别及桥梁涡激振动预测[J]. 世界桥梁, 2021, 49(2): 84-89. doi: 10.3969/j.issn.1671-7767.2021.02.014 CHEN Ping, CHEN Qiangcao, HUA Xugang, et al. Parameter identification and bridge vortex-induced vibration prediction based on structure-wake oscillator coupling model[J]. World Bridges, 2021, 49(2): 84-89. doi: 10.3969/j.issn.1671-7767.2021.02.014
[14]	周涛, 邓宇, 陈晓虎, 等. 大跨度钢箱桁组合连续梁桥涡振性能研究[J]. 工程力学., 2023, 40(2): 213-221. ZHOU Tao, DENG Yu, CHEN Xiaohu, et al. Vortex-induced vibrations of long-span continuous bridges with steel truss-stiffened box-girder[J]. Engineering Mechanics., 2023, 40(2): 213-221.
[15]	许坤, 葛耀君. 基于尾流振子模型的桥梁节段至实桥涡激共振振幅转换关系[J]. 工程力学, 2017, 34(2): 137-144. XU Kun, GE Yaojun. Conversion of the vortex-induced amplitudes of sectional models to full-scale bridges based on wake oscillator model[J]. Engineering Mechanics, 2017, 34(2): 137-144.
[16]	葛耀君, 赵林, 许坤. 大跨桥梁主梁涡激振动研究进展与思考[J]. 中国公路学报, 2019, 32(10): 1-18. GE Yaojun, ZHAO Lin, XU Kun. Review and reflection on vortex-induced vibration of main girders of long-span bridges[J]. China Journal of Highway and Transport, 2019, 32(10): 1-18.
[17]	陈政清, 黄智文, 王建辉, 等. 桥梁用TMD的基本要求与电涡流TMD[J]. 湖南大学学报(自然科学版), 2013, 40(8): 6-10. doi: 10.3969/j.issn.1674-2974.2013.08.002 CHEN Zhengqing, HUANG Zhiwen, WANG Jianhui, et al. Basic requirements of tuned mass damper for bridges and the eddy current TMD[J]. Journal of Hunan University (Natural Sciences), 2013, 40(8): 6-10. doi: 10.3969/j.issn.1674-2974.2013.08.002
[18]	黄智文. 电涡流阻尼器理论研究及其在桥梁竖向涡振控制中的应用[D]. 长沙: 湖南大学, 2016.
[19]	李寿英, 霍朝煜, 毛伟阳, 等. 齿轮齿条式电涡流阻尼墙有限元数值研究[J]. 湖南大学学报(自然科学版), 2022, 49(9): 100-107. doi: 10.55463/issn.1674-2974.49.9.12 LI Shouying, HUO Zhaoyu, MAO Weiyang, et al. FEM numerical study of eddy current damping-rack and gear wall[J]. Journal of Hunan University (Natural Sciences), 2022, 49(9): 100-107. doi: 10.55463/issn.1674-2974.49.9.12
[20]	张进秋, 彭虎, 张建, 等. 车辆悬挂LQR主动控制权矩阵权重参数优化[J]. 振动与冲击, 2018, 37(22): 214-219. ZHANG Jinqiu, PENG Hu, ZHANG Jian, et al. Weight parameters optimization for the weight matrices in a vehicle suspension LQR active control[J]. Journal of Vibration and Shock, 2018, 37(22): 214-219.
[21]	郭一峰, 徐赵东, 涂青, 等. 基于遗传算法的LQR算法中权矩阵的优化分析[J]. 振动与冲击, 2010, 29(11): 217-220, 264. doi: 10.3969/j.issn.1000-3835.2010.11.047 GUO Yifeng, XU Zhaodong, TU Qing, et al. Optimal analysis for weight matrices in LQR algorithm based on genetic algorithm[J]. Journal of Vibration and Shock, 2010, 29(11): 217-220, 264. doi: 10.3969/j.issn.1000-3835.2010.11.047
[22]	刘汉云, 陈柏翔, 韩艳, 等. 基于WOA-GRNN代理模型的Π形截面梁风嘴气动外形优化[J]. 中国公路学报, 2023, 36(8): 76-86. LIU Hanyun, CHEN Baixiang, HAN Yan, et al. Aerodynamic shape optimization of Π-shaped composite bridge deck with wind fairing based on WOA-GRNN surrogate model[J]. China Journal of Highway and Transport, 2023, 36(8): 76-86.
[23]	刘金琨. 滑模变结构控制MATLAB仿真: 基本理论与设计方法[M]. 4版. 北京: 清华大学出版社, 2019.
[24]	王林军, 史宝周, 张东, 等. 基于GA优化的LQR控制对并联机器人的控制研究[J]. 振动与冲击, 2020, 39(20): 82-90, 96. WANG Linjun, SHI Baozhou, ZHANG Dong, et al. LQR control of parallel robot based on genetic algorithms[J]. Journal of Vibration and Shock, 2020, 39(20): 82-90, 96
[25]	商祥志, 刘景旭, 路永婕, 等. 振动压路机的滑膜控制研究[J]. 力学与实践, 2024, 46(1): 127-137. doi: 10.6052/1000-0879-23-132 SHANG Xiangzhi, LIU Jingxu, LU Yongjie, et al. Research on sliding mode control of vibration roller[J]. Mechanics in Engineering, 2024, 46(1): 127-137. doi: 10.6052/1000-0879-23-132
[26]	中华人民共和国交通运输部. 公路桥桥抗风设计规范: JTG/T 3360-01—2018[S]. 北京: 人民交通出版社股份有限公司, 2018.