A Simple Generalized Method for Unified Constitutive Model of Clay and Sand
-
摘要:
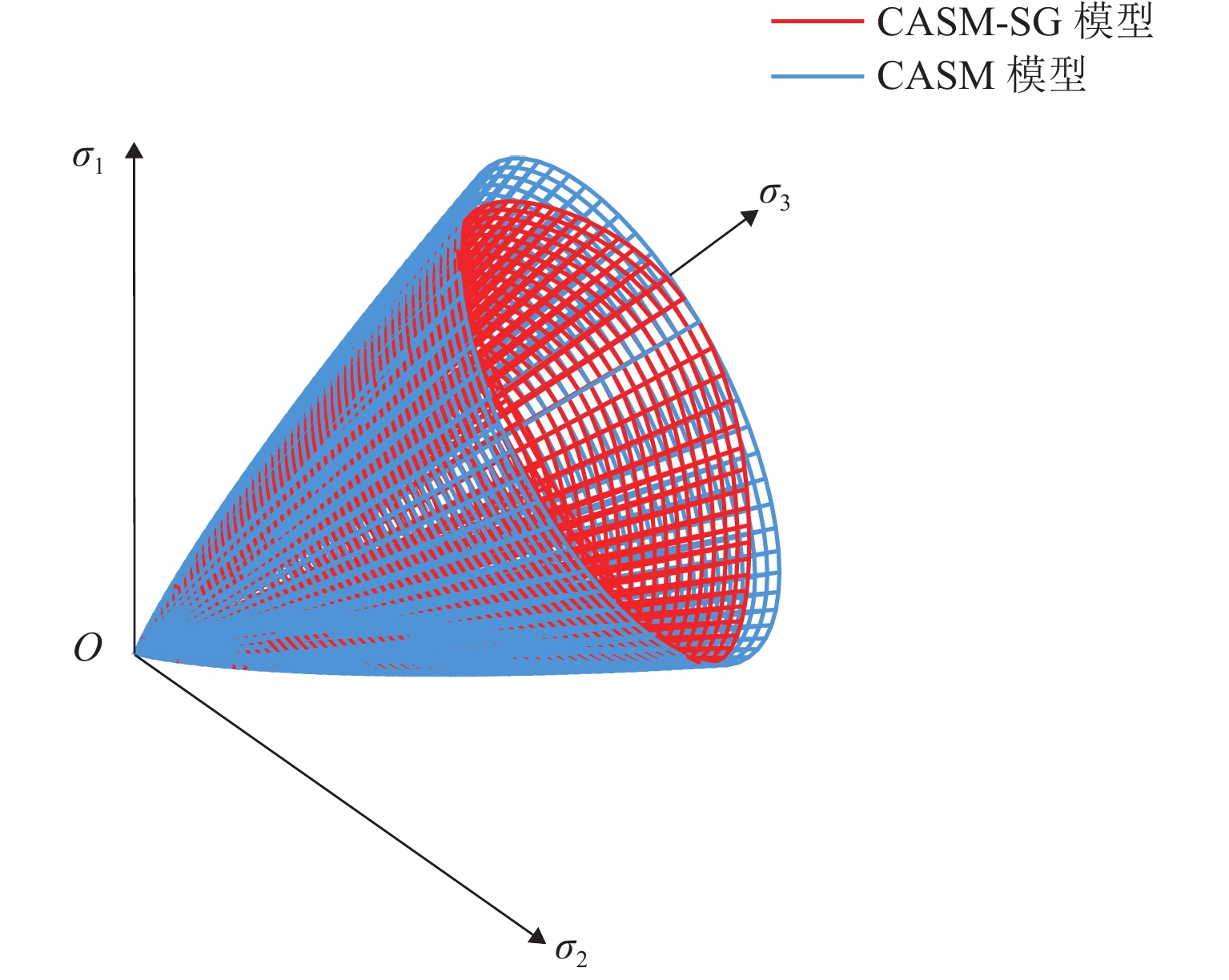
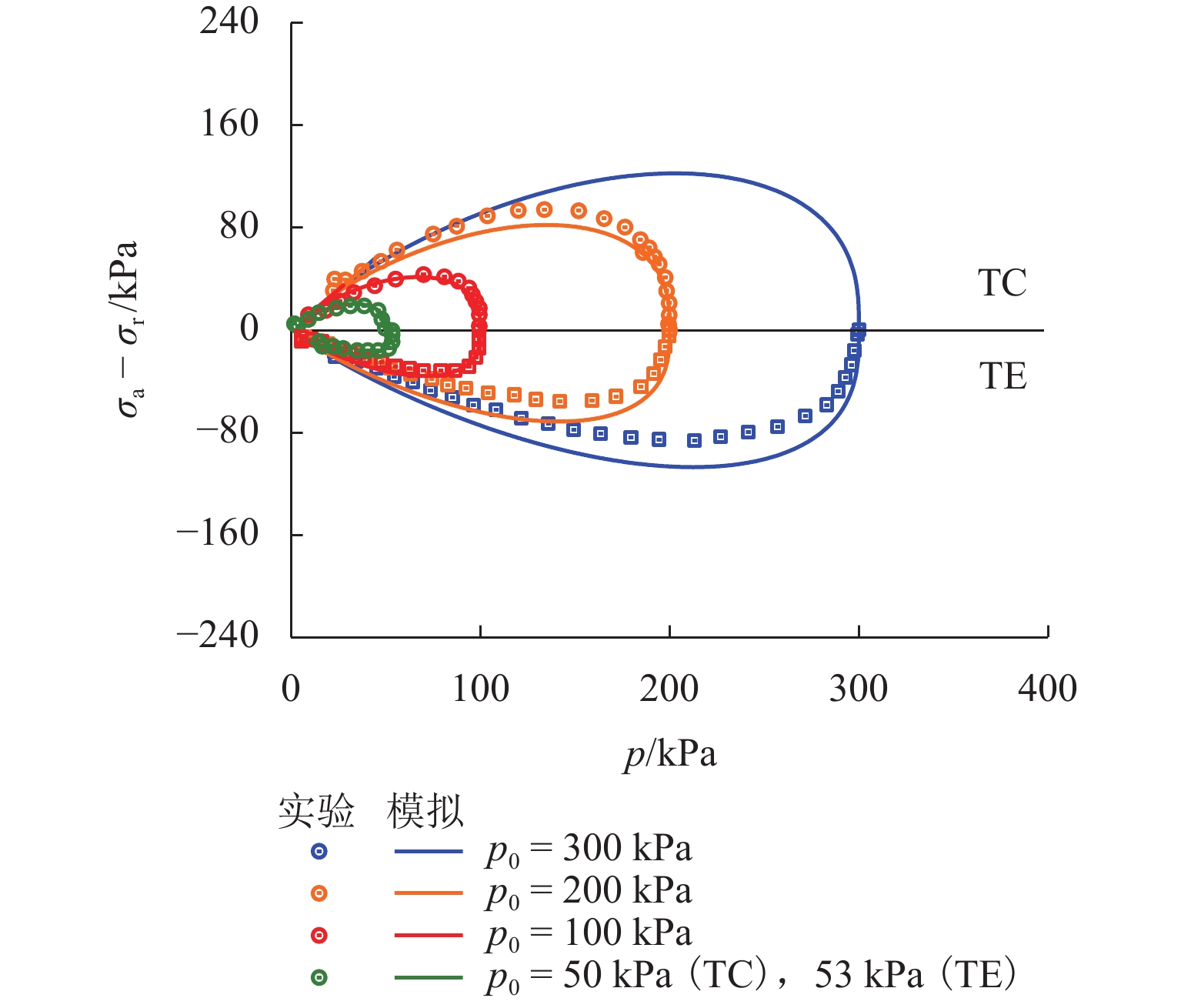
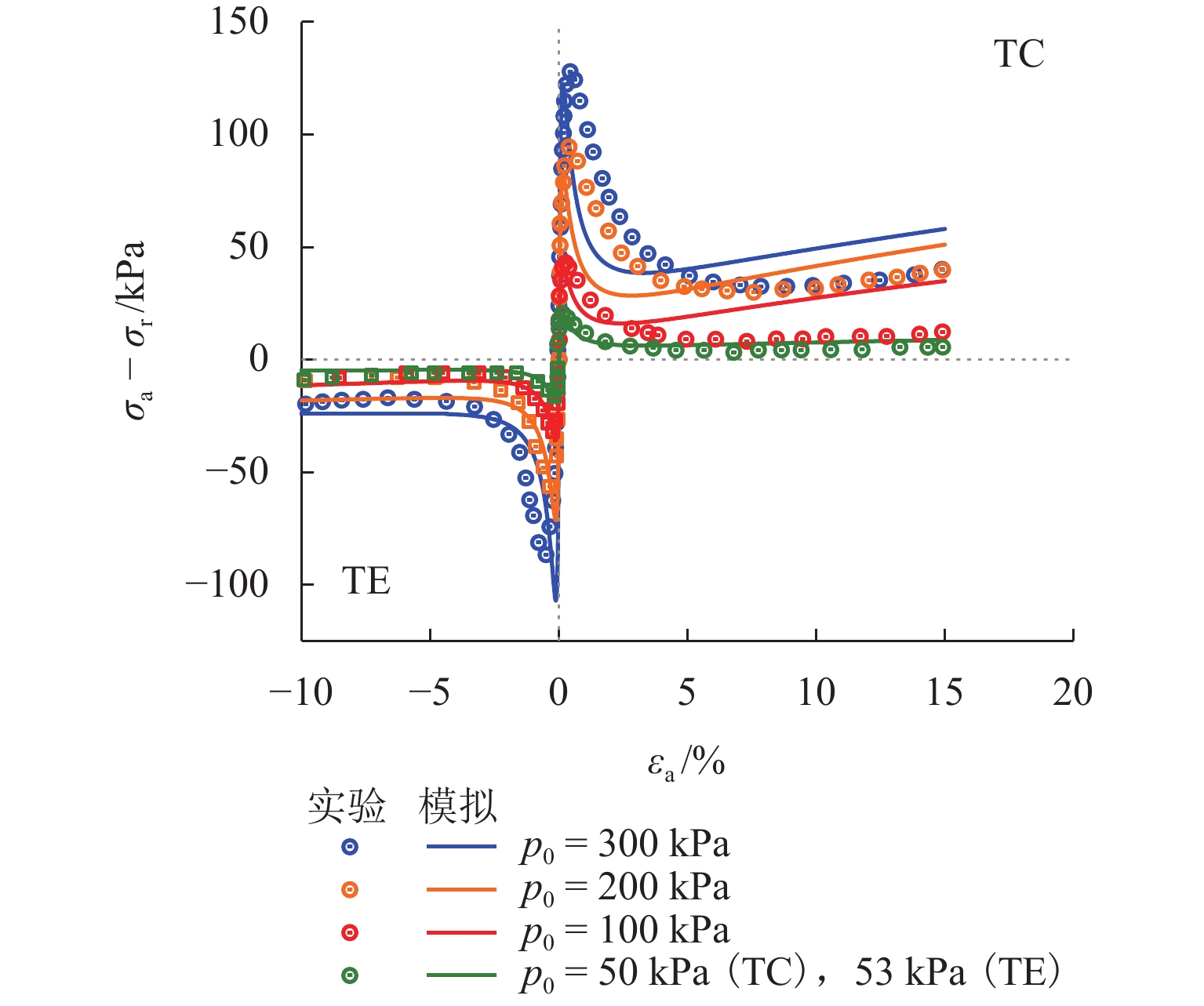
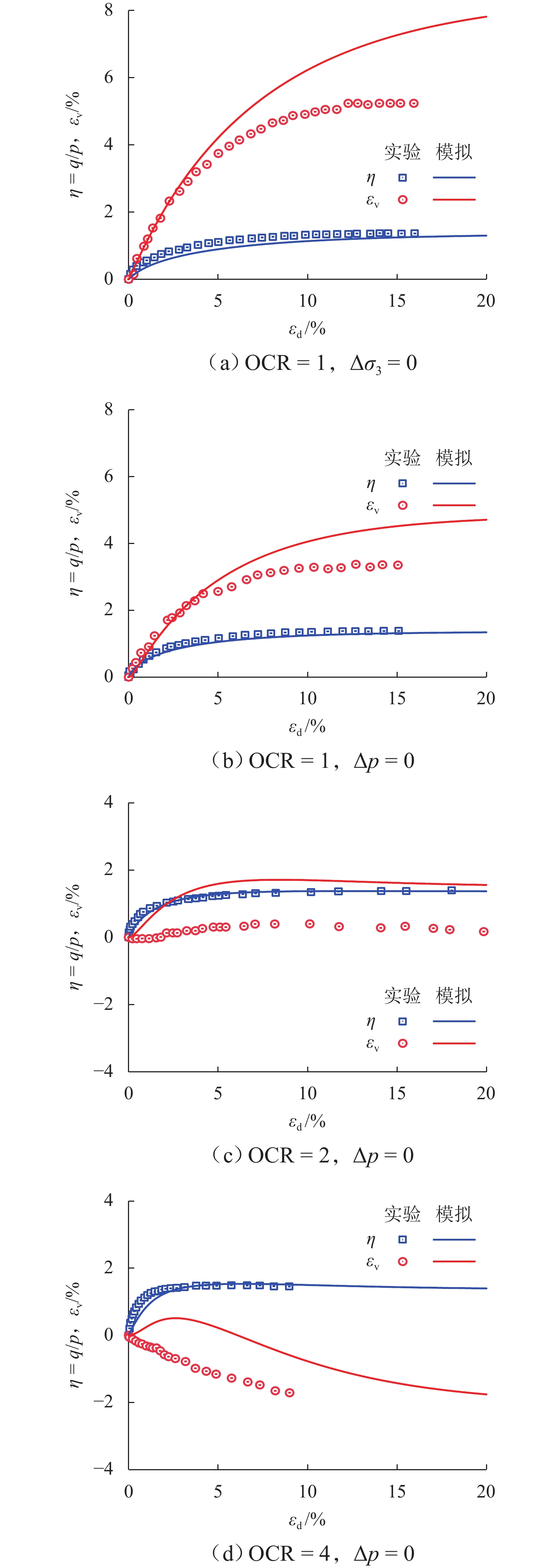
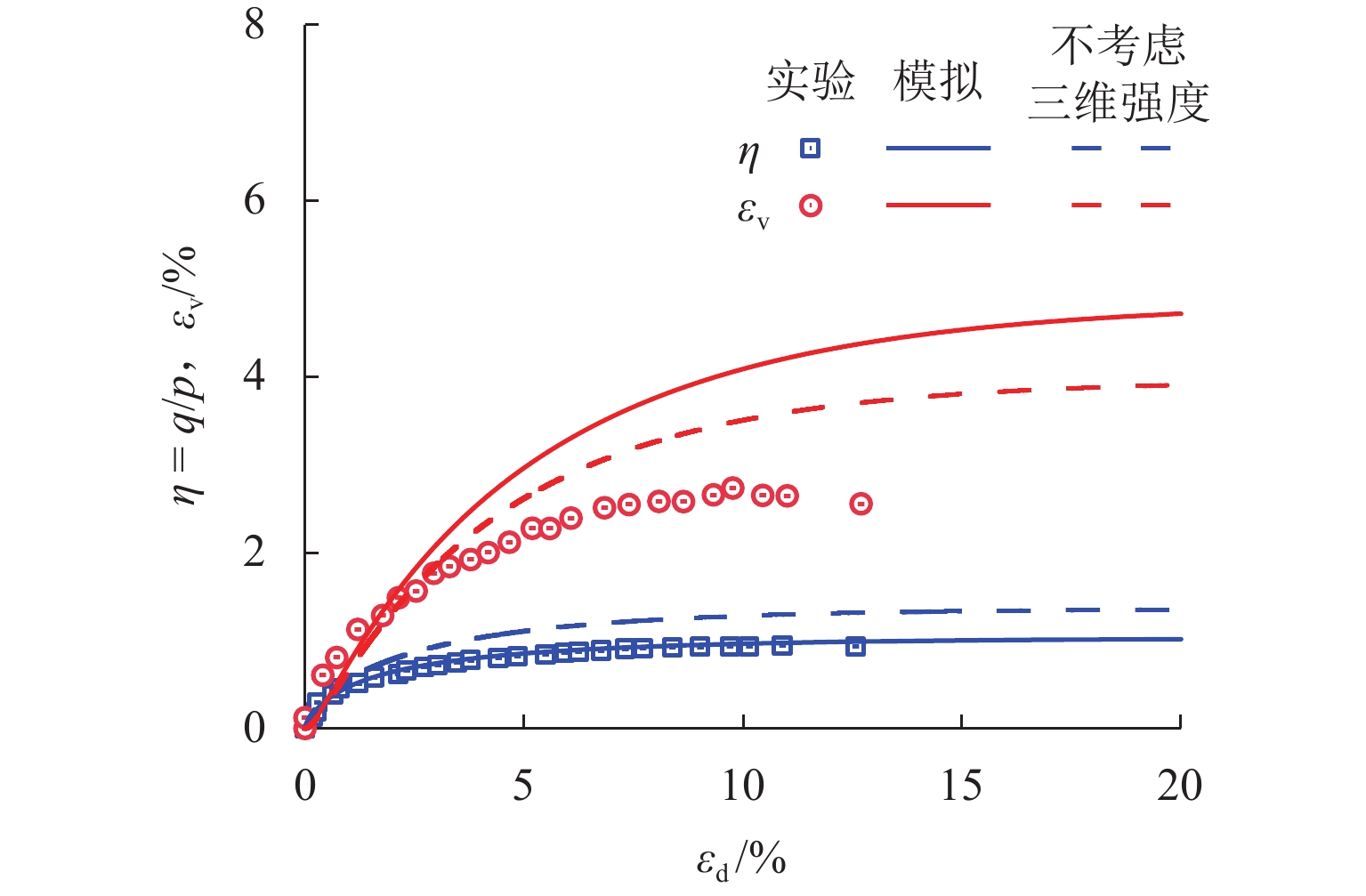
为统一描述砂土和黏土在广义应力路径下的力学响应，在具有状态参数的砂黏统一本构模型CASM的基础上，结合次加载面理论和变换应力法，提出一种适用于广义加载条件的统一临界状态本构模型（CASM-SG模型）. 该模型基于原始CASM模型，结合次加载面概念建立一种与土体初始状态相关的塑性内变量，并利用变换应力法成功将原先由三轴压缩实验确定的二维屈服包面拓展到三维应力空间；构建广义应力条件下CASM-SG模型的应力剪胀关系和硬化准则等完整本构框架，并基于一致性条件推导出其塑性模量与弹塑性刚度矩阵的显式表达式；采用新提出的模型对Hostun砂土和Fujinomori黏土在排水与不排水三轴压缩及拉伸条件下的力学行为进行模拟. 模拟结果显示：CASM-SG模型能够较为准确地捕捉砂土和黏土在不同应力路径下的力学行为；对于Fujinomori黏土，三轴拉伸强度相对三轴压缩强度降低了24%左右，CASM-SG模型能够精确捕捉这一特征；相比原始CASM模型，该模型仅增加了2个具备明确物理意义的材料参数，但体现出良好的精度与简洁性兼顾的建模优势.
Abstract:To consistently describe the mechanical response of sand and clay under generalized stress paths, a unified critical state constitutive model (CASM-SG) applicable to generalized loading conditions was proposed based on the unified constitutive clay and sand model (CASM) with state parameters and by employing the subloading surface theory and the transformed stress method. In the model based on the original CASM model, a plastic internal variable associated with the initial state of the soil was established by using the concept of subloading surface, and the original two-dimensional yield surface determined from triaxial compression tests was transformed into the three-dimensional stress space through the transformed stress method. A complete constitutive framework was constructed for the CASM-SG model under generalized stress conditions, including the stress dilatancy relationship and the hardening rule. Explicit expressions for the plastic modulus and the elastoplastic stiffness matrix were derived based on the consistency condition. Finally, the proposed model was employed to simulate the mechanical behavior of Hostun sand and Fujinomori clay under drained and undrained triaxial compression and extension conditions. The simulation results indicate that the CASM-SG model can accurately capture the mechanical behavior of both sand and clay under various stress paths. For Fujinomori clay, the triaxial extension strength decreases by approximately 24% compared with the triaxial compression strength, and the CASM-SG model captures this characteristic. Compared to the original CASM model, the CASM-SG model introduces two additional material parameters with clear physical interpretations, demonstrating a favorable balance between modeling accuracy and simplicity.
-
Key words:
- generalized stress space /
- sand /
- clay /
- constitutive model /
- transformed stress method
-
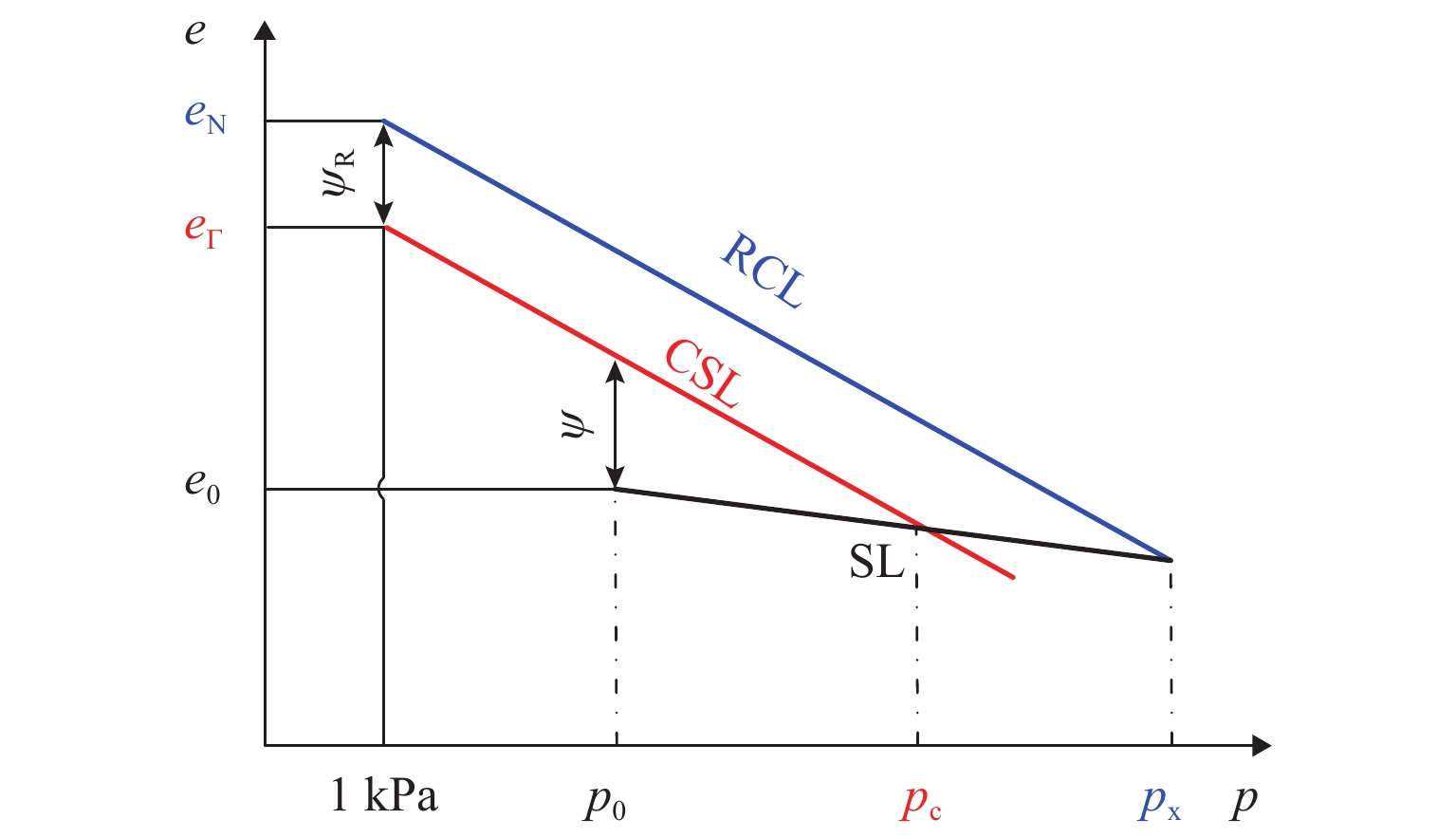
图 1 状态参数，参考状态参数在e-ln p空间中的示意[18]
Figure 1. State and reference state parameters in e-ln p space
图 3 CASM模型和CASM-SG模型在广义应力空间中的屈服面 （r = 50, n = 2, M = 1.2）
Figure 3. Yield curves of CASM and CASM-SG models in generalized stress space （r = 50, n = 2, M = 1.2）
图 4 Hostun砂土在不排水TC/TE条件下的有效应力路径
Figure 4. Effective stress paths of Hostun sand under undrained TC/TE conditions
图 5 Hostun砂土在不排水TC/TE条件下的应力-应变关系
Figure 5. Stress–strain relationship of Hostun sand under undrained TC/TE conditions
图 6 正常和超固结Fujinomori黏土在排水TC条件下的应力-应变及体变-应变曲线
Figure 6. Stress–strain and volumetric strain–strain curves of normally and over-consolidated Fujinomori clay under drained TC conditions
图 7 正常固结Fujinomori黏土在排水TE条件下的应力-应变及体变-应变曲线（Δp = 0）
Figure 7. Stress–strain and volumetric strain–strain curves of normally consolidated Fujinomori clay under drained TE conditions （Δp = 0）
-
[1] 吴杨,容浩俊,王金莲,等. 颗粒形状和中主应力对砂土力学特性耦合影响的真三轴试验研究[J]. 岩石力学与工程学报,2023,42(2): 497-507.WU Yang, RONG Haojun, WANG Jinlian, et al. A true triaxial experimental study on the coupled effect of particle shape and intermediate principal stress on the mechanical properties of sand[J]. Chinese Journal of Rock Mechanics and Engineering, 2023, 42(2): 497-507. [2] WANG Y K, GAO Y F, LI B, et al. Influence of initial state and intermediate principal stress on undrained behavior of soft clay during pure principal stress rotation[J]. Acta Geotechnica, 2019, 14(5): 1379-1401. doi: 10.1007/s11440-018-0735-5 [3] LI K F, LI X F, CHEN Q S, et al. Laboratory analyses of noncoaxiality and anisotropy of spherical granular media under true triaxial state[J]. International Journal of Geomechanics, 2023, 23(9): 04023150.1-04023150.13. [4] YUAN R, YU H S, YANG D S, et al. On a fabric evolution law incorporating the effects of b-value[J]. Computers and Geotechnics, 2019, 105: 142-154. doi: 10.1016/j.compgeo.2018.09.019 [5] 袁冉,杨文波,余海岁,等. 土体非共轴各向异性对城市浅埋土质隧道诱发地表沉降的影响[J]. 岩土工程学报,2018,40(4): 673-680.YUAN Ran, YANG Wenbo, YU Haisui, et al. Effects of non-coaxiality and soil anisotropy on tunneling-induced subsurface settlements[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(4): 673-680. [6] YUAN R, YU H S, ZHANG J R, et al. Noncoaxial theory of plasticity incorporating initial soil anisotropy [J]. International Journal of Geomechanics, 2019, 19(12): 06019017.1-06019017.10. [6] YUAN R, YU H S, ZHANG J R, et al. Noncoaxial theory of plasticity incorporating initial soil anisotropy[J]. International Journal of Geomechanics, 2019, 19(12) : 06019017.1-06019017.10. [7] YUAN R, YU H S, HU N, et al. Non-coaxial soil model with an anisotropic yield criterion and its application to the analysis of strip footing problems[J]. Computers and Geotechnics, 2018, 99: 80-92. doi: 10.1016/j.compgeo.2018.02.022 [8] Roscoe K H, Schofield A N, Wroth C P. On the yielding of soils[J]. Geotechnique, 1958, 8(1): 22-53. doi: 10.1680/geot.1958.8.1.22 [9] Roscoe K H, Burland J B. On the generalised stress-strain behaviour of ‘wet’ clay[M]. Cambridge: Cambridge University Press, 1968. [10] 田雨. 基于各向异性变换应力法的UH模型及其应用[D]. 北京:北京航空航天大学,2018. [11] 姚仰平,张奎,王祖乐,等. UH模型超固结状态演化分析及离心模型试验验证[J]. 岩土工程学报,2024,46(6): 1127-1135.YAO Yangping, ZHANG Kui, WANG Zule, et al. Evolution analysis of over-consolidated state with UH model and verification of hypergravity centrifuge experiments[J]. Chinese Journal of Geotechnical Engineering, 2024, 46(6): 1127-1135. [12] 姚仰平,田易川,崔文杰. 理想膨胀性非饱和土UH模型[J]. 岩土工程学报,2023,45(6): 1103-1112.YAO Yangping, TIAN Yichuan, CUI Wenjie. UH model for ideal expansive unsaturated soils[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(6): 1103-1112. [13] PETALAS A L, DAFALIAS Y F, PAPADIMITRIOU A G. SANISAND-F: Sand constitutive model with evolving fabric anisotropy[J]. International Journal of Solids and Structures, 2020, 188: 12-31. [14] 曹威. 定轴剪切条件下各向异性砂土本构规律与模型研究[D]. 北京:清华大学,2018. [15] 王睿,张建民,王刚. 砂土液化大变形本构模型的三维化及其数值实现[J]. 地震工程学报,2013,35(1): 91-97.WANG Rui, ZHANG Jianmin, WANG Gang. Multiaxial formulation and numerical implementation of a constitutive model for the evaluation of large liquefaction-induced deformation[J]. China Earthquake Engineering Journal, 2013, 35(1): 91-97. [16] 邹佑学,王睿,张建民. 砂土液化大变形模型在FLAC3D中的开发与应用[J]. 岩土力学,2018,39(4): 1525-1534.ZOU Youxue, WANG Rui, ZHANG Jianmin. Implementation of a plasticity model for large post-liquefaction deformation of sand in FLAC3D[J]. Rock and Soil Mechanics, 2018, 39(4): 1525-1534. [17] YU H S. Plasticity and geotechnics [M]. New York: Springer Science & Business Media, 2007. [18] YU H S. CASM: a unified state parameter model for clay and sand[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1998, 22(8): 621-653. doi: 10.1002/(SICI)1096-9853(199808)22:8<621::AID-NAG937>3.0.CO;2-8 [19] MO P Q, MARSHALL A M, FANG Y. Cavity expansion–contraction-based method for tunnel–soil–pile interaction in a unified clay and sand model: drained analysis[J]. International Journal of Geomechanics, 2021, 21(5): [20] YU H S, ZHUANG P Z, MO P Q. A unified critical state model for geomaterials with an application to tunnelling[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2019, 11(3): 464-480. doi: 10.1016/j.jrmge.2018.09.004 [21] KHONG C D. Development and numerical evaluation of unified critical state models [D]. Nottingham: University of Nottingham, 2004. [22] YAO Y P, WANG N D. Transformed stress method for generalizing soil constitutive models[J]. Journal of Engineering Mechanics, 2014, 140(3): 614-629. doi: 10.1061/(ASCE)EM.1943-7889.0000685 [23] MATSUOKA H, YAO Y P, SUN D A. The cam-clay models revised by the SMP criterion[J]. Soils and Foundations, 1999, 39(1): 81-95. doi: 10.3208/sandf.39.81 [24] YAO Y P, SUN D A. Application of lade’s criterion to cam-clay model[J]. Journal of Engineering Mechanics, 2000, 126(1): 112-119. doi: 10.1061/(ASCE)0733-9399(2000)126:1(112) [25] YAO Y P, LIU L, LUO T, et al. Unified hardening (UH) model for clays and sands[J]. Computers and Geotechnics, 2019, 110: 326-343. doi: 10.1016/j.compgeo.2019.02.024 [26] YAO Y, TIAN Y, GAO Z. Anisotropic UH model for soils based on a simple transformed stress method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2017, 41(1): 54-78. doi: 10.1002/nag.2545 [27] TIAN Y, YAO Y P. Constitutive modeling of principal stress rotation by considering inherent and induced anisotropy of soils[J]. Acta Geotechnica, 2018, 13(6): 1299-1311. doi: 10.1007/s11440-018-0680-3 [28] CUI K, WANG X W, YUAN R, et al. A unified critical state parameter model for sand and overconsolidated clay in the framework of subloading surface theory[J]. Canadian Geotechnical Journal, 2023, 60(10): 1461-1474. doi: 10.1139/cgj-2022-0287 [29] WANG X W, CUI K, YUAN R. Complete and semi-complete explicit algorithms of a unified critical state model for over-consolidated soils[J]. International Journal for Multiscale Computational Engineering, 2024, 22(2): 1-25. doi: 10.1615/IntJMultCompEng.2023047907 [30] BEEN K, JEFFERIES M G. A state parameter for sands[J]. Géotechnique, 1985, 35(2): 99-112. [31] HASHIGUCHI K. Subloading surface model in unconventional plasticity[J]. International Journal of Solids and Structures, 1989, 25(8): 917-945. doi: 10.1016/0020-7683(89)90038-3 [32] HASHIGUCHI K, MASE T, YAMAKAWA Y. Elaborated subloading surface model for accurate description of cyclic mobility in granular materials[J]. Acta Geotechnica, 2022, 17(3): 699-719. doi: 10.1007/s11440-021-01203-y [33] WANG X W, YUAN R, CUI K. Modified unified critical state model for soils considering over-consolidation and cyclic loading behaviours[J]. Scientific Reports, 2023, 13(1): 3024.1-3024.14. [34] CUI K, WANG X W, YUAN R. Unified modeling for clay and sand with a hybrid-driven fabric evolution law[J]. Applied Mathematical Modelling, 2024, 129: 522-544. doi: 10.1016/j.apm.2024.02.015 [35] RIOS S, CIANTIA M, GONZALEZ N, et al. Simplifying calibration of bonded elasto-plastic models[J]. Computers and Geotechnics, 2016, 73: 100-108. doi: 10.1016/j.compgeo.2015.11.019 [36] DOANH T, IBRAIM E, MATIOTTI R. Undrained instability of very loose Hostun sand in triaxial compression and extension. Part 1: experimental observations[J]. Mechanics of Cohesive-Frictional Materials, 2(1): 47-70. [37] NAKAI T, HINOKIO M. A simple elastoplastic model for normally and over consolidated soils with unified material parameters[J]. Soils and Foundations, 2004, 44(2): 53-70. doi: 10.3208/sandf.44.2_53 -
下载:
点击查看大图
计量
- 文章访问数: 44
- HTML全文浏览量: 15
- PDF下载量: 1
- 被引次数: 0