Theoretical Correction Method and Application of German-Standard Insertion Loss Rate of Vibration Damping Track
-
摘要:
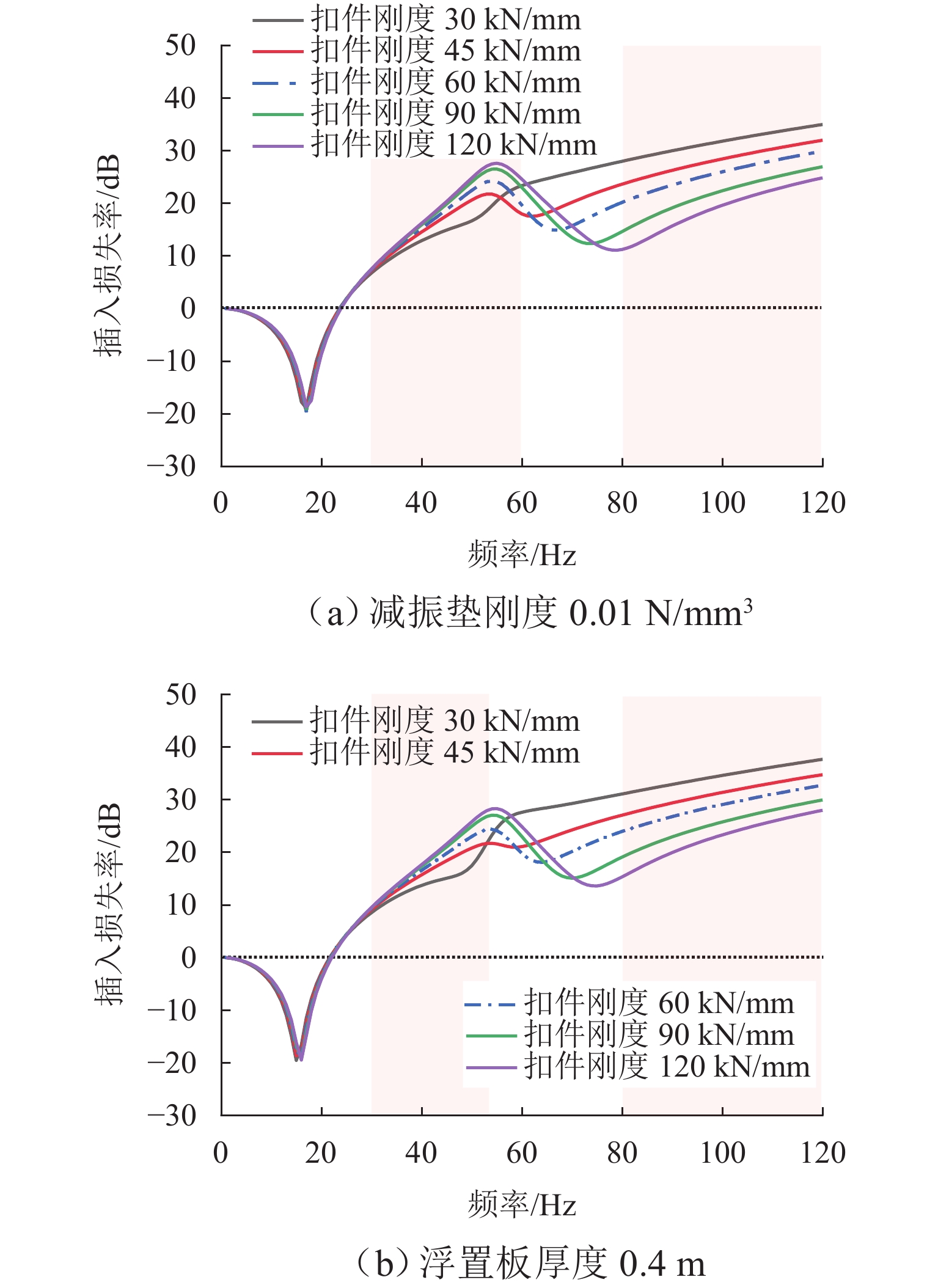
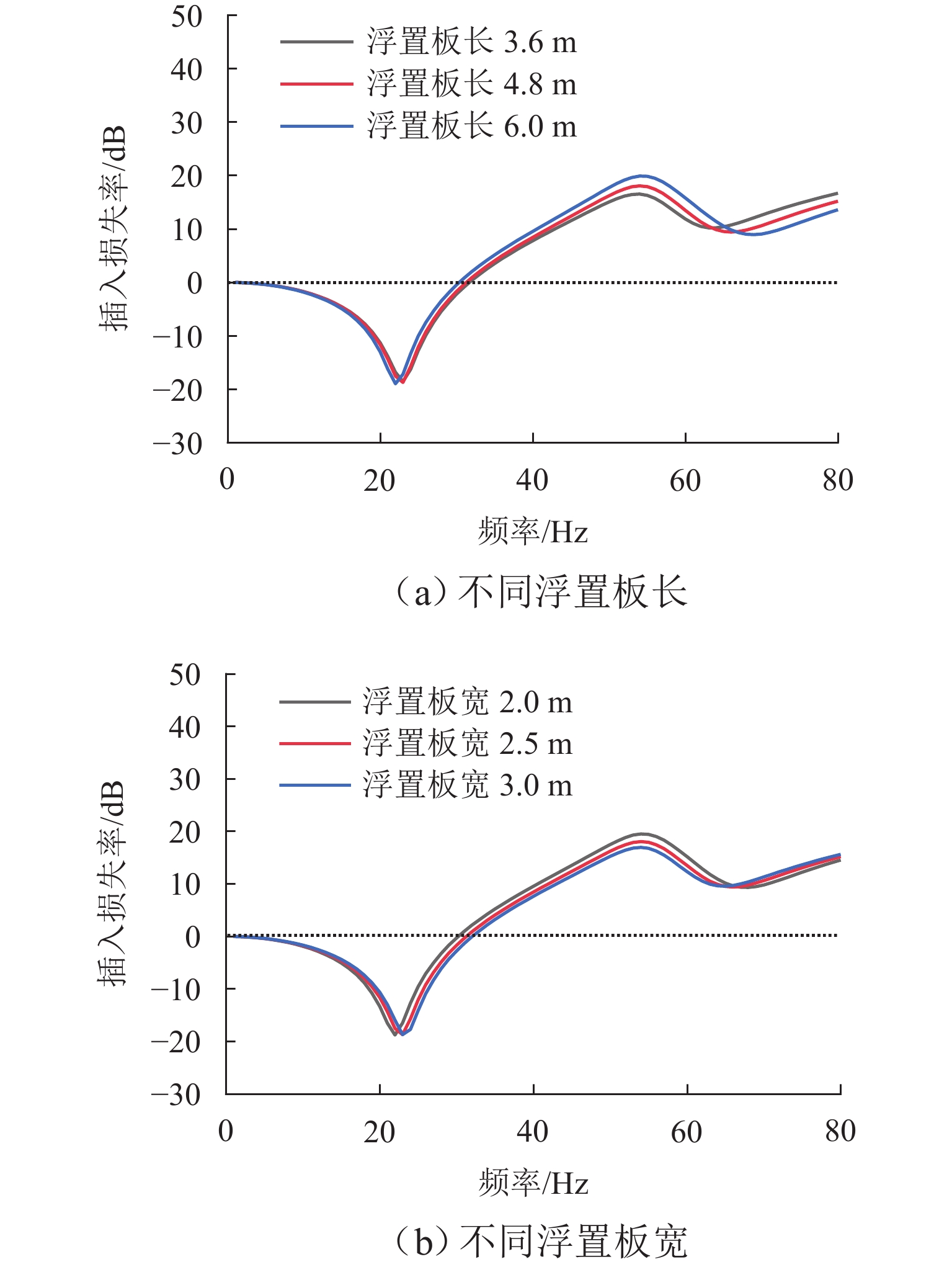
为准确高效评价轨道减振性能，德国标准DIN V 45673-4规定了插入损失率的高效计算方法，能够排除线路运营条件与轨道不平顺等随机因素的干扰，但该方法在模型等效时未考虑轨道抗弯刚度的贡献，不能准确得到实际轮轨系统共振频率，进而无法准确判断减振轨道的减振频带. 为提高计算精度，在不降低计算效率的前提下改进德标插入损失率计算模型，以弹性地基梁近似反映轨道实际结构尺寸与刚度特征，综合考虑弹性元件与轨道抗弯刚度对轨道刚度的贡献，修正模型刚度；以减振垫浮置板轨道为例，针对我国环评要求的1～80 Hz减振频带，讨论轨道尺寸及弹性元件减振优化方案. 研究结果表明：刚度修正后，轮轨系统共振频率误差由76.0%大幅降低至4.9%；单纯提高扣件损耗因子可以实现环评1～80 Hz频带的整体减振，然而在30～90 kN/mm扣件刚度范围内，单纯降低（单纯提高）扣件刚度仅能提高60～80 Hz （30～60 Hz）频带的插入损失率，但是却降低了30～60 Hz （60～80 Hz）的插入损失率，无法实现环评1～80 Hz频带的整体减振；只有当扣件刚度提升至90 kN/mm以上时，才可实现环评1～80 Hz频带的整体减振，且当减振垫刚度越低或浮置板厚度越大时，所需提高的扣件刚度越大.
Abstract:To accurately and efficiently evaluate the vibration damping performance of tracks, the German standard DIN V
45673 -4 provides a method for efficiently calculating the insertion loss rate, which can eliminate interference from stochastic factors such as line operation conditions and track irregularities. However, this method neglects the contribution of track bending stiffness in its equivalent model, leading to errors in identifying the resonant frequency of the wheel-rail system and the vibration damping frequency band of tracks. To increase the calculation precision, the model for calculating the German-standard insertion loss rate was improved on the premise that the computational efficiency was maintained. By employing the elastic foundation beam theory to approximate the actual structural dimensions and stiffness characteristics of tracks and considering the contributions of elastic components and track bending stiffness, the stiffness of the model was corrected. The plans for optimizing track dimensions and vibration damping performance of elastic components were discussed in terms of the 1–80 Hz vibration damping frequency band required by China’s environmental impact assessment by taking the floating slab tracks with vibration damping pads for example. The results show that after stiffness correction, the error in the resonant frequency of the wheel-rail system is reduced from 76.0% to 4.9%. The increase in the fastener loss factor can achieve the overall vibration damping performance within the 1–80 Hz frequency band. However, within the range of 30–90 kN/mm for fastener stiffness, reducing (increasing) the fastener stiffness improves the insertion loss rate of the 60–80 Hz (30–60 Hz) frequency band and decreases the rate of the 30–60 Hz (60–80 Hz) frequency band. This does not meet the overall vibration damping performance for the 1–80 Hz frequency band which can only be achieved when the fastener stiffness exceeds 90 kN/mm. Furthermore, lower stiffness of vibration damping pads or thicker floating slabs indicate higher improvement in fastener stiffness. -
图 2 双层弹性地基梁（浮置板轨道）
Figure 2. Double-layer elastic foundation beam (floating slab track)
图 4 减振垫浮置板轨道有限元模型
Figure 4. Finite element model of floating slab track with vibration damping pads
图 5 不同减振措施下插入损失率修正结果
Figure 5. Correction results of insertion loss rate under different vibration damping measures
图 6 减振扣件轨道轮轨一阶（39.1 Hz）
Figure 6. First-order wheel–rail frequency of vibration damping fastener track (39.1 Hz)
图 7 减振垫浮置板轨道轮轨系统共振频率
Figure 7. Resonant frequency of wheel–rail system of floating slab track with vibration damping pads
图 8 插入损失率随频率的变化
Figure 8. Changes of insertion loss rate with frequency for different loss factors
图 11 不同浮置板长宽时插入损失率随频率的变化
Figure 11. Changes of insertion loss rate with frequency for different floating slab track lengths and widths
表 1 参照系统与减振系统参数
Table 1. Parameters of reference system and vibration damping system
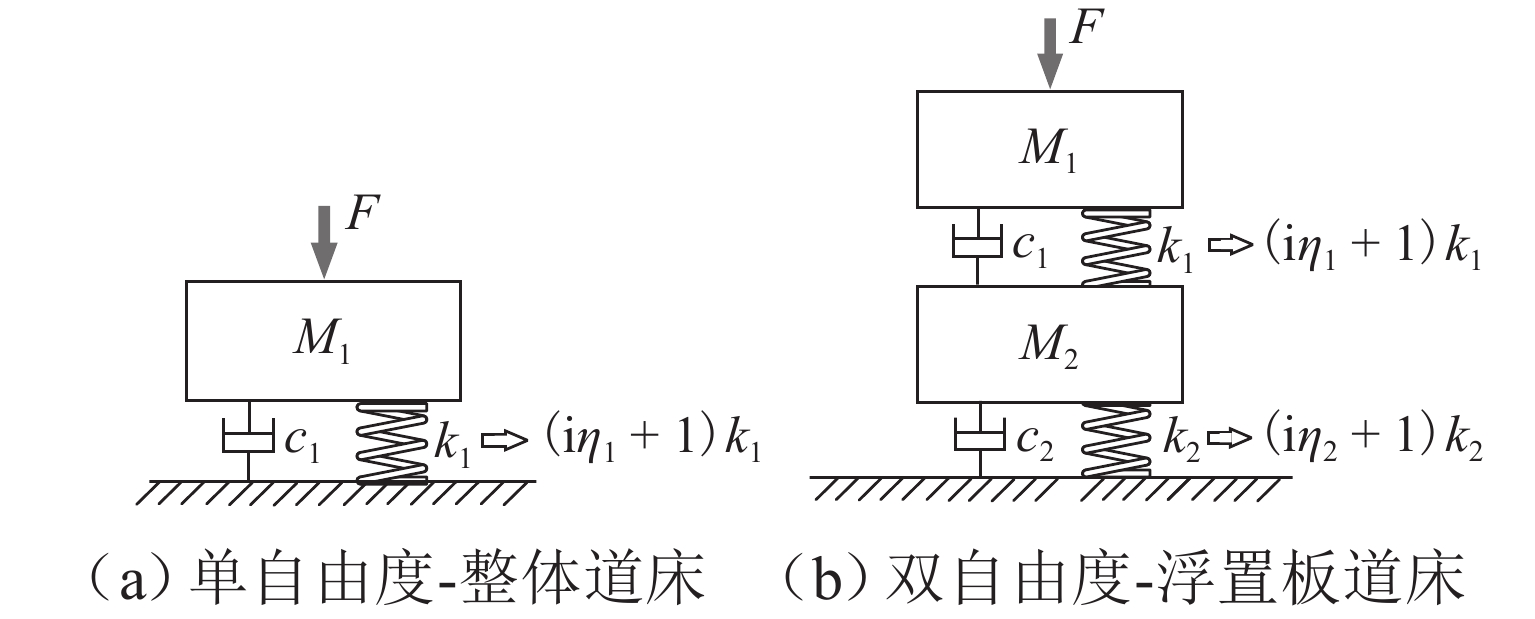
参数变量 默认变量名 质量-弹簧-阻尼体系 参照系统 减振系统 质量 $ {M_1} $ $ {M_{1{{\mathrm{Re}}} {\text{f}}}} $ $ {M_{1{\text{mit}}}} $ $ {M_2} $ $ {M_{2{{\mathrm{Re}}} {\text{f}}}} $ $ {M_{2{\text{mit}}}} $ 复刚度 $ (1 + {\mathrm{i}}{\eta _1}){k_1} $ $ (1 + {\mathrm{i}}{\eta _{1{{\mathrm{Re}}} {\text{f}}}}){k_{1{{\mathrm{Re}}} {\text{f}}}} $ $ (1 +{\mathrm{ i}}{\eta _{1{\text{mit}}}}){k_{1{\text{mit}}}} $ $ (1 + {\mathrm{i}}{\eta _2}){k_2} $ $ (1 + {\mathrm{i}}{\eta _{2{{\mathrm{Re}}} {\text{f}}}}){k_{2{{\mathrm{Re}}} {\text{f}}}} $ $ (1 + {\mathrm{i}}{\eta _{2{\text{mit}}}}){k_{2{\text{mit}}}} $ 
下载: 导出CSV
表 2 车轮受集中力时的荷载附加项
Table 2. Additional load when wheels are subject to concentrated force
荷载附加项 钢轨挠度 浮置板挠度 $ {y_{{\mathrm{p}}1}} $ $ P {w_4}\left(x - \dfrac{{{L_{\mathrm{r}}} - 2.5}}{2}\right) $ $ P {w_{12}}\left(x - \dfrac{{{L_{\mathrm{r}}} - 2.5}}{2}\right) $ $ {y_{{\mathrm{p}}2}} $ $ P {w_4}\left(x - \dfrac{{{L_{\mathrm{r}}} + 2.5}}{2}\right) $ $ P {w_{12}}\left(x - \dfrac{{{L_{\mathrm{r}}} + 2.5}}{2}\right) $
下载: 导出CSV
表 3 浮置板受均布力作用时的荷载附加项
Table 3. Additional load when floating slab track is subject to uniform force
荷载附加项 钢轨挠度 浮置板挠度 $ {y_{\mathrm{q}}} $ $ \displaystyle\int_0^x {{w_8}(x - r) q{\text{ d}}r} $ $ \displaystyle\int_0^x {{w_{16}}(x - r) q{\text{ d}}r} $
下载: 导出CSV
表 4 计算工况
Table 4. Calculation conditions
系统 扣件刚度/（kN·mm−1） 扣件损耗因子 减振垫刚度/（N·mm−3） 减振垫损耗因子 参照系统 普通扣件整体道床 45 0.2 减振系统 减振扣件 20 0.2 减振垫浮置板 45 0.2 0.02 0.1
下载: 导出CSV
表 5 有限元及修正前、后轮轨系统共振频率结果
Table 5. Finite element results and resonant frequency results of wheel–rail system before and after correction
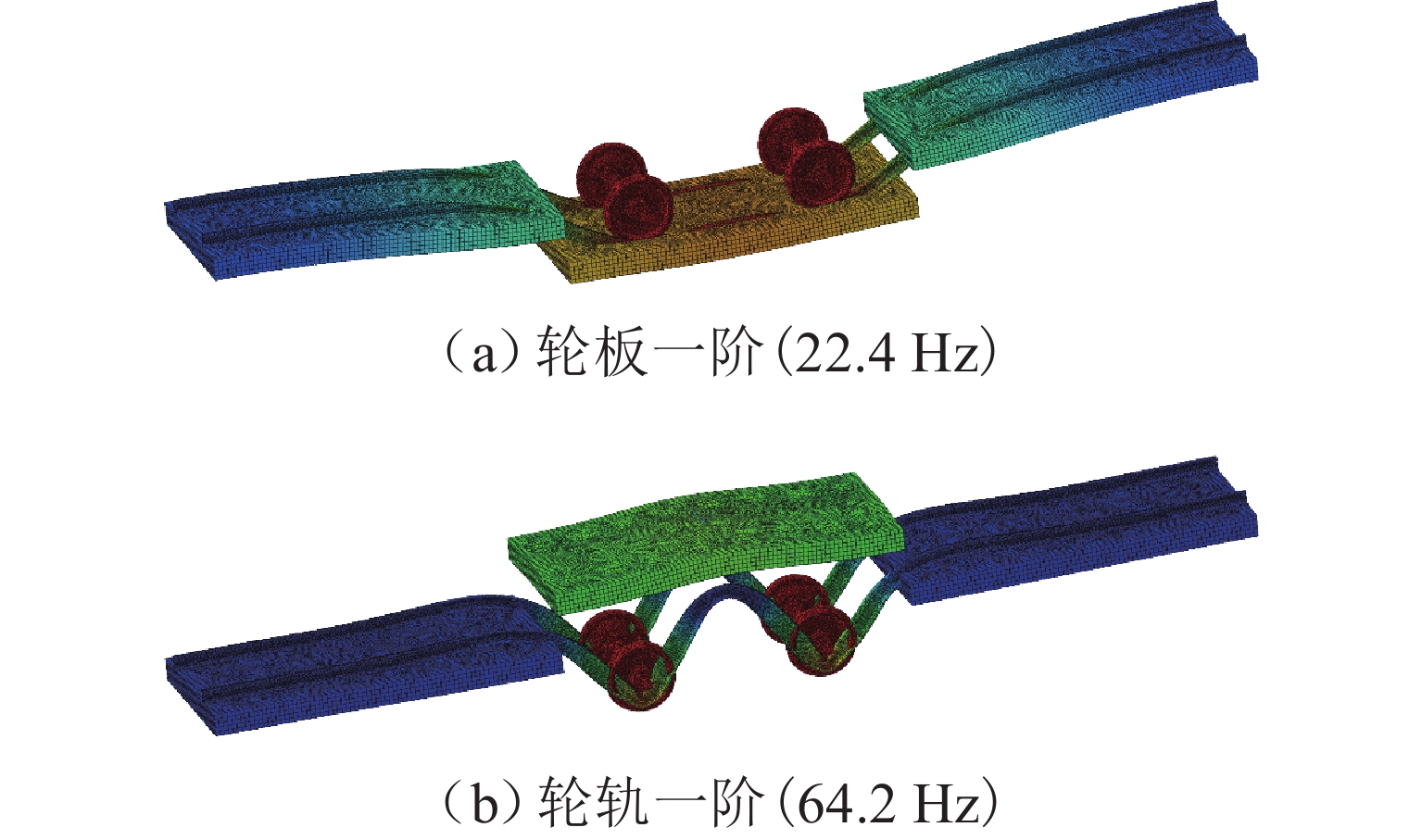
Hz 对象 减振类型 刚度修正前 刚度修正后 有限元 9 组扣件 11 组扣件 减振扣件 轮轨一阶 62.0 69.0 37.2 39.1 减振垫浮置板 轮轨一阶 89.0 98.0 66.0 64.2 轮板一阶 21.0 21.0 23.0 22.4
下载: 导出CSV
表 6 减振垫浮置板轨道插入损失率基础计算参数
Table 6. Basic calculation parameters for insertion loss rate of floating slab track with vibration damping pads
减振系统计算参数 参数值 扣件刚度/（kN·mm−1） 45 减振垫刚度/（N·mm−3） 0.02 扣件损耗因子 0.2 减振垫损耗因子 0.1 车轮质量/kg 2 × 1900 每延米钢轨质量/kg 60 浮置板长/宽/高/m 4.8/2.5/0.3 浮置板密度/（kg·m−3） 2400
下载: 导出CSV
-
[1] 刘维宁, 马蒙, 刘卫丰, 等. 我国城市轨道交通环境振动影响的研究现况[J]. 中国科学: 技术科学, 2016, 46(6): 547-559. doi: 10.1360/N092015-00334LIU Weining, MA Meng, LIU Weifeng, et al. Overview on current research of environmental vibration influence induced by urban mass transit in China[J]. Scientia Sinica (Technologica), 2016, 46(6): 547-559. doi: 10.1360/N092015-00334 [2] 王博, 赵俊娟, 卢伟健, 等. 轨道减振技术与应用[M]. 北京: 中国铁道出版社, 2023: 224-225. [3] 杜林林, 刘维宁, 刘卫丰, 等. 城市轨道交通环境振动评价指标计算与分析[J]. 都市快轨交通, 2017, 30(5): 40-45. doi: 10.3969/j.issn.1672-6073.2017.05.007DU Linlin, LIU Weining, LIU Weifeng, et al. Computation and analysis of evaluation indicators of environmental vibration induced by urban rail transit[J]. Urban Rapid Rail Transit, 2017, 30(5): 40-45. doi: 10.3969/j.issn.1672-6073.2017.05.007 [4] ZHAO L, ZHAO G T, YANG G T. Warping deformation of the track slab and their influence on the interlayer stiffness and vibration transmission characteristics of the unit ballastless track[J]. Structures, 2023, 10: 105078.1-105078.57. [5] 韦凯, 王平. 铁路轨道高聚物弹性元件刚度设计方法与应用[M]. 北京: 科学出版社, 2023: 246, 315-319. [6] 王文斌. 基于脉冲实验的地铁环境振动响应传递函数预测方法研究[D]. 北京: 北京交通大学, 2011. [7] LAGE Y E, NEVES M M, MAIA N M M, et al. Force transmissibility versus displacement transmissibility[J]. Journal of Sound Vibration, 2014, 333(22): 5708-5722. doi: 10.1016/j.jsv.2014.05.038 [8] DE-DIN. Mechanical vibration-resilient elements used in railway tracks-part 4: analytical evaluation of insertion loss of mounted track systems: DIN V 45673-4[S]. Berlin: Deutsches Institut für Normung, 2008. [9] 瞿思嫣. 基于等效弹性地基梁模型的钢轨动力分析方法研究[D]. 长沙: 中南大学, 2022: 19-21. [10] 赵坪锐. 客运专线无碴轨道设计理论与方法研究[D]. 成都: 西南交通大学, 2008. [11] VERACHTERT R, HUNT H E M, HUSSEIN M F M, et al. Changes of perceived unevenness caused by in-track vibration countermeasures in slab track[J]. European Journal of Mechanics-A/Solids, 2017, 65: 40-58. doi: 10.1016/j.euromechsol.2017.02.003 [12] 何威, 左树行, 白象忠. 弹性地基双层梁理论下的混凝土路面力学分析[J]. 应用力学学报, 2020, 37(1): 63-69, 472-473.HE Wei, ZUO Shuhang, BAI Xiangzhong. Mechanical analysis of concrete pavement via the theory of double layer beams on elastic foundation[J]. Chinese Journal of Applied Mechanics, 2020, 37(1): 63-69, 472-473. [13] 周越, 张国锋. 简谐波势能的一种简明推导[J]. 物理与工程, 2015, 25(2): 49-51. doi: 10.3969/j.issn.1009-7104.2015.02.007ZHOU Yue, ZHANG Guofeng. A simplified derivation of potential energy of simple harmonic waves[J]. Physics and Engineering, 2015, 25(2): 49-51. doi: 10.3969/j.issn.1009-7104.2015.02.007 [14] 韦凯, 豆银玲, 杨麒陆, 等. 钢弹簧浮置板轨道的随机振动分析及参数优化[J]. 华中科技大学学报(自然科学版), 2017, 45(8): 115-119.WEI Kai, DOU Yinling, YANG Qilu, et al. Random vibration analysis and parameter optimization of steel-spring floating-slab track[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2017, 45(8): 115-119. [15] 龙驭球. 弹性地基梁的计算[M]. 北京: 人民教育出版社, 1981. [16] 关庆华, 周业明, 李伟, 等. 车辆轨道系统的P2共振频率研究[J]. 机械工程学报, 2019, 55(8): 118-127. doi: 10.3901/JME.2019.08.118GUAN Qinghua, ZHOU Yeming, LI Wei, et al. Study on the P2 resonance frequency of vehicle track system[J]. Journal of Mechanical Engineering, 2019, 55(8): 118-127. doi: 10.3901/JME.2019.08.118 [17] 马维国, 关庆华, 钟文生, 等. 轨道参数对轮轨耦合系统固有频率的影响[J]. 噪声与振动控制, 2019, 39(3): 18-23, 55. doi: 10.3969/j.issn.1006-1355.2019.03.004MA Weiguo, GUAN Qinghua, ZHONG Wensheng, et al. Influence of track parameters on natural frequencies of wheel-track coupling systems[J]. Noise and Vibration Control, 2019, 39(3): 18-23, 55. doi: 10.3969/j.issn.1006-1355.2019.03.004 [18] 马超智, 高亮, 曾钦娥, 等. 高速铁路轮轨耦合振动模态特征及其影响因素研究[J]. 铁道学报, 2021, 43(12): 85-93. doi: 10.3969/j.issn.1001-8360.2021.12.011MA Chaozhi, GAO Liang, ZENG Qine, et al. Study on modal characteristics and influencing factors of wheel-rail coupling vibration of high-speed railway[J]. Journal of the China Railway Society, 2021, 43(12): 85-93. doi: 10.3969/j.issn.1001-8360.2021.12.011 [19] 易思蓉. 铁道工程[M]. 3版. 北京: 中国铁道出版社, 2015: 240-243. [20] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 机械振动与冲击, 人体暴露于全身振动的评价 第1部分: 一般要求: GB/T 13441.1—2007[S]. 北京: 中国标准出版社, 2007. [21] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 机械振动与冲击, 人体暴露于全身振动的评价 第2部分: 建筑物内的振动: GB/T 13441.1—2008[S]. 北京: 中国标准出版社, 2008. -
下载:
点击查看大图
计量
- 文章访问数: 172
- HTML全文浏览量: 86
- PDF下载量: 18
- 被引次数: 0