基于多种群遗传算法的磁浮列车自抗扰速度控制

李自康; 戴春辉; 黄翠翠; 龙志强

doi:10.3969/j.issn.0258-2724.20240113

基于多种群遗传算法的磁浮列车自抗扰速度控制

doi: 10.3969/j.issn.0258-2724.20240113

国防科技大学智能科学学院，湖南长沙 410000

基金项目: 国家自然科学基金项目（52332011）

详细信息

作者简介:
李自康（1995—），男，博士研究生，研究方向为电磁悬浮与推进控制，E-mail：lizikang24@nudt.edu.cn

通讯作者:
戴春辉（1984—），男，副研究员，博士，研究方向为电磁悬浮与推进控制、智能诊断与容错控制，E-mail：daichunhui@nudt.edu.cn

中图分类号: U238
计量
- 文章访问数: 50
- HTML全文浏览量: 29
- PDF下载量: 17
- 被引次数: 0
出版历程
- 收稿日期: 2024-03-07
- 修回日期: 2024-08-25
- 网络出版日期: 2025-03-05

Active Disturbance Rejection Speed Control for Maglev Trains Based on Multiple Population Genetic Algorithm

College of Intelligence Science and Technology, National University of Defense Technology, Changsha 410000, China

摘要

摘要:
相较传统轮轨交通方式，磁浮列车具有速度快、噪音小、平稳性高、维护成本低等不可替代的优势，为实现磁浮列车在复杂扰动环境下的精准速度运行控制，提出一种参数自整定的自抗扰控制(ADRC)方法. 通过受力分析建立磁浮列车纵向动力学模型，用于描述运行控制过程中的非线性迟滞特性；将模型不确定参数及外部扰动等因素归纳为扩张状态，设计三阶扩张状态观测器实时观测扩张状态，并基于李雅普诺夫稳定性定理对观测器的收敛性条件进行分析；针对传统ADRC控制参数多、调参困难的问题，引入多种群遗传算法(MPGA)实现参数自适应优化和调整；利用磁浮列车现场运行采集的数据开展仿真实验. 结果表明：相较传统ADRC，MPGA-ADRC在速度控制精度方面提升22.7%，跟踪平稳性提升25.6%，所提出的方法能够有效提升磁浮列车运行的稳定性和乘坐舒适性.
- 磁浮列车 /
- 自抗扰控制 /
- 扩张状态观测器 /
- 多种群遗传算法 /
- 速度控制
Abstract:
Compared with traditional wheel-rail transportation, maglev trains have some irreplaceable advantages such as high speed, low noise, smooth operation, and low maintenance cost. To realize precise speed control of maglev trains in complex disturbance environments, an active disturbance rejection control (ADRC) method with self-tuning parameters was proposed. Firstly, the longitudinal dynamic model of maglev trains was established by force analysis to describe the nonlinear hysteresis characteristics of maglev trains during operation. Secondly, the unknown parameters of the model and external disturbances were regarded as the extended state, and a third-order extended state observer was designed to observe the extended state in real time. In addition, the convergence condition of the observer was analyzed based on the Lyapunov stability theorem. Then, to solve the problem of many control parameters and difficult parameter adjustment in traditional ADRC, the multiple population genetic algorithm (MPGA) was introduced to realize adaptive optimization and adjustment of parameters. Finally, the simulation experiment was carried out based on the data collected from the real operation environment of maglev trains, and the simulation results show that compared with traditional ADRC, the speed control accuracy is increased by 22.7% and the tracking stability is improved by 25.6% by means of MPGA-ADRC method, which indicates that the proposed method can effectively improve the stability and ride comfort of maglev trains.
- maglev train /
- active disturbance rejection control /
- extended state observer /
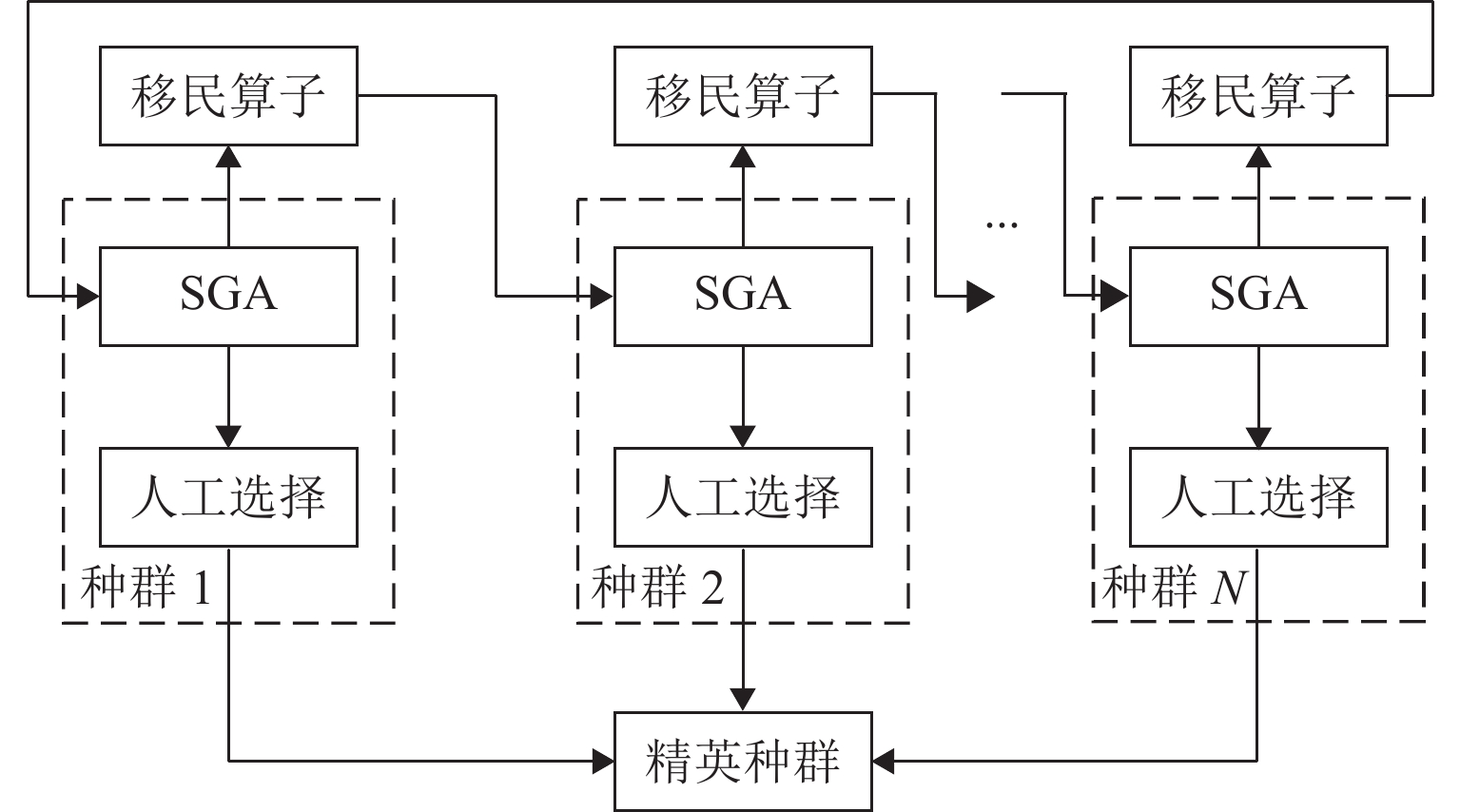
- MPGA /
- speed control

HTML全文

磁悬浮轴承是通过磁场产生的电磁力将转子悬浮在空中的一种无摩擦的高性能轴承^[1]，具有无接触、损耗低、运行速度高及寿命长等优点，因此被广泛应用在航空航天、飞轮储能、人工心脏等领域^[2-9]. 从工作原理的角度，磁悬浮轴承分为主动型、被动型和混合型. 主动型磁悬浮轴承通过传感器和功率放大器等单元，主动控制通电线圈的电流，以此调控电磁力，从而实现转子的主动悬浮；被动型磁悬浮轴承则利用永磁体间、永磁体和软磁材料间的斥力或电磁吸力，产生不可控的电磁力以实现转子悬浮^[10]；混合磁悬浮轴承综合两者特点，通过永磁体生成偏置磁场和电磁线圈生成控制磁场，减少功率放大器的数量，并降低其功耗^[11-12].

混合磁悬浮轴承按其结构型式可分为同极性结构和异极性结构. 同极性磁轴承的偏置磁场和控制磁场在不同的平面，工作产生的损耗较低但轴向尺寸较长^[13]，限制了其转子的最高临界转速. 异极性磁轴承磁极的极性相反，极性交替排列，偏置磁通与控制磁通在同一平面，相比于同极性轴承，其轴向长度短，对提升转子最高转速有利^[14-17]. Okada等^[18]将传统磁轴承永磁体在两径向轴承间形成磁通回路的方式改变为将永磁体置于径向磁轴承内部，使得磁路在内部闭合，减小了磁轴承漏磁，提高了轴承效率. 孙津济等^[19]提出一种外转子式的新型磁轴承结构，在定子内部引入第二气隙，使得电磁磁路与永磁磁路共面，且不经过永磁体，同时，将定子铁心磁极数由8个减为4个，大大降低了磁轴承损耗. 朱润泽等^[20]提出一种4极型磁轴承，将传统的8极结构变为4极，并引入辅助气隙以防止永磁体发生短路，使得轴承在减少损耗的同时降低径向两自由度间的电磁耦合，有效提高轴承性能. 钟志贤等^[21]提出一种新型4极径向磁轴承，将外定子在轴向上进行拓展，形成具有6条独立磁路的结构，使其电磁磁路与永磁磁路相互独立，实现径向两自由度的电磁力解耦，但由于轴向较长，在一定程度上会影响转子的临界转速.

本文提出一种新型异极径向混合磁轴承（heteropolar radial hybrid magnetic bearing，HRHMB），可以控制径向2个自由度，具有轴向长度短、空间利用率高、永磁磁路与电磁磁路耦合距离短等优点. 首先，介绍新型HRHMB的结构原理，采用等效磁路法解析得到该磁轴承的电磁力、位移刚度和电流刚度，并与仿真结果进行分析对比；为验证该磁悬浮轴承的静态性能，在同悬浮力约束条件下与传统偏置磁轴承^[22]进行对比；最后，通过有限元分析验证该新型磁轴承在径向两自由度间的电磁力耦合较小.

1. 新型HRHMB结构及原理

1.1 新型HRHMB结构

新型HRHMB和传统八极偏置磁轴承的结构及磁路如图1所示. 新型HRHMB主要由定子铁心、转子铁心、控制绕组及永磁体组成. 定子铁心上包含主动控制磁1、3、5、7和辅磁极2、4、6、8，4组控制绕组分别在4个主动控制磁极上，产生控制磁场；4个辅磁极交错分布在主动控制磁极之间. 8个永磁体采用平行充磁的方式两两分布在主动控制磁极两侧，与转子形成工作气隙，用以产生偏置磁场. 定子铁心上的主辅磁极沿圆周形成NS相间的异极极性分布，为异极型磁悬浮轴承的结构形式. 同时，在定子铁心的横向处引入辅助气隙，起到减少X方向的永磁体在定子极间的漏磁及加强偏置磁场的作用. 由于异极型磁轴承损耗较大，其定转子铁心采用硅钢片叠压而成以降低转子高速运转下的铁耗. 永磁体采用钕铁硼烧结而成，嵌装在主辅磁极之间.

图 1 两种混合型磁悬浮轴承结构

Figure 1. Two kinds of hybrid magnetic bearing structures

下载: 全尺寸图片幻灯片

1.2 新型HRHMB工作原理

由于新型HRHMB具有对称性，以Y向磁极为例，控制绕组产生的控制磁通路径如图1（a）虚线所示，主动控制磁极上的控制绕组通入电流产生Y向的磁通，经过气隙、转子铁心及磁轭形成回路. 当转子处于平衡位置时，由于定子结构对称，Y方向上永磁体产生的气隙磁密相同，此时线圈中未通入电流，没有控制磁通. 假设转子受到向下的扰动力时， + Y方向气隙长度变大，−Y方向气隙长度变小. 在差动控制方式下，线圈通入电流，控制绕组产生的控制磁通和永磁体产生的偏置磁通在 + Y方向气隙处叠加，−Y方向气隙处抵消，使 + Y方向气隙磁通大于−Y方向气隙磁通，导致转子产生一个 + Y方向的电磁力，将转子拉回平衡位置. 线圈通电产生不同方向的力以使转子受到其它方向的干扰时保持平衡位置.

新型HRHMB的优点在于磁通路径和轴向长度短，且由于偏置磁通由永磁体产生，因此，功耗较低. 另外，其永磁磁路和电励磁磁路耦合距离较短，利于降低径向二自由度之间的磁场力耦合. 与传统八极径向偏置磁悬浮轴承相比，磁极数量同为八极，但新型HRHMB磁极区域大，在飞轮储能系统和磁悬浮电机等透平机械中有潜在的应用前景.

2. HRHMB磁路分析

2.1 等效磁路模型

单独考虑永磁体产生的偏置磁场和通电线圈产生的控制磁场，对HRHMB磁场进行仿真，结果如图2所示.

图 2 新型异极径向混合磁轴承磁场仿真

Figure 2. Magnetic field simulation of novel HRHMB

下载: 全尺寸图片幻灯片

由磁场仿真结果可以看出：偏置磁通经过永磁体、主动控制磁极、气隙、转子铁心和定子辅磁极，漏磁通经过永磁体、定子主磁极、定子磁轭、定子极间空隙和定子辅磁极；Y方向偏置磁通漏磁主要分布在定子的极间，由于X方向第二气隙的引入，X方向永磁体产生的偏置磁通漏磁大为减小；控制磁通经过主动控制磁极、气隙、转子铁心和定子磁轭.

假设该新型磁轴承定转子铁心磁阻及涡流损耗为零，建立其等效磁路模型，如图3所示. 在偏置磁场等效磁路（图3（a））中，R_gb1 ～ R_gb8为永磁体下偏置磁路气隙磁阻，转子处在平衡位置时，其结构对称，此时R_gb1=R_gb2，R_gb3=R_gb4；R_k1 ～ R_k8为永磁体漏磁磁阻；F_p为永磁体磁动势；R_p为永磁体磁阻.

图 3 新型异极径向混合磁轴承等效磁路

Figure 3. Equivalent magnetic circuit of novel HRHMB

下载: 全尺寸图片幻灯片

${F_{\text{p}}} = {H_{\text{c}}}{l_{\text{m}}},$

(1)

${R_{\text{p}}} = {l_{\text{m}}}/\left( {{\mu _{\text{p}}}{S_{\text{p}}}} \right),$

(2)

式中：H_c为永磁体矫顽力，l_m为永磁体宽度， ${\mu _{\text{p}}}$ 为永磁体磁导率，S_p为永磁体中性面面积.

在控制磁场等效磁路（图3（b））中，R_c1、R_c2、R_c3、R_c4分别为4个控制磁极气隙的磁阻，R_a为辅助气隙磁阻，N_x、N_y分别为水平、垂直方向的线圈匝数，i_x、i_y分别为水平、垂直方向上的电流.

$\left\{ \begin{array}{l}\left[{R}_{\text{c}1}\;{R}_{\text{c}2}\;{R}_{\text{c}3}\;{R}_{\text{c}4}\right]=\left[\dfrac{{g}_{0} + y}{{\mu }_{0}{A}_{\text{r}}}\;\dfrac{{g}_{0}-y}{{\mu }_{0}{A}_{\text{r}}}\;\dfrac{{g}_{0} + x}{{\mu }_{0}{A}_{\text{r}}}\;\dfrac{{g}_{0}-x}{{\mu }_{0}{A}_{\text{r}}}\right]\\ {R}_{\text{a}}={g}_{\text{a}}/\left({\mu }_{0}{A}_{\text{r}}\right),\end{array},\right.$

(3)

式中：μ₀为空气磁导率，g₀为转子铁心在平衡位置时的气隙长度，g_a为辅助气隙长度，x、y分别为转子在X、Y轴方向的位移量，A_r为主动控制磁极气隙的面积.

2.2 新型异极径向混合磁轴承磁通计算

在高速电机和飞轮储能系统中转子最大允许的偏心位移为气隙长度的1/10，此时可认为4个径向方向偏置磁通彼此解耦^[23-24]. 将图3（a）偏置磁路图简化为Y + 、Y−、X + 、X− 4条磁路，分别计算其气隙处磁通，由于该磁轴承结构对称，由磁网络法计算Y + 、X−处可得到其他气隙处磁通.

2.2.1 Y + 方向偏置磁路磁通

偏置磁通在Y + 方向的等效磁路如图4（a）所示，φ_pmk1、φ_pmk2为漏磁磁通，φ_pmy1、φ_pmy2为永磁体下的偏置磁通；R_gb1、R_gb2为偏置磁通气隙磁阻，R_k2为漏磁磁阻，R_k1漏磁阻可以看作是端部漏磁磁阻R_k11和极间磁阻R_k12的并联磁阻，且R_k1//R_p//R_gb1.

图 4 Y + 方向等效磁路

Figure 4. Equivalent magnetic circuit along Y + direction

下载: 全尺寸图片幻灯片

漏磁磁阻和气隙磁阻分别为

$\left\{ \begin{array}{l}{R}_{\text{k}1}={R}_{\text{k2}}={R}_{\text{k}12}{R}_{\text{k}11}/({R}_{\text{k}12} + {R}_{\text{k}11}),\\ \left[{R}_{\text{gb}1}\;{R}_{\text{gb}2}\;{R}_{\text{gb}3}\;{R}_{\text{gb}4}\right]=\left[\dfrac{{g}_{0} + y}{{\mu }_{0}{A}_{\text{ra}}}\;\dfrac{{g}_{0} + y}{{\mu }_{0}{A}_{\text{ra}}}\;\dfrac{{g}_{0}-y}{{\mu }_{0}{A}_{\text{ra}}}\;\dfrac{{g}_{0}-y}{{\mu }_{0}{A}_{\text{ra}}}\right],\end{array}\right.$

(4)

式中： ${R_{{\text{k11}}}} = \ln ({r_{{\text{a}}2}}/{r_{{\text{a1}}}})/\left( {2{\mu _0}{\text{π}} {L_{\text{z}}}} \right)$ ^[25]，r_a1和r_a2为两极间半径， ${R}_{\text{k12}}=(2/{m}_{\text{y}} + 0.5)/\left(0.64{\mu }_{0}{L}_{\text{z}}\right)$ ，L_z为磁轴承轴向长度，m_y为端部漏磁路半径，A_ra为辅磁极截面积.

根据磁路基尔霍夫定律可求出Y + 方向2个永磁体产生的偏置磁通和漏磁磁通，对应（a）的磁网络矩阵如式（5）所示. 各磁阻由磁阻模型得出，可得偏置磁场的磁通 ${\phi} _{\text{pmy1}}$ 、 ${\phi}_{\text{pmy2}}$ 如式（6）所示.

$\quad\quad\quad\quad\quad \left[ {\begin{array}{*{20}{c}} {{R_{{\text{k}}1}}}&0&{ - {R_{\text{p}}}}&0 \\ 0&{{R_{{\text{k}}2}} + {R_{\text{p}}}}&0&{ - {R_{\text{p}}}} \\ { - {R_{\text{p}}}}&0&{{R_{{\text{gb}}1}} + {R_{{\text{c}}1}} + {R_{\text{p}}}}&{ - {R_{{\text{c}}1}}} \\ 0&{ - {R_{\text{p}}}}&{ - {R_{{\text{c}}1}}}&{{R_{{\text{gb2}}}} + {R_{{\text{c}}1}} + {R_{\text{p}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\phi _{{\text{pmk}}1}}} \\ {{\phi _{{\text{pmk2}}}}} \\ {{\phi _{{\text{pmy}}1}}} \\ {{\phi _{{\text{pmy2}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_{\text{p}}}/\sigma } \\ { - {F_{\text{p}}}/\sigma } \\ { - {F_{\text{p}}}/\sigma } \\ {{F_{\text{p}}}/\sigma } \end{array}} \right],$

(5)

$\quad\quad\quad\quad\quad\quad\quad\quad \left\{\begin{array}{l}{\phi }_{\text{pmy}1}=\dfrac{{F}_{\text{p}}{R}_{\text{p}}({R}_{\text{c}1}-{R}_{\text{k1}})}{\sigma [{R}_{\text{p}}({R}_{\text{k1}} + {R}_{\text{gb1}} + {R}_{\text{c1}}) + {R}_{\text{k2}}({R}_{\text{gb1}} + {R}_{\text{c1}})]({R}_{\text{p}} + {R}_{\text{gb2}} + {R}_{\text{c1}})},\\ {\phi }_{\text{pmy2}}=\dfrac{{F}_{\text{p}}{R}_{\text{p}}({R}_{\text{c}1}-{R}_{\text{k2}})}{\sigma [{R}_{\text{p}}({R}_{\text{k2}} + {R}_{\text{gb2}} + {R}_{\text{c1}}) + {R}_{\text{k1}}({R}_{\text{gb2}} + {R}_{\text{c1}})]({R}_{\text{p}} + {R}_{\text{gb1}} + {R}_{\text{c1}})},\end{array}\right.$

(6)

式中：σ为永磁体漏磁系数.

2.2.2 X-方向偏置磁路磁通

偏置磁通X−方向的等效磁路如图5所示，φ_pmk5、φ_pmk6为漏磁磁通，φ_pmx1、φ_pmx2为永磁磁极下的偏置磁通；R_gb5、R_gb6为偏置磁通气隙磁阻，R_k5、R_k6为漏磁磁阻. 气隙磁阻及漏磁磁阻分别为

图 5 X−方向等效磁路

Figure 5. Equivalent magnetic circuit along X− direction

下载: 全尺寸图片幻灯片

$\left\{ \begin{array}{l}{R}_{\text{k5}}={R}_{\text{k}6}=\left(2/{m}_{x} + 0.5\right)/\left(0.64{\mu }_{0}{L}_{{\textit{z}}}\right),\\ \left[{R}_{\text{gb}5}\;{R}_{\text{gb}6}\;{R}_{\text{gb}7}\;{R}_{\text{gb}8}\right]=\left[\dfrac{{g}_{0} + x}{{{\mu }_{0}}{A}_{\text{ra}}}\;\dfrac{{g}_{0} + x}{{{\mu }_{0}}{A}_{\text{ra}}}\;\dfrac{{g}_{0}-x}{{{\mu }_{0}}{A}_{\text{ra}}}\;\dfrac{{g}_{0}-x}{{{\mu }_{0}}{A}_{\text{ra}}}\right],\end{array}\right.$

(7)

式中: ${m_x}$ 为永磁体端部漏磁半径.

对应图5的磁网络矩阵如式（8）所示，式中各磁阻由图5磁阻模型得出，进而可得偏置磁通如式（9）所示.

$\quad\quad\quad\quad \left[ {\begin{array}{*{20}{c}} {{R_{{\text{gb}}5}} + {R_{\text{p}}} + {R_{{\text{c}}3}}}&{ - {R_{{\text{c}}3}}}&{ - {R_{\text{p}}}}&0 \\ { - {R_{{\text{c}}3}}}&{{R_{{\text{gb6}}}} + {R_{\text{p}}} + {R_{{\text{c}}3}}}&0&{ - {R_{\text{p}}}} \\ { - {R_{\text{p}}}}&0&{{R_{{\text{k5}}}} + {R_{\text{p}}}}&0 \\ 0&{ - {R_{\text{p}}}}&0&{{R_{{\text{gb6}}}} + {R_{\text{p}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\phi _{{\text{pmx1}}}}} \\ {{\phi _{{\text{pmx2}}}}} \\ {{\phi _{{\text{pmk5}}}}} \\ {{\phi _{{\text{pmk6}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_{\text{p}}}/\sigma } \\ { - {F_{\text{p}}}/\sigma } \\ { - {F_{\text{p}}}/\sigma } \\ {{F_{\text{p}}}/\sigma } \end{array}} \right],$

(8)

$\quad\quad\quad\quad\quad\quad\quad\quad \left\{\begin{array}{l}{\phi }_{\text{pmx}1}=\dfrac{{F}_{\text{p}}{R}_{\text{p}}({R}_{\text{c}3}-{R}_{\text{k5}})}{\sigma [{R}_{\text{p}}({R}_{\text{k5}} + {R}_{\text{gb5}} + {R}_{\text{c3}}) + {R}_{\text{k6}}({R}_{\text{gb5}} + {R}_{\text{c3}})]({R}_{\text{p}} + {R}_{\text{gb6}} + {R}_{\text{c3}})},\\ {\phi }_{\text{pmx2}}=\dfrac{{F}_{\text{p}}{R}_{\text{p}}({R}_{c3}-{R}_{\text{k5}})}{\sigma [{R}_{\text{p}}({R}_{\text{k6}} + {R}_{\text{gb6}} + {R}_{\text{c3}}) + {R}_{\text{k5}}({R}_{\text{gb6}} + {R}_{\text{c3}})]({R}_{\text{p}} + {R}_{\text{gb5}} + {R}_{\text{c3}})}.\end{array}\right.$

(9)

2.2.3 电磁磁路磁通

在图3（b）中，径向X、Y方向的控制磁路总磁阻分别为R_rx、R_ry，如式（19）所示.

$\left\{ \begin{array}{l} {R_{{\text{rx}}}} = {R_{{\text{c}}3}} + {R_{{\text{c}}4}} + 2{R_{\text{a}}} , \\ {R_{{\text{ry}}}} = {R_{{\text{c}}1}} + {R_{{\text{c}}2}}. \end{array} \right.$

(10)

径向X、Y方向的控制磁路磁通φ_cx、φ_cy分别为

$\left\{ \begin{array}{l} {\phi _{{\text{cx}}}} = 2{N_x}{i_x}/{R_{{\text{rx}}}}, \\ {\phi _{{\text{cy}}}} = 2{N_y}{i_y}/{R_{{\text{ry}}}}. \end{array} \right.$

(11)

2.3 悬浮力与刚度计算

由磁网络分析法求解该磁轴承的各磁路磁通，从而可得该磁轴承的刚度和承载力. 将笛卡尔坐标系的正方向作为力的正方向，根据麦克斯韦方程组可推导出径向两自由度的悬浮力分别为

$\left\{ \begin{array}{l} {F_y} = \dfrac{{{{({\phi _{{\text{pmy}}1}} + {\phi _{{\text{cy}}}})}^2} - {{({\phi _{{\text{pmy}}2}} - {\phi ^2_{{\text{cy}}}})}}}}{{2{\mu _0}{A_{\text{r}}}}} + \dfrac{{{\phi ^2_{{\text{pmy}}1}} - {\phi ^2_{{\text{pmy}}3}}}}{{2{\mu _0}{A_{{\text{ra}}}}}}, \\ {F_x} = \dfrac{{{{({\phi _{{\text{pmx}}1}} + {\phi _{{\text{cx}}}})}^2} - {{({\phi _{{\text{pmx}}2}} - {\phi ^2_{{\text{cx}}}})}}}}{{2{\mu _0}{A_{\text{r}}}}} + \dfrac{{{\phi ^2_{{\text{pmx}}1}} - {\phi ^2_{{\text{pmx3}}}}}}{{2{\mu _0}{A_{{\text{ra}}}}}} . \end{array} \right.$

(12)

联立式（9）～（12），求出该磁轴承在Y、X方向两自由度的电流刚度 $k_{i_y}$ 、 $k_{i_x}$ 和位移刚度 $k_{d_y}$ 、 $k_{d_x}$ 分别为

$\left\{ \begin{array}{l} k_{i_y}=\left.\dfrac{\partial F_y}{\partial i_y}\right|_{\substack{x=y=0,\\ i_x=i_y=0}}=\dfrac{2 \phi_{\mathrm{cy}} N}{\sigma \mu_0 g_0\left(R_{\mathrm{c} 2}+R_{\mathrm{c} 1} / R_{\mathrm{ry}}\right)}, \\ k_{i_x}=\left.\dfrac{\partial F_x}{\partial i_x}\right|_{\substack{x=y=0, \\ i_x=i_y=0}}=\dfrac{2 \phi_{\mathrm{cx}} N}{\sigma \mu_0 g_0\left(R_{\mathrm{rx}}+R_{\mathrm{a} 1}\right)}, \\ k_{d_y}=\left.\dfrac{\partial F_y}{\partial y}\right|_{\substack{x=y=0, \\ i_x=i_y=0}}=\dfrac{32\left(\dfrac{A_{\mathrm{ra}} g_0}{\mu_0}-\dfrac{R_{\mathrm{k} 12} R_{\mathrm{k} 11}}{R_{\mathrm{k} 12}+R_{k 11}}\right) S_{\mathrm{p}}^2 l_{\mathrm{m}}}{\sigma \mu_{\mathrm{p}}^2 A_{\mathrm{r}}^2\left(R_{\mathrm{p}} R_{\mathrm{k} 1}+6 R_{\mathrm{k} 2}+R_{\mathrm{p}}\right)^3}, \\ k_{d_x}=\left.\dfrac{\partial F_x}{\partial x}\right|_{\substack{x=y=0,\\ i_x=i_y=0}}=\dfrac{32\left(A_{\mathrm{ra}} g_0 / \mu_0-2 R_{\mathrm{c} 1}\right) S_{\mathrm{p}}^2 l_{\mathrm{m}}}{\sigma \mu_{\mathrm{p}}^2 A_{\mathrm{r}}^2\left(4 R_{\mathrm{c} 2}+2 R_{\mathrm{k} 3} R_{\mathrm{p}}+R_{\mathrm{p}}\right)^3}, \end{array}\right.$

(13)

式中：N为控制绕组的匝数.

3. 仿真分析

为验证磁路计算及悬浮力式的正确性，对新型磁轴承进行有限元仿真. 图1中2种磁轴承结构的主要模型参数如表1所示.

表 1 磁轴承主要参数

Table 1. Main parameters of magnetic bearing

参数	传统	新型
定子外直径/mm	130	139
转子外直径/mm	50	50
轴向长度/mm	45	45
主气隙长度/mm	0.5	0.5
辅助气隙长度/mm		1
永磁体厚度/mm	2	3
永磁体宽度/mm	15	8
磁极截面积/mm²	920	1560
最大控制电流/A	3.6	12/3

下载: 导出CSV

| 显示表格

3.1 磁场分布

新型磁悬浮轴承转子处于平衡位置时，给Y方向线圈通入不同电流时的磁密如图6所示，图中，序号1 ～ 8为图1（a）中对应的磁极位置. 当电流为0 A时，磁通仅由永磁体产生，磁极1、5处的磁密幅值高于磁极3、7处，这是由于引入辅助气隙导致减少了磁极1、5处的永磁体漏磁；随着控制电流的增大，永磁体和控制电流产生的磁通会在磁极1气隙处叠加，使得气隙磁密增大，在磁极5气隙处抵消，使得气隙磁密减小，其他磁极处的磁密基本不变.

图 6 气隙磁密随电流变化

Figure 6. Variation of magnetic density in air gap with current

下载: 全尺寸图片幻灯片

控制线圈未接入电流时，转子在Y方向上不同位置的气隙磁密如图7所示. 图中箭头为气隙增加趋势. 当转子向上偏转时，磁极3气隙处的磁通密度增强，而定子另一侧磁极7气隙处的磁通密度会减弱. 当转子不在平衡位置发生偏离时，此时转子和定子磁极的圆弧面不再平行，使得相同磁极不同位置上的气隙长度有所不同，出现磁极1、2、4、5、6、8处气隙磁通密度不均匀现象.

图 7 气隙磁密随位移变化

Figure 7. Variation of magnetic density in air gap with displacement

下载: 全尺寸图片幻灯片

3.2 电磁力仿真分析

悬浮力和位移刚度、电流刚度为磁悬浮轴承的基本特性，是衡量磁轴承性能的重要指标. 为验证磁路法分析的正确性，由式（13）对HRHMB的刚度特性进行计算并仿真，位移刚度和电流刚度如图8所示.

图 8 径向电流刚度与位移刚度

Figure 8. Radial current stiffness and displacement stiffness

下载: 全尺寸图片幻灯片

从图8（a）中可以看出，铁心材料处于不饱和状态时，转子所受到的悬浮力与绕组电流几乎成正比，同时也与转子在平衡位置附近的位移成正比. 当控制电流在−3 ～ 3 A时，通过磁路法计算出的最大电磁力为472.8 N，仿真得到的电磁力为447.7 N，等效磁路与仿真结果有所偏差，误差为5.6%，这是由于忽略了部分漏磁和定转子铁心中的磁阻造成的，在误差允许范围内.

在图8（b）中，转子位移在（−0.1 ～ + 0.1）mm时，等效磁路法和仿真结果的平均偏差为5.6%. 转子位置在 + 0.1 mm时，磁路法得到的电磁力为134.2 N，仿真的电磁力为123.2 N，偏差为8.9%，这是因为铁心磁通达到饱和引起的，而在高速电机等设备中转子最大允许的偏心位移为气隙长度的1/10，小于达到铁心饱和时的区间，故可忽略铁心饱和的影响. 另外，由于增加了第二气隙，该新型磁轴承X方向的位移刚度和电流刚度小于Y方向. 在应用中可以将Y轴放置于重力方向上，用以增强转子浮动的动态性能，同时，可以通过适当增加X轴方向上的控制线圈的匝数来提高其X方向上的电流刚度.

3.3 两种磁轴承对比

为比较新型和传统偏置磁轴承的悬浮性能及空间利用率，建立相同最大承载力和偏置磁通、转子尺寸等约束条件的仿真模型，传统磁轴承和新型HRHMB的永磁磁密分布如图9所示. 通过有限元仿真计算，在相同承载力下，新型磁轴承为传统偏置磁轴承体积的0.87倍，这表明新型磁轴承结构有着更高的空间利用率.

图 9 2种磁轴承的永磁磁通密度分布

Figure 9. Permanent magnetic flux density distribution of two types of magnetic bearings

下载: 全尺寸图片幻灯片

2种磁悬浮轴承的电流刚度和位移刚度如图10所示. 由图10（a）可以看出，新型HRHMB在X和Y方向上的位移刚度都相对较小，这表明当转子发生偏移时，通过控制系统回到平衡位置较为容易^[20]；图10（b）可以看出，新型HRHMB Y方向上的电流刚度大于传统结构磁轴承的电流刚度，这表明在相同的电流下，新型HRHMB能产生更大的悬浮力. 此外，由于引入辅助气隙，其X方向上的电流刚度会小于Y方向上的电流刚度，因此，新型HRHMB适用于卧式系统等应用场合.

图 10 2种磁轴承的位移刚度和电流刚度对比

Figure 10. Comparison of displacement stiffness and current stiffness of two types of magnetic bearings

下载: 全尺寸图片幻灯片

3.4 电磁力耦合分析

为分析新型异极径向混合磁轴承X、Y方向2个自由度间的电磁力耦合，对转子位移和控制电流对电磁力的影响进行仿真分析，并与图1（b）中的传统八极偏置磁轴承进行对比.

首先，定义转子处于坐标 $(x,y)$ 时，Y方向电磁力的相对误差为

$\delta (x,y) = \left| {\frac{{{f_Y}(x,y) - {f_Y}(0,y)}}{{{f_Y}(0,y)}}} \right| \times 100{\text{%}}$

(14)

式中： ${f_Y}(x,y)$ 为转子在坐标（x，y）时Y方向上的电磁力.

在X轴、Y轴绕组不通电情况下，X和Y方向转子不同位移对Y方向电磁力的影响和电磁力相对误差如图11所示. 由图11（a）可以看出，在x位移量的影响下，新型磁轴承转子在Y方向上受到的电磁力随Y轴位移量仍成正比，变化不明显，最大相对误差为2.76%. 而从图11（b）可以看出，传统偏置磁轴承转子在Y方向上受到的电磁力最大相对误差达到了3.87%.

图 11 转子偏心时的耦合特性

Figure 11. Coupling characteristics with eccentric rotor

下载: 全尺寸图片幻灯片

定义转子位置在（0，y）时，电磁力的相对误差为

$\kappa ({I_X},y) = \left| {\frac{{{f_Y}({I_X},y) - {f_Y}(0,y)}}{{{f_Y}(0,y)}}} \right| \times 100{\text{%}}$

(15)

式中： ${f_Y}({I_X},y)$ 和 ${f_Y}(0,y)$ 分别为转子在（0，y）处通入X方向电流I_X和不通电时Y方向的电磁力.

磁轴承x位移量和Y方向电流为0，通入X方向不同电流时，Y方向电磁力随y的关系曲线和电磁力相对误差如图12所示，由图12（a）可以看出，新型磁轴承Y方向的电磁力与Y轴位移量基本成正比关系，最大误差为3.52%，表明该新型磁轴承X方向电流对Y方向位移刚度影响较小；由图12（b）可以看出，传统偏置磁轴承X方向电流会增加转子在Y方向受的电磁力，其最大相对误差为7.6%.

图 12 转子不偏心时控制电流的耦合特性

Figure 12. Coupling characteristics of control current when rotor is not eccentric

下载: 全尺寸图片幻灯片

当转子在X方向偏心0.1 mm时，图13为磁轴承Y方向电磁力随Y轴位移量和X方向控制电流的关系和电磁力相对误差. 由图13（a）可以看出，在转子偏心条件下通入不同的X方向电流时，Y方向的电磁力仍然正比于Y轴位移量，相对误差最大值为6.5%，这表明转子在X方向发生偏移时，通入X方向电流对Y方向电磁力随Y方向位移的线性特性影响较小，有利于该新型磁悬浮轴承的控制系统设计. 由图13（b）可以看出，通入X方向电流对传统偏置磁轴承转子在Y方向上受的电磁力有较大的影响，最大相对误差为13.6%，其径向两自由度之间的运动存在一定耦合.

图 13 转子偏移0.1mm时控制电流的耦合特性

Figure 13. Coupling characteristics of control current when rotor offsets 0.1 mm

下载: 全尺寸图片幻灯片

综上可知，新型HRHMB在X方向的转子位移基本不影响Y方向的电磁力. 无论转子是否在X方向上发生偏移，X方向上的控制电流对Y方向上的电磁力基本没有影响. 其两自由度之间的电磁力耦合明显小于传统偏置磁轴承，这是由于该新型HRHMB永磁体排列组合方式使其永磁磁路与电磁磁路耦合距离短，且两磁场的相互影响效果较弱，有利于获得良好的解耦特性.

4. 结　论

对于飞轮储能系统等空间利用率要求较高的场合，本文提出了一种新型异极径向混合磁悬浮轴承，该磁轴承电磁磁路和永磁磁路耦合距离短，具有解耦性高的优点. 由等效磁路法建立了该新型轴承的磁路模型，通过解析和仿真研究得出以下结论：

1）由等效磁路法得到的新型HRHMB的承载力、位移刚度和电流刚度的理论结果，与有限元仿真结果相吻合，验证了解析结果的正确性.

2）在相同承载力、偏置磁通、转子尺寸等约束条件下，新型HRHMB结构更为紧凑，空间利用率较高，同时有着较大的电流刚度.

3）新型HRHMB在不同自由度的转子位移和控制电流变化影响下，电磁力相对误差最大值较传统偏置磁轴承小，表明该结构特殊的永磁体排列方式使得电磁磁路与永磁磁路间耦合小，径向二自由度之间电磁力解耦效果较好.

图 1 磁浮列车MPGA-ADRC控制框架

Figure 1. MPGA-ADRC frame of maglev train

下载: 全尺寸图片幻灯片

图 2 MPGA算法原理

Figure 2. Principle of MPGA

下载: 全尺寸图片幻灯片

图 3 适应度变化过程

Figure 3. Change process of fitness

下载: 全尺寸图片幻灯片

图 4 参数调整过程

Figure 4. Process of parameters’ adjustment

下载: 全尺寸图片幻灯片

图 5 基于MPGA-ADRC的磁浮列车速度控制结构

Figure 5. Speed control structure of maglev train based on MPGA-ADRC

下载: 全尺寸图片幻灯片

图 6 唐山线固定限速曲线及ATO跟踪曲线

Figure 6. Fixed speed limit curve and ATO tracking curve of Tangshan Line

下载: 全尺寸图片幻灯片

图 7 对唐山线的跟踪效果

Figure 7. Tracking effect of Tangshan Line

下载: 全尺寸图片幻灯片

图 8 速度跟踪误差

Figure 8. Speed tracking errors

下载: 全尺寸图片幻灯片

图 9 加速度误差

Figure 9. Acceleration errors

下载: 全尺寸图片幻灯片

图 10 ESO观测效果

Figure 10. Observation effect of ESO

下载: 全尺寸图片幻灯片

图 11 ESO观测误差

Figure 11. Observation errors of ESO

下载: 全尺寸图片幻灯片

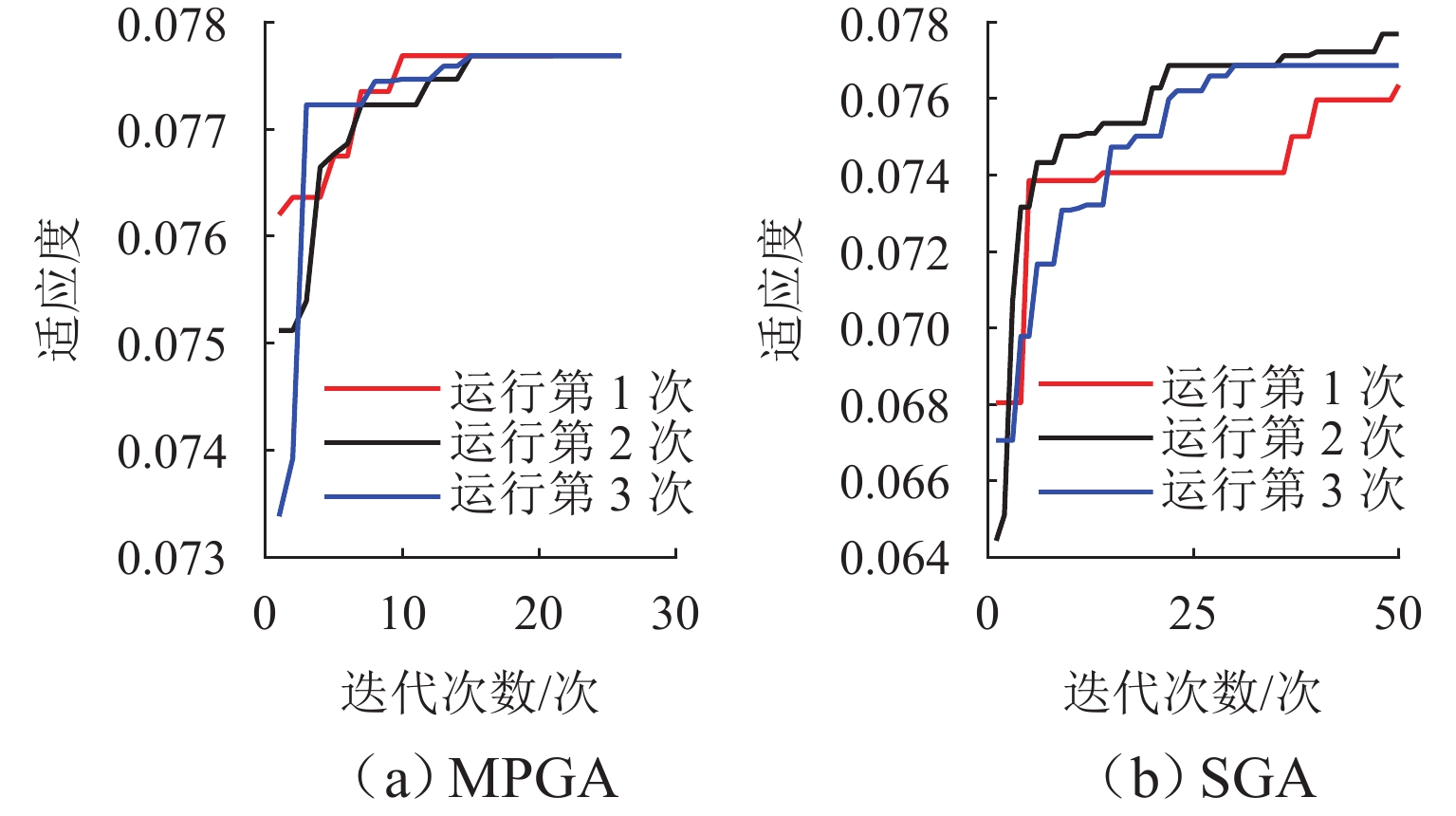
表 1 算法效果对比

Table 1. Comparison of algorithm effects

运行次数	MPGA		SGA
运行次数	迭代次数/次	最优值	迭代次数/次	最优值
第 1 次	27	0.0776	50	0.0769
第 2 次	25	0.0776	50	0.0776
第 3 次	21	0.0776	50	0.0764

下载: 导出CSV

表 2 MPGA-ADRC控制参数

Table 2. Control parameters of MPGA-ADRC

名称	控制参数
TD	$\delta = 0.9$ ， $h = 0.01$ ， ${h_0} = 0.011$
ESO	$\alpha = 0.5$ ， $\tau = 0.01$ ， ${\beta _1} = 1\;009.3$ ， ${\beta _2} = 1\;559.7$ ， ${\beta _3} = 4\;397.3$
NLSEF	${k_{\text{p}}} = 17.3$ ， ${k_{\text{d}}} = 14.8$

下载: 导出CSV

表 3 控制器性能比较

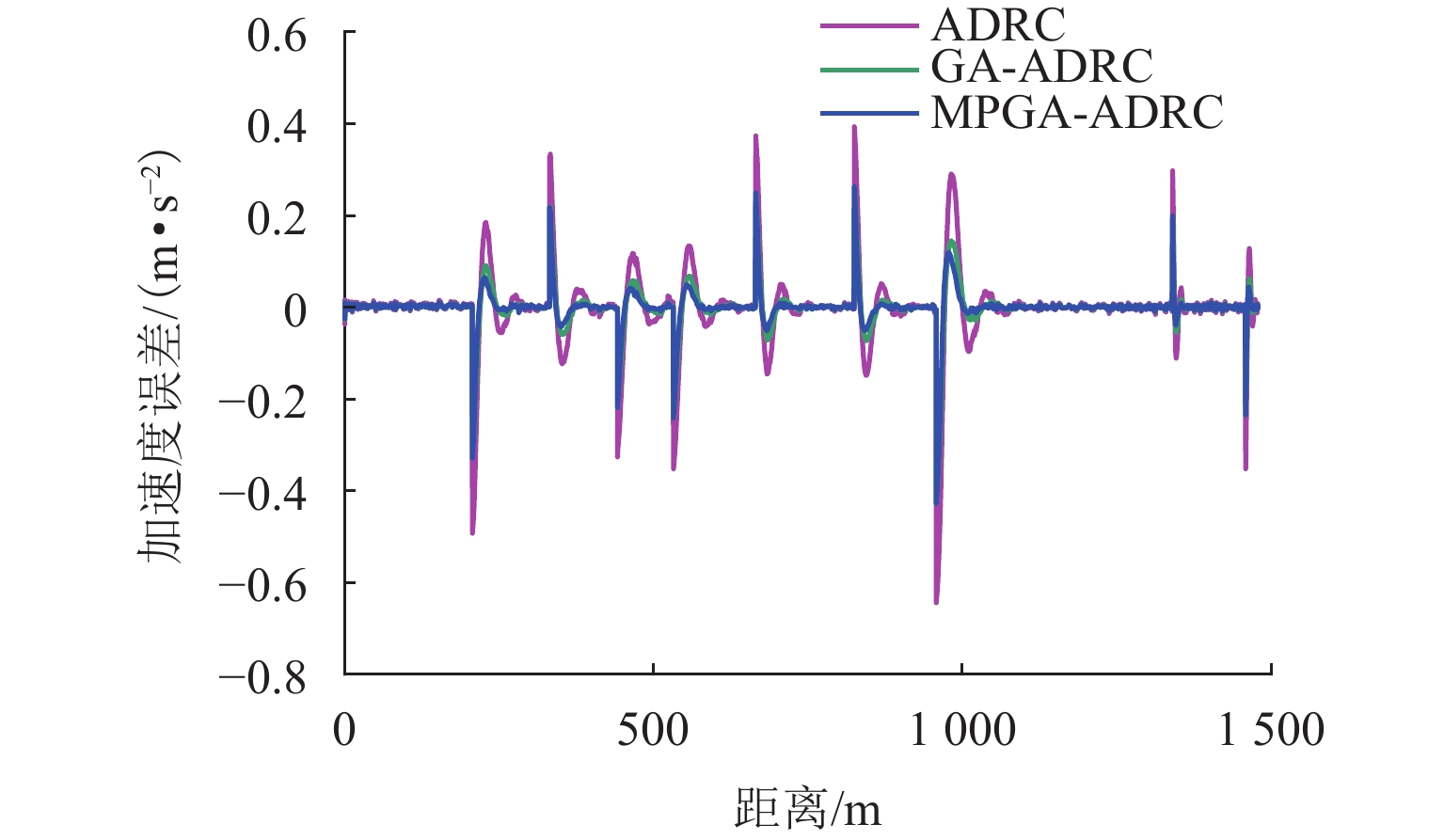
Table 3. Comparison of controllers performance

名称	最大速度误差（m·s⁻¹）	速度E_RMSE（m·s⁻¹）	加速度E_RMSE（m·s⁻²）
ADRC	0.4841	0.1468	0.1320
GA-ADRC	0.4211	0.1294	0.1135
MPGA-ADRC	0.3109	0.1135	0.0982

下载: 导出CSV

参考文献(20)

[1]	龙志强,窦峰山,王志强,等. 高速磁浮悬浮导向控制技术现状及展望[J]. 前瞻科技,2023,2(4): 78-88. LONG Zhiqiang, DOU Fengshan, WANG Zhiqiang, et al. Current status and prospect of high speed maglev levitation guidance control technology[J]. Science and Technology foresight, 2023, 2(4): 78-88.
[2]	邓自刚,刘宗鑫,李海涛,等. 磁悬浮列车发展现状与展望[J]. 西南交通大学学报,2022,57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001 DENG Zigang, LIU Zongxin, LI Haitao, et al. Development status and prospect of maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001
[3]	SUN Y G, QIANG H Y, WANG L, et al. A fuzzy-logic-system-based cooperative control for the multielectromagnets suspension system of maglev trains with experimental verification[J]. IEEE Transactions on Fuzzy Systems, 2023, 31(10): 3411-3422. doi: 10.1109/TFUZZ.2023.3257036
[4]	何之煜,徐宁. 非参数化迭代学习控制的列车自动驾驶控制算法[J]. 铁道学报,2020,42(12): 90-96. doi: 10.3969/j.issn.1001-8360.2020.12.012 HE Zhiyu, XU Ning. Research on automatic train operation algorithm based on non-parametric iterative learning control[J]. Journal of the China Railway Society, 2020, 42(12): 90-96. doi: 10.3969/j.issn.1001-8360.2020.12.012
[5]	王青元,吴鹏,冯晓云,等. 基于自适应终端滑模控制的城轨列车精确停车算法[J]. 铁道学报,2016,38(2): 56-63. doi: 10.3969/j.issn.1001-8360.2016.02.008 WANG Qingyuan, WU Peng, FENG Xiaoyun, et al. Precise automatic train stop control algorithm based on adaptive terminal sliding mode control[J]. Journal of the China Railway Society, 2016, 38(2): 56-63. doi: 10.3969/j.issn.1001-8360.2016.02.008
[6]	MAO Z H, YAN X G, JIANG B, et al. Adaptive fault-tolerant sliding-mode control for high-speed trains with actuator faults and uncertainties[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(6): 2449-2460. doi: 10.1109/TITS.2019.2918543
[7]	LIN X, DONG H R, YAO X M, et al. Neural adaptive fault-tolerant control for high-speed trains with input saturation and unknown disturbance[J]. Neurocomputing, 2017, 260: 32-42. doi: 10.1016/j.neucom.2017.02.083
[8]	JI H H, HOU Z S, ZHANG R K. Adaptive iterative learning control for high-speed trains with unknown speed delays and input saturations[J]. IEEE Transactions on Automation Science and Engineering, 2016, 13(1): 260-273. doi: 10.1109/TASE.2014.2371816
[9]	SUN Y G, HE Z Y, XU J Q, et al. Cooperative model predictive levitation control for two-points electromagnetic levitation system of high-speed maglev vehicle[J]. IEEE Transactions on Intelligent Vehicles, 2023, 99: 1-12.
[10]	龙志强,李云,王旭. 基于自抗扰控制的磁浮列车自动驾驶算法研究[C]//第27届中国控制会议. 昆明:北京航空航天大学出版社,2008: 681-685.
[11]	黄翠翠,李晓龙,杨洋,等. 基于自抗扰技术的机械电磁悬浮复合隔振控制[J]. 西南交通大学学报,2022,57(3): 582-587. doi: 10.3969/j.issn.0258-2724.20210850 HUANG Cuicui, LI Xiaolong, YANG Yang, et al. Mechanical-electromagnetic suspension compound vibration isolation control based on active disturbance rejection technology[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 582-587. doi: 10.3969/j.issn.0258-2724.20210850
[12]	王盼盼,杨杰,邹吉强,等. 基于改进自抗扰控制器的磁浮列车速度跟踪控制研究[J]. 铁道科学与工程学报,2023,20(1): 310-320. WANG Panpan, YANG Jie, ZOU Jiqiang, et al. Design maglev train speed tracking system based on improved active disturbance rejection controller[J]. Journal of Railway Science and Engineering, 2023, 20(1): 310-320.
[13]	LU Z X, CHEN C J. Research on decoupling control for module suspension system based on linear active disturbance rejection control[C]//2023 5th International Conference on Intelligent Control, Measurement and Signal Processing (ICMSP). Chengdu: IEEE, 2023: 260-265.
[14]	ZHANG B J, KE Z H, LI Z Y, et al. Yawing stability and manipulative approach design for maglev car based on active disturbance rejection control[J]. Asian Journal of Control, 2024, 26(2): 1003-1016. doi: 10.1002/asjc.3246
[15]	罗京,胡伟,刘豫湘. 中低速磁浮列车牵引特性分析和计算[J]. 电力机车与城轨车辆,2010,33(6): 21-22,26. doi: 10.3969/j.issn.1672-1187.2010.06.006 LUO Jing, HU Wei, LIU Yuxiang. Traction characteristic analysis and calculation of mid-low speed maglev trains[J]. Electric Locomotives & Mass Transit Vehicles, 2010, 33(6): 21-22,26. doi: 10.3969/j.issn.1672-1187.2010.06.006
[16]	杨光. 高速磁浮列车最优速度曲线及其跟踪控制研究[D]. 北京:北京交通大学,2007.
[17]	谢云德,龙志强. 高精度快速非线性离散跟踪微分器[J]. 控制理论与应用,2009,26(2): 127-132. XIE Yunde, LONG Zhiqiang. A high-speed nonlinear discrete tracking-differentiator with high precision[J]. Control Theory & Applications, 2009, 26(2): 127-132.
[18]	董聪,郭晓华. 广义遗传算法的逻辑结构及全局收敛性的证明[J]. 计算机科学,1998,25(5): 38-42. DONG Cong, GUO Xiaohua. Logical structure of generalized genetic algorithm and a proof of its global convergence. Computer Science, 1998, 25(5): 38-42.
[19]	SHI H F, WU S Y, KE Z H, et al. Speed-range-based novel guideway configuration with variable material and thickness for PMECB[J]. IEEE Transactions on Instrumentation and Measurement, 2024, 73: 2514913.
[20]	连文博,刘伯鸿,李婉婉,等. 基于自抗扰控制的高速列车自动驾驶速度控制[J]. 铁道学报,2020,42(1): 76-81. LIAN Wenbo, LIU\|Bohong, LI Wanwan, et al. Automatic operation speed control of high-speed train based on ADRC[J]. Journal of the China Railway Society, 2020, 42(1): 76-81.