Stochastic Vibration Analysis of Maglev Train-Bridge Coupling System Based on Pseudo Excitation Method
-
摘要:
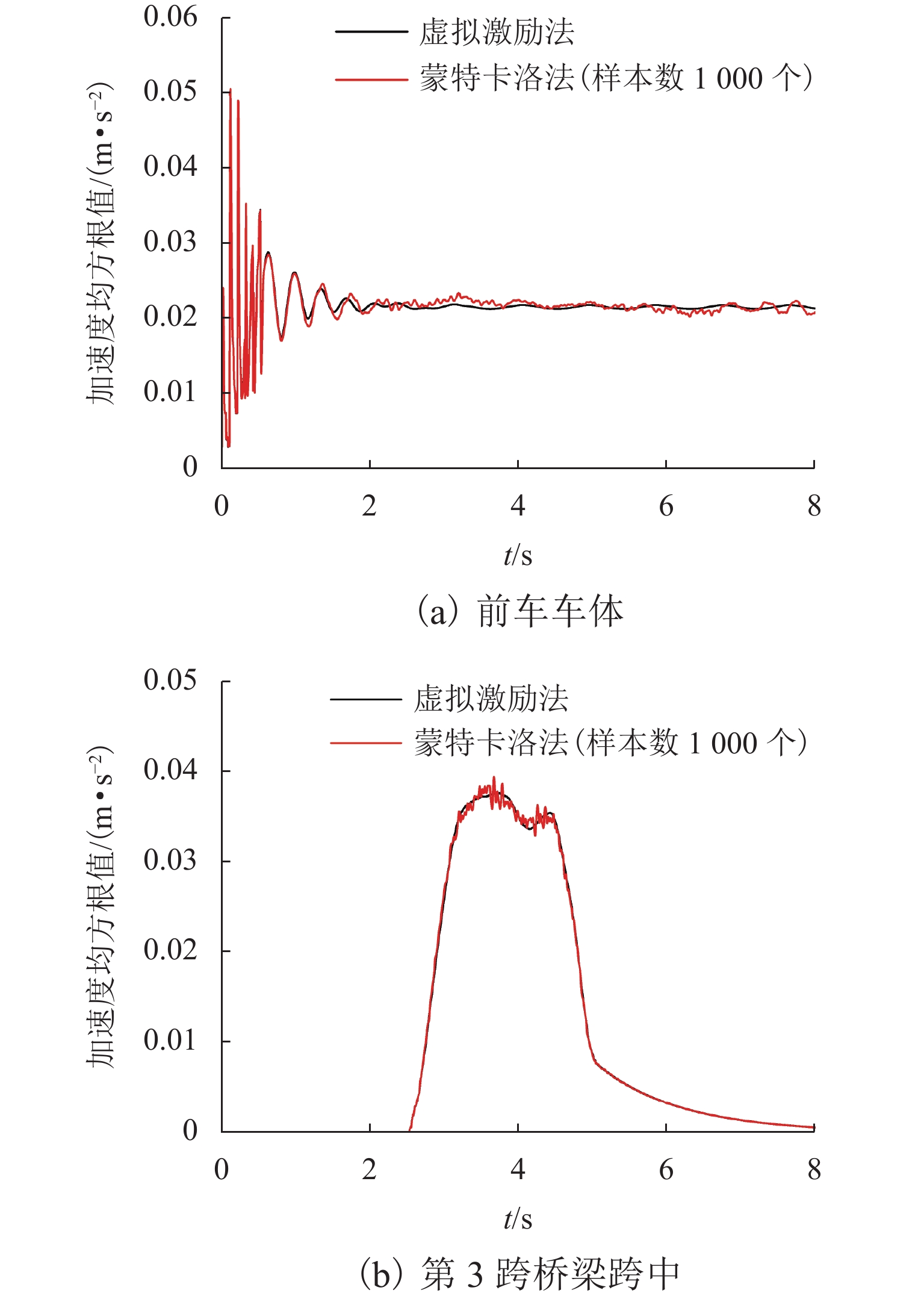
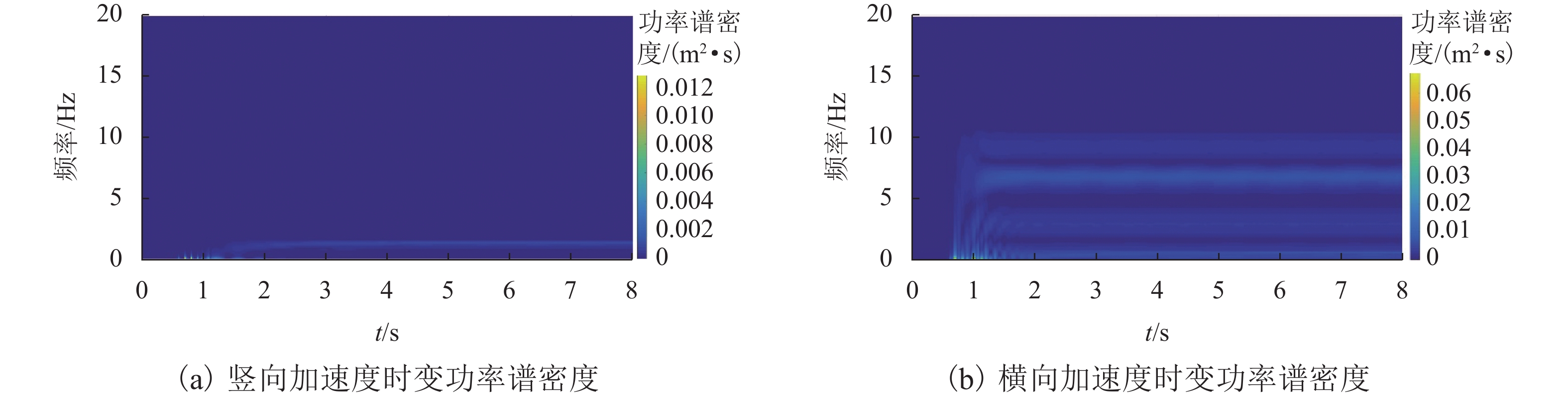
为探讨随机轨道不平顺作用下中低速磁浮列车和桥梁的动力响应，将虚拟激励法引入磁浮车桥振动分析中，提出中低速磁浮车辆-悬浮控制系统-桥梁耦合系统随机振动分析方法. 将中低速磁浮列车简化为弹簧阻尼器连接的多刚体，悬浮系统中电流使用比例-微分（PD）控制方法进行主动控制，采用有限元方法对桥梁进行建模，将随机轨道不平顺转换为一系列简谐波构成的虚拟激励；编制中低速磁浮车桥动力系统随机振动分析程序，自动生成系统随机振动方程，利用分离迭代方法对磁浮车辆控制方程和桥梁动力方程进行求解计算. 研究结果表明：虚拟激励法能够高效计算中低速磁浮车桥系统随机动力响应，其计算效率约为蒙特卡洛方法的1/11，基于虚拟激励法能够获得中低速磁浮车桥动力系统均值、标准差和时变功率谱密度等统计结果.
Abstract:To explore the dynamic responses of medium-low speed maglev trains and bridges under stochastic track irregularities, the pseudo excitation method was introduced into the vibration analysis of the maglev train-bridge system. A stochastic vibration analysis method for the medium-low speed maglev train, suspension control system, and bridge coupling system was proposed. The medium-low speed maglev train was simplified as rigid bodies connected by spring dampers, and the current in the suspension system was actively controlled using the proportional-differential (PD) control method. The bridge was modeled by using a finite element method, and the stochastic track irregularity was converted into a pseudo excitation composed of a series of simple harmonic waves. The stochastic vibration analysis program for the medium-low speed maglev train-bridge dynamic system was developed, which could automatically generate the stochastic vibration equations of the system, and the separation iteration method was used to solve the control equation of the maglev train and the dynamic equation of the bridge. The research results indicate that the pseudo excitation method can efficiently calculate the stochastic dynamic response of the medium-low speed maglev train-bridge system, with a calculation efficiency of about 1/11 of the Monte Carlo method. Based on the pseudo excitation method, statistical results such as mean, standard deviation, and time-varying power spectral density of the medium-low speed maglev train-bridge dynamic system can be obtained.
-
Key words:
- maglev train /
- train-bridge interaction /
- stochastic vibration /
- pseudo excitation method
-
桁架梁抗扭刚度大、透风性能好，具有运输方便、施工灵活等优点，在大跨度桥梁建设中得到了广泛应用. 与单层桁架梁相比，双层桁架梁在解决重载交通问题上更具优势，因此，双层桥面桁架梁已成为大跨度桁架梁桥新的设计趋势[1]. 目前已建成的双层桁架梁桥包括美国的华盛顿大桥、日本的濑户大桥以及我国的沪通长江大桥等. 随着桥梁跨径的不断增大，结构将变得更加轻柔，阻尼比更小，对风的作用愈加敏感. 以往研究表明[2-5]，桁架梁悬索桥的颤振性能在初步设计阶段通常难以满足要求，特别是当桥址处的设计风速较高时，钢桁梁的颤振稳定性已成为设计过程中的控制性因素.
目前，桁架梁桥通常利用附加气动措施来改善其颤振稳定性. 与调谐质量阻尼器等机械措施相比，气动措施可以从根本上抑制主梁振动. 常用于提高桁架梁桥颤振性能的气动措施包括：在主梁的不同位置安装稳定板、导流板或气动翼板；在桥面板的中央开槽或封槽；改变栏杆透风率、设置抗风缆等. 明石海峡大桥通过设置下中央稳定板和提高桥面板开槽率来改善大桥的颤振性能[2]；矮寨大桥通过封闭中央开槽并同时安装上、下中央稳定板来提高主梁的颤振临界风速[3]；清水河大桥采用了上中央稳定板使桥梁的颤振稳定性达到设计要求[4]；坝陵河大桥通过在下检修道安装双层气动翼板来改善桁架梁桥的颤振性能[5].
对于桁架梁桥颤振气动措施的研究，Ueda等[6]通过流迹显示和测压试验研究了竖向稳定板的制振机理发现，桁架梁的颤振是由于分离流的再附引起的，当安装竖向中央稳定板后减弱了气流的再附程度，进而抑制了主梁颤振. 陈政清等[7]从能量角度研究了中央稳定板对桁架梁悬索桥颤振稳定性的气动机理，发现中央稳定板能降低气动负阻尼，提高颤振发生时的扭弯耦合程度，从而降低颤振频率，提高桁架梁的颤振临界风速. 欧阳克俭等[8]通过数值模拟和流迹显示试验研究了中央稳定板绕流的细观作用机理，发现中央稳定板可使桥面中央区域形成上下旋涡对，进而增强桁架梁竖向自由度的参与程度. 李加武等[9]研究了抗风缆、中央稳定板、风嘴等措施对窄桁架悬索桥颤振稳定性的影响. Tang等[10]通过节段模型风洞试验和数值模拟研究了水平翼板、竖向稳定板以及改变栏杆透风率等措施对桁架梁颤振稳定性的影响，并考察了较大来流攻角条件下主梁的颤振性能. 李明等[11]研究了不同桥面板开槽率、通长或间隔设置中央稳定板对桁架梁桥颤振性能的影响，并对有效措施进行了组合，最后通过全桥气弹模型试验验证了气动措施的有效性.
以上对颤振的气动措施研究均针对传统单层板桁分离式桁架梁进行，目前关于双层桁架梁特别是板桁结合梁的颤振性能及气动措施研究较少[12-14]. 由于下层桥面的存在，双层桁架梁的气动特性比单层桥面桁架梁更为复杂. 现有单层桁架梁的有效气动措施不适用于双层桁架梁. 此外，由于板桁结合梁桥的桥面板和桁架上横梁之间不存在缝隙，这与传统的板桁分离式加劲梁的气动外形存在较大差别，使其气动性能不同于板桁分离式加劲梁. 因此，对双层板桁结合梁的颤振稳定性及制振措施研究具有重要意义.
本文以杨泗港长江大桥为研究背景，通过节段模型风洞试验，研究了双层板桁结合梁悬索桥的颤振稳定性. 同时对其颤振性能进行优化，考察了安装于上层桥面和下层桥面不同位置处的上、下稳定板和水平翼板的制振效果，并将有效的制振措施进行了组合. 在此基础上提出了最佳的颤振优化气动方案. 最后，研究了系统阻尼比对该双层板桁结合梁悬索桥颤振稳定性的影响.
1. 工程背景及桥位风参数
杨泗港长江大桥是一座单跨简支公路悬索桥，主跨为1 700 m，建成后将成为我国跨度最大、世界跨度第二大的悬索桥. 大桥位于武汉市区，为了满足日益增大的交通量，加劲梁设计采用双层板桁结合梁形式，上、下两层桥面均按双向六车道布置. 大桥的主桁宽度为28 m，高度为10 m，矢跨比为0.11，大桥主塔设计采用H型桥塔，其中汉阳侧桥塔高度为229.8 m，武昌侧桥塔高度为241.8 m，大桥总体布置如图1所示，主梁横截面如图2所示. 根据气象站提供资料确定桥位处的设计基本风速为25.6 m/s，由《公路桥梁抗风设计规范》[15]确定大桥的设计基准风速为33.2 m/s，成桥阶段的颤振检验风速为46.1 m/s.
图 1 杨泗港长江大桥总布置（单位：m）Figure 1. General layout of the Yangsigang Yangtze River Bridge (unit：m)2. 节段模型颤振试验
节段模型颤振试验在西南交通大学工业风洞第二试验段中进行，该试验段断面尺寸为2.4 m （宽） × 2.0 m （高），最大来流风速为45.0 m/s. 图3为安装在风洞中的节段模型. 为了保证该双层桁架梁节段模型包含完整的节间，节段模型的几何缩尺比设定为1∶52.67. 为加强桁架梁模型的整体刚度，节段模型的四根纵梁采用铝合金材料制作而成，并与两端的木质端板构成整体框架结构. 桁架梁的上、下桥面、竖杆、横梁以及栏杆等附属设施均采用工程塑料板整体雕刻而成，精确地模拟了主梁的气动外形. 节段模型的主要设计参数见表1.
表 1 节段模型主要试验参数Table 1. Main test parameters of section model参数名称 符号 缩尺比 实桥值 理论值 实际值 主桁高/m H 1∶52.67 10.00 0.19 0.19 主桁宽/m B 1∶52.67 28.000 0.532 0.532 单位长度质量/（kg•m−1） m 1∶52.672 53 027.00 19.13 19.14 单位长度质量惯矩/（kg•m） I 1∶52.674 7 465 823.000 0.970 0.979 一阶竖弯频率/Hz f1 0.117 1.695 一阶扭转频率/Hz f2 0.284 4.095 竖弯阻尼比/% ζ1 1 0.50 0.36 扭转阻尼比/% ζ2 1 0.50 0.37 扭弯频率比 ε 1 2.418 2.418 2.417 颤振试验在均匀流场中进行，主梁的扭转位移均方根值（σ）随风速（Ｕ）的变化曲线如图4所示. 图中：α为风攻角，由图4可知：主梁在0° 和 +3° 攻角下发生了没有明显发散点的“软颤振”，且颤振形态表现为单自由度扭转振动. 相比于经典硬颤振，软颤振没有明显的临界发散点，颤振振幅随着平均风速的增加而逐渐变大，不会像硬颤振那样直接发散[16-18]. 在41.8 m/s的实桥风速下，令节段模型静止然后释放，模型的振幅（θ）随着时间（t）的变化如图5（a）所示，扭转位移与扭转角速度的相位图如图5（b）所示. 由图5（a）可知： 节段模型的振幅随着时间增加开始逐渐变大，最后节段模型会以一个平稳的振幅持续振动. 文献[15]规定，对于无明显发散点的颤振，可以取扭转位移均方根值为0.5° 时对应的风速作为颤振临界风速. 根据该标准，该双层桁架梁在0° 和 +3° 攻角下的颤振临界风速值分别为50.5 m/s和31.2 m/s. 由此可知：+3° 攻角下该主梁的颤振临界风速小于桥梁的颤振检验风速值.
图 4 主梁的扭转位移均方根值随风速变化曲线Figure 4. Variation of the standard deviation of torsional displacements of main girder with the wind speed
图 5 +3° 攻角下主梁软颤振位移时程与相位图Figure 5. Time history and phase diagram of soft flutter displacements of main girder at an attack angle of +3°朱乐东等[19]认为软颤振是由于自激力的非线性特性引起的，软颤振可以采取类似于涡激共振的设计方法，不需要完全杜绝其发生，只要将稳定的振幅限制在一定范围内即可. 对于杨泗港长江大桥而言，+3° 攻角下大桥在来流风速为22.0 m/s左右便开始持续振动，并随着风速的提高，振幅逐渐增大. 虽然这种振动不会像经典颤振那样直接导致结构破坏，但是大桥发生软颤振的起振风速较低，发生的可能性较大. 为了确保大桥的抗风安全性，需要针对该双层桁架梁开展颤振性能优化研究，提高其颤振稳定性.
3. 颤振性能优化研究
以往研究表明[2-5,10-14]，设置稳定板、水平翼板等措施可以提高桁架梁桥的颤振稳定性. 针对最不利 +3° 攻角，通过在双层桁架梁的上、下桥面不同位置处安装上中央稳定板、下稳定板和水平翼板来优化主梁的颤振稳定性，从而寻求经济合理的颤振性能气动优化方案. 为了方便比较不同气动措施的抑振效果，定义颤振临界风速增长率为
β=(Ucr−U∗cr)/(Ucr−U∗cr)U∗crU∗cr×100%， (1) 式中：Ucr为设置气动措施后的颤振临界风速；
$ U_{{\text{cr}}}^* $ 为原方案 +3° 攻角下的颤振临界风速，即31.2 m/s.3.1 单一抑振措施
上中央稳定板是一种能有效提高主梁颤振临界风速的抑振措施，在单层桁架梁悬索桥上应用广泛[2-4,11]. 由于杨泗港长江大桥为双层桁架梁桥，在上、下层桥面分别设置上中央稳定板可能会产生不同的抑振效果，因此，对不同高度的上中央稳定板分别安装于上层桥面（工况1 ~ 5）和下层桥面（工况6 ~ 10）的情况进行了研究，如图6所示.
上中央稳定板对主梁颤振性能的影响如图7所示. 图中：h为上中央稳定板高度. 当上中央稳定板安装于下层桥面时，颤振临界风速增长率为负值，说明该方案会恶化主梁的颤振性能. 对于安装于上层桥面的上中央稳定板，当其高度小于2.10 m时，颤振临界风速增长率均小于5%，无法明显改善主梁的颤振稳定性；当其高度达到2.37 m后才有明显的制振效果，且随着上中央稳定板高度的增加，颤振临界风速增长率大幅增大，当上中央稳定板的高度达到2.63 m时，颤振临界风速提高了37%. 结合Ueda等[6]研究结果可知：对于桁架梁发生的单自由度扭转颤振，其主要是由桁架梁迎风侧边缘处分离的来流在桥面板上发生再附，且与主梁扭转运动具有一定的相位差引起的. 因此可以推断，当安装于上桥面板的上中央稳定板足够高时，可以在一定程度上有效减弱来流的再附，从而起到抑制桁架梁扭转颤振的作用. 然而，当其高度较小时，不能有效阻止来流再附，进而不能明显改善主梁的颤振稳定性.
图 7 上中央稳定板对主梁颤振性能的影响Figure 7. Effect of the upper central stabilizer on the flutter performance of the main truss girder为了研究下稳定板对主梁颤振性能的影响，分别在上、下层桥面不同位置安装与横梁等高度的下稳定板. 如图8所示，安装方式分为两种：设置单片下中央稳定板，如工况11、14；在主梁两侧对称设置双下稳定板，其中工况12、15分别为在上、下层桥面板1/3处安装双下稳定板，工况13、16分别为在上、下层桥面板1/4处安装双下稳定板，工况17为在下层桥面检修车轨道处安装双下稳定板.
下稳定板对主梁颤振性能的影响如图9所示. 由图可知：安装于上层桥面的下稳定板不能有效提高主梁的颤振临界风速，而安装于下层桥面的下稳定板有较为明显的抑振效果，其中在梁宽1/4处和检修车轨道处安装双下稳定板的制振效果最好，颤振临界风速增长率大于22%. 结合以上分析可以推断：该双层板桁结合加劲梁的扭转颤振主要是由于上层桥面上表面和下层桥面下表面的来流再附引起的. 因此，对于安装于上层桥面的下稳定板不能起到有效抑制主梁颤振的作用；对于安装于下层桥面的下稳定板，则能在不同程度上减弱主梁下层桥面下表面来流的再附，进而有效提高该桁架梁的颤振临界风速.
图 9 下稳定板对主梁颤振性能的影响Figure 9. Effect of the lower stabilizers on the flutter performance of the main truss girder为了研究水平翼板对主梁颤振稳定性的影响，分别在桁架梁两侧不同位置对称布置1.58 m宽的水平翼板进行试验，如图10所示. 工况18 ~ 21分别为在上层托架、下层托架、人行道底边和人行道栏杆顶部安装水平翼板，结果如图11. 由图可知：水平翼板的位置对主梁的颤振性能具有显著影响，布置于上层托架的水平翼板并不能有效改善主梁的颤振性能，而布置在下层托架处甚至会降低主梁的颤振临界风速. 在与上层桥面人行道底边齐平和人行道栏杆顶部的位置处安装水平翼板会使颤振临界风速增长率大于25%，主梁颤振稳定性得到明显改善. 从空气动力学角度分析，安装在人行道底部的水平翼板可以使该方向的来流提前发生分离，从而减弱来流在上桥面板上表面的再附，进而改善桁架梁的颤振稳定性.
图 11 水平翼板对主梁颤振性能的影响Figure 11. Effect of the horizontal flap on the flutter performance of the main truss girder3.2 组合抑振措施
由单一抑振措施优化试验结果可知：在上层桥面安装上中央稳定板、在下层桥面安装下稳定板以及在与人行道底边齐平的位置处安装水平翼板，均能起到改善主梁颤振性能的作用. 然而要达到较好的抑振效果，需要以上气动措施具有较大尺寸，这会在一定程度上对结构设计、施工及美观性等方面产生不利影响. 根据以往研究[10-11,20]，在联合使用不同的有效抑振措施后，其制振效果要明显优于单一措施. 为了减小气动措施带来的不利影响，并进一步提高主梁的颤振稳定性，工况22 ~ 25将1.1 m宽的水平翼板安装于与人行道底边齐平处，并与下层桥面的下稳定板进行组合，如图12所示. 图中：下稳定板高度与横梁等高，分别位于主梁中央、1/3处、1/4处和检修车轨道处. 图13为水平翼板与下稳定板组合对主梁颤振稳定性的影响，由图可知：水平翼板与下稳定板组合后可以取得更为明显的抑振效果，能大幅改善主梁的颤振稳定性，当下稳定板安装于主梁1/4处和检修车轨道处时，颤振临界风速增长率高于34%.
图 13 水平翼板与下稳定板组合对主梁颤振稳定性的影响Figure 13. Effect of the combination of the horizontal flap and the lower stabilizer on the flutter performance of main girder为了进一步降低气动措施的不利影响，在综合结构设计和气动方案的抑振效率后，拟在工况25基础上对主梁气动外形进行优化. 首先，工况26将人行道板和上层托架进行加宽，使水平翼板作为人行道板的一部分，其中，上层托架增宽至2.71 m，改变人行道板的结构，宽度由2.19 m增宽至3.61 m. 在工况26基础上，工况27将下稳定板布置在两侧检修车轨道的上方，与检修车轨道连接成整体，从而将检修车轨道视为下稳定板的一部分，这种方式相当于增加了下稳定板的高度，优化后的主梁横截面如图14所示.
对优化后的主梁进行颤振试验，发现 −3° 和0° 攻角下的颤振临界风速均高于颤振检验风速. 其中工况26主梁在 +3° 攻角下颤振临界风速为36.3 m/s，相比原断面提高了16.4%. 工况27在检修车轨道上方设置双下稳定板，主梁颤振临界风速相比原断面提高了43.3%，达到了44.7 m/s，接近颤振检验风速值，因此，确定工况27为该双层桁架梁的最优颤振性能气动优化方案.
3.3 阻尼比的影响
目前，还没有一种被广泛接受的准确估算桥梁结构阻尼比的方法，根据《公路桥梁抗风设计规范》[15]，钢桁架主梁扭转阻尼比建议取为0.50%. 由于以上试验均是在小阻尼比条件下进行的，实际大桥的扭转阻尼比有可能高于这一水平. 为了考察阻尼比对该双层桁架梁颤振性能的影响，将节段模型扭转阻尼比增加至0.52%，该值与规范所建议的阻尼值接近. 增加阻尼比后，主梁原断面与优化断面（工况26、27）的颤振临界风速见图15. 图中：ξ为扭转阻尼比. 为了方便比较，图中还给出了小阻尼比下主梁的颤振临界风速值. 由图15可知：单自由度的扭转颤振响应对系统阻尼十分敏感，系统扭转阻尼比由0.37%增加至0.52%后，主梁的颤振临界风速可提高11.9%；当扭转阻尼比为0.52%时，工况27对应的最优主梁断面的颤振临界风速为48.6 m/s，高于颤振检验风速值.
图 15 系统扭转阻尼比对主梁颤振临界风速的影响Figure 15. Effect of system torsional damping ratio on the critical flutter wind speed of the main girder需要说明，该双层桁架梁悬索桥发生的是软颤振，其振幅在一定风速范围内不会急剧增大. 因此可以采取类似于涡激振动的设计方法，将其振幅限制在一定范围内即可[19]. 对于工况27对应的最优主梁断面，在两种阻尼比条件下其扭转位移均方根值随风速变化如图16所示. 由图可知：当扭转阻尼比为0.52%时，在颤振检验风速下主梁扭转振幅均方根值为0.29°. 即使当扭转阻尼比为0.37%，在颤振检验风速下主梁扭转振幅均方根值为1.1°，这对于跨度1 700 m的大桥而言该扭转位移较小，不会对桥梁安全构成威胁. 因此，本文提出的颤振优化方案可以满足该大桥的颤振稳定性要求.
图 16 不同阻尼比条件下最优气动方案主梁的扭转位移响应Figure 16. Torsional response of the optimal truss girder in different damping ratio conditions4. 结 论
本文通过节段模型风洞试验对双层桁架梁悬索桥的颤振稳定性进行了优化研究，并得出以下结论：
1） 双层桁架梁在0° 、 +3° 攻角下发生了无明显发散点的软颤振，振动形态以单自由度扭转振动为主；+3° 攻角发生软颤振的起振风速为22.0 m/s，颤振临界风速值为31.2 m/s. 由于起振风速低，大桥有发生持续振动的风险，因此，需要对该双层桁架梁进行气动优化，以提高其颤振稳定性.
2） 在上层桥面安装上中央稳定板、下层桥面安装下稳定板以及在上层桥面人行道底边齐平处安装水平翼板均能不同程度地提高主梁颤振临界风速. 当把水平翼板与下层桥面的下稳定板组合后，主梁的颤振稳定性得到显著改善，颤振临界风速增长率高达34%.
3） 通过一系列气动优化研究，最优气动方案确定为将上层托架和人行道板加宽，使下稳定板与检修车轨道相结合. 该方案将气动措施与结构本身巧妙融合，既起到提升大桥颤振稳定性的作用，又减小了传统措施带来的不利影响，可为同类桥梁的颤振设计提供参考.
4） 增加扭转阻尼比能有效减小主梁软颤振的振动振幅. 对于本文研究的双层桁架梁，当系统阻尼比由0.37%增加至0.52%后，主梁的颤振临界风速可提高11.9%. 可以推断，对于以单自由度扭转软颤振为特征的桥梁，安装阻尼器可以有效控制主梁振动振幅.
-
图 2 简支梁桥的截面图（单位：cm）
Figure 2. Cross-section of simply supported gride bridge （unit: cm）
图 3 磁浮车辆和桥梁竖向加速度均方根值
Figure 3. Root mean squares of vertical accelerations of maglev train and bridge
图 5 磁浮车桥系统动力响应的上、下限值
Figure 5. Upper and lower limits of dynamic responses of maglev train-bridge system
图 6 前车车体竖向、横向加速度时变功率谱密度
Figure 6. Time-varying power spectral density for vertical acceleration and lateral acceleration of leading train
图 7 第3跨桥梁跨中竖向、横向加速度时变功率谱密度函数
Figure 7. Time-varying power spectral density for midspan vertical acceleration and midspan lateral acceleration of three-span bridge
表 1 磁浮车辆主要参数
Table 1. Main parameters of maglev train
参数 取值 车体质量/kg 20 000 悬浮模块质量/kg 1 000 车体绕 x 轴转动惯量/（kg·m2） 66 800 车体绕 y 轴转动惯量/ （kg·m2） 210 000 车体绕 z 轴转动惯量/（kg·m2） 193 000 悬浮模块绕 x 轴转动惯量/（kg·m2） 1 030 悬浮模块绕 y 轴转动惯量/（kg·m2） 1 800 悬浮模块绕 z 轴转动惯量/（kg·m2） 2 680 二系悬挂弹簧纵向刚度/（N·m−1） 900 000 二系悬挂弹簧竖向刚度/（N·m−1） 80 000 二系悬挂弹簧横向刚度/（N·m−1） 80 000 二系悬挂弹簧纵向阻尼/（N·s·m−1） 50 000 二系悬挂弹簧竖向阻尼/（N·s·m−1） 2 000 二系悬挂弹簧横向阻尼/（N·s·m−1） 4 000 线圈匝数/匝 96 磁导率/（× 10−6 H·m−1） 1.26 铁芯极面积/m2 0.383 额定气隙/mm 8 车体长度/m 16 
下载: 导出CSV
-
[1] 罗英昆,赵春发,梁鑫,等. 小半径竖曲线上磁浮车辆空气弹簧动态响应分析[J]. 振动与冲击,2020,39(17): 99-105.LUO Yingkun, ZHAO Chunfa, LIANG Xin, et al. Dynamic responses of air-spring suspension of a maglev vehicle negotiating a small-radius vertical curved track[J]. Journal of Vibration and Shock, 2020, 39(17): 99-105. [2] LIU W, GUO W H. Vibration analysis of EMS-type maglev vehicles traveling over a long-span bridge with double lines[J]. KSCE Journal of Civil Engineering, 2020, 24(5): 1531-1544. doi: 10.1007/s12205-020-0816-5 [3] 付善强,梁鑫,丁叁叁. 高速磁浮车-轨耦合系统动态机理与振动响应[J]. 同济大学学报(自然科学版),2023,51(3): 314-320,384.FU Shanqiang, LIANG Xin, DING Sansan. Dynamic mechanism and vibration response of high-speed maglev vehicleguideway coupling system[J]. Journal of Tongji University (Natural Science), 2023, 51(3): 314-320,384. [4] 李小珍,王渝文,胡启凯,等. 不同桥跨对中低速磁浮列车-简支梁系统竖向耦合振动影响机理研究[J]. 振动与冲击,2022,41(19): 8-15.LI Xiaozhen, WANG Yuwen, HU Qikai, et al. Influence mechanisms of different bridge spans on vertical coupled vibration of low and medium speed maglev train-simply supported beam system[J]. Journal of Vibration and Shock, 2022, 41(19): 8-15. [5] ZHAO C F, ZHAI W M. Maglev vehicle/guideway vertical random response and ride quality[J]. Vehicle System Dynamics, 2002, 38(3): 185-210. doi: 10.1076/vesd.38.3.185.8289 [6] 时瑾,魏庆朝. 线路不平顺对高速磁浮铁路动力响应特性的影响[J]. 工程力学,2006,23(1): 154-159,86. doi: 10.3969/j.issn.1000-4750.2006.01.028SHI Jin, WEI Qingchao. The effect of guideway irregularity on the dynamic characteristics of high-speed maglev railway[J]. Engineering Mechanics, 2006, 23(1): 154-159,86. doi: 10.3969/j.issn.1000-4750.2006.01.028 [7] 时瑾,魏庆朝,冯雅薇. 高速磁浮车桥系统随机振动特性仿真研究[J]. 系统仿真学报,2005,17(7): 1577-1579.SHI Jin, WEI Qingchao, FENG Yawei. Analysis of random vibration responses characteristics of maglev and elevated-beam guideway[J]. Journal of System Simulation, 2005, 17(7): 1577-1579. [8] MIN D J, JUNG M R, KIM M Y, et al. Dynamic interaction analysis of maglev-guideway system based on a 3D full vehicle model[J]. International Journal of Structural Stability and Dynamics, 2017, 17(1): 1750006.1-1750006.39. [9] TALUKDAR R P, TALUKDAR S. Dynamic analysis of high-speed MAGLEV vehicle–guideway system: an approach in block diagram environment[J]. Urban Rail Transit, 2016, 2: 71-84. doi: 10.1007/s40864-016-0039-8 [10] HAN J B, HAN H S, KIM S S, et al. Design and validation of a slender guideway for maglev vehicle by simulation and experiment[J]. Vehicle System Dynamics, 2016, 54(3): 370-385. doi: 10.1080/00423114.2015.1137957 [11] 张鹏. 磁浮列车-轨道-桥梁耦合系统随机振动分析[D]. 长沙:中南大学,2022. [12] 余志武,张鹏,丁叁叁,等. 基于概率密度演化理论的磁浮列车-轨道梁耦合系统随机动力分析[J]. 中南大学学报(自然科学版),2022,53(7): 2544-2554.YU Zhiwu, ZHANG Peng, DING Sansan, et al. Stochastic vibration analysis of maglev vehicle-guideway coupling system based on PDEM[J]. Journal of Central South University (Science and Technology), 2022, 53(7): 2544-2554. [13] 陆周瑞,陈冉,苏成. 磁浮车辆-桥梁耦合系统随机振动分析的时域显式方法研究[J]. 工程力学,2022,39(8): 19-30. doi: 10.6052/j.issn.1000-4750.2021.04.0321LU Zhourui, CHEN Ran, SU Cheng. Random vibration analysis of maglev vehicle-bridge coupled systems with the explicit time-domain method[J]. Engineering Mechanics, 2022, 39(8): 19-30. doi: 10.6052/j.issn.1000-4750.2021.04.0321 [14] 周劲松,李大光,沈钢,等. 磁浮车辆运行平稳性的虚拟激励分析方法[J]. 交通运输工程学报,2008,8(1): 5-9.ZHOU Jinsong, LI Daguang, SHEN Gang, et al. Pseudo-excitation analysis method of riding quality for maglev vehicle[J]. Journal of Traffic and Transportation Engineering, 2008, 8(1): 5-9. [15] SU X J, YANG X Z, SHI P, et al. Fuzzy control of nonlinear electromagnetic suspension systems[J]. Mechatronics, 2014, 24(4): 328-335. doi: 10.1016/j.mechatronics.2013.08.002 [16] KONG E, SONG J S, KANG B B, et al. Dynamic response and robust control of coupled maglev vehicle and guideway system[J]. Journal of Sound and Vibration, 2011, 330(25): 6237-6253. doi: 10.1016/j.jsv.2011.05.031 [17] 赵春发. 磁悬浮车辆系统动力学研究[D]. 成都:西南交通大学,2002. [18] FENG Y, ZHAO C F, ZHOU W, et al. Maglev vehicle-switch girder coupled vibration characteristics analysis based on distributed co-simulation[J]. Vehicle System Dynamics, 2023, 61(5): 1345-1366. doi: 10.1080/00423114.2022.2074470 [19] 曾庆元,杨平. 形成矩阵的“对号入座” 法则与桁梁空间分析的桁段有限元法[J]. 铁道学报,1986,8(2): 48-59.ZENG Qingyuan, YANG Ping. The “set-in-right-position” rule for forming structural matrices and the finite truss-element method for space analysis of truss bridges[J]. Journal of the China Railway Society, 1986, 8(2): 48-59. [20] 胡帛茹. 两种中低速EMS磁浮车辆动力学性能的对比分析[D]. 成都:西南交通大学,2021. [21] FRÝBA L. Dynamics of railway bridges[M]. London: Thomas Telford Publishing, 1996. [22] YANG Y B, YAO Z D, WU Y S. Vehicle-bridge interaction dynamics: with applications to high-speed railways[M]. Singapore: World Scientific, 2004. [23] 林家浩. 随机地震响应的确定性算法[J]. 地震工程与工程振动,1985,5(1): 89-94.LIN Jiahao. A deterministic method for the computation of stochastic earthquake response[J]. Earthquake Engineering and Engineering Vibration, 1985, 5(1): 89-94. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 381
- HTML全文浏览量: 127
- PDF下载量: 73
- 被引次数: 0