Characteristics Analysis of Lithium Metal Batteries with Ultra-High Energy Density under Pressure Conditions
-
摘要:
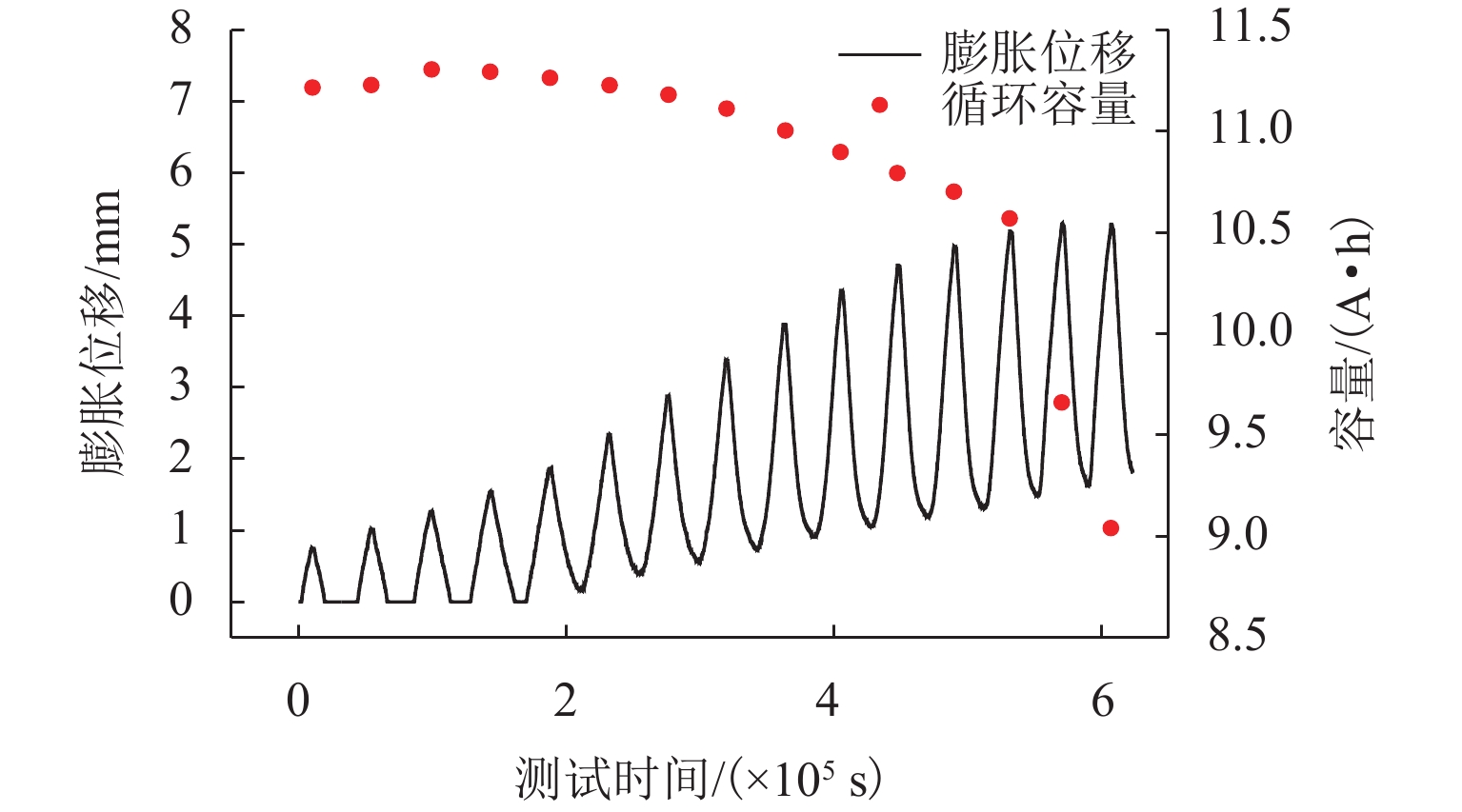
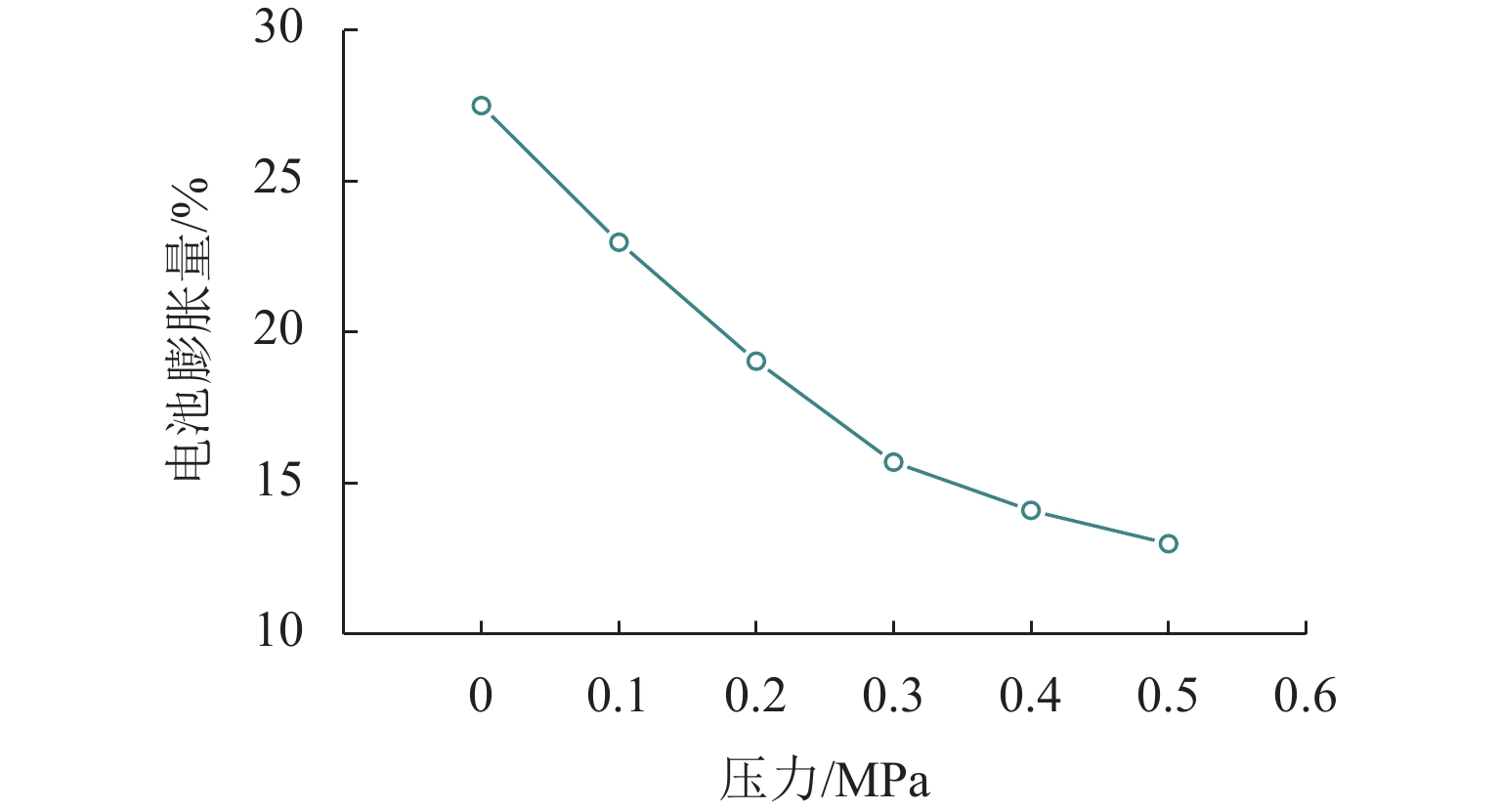
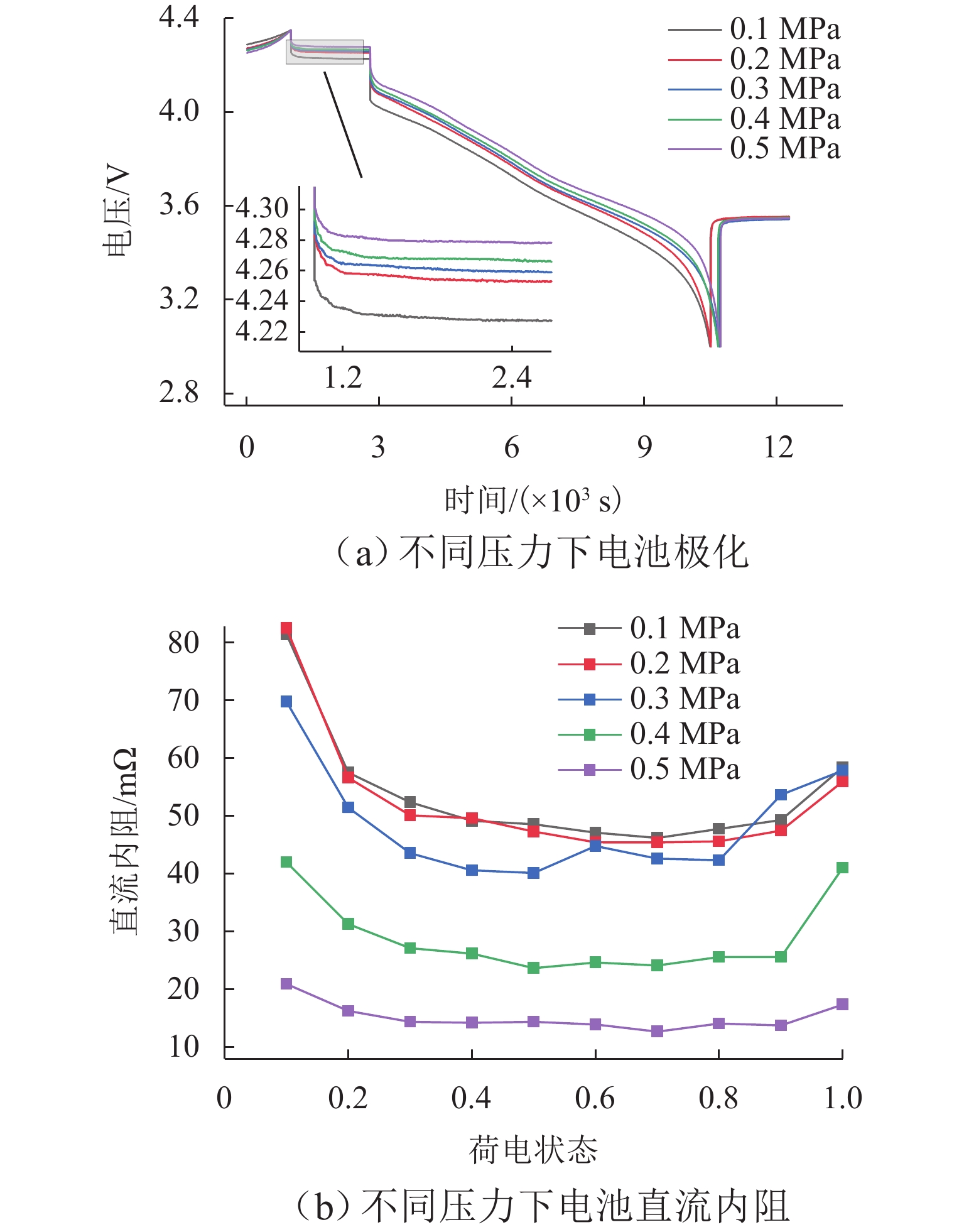
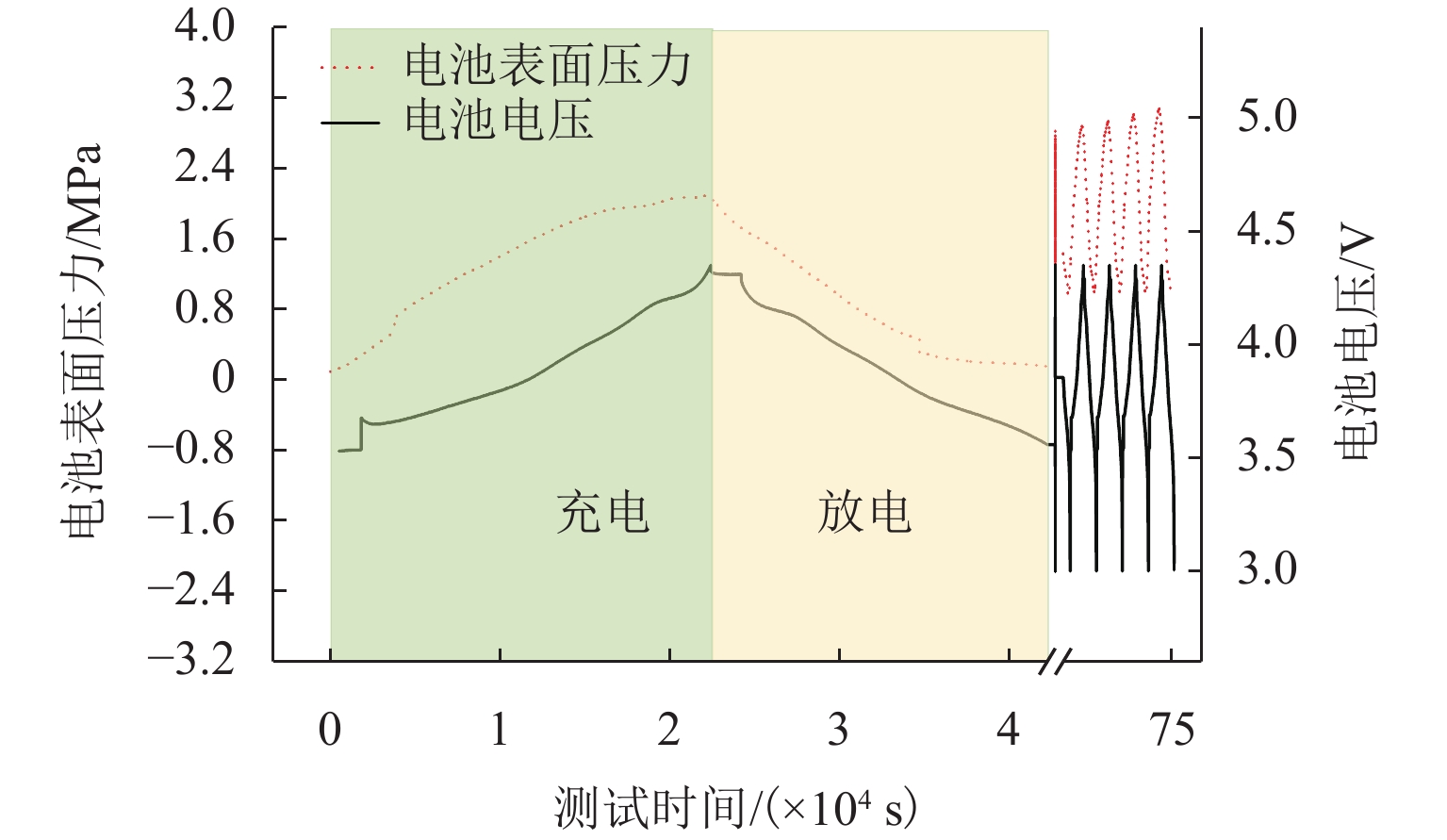
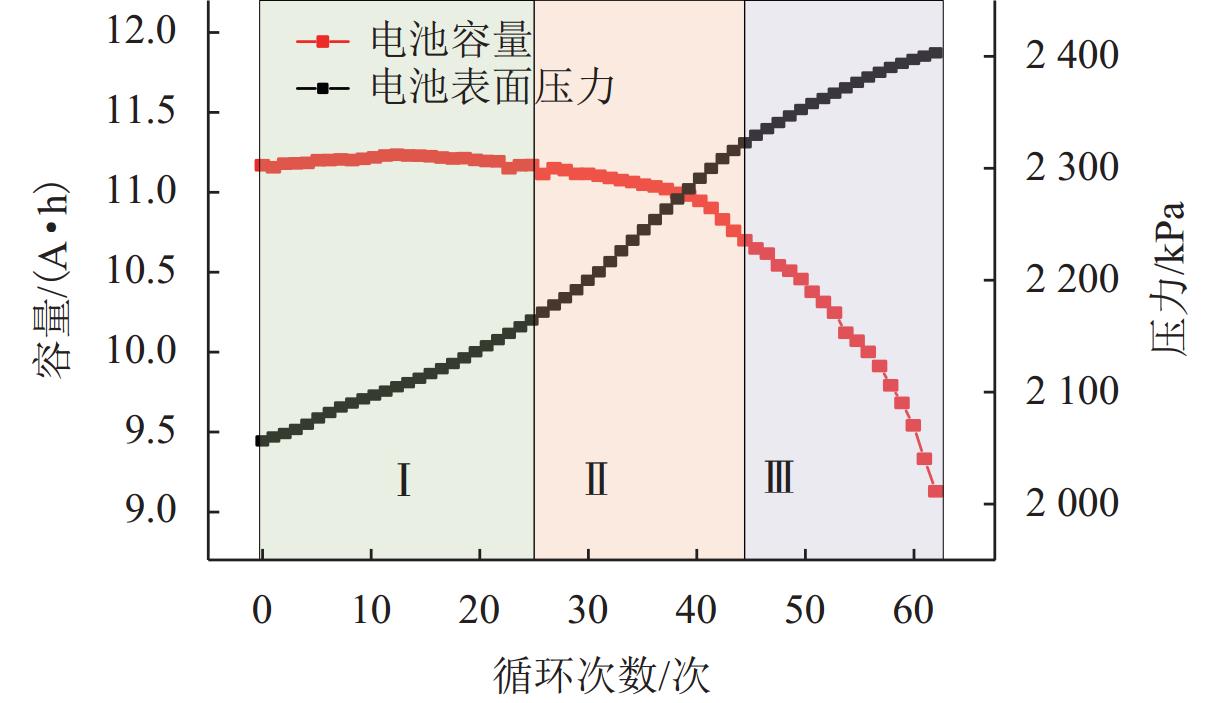
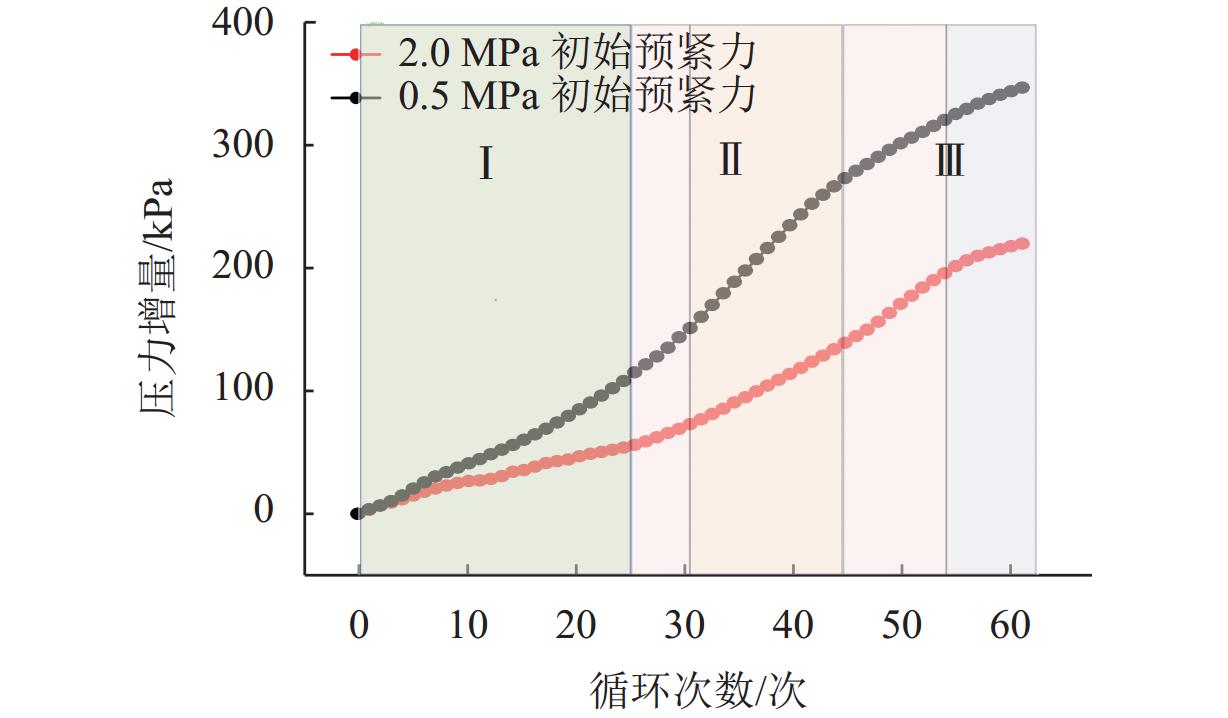
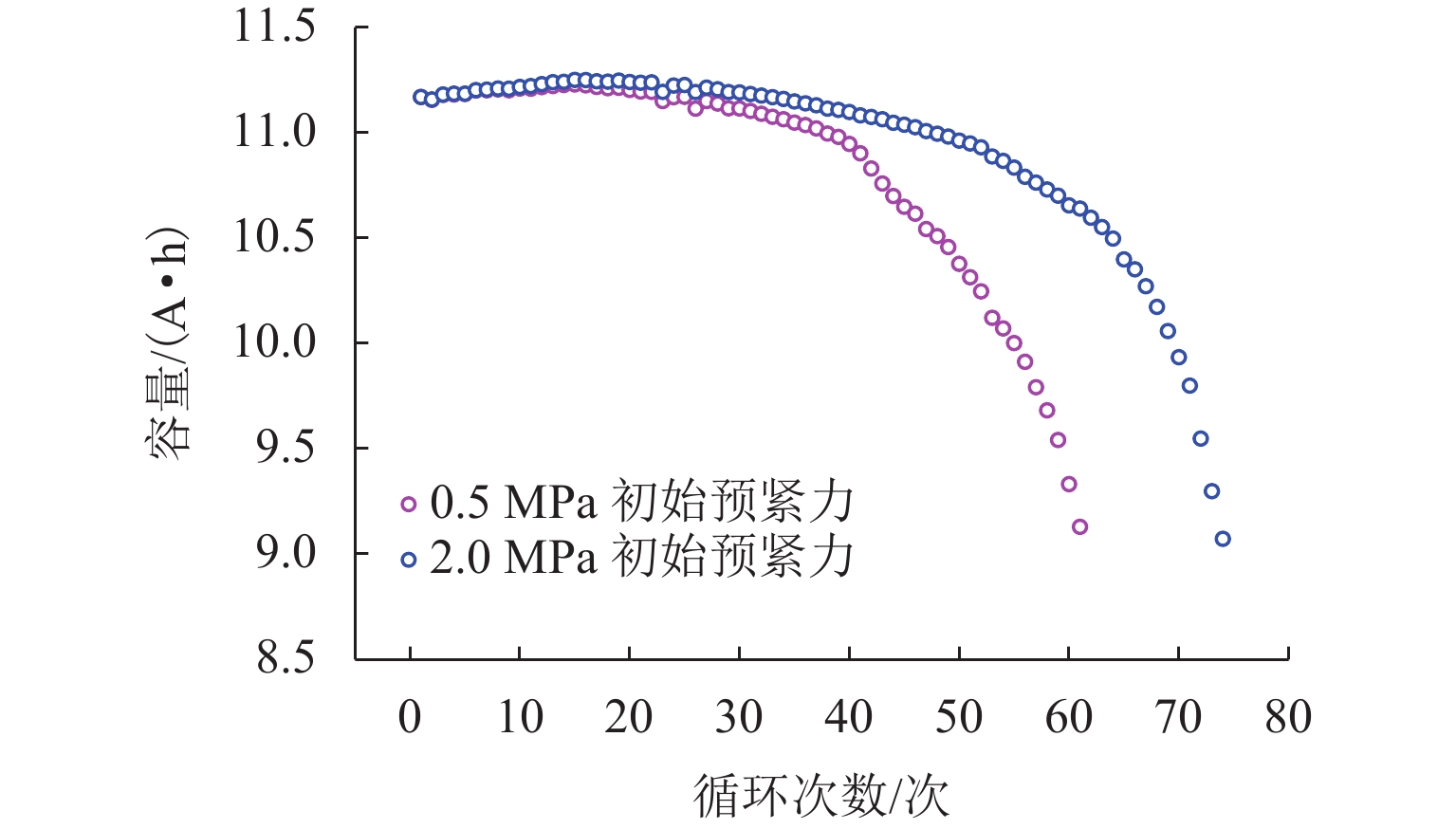
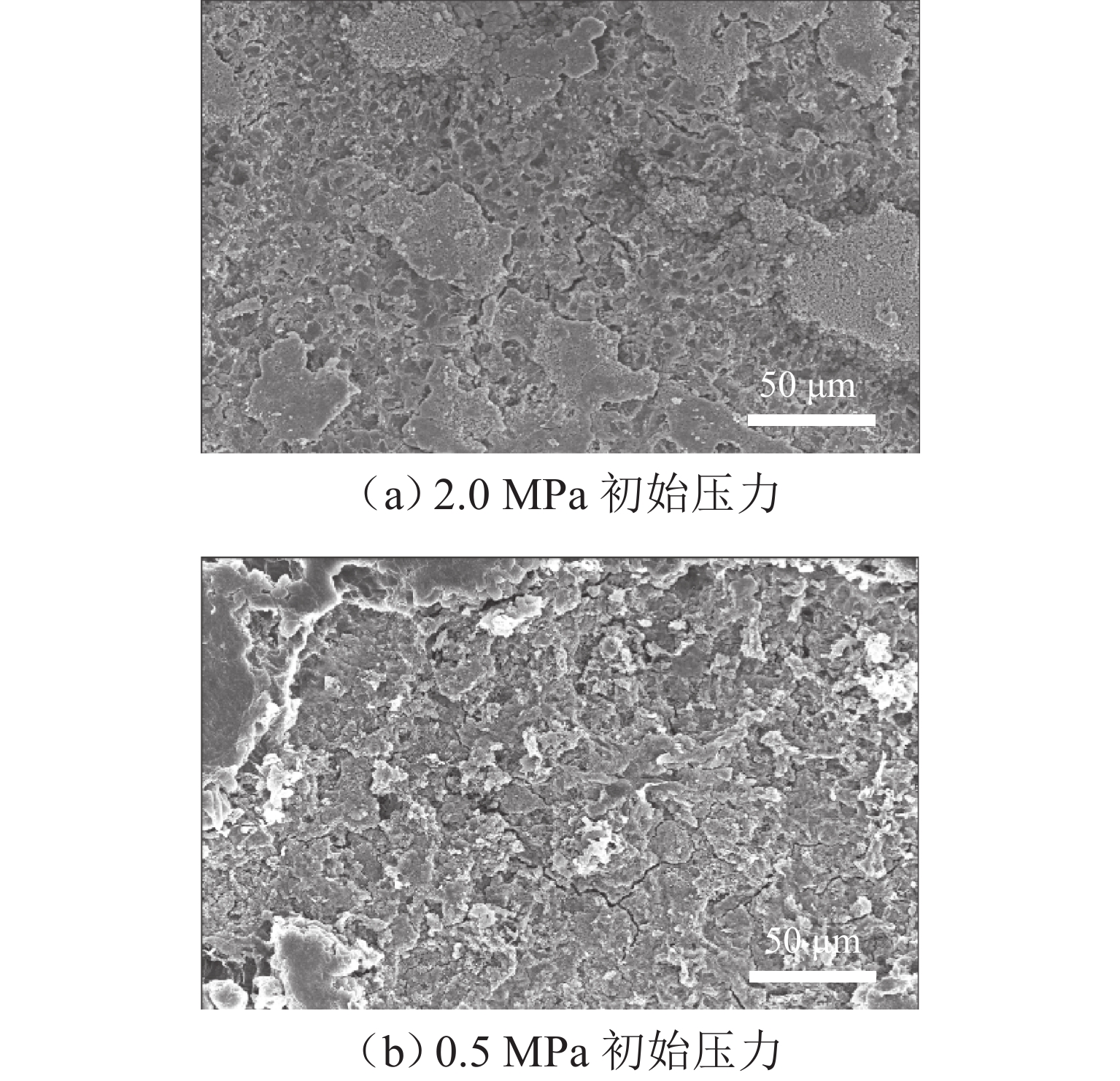
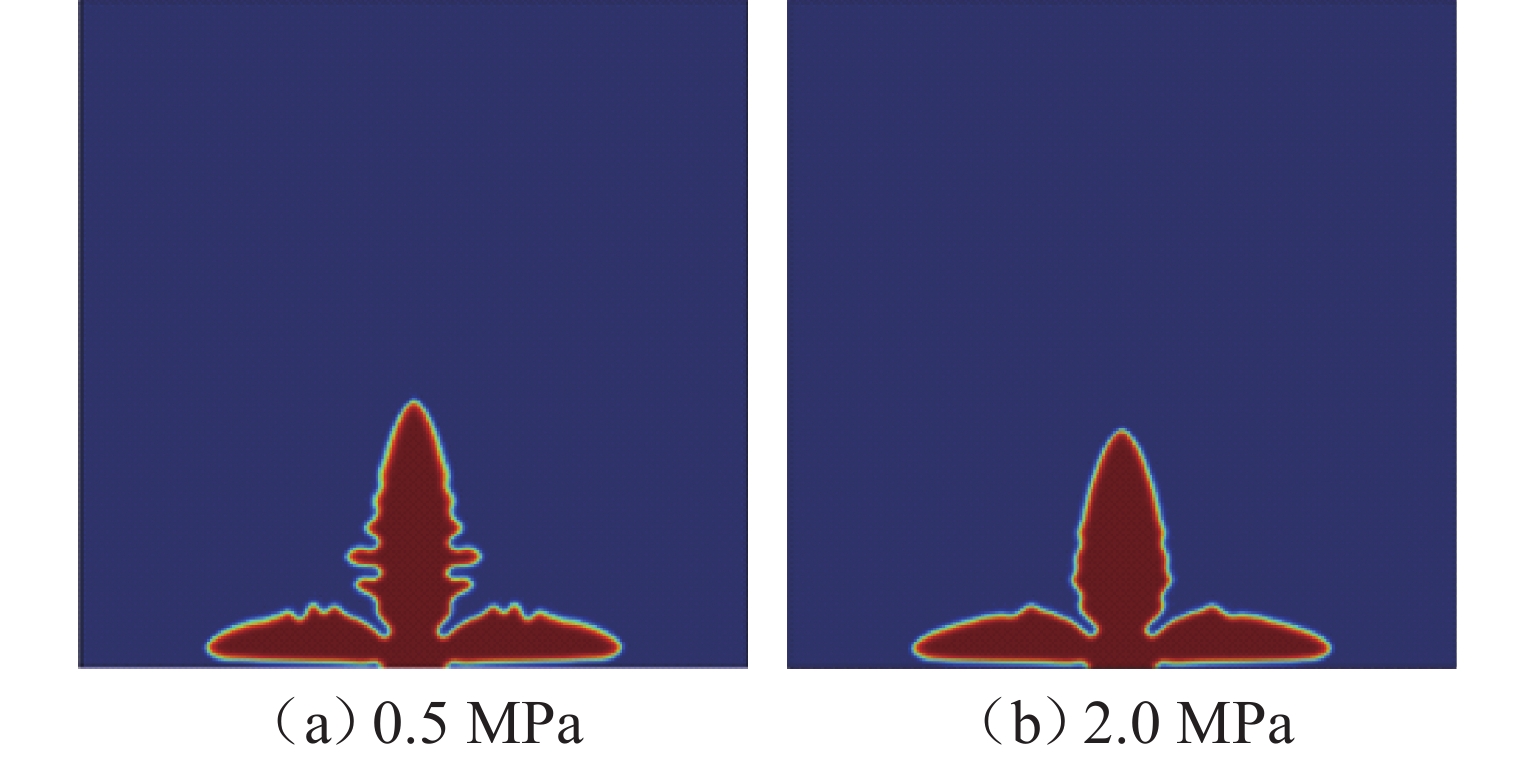
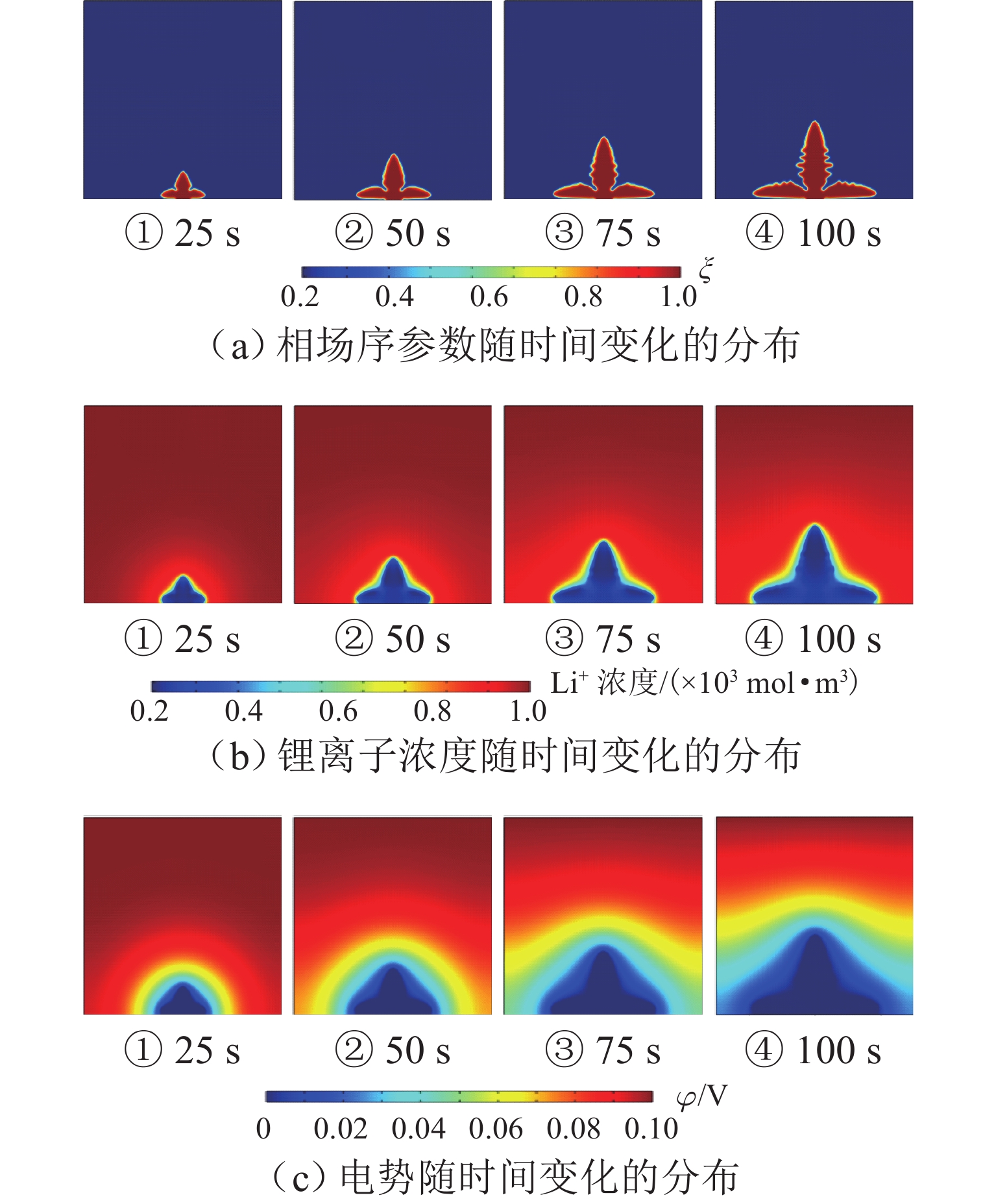
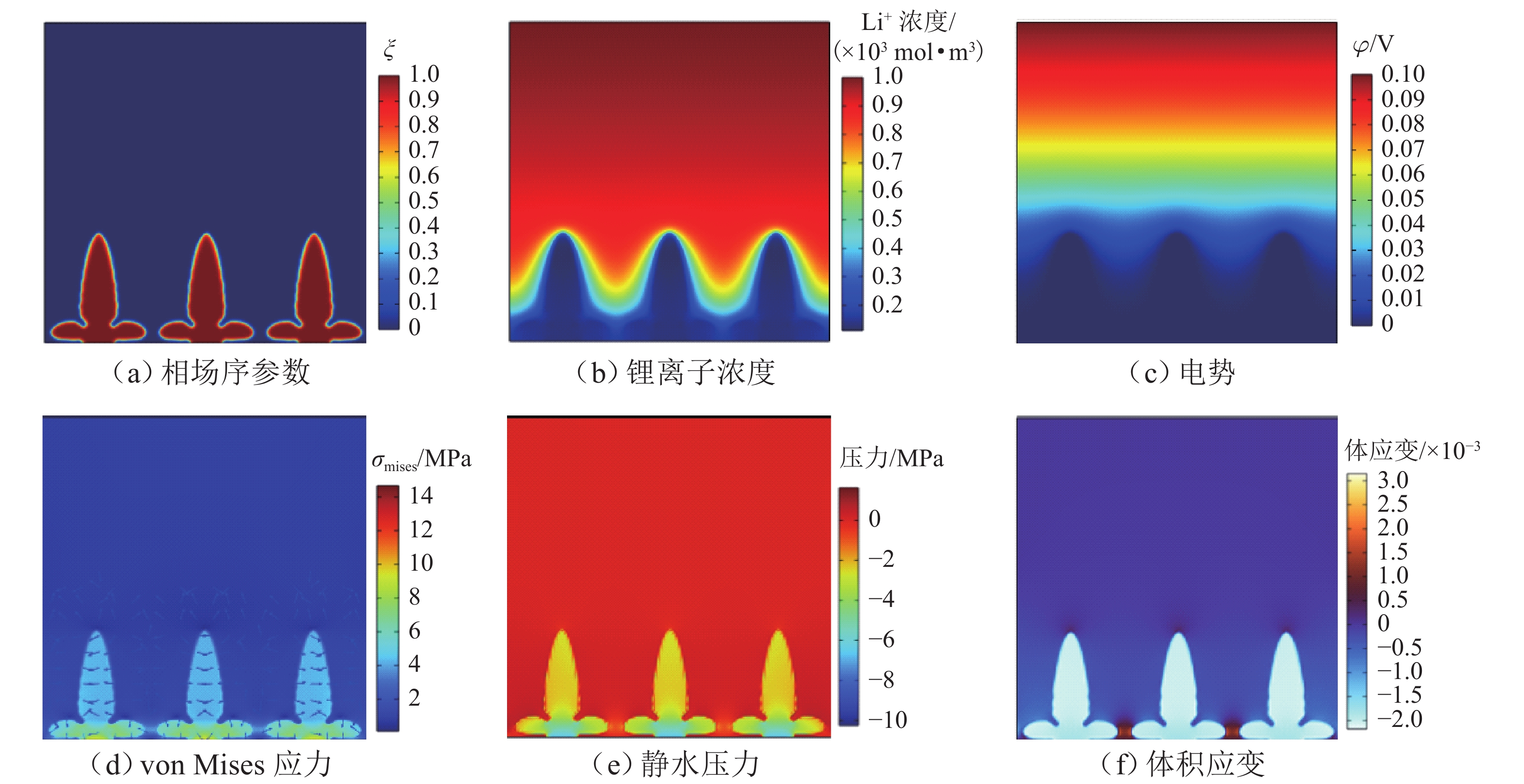
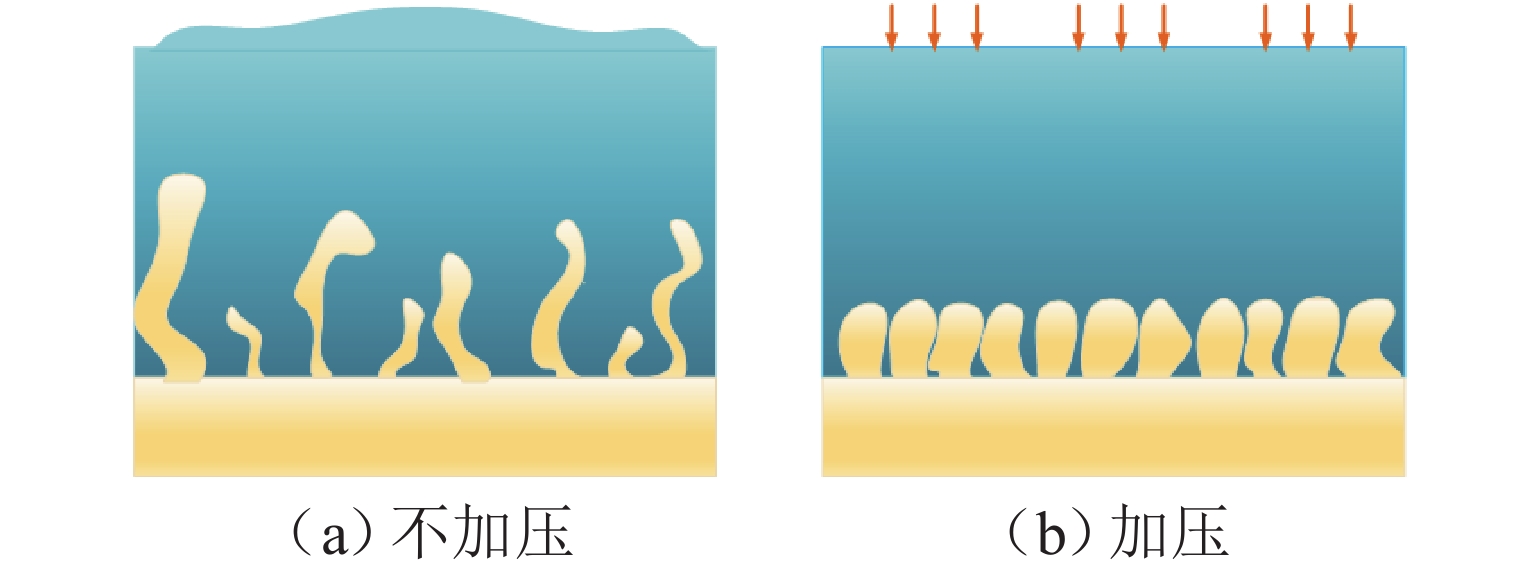
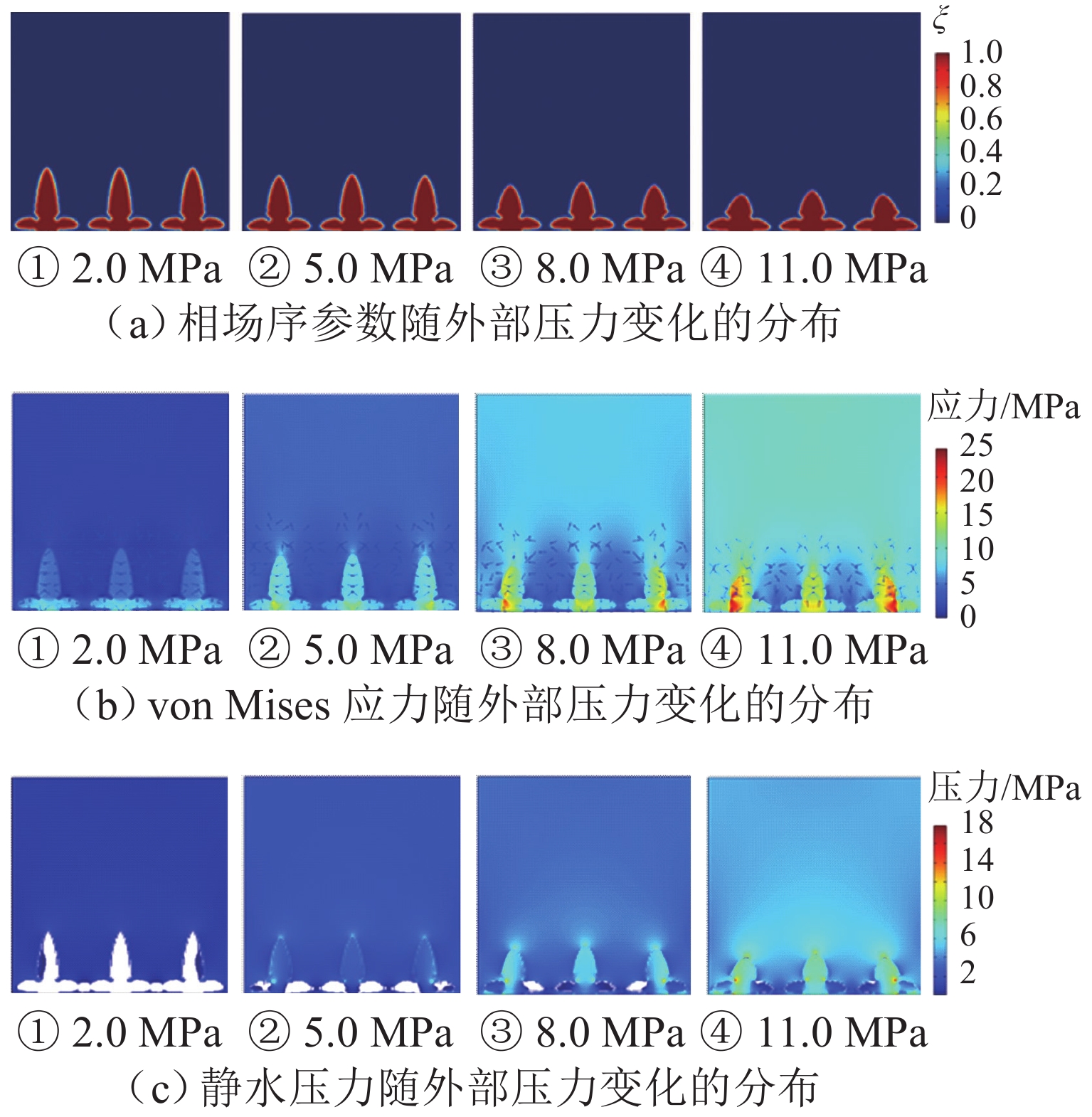
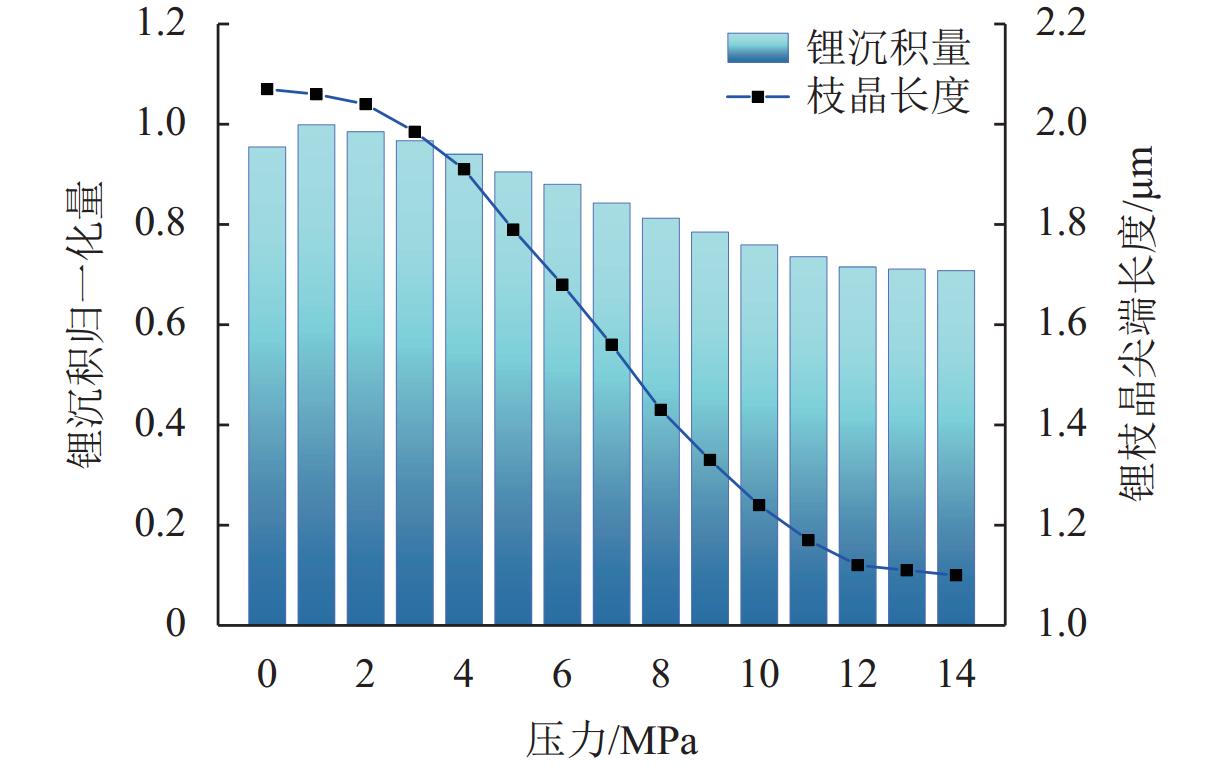
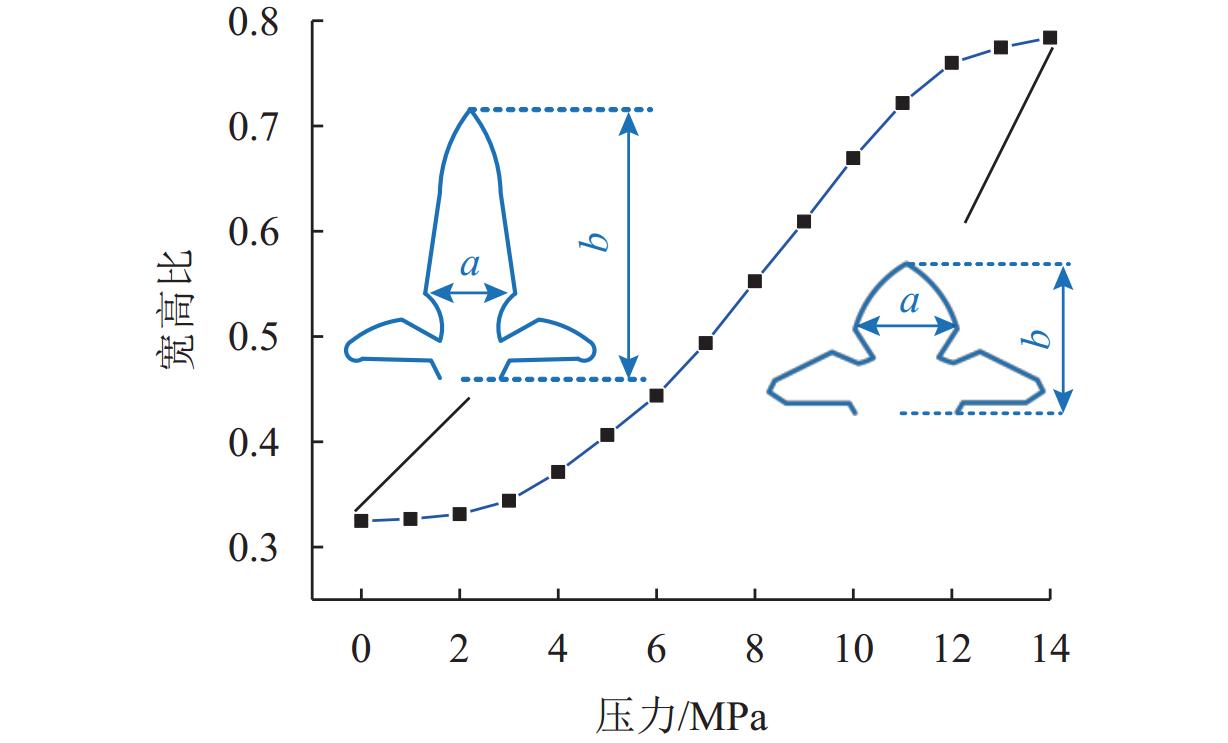
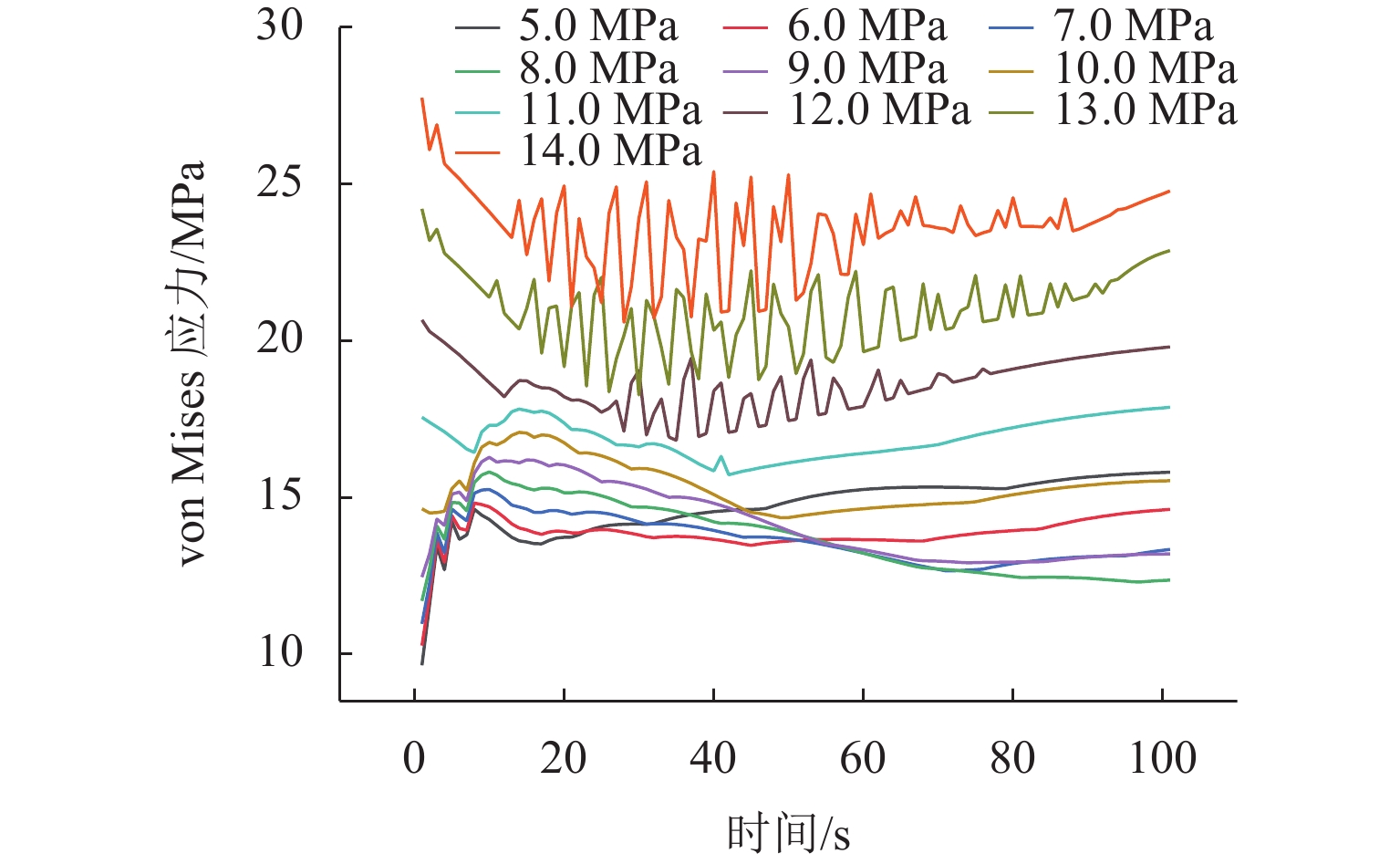
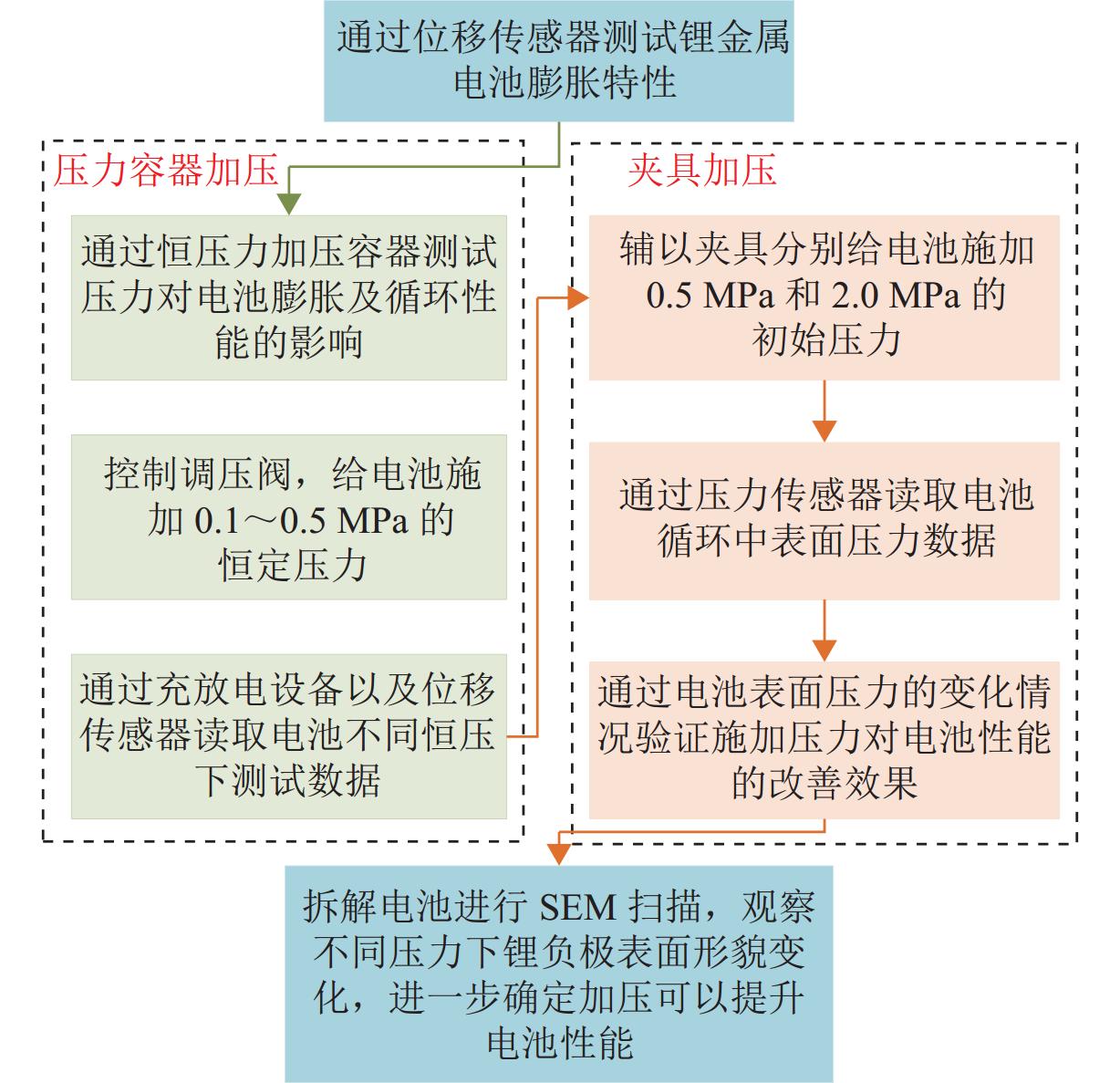
外部压力对锂金属电池的性能起着至关重要的作用. 为研究锂金属电池在不同压力条件下宏观电池性能表现和微观锂沉积特性，首先通过加压试验及电子显微镜扫描验证施加外部压力有助于改善锂金属负极表面形貌，为揭示其作用机理，并将非线性相场模型与力模型耦合，分析微观不用压力条件对锂的沉积形貌及内部应力分布的影响. 研究结果表明：在没有外部压力作用时，锂金属电池对外膨胀加速了锂枝晶的持续生长，导致容量快速衰退；模拟数据显示，随着外部压力的逐渐增大，锂枝晶的主轴长度由2.04 μm降低到1.1 μm，宽高比由0.32提升至0.79，这种光滑粗壮的形貌演变显著降低锂枝晶的比表面积，但同时也增加了力学不稳定性. 本文所提供的在不同外部压力下锂枝晶的相图，为锂金属电池压力管理设计提供理论支持.
Abstract:External pressure plays a crucial role in the performance of lithium metal batteries. In order to study the macroscopic performance and the microscopic lithium deposition characteristics of lithium metal batteries under different pressure conditions, the pressure test and scanning electron microscope (SEM) verification were conducted to verify that applying external pressure can improve the surface morphology of negative electrodes of lithium metal batteries. The nonlinear phase field model and the force model were coupled to reveal relevant mechanisms. The influence of non-pressure conditions on the deposition morphology and internal stress distribution of lithium was analyzed from the microscopic perspective. The results show that in the absence of external pressure, the external expansion of lithium metal batteries accelerates the continuous growth of lithium dendrites, which results in rapid capacity fading. According to the simulation data, as external pressure rises, the principal axis length of lithium dendrites decreases from 2.04 μm to 1.1 μm, and the aspect ratio increases from 0.32 to 0.79. The smooth and robust morphology evolution can significantly reduce the specific surface area of lithium dendrites, but at the same time, it increases the mechanical instability. The phases of lithium dendrites under different external pressures are displayed, which provides theoretical support for the pressure management and design of lithium metal batteries.
-
在高速列车制动过程中，列车的动能通过闸片与制动盘摩擦面之间的剧烈摩擦转化为热能，使制动盘在制动过程中承受着巨大的热负荷，此时制动盘上产生很大的温度梯度，从而产生较大的热应力[1-2]. 若高速列车在运行过程中发生高速下的紧急制动或持续坡道制动等恶劣制动，所产生的热应力超过了材料的屈服强度，盘面进入塑性状态，并在制动结束后在制动盘内留下残余应力[3-4].
残余应力的存在会影响材料的疲劳强度和构件的稳定性[5]，长期使用后制动盘摩擦面会产生微裂纹，甚至会引起制动盘的断裂、热变形并影响接触压力的稳定性，尤其在严苛地域条件下，导致制动盘热弹性不稳定，降低制动效能与制动盘的使用寿命[6-8]. 为提高高速列车的制动性能，国内外诸多学者针对制动盘材料[9-10]、疲劳寿命预测[11]展开研究：王东伟等[12]采用ABAQUS/Explicit热-位移瞬态分析法，探究热机耦合对高速列车制动系统动力学行为的影响；Wu等[13]采用扩展有限元法和虚拟节点多边形有限元法模拟热疲劳裂纹，并利用损伤容限法评估疲劳裂纹扩展寿命；石晓玲等[14]针对高速列车锻钢制动盘在实际运用中出现的多裂纹问题，通过1∶1制动动力试验与有限元计算相结合的方法研究了制动盘多裂纹间的作用机制；Xie等[15]对铁路制动盘深层裂纹的形成与扩展进行了研究，探讨了制动工况和服役历程对动车组制动盘裂纹快速扩展行为的影响；Belhocine等[16]使用ANSYS软件对不同材料的制动盘进行热-机耦合分析发现，制动盘在热应力作用下发生“伞状”变形，导致制动盘在制动过程中产生红热带迁移，从而影响制动盘的性能；日本Saga等[17]设计了测量制动盘动态变形的方法，研究了制动过程盘体的热变形规律. 前期研究表明，制动盘摩擦面附近的周向残余应力是驱动制动盘热疲劳裂纹扩展的主要原因[4, 18].
残余应力导致轮装制动盘变形的机理已有一定的研究，但基于动车组轮装制动盘拆解维修以及后续重复利用的工程需求，服役后轮装制动盘残余应力以及翘曲变形的仿真和预测方法仍鲜见报道. 因此，制动盘服役后的残余应力分布与翘曲变形之间的关系亟待深入研究.
本文通过试验构建了铸钢制动盘材料在不同温度下的本构模型，使用弹塑性有限元法研究了不同制动工况下制动盘的残余应力分布规律与翘曲变形量的变化规律，结合残余应力测试及制动盘变形测试，验证了仿真结果的有效性. 本文研究工作可为预测动车组制动盘长期服役后的残余应力分布及翘曲变形量变化提供方法借鉴，为动车组轮装制动盘拆解检修、后续重复利用提供参考.
1. 有限元模型的建立
1.1 材料力学性能及本构模型
从高速动车组制动盘本体取样，加工为标准拉伸试样进行单调拉伸试验,拉伸试样尺寸如图1所示. 在高速列车紧急制动过程中，制动盘摩擦面的瞬时温度可高达800 ℃，因此，试验温度为25～800 ℃. 试验设备为CMT5105型电子万能试验机，测得不同温度下的拉伸应力-应变曲线如图2所示.
参考GB/T 22315—2008标准，拟合得到不同温度下的杨氏模量、屈服强度等力学性能参数. 由应力-应变曲线能够看出，铸钢制动盘材料无明显屈服平台，对于此类非线性材料，Ramberg-Osgood模型[19]可用来描述其应力-应变（$ \sigma {\text{-}} \varepsilon $）关系，其理论表达式为
ε=σE0+0.002(σσ0.2)n， (1) 式中：E0为材料的杨氏模量，σ0.2为残余应变0.002时所对应的应力，n为材料的应变硬化指数.
使用最小二乘法对试验所得应力-应变数据进行拟合，可得到制动盘材料在不同温度下的应变硬化指数n. 材料的弹性模量、强度等力学性能参数如表1所示，σb为抗拉强度. 从表1中可以看出，随着试验温度的升高，材料的弹性模量和屈服强度不断降低，当试验温度超过400 ℃时发生明显下降.
表 1 制动盘材料不同温度下的力学性能参数Table 1. Mechanical properties of brake disc material at different temperatures温度/（℃） σ0.2/MPa σb/MPa E /GPa n 25 1055 1142 214 37.893 100 1007 1095 202 33.306 400 843 948 191 19.766 600 547 568 159 13.252 800 77 102 59 12.593 
图 2 制动盘材料不同温度下的单调拉伸应力-应变Figure 2. Monotonic tensile stress-strain curves of brake disc materials at different temperatures1.2 有限元模型的建立
制动过程的仿真模型包括制动盘、车轮与紧固件三部分，为兼顾计算精度与效率，简化了对仿真分析影响较小的圆角和倒角特征. 考虑到制动盘结构的对称性，取其1/6进行三维建模，如图3（a）所示. 利用有限元仿真软件ABAQUS开展热机耦合仿真分析，模型网格划分的结果如图3（b）所示，其中热分析部分使用三维实体单元C3D8，应力分析部分使用三维实体单元C3D8R.
高速列车在制动过程中，列车的动能会转化为摩擦面吸收的热能，假设制动盘和闸片之间理想接触，摩擦热量均匀输入，则施加在摩擦表面接触区域的热流可使用能量折算法计算，如式（2）.
q(t)=Mηa2cA(v0+at)， (2) 式中：M为单个轴重，η为制动盘的热吸收系数，a为列车制动平均减速度，A为制动摩擦面积，c为每轴制动盘数，v0为制动初速度，q(t)为制动期间随时间变化的热流密度.
对流换热系数hf是随列车速度变化的函数，制动盘摩擦面和散热筋表面与空气间换热条件不同，可分别按照式（3）计算[20].
hf={0.332λRe0.5Pr1/3/l，摩擦面，0.4Pr0.33kv0.556¯v0.556d0.444，散热筋表面， (3) 式中：λ为材料热导率，Re为雷诺数，Pr为普朗特数，l为厚度，k为热导率，v为运动黏度系数，$\bar v $为散热筋之间的平均风速，d为散热筋的内外径差.
在制动过程中，对流换热系数随列车速度减小而减小，假设环境恒定不变且列车进行匀减速，根据式（3），即可得到与时间相关的对流换热系数.
根据列车运行速度与1∶1制动动力试验中的试验速度等级，确定4种仿真工况的初速度（200、250、300、350 km/h），减速度恒定为1.0 m/s2，根据式（2）、（3）计算出不同工况下的热流密度与对流换热系数并施加到制动盘上，在制动盘盘体上的热流输入面、对流换热面的位置如图4所示.
本文使用间接耦合法计算制动盘热应力，将温度分析结果作为应力分析的输入载荷. 制动盘与车轮通过紧固件连接，在有限元模型中通过施加螺栓轴向载荷模拟紧固件预紧力；轮装制动盘与车轮共同压装于车轴上，运行过程中与车轴相对静止，故在轮毂孔上施加全约束；由于所使用的仿真模型为整体模型的1/6，还需在模型的分割面上施加对称约束. 应力分析的边界条件设置如图5所示. 在热应力计算完成后，移除螺栓的预紧力作用，使制动盘在不受结构约束的情形完全释放应力，以模拟制动盘从车轮拆卸后的残余变形情况.
2. 模拟结果分析及验证
2.1 不同工况下制动盘残余应力
图6为不同初速度下，制动结束并冷却至室温同时将制动盘紧固件拆除后的等效应力分布云图. 可见：4种工况制动后，制动盘螺栓孔上下侧都出现明显的应力集中现象，最大应力值均位于螺栓孔的靠近制动盘内沿侧；随着制动初速度的增加，摩擦面的残余应力值越来越大，高应力区域也越来越大，但残余应力的分布规律类似；制动盘摩擦面上的最大应力位于螺栓孔靠近制动盘内沿侧，故选择该位置处的节点分析制动过程中摩擦面的应力变化情况，所选择节点的位置及编号如图7所示.
图 6 不同制动初速度下制动结束拆除螺栓后等效应力分布Figure 6. Equivalent stress distribution after bolt removal at the end of braking with different initial braking speeds
图 7 制动盘螺栓孔边应力分析节点位置及编号Figure 7. Node position and number of bolt hole in brake disc for stress analysis当减速度恒定为1.0 m/s2，制动初速度不同时，输出摩擦面上应力最大节点的周向应力、径向应力、轴向应力以及温度瞬态变化曲线如图8所示.
图 8 不同制动初速度下摩擦面不同方向应力-时间曲线Figure 8. Stress-time curves in different directions on friction surface under different initial braking speeds由图8可见：整个过程中制动盘摩擦面的周向应力远大于径向与轴向应力，且制动初速度越高，最高温度值越大，产生的应力值就越大；在制动初期，制动盘摩擦面主要受到较大的周向压缩应力，径向与轴向应力较小，且此阶段摩擦面温度快速上升，材料屈服强度下降，所承受压应力会超过材料屈服强度，在摩擦面表层产生压缩塑性应变；制动过程中周向压缩应力逐渐减小，在制动结束前转变为周向拉伸应力，而制动盘最高温度也出现在制动后期；制动结束后随着制动盘的冷却，周向拉伸应力逐渐减小并趋于稳定；待制动盘完全冷却至室温并卸载螺栓载荷后，摩擦面会存在一定的残余拉应力，该残余拉应力的形成是由于在制动温升和热应力的共同作用下使表面形成了压缩塑性应变；在制动结束、冷却收缩的过程中，摩擦面附近的塑性应变在结构约束下无法完全恢复，从而在摩擦面表层形成残余拉应力，盘体内则形成残余压应力以达到应力平衡.
沿制动盘盘体轴向选择5个位置（距摩擦面的距离分别为0、5.5、11.0、16.5、22.0 mm）研究残余应力沿摩擦面轴向的梯度分布情况，距摩擦面不同深度取点位置以及距摩擦面不同深度的周向残余应力变化曲线如图9所示：由图9 （b）可见：在不同的制动初速度下，制动盘内的残余应力分布规律相似，摩擦面上的残余应力最大，并随着距摩擦面深度的增加而减小；在深度达到10 mm后残余应力由拉应力转变为压应力，在10～15 mm深度上应力有小幅增加，在15～20 mm深度上压应力开始逐渐减小且趋近于0；从制动盘摩擦面到制动盘心部，周向残余应力的大小与方向都有转变，不均匀的梯度型应力分布会使制动盘在失去外部结构约束后以翘曲变形的形式释放应力.
图 9 距摩擦面不同深度取点位置及周向应力变化曲线Figure 9. Circumferential stress changes at different depths from friction surface2.2 制动工况对变形量的影响
制动初速度与平均减速度是列车制动的2个重要因素，为了更好地描述制动盘翘曲变形规律，分别考虑这2个因素对制动盘翘曲变形的影响.
2.2.1 制动初速度对变形量的影响
制动盘在制动减速度恒为1.0 m/s2时，列车在初速度为200、250、300、350 km/h 4种工况下摩擦面上的周向塑性应变如图10所示. 由图可见，制动结束后摩擦面上形成压缩塑性应变，随着制动初速度的增加，塑性应变的区域和塑性应变量都随之增大.
图 10 不同制动初速度下摩擦面周向塑性应变Figure 10. Circumferential plastic strain of friction surface at different initial braking speeds对1∶1制动动力试验中常用的制动试验初速度为225、275、330、385 km/h，制动减速度恒为1.0 m/s2的4种制动工况进行分析，如图11所示. 由图可见：翘曲变形量随制动能量的升高而增加，当制动能量在26.2～59.0 MJ时，翘曲变形量随制动能量线性增加，当制动能量超过59.0 MJ后，翘曲变形量与制动能量呈二次函数关系.
因此，可以采用分段函数对翘曲变形量Y和制动能量W之间的关系进行拟合，如式（4）.
Y={0.024 64W−0.414 47，W=26.2～59.0MJ，3.29392×10−4W2−0.01425W+0.73364，W=59.0～80.3MJ. (4) 从图11还可看出：当制动能量超过59.0 MJ后，制动盘翘曲变形量增速逐渐变大；制动能量59.0 MJ所对应制动初速度为300 km/h，此初速度下制动盘最高温度达到了598 ℃. 拉伸试验结果表明，在温度达到600 ℃或更高时，制动盘材料的强度显著下降、塑性显著增大，当制动峰值温度达到对应水平时，摩擦面表层材料在制动时的压缩塑性应变也越大，冷却后形成的残余应力梯度和翘曲变形量也更大.
2.2.2 制动平均减速度对变形量的影响
列车制动时，制动盘与闸片的剧烈摩擦会使列车的动能转化为热能，当制动初速度一定时，制动平均减速度越大，摩擦副的制动热输入功率越大. 为探究不同制动热输入功率对制动盘翘曲变形的影响，在制动初速度均为300 km/h时，参照TL/CL 342—2014《中国标准动车组暂行技术条件》[21]中的减速度曲线，选择3、5、7级常用制动与紧急制动，将列车的减速过程等效为匀减速，对应的平均减速度分别为0.2、0.4、0.6、1.0 m/s2. 为保证曲线的连续性，额外选择0.8、1.2 m/s2的平均减速度，即在制动初速度均为300 km/h，平均减速度分别为0.2、0.4、0.6、0.8、1.0、1.2 m/s2的6种不同制动工况下对制动盘进行仿真分析，如图12所示，其中，制动盘的最大温度差为摩擦面上最高温度点与散热筋上最低温度点之差.
图 12 翘曲变形随制动减速度变化Figure 12. Variation of warping deformation with braking deceleration从图12可以看出：当平均减速度为0.2 m/s2时，制动盘翘曲变形量极小，在该工况下，制动盘摩擦面最高温度仅为324 ℃，摩擦面表层材料在该温度下仍有很高的强度，制动盘最大温度差仅为63 ℃，极低的温度梯度引起的热应力不足以产生大的塑性变形；当平均减速度从0.4 m/s2逐渐增大至1.2 m/s2时，制动盘的翘曲变形量也由0.02 mm逐渐增加到1.3 mm. 可见，当制动总能量恒定时，制动热输入功率需达到一定阈值才会使制动盘出现翘曲变形. 由图12还可看出：制动盘上的最高温度与最大温差都随制动平均减速度的增大而增大，但增幅逐渐降低；当制动热输入功率较高时，制动盘摩擦面产生的高温使表层材料强度降低，更大的温度梯度使制动盘内产生更高水平的热应力，因此平均减速度增大时，制动盘产生的翘曲变形量增加. 可以使用二次函数拟合得到翘曲变形量Y与平均减速度a间的关系，如式（5）.
Y=0.410 71a2+0.967 86a−0.432. (5) 3. 试验验证
3.1 翘曲变形与残余应力测试
从运行速度为300～350 km/h的动车组上选取一个经长期服役后的轮装制动盘，在拆卸前、后分别对制动盘的翘曲变形量进行测试，翘曲变形量的测试位置如图13所示. 在轮装制动盘拆卸前，采用塞尺对制动盘散热筋外环与车轮辐板之间的贴合间隙进行测量；在拆卸后，散热筋内环与散热筋外环间的产生明显高度差，测量变形量时，将平尺放置于螺栓安装孔所在散热筋的内环上，使用塞尺测量平尺与散热筋外环间的间隙大小. 在12个螺栓安装孔对应的散热筋外环重复进行上述测量步骤，记录测量数值并取平均值作为制动盘的翘曲变形量.
由于X射线法可以实现对工件残余应力的无损测试[22]，本文采用μ-360s型X射线残余应力分析仪对翘曲变形的制动盘进行表面残余应力测试，如图14（a）所示,在制动盘螺栓安装孔部位沿径向选取9个摩擦表面测点，测点位置如图14（b）所示.
图 14 X射线法测试摩擦面残余应力Figure 14. Residual stress of friction surface measured by X-ray method3.2 试验验证
对所选取的运行速度为300～350 km/h动车组上长期服役后的轮装制动盘的翘曲变形量进行测试发现：在轮装制动盘拆卸前，制动盘散热筋外环与车轮辐板之间的贴合间隙均小于0.1 mm；将轮装制动盘从车轮拆下后，制动盘的残余应力通过变形释放，翘曲变形量平均值为1.18 mm，如表2所示.
表 2 制动盘翘曲变形量测试结果Table 2. Test results of warping deformation of brake disc螺栓孔编号 1 2 3 4 5 6 7 8 9 10 11 12 平均 变形量/mm 1.20 1.24 1.18 1.20 1.16 1.20 1.16 1.20 1.16 1.20 1.18 1.18 1.18 X射线残余应力测试结果如图15所示. 可见：制动盘摩擦面中部的螺栓孔附近残余应力值较高，可达到260～280 MPa；残余应力的最大值均位于螺栓孔靠近制动盘内沿的一侧，摩擦面残余应力由摩擦面中部向边沿逐渐降低.
图 15 测试与仿真残余应力值对比Figure 15. Comparison of tested and simulated residual stress values2.2.1节的仿真分析可知：制动初速度为300 km/h的制动工况对应的残余翘曲变形量为1.04 mm，初速度为330 km/h的制动工况对应的残余翘曲变形量为1.39 mm，2种工况下的仿真翘曲变形量最接近实测翘曲变形量1.18 mm，故选取制动盘在制动初速度为300、330 km/h工况下的仿真结果与试验结果进行对比，如图15所示. 可见：仿真与实测制动盘残余应力分布规律和变化趋势具有很高的吻合度，且制动盘翘曲变形量与残余应力水平间呈现明显正相关关系. 从对比分析结果可知，有限元仿真结果能够较为准确地反映制动盘摩擦面的残余应力分布和翘曲变形量变化规律. 故式（4）、（5）可对动车组制动盘长期服役后形成的残余应力分布及翘曲变形量进行有效预测.
4. 结 论
1） 在高能量制动工况下，制动盘摩擦面热应力变化剧烈，冷却后形成残余应力. 在制动过程中，摩擦面先后受到的周向压缩应力和周向拉伸应力作用，待制动盘完全冷却后摩擦面会产生残余拉应力. 在解除紧固件对制动盘的结构约束后，制动盘形成翘曲变形以释放残余应力.
2） 制动减速度相同时，制动初速度越高、制动热输入的总能量越大；制动初速度相同时，制动减速度越大、制动热输入功率越高. 通过拟合制动能量、制动减速度与制动盘翘曲变形量的关系式发现，制动盘翘曲变形量与制动能量、制动减速度呈正相关关系，不同制动工况下的制动峰值温度与温度梯度会显著影响翘曲变形量的大小.
3） 对服役后的制动盘进行翘曲变形量与残余应力测试发现，制动盘在拆卸后通过翘曲变形释放应力，制动盘摩擦面中部螺栓孔附近的残余应力水平最高. 通过与对应工况下翘曲变形量相近的仿真结果进行对比表明，本文的仿真分析可有效反映制动盘残余应力分布及翘曲变形量变化规律.
-
图 1 压力条件下锂金属电池性能测试流程
Figure 1. Performance test procedure for lithium metal batteries under pressure
图 5 锂金属电池不同压力下电化学特性
Figure 5. Electrochemical properties of lithium metal batteries under different pressures
图 7 电池充放电过程中表面压力变化
Figure 7. Surface pressure changes during battery charging and discharging
图 8 锂金属电池表面压强随循环寿命的变化
Figure 8. Variation of surface pressure of lithium metal batteries with cycle life
图 9 不同压力下电池表面压强增量
Figure 9. Pressure increment on battery surface under different pressures
图 11 不同初始压力下锂金属电池负极界面形貌对比
Figure 11. Comparison of negative electrode surface morphology of lithium metal batteries under different initial pressures
图 12 不同初始压力下锂负极沉积形貌对比
Figure 12. Comparison of negative electrode deposition morphology of lithium metal batteries under different initial pressures
图 15 无外压力下锂沉积相场模拟结果
Figure 15. Simulation results of lithium deposition phase field without external pressure
图 16 外压力对锂沉积形貌影响示意
Figure 16. Influence of external pressure on lithium deposition morphology
图 17 不同外部压力条件下锂枝晶形貌演变结果
Figure 17. Evolution results of lithium dendrite morphology under different external pressures
图 18 锂离子沉积量的归一化值及枝晶长度数值
Figure 18. Normalized amount and dendrite length of lithium-ion deposition
图 20 不同外部压力作用下最大Von Mises应力变化
Figure 20. Variation of maximum Von Mises stress with external pressure
表 1 耦合模型参数值
Table 1. Coupling model parameter values
参数 符号 数值 参考文献 界面迁移速率/(m3•（J•s）−1) $ {L_\sigma } $ 10−6 [17-18] 反应速率常数/s−1 $ {L_\eta } $ 0.5 [17-18] 能量梯度系数/(J•m−1) $ {k_0} $ 1.5 × 10−6 [17-18] 势垒高度/(J•m−3) $ w $ 3.5 × 105 [17-18] 各向异性强度 $ \delta $ 0.03 [17-18] 各向异性模数 $ \omega $ 4 [17-18] 对称因子 $ \alpha $ 0.5 [17-18] 初始电解质浓度/(mol•m3) $ {c_0} $ 1.00 × 103 [17-18] 金属锂中初始锂原
子浓度/(mol•m3)$ {c_{\mathrm{s}}} $ 7.69 × 104 [17-18] 电极扩散系数/(m2•s−1) $ {D_{\mathrm{e}}} $ 2 × 10−15 [24] 电解质扩散系数/(m2•s−1) $ {D_{\mathrm{s}}} $ 2 × 10−15 [24] 电极电导率/(S•m−1) $ {\sigma _{\mathrm{e}}} $ 107 [24] 电解质电导率/(S•m−1) $ {\sigma _{\mathrm{s}}} $ 0.1 [24] 电极杨氏模量/GPa $ {E_{\mathrm{e}}} $ 7.8 [24-25] 电解质杨氏模量/GPa $ {E_{\mathrm{s}}} $ 1.0 [24-25] 电极泊松比 $ {v_{\mathrm{e}}} $ 0.42 [24-25] 电解质泊松比 $ {v_{\mathrm{s}}} $ 0.30 [24-25] Vegard 应变系数 $ {\lambda _{\mathrm{i}}} $ −8.66 × 10−4,
−7.73 × 10−4,
−5.29 × 10−4[24-25] 
下载: 导出CSV
-
[1] 秦潜聪,吴冠霖,高原,等. 面向战场条件的无人机集群分布式存储方法[J]. 西南交通大学学报,2024,59(4): 942-958. doi: 10.3969/j.issn.0258-2724.20230521QIN Qiancong, WU Guanlin, GAO Yuan, et al. Distributed storage methods for unmanned aerial vehicle clusters in battlefield[J]. Journal of Southwest Jiaotong University, 2024, 59(4): 942-958. doi: 10.3969/j.issn.0258-2724.20230521 [2] 郭林,刘飞,李佳钰,等. 基于能量管理策略的太阳能无人机航迹跟踪控制[J]. 西北工业大学学报,2023,41(2): 409-418. doi: 10.3969/j.issn.1000-2758.2023.02.019GUO Lin, LIU Fei, LI Jiayu, et al. Path tracking control of solar-powered UAV based on energy management strategy[J]. Journal of Northwestern Polytechnical University, 2023, 41(2): 409-418. doi: 10.3969/j.issn.1000-2758.2023.02.019 [3] KRAUSKOPF T, RICHTER F H, ZEIER W G, et al. Physicochemical concepts of the lithium metal anode in solid-state batteries[J]. Chemical Reviews, 2020, 120(15): 7745-7794. doi: 10.1021/acs.chemrev.0c00431 [4] 金礼芬,蒲建,杨文斌,等. 太阳能无人机的能源系统技术与发展趋势[J]. 信息记录材料,2022,23(6): 13-16. doi: 10.3969/j.issn.1009-5624.2022.6.xxjlcl202206003JIN Lifen, PU Jian, YANG Wenbin, et al. Overview of solar powered UAV development[J]. Information Recording Materials, 2022, 23(6): 13-16. doi: 10.3969/j.issn.1009-5624.2022.6.xxjlcl202206003 [5] ZHANG R, SHEN X, ZHANG Y T, et al. Dead lithium formation in lithium metal batteries: a phase field model[J]. Journal of Energy Chemistry, 2022, 71: 29-35. doi: 10.1016/j.jechem.2021.12.020 [6] CHENG X B, ZHANG R, ZHAO C Z, et al. Toward safe lithium metal anode in rechargeable batteries: a review[J]. Chemical Reviews, 2017, 117(15): 10403-10473. doi: 10.1021/acs.chemrev.7b00115 [7] ARGUELLO M E, LABANDA N A, CALO V M, et al. Dendrite formation in rechargeable lithium-metal batteries: Phase-field modeling using open-source finite element library[J]. Journal of Energy Storage, 2022, 53: 104892.1-104892.21. [8] 李志强,刘媛,李彬,等. 一种面向浮充工况的锂离子电池组早期内短路快速定量诊断方法[J/OL]. 西南交通大学学报,1-8[2025-02-17]. http://kns.cnki.net/kcms/detail/51.1277.U.20240614.1318.006.html.LI Zhiqiang, LIU Yuan, LI Bin, et al. A rapid quantitative diagnosis method for early internal short circuit of lithium-ion battery packs under float charging conditions [J/OL]. Journal of Southwest Jiaotong University, 1-8 [2025-02-17]. http://kns.cnki.net/kcms/detail/51.1277.U.20240614.1318.006.html. [9] RAMASUBRAMANIAN A, YURKIV V, FOROOZAN T, et al. Lithium diffusion mechanism through solid–electrolyte interphase in rechargeable lithium batteries[J]. The Journal of Physical Chemistry C, 2019, 123(16): 10237-10245. doi: 10.1021/acs.jpcc.9b00436 [10] MU W Y, LIU X L, WEN Z, et al. Numerical simulation of the factors affecting the growth of lithium dendrites[J]. Journal of Energy Storage, 2019, 26: 100921.1-100921.10. [11] VERMA P, PURAVANKARA S, NANDANWAR M N, et al. Insights into the morphological evolution of mossy dendrites in lithium metal symmetric and full cell: a modelling study[J]. Journal of the Electrochemical Society, 2023, 170(3): 030529.1-030529.11. [12] CHENG F, HU Y, ZHAO L X. Analysis of weak solutions for the phase-field model for lithium-ion batteries[J]. Applied Mathematical Modelling, 2020, 78: 185-199. doi: 10.1016/j.apm.2019.09.048 [13] REN Y, ZHOU Y, CAO Y. Inhibit of lithium dendrite growth in solid composite electrolyte by phase-field modeling[J]. The Journal of Physical Chemistry C, 2020, 124(23): 12195-12204. doi: 10.1021/acs.jpcc.0c01116 [14] ARGUELLO M E, GUMULYA M, DERKSEN J, et al. Phase-field modeling of planar interface electrodeposition in lithium-metal batteries[J]. Journal of Energy Storage, 2022, 50: 104627.1-104627.13. [15] JING H X, XING H, DONG X L, et al. Nonlinear phase-field modeling of lithium dendritic growth during electrodeposition[J]. Journal of the Electrochemical Society, 2022, 169(3): 032511.1-032511.6. [16] MONROE C, NEWMAN J. Dendrite growth in lithium/polymer systems: a propagation model for liquid electrolytes under galvanostatic conditions[J]. Journal of the Electrochemical Society, 2003, 150(10): A1377.1-A1377.8. [17] GUYER J E, BOETTINGER W J, WARREN J A, et al. Phase field modeling of electrochemistry Ⅰ: equilibrium[J]. Physical Review E, 2004, 69(2): 021603.1-021603.13. [18] CHEN L, ZHANG H W, LIANG L Y, et al. Modulation of dendritic patterns during electrodeposition: a nonlinear phase-field model[J]. Journal of Power Sources, 2015, 300: 376-385. doi: 10.1016/j.jpowsour.2015.09.055 [19] ZHANG R, SHEN X, CHENG X B, et al. The dendrite growth in 3D structured lithium metal anodes: Electron or ion transfer limitation?[J]. Energy Storage Materials, 2019, 23: 556-565. doi: 10.1016/j.ensm.2019.03.029 [20] MCDOWELL M T, CORTES F J Q, THENUWARA A C, et al. Toward high-capacity battery anode materials: chemistry and mechanics intertwined[J]. Chemistry of Materials, 2020, 32(20): 8755-8771. doi: 10.1021/acs.chemmater.0c02981 [21] TANG Y F, ZHANG L Q, CHEN J Z, et al. Electro-chemo-mechanics of lithium in solid state lithium metal batteries[J]. Energy & Environmental Science, 2021, 14(2): 602-642. [22] WANG M J, KAZYAK E, DASGUPTA N P, et al. Transitioning solid-state batteries from lab to market: Linking electro-chemo-mechanics with practical considerations[J]. Joule, 2021, 5(6): 1371-1390. doi: 10.1016/j.joule.2021.04.001 [23] 朱迎迎,王勇,徐淼,等. 追踪锂金属负极的压力与形貌变化[J]. 物理化学学报,2023,39(1): 77-84.ZHU Yingying, WANG Yong, XU Miao, et al. Tracking pressure changes and morphology evolution of lithium metal anodes[J]. Acta Physico-Chimica Sinica, 2023, 39(1): 77-84. [24] SHEN X, ZHANG R, SHI P, et al. How does external pressure shape Li dendrites in Li metal batteries?[J]. Advanced Energy Materials, 2021, 11(10): 2003416.1-2003416.9. [25] ZHANG X, WANG Q J, HARRISON K L, et al. Pressure-driven interface evolution in solid-state lithium metal batteries[J]. Cell Reports Physical Science, 2020, 1(2): 100012.1-100012.19. [26] 罗崇亮,余云燕,张璟,等. 硫酸盐渍土热-质迁移试验与耦合模型[J]. 西南交通大学学报,2023,58(2): 470-478.LUO Chongliang, YU Yunyan, ZHANG Jing, et al. Heat-mass transfer test and coupling model of sulfate saline soil[J]. Journal of Southwest Jiaotong University, 2023, 58(2): 470-478. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 93
- HTML全文浏览量: 32
- PDF下载量: 10
- 被引次数: 0