Vibration Fatigue Fracture Mechanism of e-Type Clip Under Rail Corrugation Excitation
-
摘要:
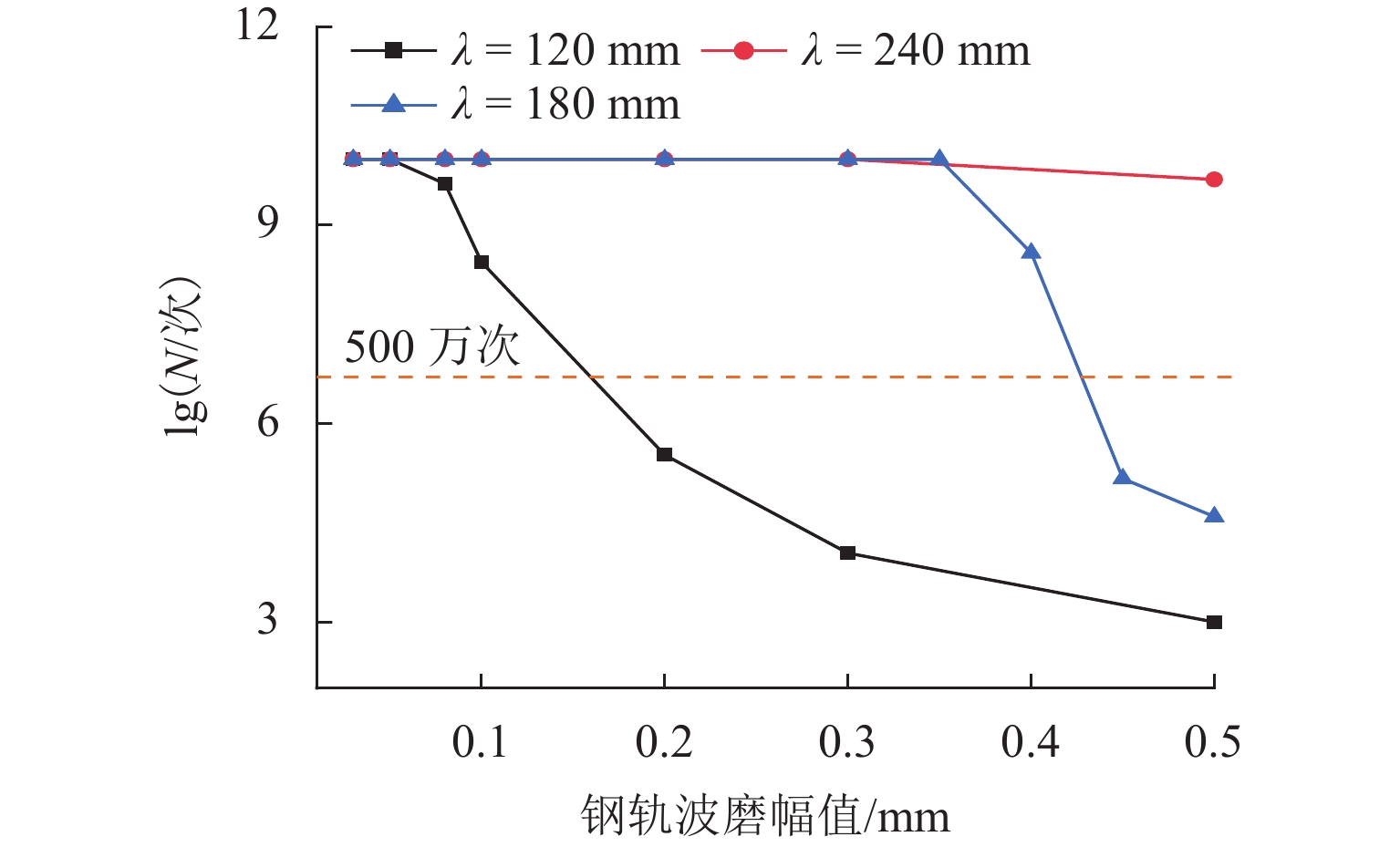
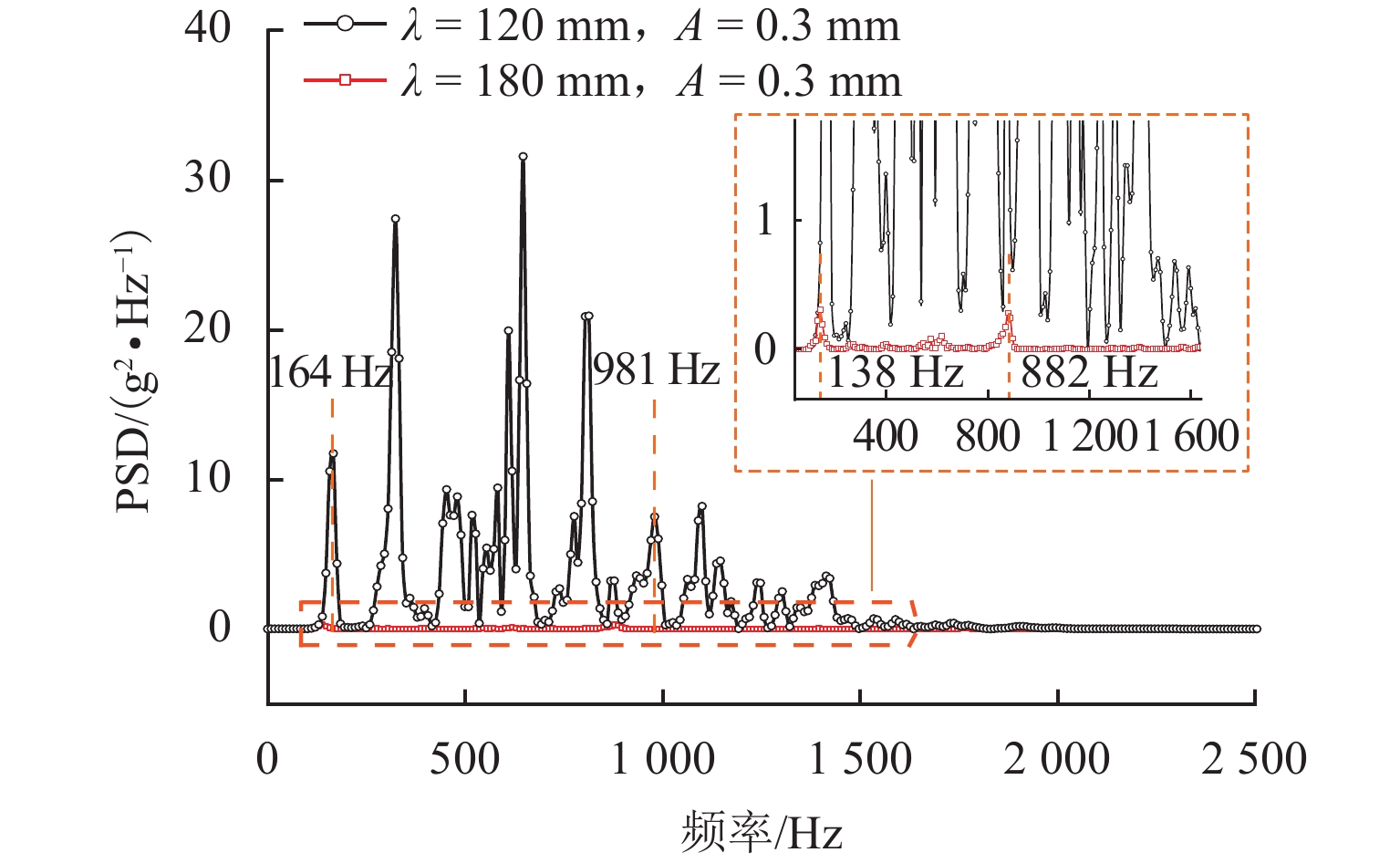
为研究地铁小半径曲线轨道上e型弹条异常断裂的原因，通过长期跟踪和测量成都地铁X号线钢轨波磨的发展情况，并基于摩擦自激振动理论，建立轮对-轨道-扣件系统的全实体单元有限元模型；采用隐式动态分析方法和谐响应分析方法，研究短波长波磨、长波长波磨对e型弹条振动疲劳寿命的影响. 研究表明：这2种类型的钢轨波磨都会导致地铁e型弹条振动疲劳寿命减小；波磨幅值越大，导致弹条的振动疲劳寿命越小；钢轨波磨不仅能够引起e型弹条产生与钢轨波磨“同频”的受迫振动，还容易激发弹条产生该频率的倍频振动；对于短波长波磨而言，由于2倍频的存在，在相同波深幅值的短波长波磨影响下，25 mm 和40 mm波长的钢轨波磨最容易导致e型弹条产生振动疲劳断裂；波长为120 mm的长波长波磨的波深幅值较大时，激发出的6倍频振动导致弹条的振动疲劳寿命急剧减小；由于振动强度的减弱，波长为240 mm的长波长波磨对弹条振动疲劳寿命的影响有限.
Abstract:To study the reason for the abnormal fracture of e-type clips on small-radius curved subway tracks, the development of rail corrugation on Line X of the Chengdu Metro over an extended period was monitored and measured. Based on the theory of friction-induced self-excited vibration, a comprehensive solid finite element model of the wheelset−rail−fastening system was established. The effects of short-pitch rail corrugation and long-pitch rail corrugation on the vibration fatigue life of e-type clips were studied by means of implicit dynamic analysis and harmonic response analysis. The study reveals that both types of rail corrugation result in a decrease in the vibration fatigue life of the e-type clips. Greater amplitude of rail corrugation indicates shorter vibration fatigue life of the clips. Rail corrugation can not only induce the e-type clip to generate forced vibrations at the frequency matching that of the rail corrugation but also easily trigger vibrations at multiples of this frequency in the e-type clips. For short-pitch rail corrugation, due to the existence of a frequency twice that of the rail corrugation, the rail corrugation with wavelengths of 25 mm and 40 mm is most likely to lead to vibration fatigue failure of the e-type clips under the influence of short-pitch and long-pitch rail corrugation with the same wave depth amplitude. When the wave depth amplitude of long-pitch rail corrugation with a wavelength of 120 mm is large, the vibration fatigue life of the clips decreases sharply due to the excited 6-fold vibration. However, the long-pitch rail corrugation with a wavelength of 240 mm has only a limited impact on the vibration fatigue life of the clips due to the attenuation of vibration intensity.
-
山区地势地形、气候极其复杂，环境敏感区众多，铁路路基工程的建设活动会给周边区域环境造成严重损害，同时，区域环境的脆弱性也会反馈于路基工程的建设活动并对其产生约束，彼此间相互作用、相互影响、相互制约[1]，通俗表现为一方利益受损，另一方利益受益的状态，但在双方博弈过程中，会存在协调平衡点，此时，“路基-环境”会产生共同创造、相互促进的关系，促使整体系统利益最大化. 因此，如何探析路基工程与环境之间的耦合状况，并通过优化调控方式促使“路基-环境”向协调平衡状态进行演变，对铁路路基绿色高效建设具有重要意义.
“路基-环境”绿色高效内涵不仅包含环境效益最大化原则，还容纳路基工程设计资源投入最小化的目的. 目前，大多数学者对于“路基-环境”绿色高效的研究较为局限于单一方面，甚至其中的一小部分，缺乏系统性思维. 在环境效益最大化原则，Su等[2]通过对不同根系与土壤之间的关系进行力学试验，为生态护坡技术的应用提供了参考；Sukmak等[3]研究石榴石残渣和轮胎衍生骨料改善不良地质的可行性，减少废弃材料对环境的损害；郑雨茜等[4]以铁路路基爆破为研究对象，从绿色施工理念的角度提出动态“三位一体”综合爆破效益评估模型. 在设计资源投入最小化目的上，李雨浓等[5]基于G1法和改进数据包络分析（DEA）模型对铁路工程材料投入进行评价，以此为依据减少材料的投入成本；鲍学英等[6]构建技术接口的关键要素均衡优化模型，分析质量、进度、成本、安全要素间的关系，并对关键要素进行均衡优化以减少管理成本. 因此，从系统整体性思维分析“路基-环境”协调发展，寻找铁路路基与环境之间和谐共存的利益平衡点具有一定的前景.
“路基-环境”绿色高效的实施必然离不开工程智能优化决策，学者进行了广泛研究. 李伟等[7]建立一个综合考虑建设和运营费用、环境影响代价及线路约束的线形优化模型，并基于改进的遗传算法生成最优选线方案；段晓晨等[8]将三维非线性智能控制技术运用实际工程，通过建立张家庄大桥运营维护成本预测模型获取最优成本值，为桥梁运营阶段的管理提供借鉴和参考；薛新功等[9]对20世纪60年代至今国内外铁路线路专业智能优化策略进行总结，详细介绍各类方法的适用性及优缺点. 上述研究集中在桥梁、选线等专业领域，缺乏对铁路路基与环境之间的相互影响的分析决策.
综上，本研究以山区铁路路基为研究对象，对“路基-环境”相容共生进行定义，构建绿色要素体系，利用耦合魔方游戏模型明确“路基-环境”调控优化的途径与方法，识别绿色关键要素作为主控变量，构建以“路基-环境”耦合协调度最优为目标、各绿色要素函数关系约束、“满载”条件约束下的耦合优化模型，基于MATLAB，采取变色龙群算法进行优化求解，得到最优状态下主控变量的最优值，通过模型最优值与工程实际值进行对比管理，促使路基工程绿色关键要素不断向最优值靠近，最终实现铁路“路基-环境”的相容共生.
1. 铁路“路基-环境”耦合魔方游戏模型
根据肖建庄等[10]对工程结构可持续性设计理论的架构，将“路基-环境”相容共生表征为路基工程建设活动对环境产生的影响维持在环境承载力所界定的合理阈值范围内，即达到一种“满载而不过载”的微妙平衡状态下，彼此间协调状态达到最优. 因此，为达到“路基-环境”相容共生的目的，本文依托铁路“路基-环境”交互影响特点，挖掘影响相容共生的绿色要素，并在此基础上提出耦合魔方游戏模型建立目标调控框架.
1.1 绿色要素体系构建
山区铁路路基工程建设活动与环境之间存在错综复杂的联系，彼此间相互作用、相互影响、相互制约，会形成大量由一对一、一对多、多对多影响路径所构成的交互影响网络，网络中任意节点的变化都会牵一发而动全身，对铁路“路基-环境”相容共生产生影响，因此，参考文献[11-13]及《铁路路基设计规范》（TB 10001—2016）[14]、《铁路工程环境保护设计规范》（TB 10501—2016）[15]，从微观层面“路基-环境”交互影响关系进行分析，如图1所示. 图中，黄色、紫色和黑色文字分别表示路基工程绿色要素、环境绿色要素和“路基-环境”影响路径.
在此基础上，对“路基-环境”交互影响网络内影响因素进行集成，从基体结构、地基处理、支挡结构、边坡防护、声屏障、防排水等设计环节提取路基工程绿色要素，分析其对地质环境、大气环境、水环境、生态环境、土壤环境、声环境的影响，识别环境绿色要素，构建铁路“路基-环境”绿色要素体系，如图2所示. 图中：$ {{\textit{z}}_1} $为路基表土清理时单位体积产生的粉尘平均浓度；$ {{\textit{z}}_{11}} $为从隧道工程弃渣场运送弃渣填筑可利用率；$ {{\textit{z}}_{12}} $为路基挖方用作填方的弃渣利用率；$ {{\textit{z}}_{14}} $、$ {{\textit{z}}_{16}} $、$ {{\textit{z}}_{18}} $分别为设计单位所设计的路基支挡结构、边坡工程防护、边坡植物防护的结构形式是否与周围环境相协调且功能有效，设计合理性能否达到要求，例如，在有滑坡体的路基地段，宜采用抗滑桩等支挡结构进行防护；$ {{\textit{z}}_{15}} $、$ {{\textit{z}}_{17}} $、$ {{\textit{z}}_{19}} $为在实际施工中施工单位是否严格遵循技术要求与组织管理，从而确保施工质量达到设计标准，例如，边坡植物防护中，严格遵循植物种类选配标准，极大提高边坡稳定性、增强水土保持能力；$ {{\textit{z}}_{20}} $表示安装声屏障前后在某特定位置上的声压级之差；$ {{\textit{z}}_{22}} $、$ {{\textit{z}}_{23}} $、$ {{\textit{z}}_{24}} $、$ {{\textit{z}}_{25}} $表示路基截排水结构在单位时间内所能通过的最大截排水量；$ {{\textit{z}}_{27}} $、$ {{\textit{z}}_{28}} $为路基施工区大气环境PM10（CO）浓度值；$ {{\textit{z}}_{30}} $为在爆破影响下介质质点往复运动的速度；$ {{\textit{z}}_{31}} $为单位面积土壤在单位时间内侵蚀量的大小；$ {{\textit{z}}_{32}} $为通过措施减少水土流失面积与未实施措施时水土流失面积之比.
图 2 铁路“路基-环境”绿色要素指标体系Figure 2. Index system for green elements of railway roadbed and environment1.2 耦合魔方游戏模型分析
基于上述相容共生定义及绿色要素体系，提出铁路“路基-环境”耦合魔方游戏模型[16]，建立铁路“路基-环境”调控优化目标框架，如图3所示. 将“路基-环境”的整个耦合过程映射为魔方的旋转操作过程，在一定时间内，将混乱状态的魔方还原成有序状态（混乱状态表现为魔方的各个小立方体颜色错乱，有序状态表现为魔方每一面颜色相同）. 其中，每个小立方体代表一个相对完整的“路基-环境”耦合子系统，关节轴起到连接各个小立方体纽带作用，确保它们能够在旋转操作中相互作用、相互影响；路基工程的建设活动为转动魔方的动力，支撑魔方不断转动；属于水、土壤、声、大气、生态、地质等环境的绿色要素代表小立方体的每一面，表现为如何达到魔方有序状态的标识；路基与环境耦合形成的一面有序状态则表示单一环境与工程达到高度协调水平；由于本文提出的是一种“有损魔方”的理想模型，受制于魔方几何约束、物理约束的结构特点，会随着魔方的旋转产生使用损坏，当旋转次数达到魔方可以承受的限值区间，魔方就会失去使用价值，同理，环境的承载力表现为魔方可以承受转动次数区间，转动次数超出了魔方承受范围，认为魔方损坏.
魔方游戏的最终得分由三方面组成：还原度、错误率以及转动效率. 还原度指魔方的有序状态，即路基与环境之间的高度耦合协调水平；错误率是转动魔方过程中失误转动次数与魔方可承受次数的比值，表现为在旋转作用下魔方受损程度，即路基工程建设活动对环境的影响效果；转动效率是魔方从无序到有序所花费的步骤，即路基工程投入转化环境效益的能力. 游戏结果一般会出现3种状况：1）玩家在规定的时间内，还原度最低，错误率高，转动效率低；2）玩家超出规定时间的限制，还原度最高，错误率最低，转动效率高；3）玩家在规定的时间，通过利用关键小方块改进方法，还原度提升，错误率较低，转动效率较高. 因此，第3种结果得分最优，结合路基工程实践，应在满足铁路“路基-环境”满载的条件下，通过调控绿色关键要素达到协调水平最优，共同实现路基工程与环境之间的相容共生.
2. 铁路“路基-环境”耦合优化模型构建
基于耦合魔方游戏模型的构建过程，有必要识别绿色关键要素，将其作为耦合优化模型的主控变量，并以此采取施压承载模型对“路基-环境”的耦合效率进行测算，保证铁路“路基-环境”处于满载状态，结合耦合协调度模型对协调水平进行测度，促使“路基-环境”耦合协调状态有向高度协调状态演变的趋势.
2.1 数据归一化
为消除量纲，使数据具有可比性，对要素进行极差归一化处理.
xi,g={xi−minximaxxi−minxi,正向要素,maxxi−ximaxxi−minxi,负向要素, (1) 式中：$ {x_i} $为第$ i $项绿色要素的实际值，$ x_{i,{\text{g}}}^{} $为第$ i $项绿色要素的归一化值.
2.2 绿色关键要素识别
在“路基-环境”交互影响关系网络中，路基绿色要素对环境绿色要素的影响路径总体呈现一对一、一对多甚至多对多的情况，具有复杂化、虚拟性的特点，难以识别关键要素. 为保障后续优化调控顺利实施，借助鲍学英等[17]构建的复杂网络模型理论，将影响路径分为路基、环境系统内部影响和“路基-环境”系统间影响，通过二维云模型、Spearman相关系数对绿色关键要素进行识别.
2.2.1 自身属性重要度
Spearman相关系数是一种利用单调方程来评价2个变量之间相关性的方法，可以在同一系统内有效得到绿色要素的自身重要度，如式（2）所示：
Wi=M∑j=1ρij,ρij=1−6K∑k=1d2KK(K2−1), (2) 式中：$ {W_i} $为路基、环境由于自身内部影响下第$ i $项绿色要素的属性重要度，$ M $为第$ i $项绿色要素与其他绿色要素有关联关系的要素个数，$ {\rho _{ij}} $为第$ i $项绿色要素与第$ j $项绿色要素之间的Spearman相关系数，$ {d_k} $为在第$ k $位专家打分中2个变量中的等级差，$ K$指专家个数.
2.2.2 影响间重要度
二维云模型是一种可以将定性概念与定量数据进行转换的方法，通过表征路基建设活动对环境的影响后果$ {E_{\text{h}}} $和概率$ {E_{\text{g}}} $可以直观看出“路基-环境”之间的影响关系，确定绿色要素影响间重要度. 具体计算如式
{Ex=1KK∑k=1uk,En=√π2×1KK∑k=1|uk−Ex|,He=√|S2−E2n|,S2=1K−1K∑k=1(uk−Ex)2, (3) Li=11+√(Ehj−Eh)2+(Egj−Eg)2,Vi={Cmaxi−Li若靠近上界,Cmixi+Li若靠近下界, (4) 式中：$ {E_{\text{x}}} $、$ {E_{\text{n}}} $、$ {H_{\text{e}}} $、$ {S^2} $分别为样本期望、熵、超熵和样本方差；$ {u_k} $为第$ k $位专家的评估分值；$ {L_i} $为第$ i $项绿色要素二维云贴进度；$ C_i^{\max} $、$ C_i^{{\mathrm{mix}}} $分别为$ i $项绿色要素贴进度所处区间范围的上限和下限；$ {V_i} $为第$ i $项绿色要素二维云评价值；$ {E_{{\text{hj}}}} $和$ {E_{{\text{gj}}}} $分别为标准风险云后果等级和概率等级的期望值，具体云评价等级标准依照参考文献[17-18].
2.2.3 综合重要度
综合重要度由自身属性重要度及影响间重要度构成，综合重要度越大，代表该绿色要素越重要. 第$ i $项绿色要素的综合重要度为
Ii=(Wi/f∑i=1Wi+Vi/f∑i=1Vi)/2,f=m,n, (5) 式中：${V_i} $为第$i $项绿色要素二维云评价值；$ \displaystyle\sum\limits_{i = 1}^{f} {{W_i}} $和$ \displaystyle\sum\limits_{i = 1}^{f} {{V_i}} $分别为自身属性重要度总值和影响路径重要度的总值；$ m $为路基工程系统的绿色要素个数，如图2中绿色要素$ {x_1} $ ～ $ {x_{19}},m=19 $；$ n $为环境系统的绿色要素个数，如图2中绿色要素$ {x_{20}} $ ～ $ {x_{26}},n=7 $.
2.3 目标函数建立
实现铁路“路基-环境”相容共生的首要目的是他们彼此间的协调状态最优，而耦合协调度模型可在多个系统或子系统之间进行协调和交互的过程中分析事物的协调发展水平. 因此，通过耦合协调度模型对协调状态的测度，可以明晰“路基-环境”耦合协调状态是否有进一步提升空间[19-20]，关系如式（6）所示
{minD=1−(Ta+Tb2(TaTb×[1−(Tb−Ta)])1/2)1/2,Ta=m∑i=1ωixi,g,Tb=n∑i=1ωixi,g, (6) 式中：$ {T_{\text{a}}} $、$ {T_{\text{b}}} $分别为路基工程、环境的综合发展水平，表示在绿色要素相互作用的影响下系统发展水平的高低；$ D $为耦合协调度，具体标准划分如表1所示[21-22]，表示为路基工程与环境之间在绿色要素作用下耦合协调状态的强弱；$ \omega _{_i}^{} $为第$ i $项绿色要素的权值.
表 1 耦合协调度划分标准Table 1. Classification criteria for ccoupling coordination degree第1分类 划分标准 第2分类及划分标准 协调发展类 0.9＜D≤1.0 优质协调 0.8＜D≤0.9 良好协调 0.7＜D≤0.8 中级协调 0.6＜D≤0.7 初级协调 过渡发展类 0.5＜D≤0.6 勉强发展 0.4＜D≤0.5 濒临失调 失调衰退类 0.3＜D≤0.4 轻度失调 0.2＜D≤0.3 中度失调 0.1＜D≤0.2 严重失调 0＜D≤0.1 极度失调 2.4 约束条件构建
2.4.1 “路基-环境”影响关系约束
参考《铁路路基设计规范》（TB 10001—2016）[14]、《铁路工程环境保护设计规范》（TB 10501—2016）[15]、《铁路声屏障工程设计规范》（TB 10505—2019）[23]、《土壤侵蚀分类分级标准》（sl190—2007）[24]、《环境空气质量标准》（GB 3095—2012）[25]、《声环境质量标准》（GB 3096—2008）[26]、《地表水环境质量标准》（GB 3838—2002）[27]、《爆破安全规程》（GB 6722—2014）[28]及文献[29]，建立铁路“路基-环境”绿色要素函数关系，并明确环境绿色要素的限制范围，具体关系如式（7）所示.
{z27=z1+y(1+2.5(z10b−1)),z28=(ts(c1−z3)es+tyz13ey(c2−z2))φfcπr2,z29=(scWc/100+swWw/100)(1−z26),z30=q(z1/310R)α,z31=0.067W1.627wLSC(0.6508−0.3436×lg(z18z19/A)),z32=(z16z17+z14z15+z17z18)/A,z33=(z2+z3)nd+∑nq+20lg(0.006z0.52102×10−5),z34=ny−z20,z35=z18z19+z21z4z5+pqz4+z7z8+ptz7,z25⩽ (7) 式中：$ y $为原来的爆破产尘浓度（mg/m3），$ b $为原来爆破的炸药量（t），$ {t_{\text{s}}} $为施工机械工作台班数（台班），$ {t_{\text{y}}} $为运输机械运渣次数（次数），$ c_{1} $、$ c_{2} $分别为施工机械、运输机械总数目（台），$ {e_{\text{s}}} $为整体施工机械燃油消耗量均值（L），$ {e_{\text{y}}} $为整体运输机械燃油消耗量均值（L），$ \varphi $为燃油CO排放系数（mg/L），$ {f_{\text{c}}} $为路基长度与监测范围的比值，$ r $为CO监测点半径（m），$ {W_{\text{c}}} $为收集处理后废水（L），$ {W_{\text{w}}} $为未收集处理径流（L），$s_{\mathrm{c}} $、$ {s_{\text{w}}} $分别为收集、未收集废水里固体悬浮物（SS）含量（mg/L），$ q $、$ \alpha $分别为爆破点至保护对象间的地形、地质条件有关的系数和衰减系数，$ R $为爆破后安全允许距离（m），$ {L_{\text{S}}} $为地形因子，$ C $为土壤可蚀性因子，$ A $为路基边坡面积（m2）；$ {n_{\text{d}}} 、{n_{\text{q}}}、 {n_{\text{y}}}$分别为电能机械设备、燃油机械设备、机车运行噪声平均值（dB），$ {p_{\text{q}}} $为路堑边坡坡面长（m），$ {p_{\text{t}}} $为路堤边坡坡面长（m）.
2.4.2 “满载”约束
在魔方游戏模型中，魔方作为一个三维物体，具备空间特征，因此，将状态空间模型与魔方相结合[30]，构成三维空间约束模型，为展现旋转过程中错误率对魔方的施压承载效果，引入超曲面概念，将三维空间映射成XOY二维超曲面状态，以X轴表示魔方横向约束，Y轴表示为魔方纵向约束，Z轴表示为魔方游戏的转动错误率，如图4所示. XYZ表现为最佳的错误率曲面. 点Ac表现为玩家在规定时间前提下错误率最佳状态，点Bc表现为玩家为降低错误率损失了时间，点Cc表现为玩家过于强调时间，错误率高于魔方承受的次数限值，魔方损坏，得分扣除.
因此，将魔方游戏施压承载模型应用于铁路“路基-环境”，确保路基工程建设活动对环境的影响始终处于XYZ曲面，使两系统在相互耦合过程中达到一种临界状态，即在不破坏环境条件下，路基工程设计资源投入最大化，构建“路基-环境”满载约束. 关系如式（8）所示.
\left\{ \begin{array}{l} 1 - c \leqslant {X_{{\text{rgs}}}} = \dfrac{{{F_{l}} \cos \;\theta }}{{{F_{s}}}} \leqslant 1 + c , \\ {F_u} = { \sqrt{\displaystyle\sum\limits_{i = 1}^f {{w_i}x^{2}_{i,{\mathrm{g}}}} }},f = m,n,\;u \in \{{l,{\mathrm{s}}}\}, \\ \cos \;\theta = \dfrac{{\displaystyle\sum\nolimits_{i = 1}^{m} \displaystyle\sum\nolimits_{i = 1}^{n} {x^2_{i,{\text{g}}}} }}{\sqrt{{{ {\displaystyle\sum\limits_{i = 1}^m {x{{_{i,{\text{g}}}^2}^{}}\displaystyle\sum\limits_{i = 1}^n {x_{i,{\text{g}}}^2} } } }}}}, \end{array} \right. (8) 式中：$ {F_{l}} $为环境理想承载力，表示为路基工程建设活动对环境的影响限值；$ {F_{s}} $为环境实际影响值，表示为路基工程建设活动对环境的实际影响效果；$ \theta $为随机旋转角度；$ {X_{{\text{rgs}}}} $为绿色耦合效率指数，表征路基工程与环境之间的施压承载状态，用于判断是否存在设计资源的浪费；$ c $为路基工程建设方的决策偏向，值越大，表示越偏向于环境保护，越小越，表示越偏向于工程设计投入高效利用，本文取值0.1；$ {X_{{\text{rgs}}}} \leqslant 1 - c $，表示路基工程建设活动强度小于环境承载力（可载）；$ 1 - c \leqslant {X_{{\text{rgs}}}} \leqslant 1 + c $，表示路基工程建设活动强度刚好处于环境承载力之内（满载）；$ 1 + c \leqslant {X_{{\text{rgs}}}} $，表示路基工程建设活动强度大于环境承载力（超载）.
3. 模型求解—变色龙群优化算法
变色龙群优化算法（CSA）是Braik于2021年提出的一种改进变色龙算法（CA）. 该算法能够通过模拟变色龙猎食动态行为进行数学建模和计算，相较于传统的模拟退火算法（SA）、粒子群算法等，具有搜索能力强，收敛速度快等特征[31-32]，且能够有效处理单、多目标复杂问题，符合本文所构建的优化调控模型. 主要步骤如下：
步骤1 搜索猎物
变色龙的搜寻食物行为如式（9）所示.
{y}_{t + 1,\lambda ,\eta }^{}=\left\{\begin{array}{ll}{y}_{t,\lambda ,\eta }^{} + {p}_{1}\left({P}_{t,\lambda ,\eta }^{}-{G}_{t,\eta }^{}\right){r}_{2} +\\ \quad{p}_{2}\left({G}_{t,\eta }^{}-{y}_{t,\lambda ,\eta }^{}\right){r}_{1},\quad{\text{当}}{r}_{q}\geqslant{P}_{\text{p}}, \\ {y}_{t,\lambda ,\eta }^{} + \mu \left(\left({u}_{\text{b}}-{l}_{\text{b}}\right){r}_{3} + {l}_{\text{b}}\right)\\ \quad \mathrm{sgn}(r_{\text{a}}-0.5),\quad{\text{当}}{r}_{q} \lt {P}_{\text{p}}, \end{array} \right. (9) 式中：$ y_{t,\lambda ,\eta }^{} $为$ t $次迭代第$ \lambda $只变色龙在$ \eta $维迭代后的位置；${p}_{1} $、${p}_{2} $为控制算法搜索能力的正系数；$ {P_{\text{p}}} $为感知猎物的概率；${r}_{q} $、${r}_{{\mathrm{a}}} $为（0,1）间的随机数；$ {{\mathrm{sgn}}} (r_{\text{a}} - 0.5) $代表变色龙旋转的方向，一般取值为±1；$ P_{t,\lambda ,\eta }^{} $为第$ t $次迭代第$ \lambda $只变色龙在$ \eta $维迭代后的最佳位置；$ G_{t,\eta }^{} $为第$ t $次迭代在$ \eta $维中的全局最优位置；$ {r_1} $,$ {r_2} $,$ {r_3} $为0到1之间产生的随机数值；$ {u_{\text{b}}} $、$ {l_{\text{b}}} $分别为搜索空间的上界和下界；$ \mu $为通过$ t $表达的变色龙搜索能力，$ \mu = {{\mathrm{e}}^{{{( - \delta t/{T_{\text{c}}})}^3}}} $，其中，$ \delta $为敏感系数，$ {T_{\text{c}}} $为最大迭代次数.
步骤2 旋转眼睛搜索
变色龙能利用眼睛360°旋转获取食物的具体位置，并且也会根据猎物的位置变化而更新自己的位置，更新位置关系如式（10）所示.
\left\{\begin{array}{l} {y}_{t + 1,\lambda }^{}={m}_{\text{b}}({y}_{t,\lambda }-{y}_{t,{\lambda },{\text{q}}}) + {y}_{t,{\lambda },{\text{q}}},\\ {m}_{\text{b}}={R}_{\text{b}}(\theta ,{V}_{\text{z}1},{V}_{\text{z2}})\\ \theta ={r}_{\text{q}}\mathrm{sgn}(r_{\text{a}}-0.5)\text{π},\end{array}\right. (10) 式中：$ {y}_{t + 1，\lambda }^{} $为第$ \lambda $只变色龙在第$ t + 1 $次迭代位置；$ y_{t,{\lambda ,{\text{q}}}} $为第$ \lambda $只变色龙第$ t $次迭代的中心位置；$ {{\boldsymbol{m}}_{\text{b}}} $为变色龙眼睛的旋转矩阵；$ {{\boldsymbol{R}}_{\text{b}}} $(·)为旋转矩阵的生成函数；$ {{\boldsymbol{V}}_{{\text{z}}1}} $，$ {{\boldsymbol{V}}_{{\text{z2}}}} $为坐标空间形成的2个正交向量.
步骤3 吐舌捕食猎物
在更新位置后，一旦猎物离自己较近，可以用吐舌的方式进行捕捉猎物，并且这时候的位置称为最优解，具体关系如式（11）所示.
\left\{ \begin{array}{l} v_{t + 1,\lambda ,\eta }^{} = v_{t,\lambda ,\eta }^{} + {\varpi _1}{r_1}\left( {{G_{t,\eta }} - {y_{t,\lambda ,\eta }}} \right) + {\varpi _2}{r_2}\left( {{P_{t,\lambda ,\eta }} - {y_{t,\lambda ,\eta }}} \right), \\ y_{t + 1,\lambda ,\eta }^{} = {y_{t,\lambda ,\eta }} + \dfrac{{ {{{\left( {v_{t,\lambda ,\eta }^{}} \right)}^2} - {{\left( {v_{t - 1,\lambda ,\eta }^{}} \right)}^2}} }}{{2a}},\\ a = 2590(1 - {{\mathrm{e}}^{ - \lg \;t}}), \end{array} \right. (11) 式中：$ v_{t,\lambda ,\eta }^{} $为第$ t $次迭代的速度；$ {\varpi _1} $、$ {\varpi _2} $分别为$ {G_{t,\eta }} $和$ {P_{t,\lambda ,\eta }} $的认知因子；$ a $为变色龙的加速度，随着$ t $的变化而非线性变化.
整体的变色龙群优化算法流程如图5所示.
4. 案例分析
选取山区某铁路路基为研究对象，全线路基包含隧道出口段和进口段两部分，共1178 m，地处区域地势地形极其复杂，高差大，工程施工多为高路堤深路堑形式，施工难度巨大. 此外，由于地处峡谷边缘区，峡谷风剧烈并伴随强降水，易引发水土流失，路基边坡防护设计任务艰巨，路基区域附近多湿地、暗河等水体，植物、动物及附近居民需求高，环境保护要求高，脆弱的环境因素会对路基工程的建设活动产生重大影响，有必要挖掘关键要素，并对其进行优化调控.
4.1 “路基-环境”绿色关键要素识别
结合现场实测数据及相关工程文件，依据鲍学英等[15]对于绿色关键要素的识别方法，构建多层复杂关联网络，通过式（1） ～ （5）分别得到路基工程及环境系统绿色要素的综合重要度，路基工程内部绿色要素$ {x_1} $ ～ $ {x_{19}} $的综合重要度依次为0.06、0.03、0.11、0.09、0.03、0.02、0.03、0.02、0.04、0.04、0.08、0.06、0.10、0.11、0.04、0.04、0.04、0.04、0.03，环境绿色要素$ {x_{20}} $ ～ $ {x_{26}} $的综合重要度依次为0.07、0.21、0.08、0.10、0.28、0.05、0.21，因此，识别影响“路基-环境”相容共生的绿色关键要素为路堑开挖尺寸、路堤填筑尺寸、支挡结构设计、支挡结构布设、工程防护结构设计、边坡工程防护布设、植物防护结构设计、边坡植物防护布设、生态声屏障结构设计、生态声屏障布设.
4.2 “路基-环境”耦合协调状况分析
通过式（1）、（6）求得路基工程与环境的耦合协调度值为0.672，通过式（8）求得绿色耦合效率值为1.65，表示该“路基-环境”处于超载状态，耦合协调度也相对较低，处于初级协调，需要降低工程上投入，并将绿色关键要素作为主控变量进行优化调控，促使“路基-环境”保持满载的状态下耦合协调度向上提升.
4.3 “路基-环境”耦合优化模型求解
基于上述分析，结合式（6） ～ （8），设置求解模型的目标函数及约束条件，基于MATLAB平台并使用式（9） ～ （11）编写变色龙群算法程序，设置相关参数，种群数量为400个，最大迭代次数为5000次. 同时，为了对比CSA算法的准确性和科学性，将SA和新型麻雀搜索算法（SSA）进行对比，在同一平台运行20次，得到最终的耦合协调度最优值及相关的变量参数. 取其中具有代表性的一次结果，如图6所示.
相比SA及SSA算法结果，CSA算法的求解效果最接近于最优值，这是由于在建模过程中，CSA算法模拟了变色龙眼睛360°旋转特征，使猎物被发现的概率增加，并能使用高速发射的粘性舌头高效率捕捉猎物，具备较强的局部最优脱困能力，精准获取全局最优值，从而求解效果较好.
CSA算法求得的山区铁路“路基-环境”绿色耦合效率值为1.04、耦合协调度最优值为0.77，表明路基工程建设活动对环境的影响处于环境承载力临界区间，“路基-环境”协调水平由初级协调提升到中级协调状态.
如图7所示，整体主控变量优化情况大致分为3个等级. $ {x_{10}} $、$ {x_{11}} $、$ {x_{12}} $、$ {x_{14}} $优化比例较高，达到70%左右，是影响该“路基-环境”相容共生最主要绿色关键要素，应优先对其进行调控；$ {x_3} $、$ {x_4} $、$ {x_9} $优化比例达到45%左右，是次要需要进行调控的要素；$ {x_{13}} $、$ {x_{15}} $、$ {x_{16}} $优化比例最小，处于20%区间，表明在这些绿色关键要素领域路基建设活动较为成熟，调控幅度较小. 基于此，在满足工程可靠性且不浪费设计资源的前提下，通过以上主控变量的分级优化调控，促使“路基-环境”耦合协调状态向相容共生转变.
图 7 主控变量最优解优化比例Figure 7. Optimization proportion of optimal solution for main control variables5. 结 论
1） 将铁路“路基-环境”复杂的耦合状况通过耦合魔方游戏模型进行展现，解释了铁路“路基-环境”的最优耦合状态为满载条件下协调水平最优，提出了铁路“路基-环境”调控框架；运用耦合协调度模型和施压承载模型对某山区铁路路基工程与环境之间的耦合状况进行分析，表明该“路基-环境”协调水平处于初级协调和“超载”状态，存在一定的优化空间.
2） 构建以山区铁路“路基-环境”协调水平最优为目标，各绿色要素函数关系及满载条件约束的耦合调控优化模型，采取变色龙群算法对主控变量进行优化求解，得到满载条件下最优耦合协调值和路堑开挖尺寸、路堤填筑尺寸、支挡结构设计、支挡结构布设、工程防护结构设计、边坡工程防护布设、植物防护结构设计、边坡植物防护布设、生态声屏障结构设计、生态声屏障布设主控变量的优化比例，为山区铁路“路基-环境”调控优化提供了思路.
3） 将变色龙群优化算法和传统算法SA及新型算法SSA进行结果对比，结果表明CSA算法全局搜索能力最优，论证了该模型的有效性与科学性.
-
图 1 小半径曲线轨道的低轨上产生的短波长波磨和长波长波磨
Figure 1. Short-pitch and long-pitch rail corrugation arising on low rail of small-radius curved tracks
图 2 发生在钢轨波磨区域的e型弹条断裂
Figure 2. e-type clip fracture occurring in rail corrugation area
图 4 地铁e型弹条振动加速度的PSD分析结果
Figure 4. PSD analysis results of vibration acceleration of e-type clip
图 9 e型弹条振动加速度的谐响应分析结果
Figure 9. Harmonic response analyis results of vibration acceleration of e-type clip
图 10 轮对-轨道-扣件系统有限元模型
Figure 10. Finite element model of wheelset‒rail‒fastening system
图 11 预测得到的轮轨系统不稳定振动的频率
Figure 11. Predicted unstable vibration frequencies in wheelset‒rail system
图 12 添加了周期性不平顺的有限元模型（振幅放大8倍）
Figure 12. Finite element model with periodic irregularity （vibration amplitude is enlarged by 8 times）
图 13 不同轨道上的弹条振动加速度
Figure 13. Vibration acceleration of e-type clip on different tracks
图 14 e型弹条振动加速的PSD分析结果
Figure 14. PSD analysis resukts of vibration acceleration of e-type clip
图 15 钢轨波磨影响下的e型弹条振动疲劳寿命云图
Figure 15. Cloud map of vibration fatigue life of e-type clip under influence of rail corrugation
图 16 短波长波磨的幅值、波长变化对弹条振动疲劳寿命的影响
Figure 16. Effect of amplitude and wavelength variation in short-pitch rail corrugation on vibration fatigue life of clip
图 18 长波长波磨的幅值变化对弹条振动疲劳寿命的影响
Figure 18. Effect of amplitude variation in long-pitch rail corrugation on vibration fatigue life of clip
图 19 长波长波磨引起的弹条振动加速度PSD分析结果
Figure 19. PSD analysis results of vibration acceleration of clip caused by long-pitch rail corrugation
表 1 2处曲线轨道的线路参数
Table 1. Line parameters of two curved tracks
位置 缓和曲线
长度/m超高/
mm曲线
半径/m曲线
长度/m第 1 处
曲线轨70 85 500 199.280 第 2 处
曲线轨60 115 350 651.031 
下载: 导出CSV
表 2 发生在弯轨上的钢轨波磨的位置信息及类型
Table 2. Types and location information of rail corrugation at curved tracks
区段 第 1 次观测
（开通前）第 2 次观测
（空载试运营）第 3 次观测
（开通后两个月）第 4 次观测
（开通后一年）R = 350 m 的曲线轨道低轨 无波磨 短波：
22～25 mm短波：
22～30 mm短波：22～30 mm、40～50 mm
长波：120～250 mmR = 350 m 的曲线轨道高轨 无波磨 无波磨 无波磨 无波磨 R = 500 m 的曲线轨道高轨和低轨 无波磨 无波磨 无波磨 无波磨 直线轨道 无波磨 无波磨 无波磨 无波磨
下载: 导出CSV
表 3 扣件系统的材料参数
Table 3. Material parameters of fastening system
部件 密度/
（g·cm−3）弹性模量/
MPa泊松比 轨距挡块 1.57 8500 0.4 弹条 7.80 2.06 × 105 0.3 铁垫板 7.80 1.73 × 105 0.26
下载: 导出CSV
表 4 不同“低通信号”下的e型弹条振动疲劳寿命
Table 4. Vibration fatigue life of e-type clips under influence of different “low-pass signals”
信号 振动疲劳寿命/（×106次） 完整信号 1.18 2.0 kHz“低通” 1.185 1.2 kHz“低通” 2.637
下载: 导出CSV
-
[1] COLLETTE C, VANHONACKER P, BASTAITS R, et al. Comparison between time and frequency studies of a corrugated curve of RER Paris network[J]. Wear, 2008, 265(9): 1249-1258. [2] TORSTENSSON P T, NIELSEN J C O. Monitoring of rail corrugation growth due to irregular wear on a railway metro curve[J]. Wear, 2009, 267(1/2/3/4): 556-561. [3] CARLBERGER A, TORSTENSSON P T, NIELSEN J C, et al. An iterative methodology for the prediction of dynamic vehicle–track interaction and long-term periodic rail wear[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2018, 232(6): 1718-1730. doi: 10.1177/0954409717747127 [4] 陈光雄. 钢轨波磨预测模型验证工况的研究[J]. 西南交通大学学报,2022,57(5): 1017-1023,1054.CHEN Guangxiong. Study on validation conditions of rail corrugation prediction models[J]. Journal of Southwest Jiaotong University, 2022, 57(5): 1017-1023,1054. [5] ZHANG H G, LIU W N, LIU W F, et al. Study on the cause and treatment of rail corrugation for Beijing metro[J]. Wear, 2014, 317(1/2): 120-128. [6] GRASSIE S L, KALOUSEK J. Rail corrugation: characteristics, causes and treatments[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1993, 207(1): 57-68. doi: 10.1243/PIME_PROC_1993_207_227_02 [7] GRASSIE S L. Rail corrugation: characteristics, causes, and treatments[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2009, 223(6): 581-596. doi: 10.1243/09544097JRRT264 [8] OOSTERMEIJER K H. Review on short pitch rail corrugation studies[J]. Wear, 2008, 265(9/10): 1231-1237. [9] VALEHRACH J, GUZIUR P, RIHA T, et al. Assessment of rail long-pitch corrugation[J]. IOP Conference Series: Materials Science and Engineering,2017,236:012048.1-012048.8. [10] 杜茂金. 南京地铁DT Ⅵ2型扣件弹条折断原因分析[J]. 城市轨道交通研究,2009,12(7): 40-42.DU Maojin. Analysis of DT Ⅵ2 type fastener broken shells in Nanjing metro[J]. Urban Mass Transit, 2009, 12(7): 40-42. [11] 肖宏,马春生,郭骁,等. e型扣件弹条断裂原因频谱分析[J]. 同济大学学报(自然科学版),2017,45(7): 1000-1008.XIAO Hong, MA Chunsheng, GUO Xiao, et al. Fractures of e-type fastening clip by spectral analysis method[J]. Journal of Tongji University (Natural Science), 2017, 45(7): 1000-1008. [12] LING L, LI W, SHANG H X, et al. Experimental and numerical investigation of the effect of rail corrugation on the behaviour of rail fastenings[J]. Vehicle System Dynamics, 2014, 52(9): 1211-1231. doi: 10.1080/00423114.2014.934844 [13] WANG P, LU J, ZHAO C Y, et al. Numerical investigation of the fatigue performance of elastic rail clips considering rail corrugation and dynamic axle load[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2020, 235(3): 339-352. [14] XIAO H, WANG J B, ZHANG Y R. The fractures of e-type fastening clips used in the subway: theory and experiment[J]. Engineering Failure Analysis, 2017, 81: 57-68. doi: 10.1016/j.engfailanal.2017.07.006 [15] XIAO H, GUO X, Wang H Y, et al. Fatigue damage analysis and life prediction of e-clip in railway fasteners based on ABAQUS and FE-SAFE[J]. Advances in Mechanical Engineering, 2018, 10(3): 1-12. [16] MA D K, SHI J, YAN Z Q, et al. Experimental and numerical investigation of the effect of the assembled state on the static-dynamic characteristics and fatigue performance of railway fastening clips[J]. Structures, 2022, 46: 1808-1822. doi: 10.1016/j.istruc.2022.11.038 [17] HASAP A, PAITEKUL P, NORAPHAIPHIPAKSA N, et al. Influence of toe load on the fatigue resistance of elastic rail clips[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2018, 232(4): 1078-1087. doi: 10.1177/0954409717707834 [18] HASAP A, PAITEKUL P, NORAPHAIPHIPAKSA N, et al. Analysis of the fatigue performance of elastic rail clip[J]. Engineering Failure Analysis, 2018, 92: 195-204. doi: 10.1016/j.engfailanal.2018.05.013 [19] 崔晓璐,彭双千,徐佳,等. 钢轨波磨区段科隆蛋扣件弹条断裂机理[J]. 西南交通大学学报,2023:1-9.CUI Xiaolu, PENG Shuangqian, XU Jia, et al. Fracture Mechanism of Cologne-Egg Fastener Clip in Corrugated Sections of Metros[J]. Journal Of Southwest Jiaotong University, 2023: 1-9. [20] SADEGHI J, SEYEDKAZEMI M, KHAJEHDEZFULY A. Nonlinear simulation of vertical behavior of railway fastening system[J]. Engineering Structures,2020,209(C):110340.13-110340.13. [21] 徐井芒,梁新缘,王凯,等. 扣件刚度非线性对波磨区轮轨瞬态滚动接触行为影响研究[J]. 西南交通大学学报,2024,59(2): 1-8.Xu Jingmang, Liang Xinyuan, Wang Kai, et al. Influence of fastener stiffness nonlinearity on wheel-rail transient rolling contact behavior in corrugated area[J]. Journal of Southwest Jiaotong University, 2024, 59(2): 1-8. [22] WANG Z Q, LEI Z Y, ZHAO Y, et al. Rail Corrugation Characteristics of Cologne Egg Fastener Section in Small Radius Curve[J]. Shock and Vibration, 2020, 2020: 1-12. [23] LIU X G, WANG P. Investigation of the generation mechanism of rail corrugation based on friction induced torsional vibration[J]. Wear, 2021, 468/469: 203593, 9. [24] GRASSIE S L. Rail corrugation: a problem solved?[J]. Wear, 2023, 530/531(9/10): 1-8. [25] DONG B J, CHEN G X, SONG Q F, et al. Study on long-term tracking of rail corrugation and the influence of parameters[J]. Wear, 2023, 523(1-2): 1-13. [26] SUN L L, YAN Z Q, XIAO J H, et al. Experimental analysis of the modal characteristics of rail fastening clips[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2019, 234(2): 134-141. [27] OREGUI M, LI Z, DOLLEVOET R. Identification of characteristic frequencies of damaged railway tracks using field hammer test measurements[J]. Mechanical Systems and Signal Processing, 2015, 54/55: 224-242. doi: 10.1016/j.ymssp.2014.08.024 [28] KINKAID N, O’REILLY O, PAPADOPOULOS P. Automotive disc brake squeal[J]. Journal of Sound and Vibration, 2003, 267(1): 105-166. doi: 10.1016/S0022-460X(02)01573-0 [29] 国家质量监督检验检疫总局,中国国家标准化管理委员会. 弹簧钢:GB/T 1222—2016[S]. 北京:中国标准出版社,2016. [30] CUI X L, BAO P Y, LI Tong, et al. Research on the failure mechanism of elastic strip fracture in corrugated sections of metros[J]. Engineering Failure Analysis, 2023, 143: 1-12. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 215
- HTML全文浏览量: 99
- PDF下载量: 26
- 被引次数: 0