Modified Intersection Method for Solving Alignment Problems Containing Incomplete Transition Curves
-
摘要:
为解决公路线形设计过程中交点法依赖的非对称基本型计算模型，在转弯曲线包含非完整缓和曲线时出现计算失效的问题，以非对称基本型计算模型为基础，通过分析计算模型在解算非完整缓和曲线场景下的失效原因，对计算模型结构与求解逻辑予以优化改进，进而提出非对称通用型计算模型. 此模型新定义了缓和曲线方向，通过判断缓和曲线曲率变化趋势与路线行进方向间的关系，将缓和曲线划分为正向和逆向两类，再根据缓和曲线在单曲线中的前后关系，建立特殊局部坐标系，通过几何推导，得出非完整缓和曲线切线增长值和曲线内移值，进而可以使用非对称基本型计算模型进行求解. 研究表明：非对称通用型计算模型突破了非对称基本型计算模型对线形组合类型的限制，允许缓和曲线起、终点曲率半径可为任意值；通过与传统线元法对同一复杂曲线段进行解算对比，控制桩号里程值及控制桩号坐标的计算差异均小于1 mm，满足工程精度要求.
Abstract:To address the issue that the asymmetric basic type calculation model, which the intersection method relies on in highway alignment design, fails to perform calculations when turning curves include incomplete transition curves, the asymmetric basic type calculation model was used as the foundation. By analyzing the causes of the model’s failure in solving incomplete transition curve scenarios, the structure and solution logic of the calculation model were optimized and improved, and an asymmetric general type calculation model was further proposed. This new model introduced a novel definition of transition curve direction. It classified transition curves into two categories, positive and negative, by judging the relationship between the curvature change trend of the transition curve and the route’s traveling direction. Then, based on the positional order of the transition curve within a single curve, a special local coordinate system was established. Through geometric derivation, the tangential growth value and curve offset value of the incomplete transition curve were obtained, enabling the subsequent use of the asymmetric basic type calculation model for further solution. The research has shown that the asymmetric general type calculation model eliminates the restrictions of the asymmetric basic type model on alignment combination types, allowing the curvature radii at the start and end points of transition curves to be arbitrary values. By comparing the calculation results of the same complex curve segment with those obtained using the traditional element method, the differences in the calculated mileage values and coordinates of the control stakes are both less than 1 mm, which meets the engineering accuracy requirements.
-
图 2 完整缓和曲线与非完整缓和曲线图示
Figure 2. Illustration of complete transition curve and incomplete transition curve
图 4 正向缓和曲线内移值$ p $和切线增长值$ q $求解模型
Figure 4. Solving model of offset value $ p $ and tangential growth value $ q $ of positive transition curve
图 5 逆向缓和曲线内移值$ p $和切线增长值$ q $求解模型
Figure 5. Solving model of offset value $ p $ and tangential growth value $ q $ of negative transition curve
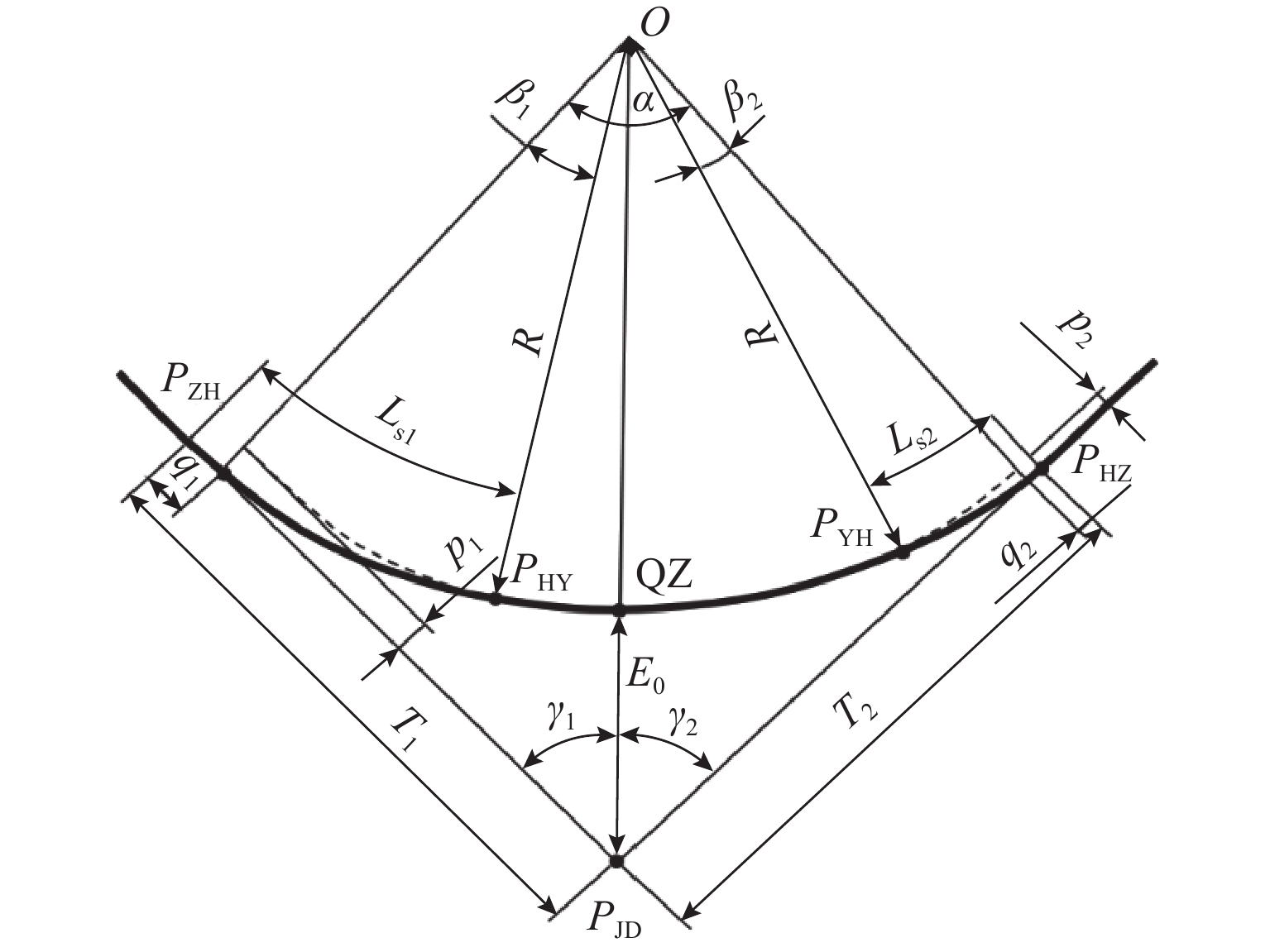
表 1 非对称通用型参数列表
Table 1. Parameters of asymmetric universal type
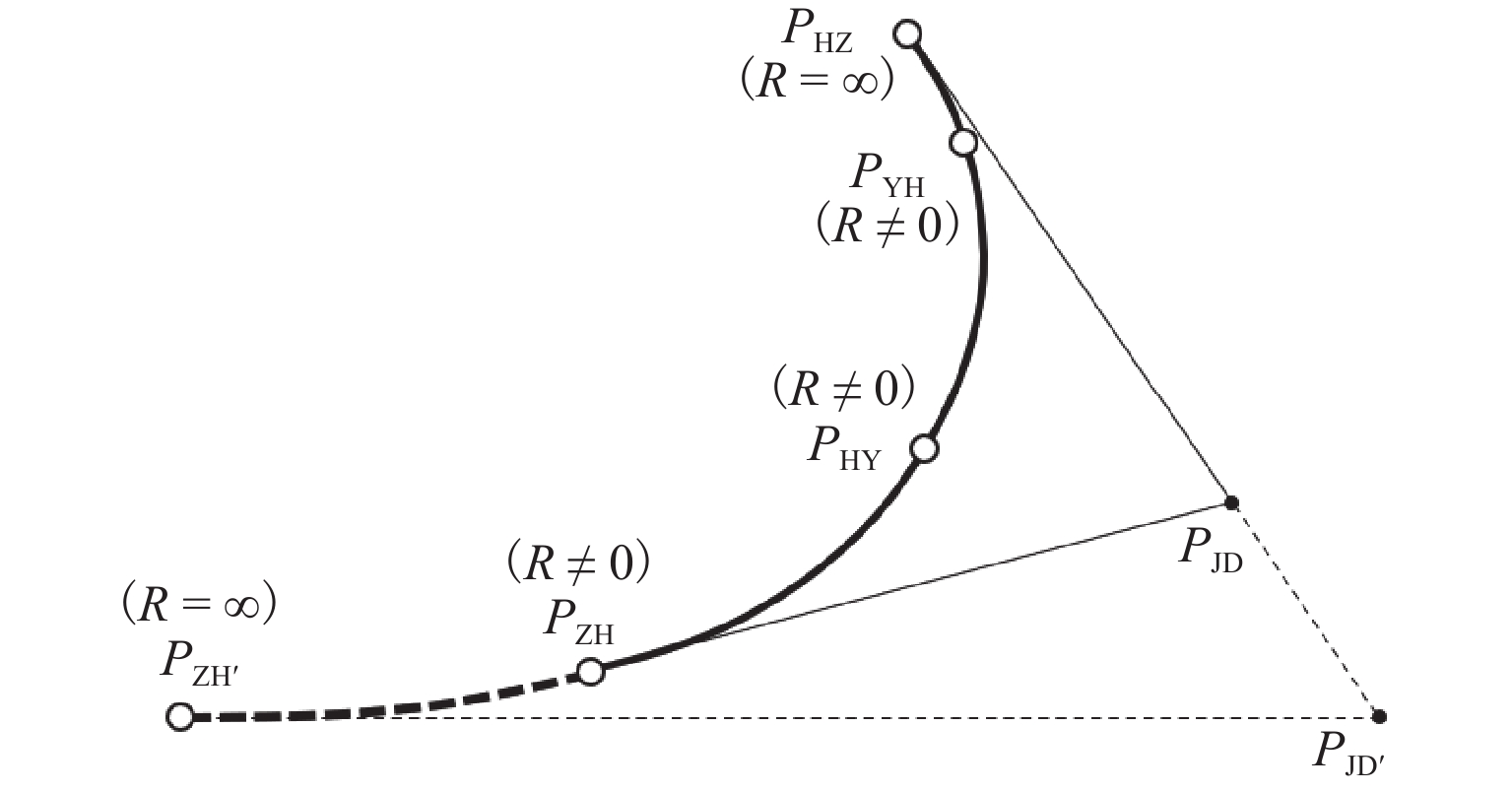
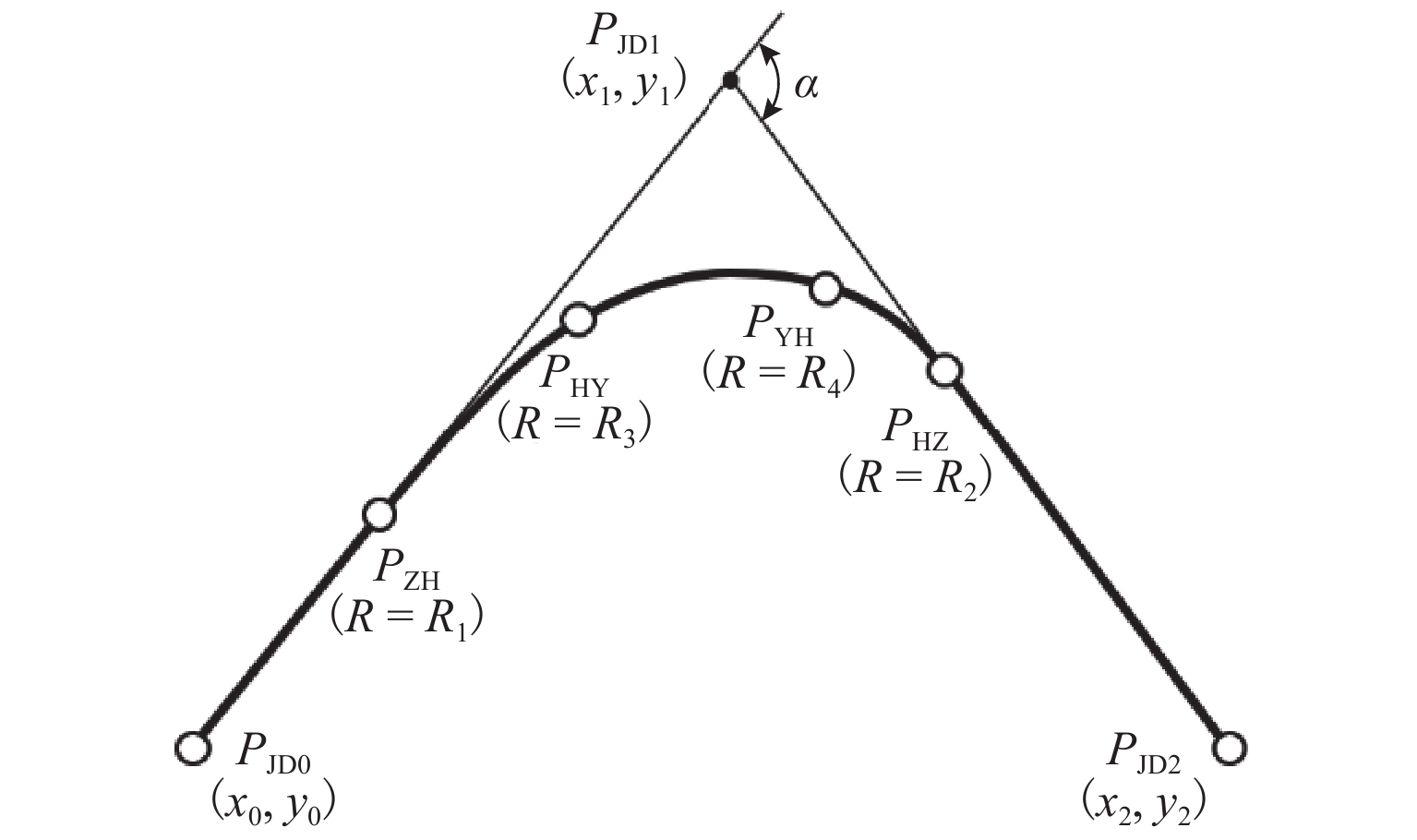
曲线段落 参数名 参数说明 前缓和曲线 $ {L}_{{\mathrm{s}}1} $ 前缓和曲线长度 $ {R}_{1} $ 前缓和曲线在$ P_{\mathrm{ZH}} $处曲率半径，当
为完整缓和曲线时，$ {R}_{1}=\infty $$ {R}_{3} $ 前缓和曲线在$ P_{\mathrm{HY}} $处曲率半径，等
于$ {R}_{{\mathrm{c}}} $圆曲线 $ {R}_{{\mathrm{c}}} $ 相接圆曲线半径 后缓和曲线 $ {L}_{{\mathrm{s}}2} $ 后缓和曲线长度 $ {R}_{2} $ 后缓和曲线在$ P_{{\mathrm{HZ}}} $处曲率半径，当
为完整缓和曲线时，$ {R}_{2}=\infty $$ {R}_{4} $ 后缓和曲线在$ P_{{\mathrm{YH}}} $处曲率半径，等
于$ {R}_{{\mathrm{c}}} $交点坐标 ($ {x}_{0},{y}_{0} $) PJD0 坐标 ($ {x}_{1},{y}_{1} $) PJD1 坐标 ($ {x}_{2},{y}_{2} $) PJD2 坐标 $ \alpha $ 转向角 
下载: 导出CSV
表 2 缓和曲线方向分类
Table 2. Classification of transition curve direction
曲线段 缓和曲线端曲率点半径关系 曲线方向 前缓和曲线 $ {R}_{1} $>$ {R}_{3} $ 正向 $ {R}_{1} $<$ {R}_{3} $ 逆向 后缓和曲线 $ {R}_{2} $>$ {R}_{4} $ 正向 $ {R}_{2} $<$ {R}_{4} $ 逆向
下载: 导出CSV
表 3 正向缓和曲线各求解步骤间参数输入输出关系
Table 3. Parameter input and output relationship between each solving step of positive transition curve
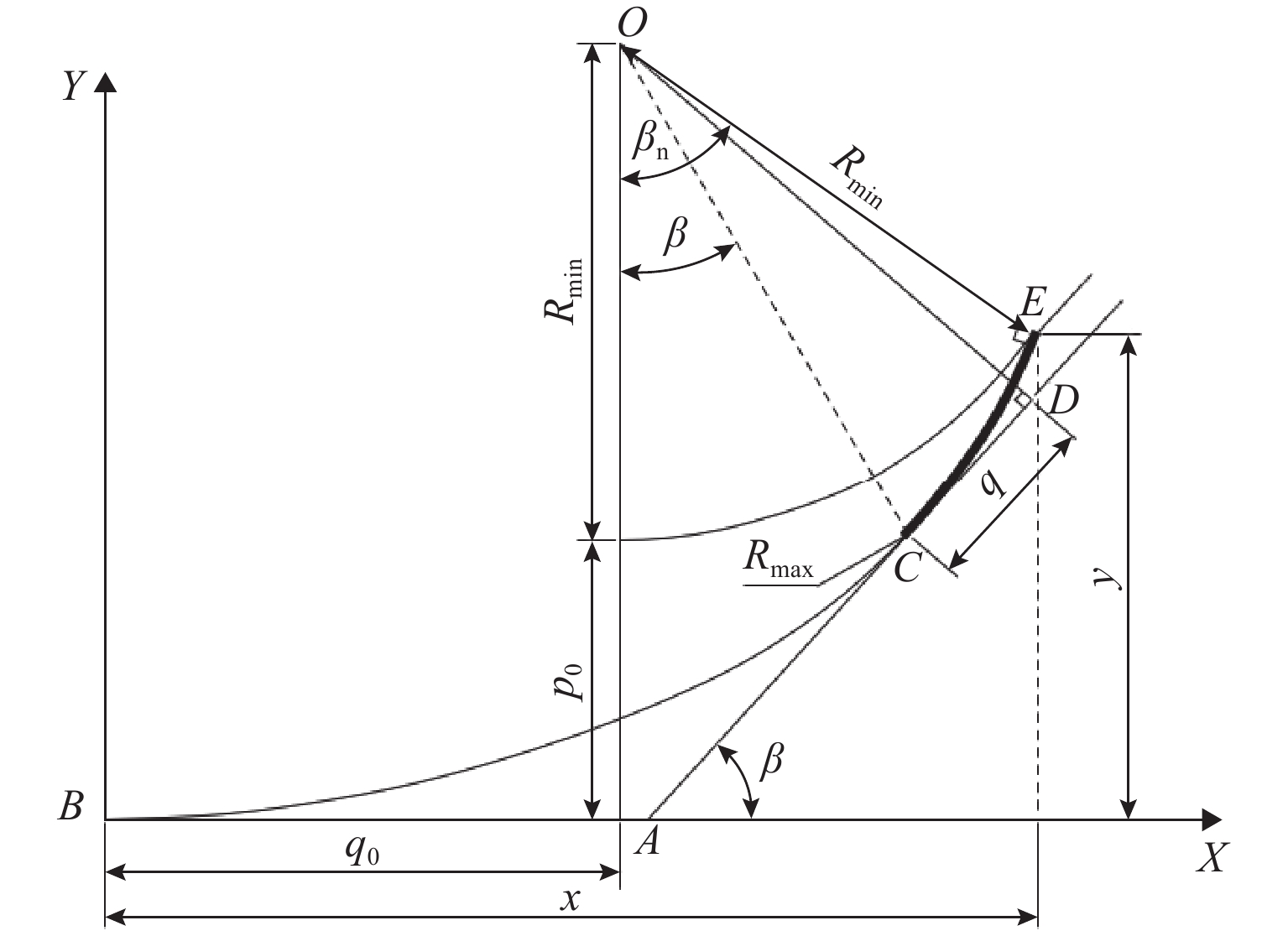
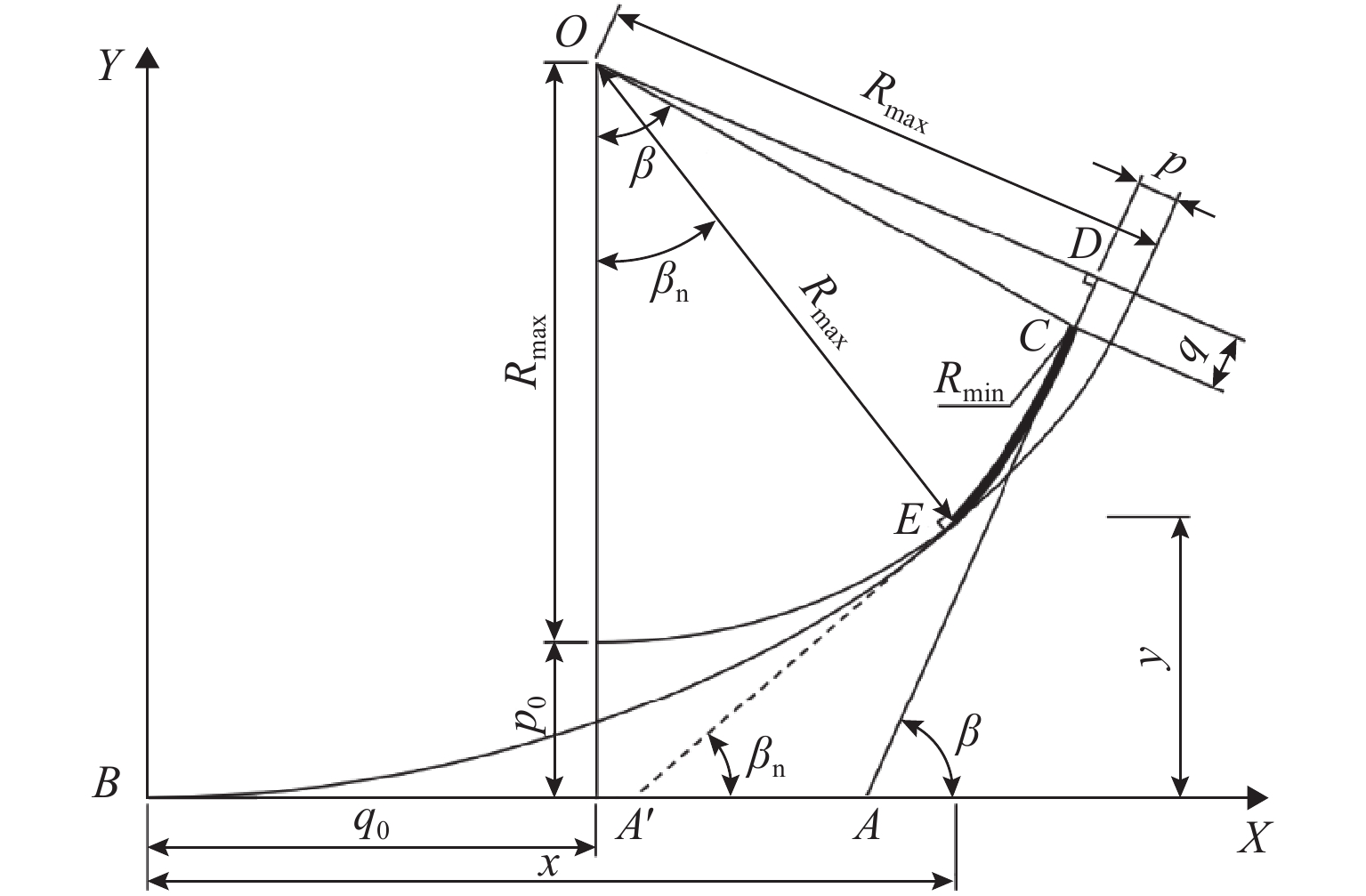
步骤 输入 输出 1 $ {L}_{{\mathrm{S}}} $、$ {R}_{{\mathrm{max}}} $、$ {R}_{{\mathrm{min}}} $ $ {L}_{{\mathrm{t}}} $、$ A $、$ {L}_{{\mathrm{m}}} $ 2 步骤 1 输出 $ x $、$ {y} $、$ {\beta }_{{\mathrm{n}}} $、$ {p}_{_0} $、$ {q}_{_0} $ 3 步骤 1 输出 $ \beta $ 4 步骤 3 输出 $ {k}_{_{AC}} $、$ {k}_{_{OD}} $ 5 步骤 2、4 输出 $ {x}_{_O} $、$ {y}_{_O} $、$ {x}_{_D} $、$ {y}_{_D} $ 6、7 步骤 2、3、5 输出 $ p $、$ q $、$ {\beta }_{{\mathrm{d}}} $
下载: 导出CSV
表 4 截取段落路线设计数据
Table 4. Design data of route section
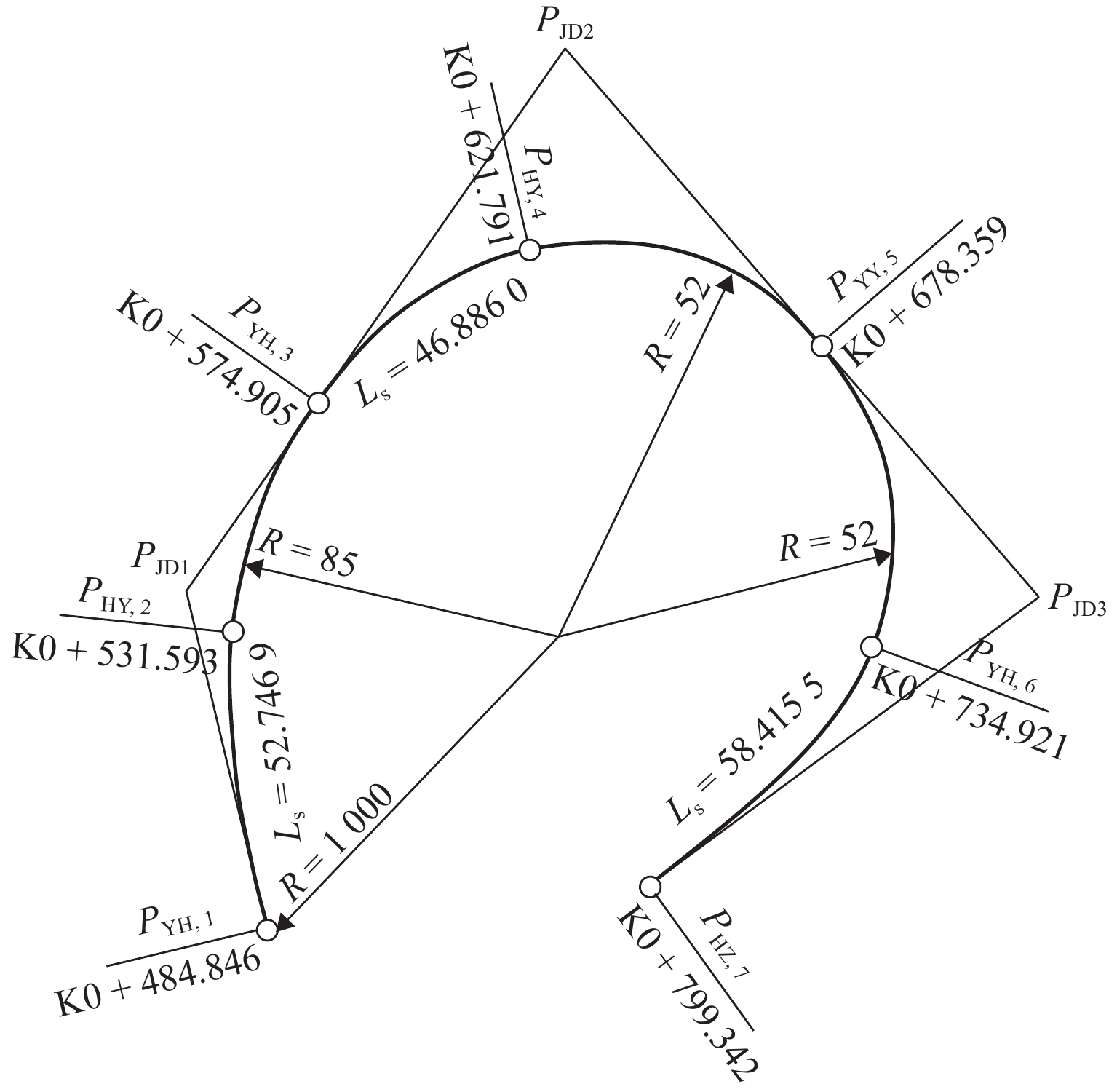
点位 前缓和曲线 圆曲线 后缓和曲线 转角 设计坐标值 切线方位角 Ls1/m R1/m R/m Ls2/m R2/m $ \alpha $ x/m y/m $ \varphi $ PJD1 52.747 1000 85 1.000×10−7 1×107 48.4839 °482328.7674 3450066.5663 346.4092 °PJD2 46.886 85 52 1.000×10−7 1×107 104.1498 °482395.2261 3450161.8571 34.8931 °PJD3 1.000×10−7 1e7 52 58.516 1×107 94.5106 °482478.8952 3450065.4611 139.0429 °
下载: 导出CSV
表 5 待校核点设计数据
Table 5. Design data of points to be checked
m 点位 坐标设计值 桩号里程 $ x $ $ y $ PYH，1 482343.0828 3450007.3520 478.846 PHY，2 482336.9930 3450059.4841 531.593 PYH，3 482351.8541 3450099.6689 574.905 PHY，4 482389.0167 3450126.5220 621.791 PYY，5 482440.2371 3450109.9994 678.359 PYH，6 482449.3910 3450056.9642 734.927 PHZ，7 482410.2139 3450014.7386 793.342
下载: 导出CSV
表 6 各交点前、后缓和曲线参数计算结果
Table 6. Calculation results of initial and terminal transition curve parameters at each intersection
交点 待求参数 前缓和曲线 后缓和曲线 $ {L}_{{\mathrm{t}}} $/m 57.64699454 1e-7 A0/m 69.99996097 3e-3 $ {L}_{{\mathrm{m}}} $/m 4.899994536 0 $ {\beta }_{{\mathrm{n}}} $ 0.339099968 °0 p0/m 1.62233421 0 q0/m 28.71337018 0 PJD1 $ \beta $ 0.002449997 °0 切点坐标/m （ 4.899991594 ,0.004001656 ）（0,0） $ {k}_{AC} $ 0.002450002 0 $ {k}_{OD} $ − 408.1629038 0 圆心$ O $坐标/m （ 28.71337018 ,86.62233421 ）（0,85） $ q $/m 24.02552159 0 $ p $/m 1.559729938 0 $ {\beta }_{{\mathrm{n}}} $/rad 0.336649971 0 $ q $/m 8.609745433 0 PJD2 $ p $/m 1.872194183 0 $ {\beta }_{{\mathrm{n}}} $/rad 0.729598901 0 $ q $/m 0 28.90335233 PJD3 $ p $/m 0 2.703741562 $ {\beta }_{{\mathrm{n}}} $/rad 0 0.561695228
下载: 导出CSV
表 7 各交点切线值计算结果
Table 7. Calculation results of tangential values at each intersection
切线长/m PJD1 PJD2 PJD3 $ {T}_{1} $ 60.92011083 75.81834455 58.97586509 $ {T}_{2} $ 40.35839291 68.66738024 85.38036815
下载: 导出CSV
表 8 各交点控制点坐标计算结果
Table 8. Calculation results of coordinates of control points at each intersection
m 点位 坐标项 PJD1 PJD2 PJD3 直缓点 (x, y) 482343.0826 ,3450007.3517 482351.8544 ,3450099.6693 482440.2369 ,3450109.9997 缓直点 (x, y) 482351.8539 ,3450099.6688 482440.2371 ,3450109.9995 482410.2142 ,3450014.7390
下载: 导出CSV
表 9 各控制桩坐标计算结果
Table 9. Calculation results of coordinates of each control stake
m 验证点位 坐标项 设计值 计算值 误差绝对值 PYH，1 (x, y) 482343.0828 ,3450007.3520 482343.0826 ,3450007.3517 2×10−4, 3×10−4 PHY，2 (x, y) 482336.9930 ,3450059.4841 482336.9929 ,3450059.484 1×10−4, 2×10−4 PYH，3 (x, y) 482351.8541 ,3450099.6689 482351.8539 ,3450099.6688 2×10−4, 1×10−4 PHY，4 (x, y) 482389.0167 ,3450126.5220 482389.0165 ,3450126.5223 2×10−4, 3×10−4 PYY，5 (x, y) 482440.2370 ,3450109.9994 482440.2369 ,3450109.9997 1×10−4, 3×10−4 PYH，6 (x, y) 482449.3910 ,3450056.9642 482449.3908 ,3450056.964 2×10−4, 3×10−4 PHZ，7 (x, y) 482410.2139 ,3450014.7386 482410.2142 ,3450014.7390 3×10−4, 4×10−4
下载: 导出CSV
表 10 各控制桩坐里程桩号计算结果
Table 10. Calculation results of mileage station of each control stake
m 验证点位 桩号校准值 计算值 误差绝对值 PYH，1 478.846 478.846 <1×10−3 PHY，2 531.593 531.593 <1×10−3 PYH，3 574.905 574.905 <1×10−3 PHY，4 621.791 621.791 <1×10−3 PYY，5 678.359 678.359 <1×10−3 PYH，6 734.342 734.927 <1×10−3 PHZ，7 739.342 793.342 <1×10−3
下载: 导出CSV
-
[1] 《中国公路学报》编辑部. 中国路基工程学术研究综述•2021[J]. 中国公路学报, 2021, 34(3): 1-49.Editorial Department of China Journal of Highway and Transport. Review on China’s subgrade engineering Research•2021[J]. China Journal of Highway and Transport, 2021, 34(3): 1-49. [2] 栾维新. 既有线改建平面设计最优化方法[J]. 西南交通大学学报, 1980, 15(3): 9-17.LUAN Weixin. Optimization method for plane realignment of existing lines[J]. Journal of Southwest Jiaotong University, 1980, 15(3): 9-17. [3] 丁建明, 李方. 公路平面线形设计的五单元导线法[J]. 东南大学学报, 1998, 28(2): 155-158.DING Jianming, LI Fang. Five element traverse method for highway horizontal alignment design[J]. Journal of Southeast University (Natural Science Edition), 1998, 28(2): 155-158. [4] 缪鵾, 詹振炎. 基于直线约束的道路线形设计通用方法[J]. 中国公路学报, 2002, 15(3): 15-17.MIU Kun, ZHAN Zhenyan. Universal method for highway’s horizontal alignment based on restrictions of straight line[J]. China Journal of Highway and Transport, 2002, 15(3): 15-17. [5] 李玉华, 孙依人, 刘佳音, 等. 路线平面线形设计计算的两点线元法原理[J]. 同济大学学报(自然科学版), 2021, 49(4): 507-516.LI Yuhua, SUN Yiren, LIU Jiayin, et al. Principle of two-point segmentary element method for horizontal alignment design and calculation[J]. Journal of Tongji University (Natural Science), 2021, 49(4): 507-516. [6] 谢峰. 基于GIS的高速公路路面管理智能决策模型研究[D]. 成都: 西南交通大学, 2012. [7] KIM E, JHA M K, SON B. Improving the computational efficiency of highway alignment optimization models through a stepwise genetic algorithms approach[J]. Transportation Research Part B: Methodological, 2005, 39(4): 339-360. doi: 10.1016/S0191-2615(04)00084-0 [8] JONG J C, JHA M K, SCHONFELD P. Preliminary highway design with genetic algorithms and geographic information systems[J]. Computer-Aided Civil and Infrastructure Engineering, 2000, 15(4): 261-271. doi: 10.1111/0885-9507.00190 [9] LEE Y, TSOU Y R, LIU H L. Optimization method for highway horizontal alignment design[J]. Journal of Transportation Engineering, 2009, 135(4): 217-224. doi: 10.1061/(ASCE)0733-947X(2009)135:4(217) [10] BOSURGI G, PELLEGRINO O, SOLLAZZO G. Using genetic algorithms for optimizing the PPC in the highway horizontal alignment design[J]. Journal of Computing in Civil Engineering, 2016, 30: 04014114. doi: 10.1061/(ASCE)CP.1943-5487.0000452 [11] 徐进, 陈莹, 张晓波, 等. 回头曲线路段的轨迹曲率特性和汽车过弯方式[J]. 西南交通大学学报, 2021, 56(6): 1143-1152.XU Jin, CHEN Ying, ZHANG Xiaobo, et al. Track curvature characteristics and vehicle cornering patterns on hairpin curves[J]. Journal of Southwest Jiaotong University, 2021, 56(6): 1143-1152. [12] 崔洪军, 魏连雨, 朱敏清, 等. 公路平面设计中有关问题的探讨[J]. 中国公路学报, 2002, 15(1): 22-25.CUI Hongjun, WEI Lianyu, ZHU Minqing, et al. Study of some horizontal curve design problems[J]. China Journal of Highway and Transport, 2002, 15(1): 22-25. [13] PAN B H, WEN C P, WANG K M, et al. Solution method and application verification of the K-curve as a highway transition curve[J]. KSCE Journal of Civil Engineering, 2021, 25(7): 2690-2700. doi: 10.1007/s12205-021-2193-0 [14] 袁胜强. 道路立交线形动态拖动设计关键技术[J]. 同济大学学报(自然科学版), 2007, 35(12): 1637-1641.YUAN Shengqiang. Critical questions of road interchange alignment dynamic drag design[J]. Journal of Tongji University (Natural Science), 2007, 35(12): 1637-1641. [15] KOBRYŃ A, STACHERA P. S-shaped transition curves as an element of reverse curves in road design[J]. The Baltic Journal of Road and Bridge Engineering, 2019, 14(4): 484-503. doi: 10.7250/bjrbe.2019-14.454 [16] ELIOU N, KALIABETSOS G. A new, simple and accurate transition curve type, for use in road and railway alignment design[J]. European Transport Research Review, 2014, 6(2): 171-179. doi: 10.1007/s12544-013-0119-8 [17] 宋占峰, 王健, 李军. 缓和曲线正交拟合的Levenberg-Marquardt算法[J]. 西南交通大学学报, 2020, 55(1): 144-149.SONG Zhanfeng, WANG Jian, LI Jun. Levenberg-marquardt algorithm for orthogonal fitting of transition curves[J]. Journal of Southwest Jiaotong University, 2020, 55(1): 144-149. [18] PEI Y L, HE Y M, RAN B, et al. Horizontal alignment security design theory and application of superhighways[J]. Sustainability, 2020, 12(6): 2222. doi: 10.3390/su12062222 [19] 潘兵宏, 王开明, 赵胜林, 等. 可用作公路缓和曲线的K型曲线数学模型及其特点分析[J]. 长安大学学报(自然科学版), 2020, 40(3): 33-41.PAN Binghong, WANG Kaiming, ZHAO Shenglin, et al. Mathematical model and characteristics analysis of K-curve that can be used as highway transition curve[J]. Journal of Chang’an University (Natural Science Edition), 2020, 40(3): 33-41. [20] MANIEI F, ARDEKAni S. Application of ellipse for horizontal alignment[J]. International Journal of Computational Engineering Research, 2013, 3(1): 35-51. [21] KOBRYŃ A. New solutions for general transition curves[J]. Journal of Surveying Engineering, 2014, 140(1): 12-21. doi: 10.1061/(ASCE)SU.1943-5428.0000113 [22] 张鹤. 公路几何设计三维线形评价模型研究[D]. 西安: 长安大学, 2019. [23] 张驰, 李永春, 吴斌, 等. 高速公路多心卵形曲线路段行车风险分析[J]. 公路, 2022, 67(3): 1-10.ZHANG Chi, LI Yongchun, WU Bin, et al. Analysis of traffic risk on the expressway sections with multi-centric oval curves[J]. Highway, 2022, 67(3): 1-10. [24] 潘兵宏, 谢振江, 赵胜林, 等. K型线与回旋线在卵形曲线上行车稳定性分析[J]. 长安大学学报(自然科学版), 2021, 41(1): 1-10.PAN Binghong, XIE Zhenjiang, ZHAO Shenglin, et al. Analysis of driving stability of K-curve and clothoid on oval curve[J]. Journal of Chang’an University (Natural Science Edition), 2021, 41(1): 1-10. [25] 徐越彤. 路线平面“两点法” 线形设计工程应用研究[D]. 大连: 大连理工大学, 2019. [26] 刘也嘉. 道路平面线形设计计算的两点法[D]. 大连: 大连理工大学, 2018. [27] 缪鹍, 詹振炎. 基于线元的公路平面线形交互设计方法研究[J]. 中国公路学报, 2001, 14(3): 25-29.MIAO Kun, ZHAN Zhenyan. Study of interactive design method for highway’s horizontal alignment based on segmentary element[J]. China Journal of Highway and Transport, 2001, 14(3): 25-29. [28] 张玲. 基于三次样条曲线拟合公路平面线形方法研究[D]. 武汉: 武汉理工大学, 2007. [29] 张航, 黄云, 龚良甫. 基于三次样条函数拟合公路平面线形方法研究[J]. 武汉理工大学学报(交通科学与工程版), 2007, 31(5): 925-927.ZHANG Hang, HUANG Yun, GONG Liangpu. Study on fitting highway alignment based on the cubic spline function[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2007, 31(5): 925-927. [30] 林雨, 杨轸, 潘晓东. 缓和曲线长度对车辆行驶轨迹的影响[J]. 西南交通大学学报, 2011, 46(2): 200-204.LIN Yu, YANG Zhen, PAN Xiaodong. Effect of spiral transition curve length on vehicle path[J]. Journal of Southwest Jiaotong University, 2011, 46(2): 200-204. [31] 杨鹏. 样条曲线在道路平面线形中的应用研究[D]. 重庆: 重庆交通大学, 2011. -
下载:
点击查看大图
计量
- 文章访问数: 48
- HTML全文浏览量: 31
- PDF下载量: 13
- 被引次数: 0