钢结构涂层的单轴拉伸试验与本构模型研究

魏亚鹏

doi:10.3969/j.issn.0258-2724.20230591

钢结构涂层的单轴拉伸试验与本构模型研究

doi: 10.3969/j.issn.0258-2724.20230591

魏亚鹏

中国铁路设计集团有限公司土建工程设计研究院，天津 300143

基金项目: 中国铁路设计集团有限公司科技研究计划重大课题（2020YY140601）；中国铁路设计集团有限公司科技开发课题（2024A0223801）

详细信息

作者简介:
魏亚鹏（1996—），男，工程师，研究方向为钢结构理论及应用，E-mail：weiyapeng@crdc.com

中图分类号: O346
计量
- 文章访问数: 73
- HTML全文浏览量: 28
- PDF下载量: 10
- 被引次数: 0
出版历程
- 收稿日期: 2023-11-07
- 修回日期: 2024-03-22
- 网络出版日期: 2025-02-18

Study on Uniaxial Tensile Test and Constitutive Model of Steel Structure Coating

WEI Yapeng

Civil Engineering Design and Research Institute, China Railway Design Corporation, Tianjin 300143, China

摘要

摘要:
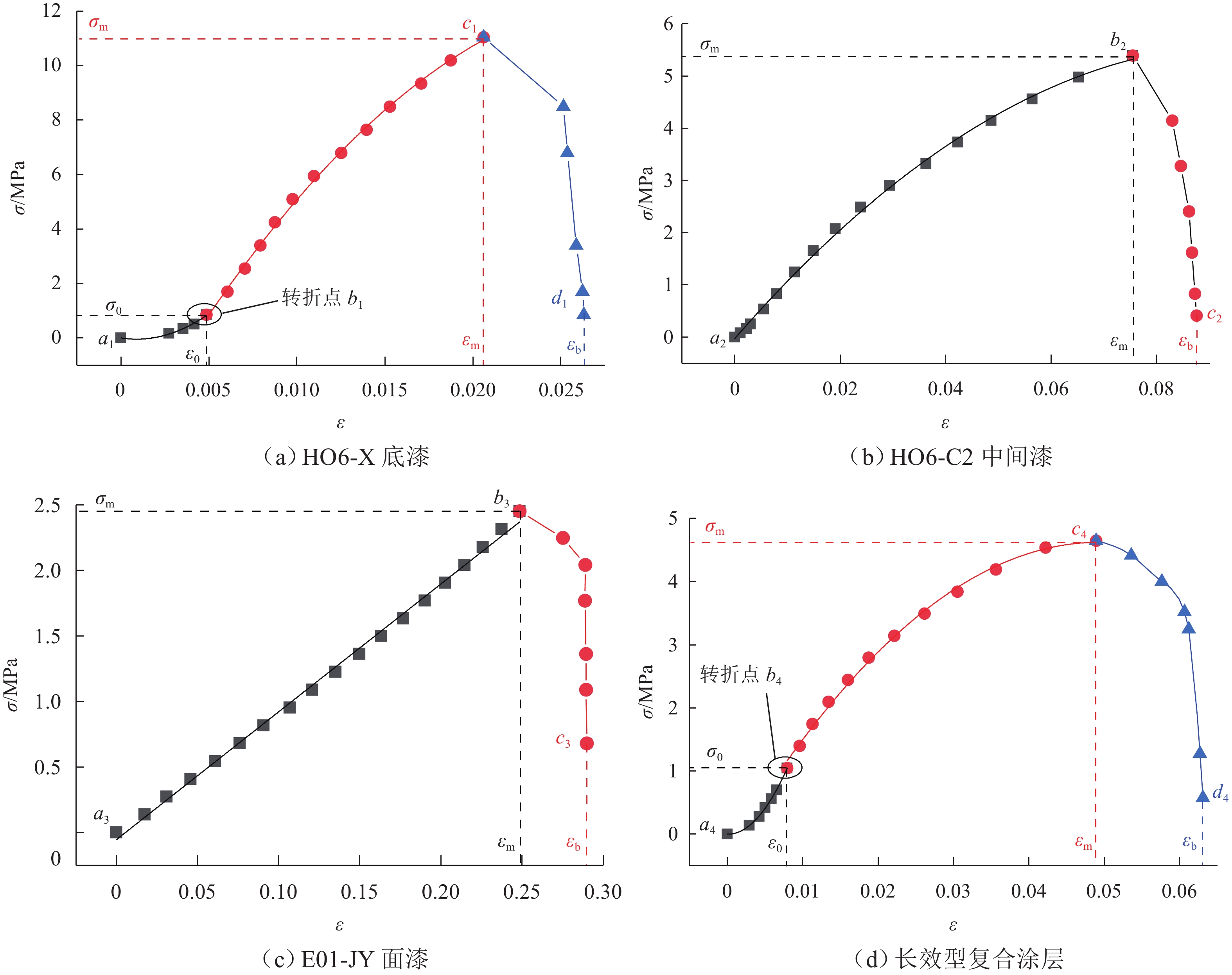
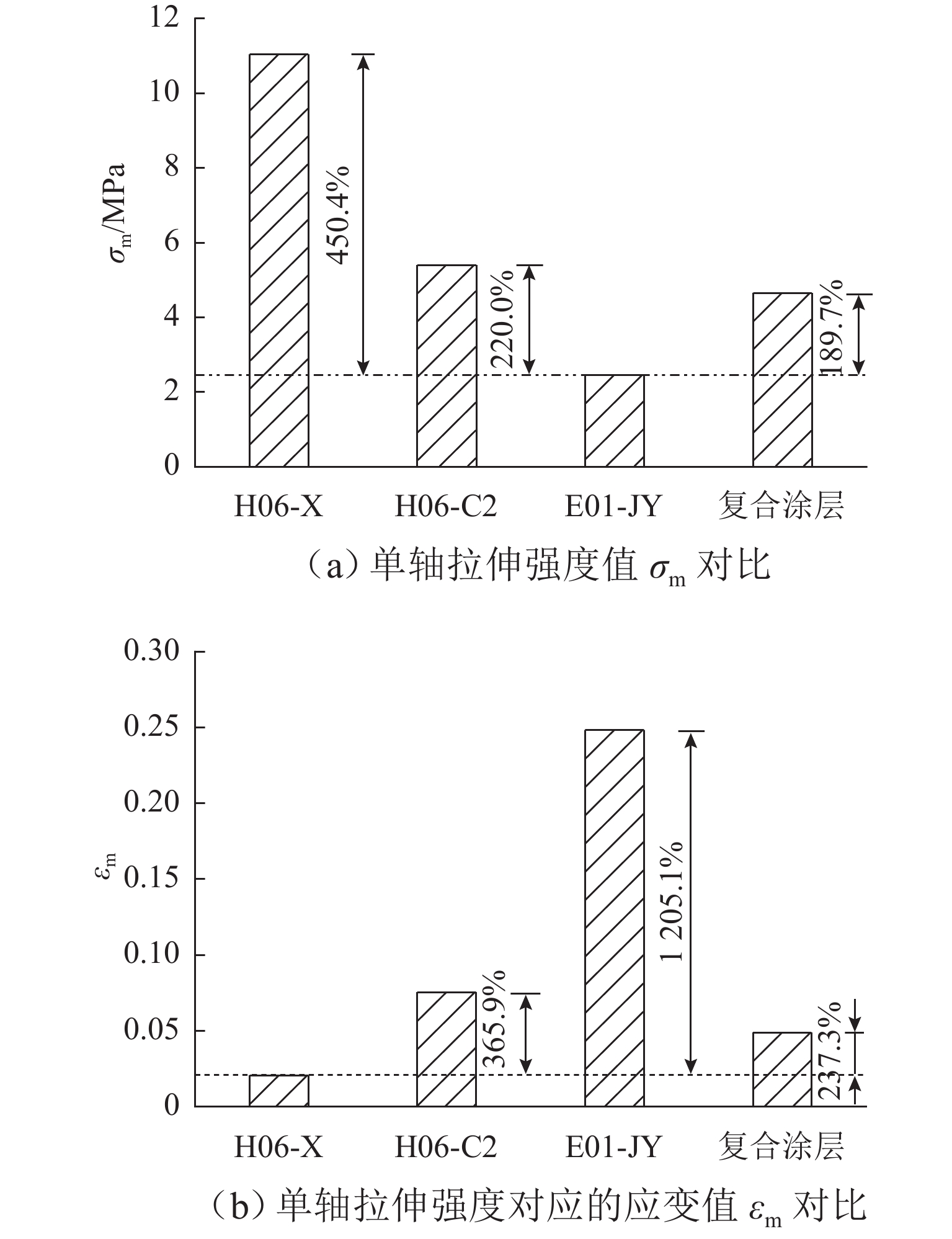
为研究钢结构桥梁涂装层的力学本构模型，以长效型涂装体系为试验对象对其分别进行单轴拉伸试验，得出面漆、中间漆、底漆和复合涂层的应力-应变曲线；通过无量纲化处理获得长效型涂装体系上升段本构方程的统一表达形式，并针对每种漆膜适用条件给出相应的本构方程. 研究结果表明：1） H06-X环氧富锌底漆（含锌量80%）和长效型复合涂层的应力-应变曲线分为弹塑型阶段、应变强化阶段和破坏阶段；H06-C2环氧厚浆云母氧化铁中间漆的应力-应变曲线分为应变强化阶段和破坏阶段；E01-JY氟碳面漆的应力-应变曲线分为近似线弹性阶段和破坏阶段. 2）依据应力-应变曲线得出了底漆、中间漆、面漆和复合涂层的弹性模量、泊松比、剪切模量、单轴拉伸强度、拉伸断裂应变等力学性能特征参数；底漆的单轴拉伸强度最强，中间漆次之，面漆最差；面漆的变形性能最佳，中间漆次之，底漆最差.
- 钢结构涂层 /
- 力学试验 /
- 本构模型 /
- 力学性能参数
Abstract:
To study the mechanical constitutive model of steel bridge coating, uniaxial tensile tests were carried out on the long-lasting coating system, obtaining the stress–strain curves for the topcoat, intermediate coat, primer, and composite coating. The unified expression for the constitutive equation of the ascending segment of the long-lasting coating system was obtained through dimensionless processing, with corresponding constitutive equations provided for each coating film. The results are as follows. 1) The stress–strain curve for H06-X epoxy zinc-rich primer (80% zinc content) and long-lasting composite coating consists of an elastic and plastic stage, a strain-hardening stage, and a failure stage; the stress–strain curve for H06-C2 epoxy thick mica ferric oxide intermediate coat consists of a strain-hardening stage and a failure stage; the stress–strain curve for E01-JY fluorocarbon topcoat consists of an approximate linear elastic stage and a failure stage. 2) Based on the stress–strain curves, the mechanical property parameters of the primer, intermediate coat, topcoat, and composite coating, such as the elastic modulus, Poisson’s ratio, shear modulus, uniaxial tensile strength, and tensile fracture strain, are obtained. The primer shows the highest uniaxial tensile strength, followed by the intermediate paint, with the topcoat being the weakest. In contrast, the topcoat exhibits the best deformability, followed by the intermediate coat, with the primer showing the worst.
- steel structure coating /
- mechanical test /
- constitutive model /
- mechanical property parameter

HTML全文

涂料被喷涂至钢桥构件的表面，并形成一定厚度的涂装层（涂层），直接将钢与腐蚀环境隔开，形成一道防腐蚀保护屏障，通过钝化缓蚀和阴极保护作用，推迟腐蚀介质与钢相接触时间. 目前，国内外钢桥的涂层体系多采用3层或4层体系，其中以富锌底漆、环氧中间漆和耐候性面漆组成的三层体系（重防腐涂装）最为常见^[1]，其中富锌底漆主要保障与钢基材的良好附着性，中间漆主要起增加厚度和提供柔韧性作用，面漆抵抗腐蚀介质和耐候性（包括美观）^[3].

钢结构桥梁涂装层厚度小且柔度高，具有明显的非线性特性,因此对涂层的本构模型、弹性模量以及泊松比等力学性能参数的研究对钢结构桥梁涂装层的设计具有重要意义. 目前国内外学者对涂层的力学性能展开了大量的试验研究和理论分析. 蔺鹏臻等^[4]利用有限元分析方法和断裂理论对重防腐涂层的界面应力与破坏准则进行研究，表明风沙冲蚀作用下涂层的界面应力破坏准则与摩尔-库伦准则相似. Hirokazu^[5]对PTFE（Polytetrafluoroethylene）膜材料进行了不同比例的双轴拉伸试验，利用分段线性函数拟合了PTFE膜的应力-应变关系曲线，通过最小二乘法求解了PTFE膜的弹性模量和泊松比等力学性能参数. Bogner^[6]通过应力-应变线性增量模型得到弹性模量计算公式. 许荔等^[7]通过对纳米涂层复合材料进行纳米划痕和纳米压痕试验得到，在试件表面进行纳米涂层喷涂可以改善试件的弹性模量和硬度. 陈辉等^[8-9]通过等粒子喷涂的方法制备了纳米涂层和普通涂层，并用试验的方法分别测量了其力学性能参数，表明纳米涂层的硬度、弹性模量、断裂韧性和结合强度均高于普通涂层. 易洪雷等^[10]通过对PES/PVC（Polyethersulfone/Polyvinyl Chloride ）膜同一平面内7个不同方向的单轴拉伸试验，证明了经过3次循环加载后的应力-应变曲线能较准确表征PES/PVC膜的弹性力学性质. 刘平等^[11]以SH-1050P膜材为试验对象进行了单、双轴拉伸试验，研究发现在单轴拉伸试验下SH-1050P膜满足双线性本构关系，并且可按应变的2%划分为弹性和塑性2个阶段，在应力比为1∶1的双轴拉伸试验条件下，SH-1050P膜的双轴弹性模量与单轴相同. 于沁灵等^[12]通过对Ferrari 1202S2膜进行多次双轴拉伸试验，利用不同的数据处理方式分别建立了双轴线性本构模型和双轴非线性本构模型. 王利钢等^[13]基于自主研制的拉伸试验机，研究了P-PVC-PVDF（Polyester fabric-polyvinyl chloride-polyvinylidene fluoride）膜材的剪切力学性能，并提出了一种改进的剪应力计算方法. 李阳^[14]利用图框法对PVC涂层膜材进行单轴拉伸试验，得出了聚酯织物膜材的剪切模量. 许珊珊等^[15-16]通过对PTFE膜材11个偏轴角度和6种拉伸速率工况下的试验研究，得出了3种破坏模式和不同工况下的膜材破坏机理.

综上所述，国内外学者对涂层的力学性能做了较多的工作，但对于钢结构桥梁底漆、中间漆和面漆复合涂层的本构模型及力学性能参数的研究还相对较少. 为此，本文以钢结构桥梁长效型涂装体系为试验对象分别进行单轴拉伸试验，研究了面漆、中间漆、底漆和复合涂层力学本构方程的统一表达形式，并针对每种漆膜的适用条件给出了具体的本构方程；得出了每种漆膜的弹性模量、泊松比、剪切模量等力学性能参数.

1. 试验材料与试验方法

1.1 试验材料与设备

本次试验采用钢结构桥梁长效型涂装体系，其底漆、中间漆和面漆的组分和配比见表1.

表 1 钢结构桥梁长效型涂装体系组分及配比

Table 1. Components and ratios of long-lasting coating system for steel bridge

对象	A组分	B组分	比例
底漆	H06-X环氧富锌底漆（含锌量80%）	H06-X固化剂	12.8∶1
中间漆	H06-C2环氧厚浆云母氧化铁中间漆	H06-C2固化剂	13.5∶1
面漆	E01-JY氟碳面漆	E01-JY固化剂	10∶1

下载: 导出CSV

| 显示表格

单轴拉伸试验机型号为WDW-J2，拉伸试验力量程为0～500 N，位移分辨率为0.01 mm，位移速度控制范围为0.01～500 mm/min. 采用高精度涂层测厚仪，量程为0～1250 μm. 采用聚酯膜制备长效型涂装体系的底漆膜、中间漆膜、面漆膜和复合涂层漆膜.

1.2 试验方法

按表1所示配比分别配制长效型涂装体系的底漆膜、中间漆膜、面漆膜及复合涂层漆膜，利用刮膜器在聚酯膜上制备以上4种漆膜，然后按照国际标准^[17]规定，每种漆膜制备3个试件，每个拉伸试件初始宽度l_b=20 mm，总长度l₀=150 mm，有效拉伸长度（标距）l=50 mm，夹持端长度取为50 mm，如图1所示. 试件在温度为25 ℃±2 ℃，相对湿度为65%±2%的条件下养护7 d. 利用高精度涂层测厚仪分别测试每个试件有效拉伸段的平均厚度t，然后利用单轴拉伸试验机以2 mm/min的拉伸速率对漆膜进行单向拉伸试验.

图 1 标准漆膜试件

Figure 1. Sample of standard coating film

下载: 全尺寸图片幻灯片

2. 涂层拉伸试验结果分析

2.1 拉伸试验的应力-应变曲线

将单轴拉伸试验荷载值T和漆膜纵向变形量 $\Delta l$ 分别代入式（1）和式（2）中，求出每种漆膜所对应的拉伸应力σ和纵向拉伸应变ε（若无特别说明，下文中的应变均指纵向应变）.

$\sigma = \frac{T}{A},$

(1)

$\varepsilon = \frac{{\Delta l}}{l},$

(2)

式中： A为漆膜的横截面积， $A = l_{\mathrm{b}} t$ .

图2给出了长效型涂装体系的底漆、中间漆、面漆以及复合涂层的应力-应变实测曲线，图中：ε_m为漆膜试件达到峰值应力σ_m时的纵向应变，ε_b为极限应变.

图 2 涂层拉伸的应力-应变实测曲线

Figure 2. Measured stress–strain curves for coatings in tension

下载: 全尺寸图片幻灯片

由图2可知：涂层在拉伸受力时，应力-应变曲线均包括明显的上升段和下降段，说明涂层材料均具有较好的韧性. 底漆和复合涂层的应力-应变曲线可分为弹塑性阶段、应变强化阶段和破坏阶段；中间漆可分为应变强化阶段和破坏阶段；面漆可分为近似线弹性阶段和破坏阶段.

2.2 涂层应力-应变曲线机理分析

涂层类高分子聚合物的应力-应变曲线依据应力转折点和应力峰值点可将其分为近似弹性阶段、弹塑性阶段、应变强化阶段和破坏阶段. 根据涂层的应力和应变特点以及涂层在达到转折点后的破环情况，可将涂层分为硬而脆、硬而韧、硬而强、软而韧、软而弱^[18].

底漆和复合涂层的弹性模量大而应变小，呈现出硬而脆的变形特点，在应力达到转折点之前，涂层先发生弹性变形后发生塑性变形，可认为涂层处于弹塑性阶段. 当涂层应力达到转折点之后，涂层原有的晶体结构被破坏，重组成强度更高，变形能力更强的微纤维束结构^[19]，随着变形的增加，应力也在逐渐增加，没有明显的屈服阶段，可认为涂层处于应变强化阶段. 在达到峰值应力后，漆膜的有效拉伸段开始逐渐出现裂纹，随着应变的增加应力急剧下降，当应变达到极限应变时试样最终断裂破坏，可定义为破坏阶段.

面漆的弹性模量小而应变大，呈现出软而韧的变形特点，在涂层应力达到峰值应力之前，涂层发生近似弹性变形，近似满足胡克定律，可认为是近似弹性阶段. 在达到峰值应力后，漆膜的有效拉伸段开始逐渐出现裂纹，随着应变的增加应力急剧下降，当应变达到极限应变时试样最终断裂破坏，可定义为破坏阶段.

中间漆具有较强的弹性模量和变形能力，呈现出硬而强的变形特点，涂层的弹塑性阶段非常短暂，迅速进入应变强化阶段，在达到峰值应力之后，进入破坏阶段.

2.3 涂层应力-应变曲线特征

1）底漆的应力-应变特征

由图2（a）可知，H06-X环氧富锌底漆（含锌量80%）的应力-应变曲线可分为3段. 在弹塑性阶段（a₁b₁段），漆膜应力增长较小，并且按照二次多项式规律先发生弹性变形，后发生塑性变形，b₁点为转折点，该点处应变ε₀=0.235ε_m，应力σ₀=0.077σ_m；然后漆膜进入应变强化阶段（b₁c₁段），漆膜的应力-应变曲线按照二次函数关系具有较大程度的增长，在c₁点达到峰值应力σ_m，与之相对应的应变ε_m为0.021；在达到峰值应力后，进入破坏阶段（c₁d₁段），漆膜的有效拉伸段开始逐渐出现裂纹，随着应变的增加应力逐渐下降，当达到极限应变ε_b时漆膜最终断裂破坏. 因此，H06-X环氧富锌底漆（含锌量80%）上升段的本构方程按照最小二乘法拟合为

$\sigma=\left\{ \begin{aligned} &55246.647{\varepsilon }^{2}-99.227\varepsilon + 0.004,\\ &\quad R^2 = 0.998, \;\varepsilon \leqslant {\varepsilon }_{0},\;a_1b_1段,\\ & -18706.511{\varepsilon }^{2} + 1125.877\varepsilon -4.313,\\ &\quad R^2 = 0.985,\;{\varepsilon }_{0} < \varepsilon \leqslant {\varepsilon }_{\text{m}},\;b_1c_1段. \end{aligned}\right.$

(3)

2）中间漆的应力-应变特征

由图2（b）可知，H06-C2环氧厚浆云母氧化铁中间漆的应力-应变曲线可分为2段. 在拉伸过程中漆膜的弹塑性阶段非常短暂，迅速进入应变强化阶段（a₂b₂段），漆膜的应力-应变曲线按二次多项式规律具有较大程度的增长，在b₂点达到峰值应力σ_m，与之对应的应变ε_m=0.075；在达到峰值应力后，进入破坏阶段（b₂c₂段），漆膜的有效拉伸段开始逐渐出现裂纹，随着应变的增加应力逐渐下降，当应变达到极限应变ε_b时漆膜最终断裂破坏. 因此，H06-C2环氧厚浆云母氧化铁中间漆上升段的本构方程按照最小二乘法拟合为

$\begin{split} &\sigma =-\text{597}\text{.587}{\varepsilon }^{2}\text{+116}\text{.028}\varepsilon -\text0.0\text{30}, \\ &\quad R^2 = 0.999,\;a_2b_2段\text{ ， }\varepsilon \leqslant {\varepsilon }_{\text{m}}. \end{split}$

(4)

3）面漆的应力-应变特征

由图2（c）可知，E01-JY氟碳面漆的应力-应变曲线可分为两段. 在近似线弹性阶段（a₃b₃段），应力-应变曲线按线性规律变化，在b₃点达到峰值应力σ_m，与之相对应的应变ε_m为0.248；在达到峰值应力后，进入破坏阶段（b₃c₃段），漆膜的有效拉伸段开始逐渐出现裂纹，随着应变的增加应力急剧下降，当应变达到极限应变ε_b时试样最终断裂破坏. 因此，E01-JY氟碳面漆上升段的本构方程按照最小二乘法拟合为

$\sigma =\text{9}\text{.76}\varepsilon -0.053,\quad R^2 =0.998,\; a_3b_3段\text{ , }\varepsilon \leqslant {\varepsilon }_{\text{m}}.$

(5)

4）复合涂层的应力-应变特征

由图2（d）可知，由H06-X环氧富锌底漆（含锌量80%）、H06-C2环氧厚浆云母氧化铁中间漆和E01-JY氟碳面漆组成的复合涂层的应力-应变曲线可分为三段. 在弹塑性阶段（a₄b₄段），漆膜应力增长较小，并且按照二次多项式规律先发生弹性变形，后发生塑性变形，b₄点为转折点，在该阶段应变ε₀为0.163ε_m，应力σ₀=0.225σ_m；然后漆膜进入应变强化阶段（b₄c₄段），应力-应变曲线按照二次函数关系具有较大程度的增长，在c₄点达到峰值应力σ_m，与之相对应的应变ε_m=0.049；在达到峰值应力后，进入破坏阶段（c₄d₄段），漆膜的有效拉伸段开始逐渐出现裂纹，随着应变的增加应力逐渐下降，当达到极限应变ε_b时漆膜最终断裂破坏. 因此，长效型复合涂层上升段的本构方程按照最小二乘法拟合为

$\sigma =\left\{\begin{aligned} &\sigma =\text{16 970}\text{.810}{\varepsilon }^{2}-\text{3}\text{.729}\varepsilon + \text{4}\text{.602},\\ &\quad R^2 = 0.998,\; a_4b_4段,\;\varepsilon \leqslant {\varepsilon }_{0},\\ & \sigma =-\text{2 023}\text{.240}{\varepsilon }^{2} + 1\text{99}\text{.523}\varepsilon -\text{0}\text{.296 },\\ &\quad R^2 = 0.999,\; b_4c_4段,\;{\varepsilon }_{0} < \varepsilon \leqslant {\varepsilon }_{\text{m}}. \end{aligned}\right.$

(6)

3. 涂层拉伸试验结果分析

3.1 拉伸试验的应力-应变曲线

为获得涂层的弹性模量、泊松比（υ）、剪切模量、单轴拉伸强度及拉伸断裂应变等力学性能参数，依据2.1节的涂层应力-应变实测曲线，采用峰值应力σ_m处的割线模量E_t作为涂层弹性模量E的代表值，见式（7）. H06-X环氧富锌底漆（含锌量80%）、H06-C2环氧厚浆云母氧化铁中间漆、E01-JY氟碳面漆和复合涂层的弹性模型值见表2.

表 2 涂层力学性能参数

Table 2. Mechanical property parameters for coatings

涂层种类	E/MPa	υ	G/MPa	σ_m /MPa	ε_m	ε_b
H06-X底漆	535.7	0.20	223.2	11.0	0.021	0.026
H06-C2中间漆	71.5	0.06	33.8	5.4	0.075	0.086
E01-JY面漆	9.9	0.03	4.8	2.5	0.248	0.289
复合涂层	95.1	0.13	41.9	4.7	0.049	0.062

下载: 导出CSV

| 显示表格

$E = {E_{\text{t}}} = \frac{{{\sigma _{\text{m}}}}}{{{\varepsilon _{\text{m}}}}}.$

(7)

通过试验测得当拉伸应力达到峰值应力时漆膜试件的宽度为l_bm，然后利用式（8）计算出H06-X环氧富锌底漆（80%锌含）、H06-C2环氧厚浆云母氧化铁中间漆、E01-JY氟碳面漆和复合涂层的泊松比值，见表2.

$\upsilon =\frac{\left|{\varepsilon }_{{\mathrm{h}}}\right|}{{\varepsilon }_{\text{m}}}=\frac{\left|{l}_{\text{bm}}-l_{\mathrm{b}}\right|}{{\varepsilon }_{\text{m}}},$

(8)

式中：ε_h为漆膜的横向应变；l_b为漆膜试件的初始宽度.

H06-X环氧富锌底漆（含锌量80%）、H06-C2环氧厚浆云母氧化铁中间漆、E01-JY氟碳面漆和复合涂层的剪切模量G可利用式（9）得出，结果见表2.

$G=\frac{E}{2(1 + \upsilon )}.$

(9)

依据图2所示的涂层应力-应变实测曲线，定义峰值应力σ_m为涂层的单轴拉伸强度，极限应变ε_b为涂层的拉伸断裂应变，则底漆、中间漆、面漆和复合涂层的单轴拉伸强度σ_m、单轴拉伸强度σ_m所对应的应变ε_m以及涂层的拉伸断裂应变ε_b见表2.

3.2 涂层力学本构模型

对H06-X环氧富锌底漆（含锌量80%）、H06-C2环氧厚浆云母氧化铁中间漆、E01-JY氟碳面漆和复合涂层的应力-应变曲线的上升段进行对比分析，以期获得统一形式的上升段本构方程. 首先，将式（3）～（6）进行无量纲化处理，然后，将4种漆膜上升段的本构方程统一归纳成式（10）.

$\frac{\sigma }{{{\sigma _{\text{m}}}}} = \alpha {\left( {\frac{\varepsilon }{{{\varepsilon _{\text{m}}}}}} \right)^2} + \beta {\frac{\varepsilon }{{{\varepsilon _{\text{m}}}}}} + \gamma.$

(10)

1）对于H06-X环氧富锌底漆（含锌量80%）和复合涂层，即当ε₀>0时，有

$\frac{\sigma }{{{\sigma _{\text{m}}}}} =\left\{ \begin{aligned} \alpha {\left( {\frac{\varepsilon }{{{\varepsilon _{\text{m}}}}}} \right)^2} + \beta {\frac{\varepsilon }{{{\varepsilon _{\text{m}}}}}} + \gamma,\quad {\text{ 0 < }}\frac{\varepsilon }{{{\varepsilon _{\text{m}}}}} \leqslant \frac{{{\varepsilon _0}}}{{{\varepsilon _{\text{m}}}}}, \\ \eta {\left( {\frac{\varepsilon }{{{\varepsilon _{\text{m}}}}}} \right)^2} + \kappa {\frac{\varepsilon }{{{\varepsilon _{\text{m}}}}}} + \lambda,\quad {\text{ }}\frac{{{\varepsilon _0}}}{{{\varepsilon _{\text{m}}}}}{\text{ < }}\frac{\varepsilon }{{{\varepsilon _{\text{m}}}}} \leqslant 1 . \end{aligned}\right.$

(11)

2）对于H06-C2环氧厚浆云母氧化铁中间漆，即当ε₀=0时，有

$\frac{\sigma }{{{\sigma _{\text{m}}}}} = \alpha {\left( {\frac{\varepsilon }{{{\varepsilon _{\text{m}}}}}} \right)^2} + \beta {\frac{\varepsilon }{{{\varepsilon _{\text{m}}}}}} + \gamma，\quad {\text{ 0 = }}\frac{{{\varepsilon _0}}}{{{\varepsilon _{\text{m}}}}}{\text{ < }}\frac{\varepsilon }{{{\varepsilon _{\text{m}}}}} \leqslant 1.$

(12)

3）对于E01-JY氟碳面漆，即当ε₀=0且a=0时，有

$\frac{\sigma }{{{\sigma _{\text{m}}}}} = \beta {\frac{\varepsilon }{{{\varepsilon _{\text{m}}}}}} + \gamma，\quad {\text{ 0 = }}\frac{{{\varepsilon _0}}}{{{\varepsilon _{\text{m}}}}}{\text{ < }}\frac{\varepsilon }{{{\varepsilon _{\text{m}}}}} \leqslant 1,$

(13)

式（10）～（13）中：α和η为二次项系数，β和κ为一次项系数，γ和λ为常数项.

由图2可知：底漆、中间漆、面漆和复合涂层的应力-应变曲线的下降段相差较大，数据也比较离散，暂无明显规律可循. 因此为获得较为可靠的涂层应力-应变曲线下降段的变化特征，还需在确定标准试验方法的基础上进行大量试验研究.

3.3 涂层抗拉强度及变形能力对比分析

为了探究不同漆膜的单轴拉伸强度和变形能力，对钢结构桥梁长效型涂装体系的单轴拉伸强度值σ_m及其对应的应变ε_m进行了对比分析，如图3.

图 3 长效型涂装体系σ_m和ε_m对比分析

Figure 3. Comparative analysis of σ_m and ε_m of long-lasting coating system

下载: 全尺寸图片幻灯片

由图3（a）可知：H06-X环氧富锌底漆（含锌量80%）、H06-C2环氧厚浆云母氧化铁中间漆、长效型复合涂层的单轴拉伸强度值分别为E01-JY氟碳面漆的450.4%、220.0%、102.2%和189.7%. 因此，钢结构桥梁涂装体系的单轴拉伸强度底漆最强、中间漆次之，面漆最差；长效型复合涂层的单轴拉伸强度接近中间漆.

由图3（b）可知：H06-C2环氧厚浆云母氧化铁中间漆、E01-JY氟碳面漆和长效型复合涂层的单轴拉伸强度所对应的应变ε_m分别为H06-X环氧富锌底漆（含锌量80%）的365.9%、1205.1%和237.3%. 因此，钢结构桥梁涂层的变形性能面漆最强、中间漆次之，底漆最差；长效型复合涂层的变形性能接近中间漆.

4. 结　论

1） H06-X环氧富锌底漆（含锌量80%）和长效型复合涂层的应力-应变关系分为弹塑型阶段、应变强化阶段和破坏阶段，并且在弹塑性阶段和应变强化阶段的表达式均满足二次多项式.

2） H06-C2环氧厚浆云母氧化铁中间漆的应力-应变曲线分为应变强化阶段和破坏阶段，并且在应变强化阶段的表达式可用一元二次函数表征.

3） E01-JY氟碳面漆的应力-应变曲线分为近似线弹性阶段和破坏阶段，并且近似线弹性阶段的表达式满足线性关系.

4）将长效型涂装体系上升段的本构方程归纳成了统一形式，并且针对每种漆膜的适用条件给出了具体的表达式.

5）得出了底漆、中间漆、面漆和复合涂层的弹性模量、泊松比、剪切模量、单轴拉伸强度和拉伸断裂应变等力学性能参数.

6钢结构桥梁长效型涂装体系单轴拉伸强度底漆最强、中间漆次之，面漆最差，复合涂层的单轴拉伸强度接近中间漆；变形性能面漆最强、中间漆次之，底漆最差，复合涂层的变形性能接近中间漆.

图 1 标准漆膜试件

Figure 1. Sample of standard coating film

下载: 全尺寸图片幻灯片

图 2 涂层拉伸的应力-应变实测曲线

Figure 2. Measured stress–strain curves for coatings in tension

下载: 全尺寸图片幻灯片

图 3 长效型涂装体系σ_m和ε_m对比分析

Figure 3. Comparative analysis of σ_m and ε_m of long-lasting coating system

下载: 全尺寸图片幻灯片

表 1 钢结构桥梁长效型涂装体系组分及配比

Table 1. Components and ratios of long-lasting coating system for steel bridge

对象	A组分	B组分	比例
底漆	H06-X环氧富锌底漆（含锌量80%）	H06-X固化剂	12.8∶1
中间漆	H06-C2环氧厚浆云母氧化铁中间漆	H06-C2固化剂	13.5∶1
面漆	E01-JY氟碳面漆	E01-JY固化剂	10∶1

下载: 导出CSV

表 2 涂层力学性能参数

Table 2. Mechanical property parameters for coatings

涂层种类	E/MPa	υ	G/MPa	σ_m /MPa	ε_m	ε_b
H06-X底漆	535.7	0.20	223.2	11.0	0.021	0.026
H06-C2中间漆	71.5	0.06	33.8	5.4	0.075	0.086
E01-JY面漆	9.9	0.03	4.8	2.5	0.248	0.289
复合涂层	95.1	0.13	41.9	4.7	0.049	0.062

下载: 导出CSV

参考文献(19)

[1]	KAMANI P K. Corrosion management & coatings[J]. Paintindia, 2016, 1: 100-105.
[2]	戴润达. 钢桥梁的长效防腐涂装[J]. 涂料工业,2018,48(12): 74-79. doi: 10.12020/j.issn.0253-4312.2018.12.74 DAI Runda. Research on long-lasting anticorrosive coating of steel bridge[J]. Paint & Coatings Industry, 2018, 48(12): 74-79. doi: 10.12020/j.issn.0253-4312.2018.12.74
[3]	TOUBIA E A, EMAMI S. Experimental evaluation of structural steel coating systems[J]. Journal of Materials in Civil Engineering, 2016, 28(12): 4016147.1-4016147.10.
[4]	蔺鹏臻,魏亚鹏,乔叶伟. 风沙冲蚀下钢结构涂层的界面应力与破坏准则[J]. 西南交通大学学报,2023,58(1): 236-243. doi: 10.3969/j.issn.0258-2724.20210189 LIN Pengzhen, WEI Yapeng, QIAO Yewei. Interfacial stress and failure criteria of steel structure coatings under wind-sand erosion[J]. Journal of Southwest Jiaotong University, 2023, 58(1): 236-243. doi: 10.3969/j.issn.0258-2724.20210189
[5]	HIROKAZU M. A multi-step linear approximation method for nonlinear analysis of stress and deformation of coated plain-weave fabric[J]. Journal of Textile Engineering, 2006, 52(5): 189-195. doi: 10.4188/jte.52.189
[6]	BOGNER B H. The mechanical behaviour of coated fabrics used in prestressing textile engineering structures: theory, simulation and numerical analysis to be used in a fem-model[J]. Journal of the International Association for Shell and Spatial Structures, 2008, 49(1): 39-47.
[7]	许荔,江晓禹,钱林茂. 树脂基纳米涂层复合材料力学性能试验研究[J]. 西南交通大学学报,2005,40(3): 347-350. doi: 10.3969/j.issn.0258-2724.2005.03.014 XU Li, JIANG Xiaoyu, QIAN Linmao. Experimental study on mechanical properties of resin matrix nano-coating composites[J]. Journal of Southwest Jiaotong University, 2005, 40(3): 347-350. doi: 10.3969/j.issn.0258-2724.2005.03.014
[8]	陈辉,苟国庆,刘艳,等. 等离子喷涂WC-17Co纳米涂层形成及强韧化机理[J]. 西南交通大学学报,2008,43(5): 633-637. doi: 10.3969/j.issn.0258-2724.2008.05.015
[9]	CHEN Hui, GOU Guoqing, LIU Yan, et al. Formation and strengthening mechanisms of plasma sprayed nanostructured WC-Co coating[J]. Journal of Southwest Jiaotong University, 2008, 43(5): 633-637.
[10]	易洪雷,丁辛,陈守辉. PES/PVC膜材料拉伸性能的各向异性及破坏准则[J]. 复合材料学报,2005,22(6): 98-102. doi: 10.3321/j.issn:1000-3851.2005.06.017 YI Honglei, DING Xin, CHEN Shouhui. Orthotropic behavior and strength criterion of pes/pvc membrane materials under tensile loading[J]. Acta Materiae Compositae Sinica, 2005, 22(6): 98-102. doi: 10.3321/j.issn:1000-3851.2005.06.017
[11]	刘平,吴刚,唐柏鉴,等. PVDF涂层织物拉伸力学性能试验研究[J]. 东南大学学报(自然科学版),2017,47(6): 1195-1200. LIU Ping, WU Gang, TANG Baijian, et al. Experimental study on mechanical properties of PVDF textile[J]. Journal of Southeast University (Natural Science Edition), 2017, 47(6): 1195-1200.
[12]	于沁灵,龚景海,郭晓,等. 涂层织物类膜材的拉伸试验及力学参数研究[J]. 空间结构,2020,26(4): 64-69. YU Qinling, GONG Jinghai, GUO Xiao, et al. Tensile test and mechanical parameters of coated fabric membrane[J]. Spatial Structures, 2020, 26(4): 64-69.
[13]	王利钢,陈务军,高成军. 聚酯纤维机织物-聚氯乙烯-聚偏氟乙烯膜材双轴剪切力学性能试验[J]. 复合材料学报,2015,32(4): 1118-1124. WANG Ligang, CHEN Wujun, GAO Chengjun. Test on biaxial shear mechanical performance of polyester fabric-polyvinyl chloride-polyvinylidene fluoride membrane[J]. Acta Materiae Compositae Sinica, 2015, 32(4): 1118-1124.
[14]	李阳. 建筑膜材料和膜结构的力学性能研究与应用[D]. 上海:同济大学,2007. LI Yang. Study and Applications on Mechanical Properties of Membrane Materials and Structures[D]. Shanghai: Tongji University, 2007.
[15]	许珊珊,张营营,徐俊豪,等. PVC涂层织物膜材的非线性各向异性本构关系模型[J]. 建筑材料学报,2020,23(5): 1098-1103. doi: 10.3969/j.issn.1007-9629.2020.05.015 XU Shanshan, ZHANG Yingying, XU Junhao, et al. Nonlinear anisotropic constitutive model of PVC coated fabric membrane[J]. Journal of Building Materials, 2020, 23(5): 1098-1103. doi: 10.3969/j.issn.1007-9629.2020.05.015
[16]	张营营,徐俊豪,曹原,等. PTFE膜材料的偏轴拉伸性能及破坏机理[J]. 哈尔滨工业大学学报,2016,48(12): 135-141,164. ZHANG Yingying, XU Junhao, CAO Yuan, et al. Off-axial tensile behaviors and failure mechanisms of PTFE coated fabrics[J]. Journal of Harbin Institute of Technology, 2016, 48(12): 135-141,164.
[17]	European Committee for Standardization. Plastics determination of Tensile Properties: ISO 527 -3-2018[S]. Belgium Brusse: European Committee for Standardization, 2018.
[18]	何平笙. 高聚物的力学性能[M]. 第3版. 合肥:中国科学技术大学出版社,2021:218.
[19]	束德林. 工程材料力学性能[M]. 第3版. 北京:机械工业出版社,2016:192-195.