Cause of Rail Corrugation on Ladder Sleeper Track
-
摘要:
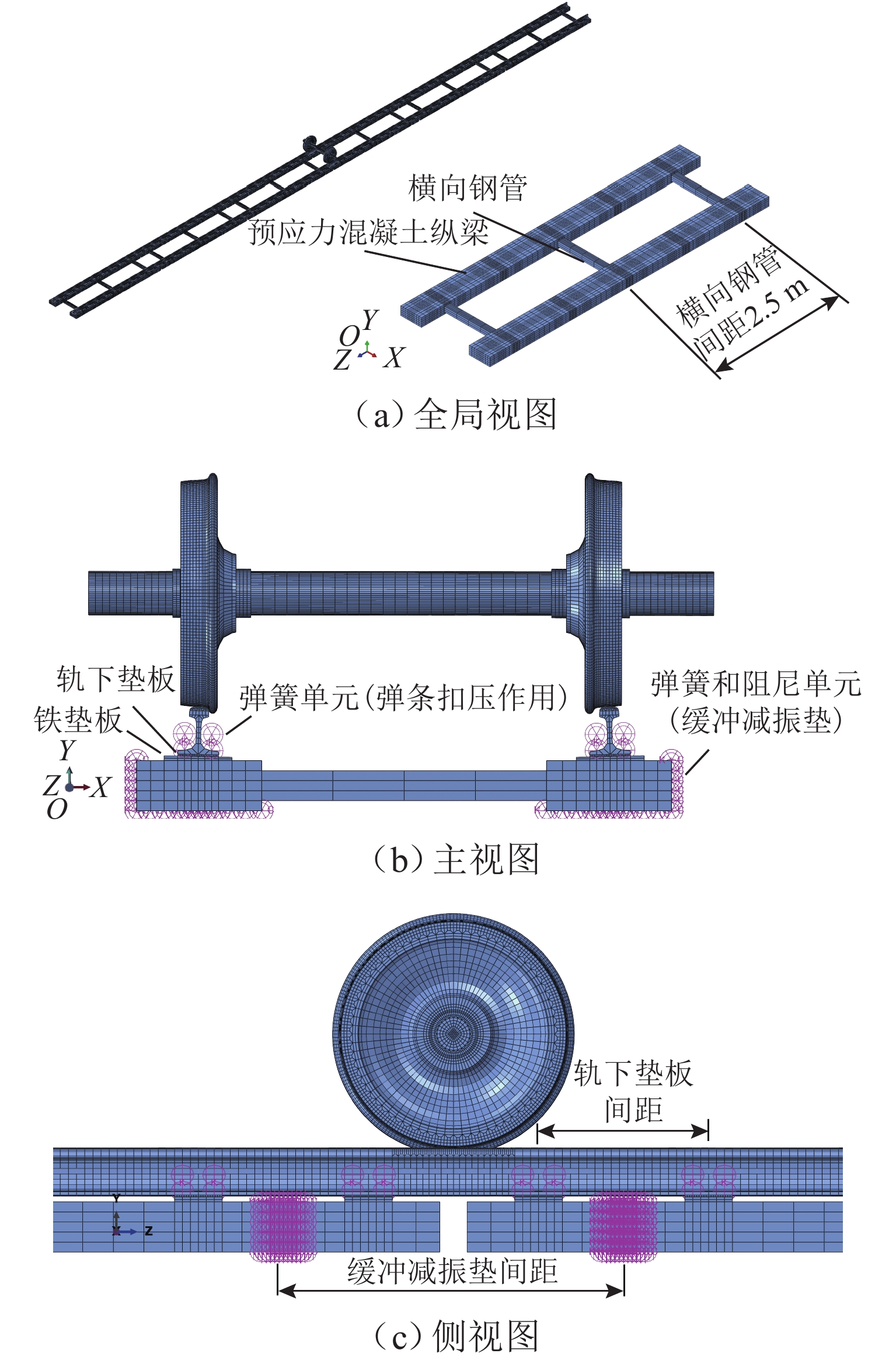
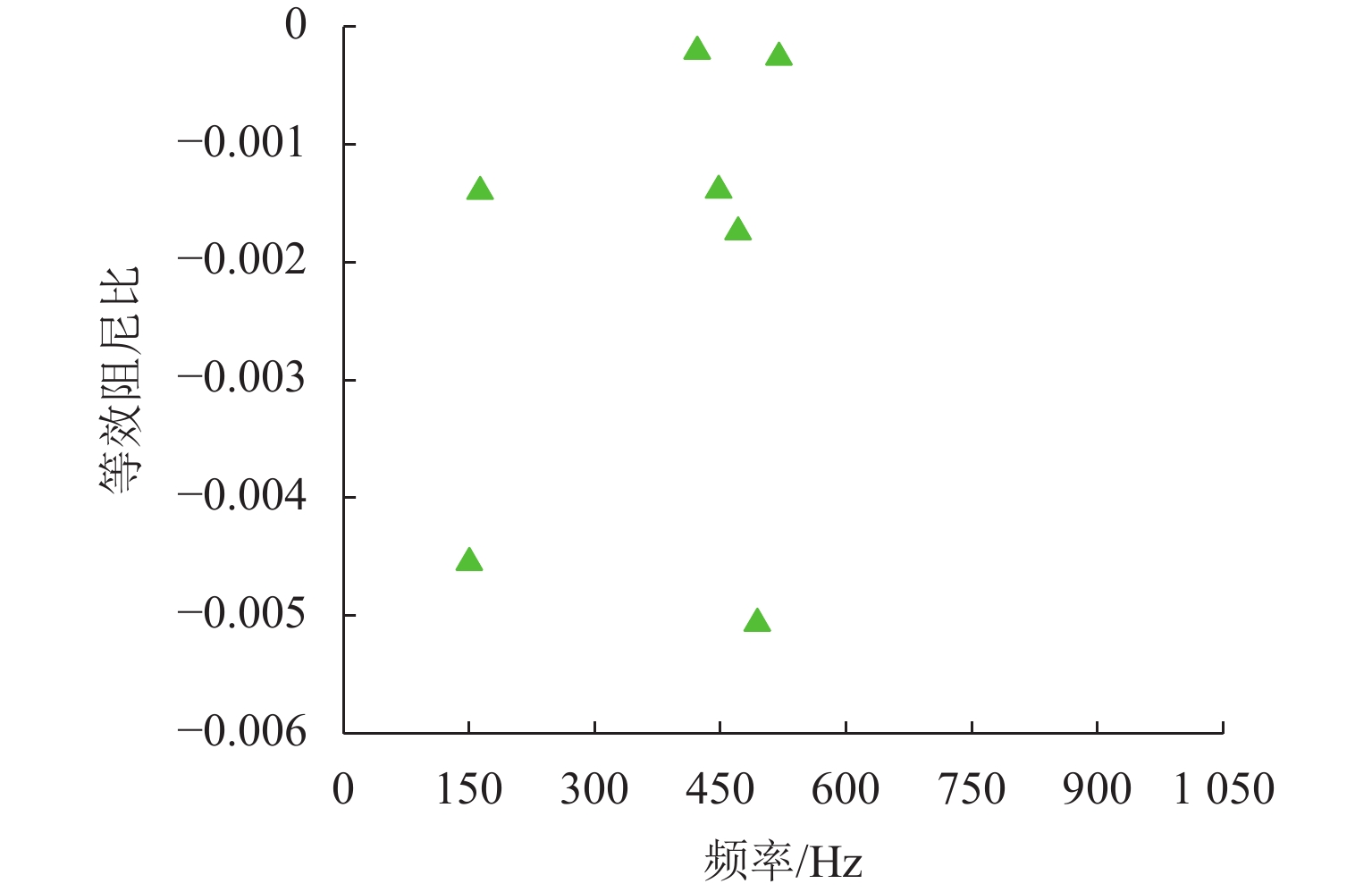
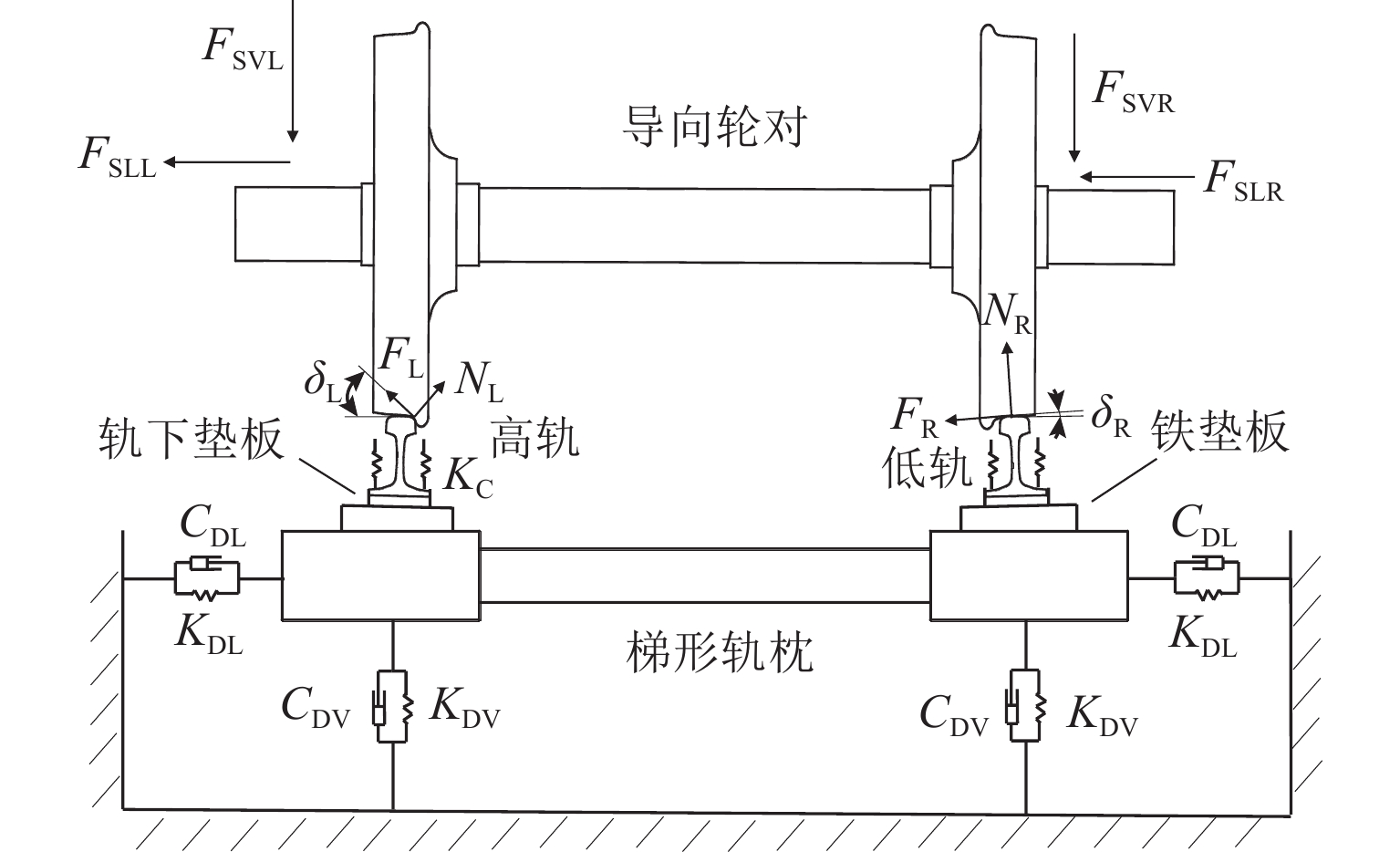
为研究地铁小半径曲线段梯形轨枕轨道上内轨波磨的形成机理，基于饱和轮轨蠕滑力引发的摩擦自激振动导致钢轨波磨的理论，建立导向轮对-梯形轨枕轨道系统有限元模型，模型中采用实体单元对扣件系统进行建模；应用复特征值分析和瞬时动态分析分别求解轮轨系统的运动稳定性和时域动态响应；研究了缓冲减振垫参数和梯形轨枕结构对轮轨系统摩擦自激振动的影响. 研究结果表明：饱和轮轨蠕滑力引发的频率为150 Hz的摩擦自激振动是小半径曲线段梯形轨枕轨道上内轨波磨的成因，预测得到的波磨波长约为69 mm，与实测结果很接近；参数敏感性分析表明，增大侧向缓冲垫阻尼及铺设横向钢管间距为1.25 m的梯形轨枕可以在一定程度上抑制梯形轨枕轨道上的钢轨波磨.
Abstract:To study the formation mechanism of inner rail corrugation on the ladder sleeper track in the small-radius curve, a finite element model of the leading wheelset–ladder sleeper track system was developed based on the theory that self-excited frictional vibration triggered by saturated wheel-rail creep force causes rail corrugation. In this model, solid elements were used to model the fastening system. Complex eigenvalue analysis and transient dynamic analysis were applied to solve the motion stability and dynamic time-domain response of the wheel-rail system, respectively. Furthermore, the effects of the parameters of the cushioning pad and ladder sleeper structure on the self-excited frictional vibration of the wheel-rail system were studied. The results show that the self-excited frictional vibration with a frequency of 150 Hz caused by the saturated wheel-rail creep force is the cause of inner rail corrugation on the ladder sleeper track in the small-radius curve section. The predicted corrugation wavelength is 69 mm, which agrees well with the measured wavelength. Parameter sensitivity analysis shows that increasing the damping of the lateral cushioning pad and laying ladder sleepers with a spacing of 1.25 m between lateral steel pipes can suppress rail corrugation on the ladder sleeper track to a certain extent.
-
钢轨波磨是铁路行业尚未解决的难题，在地铁线路上尤为严重. 任何一条地铁线路上，只要曲线轨道半径低于350 m，则该轨道内轨上出现波磨的几率接近100%；然而在大半径曲线轨道（R≥650～800 m）和直线轨道上，很少出现钢轨波磨：这是地铁线路上钢轨波磨的普遍规律[1-2]. 当列车通过波磨轨道时，轮轨界面上的剧烈振动加剧了车辆和轨道部件的疲劳断裂，甚至危害行车安全[3-4].
目前钢轨波磨的形成机理可分为3类：1） 轮轨表面初始不平顺激励下，轮轨界面的瞬时动力作用引起摩擦功波动导致钢轨波磨[5-10]；2） 轮轨系统的粘-滑振动引起了钢轨波磨[11-13]；3） 饱和轮轨蠕滑力激发了轮轨摩擦耦合系统的自激振动导致钢轨波磨[14-19]. 第一类理论模型为它激振动模型，该理论可以较好地解释地铁线路上的部分波磨现象，但不足以解释地铁线路上波磨主要出现在小半径曲线内轨，在大半径曲线和直线轨道上波磨发生率较低这一普遍现象；第二类理论模型预测得出的波磨频率约为20～80 Hz[12-13]，远小于地铁线路上绝大多数波磨的通过频率；第三类波磨理论由陈光雄教授提出，该理论认为当车辆通过小半径曲线轨道时，导向轮对上的轮轨蠕滑力饱和，引发了轮轨系统的摩擦自激振动，致使钢轨表面出现波磨，该理论可以合理地解释地铁线路上规律性的波磨现象，正逐渐被学者们认可[20-23].
梯形轨枕因其具有良好的减振降噪效果被铺设在减振要求高的地段[24]. 然而，在小半径曲线梯形轨枕轨道上出现了严重的钢轨波磨[25]，目前对于梯形轨枕轨道波磨成因的研究还不充分. 本文基于轮轨系统摩擦自激振动导致钢轨波磨的观点对小半径曲线上的梯形轨枕轨道波磨展开研究，建立了导向轮对-梯形轨枕轨道系统有限元模型. 该模型采用实体单元对扣件系统进行建模，考虑了弹条的扣压作用以及轨距挡块的横向限位作用，建模方式更加符合实际工况. 应用复特征值分析和瞬时动态分析分别求解了该摩擦耦合系统的运动稳定性和时域动态响应，揭示了小半径曲线上梯形轨枕轨道波磨的成因.
1. 数值模型和理论方法
1.1 导向轮对-梯形轨枕轨道系统有限元模型
当车辆通过小半径曲线梯形轨枕轨道时，导向轮对与钢轨的接触位置如图1所示. 外轮的轮缘与高轨的轨距面接触，内轮的踏面与低轨的轨顶面接触. 图1中：δL、δR分别为外轮、内轮与钢轨间的接触角，FL和NL分别为外轮与高轨接触界面上的横向蠕滑力和法向接触力，FR和NR分别为内轮与低轨接触界面上的横向蠕滑力和法向接触力，FSVL和FSVR为作用在导向轮对左、右轴端的垂向悬挂力，FSLL和FSLR为作用在导向轮对左、右轴端的横向悬挂力，KC为弹条刚度，KDL和CDL分别为横向缓冲垫的刚度和阻尼，KDV和CDV分别为垂向减振垫的刚度和阻尼.
图 1 导向轮对-梯形轨枕轨道系统接触模型简图Figure 1. Contact model of leading wheelset‒ladder sleeper track system扣件系统由轨下垫板、弹条、轨距挡块、铁垫板等组成，轨距挡块约束着钢轨的横向运动，弹条产生的扣压力将钢轨紧紧地压在轨道上，钢轨的纵向运动通过钢轨与轨下垫板间的摩擦力来约束，螺旋道钉将铁垫板固定在梯形轨枕上. 为了简化模型，本文仅对扣件系统中的轨下垫板和铁垫板进行实体单元建模.
依托于图1所示的轮轨系统接触模型，使用ABAQUS有限元分析软件建立了导向轮对-梯形轨枕轨道系统有限元模型，如图2所示. 车轮廓形为LM磨耗型踏面，轮对滚动圆半径为0.42 m；钢轨廓形为60 kg/m标准钢轨截面，模型中单根钢轨的长度为36 m；轨下垫板离散地分布在钢轨底部，相邻轨下垫板/铁垫板间的距离为0.625 m；梯形轨枕由横向钢管和预应力混凝土纵梁组合而成，相邻横向钢管间的距离为2.5 m；导向轮对、钢轨、轨下垫板、铁垫板和梯形轨枕通过实体单元建模，整个有限元模型采用C3D8I实体单元划分，模型中共包含
422968 个单元，606942 个节点. 轮轨间的接触以及钢轨和轨下垫板间的接触采用面-面接触算法和有限滑移准则进行建模. 轮轨间的摩擦系数为0.40，钢轨与轨下垫板间的摩擦系数为0.75[26]. 通过垂向压缩弹簧来模拟弹条的扣压作用，通过“Equation”约束模拟轨距挡块的横向限位作用，通过“Tie”约束模拟轨下垫板和铁垫板以及铁垫板和梯形轨枕的连接关系. 模型中采用接地弹簧和阻尼单元模拟侧向缓冲垫和垂向减振垫对梯形轨枕的缓冲减振作用，相邻缓冲减振垫间的距离为1.25 m. 缓冲减振垫的刚度为2 × 107 N/m，阻尼为7 × 104 N·s/m[27]. 各部件的材料参数见表1.
图 2 导向轮对-梯形轨枕轨道系统有限元模型Figure 2. Finite element model of leading wheelset‒ladder sleeper track system表 1 材料参数Table 1. Material parameters部件 密度/
（×103 kg·m−3）弹性模量/MPa 泊松比 钢轨/轮对 7.80 210000 0.30 轨下垫板 1.19 12 0.45 铁垫板 7.80 173000 0.30 横向钢管 7.80 210000 0.30 混凝土纵梁 2.50 36000 0.20 1.2 轮轨摩擦耦合系统自激振动的有限元分析方法
采用复特征值分析来求解导向轮对-梯形轨枕轨道系统的运动稳定性. 在小半径曲线轨道段，导向轮对上的轮轨蠕滑力达到饱和，约等于滑动摩擦力. 在此情形下，轮轨摩擦耦合系统的运动方程为
M¨u+C˙u+Ku=0, (1) 式中：M、C、K分别为系统的质量、阻尼和刚度矩阵，u为节点位移向量.
式（1）的通解为[28]
u(t)=z∑i=1φieλit=z∑i=1φie(αi+jωi)t, (2) 式中：z为拟提取的特征值阶数；${\lambda _i} = {\alpha _i} + {\mathrm{j}}{\omega _i}$，为第i阶特征值；${{\boldsymbol{\varphi}} _i} $为特征向量；t为时间.
由式（2）可以看出，当特征值实部为正时，节点位移随时间指数式增长，这意味着轮轨系统发生了不稳定振动. 通常采用等效阻尼比$ \xi $来判断系统发生自激振动的趋势，如式（3）.
ξ=−2αi|ωi|. (3) 当$ \xi <$0时，轮轨摩擦耦合系统发生了自激振动. 而且，$ \xi $越小，轮轨系统发生自激振动的趋势越强，钢轨波磨更易发生.
复特征值分析是一种频域分析方法，而瞬时动态分析是一种时域非线性分析方法，可以获取摩擦自激振动发生时系统的动态响应. 本文使用ABAQUS/Standard隐式求解器计算了轮轨系统的动态响应. 该求解器采用Newmark方法计算每个增量步结束时刻系统的平衡方程，进而获取节点的位移和速度[29]，如式（4）、（5）.
u|t+Δt=u|t+Δt˙u|t+Δt2((12−β)¨u|t+β¨u|t+Δt), (4) ˙u|t+Δt=˙u|t+Δt((1−γ)¨u|t+γ¨u|t+Δt), (5) 式中：Δt为积分步长，β = （1–α2）/4，γ = 0.5–α，−0.5≤α≤0.
2. 计算结果分析
2.1 小半径曲线段导向轮对-梯形轨枕轨道系统摩擦自激振动分析
复特征值分析的步骤为：
步骤1 在导向轮对轴端施加垂向悬挂力和横向悬挂力；
步骤2 引入轮轨间的摩擦耦合作用；
步骤3 提取轮轨系统的固有频率；
步骤4 进行复特征值分析，提取轮轨系统的摩擦自激振动.
通过定义轮对的横向滑动速度引入导向轮对和钢轨间的摩擦耦合作用. 应用复特征值分析提取了50～
1200 Hz内导向轮对-梯形轨枕轨道系统的摩擦自激振动，如图3所示. 可以看到，在该频率范围内系统共存在7个自激振动，对应频率分别为150.35、163.07、422.16、447.81、471.05、493.97 Hz和519.94 Hz.
图 3 导向轮对-梯形轨枕轨道系统的自激振动频率分布Figure 3. Distribution of self-excited vibration frequencies of leading wheelset‒ladder sleeper track system图4为7个自激振动的振动模态，自激振动主要发生在低轨和内轮上，与钢轨波磨发生在小半径曲线梯形轨枕轨道内轨上相吻合. 根据等效阻尼比越小，自激振动发生趋势越强的原则，可知频率为150.35 Hz和493.97 Hz的自激振动更易发生.
图 4 导向轮对-梯形轨枕轨道系统的自激振动振型Figure 4. Mode shapes of self-excited vibrations of leading wheelset‒ladder sleeper track system图5为曲线半径为350 m的梯形轨枕轨道上的内轨波磨，其波长$\lambda $为60～80 mm. 列车通过该轨道的平均速度$v $为37 km/h，由$\lambda = v/f$可得波磨通过频率为130～180 Hz[27]. 综上可得：当车辆通过小半径曲线段梯形轨枕轨道时，发生在导向轮对内侧轮轨界面上频率为150.35 Hz的自激振动致使内轨上出现了波长为60～80 mm的波磨.
2.2 轮轨法向接触力变化
应用瞬时动态分析求解轮轨系统的动态响应分2个步骤完成：第一步，在导向轮对的轴端施加垂向悬挂力和横向悬挂力；第二步，设置轮对运行速度为40 km/h，运行时间为0.15 s，采样间隔为5 × 10–5 s. 由于未施加任何外部激励且钢轨表面无初始不平顺，因此，计算所得的轮轨系统的响应为自激振动响应. 图6所示为轮轨界面上的法向接触力的时间历程曲线. 从图中可以看出，内侧轮轨界面上的法向接触力波动幅值要大于外侧轮轨界面上的，其中外轮与高轨间法向接触力的波动幅值约为20 kN，而内轮与低轨间法向接触力的波动幅值约为30 kN.
图7为轮轨法向接触力的功率谱密度分析结果. 可以看到，内外侧轮轨界面上法向接触力的振动主频为160 Hz. 由$\lambda = v/f$可得波长约为69 mm，该预测结果与线路上梯形轨枕轨道波磨的波长（60～80 mm）接近.
图 7 轮轨法向接触力的功率谱密度分析Figure 7. Power spectral density analysis of wheel-rail normal contact force2.3 侧向缓冲垫阻尼对轮轨系统摩擦自激振动的影响
不同侧向缓冲垫阻尼CDL，轮轨系统自激振动频率的分布如图8所示. 从图中可以看出：轮轨系统自激振动的数量不随侧向缓冲垫阻尼变化，轮轨系统产生了7个自激振动；侧向缓冲垫阻尼对400～600 Hz内的自激振动的影响很小，而对150～200 Hz内的2个自激振动有较大影响，2个自激振动的等效阻尼比随侧向缓冲垫阻尼值的增大而增大，这说明系统发生自激振动的趋势减弱. 因此，增大侧向缓冲垫阻尼可以在一定程度上抑制梯形轨枕轨道上的内轨波磨.
图 8 不同侧向缓冲垫阻尼下轮轨系统自激振动频率的分布Figure 8. Distribution of self-excited vibration frequencies of wheel-rail system under different damping levels of lateral cushioning pad2.4 垂向减振垫刚度对轮轨系统摩擦自激振动的影响
图9所示为不同垂向减振垫刚度KDV，轮轨系统自激振动频率的分布. 从图9可以看出，当垂向KDV=10 kN/mm时，轮轨系统有6个自激振动，最小等效阻尼比为–
0.00789 ；当KDV=20 kN/mm时，轮轨系统有7个自激振动，最小等效阻尼比为−0.00506 ；当KDV=30 kN/mm时，轮轨系统有6个自激振动，最小等效阻尼比为−0.00679 ；当KDV=40 kN/mm时，轮轨系统有6个自激振动，最小等效阻尼比为−0.00798 . 由以上分析可知，当KDV=20 kN/mm时，最小等效阻尼比高于其余3种工况，这意味着系统发生自激振动的趋势减弱. 过小或过大的垂向减振垫刚度均不利于抑制梯形轨枕轨道上的内轨波磨.
图 9 不同垂向减振垫刚度下轮轨系统自激振动频率的分布Figure 9. Distribution of self-excited vibration frequencies of wheel-rail system under different stiffness levels of vertical damping pad2.5 梯形轨枕结构对轮轨系统摩擦自激振动的影响
图10所示为4种不同结构的梯形轨枕. 每块轨枕上横向钢管的数量N=2根时，对应结构的梯形轨枕相邻横向钢管间的距离为5.000 m；N=3根时，对应结构的梯形轨枕相邻横向钢管间的距离为2.500 m；N=5根时，对应结构的梯形轨枕相邻横向钢管间的距离为1.250 m；N=9根时，对应结构的梯形轨枕相邻横向钢管间的距离为0.625 m. 需要说明的是，横向钢管间距的设计值为2.500 m.
图11所示为4个不同结构的导向轮对-梯形轨枕轨道系统自激振动频率的分布. 从图中可以看出：梯形轨枕结构对轮轨系统的摩擦自激振动有显著影响，并非每块梯形轨枕上的横向钢管数量越多，轮轨系统就越稳定. 如蓝色椭圆圈内所示，当每块梯形轨枕上安装9根横向钢管时，轮轨系统产生自激振动的等效阻尼比反而更小，轮轨系统更不稳定，钢轨波磨更易出现. 红色椭圆圈内所示为低频段的2个自激振动，当每块梯形轨枕上安装2根横向钢管时，等效阻尼比更低，轮轨系统更易趋于不稳定. 当每块梯形轨枕上安装5根横向钢管时，等效阻尼比最大，轮轨系统发生自激振动的趋势减弱. 因此，在地铁小半径曲线地段，铺设横向钢管间距为1.250 m的梯形轨枕可以一定程度抑制梯形轨枕轨道波磨.
图 11 不同结构的轮轨系统的自激振动频率分布Figure 11. Distribution of self-excited vibration frequencies of wheel-rail systems with different structures3. 结 论
本文研究了地铁小半径曲线梯形轨枕轨道上的内轨波磨，建立了导向轮对-梯形轨枕轨道系统有限元模型，模型中采用实体单元对扣件系统进行建模，应用复特征值分析和瞬时动态分析分别求解了轮轨系统的运动稳定性和时域动态响应. 研究了缓冲减振垫参数及梯形轨枕结构对轮轨系统摩擦自激振动的影响，得到以下结论：
1） 饱和轮轨蠕滑力引起的频率为150 Hz的轮轨系统共振振动是地铁线路小半径曲线段梯形轨枕轨道上波长为60～80 mm内轨波磨的成因.
2） 增大侧向缓冲垫阻尼可以一定程度上抑制梯形轨枕轨道上的内轨波磨，过小或过大的垂向减振垫刚度均不利于抑制钢轨波磨.
3） 改变单块梯形轨枕上横向钢管的数量实际上是改变了导向轮对–梯形轨枕轨道系统的刚度矩阵，进而影响了轮轨系统发生自激振动的趋势以及钢轨波磨的发展趋势. 铺设横向钢管间距为1.250 m结构的梯形轨枕可以抑制梯形轨枕轨道上的钢轨波磨.
-
图 1 导向轮对-梯形轨枕轨道系统接触模型简图
Figure 1. Contact model of leading wheelset‒ladder sleeper track system
图 2 导向轮对-梯形轨枕轨道系统有限元模型
Figure 2. Finite element model of leading wheelset‒ladder sleeper track system
图 3 导向轮对-梯形轨枕轨道系统的自激振动频率分布
Figure 3. Distribution of self-excited vibration frequencies of leading wheelset‒ladder sleeper track system
图 4 导向轮对-梯形轨枕轨道系统的自激振动振型
Figure 4. Mode shapes of self-excited vibrations of leading wheelset‒ladder sleeper track system
图 7 轮轨法向接触力的功率谱密度分析
Figure 7. Power spectral density analysis of wheel-rail normal contact force
图 8 不同侧向缓冲垫阻尼下轮轨系统自激振动频率的分布
Figure 8. Distribution of self-excited vibration frequencies of wheel-rail system under different damping levels of lateral cushioning pad
图 9 不同垂向减振垫刚度下轮轨系统自激振动频率的分布
Figure 9. Distribution of self-excited vibration frequencies of wheel-rail system under different stiffness levels of vertical damping pad
图 11 不同结构的轮轨系统的自激振动频率分布
Figure 11. Distribution of self-excited vibration frequencies of wheel-rail systems with different structures
表 1 材料参数
Table 1. Material parameters
部件 密度/
（×103 kg·m−3）弹性模量/MPa 泊松比 钢轨/轮对 7.80 210000 0.30 轨下垫板 1.19 12 0.45 铁垫板 7.80 173000 0.30 横向钢管 7.80 210000 0.30 混凝土纵梁 2.50 36000 0.20 
下载: 导出CSV
-
[1] CUI X L, CHEN G X, OUYANG H J. Study on the effect of track curve radius on friction-induced oscillation of a wheelset–track system[J]. Tribology Transactions, 2019, 62(4): 688-700. doi: 10.1080/10402004.2019.1601317 [2] 陈光雄. 钢轨波磨预测模型验证工况的研究[J]. 西南交通大学学报,2022,57(5): 1017-1023,1054. doi: 10.3969/j.issn.0258-2724.20200842CHEN Guangxiong. Study on validation conditions of rail corrugation prediction models[J]. Journal of Southwest Jiaotong University, 2022, 57(5): 1017-1023,1054. doi: 10.3969/j.issn.0258-2724.20200842 [3] WANG P, LU J, ZHAO C Y, et al. Numerical investigation of the fatigue performance of elastic rail clips considering rail corrugation and dynamic axle load[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2021, 235(3): 339-352. doi: 10.1177/0954409720926016 [4] 关庆华,张斌,熊嘉阳,等. 地铁钢轨波磨的基本特征、形成机理和治理措施综述[J]. 交通运输工程学报,2021,21(1): 316-337.GUAN Qinghua, ZHANG Bin, XIONG Jiayang, et al. Review on basic characteristics, formation mechanisms, and treatment measures of rail corrugation in metro systems[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 316-337. [5] TORSTENSSON P T, SCHILKE M. Rail corrugation growth on small radius curves—measurements and validation of a numerical prediction model[J]. Wear, 2013, 303(1/2): 381-396. [6] HIENSCH M, NIELSEN J C O, VERHEIJEN E. Rail corrugation in The Netherlands—measurements and simulations[J]. Wear, 2002, 253(1/2): 140-149. [7] SHENG X, THOMPSON D J, JONES C J C, et al. Simulations of roughness initiation and growth on railway rails[J]. Journal of Sound and Vibration, 2006, 293(3/4/5): 819-829. [8] ROBLES R, CORREA N, VADILLO E G, et al. Comprehensive efficient vertical and lateral track dynamic model to study the evolution of rail corrugation in sharp curves[J]. Journal of Sound and Vibration, 2023, 545: 117448. 1-117448.18. [9] WU T X, THOMPSON D J. An investigation into rail corrugation due to micro-slip under multiple wheel/rail interactions[J]. Wear, 2005, 258(7/8): 1115-1125. [10] JIN X S, WEN Z F, WANG K Y, et al. Three-dimensional train–track model for study of rail corrugation[J]. Journal of Sound and Vibration, 2006, 293(3/4/5): 830-855. [11] EADIE D T, KALOUSEK J, CHIDDICK K C. The role of high positive friction (HPF) modifier in the control of short pitch corrugations and related phenomena[J]. Wear, 2002, 253(1/2): 185-192. [12] SUN Y Q, SIMSON S. Wagon–track modelling and parametric study on rail corrugation initiation due to wheel stick-slip process on curved track[J]. Wear, 2008, 265(9/10): 1193-1201. [13] LIU X G, WANG P. Investigation of the generation mechanism of rail corrugation based on friction induced torsional vibration[J]. Wear, 2021, 468/469: 203593.1-203593.9. [14] CHEN G X, ZHANG S, WU B W, et al. Field measurement and model prediction of rail corrugation[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2020, 234(4): 381-392. doi: 10.1177/0954409719877318 [15] CHEN G X, ZHOU Z R, OUYANG H, et al. A finite element study on rail corrugation based on saturated creep force-induced self-excited vibration of a wheelset–track system[J]. Journal of Sound and Vibration, 2010, 329(22): 4643-4655. doi: 10.1016/j.jsv.2010.05.011 [16] QIAN W J, CHEN G X, OUYANG H, et al. A transient dynamic study of the self-excited vibration of a railway wheel set–track system induced by saturated creep forces[J]. Vehicle System Dynamics, 2014, 52(9): 1115-1138. doi: 10.1080/00423114.2014.924629 [17] QIAN W J, HUANG Z Q, OUYANG H, et al. Numerical investigation of the effects of rail vibration absorbers on wear behaviour of rail surface[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2019, 233(3): 424-438. doi: 10.1177/1350650118785061 [18] CUI X L, CHEN G X, YANG H G, et al. Effect of the wheel/rail contact angle and the direction of the saturated creep force on rail corrugation[J]. Wear, 2015, 330/331: 554-562. doi: 10.1016/j.wear.2014.12.046 [19] 吴波文,陈光雄,赵晓男,等. 地铁先锋扣件地段钢轨波磨成因[J]. 西南交通大学学报,2020,55(3): 650-657. doi: 10.3969/j.issn.0258-2724.20180371WU Bowen, CHEN Guangxiong, ZHAO Xiaonan, et al. Formation mechanisim of rail corrugation occurring on tight curved track with vanguard fasteners[J]. Journal of Southwest Jiaotong University, 2020, 55(3): 650-657. doi: 10.3969/j.issn.0258-2724.20180371 [20] WANG Z Q, LEI Z Y. Analysis of influence factors of rail corrugation in small radius curve track[J]. Mechanical Sciences, 2021, 12(1): 31-40. doi: 10.5194/ms-12-31-2021 [21] WANG Y, XIAO H, NADAKATTI M M, et al. Mechanism of rail corrugation combined with friction self-excited vibration and wheel-track resonance[J]. Construction and Building Materials, 2023, 400: 132782.1-132782.16. [22] EL BESHBICHI O, WAN C, BRUNI S, et al. Complex eigenvalue analysis and parameters analysis to investigate the formation of railhead corrugation in sharp curves[J]. Wear, 2020, 450/451: 203150.1-203150.10. [23] FOURIE D, FRÖHLING R, HEYNS S. Railhead corrugation resulting from mode-coupling instability in the presence of veering modes[J]. Tribology International, 2020, 152: 106499.1-106499.12. [24] 李响,任尊松,王子. 基于梯形轨枕轨道振动特性的钢轨波磨研究[J]. 铁道学报,2020,42(10): 38-44. doi: 10.3969/j.issn.1001-8360.2020.10.006LI Xiang, REN Zunsong, WANG Zi. Study on rail corrugation of ladder-type sleeper track based on vibration characteristics[J]. Journal of the China Railway Society, 2020, 42(10): 38-44. doi: 10.3969/j.issn.1001-8360.2020.10.006 [25] YAN Z Q, MARKINE V, GU A J, et al. Optimisation of the dynamic properties of ladder track to minimise the chance of rail corrugation[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2014, 228(3): 285-297. doi: 10.1177/0954409712472329 [26] OREGUI M, LI Z, DOLLEVOET R. An investigation into the modeling of railway fastening[J]. International Journal of Mechanical Sciences, 2015, 92: 1-11. doi: 10.1016/j.ijmecsci.2014.11.019 [27] LI W, WANG H Y, WEN Z F, et al. An investigation into the mechanism of metro rail corrugation using experimental and theoretical methods[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2016, 230(4): 1025-1039. doi: 10.1177/0954409715596182 [28] 崔晓璐,唐传平,包鹏羽,等. 高速列车制动区段钢轨波磨抑制方法[J]. 西南交通大学学报,2023,58(3): 656-664. doi: 10.3969/j.issn.0258-2724.20220256CUI Xiaolu, TANG Chuanping, BAO Pengyu, et al. Rail corrugation suppressing method on braking sections of high-speed trains[J]. Journal of Southwest Jiaotong University, 2023, 58(3): 656-664. doi: 10.3969/j.issn.0258-2724.20220256 [29] CUI X L, CHENG Z, YANG Z C, et al. Study on the phenomenon of rail corrugation on high-speed rail based on the friction-induced vibration and feedback vibration[J]. Vehicle System Dynamics, 2022, 60(2): 413-432. doi: 10.1080/00423114.2020.1817507 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 213
- HTML全文浏览量: 74
- PDF下载量: 31
- 被引次数: 0