Influence Analysis of Vibration Control Parameters for High-Speed Maglev Train-Bridge Coupling
-
摘要:
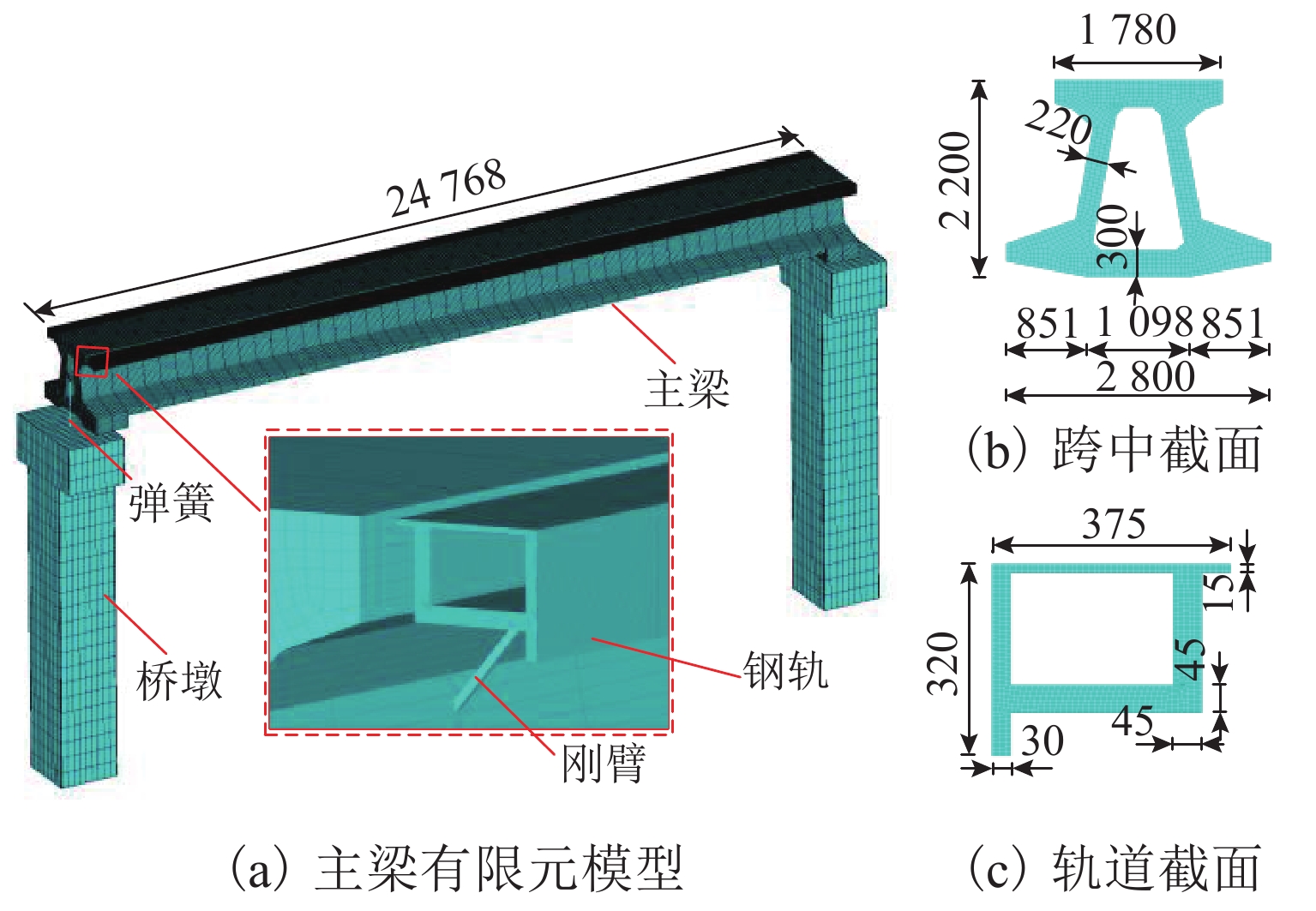
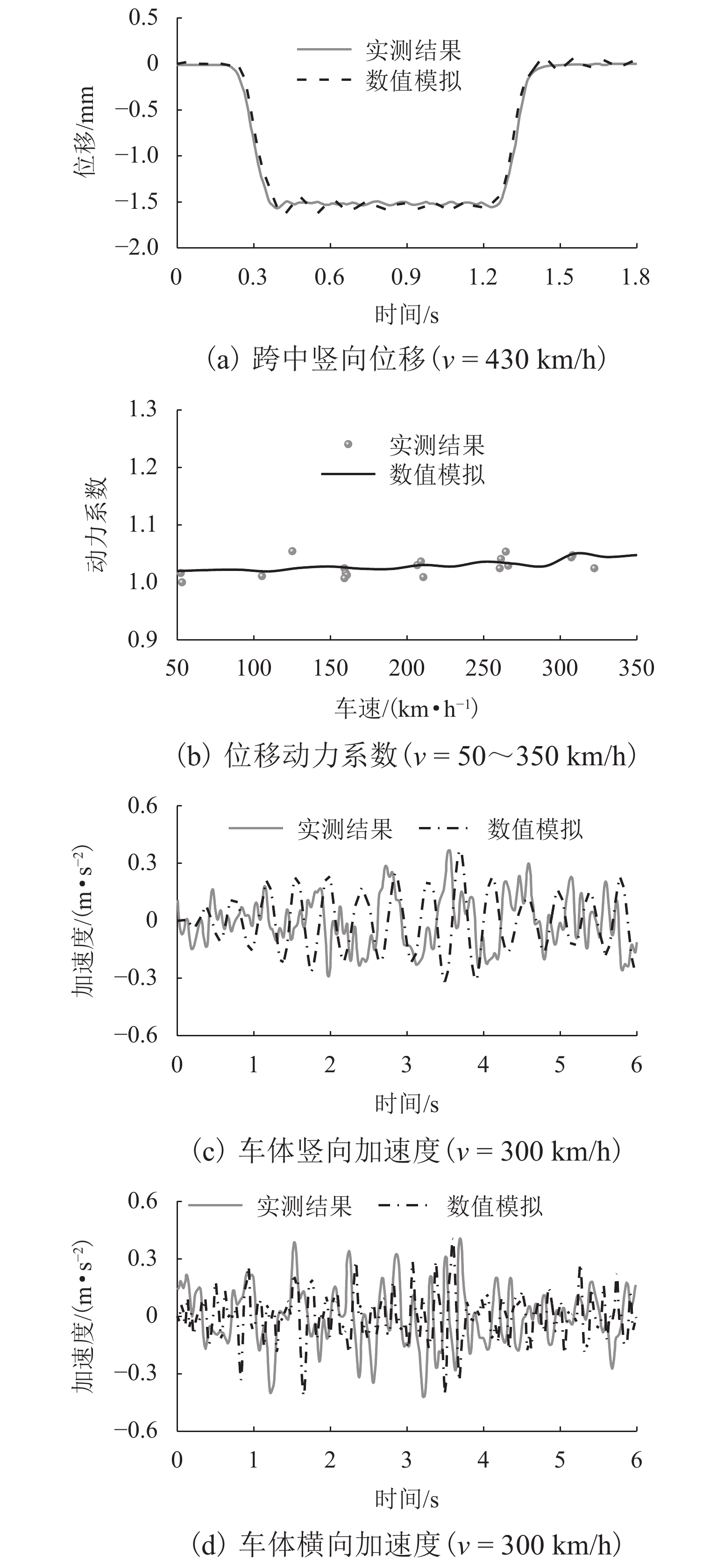
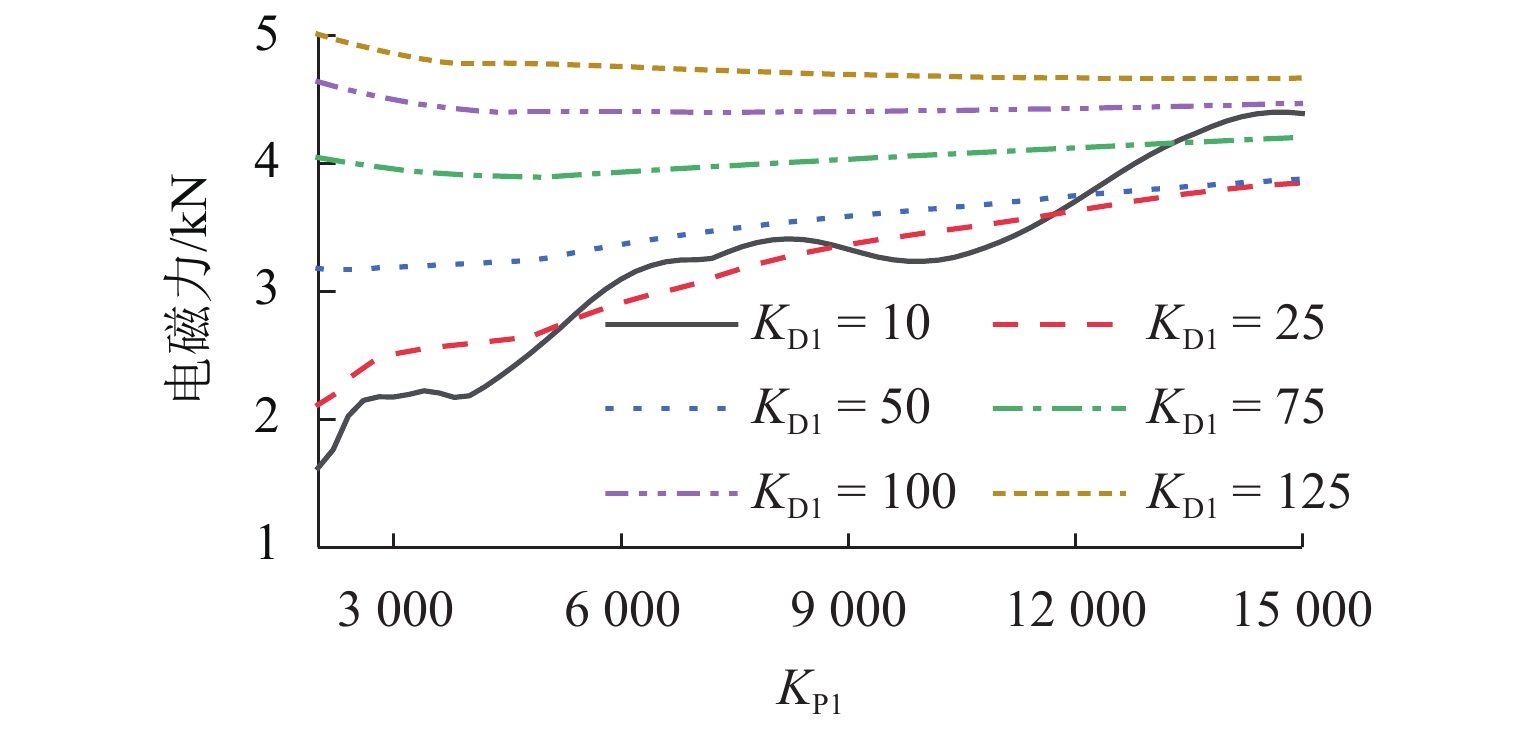
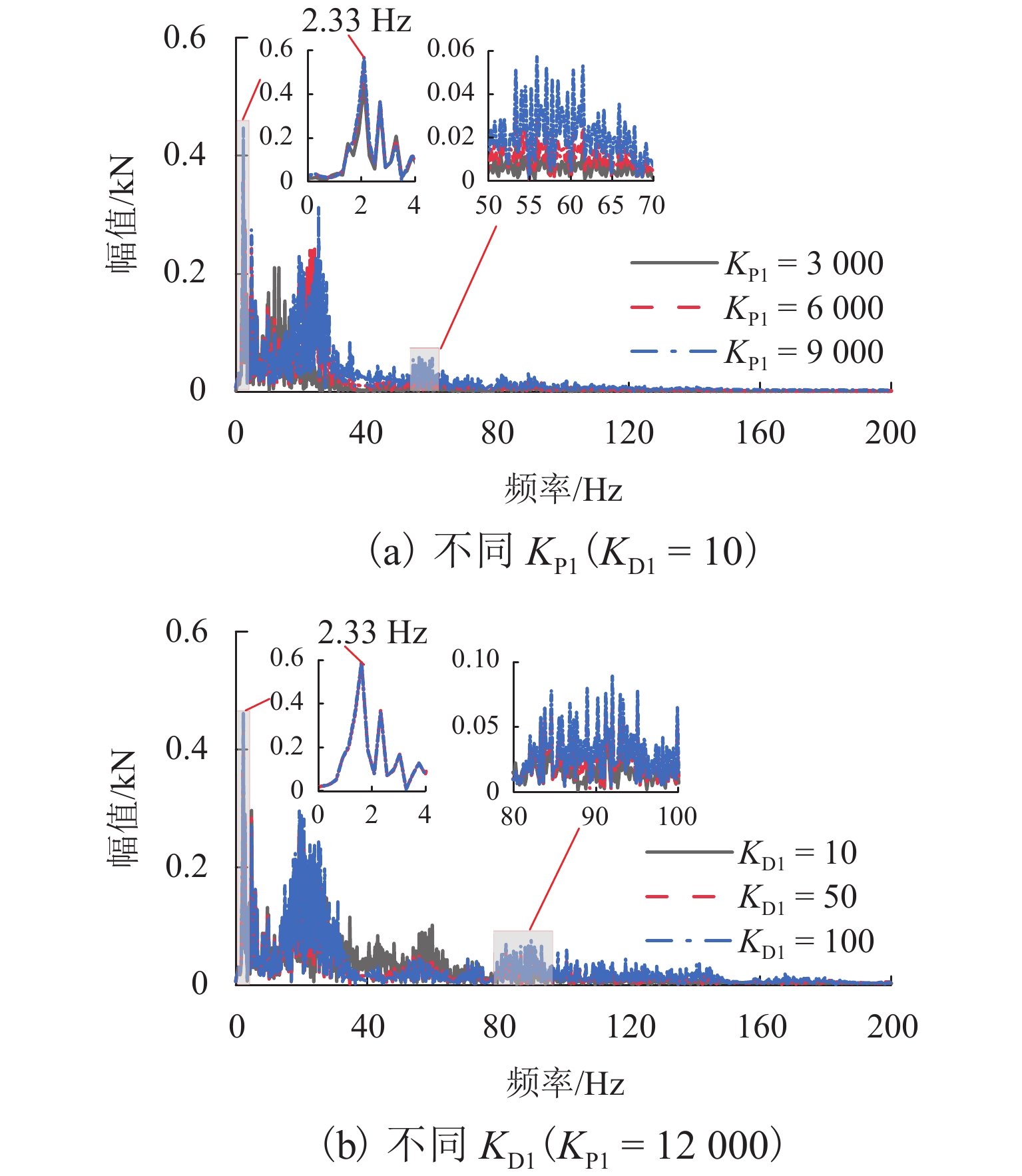
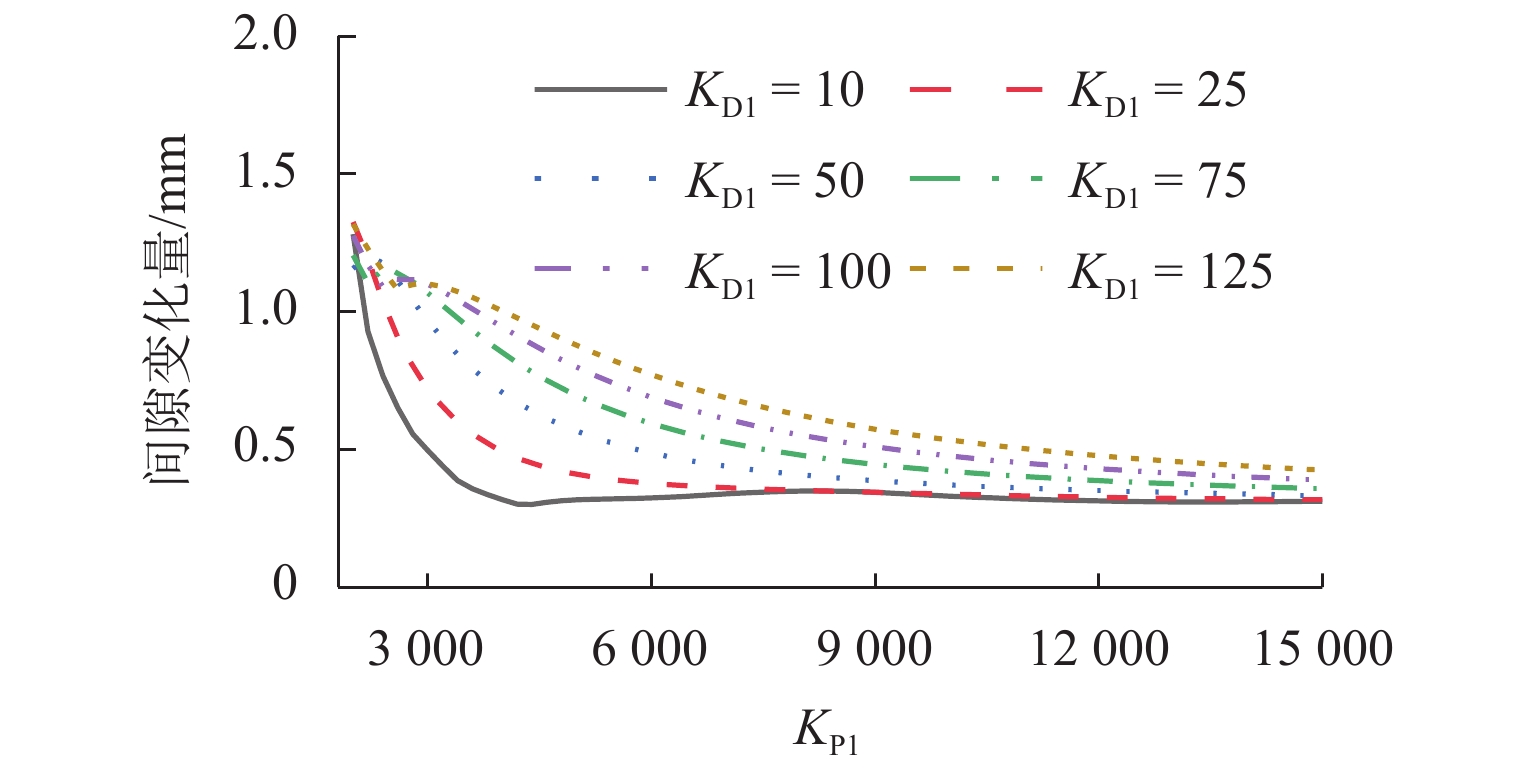
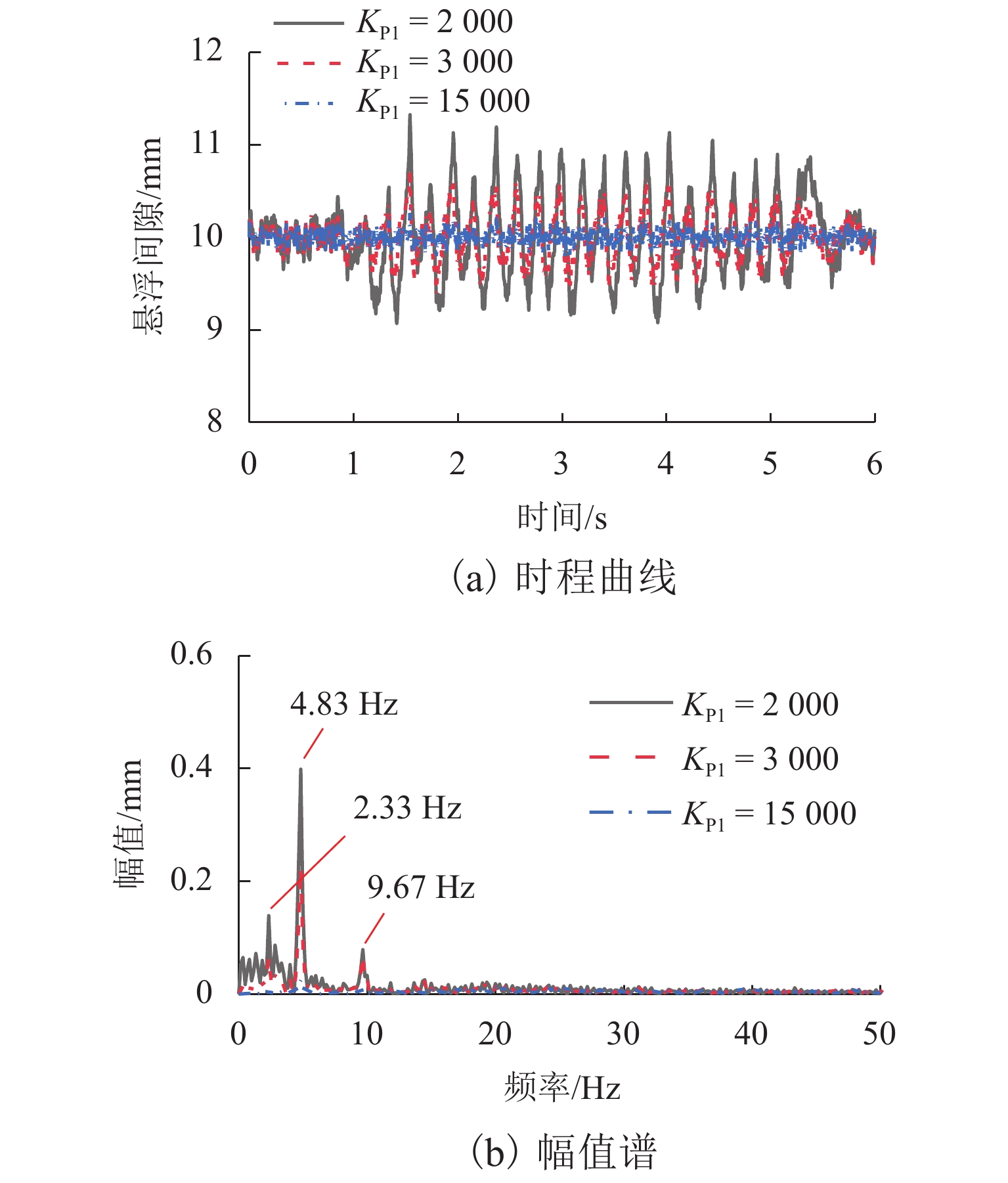
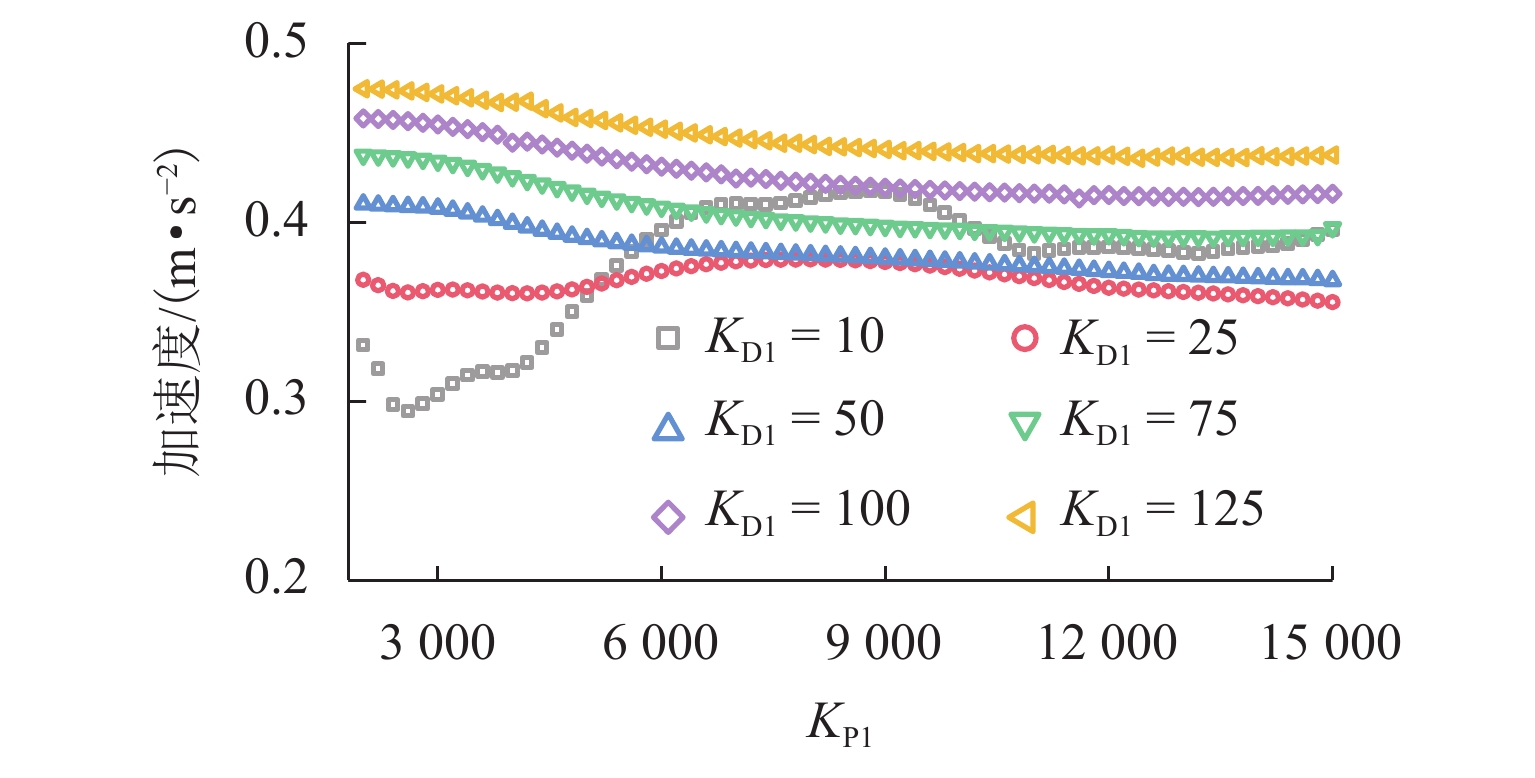
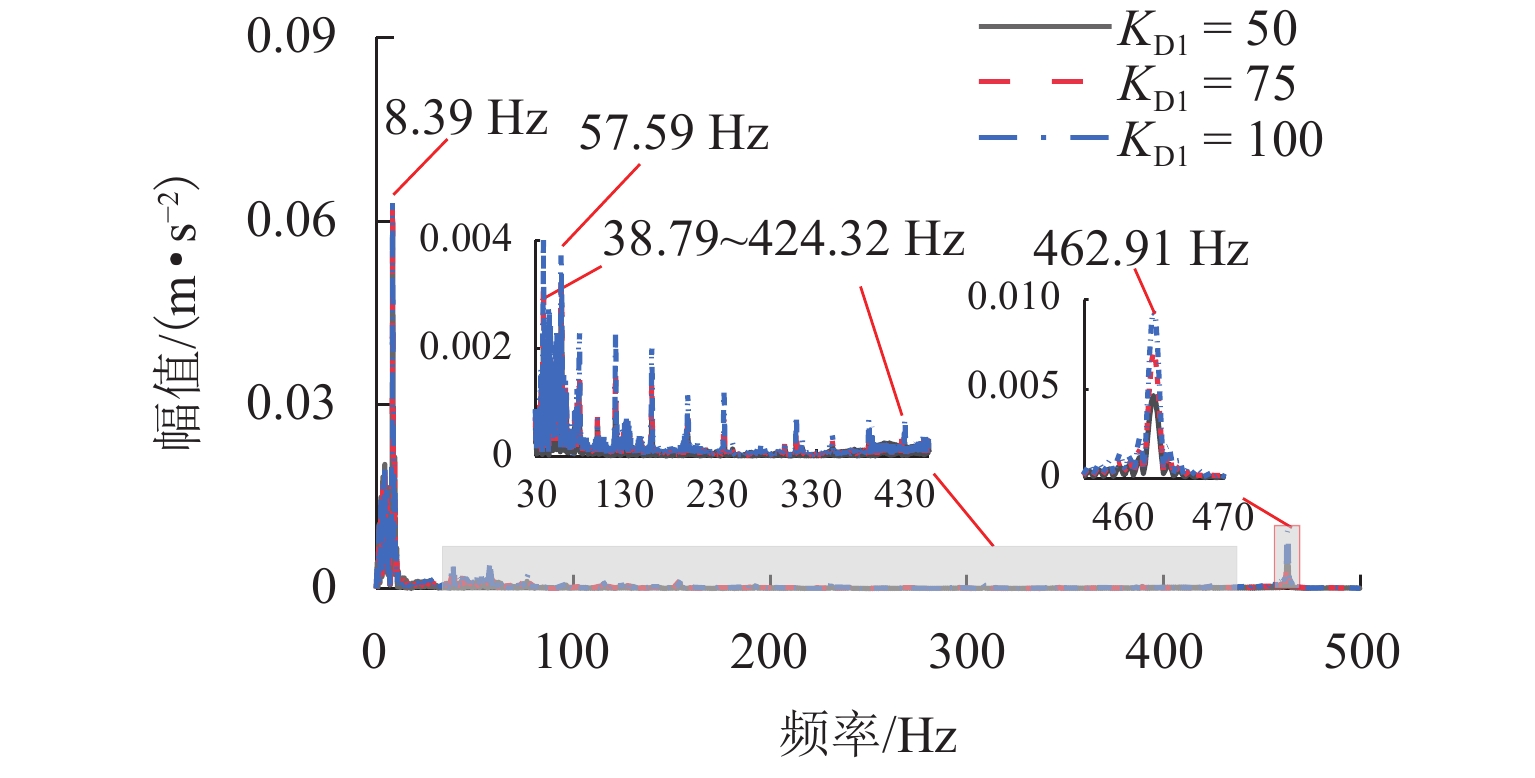
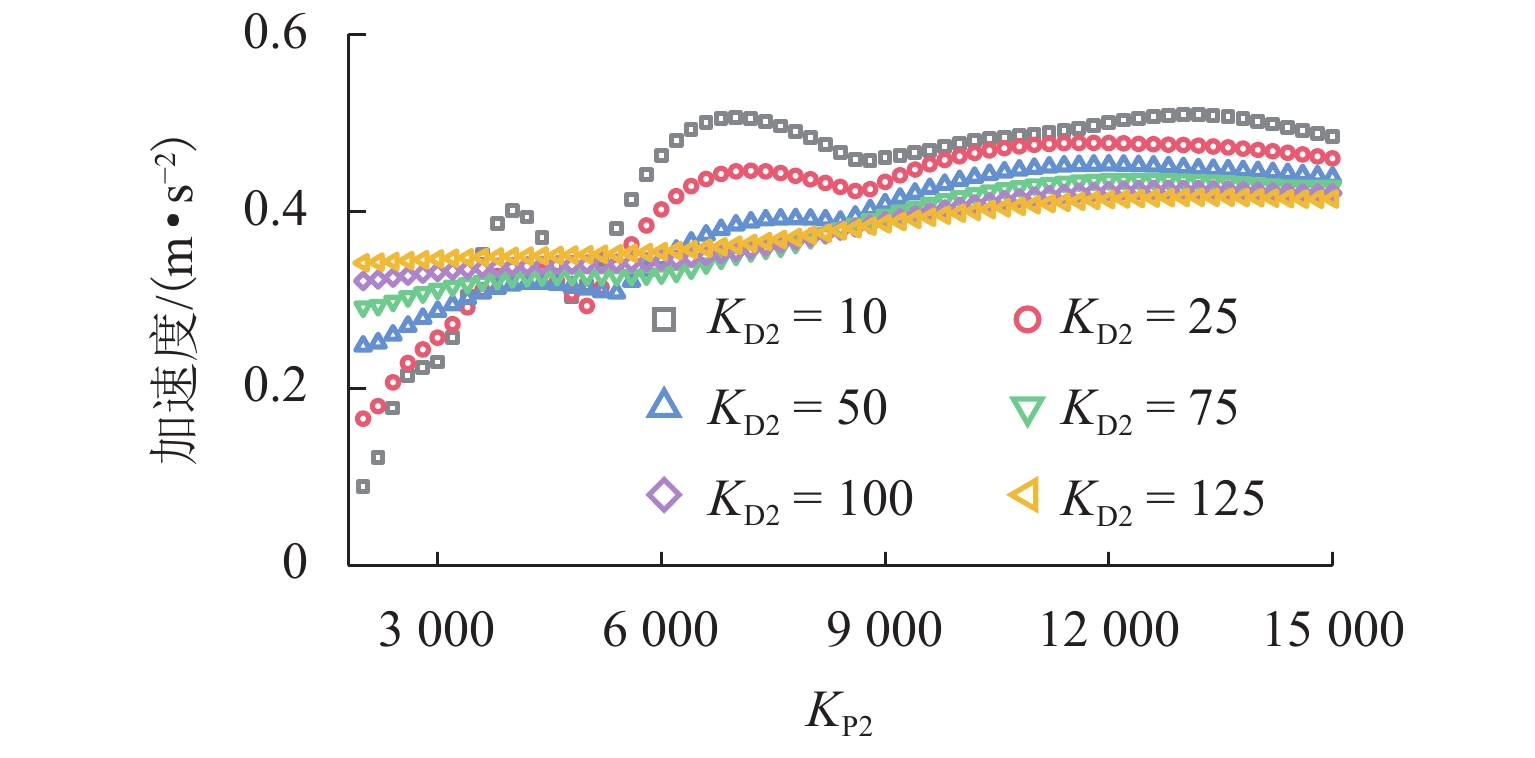
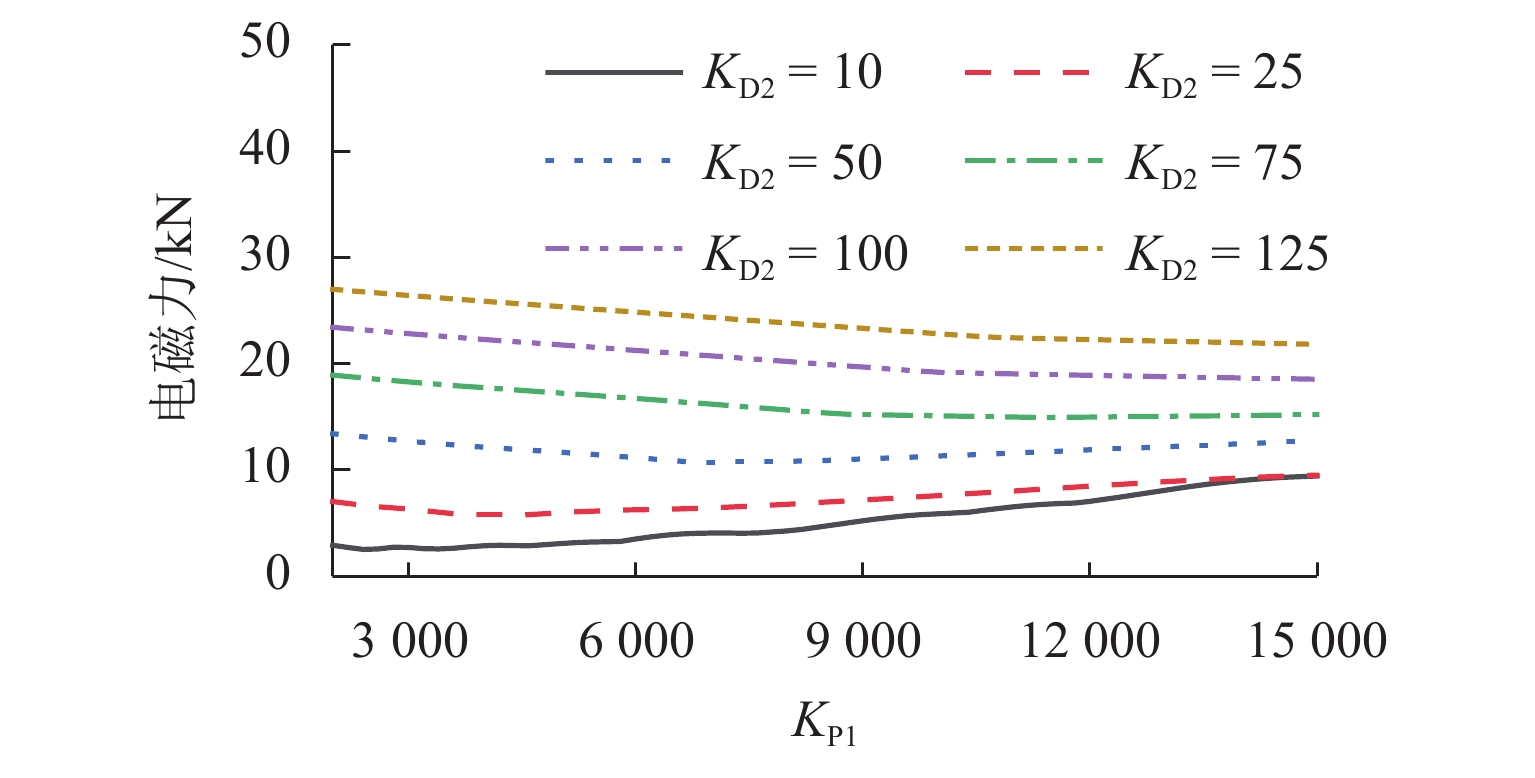
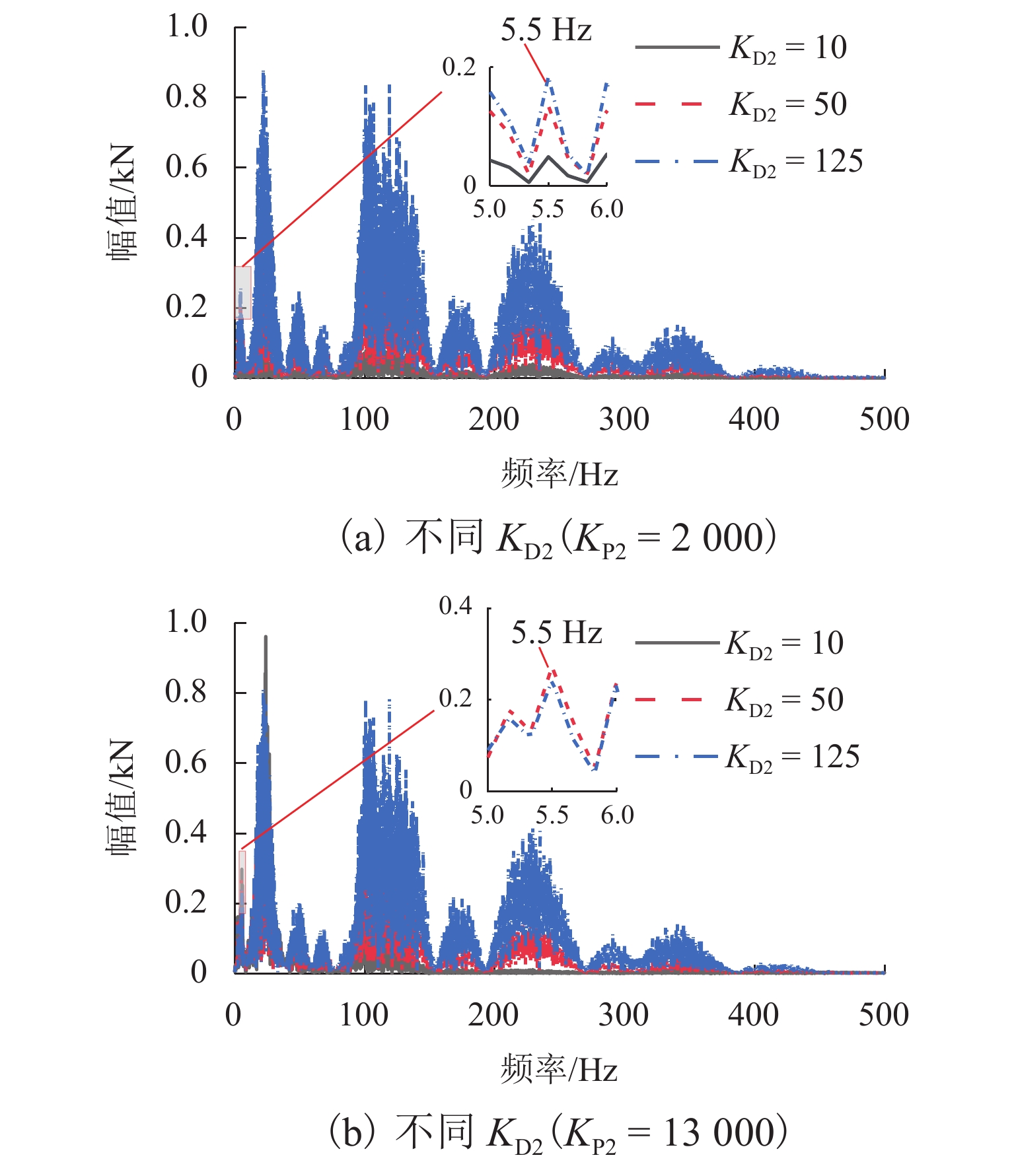
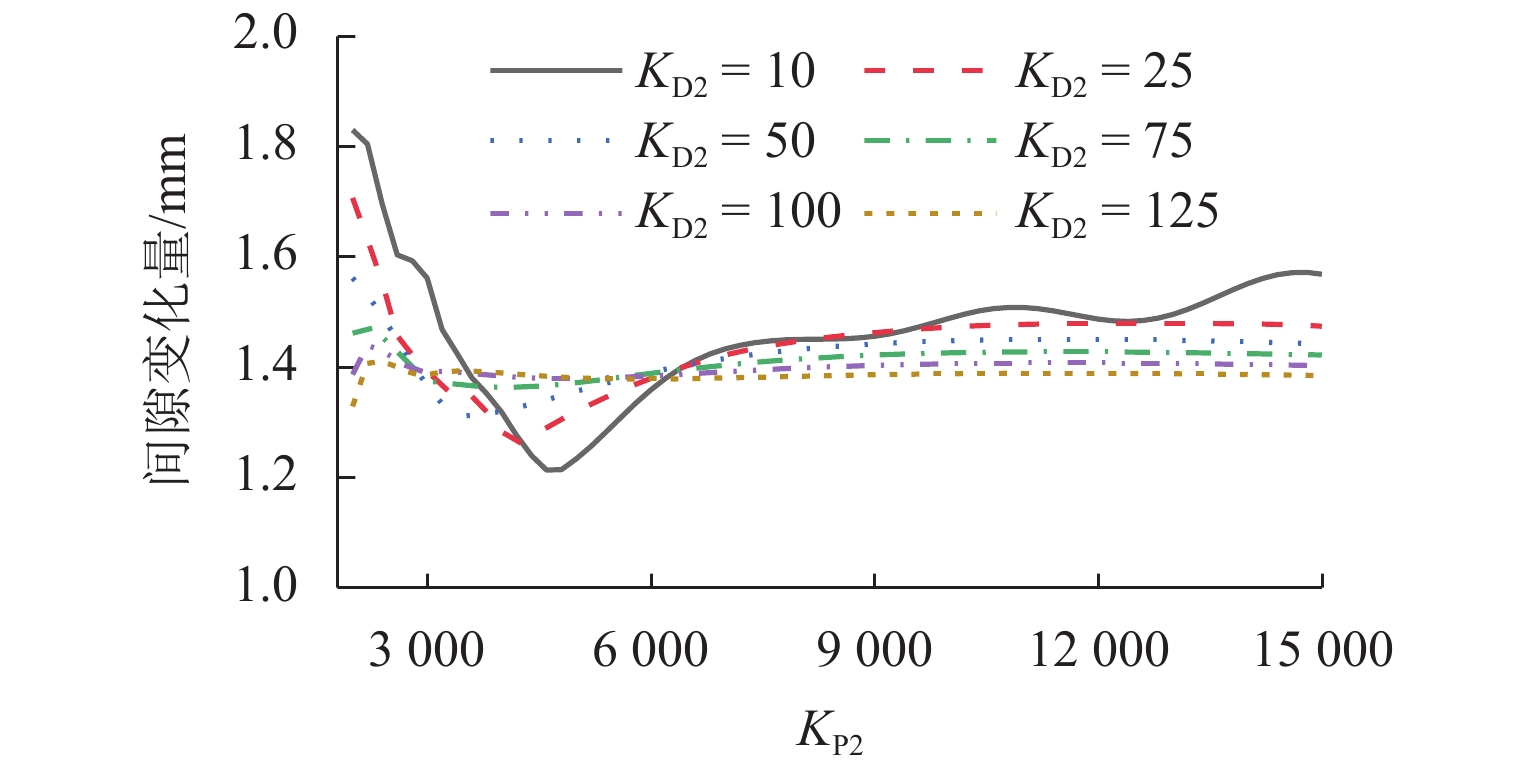
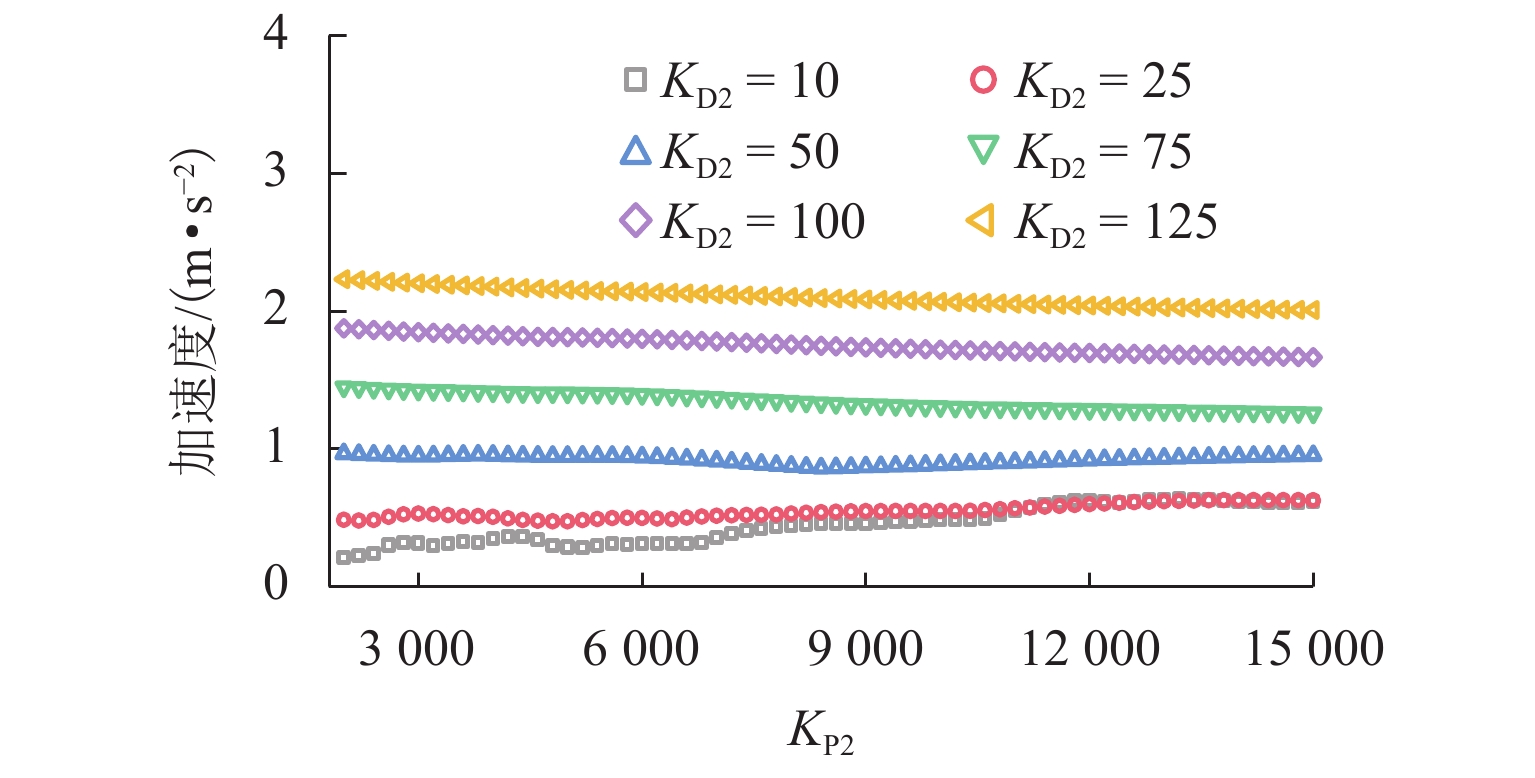
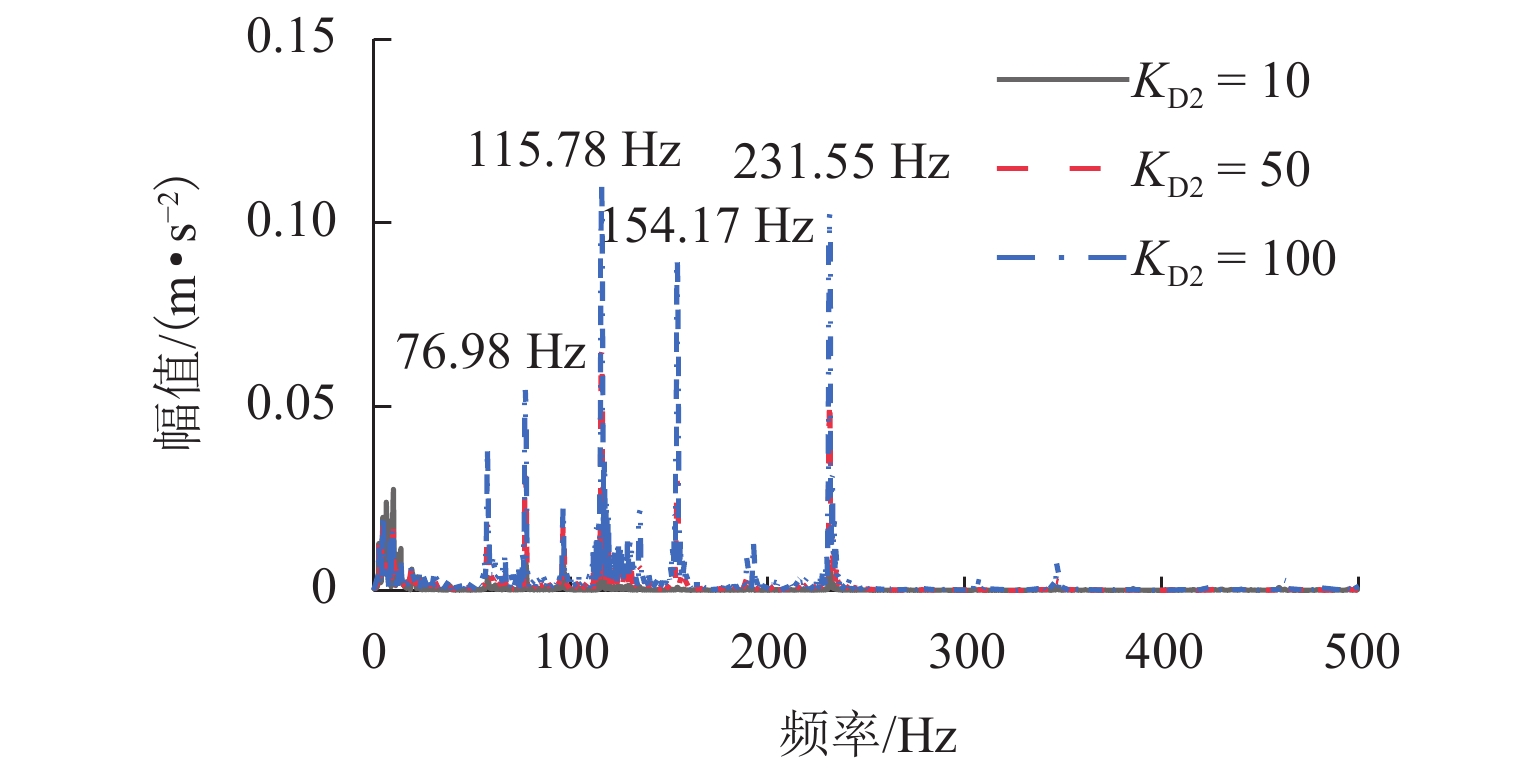
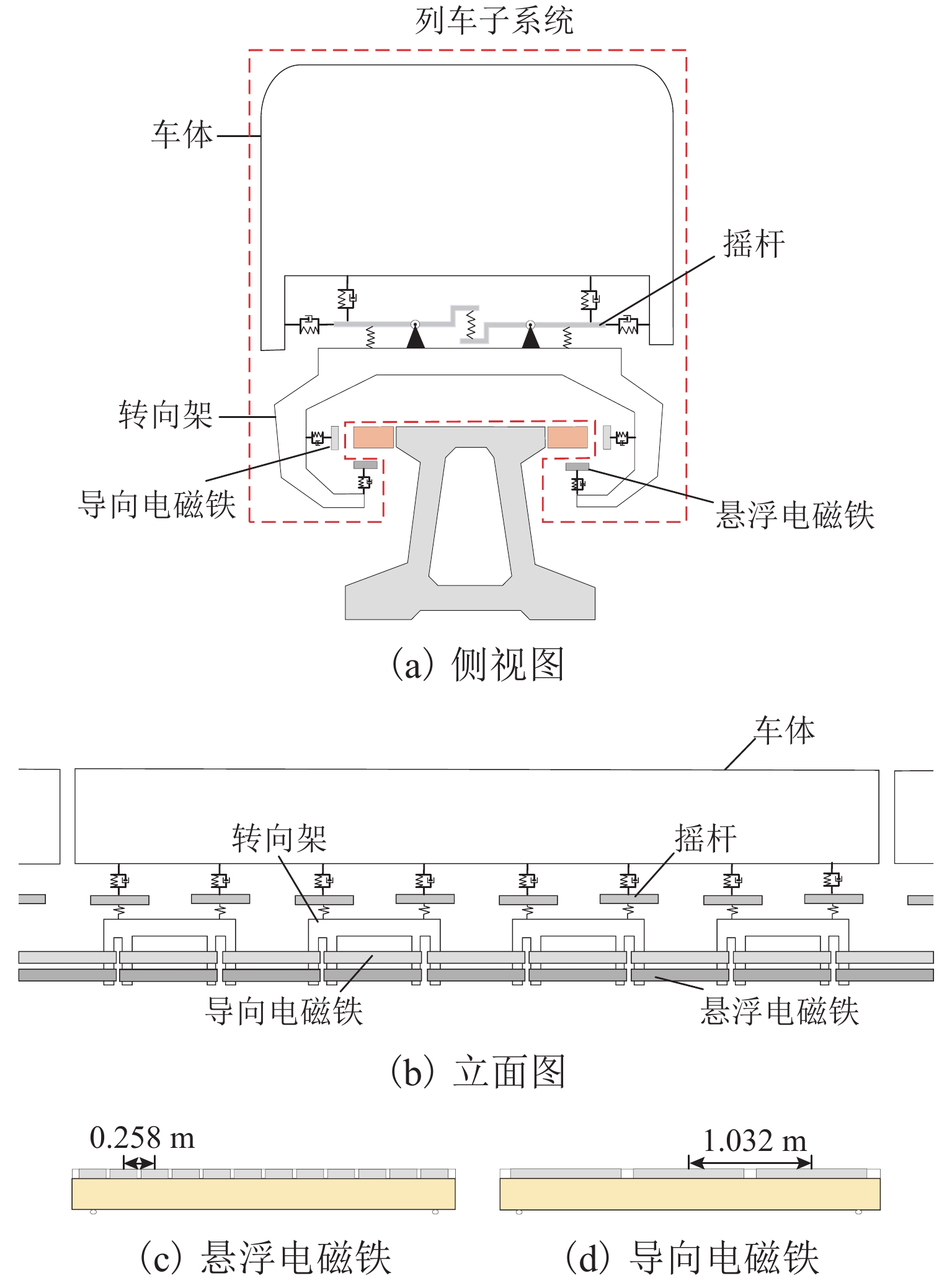
磁浮列车悬浮系统控制参数取值不当可能导致车-桥系统异常振动. 因此，明确悬浮系统控制参数与磁浮车-桥系统动力响应之间的关系十分重要. 首先，建立包含比例-微分控制的5节编组磁浮列车动力学模型和20跨简支梁桥有限元模型；其次，与实测结果进行对比验证所建立模型的正确性；最后，计算车速430 km/h时不同控制参数下列车和桥梁的动力响应. 结果表明：增大比例系数会使悬浮和导向系统刚度增大，增大微分系数会使悬浮和导向系统阻尼增大；车体竖向加速度随比例和微分系数的增大而增大，车体横向加速度随比例系数的增大而增大；悬浮间隙和桥梁竖向加速度均随比例系数的增大而减小，随微分系数的增大而增大；导向间隙随微分系数的增大而减小，比例系数对导向间隙的影响较小；桥梁横向加速度随比例系数的增大而减小，随微分系数的增大而增大；桥梁竖向加速度主要受电磁力中悬浮电磁铁长度特征频率1倍～12倍频的影响，桥梁横向加速度主要受导向磁极长度特征频率及其2倍频和导向电磁铁长度特征频率2倍频及4倍频的影响；为减小车-桥系统动力响应，综合建议竖向比例和微分系数的取值范围分别为3000～4000和10～25，横向比例和微分系数的取值范围分别为4000～5000和10～25.
Abstract:Improper control parameters of the suspension system of maglev trains may lead to abnormal vibration of the train-bridge system. Therefore, it is important to clarify the relationship between the control parameters of the suspension system and the dynamic response of the maglev train-bridge system. Firstly, the dynamic model of a 5-car maglev train with proportional-differential control, as well as the finite element model of a 20-span simply supported beam bridge was established. Secondly, the correctness of the models was verified by comparing them with the measured results. Finally, the dynamic responses of the train and bridge under different control parameters at 430 km/h were calculated. The results show that increasing the proportional coefficient will increase the stiffness of the suspension and guidance system, and increasing the differential coefficient will increase the damping of the suspension and guidance system. The vertical acceleration of the car body increases with the increase in the proportional and differential coefficients, and the lateral acceleration of the car body increases with the increase in the proportional coefficient. The suspension gap and the vertical acceleration of the bridge decrease with the increase in the proportional coefficient, and they increase with the increase in the differential coefficient. The guidance gap decreases with the increase in the differential coefficient, and the proportional coefficient has little effect on the guidance gap. The lateral acceleration of the bridge decreases with the increase in the proportional coefficient and increases with the increase in the differential coefficient. The vertical acceleration of the bridge is mainly affected by a characteristic frequency of 1–12 times of the length of the suspended electromagnet in the electromagnetic force, and the lateral acceleration of the bridge is mainly affected by the characteristic frequency and frequency of 2 times of the length of the guidance pole, as well as the characteristic frequency of 2 times and 4 times of the length of the guidance electromagnet. In order to reduce the dynamic response of the train-bridge system, it is suggested that the values of vertical proportional and differential coefficients should be 3 000–4 000 and 10–25, respectively, and the values of lateral proportional and differential coefficients should be 4 000–5 000 and 10–25, respectively.
-
轨底坡是铁路轨道的重要几何参数. 合理的轨底坡可以改善轮轨匹配关系，有效降低轮轨接触压力，减少轮轨磨耗，降低轮轨接触疲劳损伤，提高轮轨使用寿命，同时也可提高车辆运行的平稳性[1]，但在线路设计、验收和维护过程中几乎很少关注轨底坡. 《高速铁路轨道工程质量验收标准》（TB 10745—2010）[2]中无轨底坡的验收标准，并且在日常的轨道养护维修规则中也未提及关于轨底坡的相关规定. 在线路精调过程中只保证钢轨垂向平顺度和轨距不平顺符合要求，不对轨底坡进行测量和精调.
关于轨底坡的研究从未间断过. 陶功权等[3]建立了B型地铁车辆动力学模型，从动力学角度提出了LM、S1002和 DIN5573 三种不同车轮型面最优的轨底坡匹配；同时从静力学分析的角度提出了地铁车轮型面的最优轨底坡匹配[4]. 陈超[5]分析了LM型面不同轨底坡与磨耗之间的关系，给出了直线段和曲线段的轨底坡推荐值. 周宇等[6]建立基于临界平面法的裂纹萌生寿命预测模型，研究了不同轨底坡对曲线段钢轨疲劳裂纹寿命的影响. 都敏等[7]通过建立弹塑性有限元模型，从轮轨接触应力角度分析了不同轨底坡对磨耗的影响. 刘鹏飞等[8]针对30 t轴重重载线路研究了LM车轮踏面在不同轨底坡下对轮轨接触几何关系，分析了车辆动态曲线通过时轮轨横向力、磨耗指数等因素的影响. 邓建辉等[9]采用不同钢轨材料与LM踏面相匹配，分析了在不同轨底坡条件下轮轨接触斑状态，观测了现场损伤情况. 司道林等[10]通过不同轨底坡条件下，CHN75钢轨与LM车轮踏面的静态轮轨接触，分析了轨道的曲线动态通过性能，给出了1∶20轨底坡适合重载铁路的结论. 李霞等[11]改进了三维接触几何参数算法和三维弹性体非赫兹接触理论，并对比分析了不同轨底坡对轮轨接触参数、摩擦功和接触应力等影响. 关庆华等[12]对比了标准轨底坡条件下，利用基于赫兹接触理论的法向接触刚度计算公式与经验方法的差异. 李霞等[13]对比分析了在两种轨底坡条件下LM和LMA车轮踏面与CHN60钢轨踏面匹配应力结果，得出LM-CHN60 和轨底坡1∶20、LMA-CHN60和轨底坡1∶40匹配较好的结论. 曾向荣等[1]通过国内外对铁路系统的轨底坡取值情况和现场光带的调查，提出了轨底坡建议值. 沈钢等[14]从减轻钢轨侧磨角度，分析了在曲线轨道上设置内外轨合理的轨底坡配比后车辆曲线通过时的滚动圆半径差和轮轮导向性能对侧磨的影响. Sadefhi等[15]基于理论分析和试验评价了轨底坡对铁路轨道几何条件的影响，提出了综合考虑轨底坡影响的轨道几何评价指数.
综上所述，过去对于轨底坡的研究均基于同一轨道上具有相同轨底坡的前提，研究轨底坡对轮轨接触关系和车辆动力学行为的影响. 针对线路中轨底坡存在一定离散性的情况，特别是同一轨道上出现轨底坡变化对车辆动力学行为的影响，值得深入研究. 本文在同一侧钢轨具有不同轨底坡的情况下，分析轨底坡变化对车辆动力学性能的影响，提出轨道线路轨底坡调整与维修的合理化建议，对现有轨道设计与工务维修提供参考.
1. 轮轨静态接触几何分析
轮轨静态接触几何计算是进行轮轨系统关系分析的基础. 迹线法是常用的轮轨接触几何关系计算方法，该方法的算法和数值实现过程参考文献[16-17]. 轮轨接触点分布分析是对现场轮轨接触光带预测的重要指标，同时轮轨接触点分布对车轮踏面磨耗分布具有非常重要的影响. 接触点过于集中会使得车轮磨耗过于集中，容易形成车轮凹磨，以及钢轨局部应力集中，影响车辆运行稳定性[18]. 图1计算了轨底坡从倾斜角度从1∶10到1∶100中的最大、中间和最小3种情况的轮轨接触点分布. 图中车轮廓形与钢轨廓形连接红线为轮轨接触点位置连线，车轮横移量标识在虚线上方数字（左移为正，单位：mm）. 可以看出：随轨底坡角度变小轮轨接触点在钢轨表面位置从由外向轨距角内侧偏移，且接触区域逐渐变大. 由此可知：当轨底坡从1∶10突变到1∶100，接触光带将由窄变宽. 通过观测某客运专线一直线轨底坡波动区段同侧钢轨上接触光带，发现接触光带由钢轨中心外侧较窄变成较宽且覆盖轨顶，随后由较宽且覆盖轨顶变较窄的现象.
图 1 CHN60与LMD 不同轨底坡下接触点对分布Figure 1. Distribution of contact points on CHN60 and LMD for different rail cants等效锥度是轮轨匹配除接触点以外的另一重要因素，也是轮对恢复对中能力的体现，图2给出了在不同轨底坡下等效锥度随轮对横移量的变化. 针对LMD型面与CHN60型面在不同的轨底坡匹配中，轨底坡在1∶10～1∶100变化，在横移量小于6 mm时等效锥度呈现从最小到最大（轨底坡1∶30的情况），随后趋于平稳的过程. 在横移量较小的情况下，轨底坡从1∶10到1∶30过程，等效锥度波动比较明显.
图 2 不同轨底坡下等效锥度随轮对横移量的变化Figure 2. Equivalent conicity vs. wheelset’s lateral displacement for different rail cants2. 轨底坡对车辆动力学性能的影响
2.1 车辆动力学模型
使用多体动力学软件SIMPACK建立某高速车辆动力学模型. 由于前后转向架采用相同的参数，采用SIMPACK子结构模型方式搭建整车模型. 该模型包括1个车体、2个构架、4条轮对、8个轴箱共15个刚体. 轮对通过一系悬挂、轴箱转臂与构架相连，轮对采用轴箱转臂定位方式，一系悬挂由钢弹簧、减振器组成，采用弹簧阻尼单元模拟. 构架通过二系悬挂与车体相连，二系悬挂包括2个空气弹簧、2个横向减振器和横向止挡、2个牵引拉杆、2个抗蛇行减振器和1个抗侧滚扭杆. 模型中考虑一系垂向减振器、二系横向减振器、抗蛇行减振器和横向止挡的非线性特性，其非线性特性见图3.
采用标准60 kg/m CHN60钢轨型面，轨距为1435 mm，采用实测轨底坡，车轮半径为420 mm，车轮型面为LMD，轮背内侧距为1353 mm. 采用沈氏理论计算轮轨蠕滑力，轮轨摩擦系数为0.35.
图 3 一系、二系减振器和横向止挡的非线性特性Figure 3. Nonlinear characteristics of primary and secondary suspension damper, and secondary lateral stop2.2 动力学仿真分析
轨道作为车辆运行的承载体，轨道参数的变化最为直观的表现则体现在车辆运行品质. 本文针对轨道养护中只关注高低、方向和水平不平顺，忽略轨底坡突变的情况，以车辆运行平稳性和舒适性作为评价指标，分析标准轨底坡和实测线路轨底坡的变化对车辆的影响. 线路轨底坡输入为国内某条运营速度200 km/h的客运专线直线段实测数据，此线路运行车辆为城际动车组. 本文测试区段为填充式垫板区段，测量间隔为25 m，测量结果如表1所示. 通过使用轨道几何尺寸检测小车与轨底坡测量仪检测发现，此段线路未发现轨面高低、方向、水平、扭曲等不平顺超标，但测量发现轨底坡发生较大变化. 通过对现场的观察发现造成轨底坡变化的原因有：线路中使用充填式垫板和橡胶垫板两种类型，充填式垫板充填不密实，设置角度发生变化；长时间运行后，充填式垫板发生压溃等；橡胶垫板，由于钢轨内外侧扣件扣压力不一致，即两侧基于扣件螺栓的扭矩不一致；在轨道精调过程中出现安装偏置的情况；橡胶垫板在使用过程中出现断裂等情况，以上情况均会出现轨底坡变化，其中充填式垫板中表现的轨底坡变化最为明显. 仿真中轨底坡布置分为标准轨底坡（1∶40）、对称布置轨底坡（即右轨轨底坡与实测左轨相同），非对称布置轨底坡（左、右轨均用实测轨底坡）3种情况. 曲线几何参数为客运专线实际曲线参数，曲线半径3500 m、超高125 mm、缓和曲线长 250 m. 轨底坡则采用直线工况对应轨底坡，采用京津线实测轨道不平顺作为轨道激励. 在计算过程中，为排除轮轨磨耗对计算结果的影响，轮轨型面均采用标准型面，同时根据实测轨道的位置，将钢轨的型面按照实测轨底坡情况进行旋转，保证不同截面钢轨最高点和横向轨距点位置均在同一平面上，按照测试纵向里程位置进行设置，即轨底坡参数体现在轨面数据旋转上，钢轨截面之间通过B样条曲线形成映射，保证截面之间的平顺.
表 1 实测线路轨底坡Table 1. Measured cants on tracks距离 /m 曲/直线段 距离 /m 曲/直线段 左轨 左轨 左轨 左轨 0 1∶40 1∶40 625 1∶35 1∶30 150 1∶40 1∶40 650 1∶50 1∶10 175 1∶10 1∶25 675 1∶20 1∶50 200 1∶15 1∶20 700 1∶40 1∶25 225 1∶25 1∶40 725 1∶25 1∶10 250 1∶45 1∶50 750 1∶45 1∶50 275 1∶65 1∶65 775 1∶40 1∶30 300 1∶100 1∶15 800 1∶40 1∶40 325 1∶40 1∶30 825 1∶20 1∶10 350 1∶35 1∶50 850 1∶50 1∶35 375 1∶10 1∶20 875 1∶30 1∶40 400 1∶40 1∶40 900 1∶15 1∶100 425 1∶30 1∶40 925 1∶65 1∶65 450 1∶50 1∶45 950 1∶50 1∶45 475 1∶10 1∶25 975 1∶40 1∶25 500 1∶25 1∶40 1000 1∶20 1∶15 525 1∶50 1∶20 1025 1∶25 1∶10 550 1∶10 1∶50 1050 1∶40 1∶40 575 1∶30 1∶35 1100 1∶40 1∶40 600 1∶20 1∶20 1200 1∶40 1∶40 针对不同的轨底坡设置，通过使用Hopf分岔的方法计算了车辆的临界速度，如图4所示，临界速度随轨底坡变化（从1∶10到1∶100）呈现先提高，到1∶40时达到最大，随后下降最后趋于平缓的趋势. 由此可见，轨底坡的波动变化势必引起车辆临界速度的改变，进而影响车辆的运行平稳性.
故针对同一轨道的轨底坡变化，计算得出车辆在直线和曲线线路条件下垂向和横向sperling平稳性指标分别如图5、6所示. 垂向、横向平稳性指标均小于2.5，达到GB 5599—2019[19]标准规定的“优”级. 车辆在直线和曲线线路上的垂向和横向平稳性均随速度线性增大，其中横向平稳性随速度影响较大；图5可知：直线段和曲线段垂向平稳性指标随速度增加较为缓和，直线段标准轨底坡情况下维持在0.8. 垂向平稳性指标在对称和非对称布置轨底坡情况较标准轨底坡情况，分别增加了32.96%和34.52%. 直线段轨底坡变化对车辆垂向平稳性影响较大，而曲线段影响比较小.
图 4 不同轨底坡车辆Hopf分岔非线性临界速度Figure 4. Nonlinear critical velocity of Hopf bifurcation of vehicle for different rail cants
图 5 基于sperling的车辆直线和曲线上垂向平稳性Figure 5. Sperling vertical stability of vehicle on straight and curved sections由图6可知：直线线路条件下横向平稳性大于垂向平稳性，对称不规则轨底坡布置和非对称不规则轨底坡布置的平稳性均大于标准轨底坡布置条件，与标准条件相比平稳性指标最大值增加40.65%，曲线条件下增加18.23%. 曲线段的平稳性在3种轨底坡条件下基本一致. 因为车辆以不同速度通过曲线时，由于欠/过超高的存在造成车辆自身的振动大于轨底坡的影响，而直线段的影响主要由轨底坡决定.
本文也根据UIC 513：1994[20]车辆乘坐舒适度标准对车辆的舒适性进行了分析，其直线段和曲线段运行的车辆舒适性和平稳性两者表征基本一致.
图 6 基于sperling的车辆直线和曲线上横向平稳性Figure 6. Sperling lateral stability of vehicle on straight and curved sections从图5、6可以看出：轨底坡的变化在直线段对车辆运行的影响较大，从车体的横向晃动水平也可以看出（图7）：轨底坡角度差变化较大的区段，车体横向晃动也比较明显，且与轨底坡角度变化具有伴随状态. 针对车体横向晃动进行频率分析（图8），发现非对称变化轨底坡布置情况下车体晃动频率表现为1.33 Hz，对称变化轨底坡布置情况下为1.62 Hz；若车辆运行速度不变，轨底坡变化间隔缩短一倍，则车辆横向晃动频率则可能随之增加，引起车辆构架加速度报警，进而增加车辆横向晃动的风险. 在曲线段同样存在车辆从过超高进入欠超高状态，发生车轮向曲线外侧横移加之高低股轨底坡差异，造成滚动圆半径差的突变，会加剧车辆的横向晃动.
图 8 不同轨底坡条件下车辆车体横向晃动频率Figure 8. Transverse shaking frequency at car body for different rail cants3. 轨底坡变化对车轮磨耗和滚动接触疲劳分析
本节主要研究同一线路（直线、曲线）轨底坡变化对车辆运行中车轮磨耗和滚动接触疲劳的影响. 采取与上一节一致的工况条件，均针对导向车轮，利用磨耗指数和疲劳损伤指数作为评价指标.
3.1 车轮磨耗分析
采用磨耗指数作为车轮磨耗评价指标，以此分析同一轨道不同轨底坡对车轮磨耗的影响. 其中，第
i（i=1,2,⋯,8） 个车轮每一个计算时间步t下的磨耗指数为Wi,t=|Tx,iγx,i|+|Ty,iγy,i|, (1) 式中：
Tx,i 、Ty,i 分别为第i个车轮纵向和横向蠕滑力；γx,i 、γy,i 分别为第i个车轮接触斑处纵向和横向蠕滑率.然后再利用式（2）计算车辆通过直线或曲线时第 i 个车轮经过 N 个时间步后磨耗指数移动均方根（root mean square, RMS）值为
WRMS,i=√N∑n=1W2i,ntN, (2) 式中：
Wi,nt 为第 i 个车轮的 n 个时间步下的磨耗指数.利用式（1）、（2）计算不同轨底坡布置条件下轮轨磨耗指数均方根值，
N 取值为500. 由于导向轮对轮轨间相互作用更为剧烈，所以本文采用导向轮的计算结果来讨论不同轨底坡布置对车轮磨耗的影响，利用导向轮磨耗指数最大RMS值统计分析变化规律.图9为车辆以250 km/h 的速度在直线段不同轨底坡布置的车轮磨耗指数对比结果. 同一轮对左右轮的磨耗指数基本一致，但受到轨道坡非对称布置的影响比较大，磨耗指数随着相连钢轨轨底坡的变化而发生变化，且随着非对称布置的轨底坡偏差大而发生在后一段钢轨上，这由于经历轨底坡的大变化，车轮与钢轨接触点发生较大跳跃，造成左右轮径差发生变化，使得车辆发生横向较大蠕滑和横移，增大轮轨间的磨耗指数.
图 9 速度250 km/h条件下直线段不同轨底坡布置的车轮磨耗指数Figure 9. Wheel wear index at 250 km/h on straight section for different rail cants直线段不同轨底坡布置车轮的最大磨耗指数均随速度增加而增加（如图10所示），左右轮的磨耗指数相差较小. 其中在速度大于180 km/h条件下，非对称布置轨底坡对车轮磨耗指数的影响均大于对称布置，同时也大于标准布置轨底坡，两种轨底坡变化情况相对于标准轨底坡情况最大磨耗指数分别增加136.71%和27.65%；轨底坡对称布置和标准轨底坡布置对车轮磨耗指数的影响随速度缓慢增加后加速发展. 非对称布置情况则随速度成指数形式增长. 由图9、10可知：轨底坡非对称布置在直线条件下受速度影响较大.
图 10 不同速度条件下直线段不同轨底坡布置的车轮磨耗指数Figure 10. Wheel wear index at different velocities on straight section for different rail cants与直线段的表征不同，由于车辆通过曲线段的欠/过超高情况下，轨底坡的不规则的影响小于曲线参数设置对车辆的影响，故出现了不同轨底坡设置的磨耗指数在速度250 km/h时相一致的情况. 从图11可以看出：导向轮最大磨耗指数也表现为随速度成线性增加的趋势.
图 11 不同速度条件下曲线段不同轨底坡布置的车轮磨耗指数Figure 11. Wheel wear index at different velocities on curved section for different rail cants3.2 车轮滚动接触疲劳分析
本文采用基于安定图基础上EKBERG提出的表面疲劳指数来评价轮轨接触状态的疲劳程度，从而考量轨道不同轨底坡对车轮表面疲劳的影响. 车轮表面疲劳指数如式（3）所示.
δsurf=μ−2πabk3Fz, (3) μ=√T2x+T2yFz, (4) 式中：μ为轮轨接触位置的牵引系数； a和b分别为轮轨椭圆接触斑的短半轴和长半轴；k为材料纯剪切屈服强度；Fz为轮轨接触斑处法向力；
Tx 和Ty 分别为轮轨接触斑处纵向蠕滑力和横向蠕滑力.由式（3）、（4）可知：轮轨较差的牵引和导向性能（使得纵向/横向蠕滑力数增大）或较糟糕的轮轨几何接触关系（接触斑面积小或轮轨法向力大）均可导致表面疲劳指数增大，加速轮轨材料的疲劳破坏. 表面疲劳指数是基于安定图提出的，因此不能预测轮轨材料的疲劳寿命，而是评价轮轨材料表面发生疲劳损坏的可能性；
δsurf > 0, 此时轮轨材料变形将发生棘轮效应，塑性变形会持续累积，即能预测表面疲劳出现的可能性.不同速度等级下的车轮疲劳指数如图12所示. 由图12（a）可知：直线段非对称轨底坡布置的表面疲劳指数在不同速度条件下均大于对称轨底坡布置，对称轨底坡布置大于标准轨底坡布置条件，其中非对称布置条件下的车轮表面疲劳指数在0.175左右波动，对称布置条件下车轮表面疲劳指数在1.600左右波动，而标准轨底坡布置则在1.400左右波动.
直线段对称变化和非对称轨底坡布置的左轮表面疲劳指数的最大值比标准条件分别增大25.14%和15.86%；右侧车轮的表面疲劳指数分别增大24.96%和18.29%.
由图12（b）可知：对于曲线段内轨侧车轮，表面疲劳指数在3种轨底坡布置条件下，均随速度增加发生较大的线性增加，且增加幅度一致. 而高股车轮表面疲劳指数基本维持不变，非对称布置条件车轮表面疲劳指数略大于其他两种轨底坡布置情况.
图 12 直线、曲线不同速度等级的车轮疲劳指数Figure 12. Surface fatigue index of wheel at different velocities on straight and curved sections4. 结 论
本文从轮轨关系和车辆动力学两个方面分析了轨底坡变化对车辆动力学行为和轮轨损伤的影响. 从车辆运行的角度分析轨道养护维修的策略. 研究结果表明：
1） 直线段和曲线段在同一轨道上采用对称和非对称轨底坡布置，其车辆垂向、横向平稳性和舒适性指标均大于采用标准轨底坡布置情况. 其中直线段同一轨道对称和非对称轨底坡布置对车辆的平稳性影响较大. 在曲线段同一轨道对称和非对称轨底坡布置对车辆的横向平稳性影响较大.
2） 直线段不同轨底坡布置车轮的最大磨耗指数均随速度呈指数函数增加，左右轮的磨耗指数相差较小. 曲线段不同轨底坡布置车轮的最大磨耗指数均随速度呈线性增加且均大于直线段. 故车辆通过欠/过超高情况下，轨底坡的不规则的影响小于曲线参数设置对车辆的影响.
3） 在直线段相对于标准布置轨底坡的车轮疲劳指数最小，对称轨底坡布置小于非对称布置，三种情况车轮疲劳指数受速度影响较小. 曲线段低股侧车轮表面疲劳指数则与速度成线性增加的趋势，高股侧车轮则受速度影响较小.
综上所述，直线段的轨底坡变化对车辆动力学行为的影响最为直接. 在线路设计、施工、动静态验收和日常养护维修中，从车辆运行的平稳性和舒适性，以及车轮的磨耗以损伤角度，需要对同一轨道内的轨底坡变化予以关注. 在线路维修中针对同一轨道内轨底坡变化情况，如果不方便进行轨底坡调整时可以采用钢轨打磨的方式进行轨面调整，以满足轨底坡的要求.
-
图 5 不同控制参数下车体竖向加速度最大值
Figure 5. Maximum values of vertical acceleration of car body under different control parameters
图 6 不同控制参数下悬浮电磁力最大值
Figure 6. Maximum values of suspended electromagnetic force under different control parameters
图 7 不同控制参数下悬浮电磁力幅值谱
Figure 7. Amplitude spectrum of suspended electromagnetic force under different control parameters
图 8 不同控制参数下中间悬浮磁极间隙变化量
Figure 8. Variation of intermediate suspended pole gap under different control parameters
图 9 不同控制参数下悬浮间隙时程曲线及其幅值谱（KD1=25）
Figure 9. Suspension gap time history curve and amplitude spectrum under different control parameters （KD1 = 25）
图 10 不同控制参数下主梁跨中竖向加速度最大值
Figure 10. Maximum values of vertical acceleration at midspan of girder under different control parameters
图 11 不同KD1下主梁跨中竖向加速度幅值谱（KP1=6000）
Figure 11. Amplitude spectrum of vertical acceleration at midspan of girder under different KD1 （KP1 = 6 000）
图 12 不同控制参数下车体横向加速度最大值
Figure 12. Maximum values of lateral acceleration of car body under different control parameters
图 13 不同控制参数下导向电磁力最大值
Figure 13. Maximum values of guidance electromagnetic force under different control parameters
图 14 不同控制参数下导向电磁力幅值谱
Figure 14. Amplitude spectrum of guidance electromagnetic force under control parameters
图 15 不同控制参数下中间导向磁极间隙变化量
Figure 15. Variation of intermediate guidance pole gap under different control parameters
图 16 不同控制参数下主梁跨中横向加速度最大值
Figure 16. Maximum values of lateral acceleration at midspan of girder under different control parameters
图 17 不同KD2下主梁跨中横向加速度幅值谱（KP2=6000）
Figure 17. Amplitude spectrum of lateral acceleration at midspan of girder under different KD2 （KP2 = 6 000）
表 1 车辆模型参数
Table 1. Parameters of train model
参数 数值 车体质量/（× 104 kg） 3.90 车体侧滚质量惯性矩/（× 104 kg•m2） 6.46 车体摇头质量惯性矩/（× 104 kg•m2） 1.75 车体点头质量惯性矩/（× 104 kg•m2） 1.76 一系/二系弹簧竖向刚度/（×106 N•m−1） 20/2 一系/二系弹簧竖向阻尼/（×103 N•s•m−1） 5/5 一系/二系弹簧横向刚度/（×106 N•m−1） 28/2 一系/二系弹簧横向阻尼/（×102 N•s•m−1） 5/20 空气弹簧刚度竖向/（× 106 N•m−1） 1.90 
下载: 导出CSV
表 2 桥梁模型参数
Table 2. Parameters of bridge model
参数 数值 主梁/钢轨/桥墩密度/（kg•m−3） 2551/7850/2500 主梁/钢轨/桥墩弹性模量/GPa 44.5/206.0/30.0 主梁/钢轨/桥墩泊松比 0.2/0.3/0.2
下载: 导出CSV
-
[1] SU X Y, XU Y L, YANG X F. Neural network adaptive sliding mode control without overestimation for a maglev system[J]. Mechanical Systems and Signal Processing, 2022, 168: 108661.1-108661.12. [2] 马卫华,胡俊雄,李铁,等. EMS型中低速磁浮列车悬浮架技术研究综述[J]. 西南交通大学学报,2023,58(4): 720-733.MA Weihua, HU Junxiong, LI Tie, et al. Technologies research review of electro-magnetic suspension medium-low-speed maglev train levitation frame[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 720-733. [3] 熊嘉阳,邓自刚. 高速磁悬浮轨道交通研究进展[J]. 交通运输工程学报,2021,21(1): 177-198.XIONG Jiayang, DENG Zigang. Research progress of high-speed maglev rail transit[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 177-198. [4] WANG L D, BU X M, HU P, et al. Dynamic reliability analysis of running safety and stability of a high-speed maglev train on a guideway bridge[J]. International Journal of Structural Stability and Dynamics, 2023: 1-41. [5] 翟明达,朱朋博,李晓龙,等. 常导电磁型高速磁浮列车主动导向能力的评估与验证[J]. 西南交通大学学报,2022,57(3): 514-521.ZHAI Mingda, ZHU Pengbo, LI Xiaolong, et al. Evaluation and verification for active guidance ability of EMS maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 514-521. [6] 陆海英,韩霄翰,李忠继,等. 中低速磁浮系统起浮阶段的振动特性分析[J]. 中国机械工程,2019,30(3): 318-324.LU Haiying, HAN Xiaohan, LI Zhongji, et al. Analysis of vibration characteristics of low-medium speed maglev levitation systems in lifting stages[J]. China Mechanical Engineering, 2019, 30(3): 318-324. [7] 翟婉明,赵春发. 现代轨道交通工程科技前沿与挑战[J]. 西南交通大学学报,2016,51(2): 209-226.ZHAI Wanming, ZHAO Chunfa. Frontiers and challenges of sciences and technologies in modern railway engineering[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 209-226. [8] 韩霄翰,李忠继,池茂儒. 轨道梁结构对中低速磁浮车轨耦合振动的影响[J]. 铁道机车车辆,2019,39(5): 36-42.HAN Xiaohan, LI Zhongji, CHI Maoru. Influence of track beam structure on the mid-low maglev vehicle-rail coupling vibration[J]. Railway Locomotive & Car, 2019, 39(5): 36-42. [9] FENG Y, ZHAO C F, WU D H, et al. Effect of levitation gap feedback time delay on the EMS maglev vehicle system dynamic response[J]. Nonlinear Dynamics, 2023, 111(8): 7137-7156. doi: 10.1007/s11071-022-08225-5 [10] 赵春发,翟婉明. 常导电磁悬浮动态特性研究[J]. 西南交通大学学报,2004,39(4): 464-468.ZHAO Chunfa, ZHAI Wanming. Dynamic characteristics of electromagnetic levitation systems[J]. Journal of Southwest Jiaotong University, 2004, 39(4): 464-468. [11] 蔡文涛,王春江,滕念管,等. 高速磁浮双向主动控制系统模型参数分析[J]. 力学季刊,2020,41(3): 477-485.CAI Wentao, WANG Chunjiang, TENG Nianguan, et al. Study on the parameters of bi-directional active control system for high speed maglev[J]. Chinese Quarterly of Mechanics, 2020, 41(3): 477-485. [12] 梁鑫,罗世辉,马卫华. 单磁铁悬浮控制系统反馈参数动力学特性分析[J]. 噪声与振动控制,2012,32(5): 62-66,135.LIANG Xin, LUO Shihui, MA Weihua. Dynamic characteristics of feedback coefficient of single magnet suspension control system[J]. Noise and Vibration Control, 2012, 32(5): 62-66,135. [13] 汤港归,汪斌,夏翠鹏,等. 磁浮车辆起浮参数控制及其动力性能研究[J]. 铁道科学与工程学报,2023,20(3): 790-801.TANG Ganggui, WANG Bin, XIA Cuipeng, et al. Control of levitation parameters and dynamic performance of maglev vehicle[J]. Journal of Railway Science and Engineering, 2023, 20(3): 790-801. [14] SUN Y G, HE Z Y, XU J Q, et al. Dynamic analysis and vibration control for a maglev vehicle-guideway coupling system with experimental verification[J]. Mechanical Systems and Signal Processing, 2023, 188: 109954.1-109954.18. [15] 杨志南,冯洋,刘东生,等. 悬浮控制参数对磁浮车辆与道岔梁耦合振动的影响分析[J]. 机械,2022,49(2): 38-46.YANG Zhinan, FENG Yang, LIU Dongsheng, et al. Influence of levitation control parameters on coupled vibration between maglev vehicles and switch girder[J]. Machinery, 2022, 49(2): 38-46. [16] XIANG H Y, TIAN X F, LI Y L, et al. Dynamic interaction analysis of high-speed maglev train and guideway with a control loop failure[J]. International Journal of Structural Stability and Dynamics, 2022, 22(10): 2241012.1-224101228. [17] GUO W, CHEN X Y, YE Y T, et al. Coupling vibration analysis of high-speed maglev train-viaduct systems with control loop failure[J]. Journal of Central South University, 2022, 29(8): 2771-2790. doi: 10.1007/s11771-022-5119-1 [18] 谢云德,常文森. 电磁型(EMS)磁悬浮列车系统铅垂方向的建模与仿真[J]. 铁道学报,1996,18(4): 47-54.XIE Yunde, CHANG Wensen. Modeling and simulation of electromagnetic (EMS) maglev train system in vertical direction[J]. Journal of the China Railway Society, 1996, 18(4): 47-54. [19] ZHANG L, HUANG J Y. Dynamic interaction analysis of the high-speed maglev vehicle/guideway system based on a field measurement and model updating method[J]. Engineering Structures, 2019, 180: 1-17. doi: 10.1016/j.engstruct.2018.11.031 [20] 张宝安,虞大联,李海涛,等. 高速磁浮悬浮架柔性特征对曲线通过性能的影响[J]. 西南交通大学学报,2022,57(3): 475-482.ZHANG Baoan, YU Dalian, LI Haitao, et al. Influence of flexibility characteristics of levitation chassis on curve negotiation performance of high-speed maglev vehicle[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 475-482. [21] ZHAO C F, ZHAI W M. Maglev vehicle/guideway vertical random response and ride quality[J]. Vehicle System Dynamics, 2002, 38(3): 185-210. doi: 10.1076/vesd.38.3.185.8289 [22] SHI J, FANG W S, WANG Y J, et al. Measurements and analysis of track irregularities on high speed maglev lines[J]. Journal of Zhejiang University-Science A, 2014, 15(6): 385-394. doi: 10.1631/jzus.A1300163 [23] WANG Z L, XU Y L, LI G Q, et al. Modelling and validation of coupled high-speed maglev train-and-viaduct systems considering support flexibility[J]. Vehicle System Dynamics, 2019, 57(2): 161-191. doi: 10.1080/00423114.2018.1450517 [24] SHI J, WANG Y J. Dynamic response analysis of single-span guideway caused by high speed maglev train[J]. Latin American Journal of Solids and Structures, 2011, 8(3): 213-228. doi: 10.1590/S1679-78252011000300001 [25] XU Y L, WANG Z L, LI G Q, et al. High-speed running maglev trains interacting with elastic transitional viaducts[J]. Engineering Structures, 2019, 183: 562-578. doi: 10.1016/j.engstruct.2019.01.012 [26] 徐金辉,王平,汪力,等. 基于频域分析方法的轨道高低不平顺敏感波长的研究[J]. 中南大学学报(自然科学版),2016,47(2): 683-689.XU Jinhui, WANG Ping, WANG Li, et al. Sensitive wavelengths of vertical track irregularities by frequency-domain method[J]. Journal of Central South University (Science and Technology), 2016, 47(2): 683-689. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 467
- HTML全文浏览量: 226
- PDF下载量: 75
- 被引次数: 0