Modeling and Robust Control of Magnetic Bearing-Rotor System Considering Interface Contact
-
摘要:
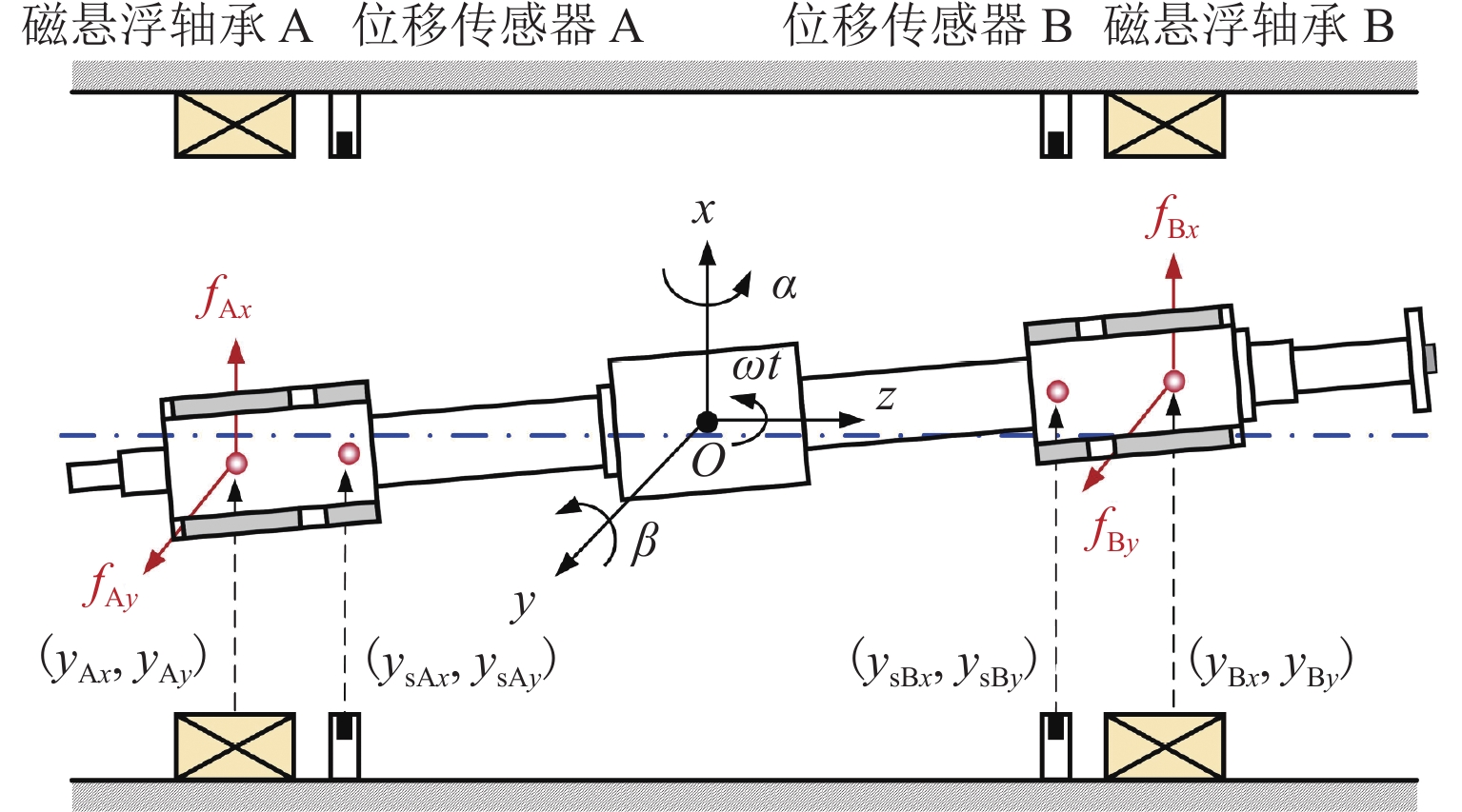
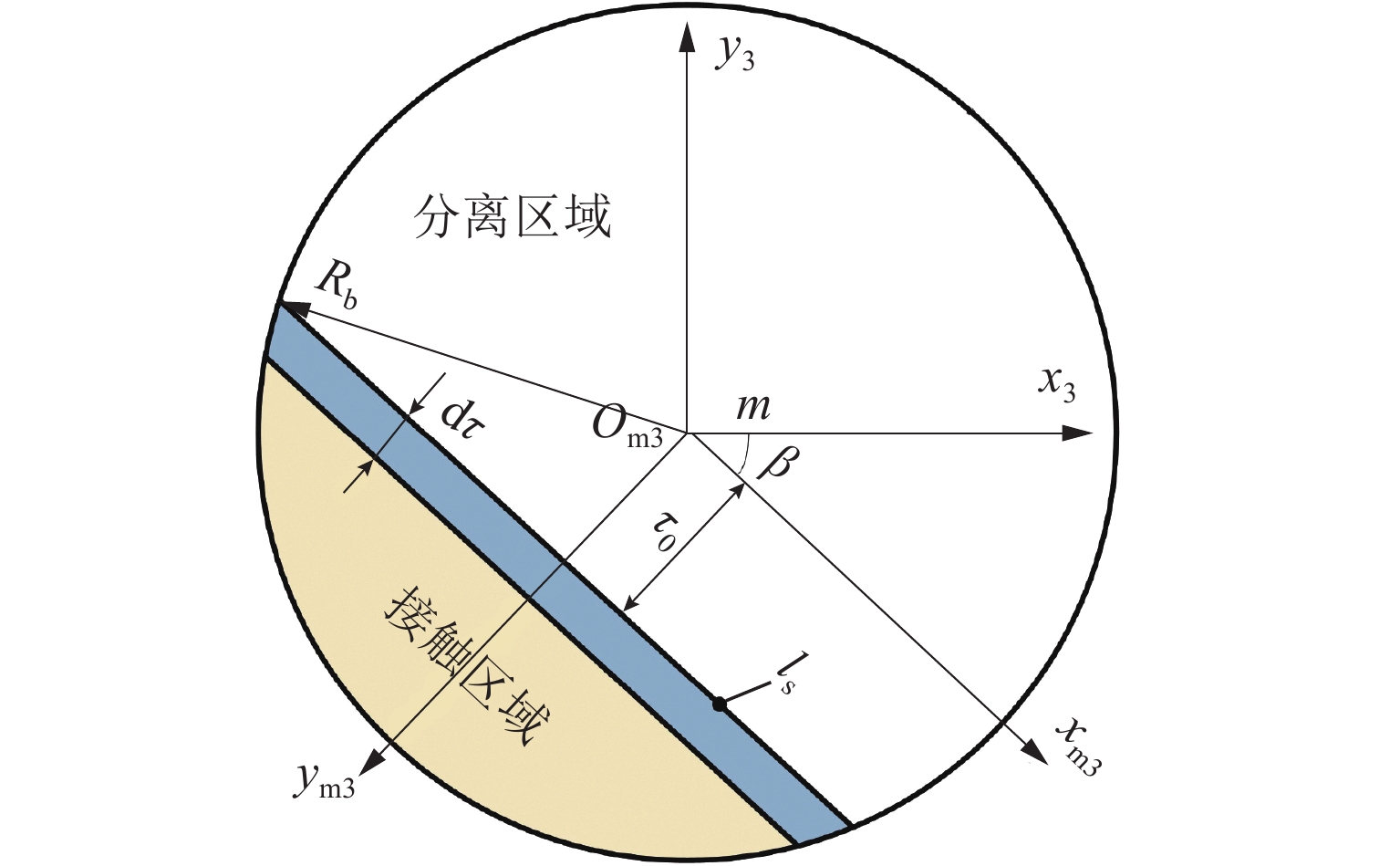
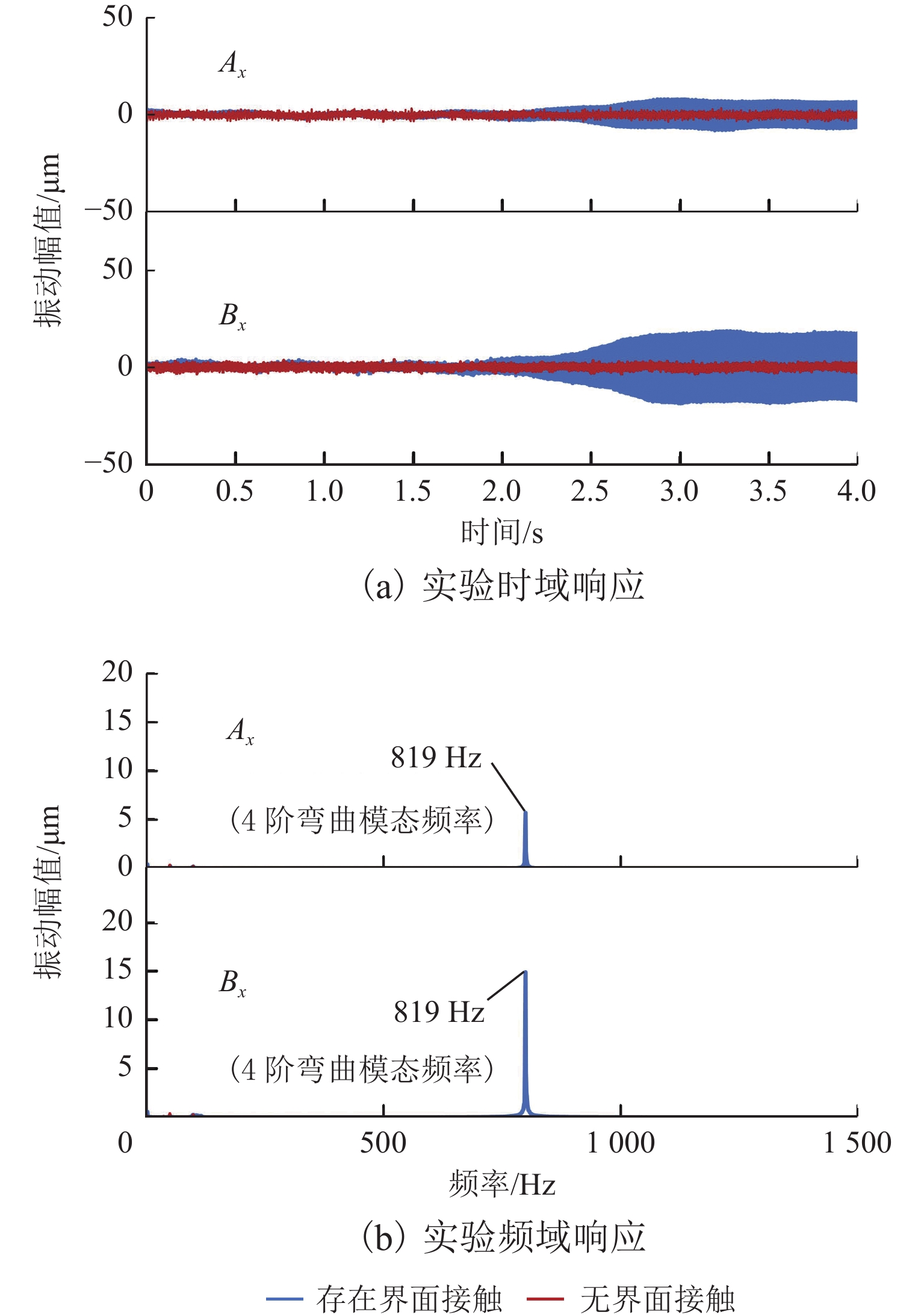
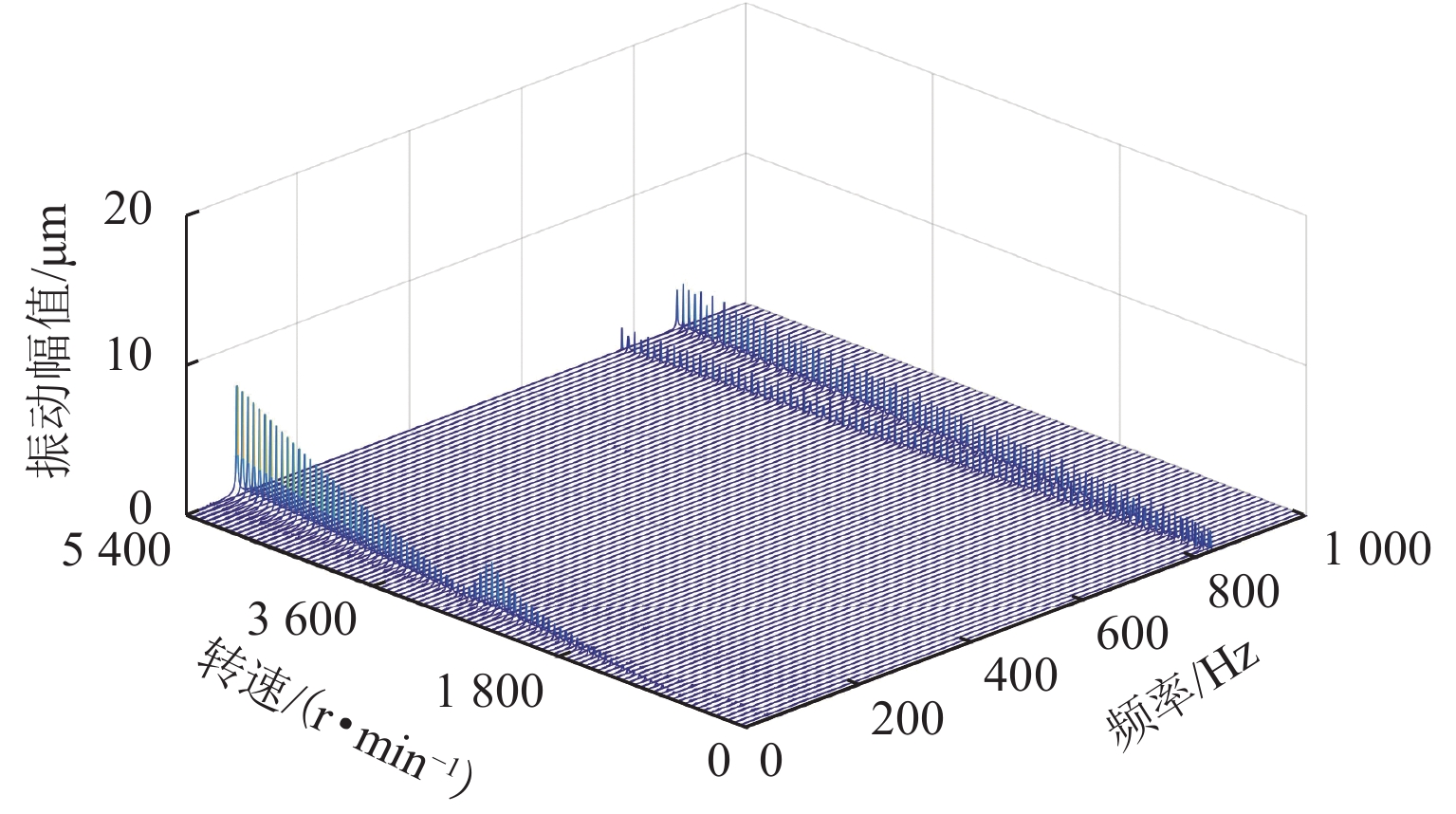
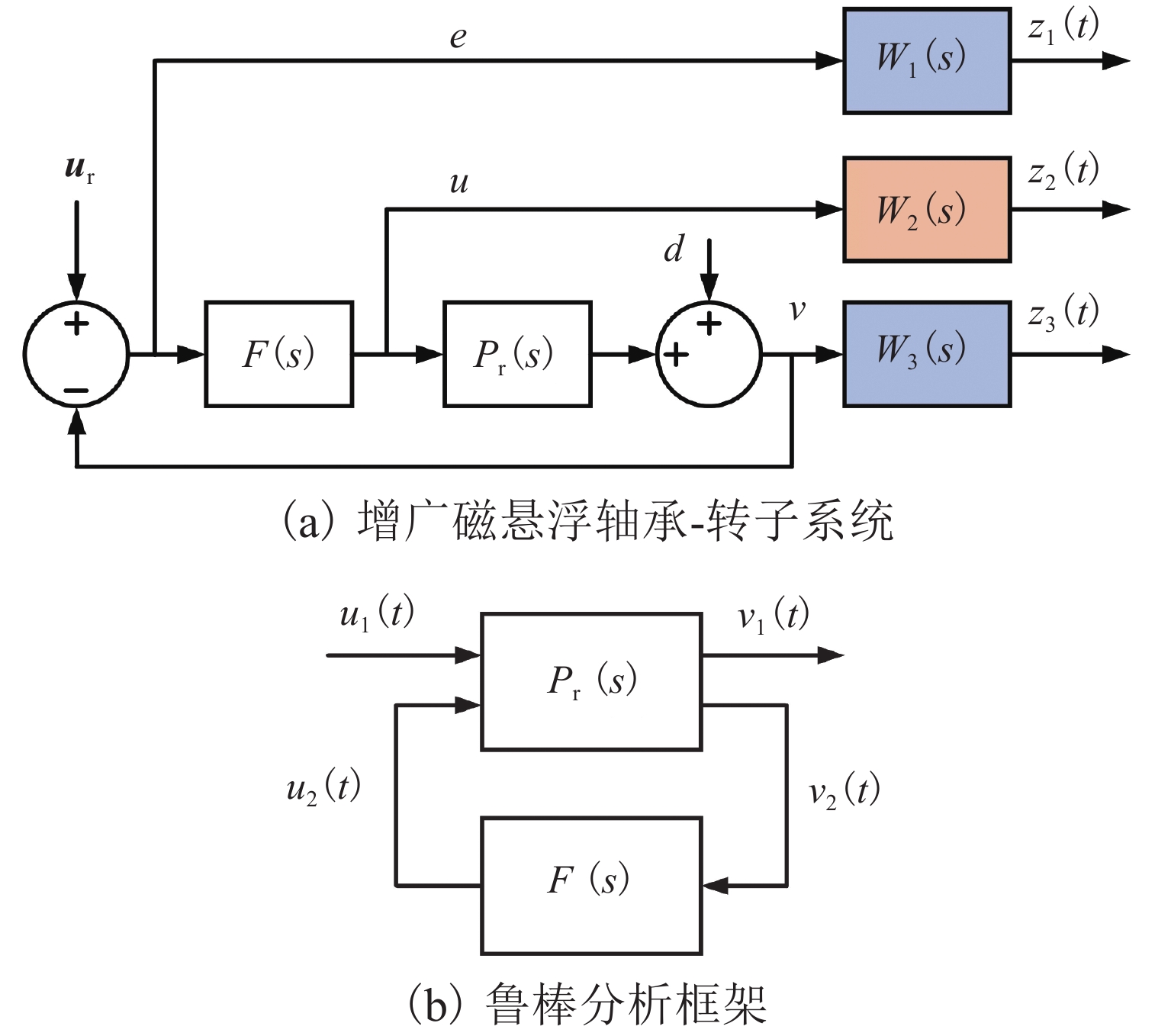
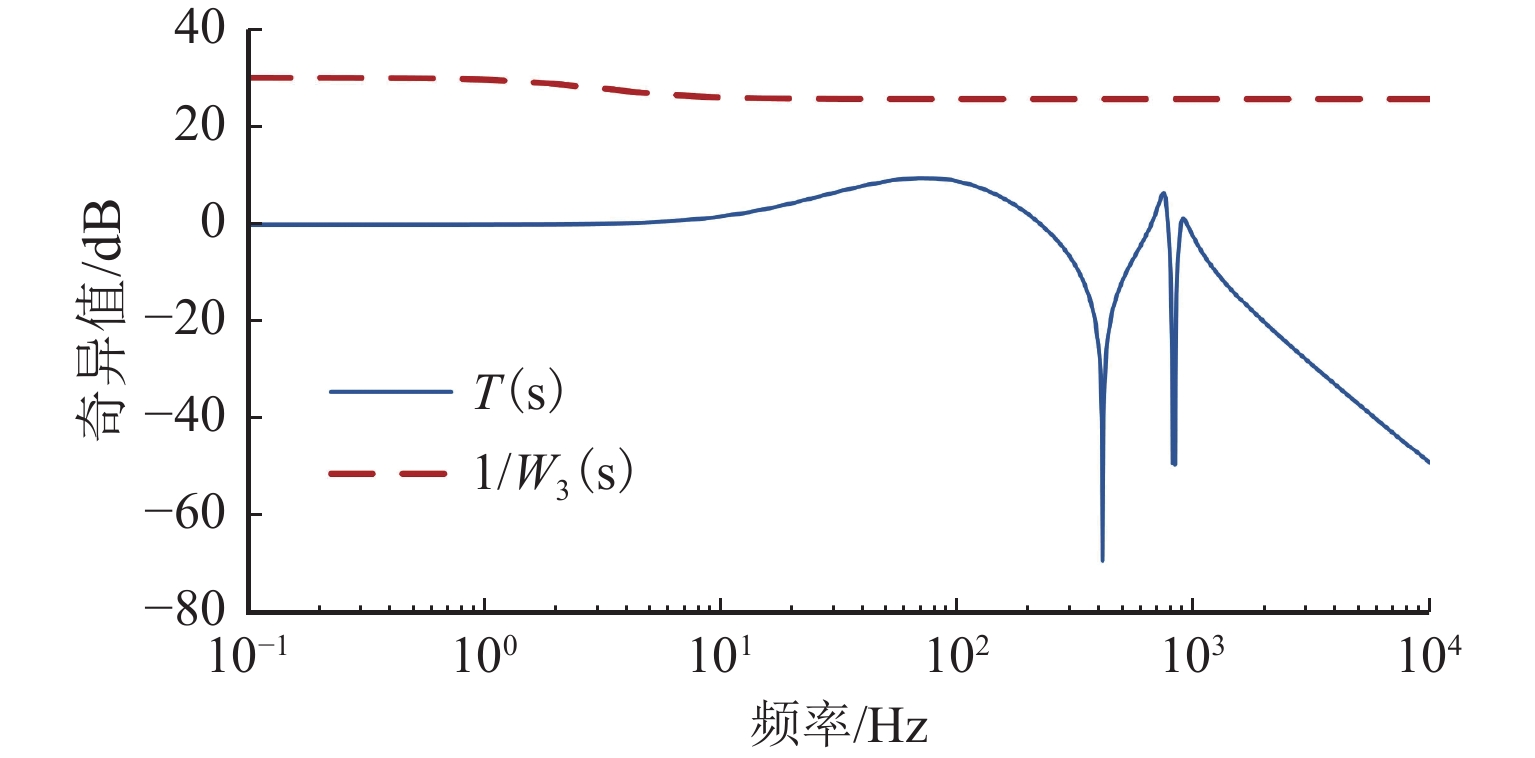
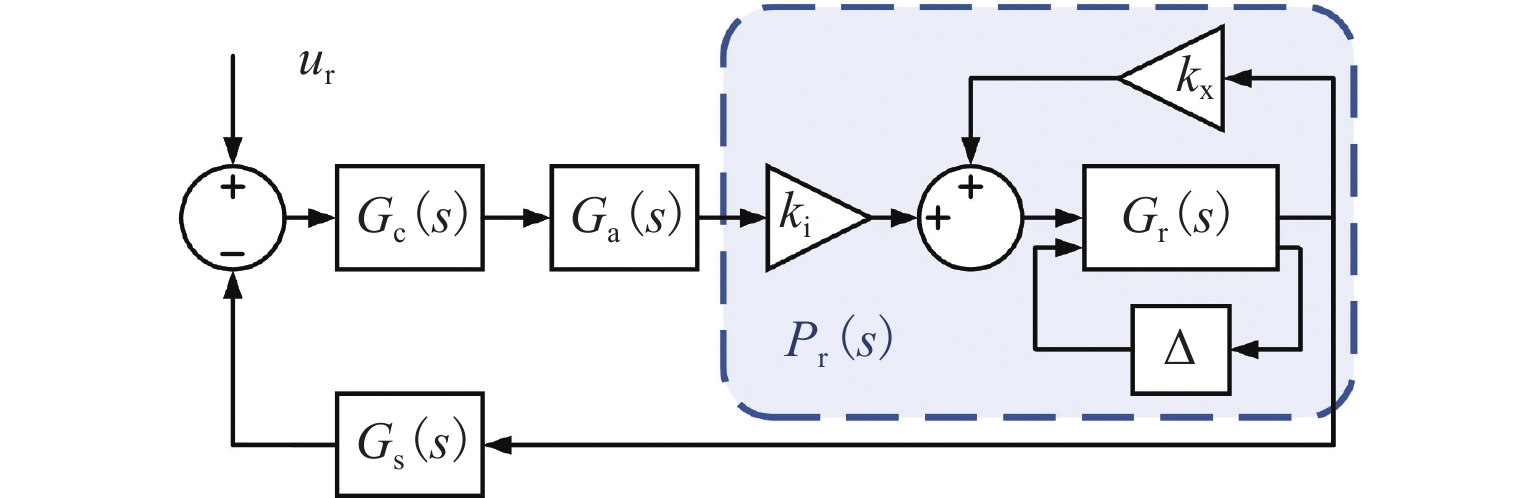
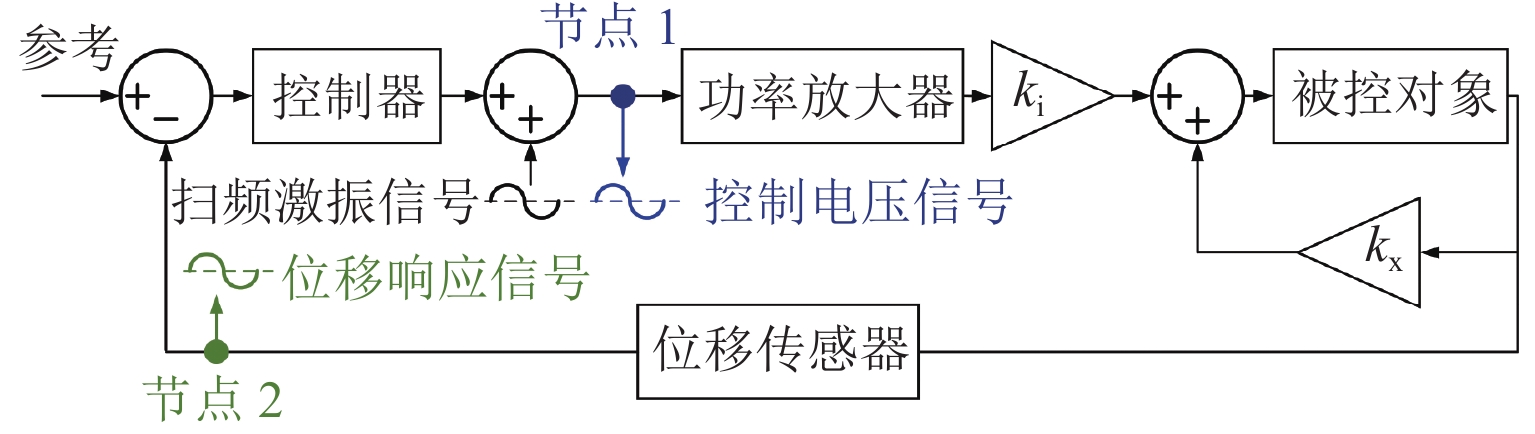
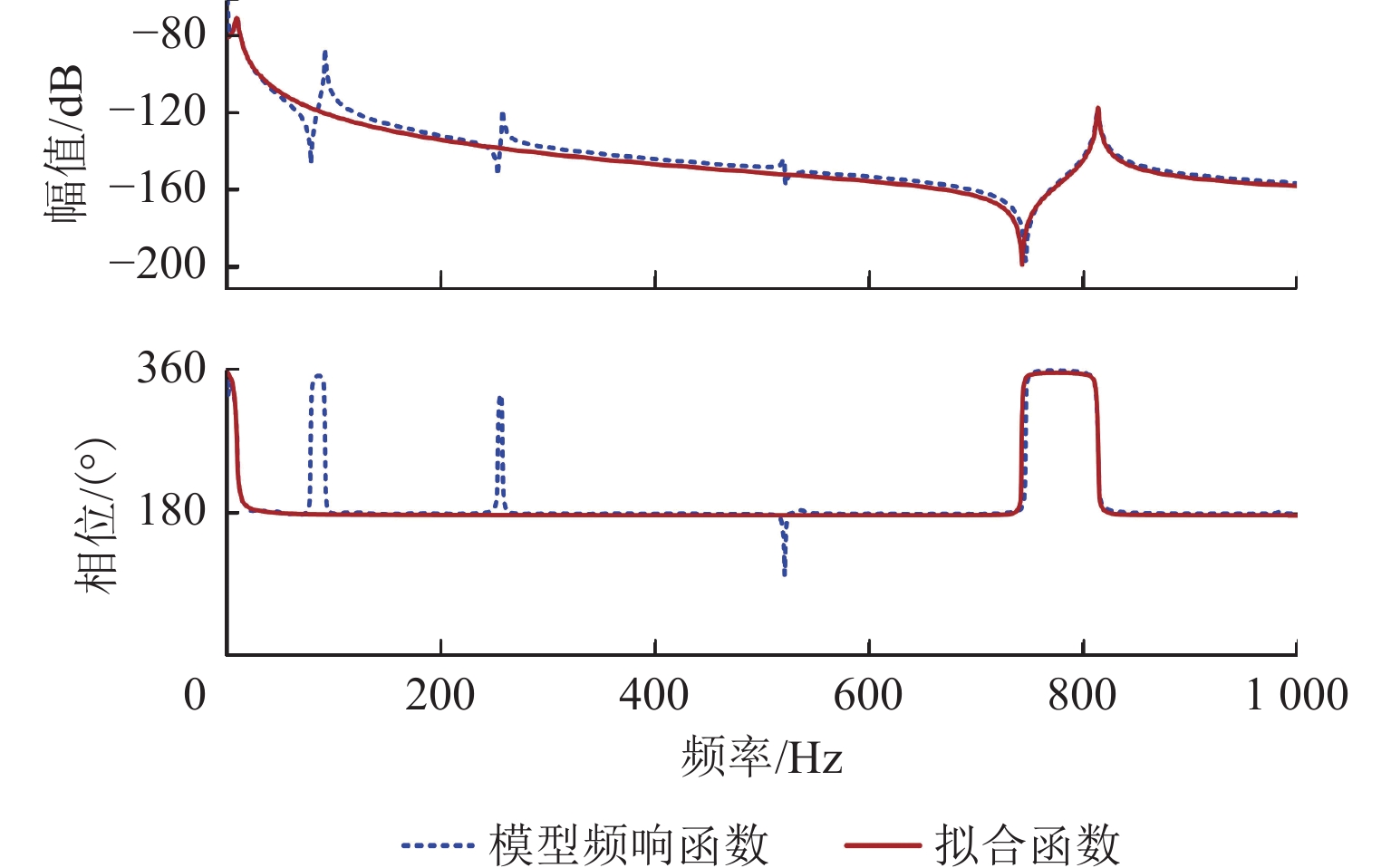
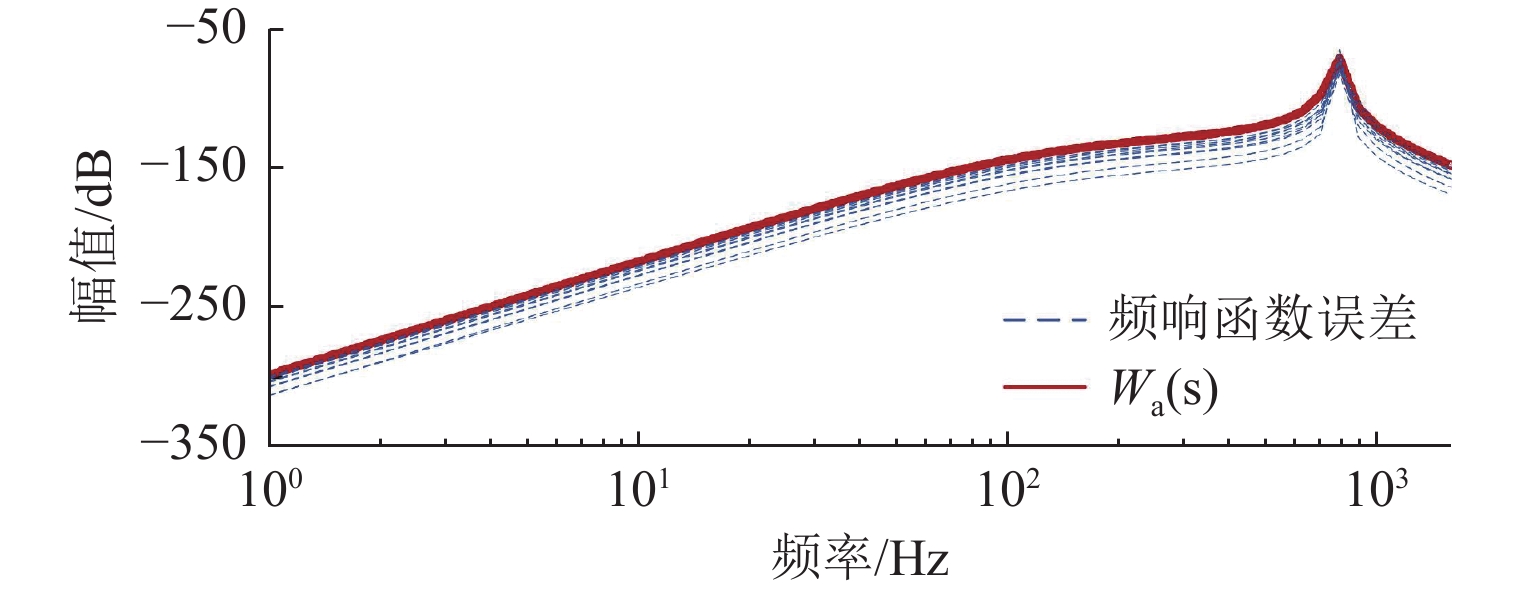
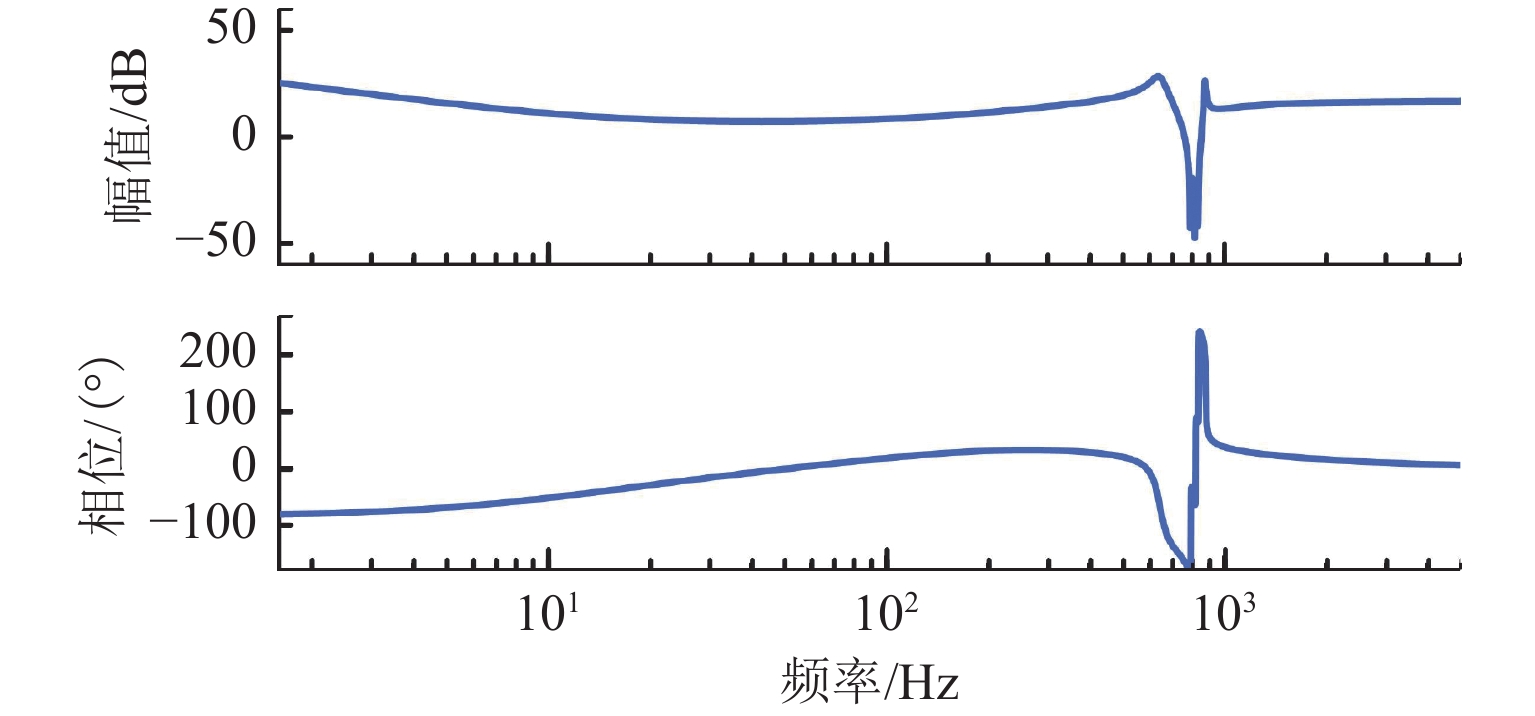
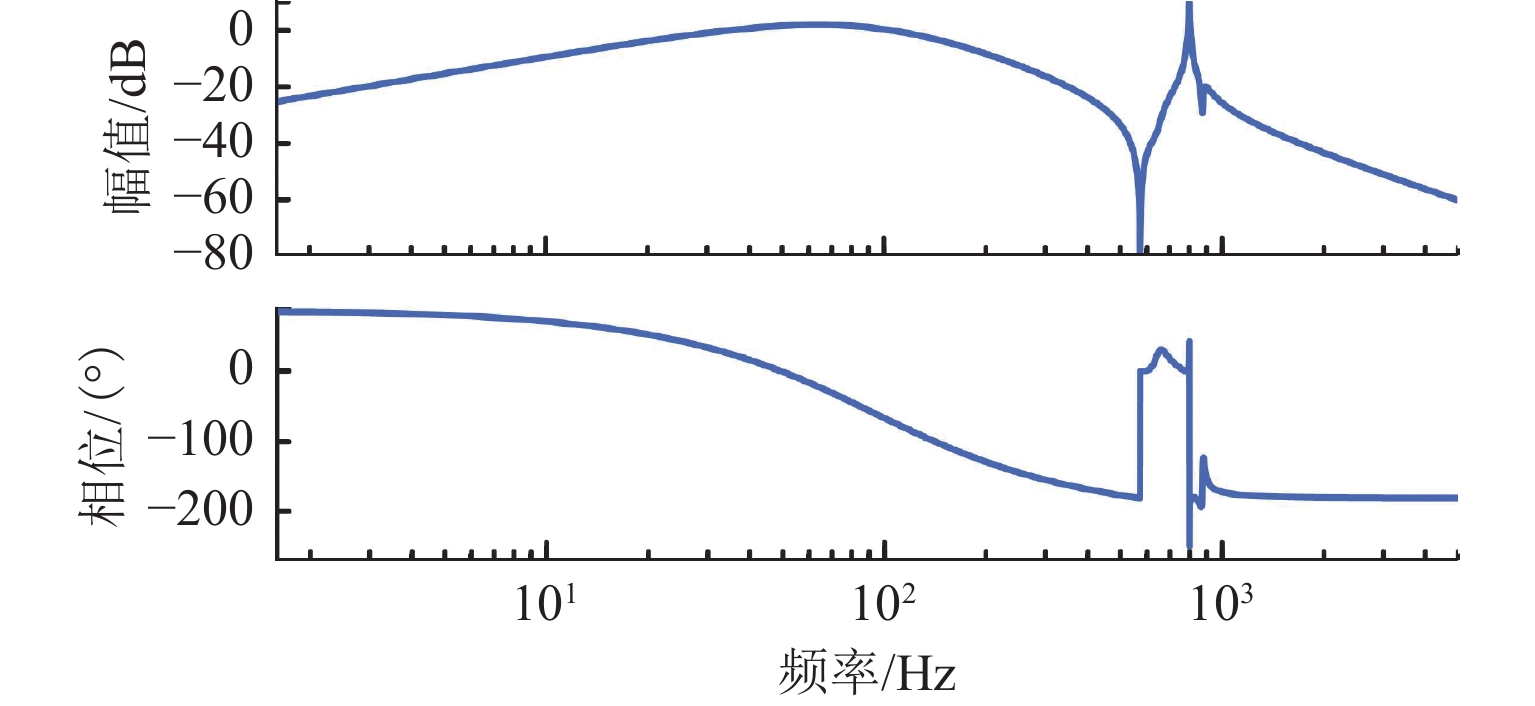
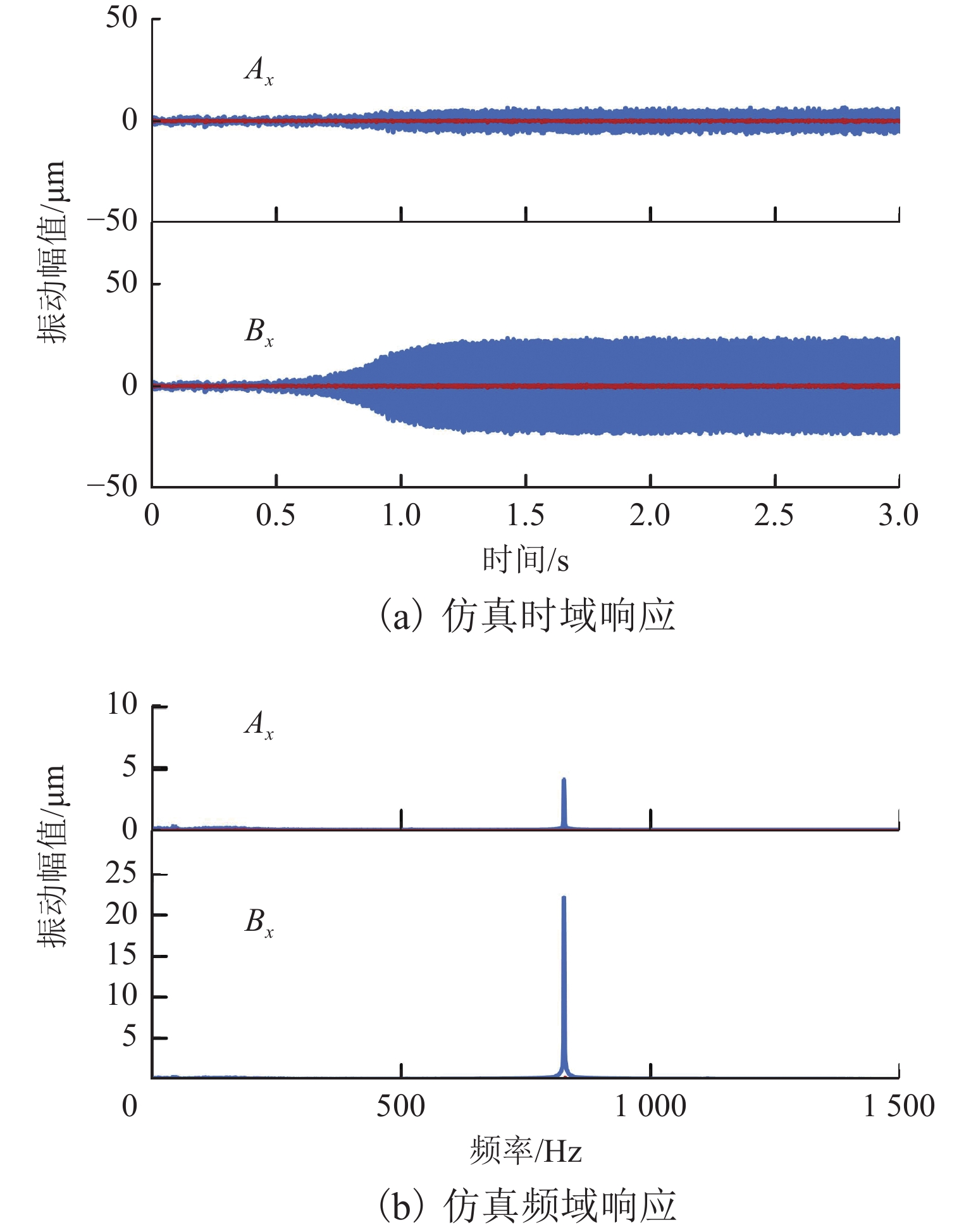
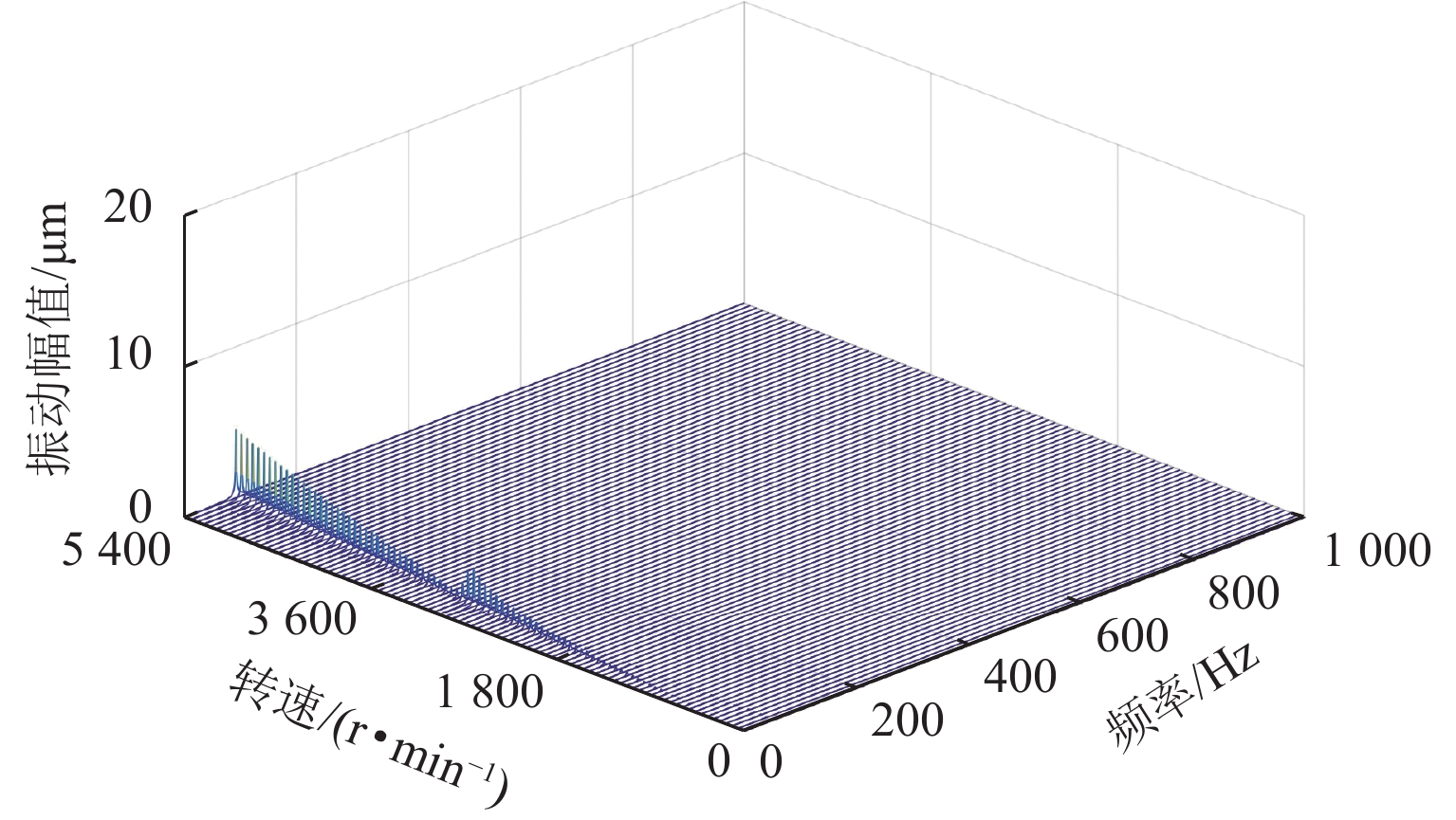
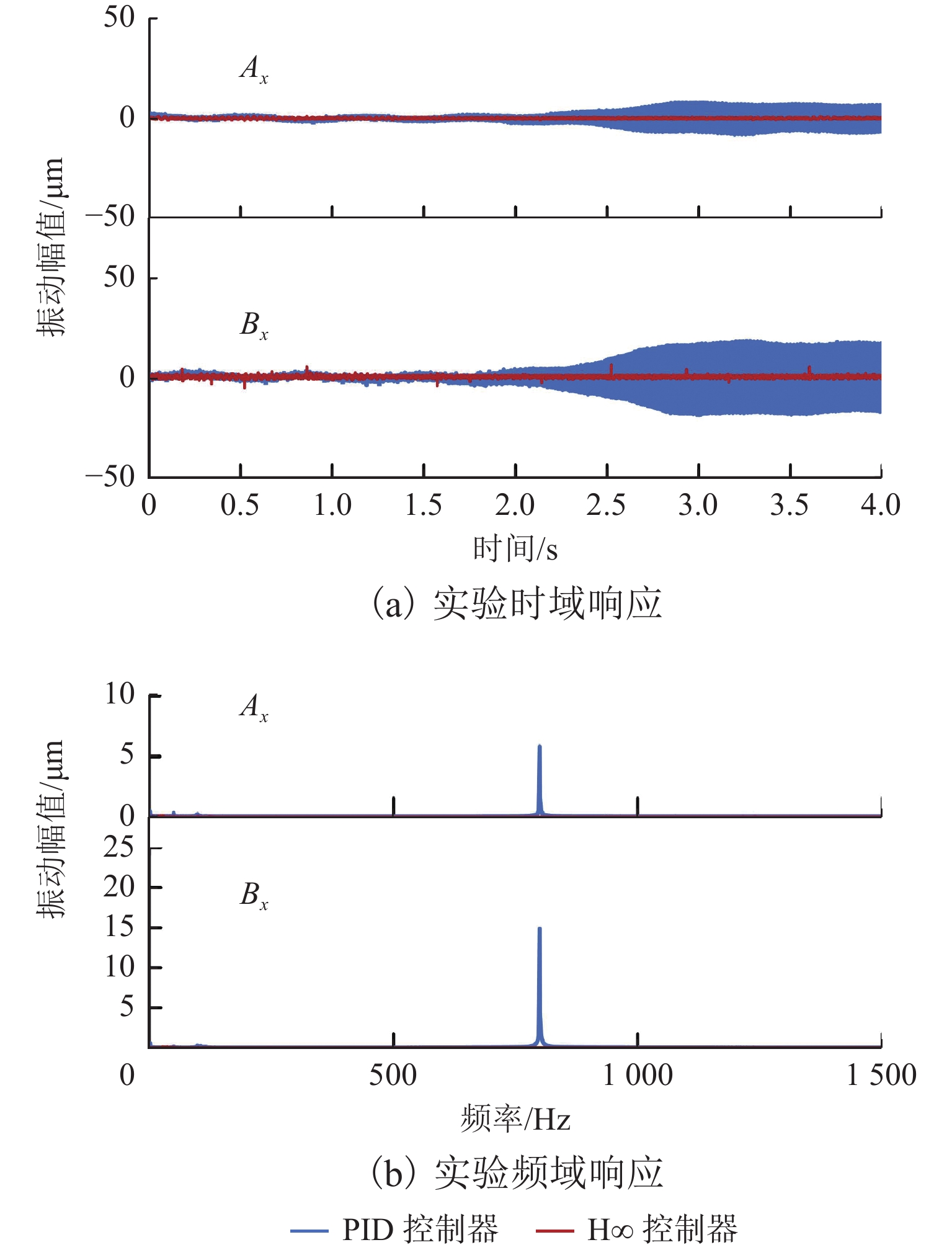
磁悬浮轴承-转子系统中，螺栓连接装配形成的界面接触会在转子悬浮状态下激发弯曲模态振动，同时振动频率随转速明显变化. 为实现全转速范围内对弯曲模态振动的主动控制，提出一种考虑频率不确定性的H∞鲁棒控制器设计方法. 首先，通过建立考虑界面接触的动力学模型进行仿真预测，获得振动频率的变化范围；其次，通过频响拟合的方式对转子传递函数进行重构，并将仿真得到的振动频率变化范围以加性不确定性方式引入到重构传递函数中，得到考虑模态频率不确定性的被控对象模型；最后，基于该模型设计兼顾参数摄动和外力扰动的鲁棒性、闭环系统稳定性和防止控制电压饱和等多功能的H∞ 鲁棒控制器. 数值仿真结果表明：该控制器在模态频率处具有宽频带阻的频响特性，能够抑制磁悬浮轴承转子系统的弯曲模态振动；采用该方法设计的H∞ 鲁棒控制器后，转子弯曲模态振动幅值最少减小90%.
Abstract:In magnetic bearing-rotor systems, the bending mode vibration may be excited by the interface contact formed by bolt joints during rotor levitation, and the vibration frequency varies with rotation speed. To actively control bending mode vibration at any speed, the design method of a robust H∞ controller considering frequency uncertainty was proposed. Firstly, the dynamic model considering interface contact was established for numerical simulation, and the vibration frequency variation was obtained. Then, the rotor transfer function was reconstructed by frequency response fitting, and the variation range of vibration frequency obtained by simulation was introduced into the reconstructed transfer function by means of additive uncertainty. As a result, a controlled object model considering mode frequency uncertainty was obtained. Finally, based on the model, the robust H∞ controller was designed by taking the robustness to parameter perturbations and external disturbance, closed-loop system stability, control voltage saturation, and other functions into account. The numerical simulation results show that the controller has the frequency response characteristic of wide band resistance at the mode frequency, which is able to suppress the bending mode vibration of the magnetic bearing-rotor system. After the robust H∞ controller designed by this method is used, the bending mode vibration amplitude of the rotor is reduced by more than 90%.
-
Key words:
- active magnetic bearing /
- interface contact /
- mode vibration /
- robust control
-
图 6 磁悬浮轴承转子系统静态悬浮仿真响应
Figure 6. Static levitation simulation response of magnetic bearing-rotor system
图 7 磁悬浮轴承转子系统静态悬浮实验响应
Figure 7. Static levitation experiment response of magnetic bearing-rotor system
图 13 被控对象扫频试验原理框图
Figure 13. Sweep frequency experiment principle for controlled object
表 1 径向磁悬浮轴承结构参数
Table 1. Structural parameters of radial magnetic bearing
参数 取值 单个磁极匝数 N/匝 75 单个磁极面积 A/m2 4.05 × 10－4 偏置电流 I0/A 2 单边气隙 C0/mm 0.25 
下载: 导出CSV
表 2 理论和试验弯曲模态频率
Table 2. Theoretical and experimental bending mode frequencies
Hz 弯曲模态阶数 理论值 试验值 1 91.26 91.83 2 255.14 257.12 3 526.41 519.53 4 816.02 817.46 5 1046.77 1032.57
下载: 导出CSV
-
[1] SCHWEITZER G, MASLEN E, BLEULER H, et al. Magnetic bearing:theory, design and application to rotating machinery[M]. Berlin:Springer-Verilog, 2009:11-12. [2] YANNICK P,JEFFREY S,王小明. 应用API617第8版配备磁悬浮轴承的透平膨胀机-压缩机[J]. 风机技术,2016,58(5): 6-18. [3] HUTTERER M, SCHRÖDL M. Modeling and mu-synthesis control of a flexible rotor stabilized by active magnetic bearings including current free control[J]. Journal of Sound and Vibration, 2023, 546:117439.1-117439.18. [4] INOUE T, LIU J, ISHIDA Y, et al. Vibration control and unbalance estimation of a nonlinear rotor system using disturbance observer[J]. Journal of Vibration and Acoustics, 2009, 131(3): 031010.1-031010.8. [5] LI K X, PENG C, DENG Z Q, et al. Field dynamic balancing for active magnetic bearings supporting rigid rotor shaft based on extended state observer[J]. Mechanical Systems and Signal Processing, 2021, 158: 107801.1-107801.14. [6] TANG E Q, HAN B C, ZHANG Y. Optimum compensator design for the flexible rotor in magnetically suspended motor to pass the first bending critical speed[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1): 343-354. doi: 10.1109/TIE.2015.2472534 [7] JIN C W, XIONG F, BAO Z P, et al. Research on modal vibration suppression of maglev steel strip based on phase compensator[J]. Journal of Sound and Vibration, 2018, 434: 78-91. doi: 10.1016/j.jsv.2018.07.043 [8] PENG C, ZHENG S Q, HUANG Z Y, et al. Complete synchronous vibration suppression for a variable-speed magnetically suspended flywheel using phase lead compensation[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5837-5846. doi: 10.1109/TIE.2017.2782204 [9] ZHENG S Q, HAN B C, WANG Y G, et al. Optimization of damping compensation for a flexible rotor system with active magnetic bearing considering gyroscopic effect[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(3): 1130-1137. doi: 10.1109/TMECH.2014.2344664 [10] ROY H K, DAS A S, DUTT J K. An efficient rotor suspension with active magnetic bearings having viscoelastic control law[J]. Mechanism and Machine Theory, 2016, 98: 48-63. doi: 10.1016/j.mechmachtheory.2015.11.012 [11] TANG E Q, FANG J C, HAN B C. Active vibration control of the flexible rotor in high energy density magnetically suspended motor with mode separation method[J]. Journal of Engineering for Gas Turbines and Power, 2015, 137(8): 082503.1-082503.10. [12] HAN X M, ZHOU J, ZHOU Y. Analysis and suppression of self-excited vibration of flexible rotor AMBs system[J]. Journal of Vibration Engineering & Technologies, 2021, 9(8): 1911-1922. [13] 魏彤,房建成. 基于双频Bode图设计磁悬浮弹性转子陷波器[J]. 光学精密工程,2008,16(5): 789-796.WEI Tong, FANG Jiancheng. Design of magnetically suspended elastic rotor Notch filter based on two-frequency Bode diagram[J]. Optics and Precision Engineering, 2008, 16(5): 789-796. [14] 崔培玲,赵光再,房建成,等. 基于相移陷波器的磁轴承不平衡振动全频自适应控制[J]. 振动与冲击,2015,34(20): 16-20,36.CUI Peiling, ZHAO Guangzai, FANG Jiancheng, et al. Adaptive control of unbalance vibration for magnetic bearings based on phase-shift Notch filter within the whole frequency range[J]. Journal of Vibration and Shock, 2015, 34(20): 16-20,36. [15] MUSHI S E, LIN Z, ALLAIRE P E. Stability analysis for a flexible rotor on active magnetic bearings subject to aerodynamic loads[C]//Proceedings of the 12th international symposium on magnetic bearings. Yokohama:[s.n.], 2010:22-25. [16] RAN S L, HU Y F, WU H C. Design, modeling, and robust control of the flexible rotor to pass the first bending critical speed with active magnetic bearing[J]. Advances in Mechanical Engineering, 2018, 10(2): 1-13. [17] 谭大力,陈进,廖明夫,等. 圆柱面配合激起的转子失稳振动研究[J]. 机械科学与技术,2014,33(12): 1786-1790.TAN Dali, CHEN Jin, LIAO Mingfu, et al. Instability caused by cylindrical surface fit in rotor system[J]. Mechanical Science and Technology for Aerospace Engineering, 2014, 33(12): 1786-1790. [18] 曾瑶,陈亮,蒋云帆,等. 圆柱面配合对柔性转子稳定性的影响[J]. 燃气涡轮试验与研究,2019,32(2): 42-48. doi: 10.3969/j.issn.1672-2620.2019.02.008ZENG Yao, CHEN Liang, JIANG Yunfan, et al. Analysis on the impact of cylindrical surface fit on flexible rotor[J]. Gas Turbine Experiment and Research, 2019, 32(2): 42-48. doi: 10.3969/j.issn.1672-2620.2019.02.008 [19] LIU Y, LIU H, YI J, et al. Investigation on the stability and bifurcation of a rod-fastening rotor bearing system[J]. Journal of Vibration and Control, 2015, 21(14): 2866-2880. doi: 10.1177/1077546313518817 [20] WU X L, JIAO Y H, CHEN Z B, et al. Establishment of a contact stiffness matrix and its effect on the dynamic behavior of rod-fastening rotor bearing system[J]. Archive of Applied Mechanics, 2021, 91(7): 3247-3271. doi: 10.1007/s00419-021-01963-9 [21] 魏彤,房建成. 磁悬浮控制力矩陀螺高速转子高频自激振动的抑制[J]. 宇航学报,2006,27(2): 291-296. doi: 10.3321/j.issn:1000-1328.2006.02.029WEI Tong, FANG Jiancheng. Self-excited vibration depression of high-speed rotor in magnetically suspended control moment gyroscope[J]. Journal of Astronautics, 2006, 27(2): 291-296. doi: 10.3321/j.issn:1000-1328.2006.02.029 [22] ZHOU Y, ZHOU J, MAHFOUD J, et al. Modelling and Validation of Rotor-Active Magnetic Bearing System Considering Interface Contact[C]//Proceedings of the 11th IFToMM International Conference on Rotordynamics. Mechanisms and Machine Science. Berlin:Springer, 2023:374-390. -
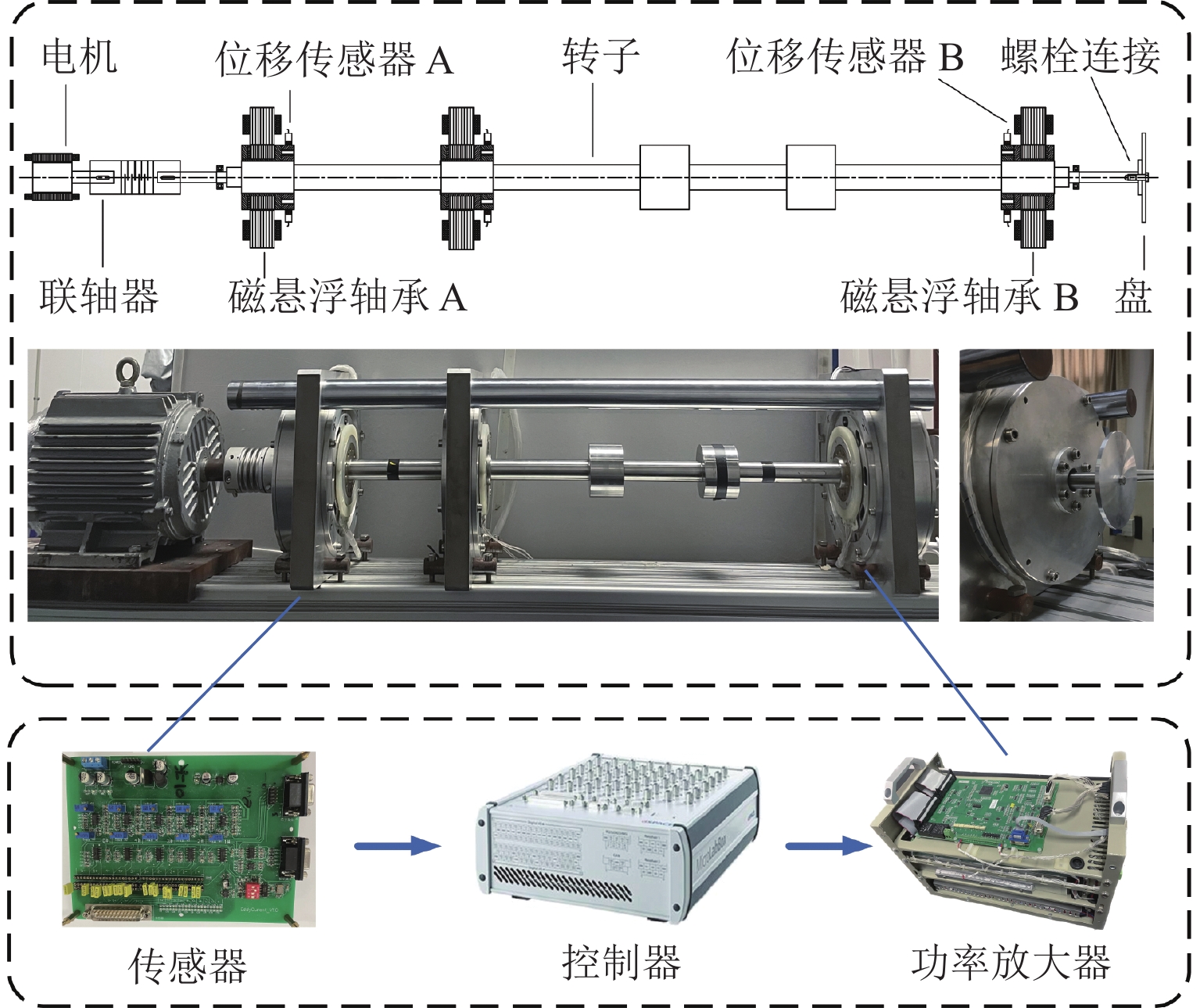
下载:
点击查看大图
计量
- 文章访问数: 119
- HTML全文浏览量: 46
- PDF下载量: 34
- 被引次数: 0