不同强度混凝土填充高强方钢管抗剪性能对比分析

王佳丽; 王莹; 陈西文; 杨东旭; 赖志超

doi:10.3969/j.issn.0258-2724.20230485

不同强度混凝土填充高强方钢管抗剪性能对比分析

doi: 10.3969/j.issn.0258-2724.20230485

福州大学土木工程学院，福建福州 350000

基金项目: 国家自然科学基金项目（51978170）

详细信息

作者简介:
王佳丽（1996—），女，博士研究生，研究方向为钢与混凝土组合结构，E-mail：1057508310@qq.com

通讯作者:
赖志超（1986—），男，教授，博士，研究方向为钢与混凝土组合结构，E-mail：laiz@fzu.edu.cn

中图分类号: TU398
计量
- 文章访问数: 104
- HTML全文浏览量: 75
- PDF下载量: 7
- 被引次数: 0
出版历程
- 收稿日期: 2023-09-19
- 修回日期: 2023-12-20
- 网络出版日期: 2025-01-09

Comparison of Shear Behaviors of Different Concrete-Filled High-Strength Steel Tubes

College of Civil Engineering, Fuzhou University, Fuzhou 350000, China

摘要

摘要:
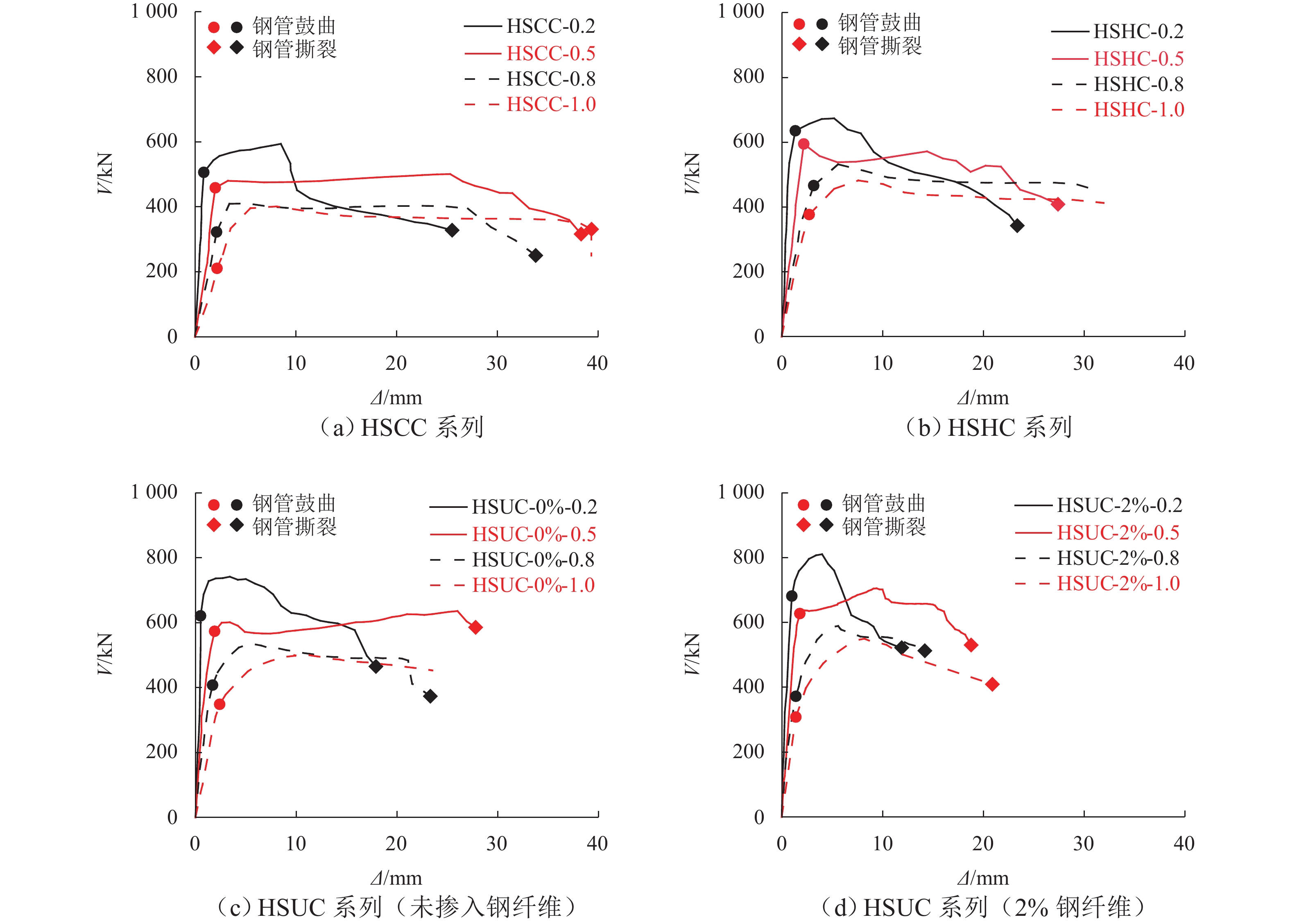
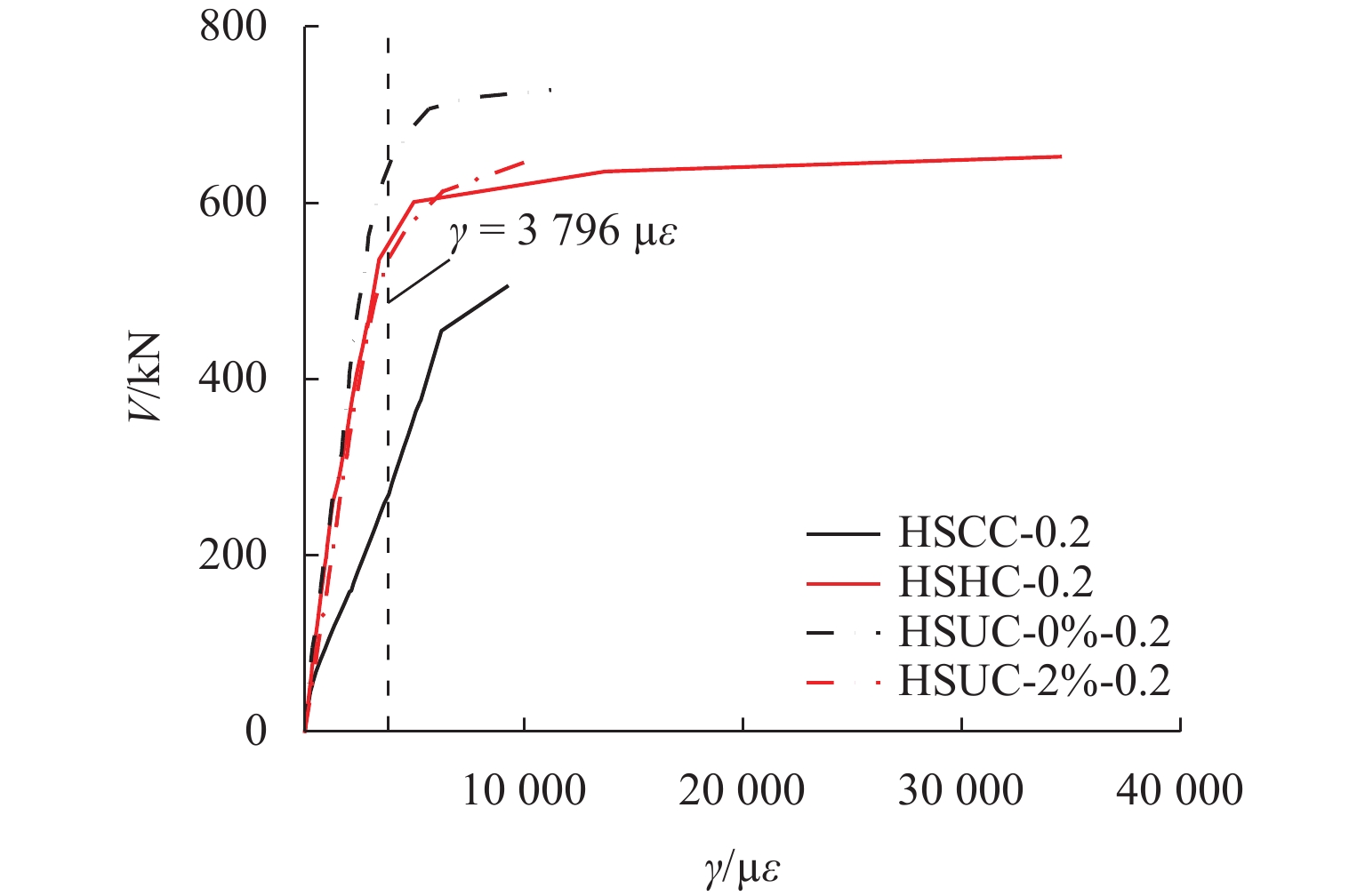
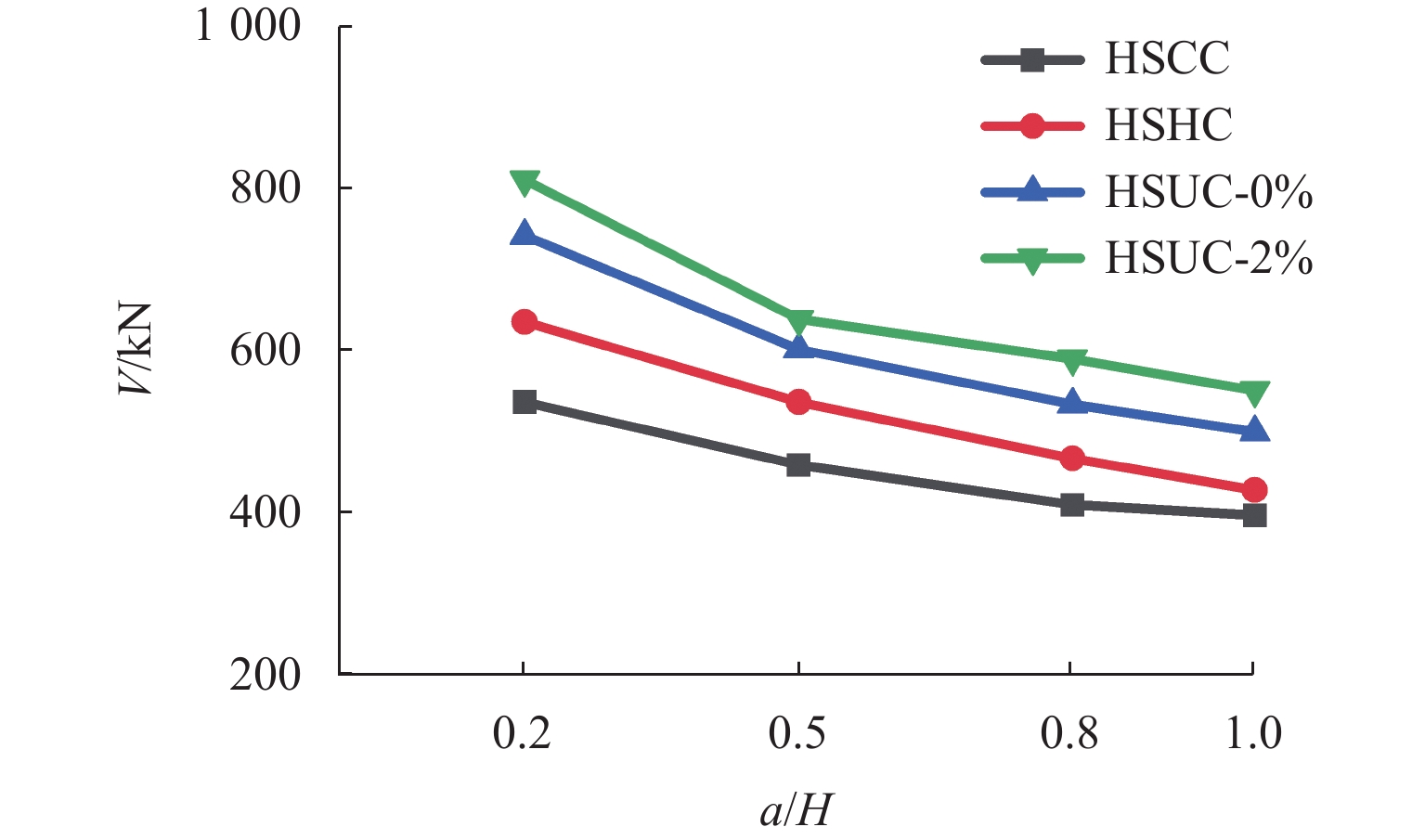
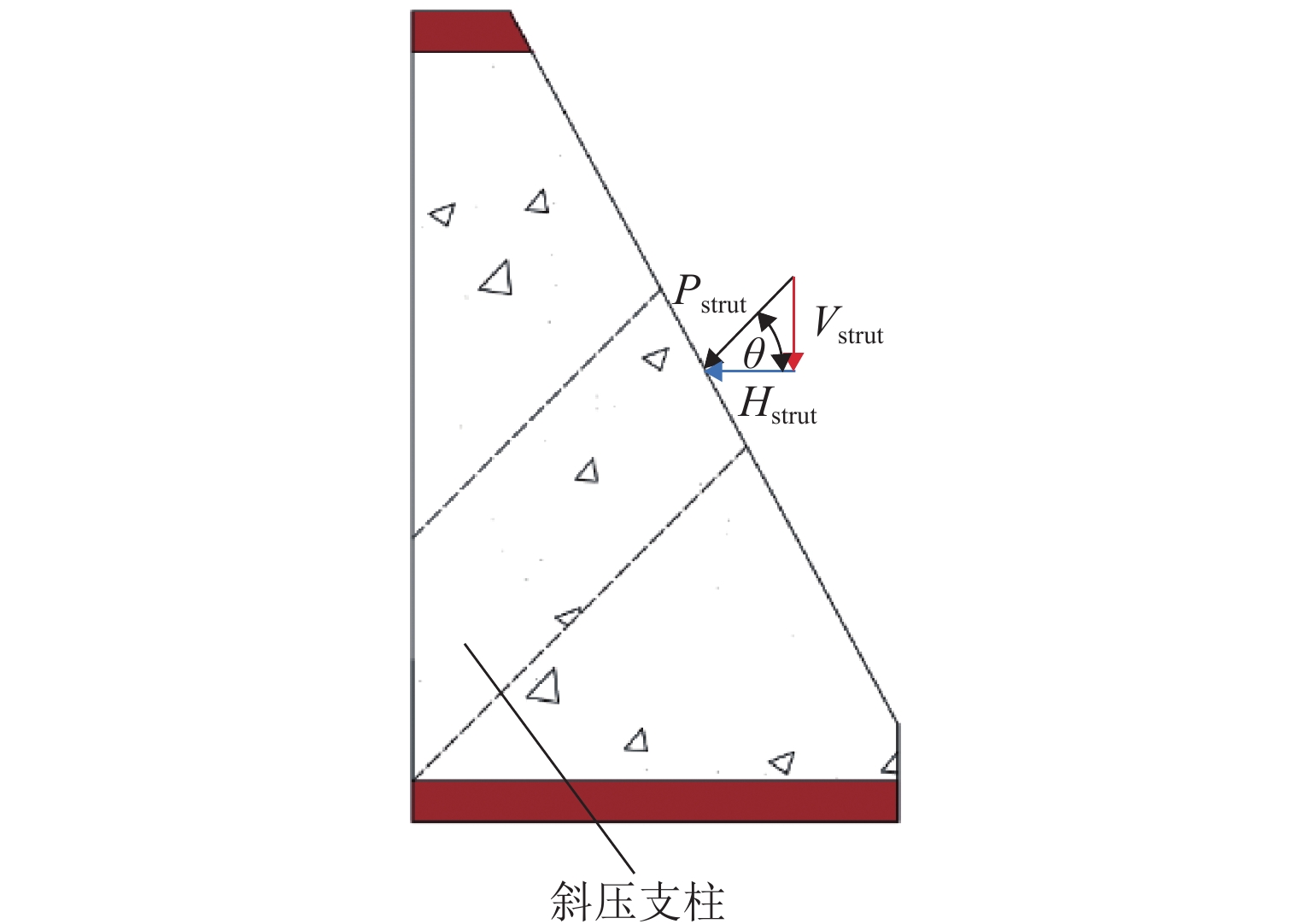
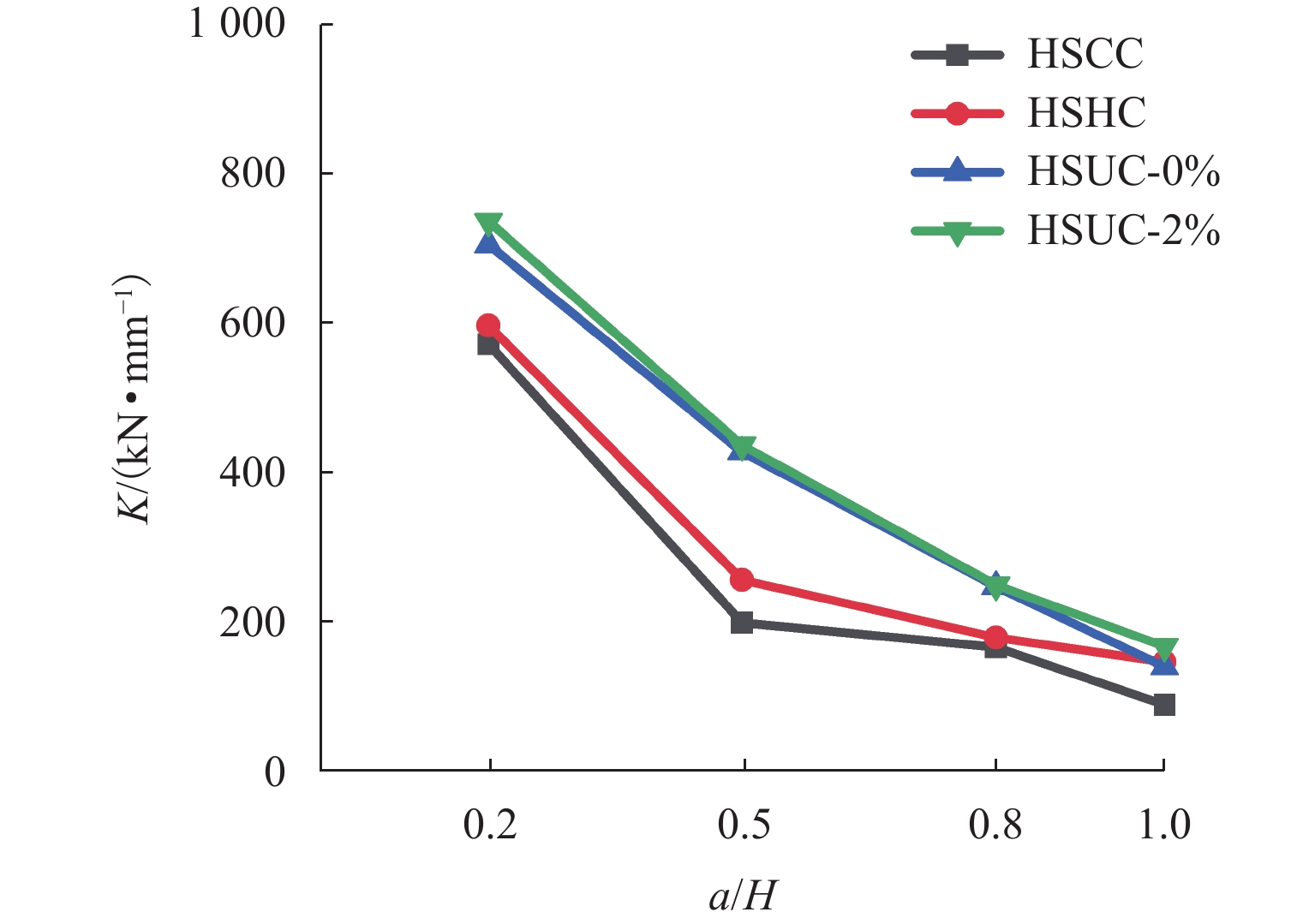
为研究剪跨比和混凝土强度对高强方钢管混凝土试件抗剪性能的影响，共设计16个高强方钢管混凝土试件. 通过试验获得试件的破坏模式和剪力-位移曲线，对比剪跨比、核心混凝土强度等参数对破坏模式、剪力-位移曲线、剪力-剪应变曲线、抗剪强度和刚度的影响. 研究结果表明：与普通钢管混凝土试件一致，剪跨比是控制高强方钢管混凝土试件破坏模式的主要参数，当剪跨比为0.2或0.5时，发生剪切破坏；当剪跨比为0.8或1.0时，发生弯剪破坏；采用超高性能混凝土填充高强方钢管（剪跨比为1.0），试件的变形能力降低61.4%，抗剪强度和刚度分别提高了38.9%和85.7%，且有效延缓钢管局部屈曲和降低试件的破坏程度；核心混凝土主斜裂缝产生的倾角随剪跨比增大而减小，但不受混凝土强度影响. 本文抗剪强度试验值/抗剪强度计算值 (V_exp/V_u) 的均值为0.97，方差为0.03，精度高，离散性小，认为该公式可较准确地预测高强钢管混凝土的抗剪强度.
- 钢管混凝土 /
- 高强钢管 /
- 抗剪性能 /
- 破坏模式 /
- 设计方法
Abstract:
A total of 16 concrete-filled high-strength steel tube specimens were designed to evaluate the effects of shear-to-span ratio and concrete strength on the shear behavior of concrete-filled high-strength steel tube specimens. The failure mode and shear-displacement curve of the specimens were obtained through the test, and the effects of shear-to-span ratio, core concrete strength, and other parameters on the failure mode, shear-displacement curve, shear-shear strain curve, shear strength, and shear stiffness were compared. The results show that similar to conventional concrete-filled steel tube specimens, the shear-to-span ratio is the key parameter controlling the failure mode of the concrete-filled high-strength steel tube specimens. When the shear-to-span ratio is 0.2 or 0.5, shear failure occurs; when the shear-to-span ratio is 0.8 or 1.0, shear-flexural failure occurs. By implementing ultra-high performance concrete (UHPC), the deformation capacity of the concrete-filled high-strength steel tube specimens (with a shear-to-span ratio of 1.0) is reduced by 61.4%. However, shear strength and stiffness increase by 38.9% and 85.7%, respectively. Additionally, local buckling of the steel tubes is effectively delayed, and the damage degree of the specimens is reduced. The inclination angle of the main diagonal cracks in the core concrete decreases with an increase in the shear-to-span ratio but is not affected by the concrete strength. The average value of tested shear strength/calculated shear strength (V_exp/V_u) is 0.97, with a deviation of 0.03, showing higher accuracy and smaller dispersion. It is considered that the formula can accurately predict the shear strength of concrete-filled high-strength steel tubes.
- concrete-filled steel tube /
- high-strength steel tube /
- shear behavior /
- failure mode /
- design method

HTML全文

超导电动悬浮列车（EDS）以其低能耗、低噪声、高速度及自稳定性等优点，近年来获得了显著发展. 磁悬浮列车的设计速度已达到600 km/h，如何实现高速稳定运行已成为磁悬浮列车空气动力学研究的关键方向之一^[1-2]. 目前，日本已于山梨试验线完成超导电动悬浮列车最高603 km/h试运行，证明超导电动悬浮的有效性^[3-4]. 磁浮列车行车速度增加至600 km/h恶化了高速磁浮列车的气动特性，严重影响高速磁浮列车运行平稳性及乘坐舒适性^[5].

国内外学者对磁浮列车气动特性已开展较多研究. 针对常导高速磁浮列车：丁叁叁等^[6-7]指出磁浮列车底部流量直接影响磁浮列车气动升力，并提出在头尾车鼻尖增加导流板用于控制间隙流量从而控制磁浮列车气动升力；Zhou等^[8]采用IDDES（improved delayed detached eddy simulation）方法计算了磁浮列车明线气动特性，给出了轨道附近列车风安全限值；孟石等^[9]研究了轨道间隙对磁浮列车气动特性影响，发现轨道间隙越大，头车升力减小，尾车升力增大；此外还有学者探究流线型鼻尖对磁浮列车气动噪声的影响^[10]. 针对钉扎磁浮列车：李一凡等^[11]基于钉扎磁浮列车分析了底部流动对磁浮列车升力特性的影响，指出底部间隙流量减小，升力及点头力矩均减小；王潇飞等^[12]则探究钉扎磁浮列车轨道结构对磁浮列车气动特性的影响. 而日本自20世纪70年代开始研究超导电动磁浮列车，山梨试验线测试结果表明，磁浮列车流线型长度增加，车体压力变化更为平缓，升力则一定程度减小^[13]. Yamamoto等^[14]对比了不同的列车截面发现，底部近似方形的列车截面可有效减小气动湍流，同时指出不同车体截面气动特性差异较大. Lin等^[15]研究了超导电动悬浮列车在不同悬浮间隙下的气动特性，发现悬浮间隙越大，阻力变化较小，升力则减小，且低频涡流对磁浮列车升力和阻力有显著影响.

在运行过程中，磁浮列车外流场气动特性直接反映于车体受到气动荷载. 列车起浮运行后仅受到电磁悬浮推进力及气动荷载的作用，为实现高速稳定运行，探究气动荷载作用特征的重要性逐步提升^[16]. 相关研究表明，磁浮列车受到的气动力与运行速度的平方成正比，可以预见的是提速至600 km/h下气动荷载也将显著增加^[17]. 刘堂红等^[18]计算了磁浮列车以相对860 km/h交会时的气动特性，同时将气动荷载作用于包含车体、悬浮架详细车辆动力学模型中，结果表明，磁浮列车车体产生了较大的横向振动. 南凯威等^[19]计算了TR08型磁浮列车明线及交会工况下气动荷载时程特征，结果表明，当磁浮列车速度增大到600 km/h时，悬浮间隙将超过安全极限. Wu等^[20]建立了磁浮列车垂向动力学模型，通过特征值方法和直接积分法研究气动荷载对悬架稳定性的影响规律.

上述国内外文献表明，磁浮列车与轨道之间的间隙流动直接影响磁浮列车气动特性. 但现有研究大多基于常导高速磁浮列车模型开展，对于超导电动悬浮列车的研究较少. 受限于超导电动悬浮的结构不同，流动特性存在一定差异^[21]. 本文以某型超导电动悬浮列车为研究对象，采用CFD（computational fluid dynamics）数值计算方法对三编组磁浮列车明线工况气动特性进行分析，并将悬浮架视为独立部件，分析其附近的详细空气流动在此基础上通过SIMPACK和Simulink建立车辆动力学模型，并使用精细化电磁力计算方法计算电磁力，分析不同气动荷载加载方式下磁浮列车动力学响应差异.

1. 数值计算方法

1.1 数值计算及边界条件

本研究选用的某型超导电动悬浮列车模型如图1所示，由头车、中间车和尾车三编组组成，头车与尾车外形一致，保留风挡特征. 磁浮列车车体与悬浮架非刚性连接，其简化模型如图1（c）所示. 使用磁浮列车车体高度H作为归一化长度，H为3.35 m. 车体总长为24.87H，建立简化超导电动悬浮列车悬浮架外形，悬浮架宽为0.95H，车体宽0.89H，头尾车流线型长度为4.24H，磁浮列车稳定运行悬浮高度为100 mm. 磁浮列车车体及悬浮架底部均简化为平面，不考虑车轮等部件.

图 1 磁浮列车几何模型

Figure 1. Geometric model of maglev train

下载: 全尺寸图片幻灯片

本文主要研究磁浮列车明线稳定运行气动特性，采用相对运动方法模拟列车高速运行^[22]. 建立计算域如图2所示，流体域长、宽、高分别为125.41H、71.64H和35.72H，磁浮列车头车鼻尖距离32.36H. 为保证尾流充分发展，尾车鼻尖距离计算域出口边界68.18H，计算域参数满足列车空气动力学计算标准TB/T 3503.4—2018.

图 2 计算域示意

Figure 2. Computational domain

下载: 全尺寸图片幻灯片

为获得准确计算结果，需对计算域赋予正确的边界条件. 超导电动悬浮列车设计速度600 km/h，大于0.30 Ma，因此需要考虑空气压缩性. 入口边界选用压力远场边界，设置边界马赫数为0.49 Ma（对应600 km/h）. 出口边界选用压力出口. 地面及U型轨道表面设置为滑移壁面，设置壁面滑移矢量与气体流动方向相同以避免轨道壁面效应影响. 车体表面为光滑壁面，计算域左、右侧及顶面设置为对称边界.

1.2 有限元网格及网格无关性验证

网格离散方法中采用四面体网格，在头（尾）车、风挡及4个悬浮架附近设置加密区，头尾车加密区内最大体网格为100 mm，最大面网格为100 mm. 悬浮架最大面网格为50 mm，由于车体流线型特征较为复杂，曲率较大部分设置面网格尺寸为20 mm. 网格示意如图3.

图 3 计算网格及加密区

Figure 3. Computational grid and area of encryption

下载: 全尺寸图片幻灯片

网格无关性验证共设置粗糙、中等及精细3类网格，具体网格尺寸如表1所示：为适应湍流模型，控制壁面第一层网格Y + 值在1附近，棱柱层统一采用0.02 mm，增长率设置为1.2，共30层. 采用无量纲压力系数C_p、升力系数C_L及阻力系数C_D评判磁浮列车网格无关性，如式（1）、（2）、（3）所示.

表 1 网格参数

Table 1. Grid parameters

网格质量	数量/ （×10⁷个）	车体最大面网格/mm	加密区最大体网格/mm
粗糙	4.74	100	200
中等	6.60	100	100
精细	7.92	80	100

下载: 导出CSV

| 显示表格

${C_p} = \frac{p}{{0.5\rho {v^2}S}},$

(1)

${C_L} = \frac{L}{{0.5\rho {v^2}S}},$

(2)

${C_D} = \frac{D}{{0.5\rho {v^2}S}},$

(3)

式中： $\rho$ 为流体密度，25 ℃时空气取值为1.17 kg/m³；p为测点压力；v为列车运行速度，取166.67 m/s；L为车体升力；D为车体阻力；S为车体截面积取9.19 m²

提取车底中线压力系数如图4所示，其中横轴正方向为头车鼻尖. 车底压力系数在头车鼻尖处及一位悬浮架后端出现一定程度分离. 放大相关位置可以发现，尽管幅值有一定差异，但仍具有相同的规律特征.

图 4 车底中线压力系数

Figure 4. Center line pressure coefficient beneath vehicle

下载: 全尺寸图片幻灯片

表2为3套网格无关性验证，其中下标h代表头车，t代表尾车，C_L,h为头车升力系数，其余类似. 提取头（尾）车的升力及阻力进行计算，以精细网格计算结果为标准. 中等网格尾车升力最大相对误差达到5.85%，粗糙网格尾车阻力最大误差达到8.51%，3套网格误差均不超过10.00%，网格对计算结果影响较小. 为提高计算效率并保证准确性，计算采用中等网格策略.

表 2 网格无关性验证

Table 2. Verification of grid independence

网格	${C_{L,h}}$	${C_{L,t}}$	${C_{D,h}}$	${C_{D,t}}$
粗糙	0.0826	−0.0665	0.0975	0.0828
中等	0.0875	−0.0755	0.0954	0.0861
精细	0.0868	−0.0713	0.0975	0.0905

下载: 导出CSV

| 显示表格

1.3 有限元计算方法及验证

采用商业软件Fluent完成数值计算，使用定常方法计算磁浮列车稳定流动特征，采用基于剪切应力的SST k-ω湍流模型避免网格诱导分离. 考虑压缩性选用25 ℃时理想气体作为计算流体；采用基于高斯节点的方法进行梯度离散；动量方程、湍流动能方程及湍流耗散率方程采用二阶迎风离散格式.

由于超导电动悬浮列车尚无实车试验数据，因此，采用TR08现场试验数据进行数值方法的验证^[23]. 建立轨道及三编组磁浮列车气动外形模型，如图5所示. 边界条件除入口和滑移壁面速度更改为430 km/h，其余保持一致. 采用相同网格策略及边界层参数. 测点p₁、p₂、p₃选择如图5所示，时均压力系数与试验相对误差如表3所示，最大误差为9.83%，满足工程误差需要，证明数值方法有效.

图 5 TR08测点示意（单位：m）

Figure 5. Measuring points of TR08 (unit: m)

下载: 全尺寸图片幻灯片

表 3 时均压力系数计算方法验证

Table 3. Validation of time-averaged pressure coefficient calculation method

测点	实测值	计算值	相对误差/%
p₁	0.240	0.21641	9.83
p₂	0.034	0.03294	3.13
p₃	0.016	0.01547	3.31

下载: 导出CSV

| 显示表格

2. 超导电动悬浮列车气动特性

2.1 车体表面压力分布

以磁浮列车明线600 km/h运行为例，车体表面压力分布如图6所示. 由图6可知：头车鼻尖出现流动驻点使得鼻尖位置动压减少，静压增大，鼻尖附近出现较大的正压力；自头车鼻尖向后发展，车体上表面由正压逐渐回落至常压，并随着空气沿磁浮列车表面加速运动，车体附近流动逐步加速，车体流线型区域表面为低压；尾车流线型区域流动截面逐渐增大，引起膨胀效应产生负压，尾车鼻尖由于顶部及底部同时产生膨胀流动，正压分布区域相比头车鼻尖更大.

图 6 磁浮列车表面压力分布

Figure 6. Pressure distribution in surface of maglev train

下载: 全尺寸图片幻灯片

磁浮列车车体底部主要为常压分布. 4个悬浮架底部则为不同程度负压，靠近悬浮架的车体底部呈现正压. 一位及四位悬浮架靠近磁浮列车鼻尖，流动截面变化速率更大，流动加剧，其底部负压明显大于二位及三位悬浮架.

2.2 车身周围扰流特征

磁浮列车空间涡结构采用Q准则识别，如式（4）.

$Q = \frac{1}{2}\left( {\left\| \varOmega \right\|_F^2 - \left\| S \right\|_F^2} \right) \text{，}$

(4)

式中：Ω为涡量张量，S为应变速率张量.

提取车体附近Q=80 s⁻¹等值面涡流，采用速度幅度染色车体及尾车附近涡流，如图7所示.

图 7 磁浮列车空间涡流

Figure 7. Space vortex of maglev train

下载: 全尺寸图片幻灯片

车体附近主要有涡流A、B、C：其中涡流A出现在头车鼻尖附近轨道梁侧壁正上方，并沿车体向后上方延伸直到尾流区域散逸；涡流B为磁浮列车尾车上表面及四位悬浮架顶部膨胀流动产生的尾涡并向后延伸；涡流C为尾车底部产生的分离涡流，在较短距离内耗散.

悬浮架附近主要有涡流D、E：悬浮架前端与轨道侧壁形成涡流D并向后扩散流动，逐步减慢，在风挡后方散逸消失；由于横向宽度变化，悬浮架与车体过渡段底部存在小型涡流E.

纵截面向提取磁浮列车Y=0截面，如图8（a）所示；横截面提取任意相邻悬浮架中间截面、头尾车鼻尖前端及尾流充分发展位置，如图8（b）所示. 由图8可知：头车鼻尖前端挤压U型轨道内部气体，车体流线型表面向上导流加速，少部分气体流入车体底部；受轨道侧壁梁限制，头车压缩U型轨内部空气流动，在侧壁梁顶部逐步形成涡流A，沿流动方向，涡流A占主要并沿着车体表面逐步从侧面移动至车体顶面；尾车鼻尖产生涡流B，主要由于膨胀流动使得侧壁梁外侧空气流入后形成；涡流C为磁浮列车底部与轨道内车轮踏面形成的膨胀涡流；在−14.33H截面位置，涡流A及涡流B仍然存在，涡流C已基本耗散消失.

图 8 不同截面涡量流线

Figure 8. Vortex streamlines of different sections

下载: 全尺寸图片幻灯片

2.3 悬浮架附近详细流动特征

通过上述对磁浮列车表面压力分布及整车流动分析发现，悬浮架外形对于车体附近流动存在一定影响. 为探究悬浮架附近详细气动特性，同时避免鼻尖对悬浮架流动的影响，以二位悬浮架为例分析悬浮架附近流动特征. 提取同一悬浮架表面压力云图及流动迹线，如图9所示.

图 9 悬浮架附近压力及流动迹线

Figure 9. Pressure and flow trace near suspension frame

下载: 全尺寸图片幻灯片

由图9可知：悬浮架前端将气流分为三部分，F部分气流导流至悬浮架上方，G部分气流被悬浮架外形压缩继续向后流动，此外还有H气体被导流压缩至悬浮架底部；悬浮架后端与车体过渡部分随着横向间隙增大，流速减小，出现扩张流动形成流动I.

进一步分析悬浮架底部流动特征，以悬浮架几何中心为0点，分别提取图9中所示悬浮架前（后）端、车体过渡段中点及悬浮架三等分截面处压力及速度云图，如图10所示.

图 10 悬浮架截面压力及速度云图

Figure 10. Pressure and velocity contours of suspension frame section

下载: 全尺寸图片幻灯片

由图10可知：沿空气流动方向分析，车体两侧压力场及速度场分布左右对称；1.38H截面位置为悬浮架前端，此位置磁浮列车横向间隙较大，轨道内由于即将受到悬浮架外形影响产生一定的拥塞流动，压力呈现正压，轨道内流速明显降低；随着空气向后流动进入悬浮架与车体过渡位置1.02H，横向间隙开始减小，对横向间隙流动空间继续压缩，压力增大，速度减小，悬浮架底部流速逐渐回归到流场速度，压力也回归常压；0.47H、0及−0.47H截面为悬浮架导向间隙流动，由于横向间隙减小，流动速度有所增大，静压减小，底部均为不同程度负压，0位置对应风挡截面，车体上附近流速减小；随后再次进入悬浮架与车体过渡区域截面−1.02H，横向间隙开始增大，流速减小，轨道内负压逐步增大至常压；随后进入悬浮架后端−1.38H，横向间隙已增大至车体宽度，流速进一步减小，静压增大，横向间隙内主要为正压.

3. 加载方式对列车动力学影响

有限元数值方法计算得到的磁浮列车气动荷载是由压力场的矢量和产生. 结果表明，磁浮列车车体与悬浮架附近压力分布差异较大，可以推断作用于磁浮列车车体与悬浮架的气动荷载同样有较大的差异. 同时车体结构也表明，磁浮列车车体与悬浮架之间通过二系悬挂连接，悬浮架与车体之间存在相对运动. 为更好地计算磁浮列车受到气动荷载作用下的响应，提出一种气动荷载提取方式（B），即将悬浮架外形受到的气动荷载区别于车体单独提取，并与常规仅区分车体的提取方式（A）获得的气动荷载进行对比. 将2种提取方式得到的气动荷载作用于车辆动力学模型中获得动力学响应.

3.1 2种提取方式下气动荷载差异

图11为不同提取方式下车体的气动荷载. 由图11可知，气动力均随速度增加而增大. 1）整体提取方式中，头车与中间车升力差异较小，均为正升力；尾车则为负升力，气动升力幅值大小基本相同. 2）分部件提取方式中，三车体均为升力，升力由大到小分别为头车、尾车以及中间车；分部件提取的头（尾）车车体气动升力约为整体提取方式的5倍. 3）相比于整体提取方式，分部件提取方式时，中间车升力增大约1倍；不同提取方式下，头车及尾车阻力差异明显大于中间车；分部件提取得到的三车体阻力约为总阻力的75%，其中头车约占33%，尾车占26%，证明磁浮列车阻力主要由车体产生且头车阻力大于尾车阻力.

图 11 不同提取方式下车体气动荷载

Figure 11. Aerodynamic load of vehicle body under different extraction methods

下载: 全尺寸图片幻灯片

分部件提取方式中，单独提取悬浮架所受气动荷载如图12所示. 一～四位悬浮架升力均为负值，为整车升力的−10.8倍，一位及四位悬浮架升力绝对值明显大于二位及三位悬浮架；一～四位悬浮架的阻力由大到小排列为四位、一位、二位和三位悬浮架，悬浮架外形产生的阻力均不超过4 kN.

图 12 悬浮架气动荷载

Figure 12. Aerodynamic load of suspension frame

下载: 全尺寸图片幻灯片

3.2 动力学模型及气动力作用下车辆动力学分析

三编组车辆动力学模型如图13所示，主要包括3个车体、4个悬浮架及超导磁体单元，其中，二位及三位悬浮架为铰接式悬浮架，同时承载2个车体. 超导磁体单元与悬浮架之间连接刚度相比二系悬挂刚度大一个数量级，因此，将超导磁体单元与构架间简化为刚性连接，并将两部件视为悬浮架整体. 以上构件均视为刚体，每个刚体考虑对应的横向、垂向、侧滚、点头及摇头5个方向自由度，共35个自由度. 由于本文磁浮列车明线运行，其横向力、侧滚力矩及摇头力矩均为0附近的极小值，因此，不再将此3个自由度荷载作为输入. 采用电磁力快速计算模型^[24]对超导电动悬浮列车电磁力进行计算.

图 13 磁浮列车动力学模型

Figure 13. Dynamics model of maglev train

下载: 全尺寸图片幻灯片

对应2种气动荷载提取方式（A、B），磁浮列车也提出2种气动荷载加载方式，分别为集中加载方式（a）和分部件加载方式（b），2种加载方式下磁浮列车受力分析如所示. 加载方式a下，整体提取的气动力 ${F_{{\mathrm{air}}}}$ 仅作用在车体，悬浮架则通过二系悬挂传递荷载；加载方式b中，车体及悬浮架分别受到车体气动力 ${F_{{\mathrm{air\_car}}}}$ 及悬浮架气动力 ${F_{{\mathrm{air\_bogie}}}}$ 作用. 2种加载方式下，磁浮列车气动荷载合力一致，但车体与悬浮架之间的受力有一定差异.

图 14 不同加载方式示意

Figure 14. Different loading modes

下载: 全尺寸图片幻灯片

以悬浮架无气动荷载作用下稳定悬浮高度为基准，Y轴正向为相对于无气动荷载作用时上浮高度，一～四位悬浮架悬浮高度变化量如图15所示. 由于头车及中间车升力通过二系悬挂向下传递，带动一、二及三位悬浮架出现一定程度上浮，二位及三位悬浮架上升程度大于一位悬浮架，最大上升量达到5.50 mm，由于尾车负升力影响四位悬浮架下沉约6.97 mm.

图 15 悬浮架悬浮高度变化量

Figure 15. Change in suspension height of suspension frame

下载: 全尺寸图片幻灯片

悬浮高度变化直接影响悬浮力，由于超导电动悬浮列车的被动悬浮稳定特征，2种加载方式下，悬浮架悬浮间隙变化量最大差异为1.05 mm. 四位悬浮架悬浮力变化量如图16所示.

图 16 悬浮力变化量

Figure 16. Change in suspension force

下载: 全尺寸图片幻灯片

悬浮力大小与悬浮架位移呈反比例关系，四位悬浮架悬浮力增大，一、二及三位悬浮架则减小. 2种加载方式下，悬浮力最大变化了2.92 kN；一位及四位独立悬浮架悬浮力差异较小，二位及三位铰接式悬浮架差异较大；有、无气动荷载对比时悬浮力最大变化量达到15.98 kN.

2种加载方式下，磁浮列车车体高度基本不变，悬浮架与车体之间的相对变化反映在二系悬挂空气弹簧力变化. 图17给出了2种气动荷载加载方式下磁浮列车二系空簧力变化量随速度变化曲线. 由图17可知：1）以磁浮列车无气动荷载作用下空簧受力为基准，加载方式a作用下，尾车车体受到负升力，反映为下压，因此，四位悬浮架空簧力增大；其余位置受车体升力影响，空簧力均减小；加载方式a下，磁浮列车空簧力最大变化量为4.94 kN. 2）加载方式b下，车体与悬浮架受力相反，空气弹簧呈减小拉伸趋势，所有空簧力均减小；一位及四位悬浮架为独立悬浮架，其前端及后端空簧变化量差异较小；二位及三位悬浮架为铰接式悬浮架，同时承载2个车体，空簧前后端存在一定差异，以二位悬浮架为例，前端头车升力较大，对应前端空簧力减少的也更多；加载方式b下，空簧力最大变化量达到18.7 kN，为加载方式a的2.86倍.

图 17 空簧力变化量

Figure 17. Chang in air spring force

下载: 全尺寸图片幻灯片

4. 结　论

基于某型磁浮列车几何模型，计算分析其明线气动特性及气动荷载，在此基础上探究2种加载方式下车辆响应，得出以下结论：

1） U型轨包车结构直接影响磁浮列车车体附近流动特性. 头车鼻尖压缩轨道内空气并沿头车流线型表面向上导流至轨道外，在侧壁梁顶部形成涡流. 尾车后端膨胀分离流动则被一定程度限制在U型轨道内部.

2）超导电动悬浮列车车体和悬浮架宽度不一致，导致悬浮架附近流动规律出现明显变化. 悬浮架从前至后压力分布为正压—负压—正压，其中悬浮架底部及侧面主要以负压为主. 一位及四位悬浮架受头尾车流线型影响，底部压力远小于二位和三位底部压力.

3）基于气动特性差异，提出2种气动荷载提取方式. 以600 km/h速度运行为例，整体提取方式中，头车与中间车升力均为正并且相近，头车和中间车升力均大于尾车负升力；分部件提取方式中，车体受到升力均为正，头车和尾车大小相近，均大于中间车；四位悬浮架升力均为负，幅值大小依次为一位和四位升力相近，均大于二位及三位悬浮架升力. 分部件提取方式中，车体气动升力相比于整车提取方式增大约5倍，增加了气动荷载作用下的不确定性，悬浮架负升力幅值占车体升力的91.5%，悬浮架阻力约占整车的四分之一.

4）相比于整体气动荷载作用，分布荷载作用下磁浮列车响应主要反映为空气弹簧变化量. 悬浮架受气动荷载作用，高度变化量不超过7 mm，不同加载方式悬浮架高度变化基本一致. 分部件加载方式相比于整车加载方式，空簧力变化量增大1.86倍. 分部件加载方式可更加准确反应二悬挂空气弹簧受力特征，为车辆动力学提供更为准确的计算参考.

致谢：

图 1 试验加载装置

Figure 1. Testing apparatus

下载: 全尺寸图片幻灯片

图 2 加载夹具和支座夹具详图

Figure 2. Loading and support fixtures

下载: 全尺寸图片幻灯片

图 3 加载制度

Figure 3. Loading system

下载: 全尺寸图片幻灯片

图 4 测点布置

Figure 4. Measuring point arrangement

下载: 全尺寸图片幻灯片

图 5 剪切破坏

Figure 5. Shear failure

下载: 全尺寸图片幻灯片

图 6 弯剪破坏

Figure 6. Shear-flexural failure

下载: 全尺寸图片幻灯片

图 7 核心混凝土破坏模式（a/H=0.2）

Figure 7. Damage mode of core concrete （a/H = 0.2）

下载: 全尺寸图片幻灯片

图 8 核心混凝土破坏模式（a/H=0.8）

Figure 8. Damage mode of core concrete （a/H = 0.8）

下载: 全尺寸图片幻灯片

图 9 剪力-位移关系曲线图

Figure 9. Shear-displacement relationship curve

下载: 全尺寸图片幻灯片

图 10 剪力-剪应变关系曲线

Figure 10. Shear-shear strain curve

下载: 全尺寸图片幻灯片

图 11 不同研究参数对抗剪强度的影响

Figure 11. Effect of different parameters on shear strength

下载: 全尺寸图片幻灯片

图 12 斜压支柱示意

Figure 12. Diagonal compression strut

下载: 全尺寸图片幻灯片

图 13 不同研究参数对抗剪刚度的影响

Figure 13. Effect of different parameters on shear stiffness

下载: 全尺寸图片幻灯片

图 14 试验值与计算值的比较

Figure 14. Comparison between tested and calculated values

下载: 全尺寸图片幻灯片

表 1 试件主要参数

Table 1. Main parameters of specimens

序号	试件编号	L/mm	B/mm	H/mm	$\rho$ /%	$f_{\mathrm{y}}$ /MPa	$f_{{\mathrm{c}}1}$ /MPa	t/mm	$E_{\mathrm{s}}$ /GPa	$E_{\mathrm{c}}$ /GPa
1	HSCC-0.2	1000	120	120		747	30	3	206	32.7
2	HSCC-0.5	1000	120	120		747	30	3	206	32.7
3	HSCC-0.8	1000	120	120		747	30	3	206	32.7
4	HSCC-1.0	1000	120	120		747	30	3	206	32.7
5	HSHC-0.2	1000	120	120		782	90	3	206	43.4
6	HSHC-0.5	1000	120	120		782	90	3	206	43.4
7	HSHC-0.8	1000	120	120		782	90	3	206	43.4
8	HSHC-1.0	1000	120	120		782	90	3	206	43.4
9	HSUC-0%-0.2	1000	120	120		747	115	3	206	41.9
10	HSUC-0%-0.5	1000	120	120		747	115	3	206	41.9
11	HSUC-0%-0.8	1000	120	120		747	115	3	206	41.9
12	HSUC-0%-1.0	1000	120	120		747	115	3	206	41.9
13	HSUC-2%-0.2	1000	120	120	2	775	135.4	3	206	44.8
14	HSUC-2%-0.5	1000	120	120	2	775	135.4	3	206	44.8
15	HSUC-2%-0.8	1000	120	120	2	775	135.4	3	206	44.8
16	HSUC-2%-1.0	1000	120	120	2	775	135.4	3	206	44.8

下载: 导出CSV

表 2 混凝土配合比

Table 2. Concrete mix proportions kg/m³

混凝土类别	水	水泥	硅灰	粗骨料	细骨料	减水剂	钢纤维体积掺量
普通（C30）	180.0	370.0		1042.0	766.0	7.40
高强（C90）	156.8	579.4	102.2	1050.8	617.2	15.48
UHPC （无钢纤维）	221.7	852.5	255.7	920.7	80.1	21.30
UHPC （2% 钢纤维）	221.7	852.5	255.7	920.7	80.1	21.30	2%

下载: 导出CSV

表 3 试验结果

Table 3. Test results

试件编号	V_exp/ kN	$\Delta_{\mathrm{y}}$ / mm	$\varDelta_{\mathrm{u}}$ / mm	K/ （kN·mm⁻¹）	破坏模式
HSCC-0.2	536	0.9	9.5	573	剪切破坏
HSCC-0.5	458	2.3	28.4	201	剪切破坏
HSCC-0.8	409	2.4	29.7	168	弯剪破坏
HSCC-1.0	396	4.4	>30.0	91	弯剪破坏
HSHC-0.2	635	1.1	7.2	598	剪切破坏
HSHC-0.5	536	2.1	22.6	258	剪切破坏
HSHC-0.8	466	2.5	27.7	181	弯剪破坏
HSHC-1.0	427	2.9	>30.0	148	弯剪破坏
HSUC-0%-0.2	741	1.1	14.5	706	剪切破坏
HSUC-0%-0.5	601	1.4	27.8	429	剪切破坏
HSUC-0%-0.8	533	2.1	21.2	249	弯剪破坏
HSUC-0%-1.0	499	3.5	23.5	142	弯剪破坏
HSUC-2%-0.2	810	1.1	6.1	737	剪切破坏
HSUC-2%-0.5	638	1.6	14.2	438	剪切破坏
HSUC-2%-0.8	589	2.3	22.4	251	弯剪破坏
HSUC-2%-1.0	550	3.3	23.3	169	弯剪破坏

下载: 导出CSV

表 4 试验值与计算值比较

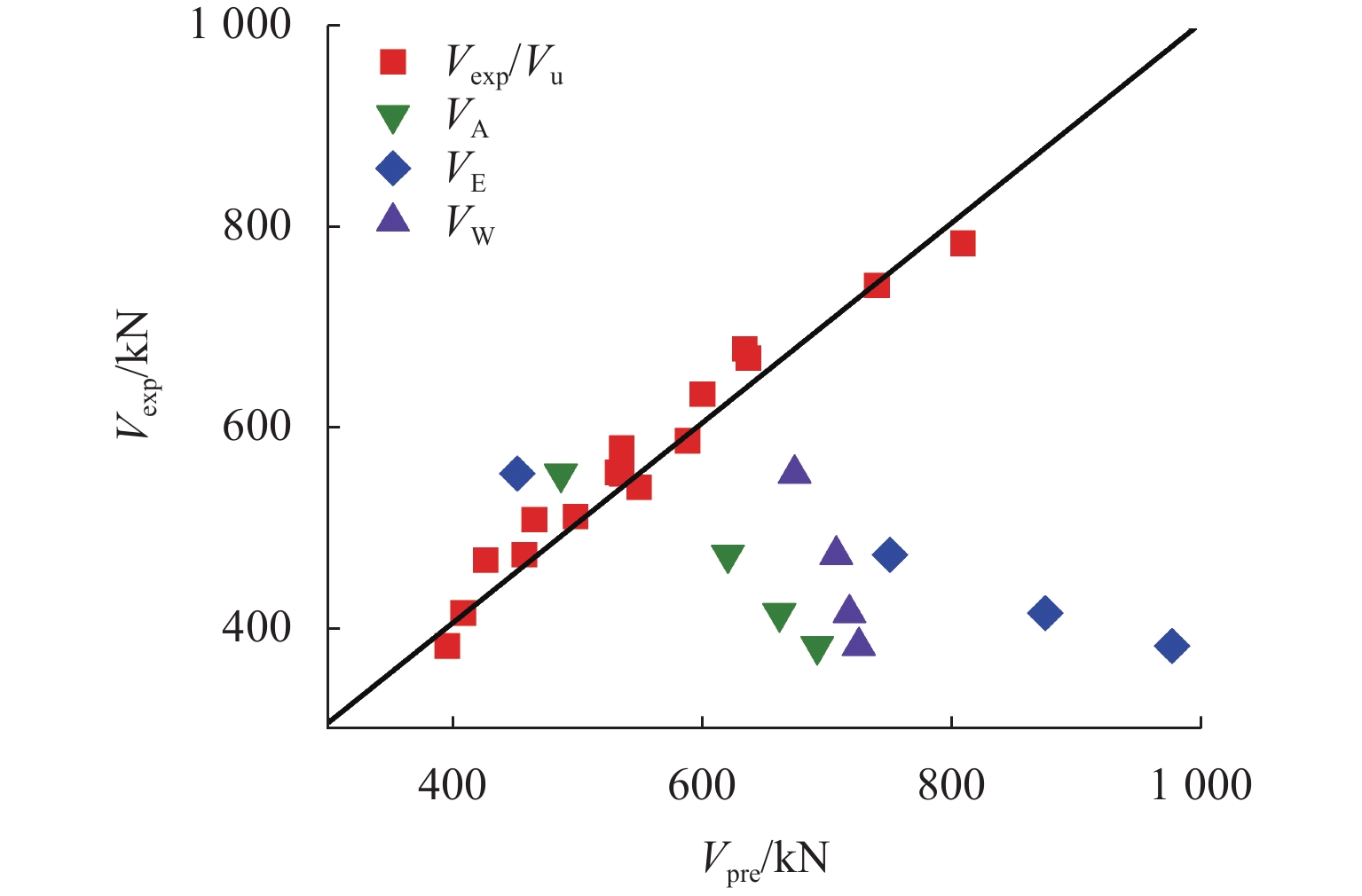
Table 4. Comparison between tested and calculated values

试件编号	V_exp/kN	文献[20]		文献[21]		文献[22]		文献[23]
试件编号	V_exp/kN	V_u/kN	V_exp/V_u	V_A/kN	V_exp/V_A	V_E/kN	V_exp/V_E	V_W/kN	V_exp/V_W
HSCC-0.2	536	553.5	0.97	487.2	1.10	452.3	1.19	675.0	0.79
HSCC-0.5	458	472.4	0.97	487.2	0.94	452.3	1.01	675.0	0.68
HSCC-0.8	409	414.0	0.99	487.2	0.84	452.3	0.90	675.0	0.61
HSCC-1.0	396	381.1	1.01	487.2	0.81	452.3	0.88	675.0	0.59
HSHC-0.2	635	678.0	0.94	621.3	1.02	751.4	0.85	708.5	0.90
HSHC-0.5	536	578.8	0.93	621.3	0.86	751.4	0.71	708.5	0.76
HSHC-0.8	466	507.2	0.92	621.3	0.75	751.4	0.62	708.5	0.66
HSHC-1.0	427	466.9	0.91	621.3	0.69	751.4	0.57	708.5	0.60
HSUC-0%-0.2	741	741.4	1.00	662.6	1.12	876.1	0.85	718.9	1.03
HSUC-0%-0.5	601	632.8	0.95	662.6	0.91	876.1	0.69	718.9	0.84
HSUC-0%-0.8	533	554.6	0.96	662.6	0.80	876.1	0.61	718.9	0.74
HSUC-0%-1.0	499	510.5	0.98	662.6	0.75	876.1	0.57	718.9	0.69
HSUC-2%-0.2	810	783.7	1.03	693.1	1.17	977.8	0.83	726.5	1.11
HSUC-2%-0.5	638	669.0	0.95	693.1	0.92	977.8	0.65	726.5	0.88
HSUC-2%-0.8	589	586.3	1.00	693.1	0.85	977.8	0.60	726.5	0.81
HSUC-2%-1.0	550	539.7	1.02	693.1	0.79	977.8	0.56	726.5	0.76
均值			0.97		0.90		0.75		0.78
方差			0.03		0.14		0.18		0.15

下载: 导出CSV

参考文献(24)

[1]	韩林海. 钢管混凝土结构:理论与实践[M]. 2版. 北京:科学出版社,2007.
[2]	LAI Z C, VARMA A H, GRIFFIS L G. Analysis and design of noncompact and slender CFT beam-columns[J]. Journal of Structural Engineering, 2016, 142(1): 04015097.1-04015097.14.
[3]	WANG Y, LIN H, LAI Z C, et al. Flexural behavior of high-strength rectangular concrete-filled steel tube members[J]. Journal of Structural Engineering, 2022, 148(1): 4021230.1-4021230.15.
[4]	WANG F Y, ZHAO O, YOUNG B. Testing and numerical modelling of S960 ultra-high strength steel angle and channel section stub columns[J]. Engineering Structures, 2020, 204: 109902.1-109902.12.
[5]	RICHARD P, CHEYREZY M. H. Reactive powder concretes with high ductility and 200-800 MPa compressive strength[J]. Special Publication, 1994, 144(24): 507-518.
[6]	管民生,黄献奇,杜宏彪,等. 矩形钢管高强混凝土框架抗震性能分析[J]. 西南交通大学学报,2019,54(3): 483-491. doi: 10.3969/j.issn.0258-2724.20170809 GUAN Minsheng, HUANG Xianqi, DU Hongbiao, et al. Seismic behavior of rectangular high-strength concrete-filled steel tube frame structure[J]. Journal of Southwest Jiaotong University, 2019, 54(3): 483-491. doi: 10.3969/j.issn.0258-2724.20170809
[7]	YE Y, HAN L H, TAO Z, et al. Experimental behaviour of concrete-filled steel tubular members under lateral shear loads[J]. Journal of Constructional Steel Research, 2016, 122: 226-237. doi: 10.1016/j.jcsr.2016.03.012
[8]	黄勇,陈伟刚,段莉. 钢管混凝土短柱(剪力键)受剪性能试验研究[J]. 建筑结构学报,2011,32(12): 178-185. HUANG Yong, CHEN Weigang, DUAN Li. Experimental study on shear resistance performance of concrete filled steel tube shear block stub columns[J]. Journal of Building Structures, 2011, 32(12): 178-185.
[9]	李志强,陈以一,王伟. 矩形钢管混凝土中短柱弯-剪性能试验研究[J]. 建筑结构学报,2015,36(7): 1-9. LI Zhiqiang, CHEN Yiyi, WANG Wei. Experimental research on bending and shearing behavior of middle and short concrete filled steel tubular columns[J]. Journal of Building Structures, 2015, 36(7): 1-9.
[10]	史艳莉,周绪红,鲜威,等. 无端板矩形钢管混凝土构件基本剪切性能研究[J]. 工程力学,2018,35(12): 25-33. SHI Yanli, ZHOU Xuhong, XIAN Wei, et al. Research on basic shear performance of concrete filled rectangular steel tubular members without end-plate[J]. Engineering Mechanics, 2018, 35(12): 25-33.
[11]	丁威. 矩形钢管混凝土双剪截面研究及其工程应用[D]. 广东:广东工业大学,2019.
[12]	MANSOURI A. Shear strength of concrete-filled steel tubes based on experimental results[J]. Journal of Structural Engineering, 2020, 146(6): 04020097.1-04020097.14.
[13]	LEHMAN D, ROEDER C, HEID A, et al. Shear response of concrete filled tubes part 1: experiments[J]. Journal of Constructional Steel Research, 2018, 150: 528-540. doi: 10.1016/j.jcsr.2018.08.027
[14]	LEHMAN D, ROEDER C, HEID A, et al. Shear response of concrete filled tubes part II: analytical study[J]. Journal of Constructional Steel Research, 2019, 153: 169-178. doi: 10.1016/j.jcsr.2018.08.019
[15]	颜燕祥,徐礼华,蔡恒,等. 高强方钢管超高性能混凝土短柱轴压承载力计算方法研究[J]. 建筑结构学报,2019,40(12): 128-137. YAN Yanxiang, XU Lihua, CAI Heng, et al. Calculation methods of axial bearing capacity of short square UHPC filled high strength steel tubular columns[J]. Journal of Building Structures, 2019, 40(12): 128-137.
[16]	操礼林,石启印,王震,等. 高强U形外包钢-混凝土组合梁受弯性能[J]. 西南交通大学学报,2014,49(1): 72-78. doi: 10.3969/j.issn.0258-2724.2014.01.012 CAO Lilin, SHI Qiyin, WANG Zhen, et al. Bending performances of high-strength steel-encased composite beams[J]. Journal of Southwest Jiaotong University, 2014, 49(1): 72-78. doi: 10.3969/j.issn.0258-2724.2014.01.012
[17]	YAN Y X, XU L H, LI B, et al. Axial behavior of ultra-high performance concrete (UHPC) filled stocky steel tubes with square sections[J]. Journal of Constructional Steel Research, 2019, 158: 417-428. doi: 10.1016/j.jcsr.2019.03.018
[18]	HU J Y, HUANG Y F, LI W J, et al. Compressive behaviour of UHPC-filled square high-strength steel tube stub columns under eccentric loading[J]. Journal of Constructional Steel Research, 2022, 198: 107558.1-107558.15.
[19]	LAI Z C, ZHOU W S, WANG Y, et al. Flexural behavior and design of rectangular ultra-high performance concrete-filled high-strength steel tube members[J]. Engineering Structures, 2023, 286: 116125.1-116125.15.
[20]	哈尔滨工业大学,中国建筑科学研究院. 钢管混凝土结构技术规程:CECS 28—2012[S]. 北京:中国计划出版社,2012.
[21]	American Association of State Highway and Transportation Officials (AASHTO). AASHTO LRFD bridge design specifications[S]. Washington, D. C.: AASHTO, 2014.
[22]	CEN. Design of composite steel and concrete structures part 1-1: general rules and rules for buildings: DS/EN 1994-1-1[S]. Belgium: [s.n.], 1994.
[23]	WSDOT. Bridge design manual LRFD[S]. Olympia: [s.n.], 2018.
[24]	KENARANGI H, BRUNEAU M. Shear strength of composite circular reinforced concrete-filled steel tubes[J]. Journal of Structural Engineering, 2020, 146(1): 04019180.1-04019180.15.