长大隧道施工车辆时刻表和运行路径协同优化

胡路; 李东婕; 陈飞; 蒋阳升

doi:10.3969/j.issn.0258-2724.20230457

长大隧道施工车辆时刻表和运行路径协同优化

doi: 10.3969/j.issn.0258-2724.20230457

胡路^{1, 2,},
李东婕^{1, 2},
陈飞^{1, 2},
蒋阳升^{1, 2, ,}

1.
西南交通大学交通运输与物流学院，四川成都 610031
2.
西南交通大学综合交通大数据应用技术国家工程实验室，四川成都 610031

基金项目: 国家自然科学基金项目（72371209，62203367）；中央高校校基金项目（2682022CX026）

详细信息

作者简介:
胡路（1985—），男，副教授，博士，研究方向为共享交通和城市轨道交通，E-mail：hulu@swjtu.edu.cn

通讯作者:
蒋阳升（1975—），男，教授，博士生导师，研究方向为交通系统建模与优化，E-mail：jiangyangsheng@swjtu.cn

中图分类号: U455.2
计量
- 文章访问数: 53
- HTML全文浏览量: 25
- PDF下载量: 5
- 被引次数: 0
出版历程
- 收稿日期: 2023-09-06
- 修回日期: 2023-12-15
- 网络出版日期: 2025-04-09

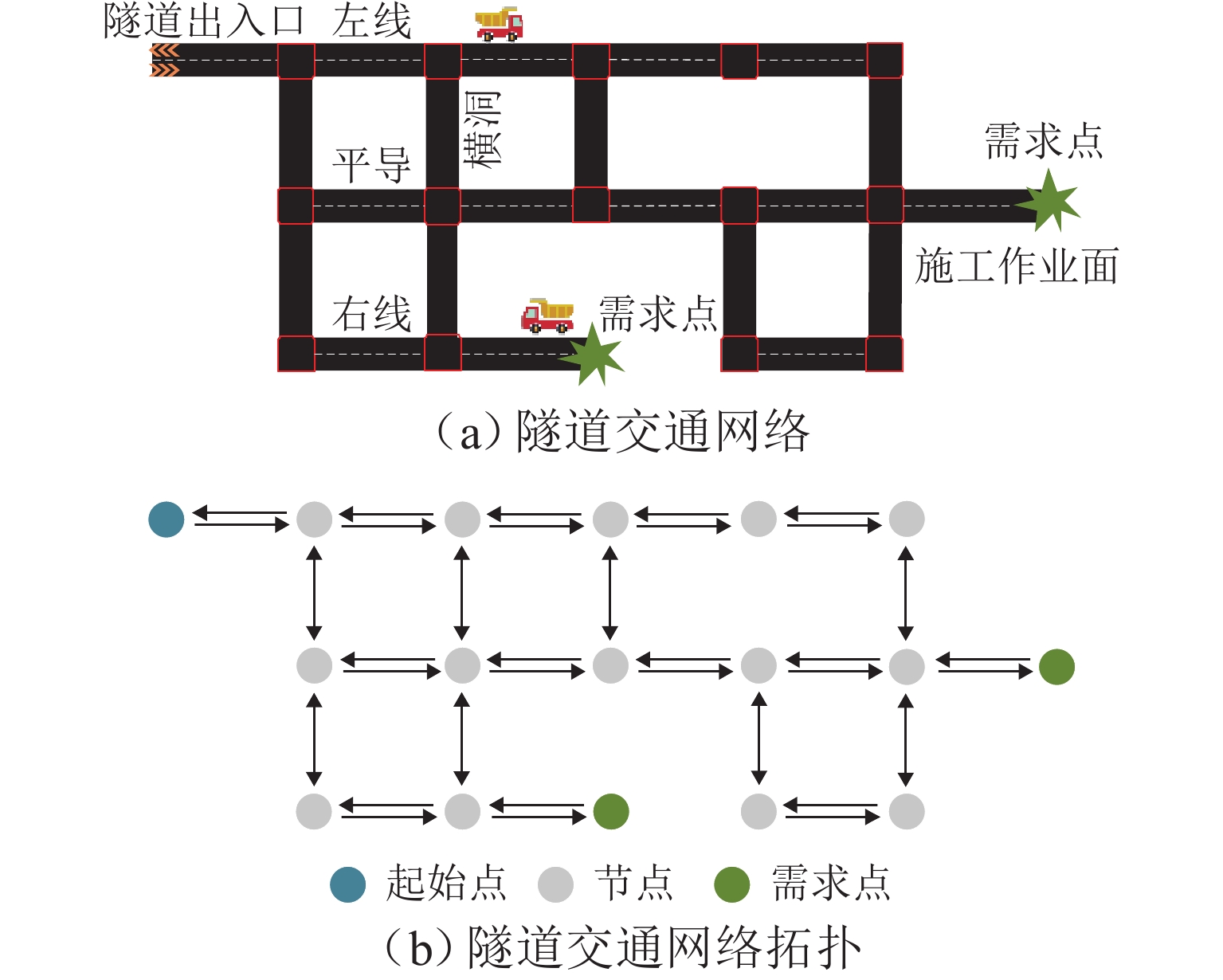
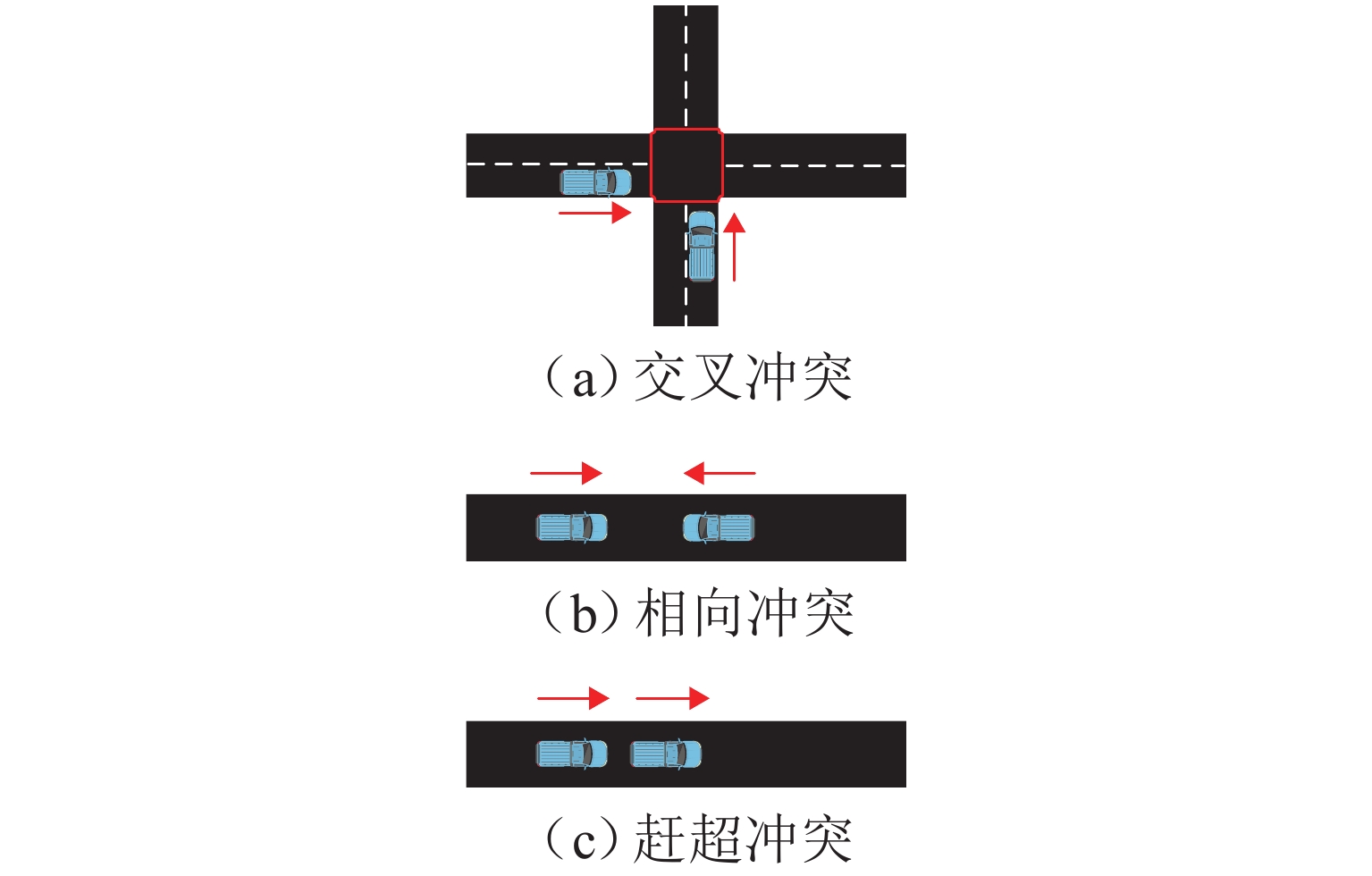
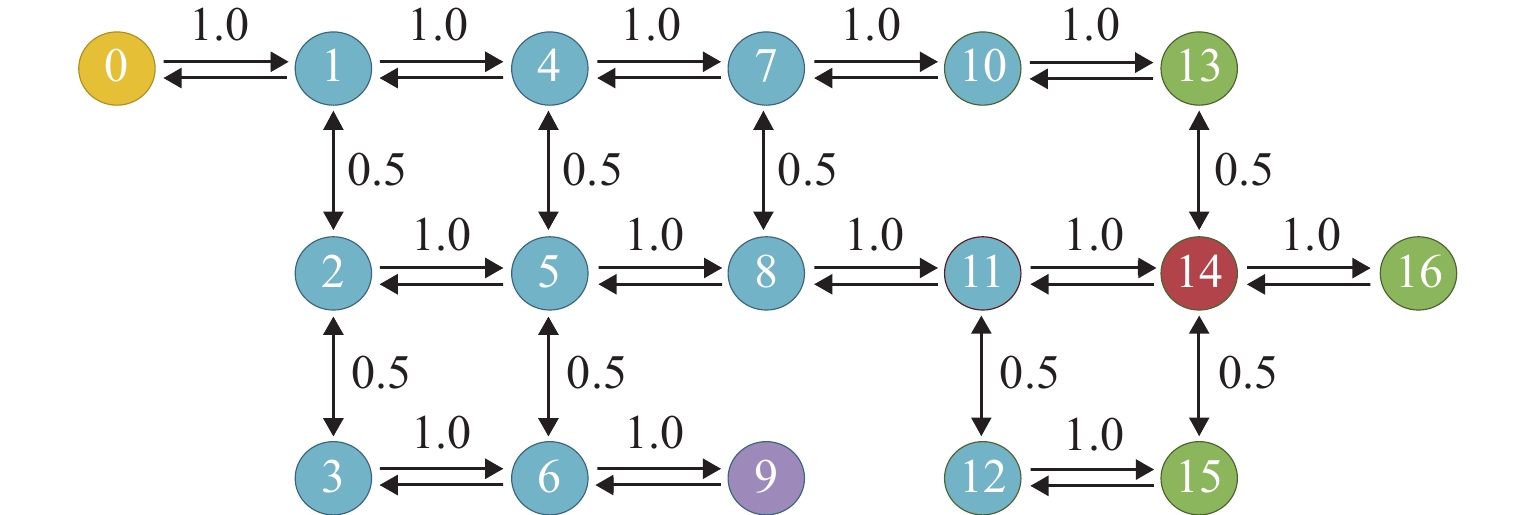
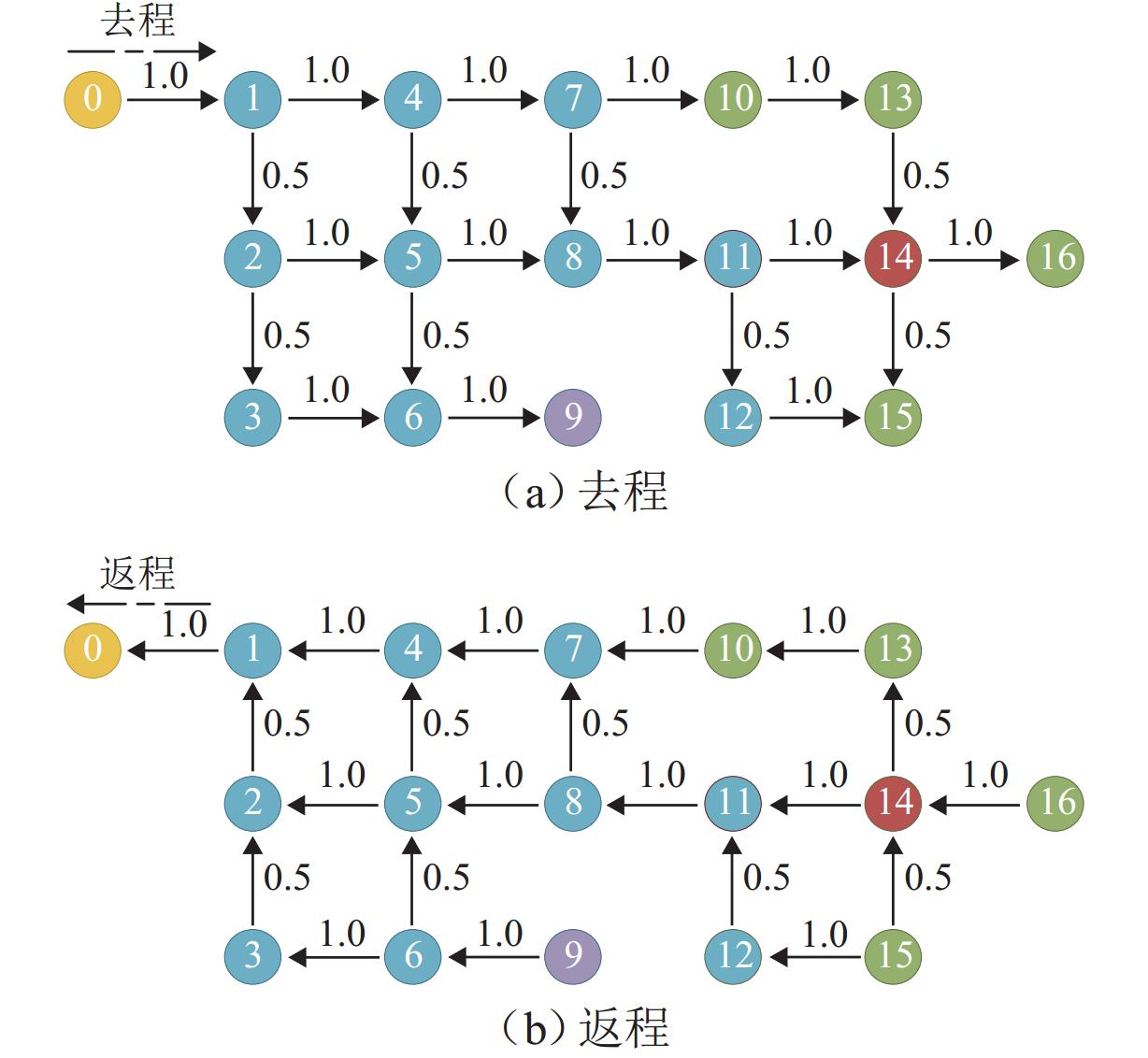
Collaborative Optimization of Vehicle Timetable and Operation Path for Long Tunnel Construction

HU Lu^{1, 2
,},
LI Dongjie^{1, 2},
CHEN Fei^{1, 2},
JIANG Yangsheng^{1, 2
, ,}

1.
School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China
2.
National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
针对隧道内部运输组织管理停留在宏观组织策略层面，缺乏对施工车辆时刻表和运行路径做出精细化决策的问题，针对长大隧道内部交通网络，绘制隧道内部交通网络拓扑图，构建考虑交通冲突的长大隧道内部多工种施工车辆时刻表和运行路径优化模型，在疏解隧道内部车流间交通冲突的前提下最小化施工车辆的总运行（行驶）时间，以提高生产效率；在此基础上，将优化模型进行线性化处理，重构为整数线形规划模型，通过GUROBI求解器进行求解. 研究结果表明：隧道运输组织方案在优化前后，车辆的总运行（行驶）时间保持512 min不变，而交叉冲突从19个减至0个，相向冲突从2个减至0个，即优化方案在不增加施工车辆总运行时间的前提下，完全避免了交通冲突，保证施工车辆的运输安全，具备可实操性.
- 长大隧道 /
- 隧道交叉口 /
- 施工运输组织 /
- 交通冲突 /
- 时刻表 /
- 行车路径
Abstract:
At present, the transportation organization and management within the tunnel still remain at the macro level, lacking refined decision-making on construction vehicle timetables and operation paths. To address the above issues, this article draws the internal traffic network topology map of the long tunnels, and proposes a collaborative optimization model for the timetable and operation path of multiple types of construction vehicles in long tunnels, which minimizes the total operating time of construction vehicles while alleviating traffic conflicts within the tunnel, improves production efficiency, and ensures system safety. And the optimization model is reconstructed into an integer linear programming model to be solved using GUROBI. The case results show that before and after the optimization of the construction transportation organization scheme, the total operating time of vehicles remains unchanged at 512 minutes, while the number of cross conflicts is reduced from 19 to 0, and the number of opposite conflicts is reduced from 2 to 0. This means that the optimization scheme completely avoids traffic conflicts without increasing the total running time of construction vehicles.
- long tunnel /
- tunnel junctions /
- construction transportation organization /
- traffic conflict /
- timetable /
- vehicle routing

HTML全文

图 1 隧道内部基本交通单元拓扑

Figure 1. Topological diagram of basic traffic units inside the tunnel

下载: 全尺寸图片幻灯片

图 2 隧道内部交通网络拓扑

Figure 2. Topological diagram of traffic network inside the tunnel

下载: 全尺寸图片幻灯片

图 3 交通冲突类型

Figure 3. Types of traffic conflicts

下载: 全尺寸图片幻灯片

图 4 隧道网络拓扑图

Figure 4. Tunnel network topology diagram

下载: 全尺寸图片幻灯片

图 5 去返程方向的隧道网络拓扑图

Figure 5. Tunnel network topology diagram in inbound and outbound directions

下载: 全尺寸图片幻灯片

图 6 隧道运输组织初始方案时空轨迹图

Figure 6. Space-time trajectory map of initial scheme of tunnel transportation organization

下载: 全尺寸图片幻灯片

图 7 隧道运输组织优化方案时空轨迹图

Figure 7. Space-time trajectory map of optimization scheme of tunnel transportation organization

下载: 全尺寸图片幻灯片

表 1 施工运输组织初始方案

Table 1. Initial construction organization scheme

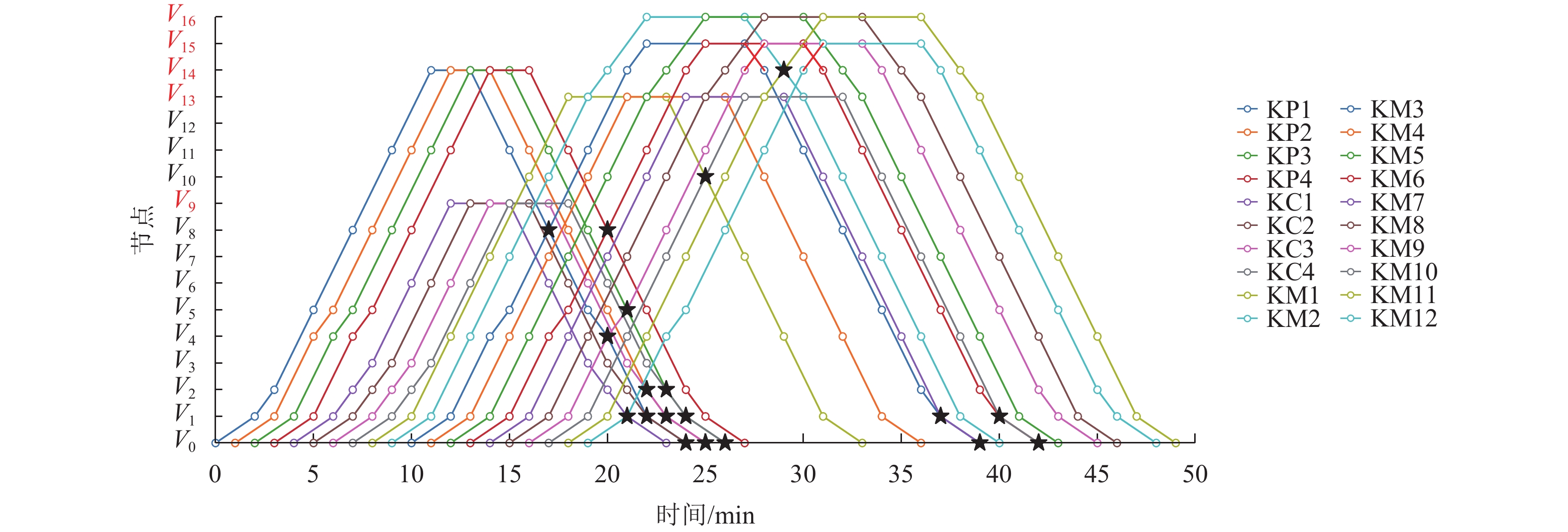
编号	车辆进入隧道运行方案		车辆离开隧道运行方案
编号	始发时刻	运行路径	始发时刻	运行路径
KP1	0	0-1-2-5-8-11-14	13	14-11-8-5-4-1-0
KP2	1	0-1-4-5-8-11-14	14	14-11-8-5-2-1-0
KP3	2	0-1-4-5-8-11-14	15	14-11-8-5-2-1-0
KP4	3	0-1-4-5-8-11-14	16	14-11-8-5-2-1-0
KC1	4	0-1-2-3-6-9	15	9-6-3-2-1-0
KC2	5	0-1-2-3-6-9	16	9-6-3-2-1-0
KC3	6	0-1-2-3-6-9	17	9-6-3-2-1-0
KC4	7	0-1-2-3-6-9	18	9-6-3-2-1-0
KM1	8	0-1-4-7-10-13	23	13-10-7-4-1-0
KM2	9	0-1-4-7-10-13-14-16	27	16-14-13-10-7-4-1-0
KM3	10	0-1-4-5-8-11-14-15	27	15-14-11-8-5-2 1-0
KM4	11	0-1-4-7-10-13	26	13-10-7-4-1-0
KM5	12	0-1-4-7-10-13-14-16	30	16-14-13-10-7-4-1-0
KM6	13	0-1-4-5-8-11-14-15	30	15-14-11-8-5-2-1-0
KM7	14	0-1-4-7-10-13	29	10-7-4-1-0
KM8	15	0-1-4-7-10-13-14-16	33	16-14-13-10-7-4-1-0
KM9	16	0-1-4-5-8-11-14-15	33	15-14-11-8-5-2-1-0
KM10	17	0-1-4-7-10-13	32	13-10-7-4-1-0
KM11	18	0-1-4-7-10-13-14-16	36	16-14-13-10-7-4-1-0
KM12	19	0-1-4-5-8-11-14-15	36	15-14-11-8-5-2-1-0

下载: 导出CSV

表 2 施工运输组织优化方案

Table 2. Optimization construction organization scheme

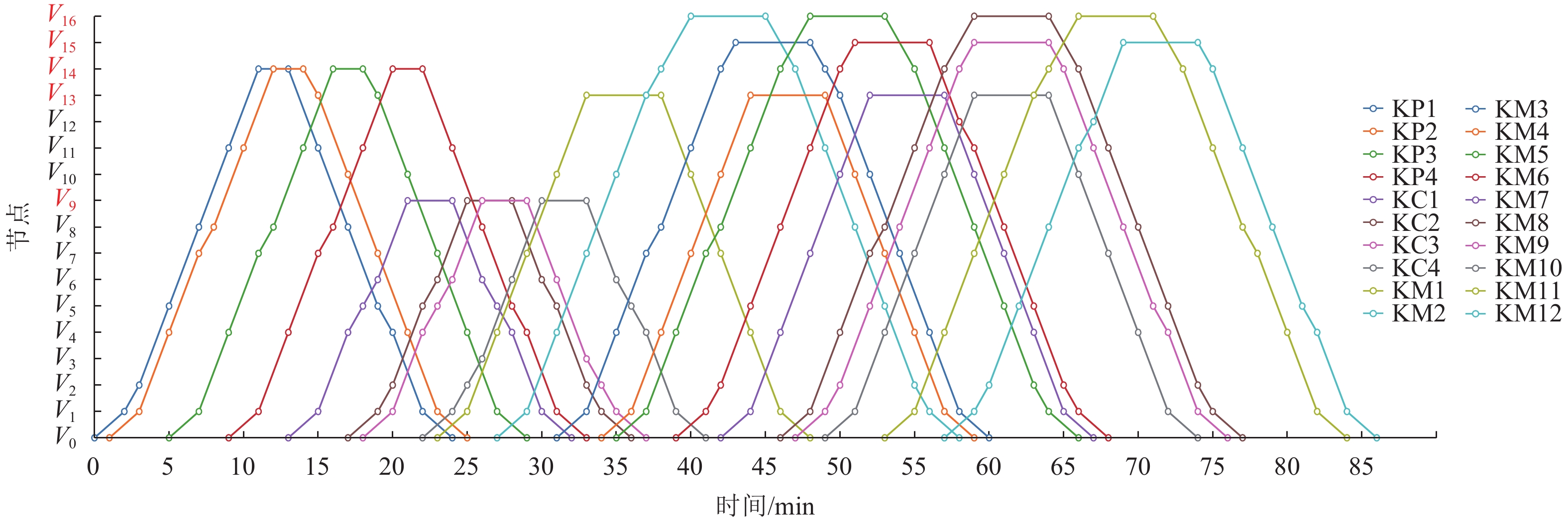
编号	车辆进入隧道运行方案		车辆离开隧道运行方案
编号	始发时刻	运行路径	始发时刻	运行路径
KP1	0	0-1-2-5-8-11-14	13	14-11-8-5-4-1-0
KP2	1	0-1-4-7-8-11-14	14	14-13-10-7-4-1-0
KP3	5	0-1-4-7-8-11-14	18	14-13-10-7-4-1-0
KP4	9	0-1-4-7-8-11-14	22	14-11-8-5-4-1-0
KC1	13	0-1-4-5-6-9	24	9-6-5-4-1-0
KC2	17	0-1-2-5-6-9	28	9-6-5-2-1-0
KC3	18	0-1-4-5-6-9	29	9-6-3-2-1-0
KC4	22	0-1-2-3-6-9	33	9-6-5-4-1-0
KM1	23	0-1-4-7-10-13	38	13-10-7-4-1-0
KM2	27	0-1-4-7-10-13-14-16	45	16-14-11-8-5-2-1-0
KM3	31	0-1-4-7-8-11-14-15	48	15-14-13-10-7-4-1-0
KM4	34	0-1-4-7-10-13	49	13-10-7-4-1-0
KM5	35	0-1-4-7-8-11-14-16	53	16-14-11-8-5-2-1-0
KM6	39	0-1-2-5-8-11-14-15	56	15-12-11-8-5-2-1-0
KM7	42	0-1-4-7-10-13	57	13-10-7-4-1-0
KM8	46	0-1-4-7-8-11-14-16	64	16-14-11-8-5-2-1-0
KM9	47	0-1-2-5-8-11-14-15	64	15-14-11-8-5-4-1-0
KM10	49	0-1-4-7-10-13	64	13-10-7-4-1-0
KM11	53	0-1-4-7-10-13-14-16	71	16-14-11-8-7-4-1-0
KM12	57	0-1-2-5-8-11-12-15	74	15-14-11-8-5-4-1-0

下载: 导出CSV

表 3 初始和优化方案的目标函数值和交通冲突数量

Table 3. Objective function values and number of traffic conflicts for initial and optimization schemes

方案	目标函数值/min	交通冲突数量/个
方案	目标函数值/min	交叉	相向	赶超
初始方案	512	19	2	0
优化方案	512	0	0	0

下载: 导出CSV

参考文献(19)

[1]	秦峰,王少飞,肖博,等. 截至2021年底中国10km以上特长公路隧道统计[J]. 隧道建设(中英文),2022,42(6): 1111-1116 QIN Feng, WANG Shaofei, XIAO Bo, et al. Statistics of super-long highway tunnels over 10 km in China as of the end of 2021[J]. Tunnel Construction, 2022, 42(6): 1111-1116.
[2]	巩江峰,唐国荣,王伟,等. 截至2021年底中国铁路隧道情况统计及高黎贡山隧道设计施工概况[J]. 隧道建设(中英文),2022,42(3): 508-517 GONG Jiangfeng, TANG Guorong, WANG Wei, et al. Statistics of China’s railway tunnels by the end of 2021 and design & construction overview of Gaoligongshan tunnel[J]. Tunnel Construction, 2022, 42(3): 508-517.
[3]	麦继婷,陈春光. 秦岭特长隧道内温度预测[J]. 西南交通大学学报,1998(2): 41-45.
[4]	杜志刚,卓诗琪,傅金乾,等. 城市长大隧道交通安全应急设计优化研究框架[J]. 武汉理工大学学报(交通科学与工程版),2023,47(1): 37-41 DU Zhigang, ZHUO Shiqi, FU Jinqian, et al. Research framework for optimization of traffic safety emergency design of urban long tunnel[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2023, 47(1): 37-41.
[5]	SOUSA R L, EINSTEIN H H. Lessons from accidents during tunnel construction[J]. Tunnelling and Underground Space Technology, 2021, 113: 103916.1-103916.28.
[6]	ZHU Y M, ZHOU J J, ZHANG B, et al. Statistical analysis of major tunnel construction accidents in China from 2010 to 2020[J]. Tunnelling and Underground Space Technology, 2022, 124: 104460.1-104460.14.
[7]	JIANG X H, LI K, CUI X Y. Study on traffic organization around pivotal tunnel entrance/exit[J]. IOP Conference Series: Materials Science and Engineering, 2020, 741(1): 012048.1-012048.6.
[8]	LIU M K, XU Z P. Research on urban path selection of construction vehicles based on bi-objective optimization[J]. PLoS One, 2022, 17(10): 0275678.1-0275678.16.
[9]	林杉,许宏科,刘占文. 一种高速公路隧道交通流元胞自动机模型[J]. 长安大学学报(自然科学版),2012,32(6): 73-77 LIN Shan, XU Hongke, LIU Zhanwen. One cellular automaton traffic flow model for expressway tunnel[J]. Journal of Chang’an University (Natural Science Edition), 2012, 32(6): 73-77.
[10]	高壮. 重载铁路无砟轨道施工技术及物流组织研究[J]. 价值工程,2019,38(2): 105-107 GAO Zhuang. Research on construction technology and logistics organization of ballastless track for long and heavy haul railway[J]. Value Engineering, 2019, 38(2): 105-107.
[11]	ZHANG Y X, PENG Q Y, YAO Y, et al. Solving cyclic train timetabling problem through model reformulation: extended time-space network construct and alternating direction method of multipliers methods[J]. Transportation Research Part B: Methodological, 2019, 128: 344-379. doi: 10.1016/j.trb.2019.08.001
[12]	王志建,刘士杰,周锦瑶,等. 考虑个性化出行需求的多模式公交路径规划[J]. 西南交通大学学报,2022,57(6): 1319-1325,1333. WANG Zhijian,LIU Shijie,ZHOU Jinyao,et al. Multimodal public transportation route planning considering personalized travel demand[J]. Journal of Southwest Jiaotong University,2022,57(6): 1319-1325,13333.
[13]	CHERIF G, TROUILLET B, TOGUYENI A K A. Modeling and routing problems of automated port using T-TPN and Beam search[C]//2022 8th International Conference on Control, Decision and Information Technologies (CoDIT). Turkey. IEEE, 2022: 1201–1206.
[14]	徐翔斌,李紫阳. 基于离散时空网络的多自动引导车路径规划问题[J]. 科学技术与工程,2021,21(33): 14209-14219 doi: 10.3969/j.issn.1671-1815.2021.33.025 XU Xiangbin, LI Ziyang. Path planning problem of multiple automatic guided vehicle based on discrete space-time network[J]. Science Technology and Engineering, 2021, 21(33): 14209-14219. doi: 10.3969/j.issn.1671-1815.2021.33.025
[15]	ZHANG Z, GUO Q, YUAN P J. Conflict-free route planning of automated guided vehicles based on conflict classification[C]//2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC). Banff IEEE, 2017: 1459–1464.
[16]	李珣,程硕,吴丹丹,等. 车路协同下基于元胞自动机的精细交通流模型[J]. 西南交通大学学报,2023,60(1): 225-232.
[17]	李英帅,马泽超,王雯婧,等. 考虑非机动车影响的直线式单泊位公交停靠站设置优化[J]. 交通信息与安全,2021,39(5): 137-143.
[18]	中铁一局集团有限公司. 铁路隧道工程施工技术指南:TZ 204—2008[S]. 北京:中国铁道出版社,2009.
[19]	鲜国. 成兰铁路跃龙门隧道动态施工组织管理研究[J]. 隧道建设(中英文),2020,40(3): 452-463 XIAN GUO. Dynamic construction organization management of yuelongmen tunnel of chengdu-lanzhou railway[J]. Tunnel Construction, 2020, 40(3): 452-463.