Quantitative Research on Misalignment Magnitude of Rotor-Magnetic Bearing System with Axis Misalignment Under Shock Excitation
-
摘要:
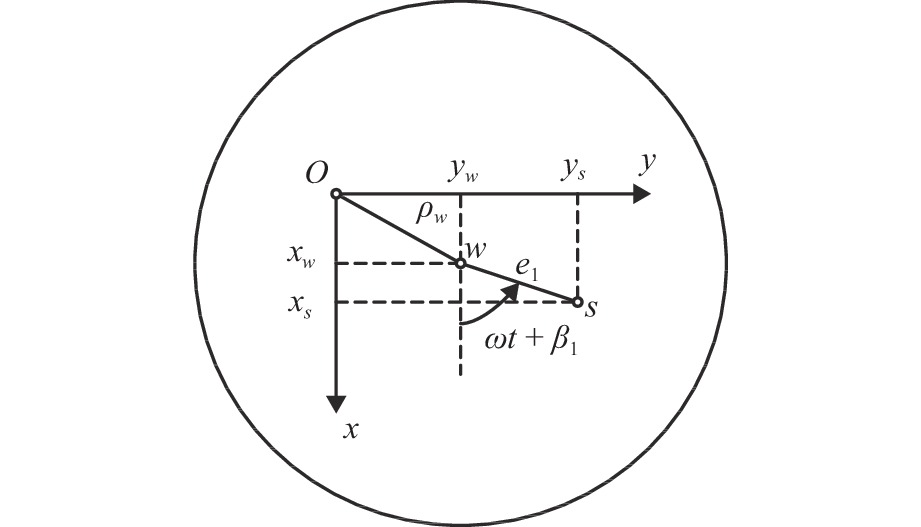
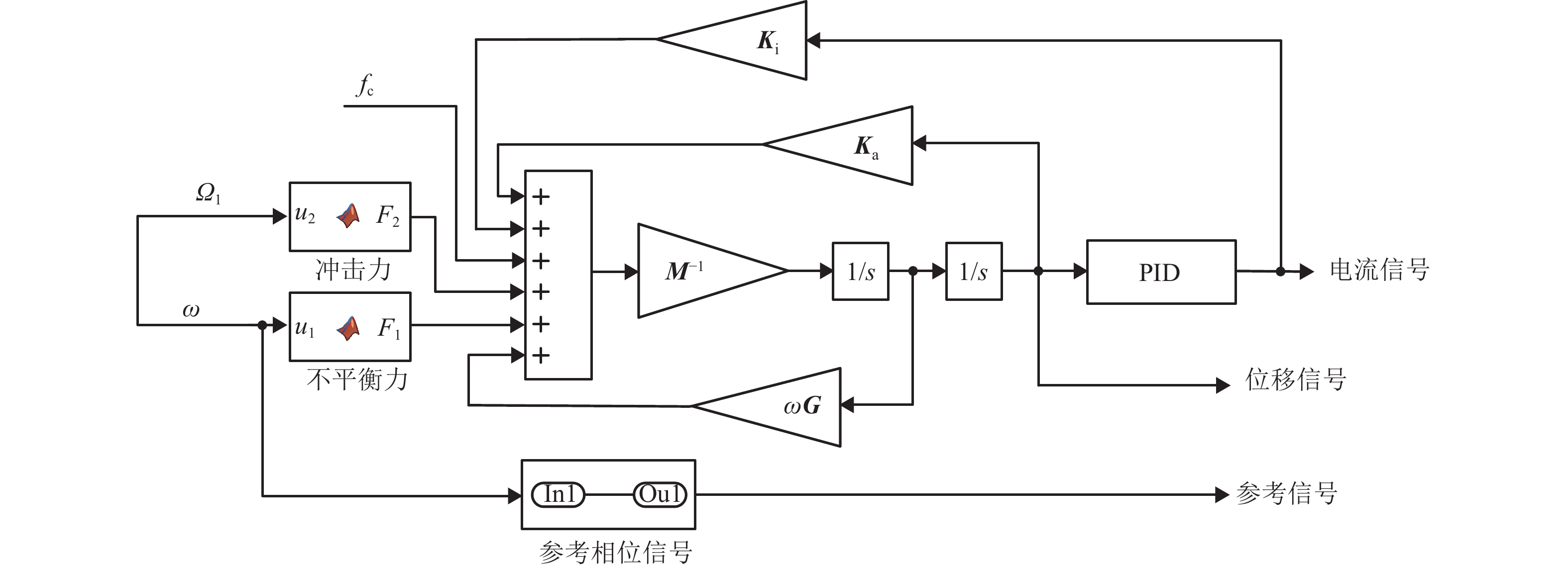
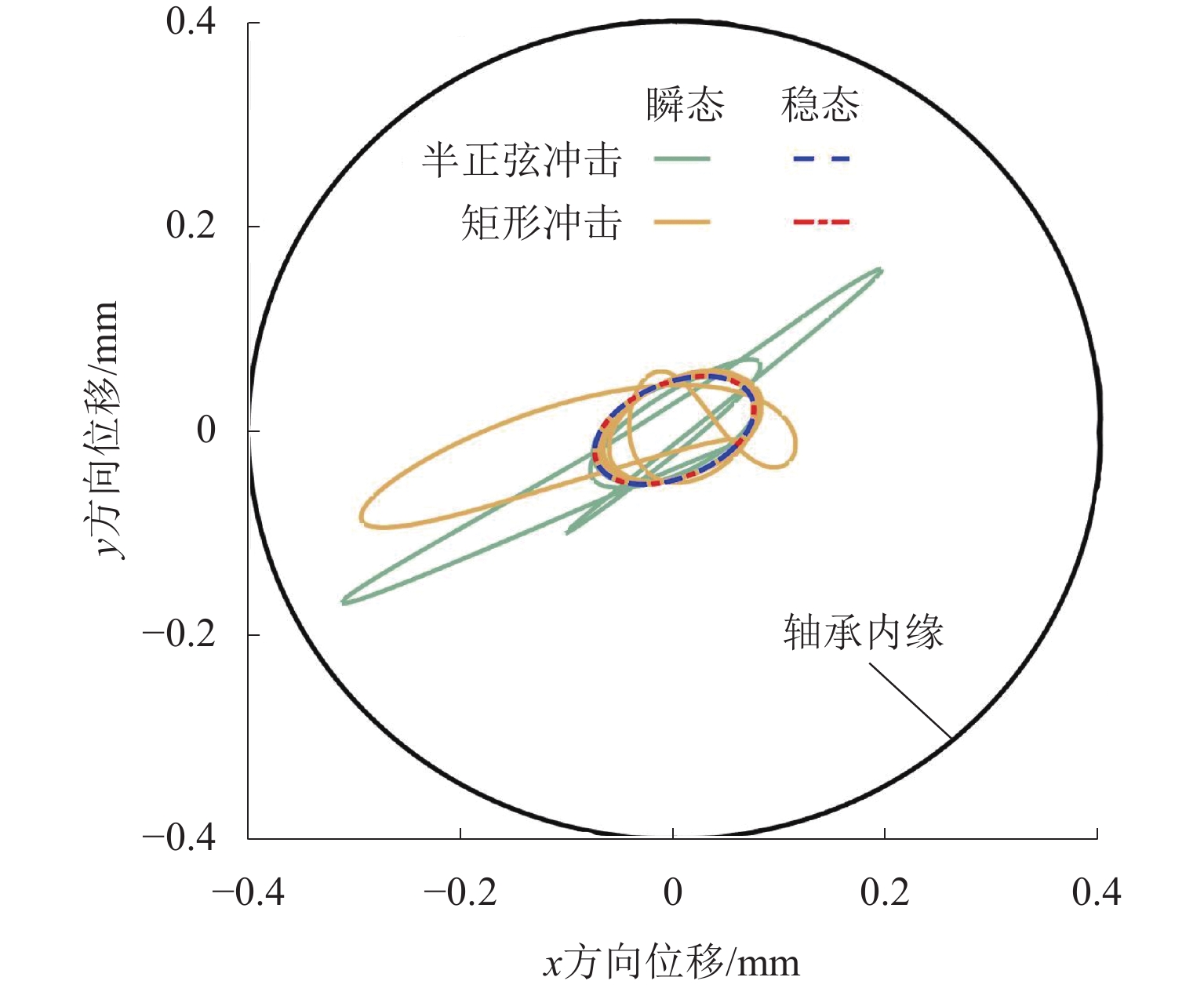
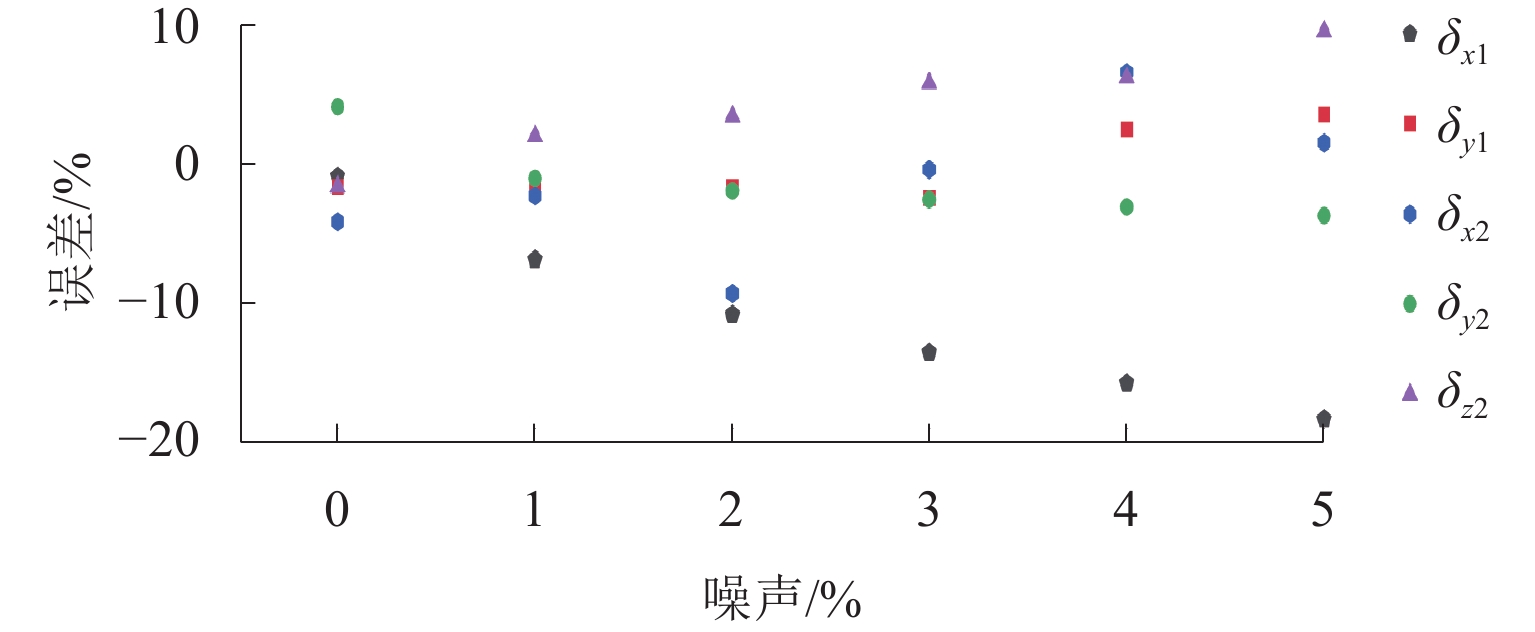
为研究和识别转子系统在轴承处发生的平行角度混合不对中，提出一种频谱辨识转子-磁轴承系统固有不对中量大小的方法. 采用动量矩定理将圆盘不平衡力对转轴的影响等效到转子轴向力上，建立考虑轴向径向耦合效应的刚性双偏置圆盘转子-磁轴承系统的动力学模型；通过SIMULINK仿真得到系统时域下的位移和电流响应，分析不对中条件下转子系统动力学特性，并利用快速傅里叶变换将时域响应转换为频域响应，基于频域下最小二乘算法得到转子系统不对中量大小. 结果表明：在冲击激励影响条件下，采用该方法计算的不对中量大小误差均在5.0%以内，当转子受到外界扰动力时，该算法能够准确定量识别转子的不对中量，可为不对中转子-磁轴承系统故障诊断及自修复提供理论参考.
Abstract:A spectral identification method for calculating the magnitude of inherent misalignment in a rotor-magnetic bearing system was proposed to study and identify mixed parallel misalignment of the rotor system occurring at the bearing. The momentum moment theorem was used to equate the effect of the disc unbalance force on the rotating shaft to the axial force of the rotor and establish a dynamics model of the rigid double offset disc rotor-magnetic bearing system considering the axial and radial coupling effects. The SIMULINK simulation was used to calculate the displacement and current response of the system in the time domain, and the dynamics characteristics of the rotor system under the misalignment condition were analyzed. Furthermore, the fast Fourier transform was utilized to convert the response in the time domain into that in the frequency domain. The magnitude of the misalignment of the rotor system was then calculated based on the least squares algorithm in the frequency domain. The results show that the error in the calculated magnitude of misalignment by using this method is within 5.0% under the influence of shock excitation, indicating that even if the rotor is affected by external disturbance forces, the algorithm can accurately quantify the rotor’s misalignment. This provides a theoretical reference for fault diagnosis and self-repair of misaligned rotor-magnetic bearing systems.
-
图 1 刚性双偏置圆盘转子-磁轴承系统模型
Figure 1. Model of a rigid double offset disc rotor-magnetic bearing system
图 2 圆盘1形心和重心位置关系
Figure 2. Relationship between shape center and gravity center for disc 1
图 5 不同转速下径向磁轴承处位移、电流稳态响应
Figure 5. Steady-state response of displacement and current at radial magnetic bearing at different rotational speeds
图 6 不同转速下混合磁轴承处位移、电流稳态响应
Figure 6. Steady-state response of displacement and current at hybrid magnetic bearing at different rotational speeds
图 7 不同噪声影响下计算的不对中量误差百分比
Figure 7. Percentage of misalignment error calculated under different noise interferences
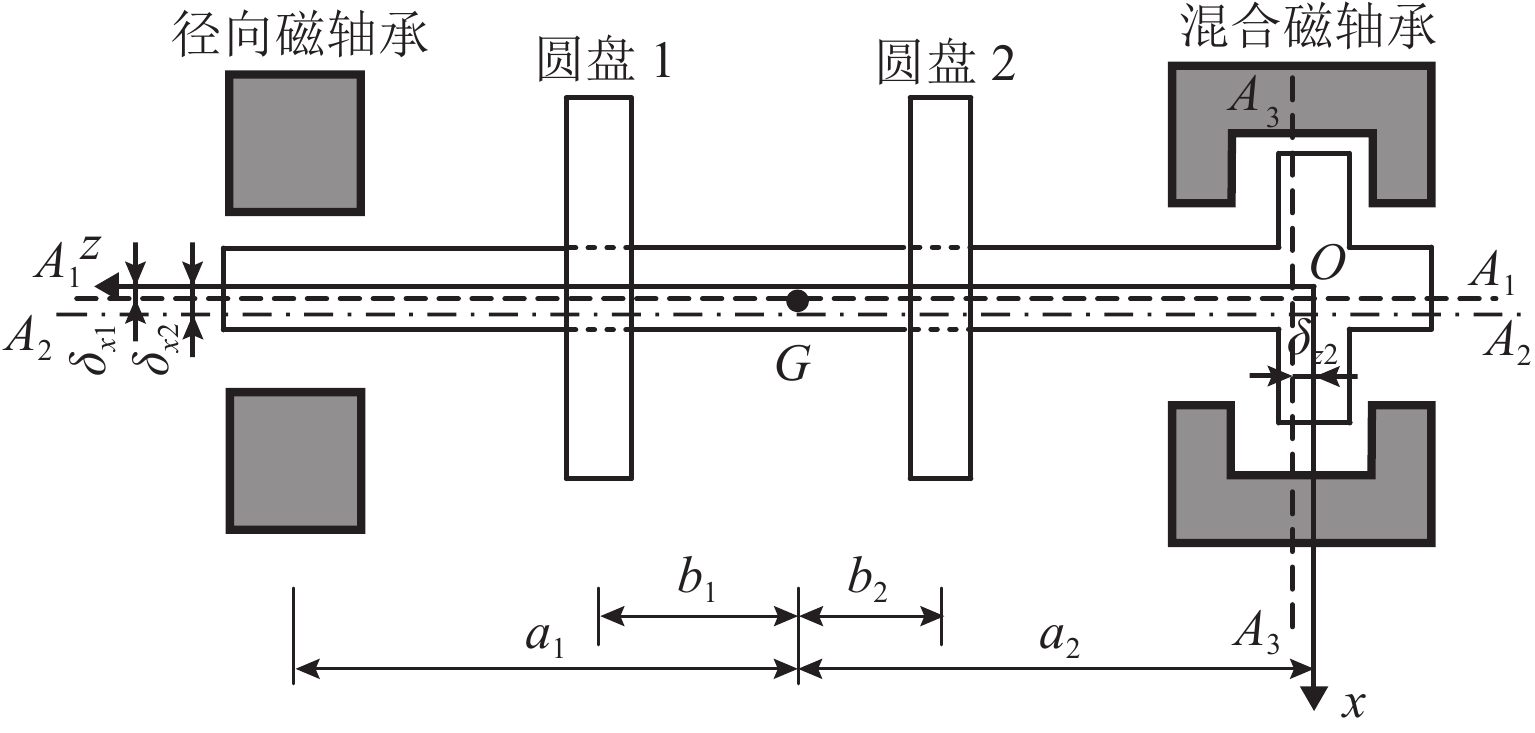
表 1 系统结构参数与仿真参数
Table 1. System structure parameters and simulation parameters
参数 数值 参数 数值 m/kg
l/m3.910
0.400s0/mm 0.400 md1/kg 1.065 δx1，δx2/mm 0.140，0.150 md2/kg 2.081 δy1，δy2/mm 0.160，0.145 e1，e2/μm 80，100 δz2，Δx1/mm 0.130，0.100 $ {e_{{\textit{z}}1}}，{e_{{\textit{z}}2}} $/μm 8，10 Δy1，Δx2/mm 0.130，0.120 β1，β2/（°） 20，30 Δy2，Δz2/mm 0.110，0.150 Id/（kg·m2） 0.0455 KP/（A·m−1） 5500 a1/mm 0.226 KI/（A·（m·s）−1） 8000 a2/mm 0.174 KD/（A·s·m−1） 3 b1/mm 0.126 R
t/ms20
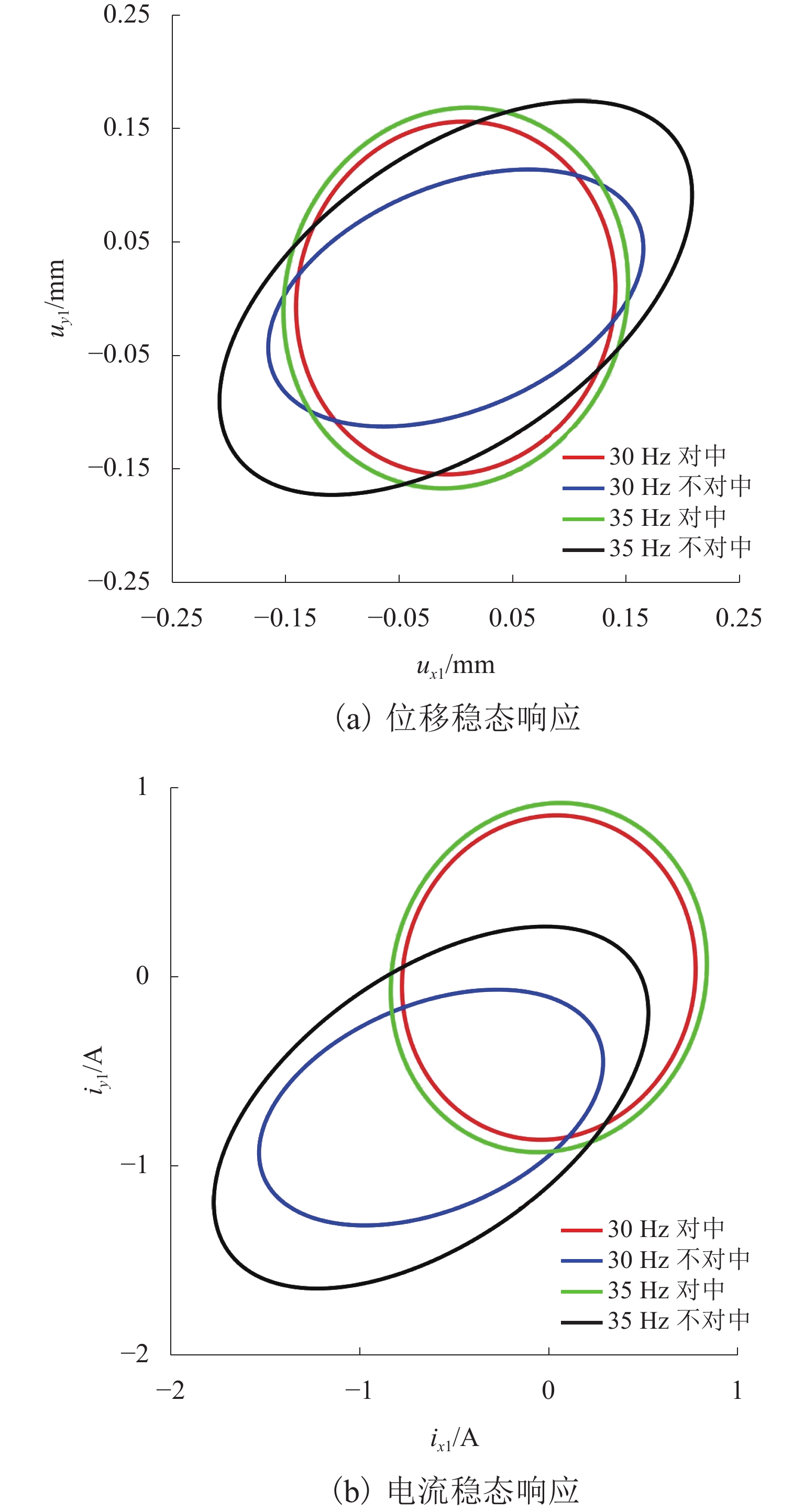
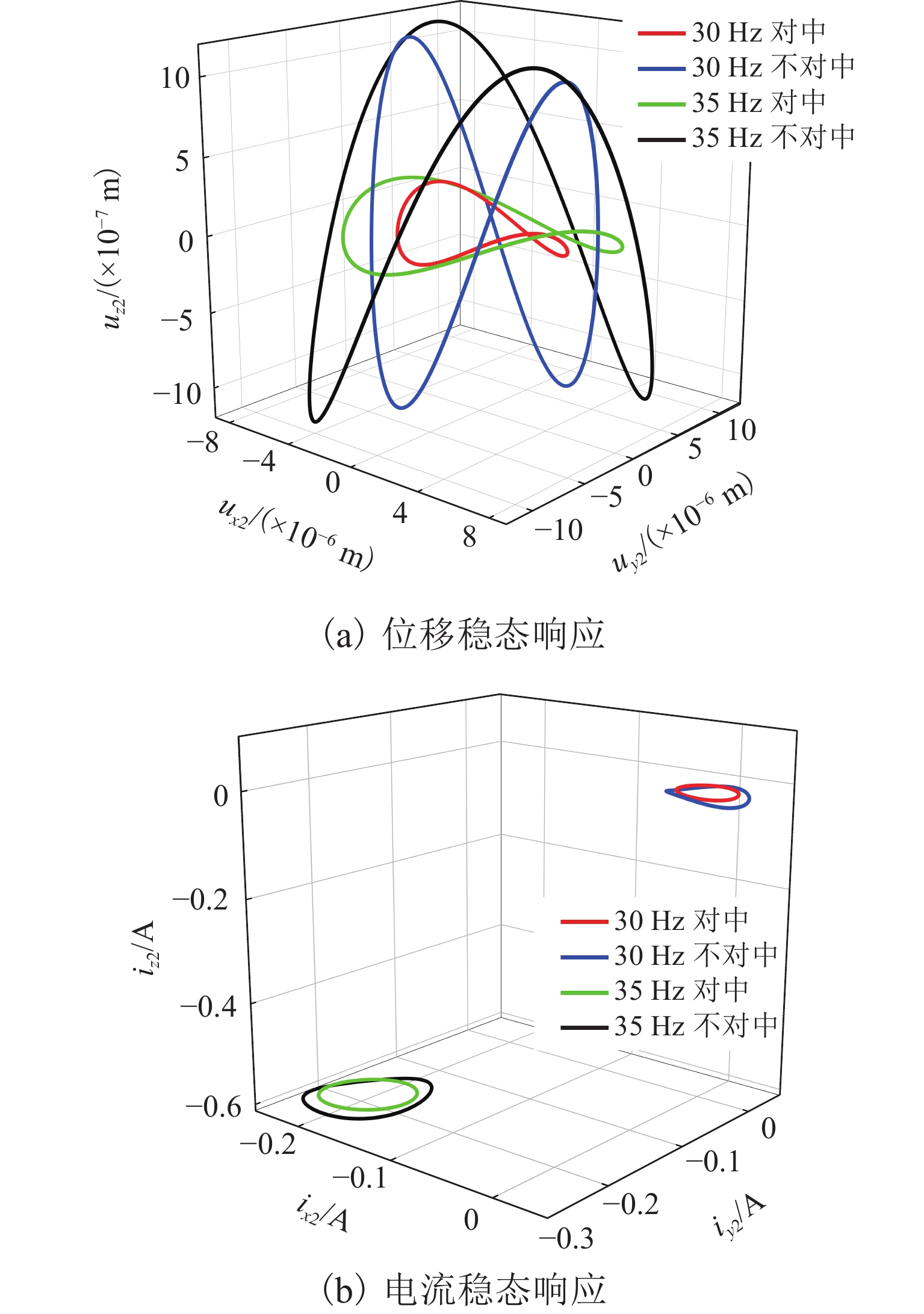
6Ip1/（kg·m2） 0.0019 b2/mm 0.074 Ip2/（kg·m2） 0.0059 
下载: 导出CSV
表 2 频域下的径向磁轴承处转子位移和控制电流响应
Table 2. Rotor displacement and control current response at radial magnetic bearing in frequency domain
频率/
Hzi 位移 电流 幅值/A 相位/（°） 幅值/m 相位/（°） 30 0 3.69 × 10−9 −16.09 0.929 −132.73 1 1.36 × 10−4 −32.43 0.754 152.99 35 0 1.13 × 10−9 112.79 0.930 −133.20 1 1.83 × 10−4 −61.97 1.016 124.49
下载: 导出CSV
表 3 无噪声影响下不对中量实际值和估计值比较
Table 3. Comparison of actual and estimated values of misalignment without noise interference
不对中量 实际值/mm 估计值/mm 误差/% δx1 0.140 0.1388 −0.857 δy1 0.160 0.1575 −1.563 δx2 0.150 0.1439 −4.067 δy2 0.145 0.1456 0.414 δz2 0.130 0.1285 −1.154
下载: 导出CSV
-
[1] 陈宏,雷文平,陈磊,等. 一种转子动态不对中量计算方法[J]. 中国机械工程,2016,27(17): 2379-2383. doi: 10.3969/j.issn.1004-132X.2016.17.018CHEN Hong, LEI Wenping, CHEN Lei, et al. A novel quantitive calculation method of dynamic misalignment in rotor systems[J]. China Mechanical Engineering, 2016, 27(17): 2379-2383. doi: 10.3969/j.issn.1004-132X.2016.17.018 [2] 甄满,田拥胜,孙涛,等. 具有不对中故障的双跨转子系统非线性动力学特性[J]. 机械工程学报,2020,56(16): 109-117. doi: 10.3901/JME.2020.16.109ZHEN Man, TIAN Yongsheng, SUN Tao, et al. Nonlinear dynamics of two-span rotor-bearing system with flexible coupling misalignment[J]. Journal of Mechanical Engineering, 2020, 56(16): 109-117. doi: 10.3901/JME.2020.16.109 [3] SHARI A, ALI A A, ALMUDHAFFER M. Combination of FFT & ICA methods for faults analysis of rotating machine[C]//Proceedings of the Information Conference on Information and Communication Technology. New York:[s.n.],2019:196-202. [4] KUPPA S K, LAL M. Dual flexible rotor system with active magnetic bearings for unbalance and coupling misalignment faults analysis[J]. Sādhanā,2019, 44:188.1-188.16. [5] LEES A W, SINHA J K, FRISWELL M I. Estimating rotor unbalance and misalignment from a single Run-down[J]. Materials Science Forum, 2003, 440/441: 229-236. doi: 10.4028/www.scientific.net/MSF.440-441.229 [6] KUMAR P, TIWARI R. Development of a novel approach for quantitative estimation of rotor unbalance and misalignment in a rotor system levitated by active magnetic bearings[J]. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering, 2021, 45: 769-786. doi: 10.1007/s40997-020-00364-7 [7] KÄRKKÄINEN A, HELFERT M, AESCHLIMANN B, et al. Dynamic analysis of rotor system with misaligned retainer bearings[J]. Journal of Tribology-transactions of The Asme, 2008, 130: 319-320. [8] KUMAR P, TIWARI R. A numerical study on the effect of unbalance and misalignment fault parameters in a rigid rotor levitated by active magnetic bearings. [C]//ASME 2019 GasTurbine India Conference. [S.L.]:American Society of Mechanical Engineers,2019:1-7. [9] KUMAR P, TIWARI R. Dynamic analysis and identification of unbalance and misalignment in a rigid rotor with two offset discs levitated by active magnetic bearings: a novel trial misalignment approach[J]. Propulsion and Power Research, 2021, 10(1): 58-82. doi: 10.1016/j.jppr.2020.06.003 [10] TIWARI R, KUMAR P. An innovative virtual trial misalignment approach for identification of unbalance, sensor and active magnetic bearing misalignment along with its stiffness parameters in a magnetically levitated flexible rotor system[J]. Mechanical Systems and Signal Processing, 2022, 167: 108540.1-108540.30. [11] 汤华涛,吴新跃,刘海涛. 转子横向运动对轴向振动的影响分析[J]. 华中科技大学学报(自然科学版),2013,41(10): 74-78.TANG Huatao, WU Xinyue, LIU Haitao. Influence of a rotor′s lateral motion on its axial vibration[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2013, 41(10): 74-78. [12] 朱熀秋,王绍帅. 六极径向–轴向主动磁轴承电磁特性分析及实验研究[J]. 中国电机工程学报,2020,40(5): 1653-1663.ZHU Huangqiu, WANG Shaoshuai. Electromagnetic characteristics analysis and experiment study of six-pole radial-axial active magnetic bearing[J]. Proceedings of the CSEE, 2020, 40(5): 1653-1663. [13] 汪希平,朱礼进,于良,等. 主动磁轴承转子系统动力学特性的研究[J]. 机械工程学报,2001,37(11): 7-12. doi: 10.3321/j.issn:0577-6686.2001.11.002WANG Xiping, ZHU Lijin, YU Liang, et al. Investigation on dynamic performance of active magnetic bearing rotor system[J]. Chinese Journal of Mechanical Engineering, 2001, 37(11): 7-12. doi: 10.3321/j.issn:0577-6686.2001.11.002 [14] DARPE A, CHAWLA A, GUPTA K. Analysis of the response of a crachked Jeffcott rotor to axial excitation[J]. Jouranl of Sound and Vibration, 2002, 249(3): 429-445. doi: 10.1006/jsvi.2001.3870 [15] 邹博,徐园平,周瑾. 冲击激励下磁悬浮转子系统的响应特性分析[J]. 机械制造与自动化,2020,49(5): 41-43.ZOU Bo, XU Yuanping, ZHOU Jin. Analysis of response characteristics of magnetic suspension rotor system under shock excitation[J]. Machine Building & Automation, 2020, 49(5): 41-43. [16] 陈伟,吴泽宇,韩佳奇,等. 突加基础冲击激励下转子系统振动特性试验[J]. 航空动力学报,2023,38(4): 878-888.CHEN Wei, WU Zeyu, HAN Jiaqi, et al. Test on vibration characteristics of rotor system under sudden base shock excitation[J]. Journal of Aerospace Power, 2023, 38(4): 878-888. [17] SINGH S, TIWARI R. Model-based fatigue crack identification in rotors integrated with active magnetic bearings[J]. Journal of Vibration and Control, 2017, 23(6): 980-1000. doi: 10.1177/1077546315587146 -
下载:
点击查看大图
计量
- 文章访问数: 171
- HTML全文浏览量: 49
- PDF下载量: 49
- 被引次数: 0