Fatigue Damage of Tied-Arch Bridge Hangers Based on Train-Bridge Coupling
-
摘要:
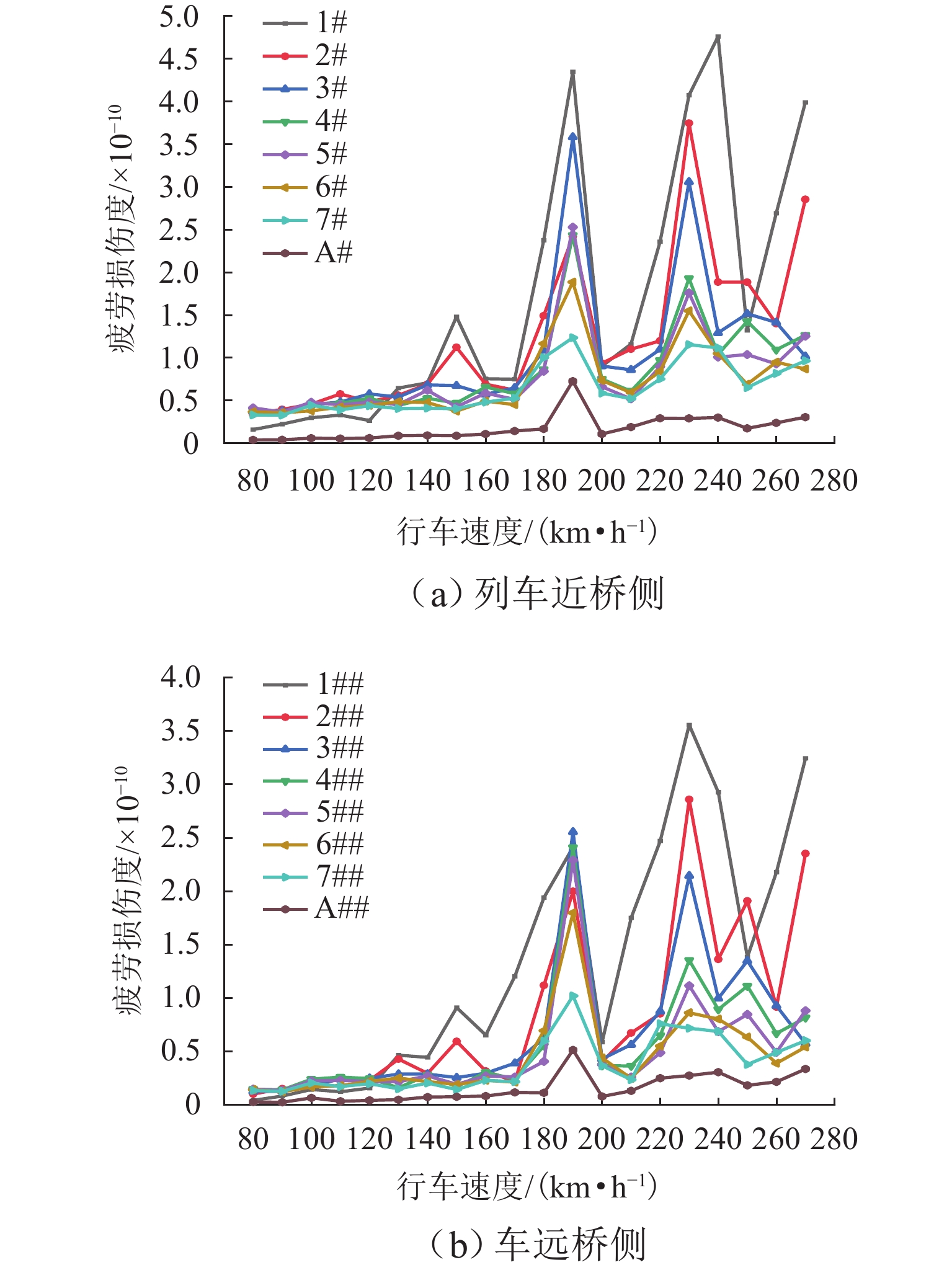
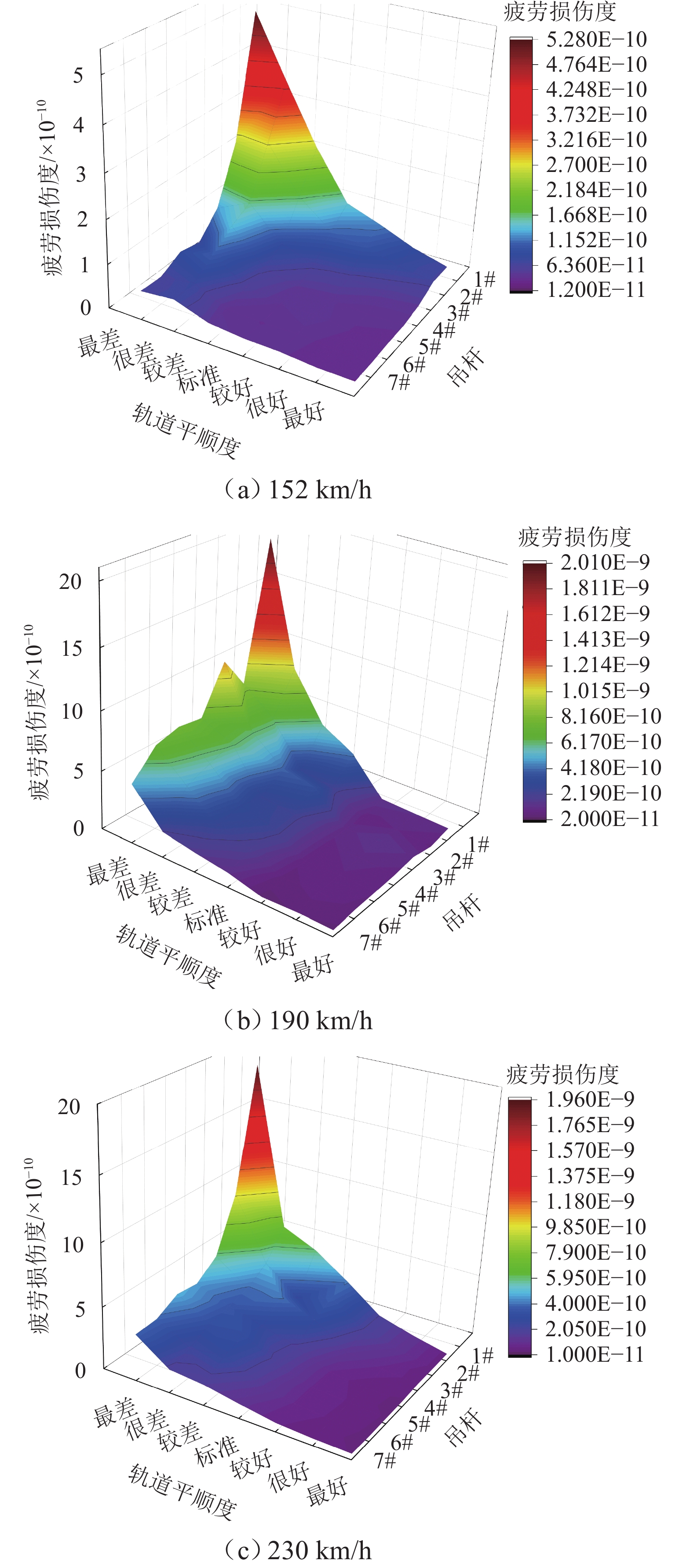
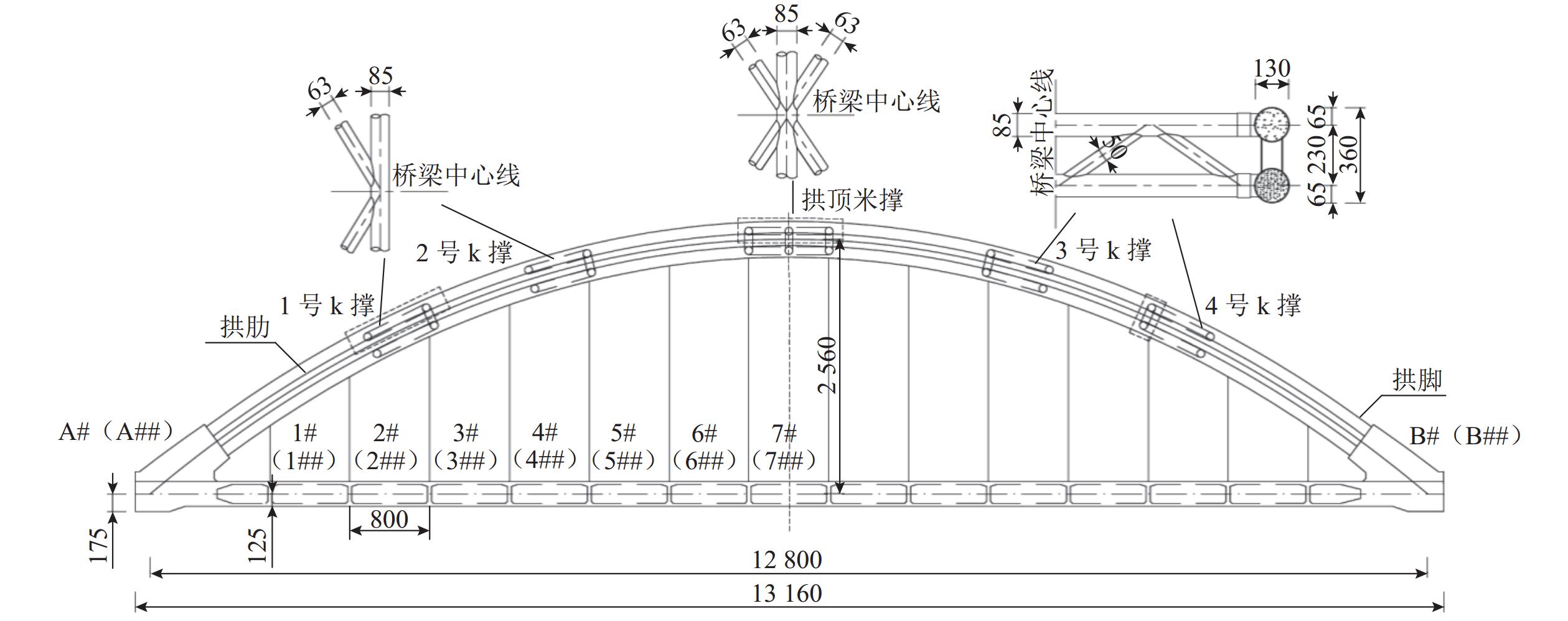
为研究高速列车经过钢管混凝土系杆拱桥时对吊杆造成的疲劳损伤，依托广西钦州钦江大桥为背景开展现场动载试验，对桥梁模态、位移、加速度和动应力进行测试；利用有限元软件ANSYS建立桥梁模型，通过对比实测频率、振型来验证桥梁有限元模型的正确性；将桥梁模型与多体动力学软件SIMPACK建立的CRH2列车模型结合，实现车-桥耦合并进行联合仿真，通过将相同工况下的模拟计算结果与实测结果对比，验证车-桥耦合振动系统的可靠性，并在此基础上依据Palmgren-Miner线性疲劳损伤准则，研究不同行车速度和轨道平顺度对吊杆的疲劳损伤. 结果表明：联合仿真计算效率高，其计算结果可靠；系杆拱桥短吊杆相较于长吊杆，对不同车速、轨道平顺度造成的耦合振动更为敏感，列车以190 km/h过桥时对1# 吊杆的疲劳损伤为7# 吊杆的3.5倍；吊杆疲劳损伤度随着车速的增加呈波浪式递增趋势，且存在接近桥梁固有频率下的临界速度；桥梁轨道平顺度的优化与恶化成倍影响着吊杆的疲劳损伤.
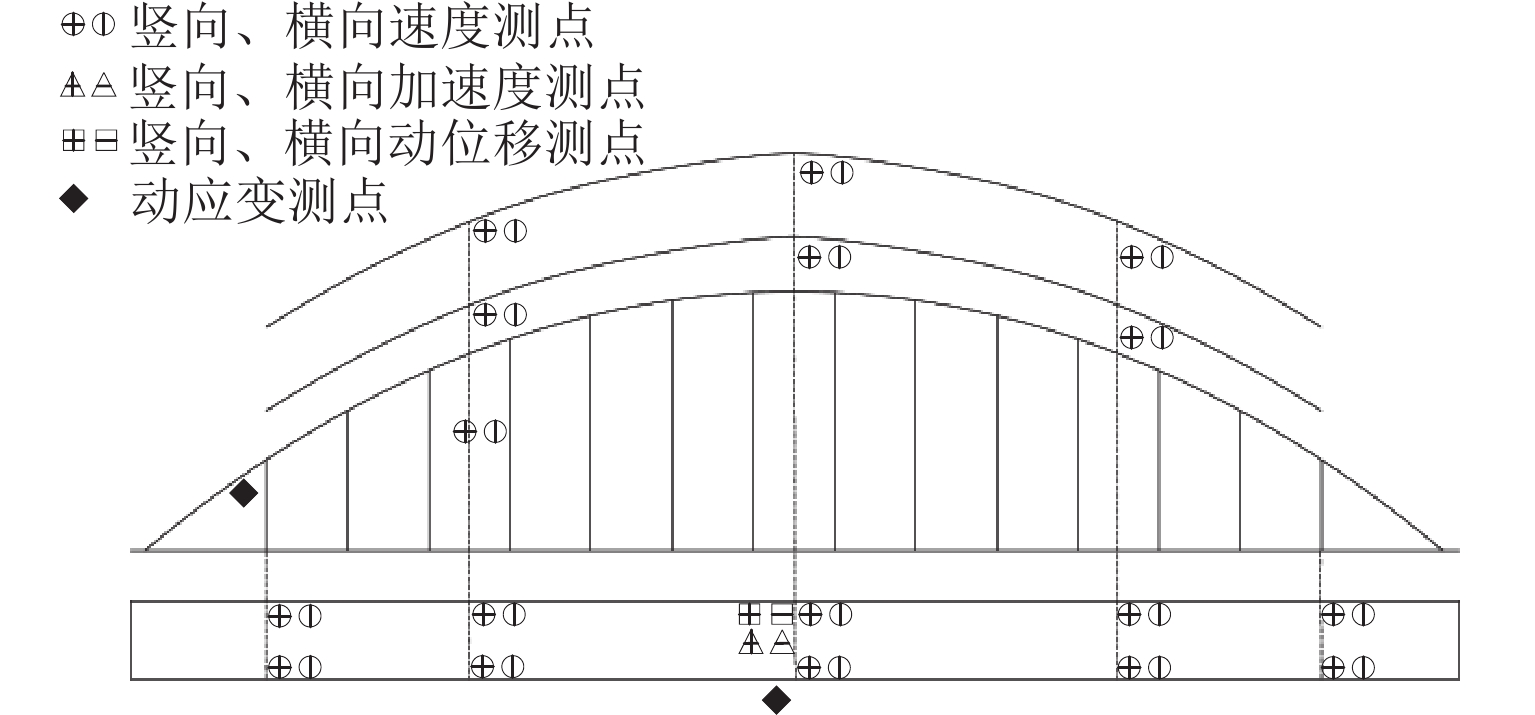
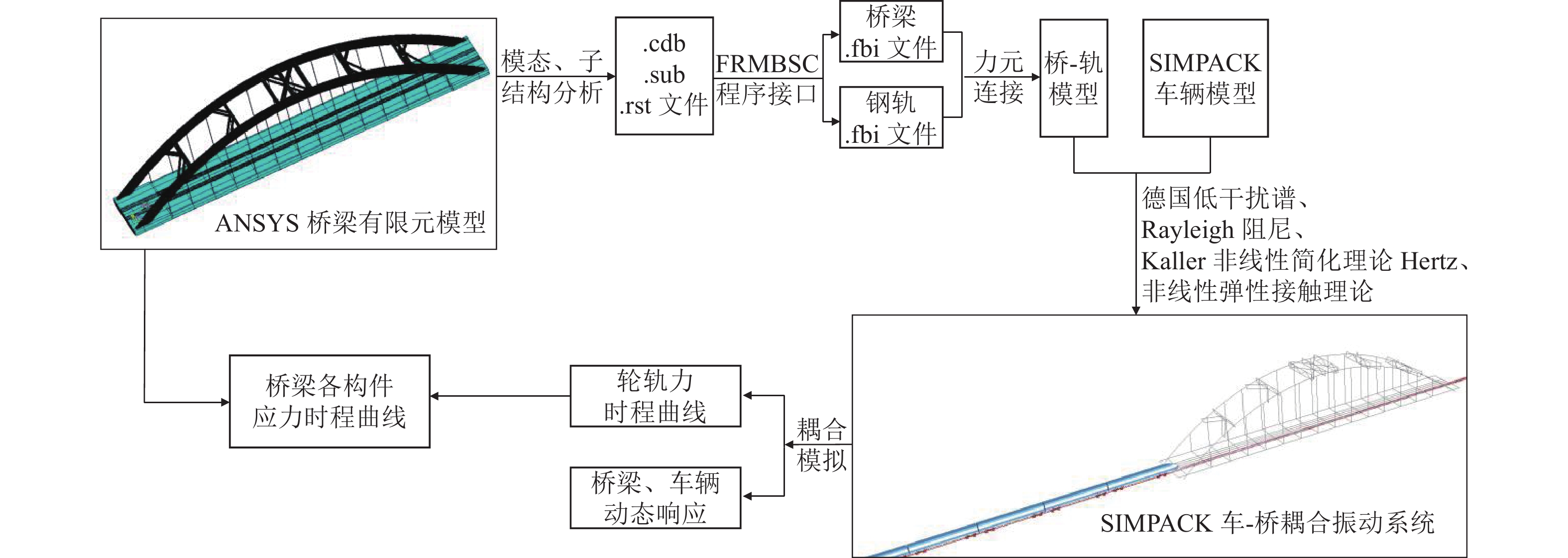
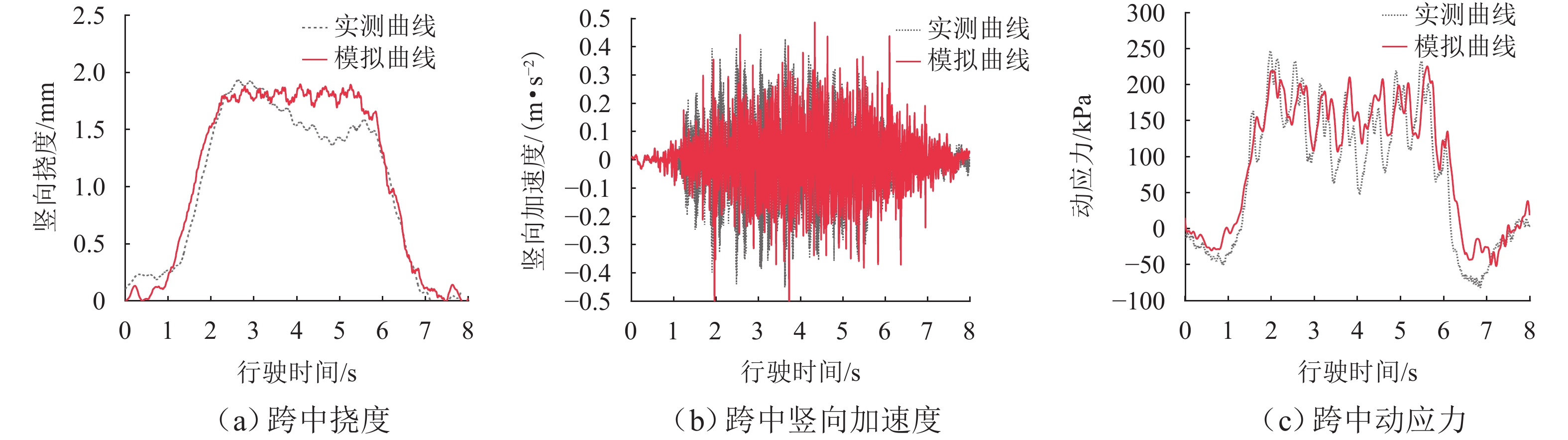
Abstract:To study the fatigue damage inflicted on hangers by high-speed trains passing over a concrete-filled steel-tube tied-arch bridge, field dynamic load tests were conducted against the backdrop of the Qinjiang Bridge in Qinzhou, Guangxi Province. These tests measured the bridge’s modal parameters, displacement, acceleration, and dynamic stress. By using the finite element software ANSYS, a bridge model was established, and its accuracy was verified by comparing measured frequencies and vibration patterns. The bridge model was then integrated with a CRH2 train model developed in the multibody dynamics software SIMPACK to achieve train-bridge coupling and conduct joint simulations. By comparing simulation results under identical conditions with actual measurements, the reliability of the train-bridge coupled vibration system was validated. On this basis, the Palmgren-Miner linear fatigue damage criterion was applied to investigate the impact of different operating speeds and track smoothness on the fatigue damage of the hanger. The results show that the joint simulation is efficient and reliable. Short hangers on the tied-arch bridge are more sensitive to coupled vibrations caused by different speeds and track smoothness than long hangers. For instance, the fatigue damage of the train to hanger 1# at a speed of 190 km/h is 3.5 times that of hanger 7#. With the increase in train speed, the fatigue damage degree of hangers shows a wave-like increasing trend instead of a continuous increase, exhibiting a critical speed near the bridge’s natural frequency. Optimizing or deteriorating the track smoothness of the bridge exponentially affects the fatigue damage of the hanger.
-
Key words:
- fatigue damage /
- tied-arch bridge /
- train-bridge coupling /
- dynamic load test /
- railroad bridge
-
图 5 实测、模拟结果对比（152 km/h）
Figure 5. Comparison of actual measurement and simulation results （152 km/h）
图 6 不同车速对桥梁构件的疲劳损伤度
Figure 6. Fatigue damage degree of bridge members at different vehicle speeds
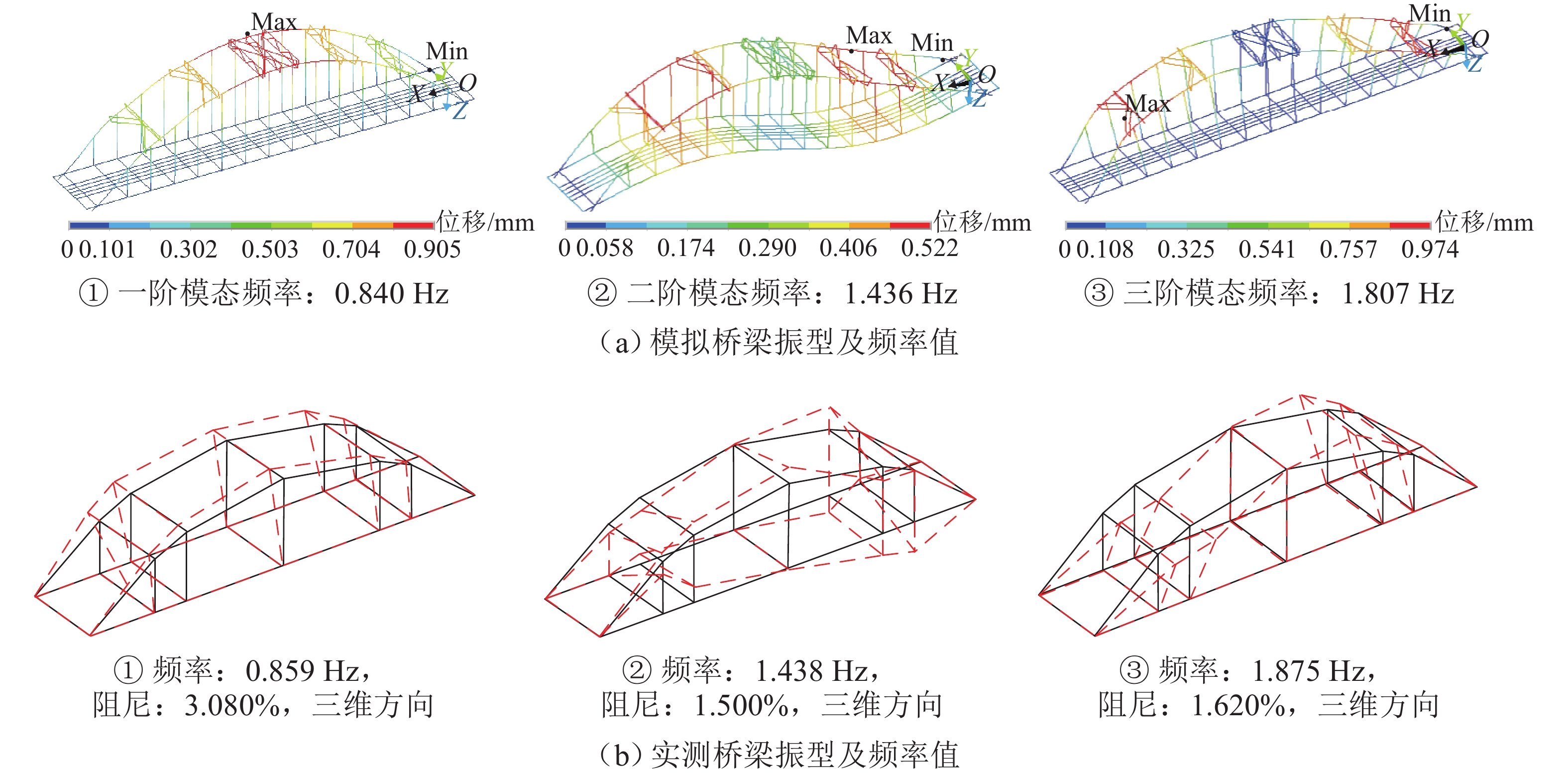
表 1 桥梁频率、振型
Table 1. Bridge frequencies and vibration patterns
阶数 振型主要特征 模拟计算值/Hz 实测值/Hz 1 全桥横向正对称 0.840 0.859 2 全桥竖向反对称 1.436 1.438 3 全桥一阶扭转 1.807 1.875 
下载: 导出CSV
表 2 CRH2列车关键参数
Table 2. Key parameters of CRH2 train
参数 质量/kg 车体转动惯量/（kg•m2） 间距/m 车体 转向架 轮对 侧滚 点头 摇头 转向架 轮对 动车 36 630 2 547 1 784 118 000 1 775 000 1670 00017.5 2.5 拖车 31 600 2 300 1 700 102 000 1 570 000 143 0000 17.5 2.5
下载: 导出CSV
表 3 构件应力幅频次表（近桥侧）
Table 3. Stress amplitude frequency table for members（near the bridge side）
应力幅值/MPa 构件应力幅频数/次 1# 2# 3# 4# 5# 6# 7# A# [0,1） 49 69 102 133 110 101 139 146 [1,2） 36 34 31 17 22 22 9 28 [2,3） 27 25 9 2 4 0 1 0 [3,4） 22 12 3 0 0 0 0 0 [4,6） 17 6 0 0 0 0 0 1 [6,8） 1 1 0 0 0 0 0 0 [8,10） 1 0 0 1 1 1 1 0 [10,12） 0 1 1 0 0 0 0 0
下载: 导出CSV
表 4 构件应力幅频次表（远桥侧）
Table 4. Stress amplitude frequency table for members（Far bridge side）
应力幅值/MPa 构件应力幅频数/次 1## 2## 3## 4## 5## 6## 7## A## [0,1） 59 77 97 117 100 108 134 160 [1,2） 47 36 36 20 28 26 9 16 [2,3） 27 19 10 3 4 2 0 1 [3,4） 15 12 1 0 0 0 0 0 [4,6） 13 6 0 0 0 0 0 1 [6,8） 1 0 1 1 1 1 1 0 [8,10） 0 1 0 0 0 0 0 0
下载: 导出CSV
表 5 不同轨道平顺度下疲劳参数值
Table 5. Fatigue parameter values under different track smoothness
轨道平顺度 等效应力
幅/MPa应力循环
次数/次疲劳损伤度
放缩系数最差 6.3 224 4.6 很差 5.2 208 2.3 较差 4.5 212 1.4 标准 4.2 196 1.0 较好 3.0 202 3.2 很好 2.9 196 3.6 最好 2.8 195 4.0
下载: 导出CSV
-
[1] 赵露薇,王青娥,王贵春. 车流作用下大跨度拱桥车桥耦合振动分析[J]. 铁道科学与工程学报,2022,19(4): 1004-1013.ZHAO Luwei, WANG Qing’e, WANG Guichun. Vehicle-bridge coupling vibration analysis of long-span arch bridge under the action of traffic flow[J]. Journal of Railway Science and Engineering, 2022, 19(4): 1004-1013. [2] 姚敦荣,邓年春. 大跨度钢管混凝土拱桥车桥耦合振动分析[J]. 铁道科学与工程学报,2022,19(12): 3693-3704.YAO Dunrong, DENG Nianchun. Vehicle-bridge coupling vibration analysis of long-span concrete-filled steel tubular arch bridge[J]. Journal of Railway Science and Engineering, 2022, 19(12): 3693-3704. [3] 秦世强,冯嘉诚,唐剑,等. 大跨度铁路连续刚构-CFST拱桥动力特性试验研究[J]. 铁道科学与工程学报,2021,18(12): 3247-3256.QIN Shiqiang, FENG Jiacheng, TANG Jian, et al. Experimental study on dynamic characteristics of long-span railway continuous rigid frame-CFST arch bridge[J]. Journal of Railway Science and Engineering, 2021, 18(12): 3247-3256. [4] LIU J P, CHEN B C, LI C, et al. Recent application of and research on concrete arch bridges in China[J]. Structural Engineering International, 2023, 33(3): 394-398. doi: 10.1080/10168664.2022.2058441 [5] SHAO Y, SUN Z G, CHEN Y F. Analysis of the impact effect of the suspender system in a half-through concrete filled steel tubular arch bridge[J]. Applied Mechanics and Materials, 2013, 477/478: 705-709. doi: 10.4028/www.scientific.net/AMM.477-478.705 [6] BARTON S C, VERMAAS G W, DUBY P F, et al. Accelerated corrosion and embrittlement of high-strength bridge wire[J]. Journal of Materials in Civil Engineering, 2000, 12(1): 33-38. doi: 10.1061/(ASCE)0899-1561(2000)12:1(33) [7] HUANG D Z. Dynamic and impact behavior of half-through arch bridges[J]. Journal of Bridge Engineering, 2005, 10(2): 133-141. doi: 10.1061/(ASCE)1084-0702(2005)10:2(133) [8] 李慧乐,夏禾,张楠,等. 基于车桥耦合动力分析的钢桥疲劳损伤与剩余寿命评估[J]. 铁道学报,2017,39(1): 104-110. doi: 10.3969/j.issn.1001-8360.2017.01.015LI Huile, XIA He, ZHANG Nan, et al. Assessment of fatigue damage and remaining life of steel bridges based on train-bridge coupling dynamic analysis[J]. Journal of the China Railway Society, 2017, 39(1): 104-110. doi: 10.3969/j.issn.1001-8360.2017.01.015 [9] 崔圣爱,张猛,曾光,等. 基于车桥耦合振动的双层六线铁路桥梁疲劳性能评估[J]. 东南大学学报(自然科学版),2023,53(1): 67-75.CUI Sheng’ai, ZHANG Meng, ZENG Guang, et al. Fatigue performance assessment of double-deck six-line railway bridge based on vehicle-bridge coupling vibration[J]. Journal of Southeast University (Natural Science Edition), 2023, 53(1): 67-75. [10] 朱志辉,王力东,龚威,等. 多种垂向轮轨关系的对比及改进的车-线-桥系统迭代模型的建立[J]. 中南大学学报(自然科学版),2017,48(6): 1585-1593. doi: 10.11817/j.issn.1672-7207.2017.06.023ZHU Zhihui, WANG Lidong, GONG Wei, et al. Comparative analysis of several types of vertical wheel/rail relationship and construction of an improved iteration model for train-track-bridge system[J]. Journal of Central South University (Science and Technology), 2017, 48(6): 1585-1593. doi: 10.11817/j.issn.1672-7207.2017.06.023 [11] 朱志辉,赵婷婷,王力东,等. 基于随机振动模型的重载铁路拱桥吊杆应力冲击系数研究[J]. 振动工程学报,2017,30(6): 955-964.ZHU Zhihui, ZHAO Tingting, WANG Lidong, et al. Stress impact factor of the suspenders of heavy-haul railway arch bridge based on random vibration model[J]. Journal of Vibration Engineering, 2017, 30(6): 955-964. [12] MALM R, ANDERSSON A. Field testing and simulation of dynamic properties of a tied arch railwaybridge[J]. Engineering Structures, 2006, 28(1): 143-152. doi: 10.1016/j.engstruct.2005.07.011 [13] YANG S C, HWANG S H. Train-track-bridge interaction by coupling direct stiffness method and mode superposition method[J]. Journal of Bridge Engineering, 2016, 21(10): 04016058.1-04016058.16. [14] GOU H Y, ZHOU W, YANG C W, et al. Dynamic response of a long-span concrete-filled steel tube tied arch bridge and the riding comfort of monorail trains[J]. Applied Sciences, 2018, 8(4): 650.1-650.22. [15] 杨超,李青宁,丰维方,等. 钢—混凝土组合梁的等效截面[J]. 四川建筑科学研究,2012,38(1): 37-39. doi: 10.3969/j.issn.1008-1933.2012.01.009YANG Chao, LI Qingning, FENG Weifang, et al. Static properties comparison of steel-concrete composite beams being equivalent as stiffness[J]. Sichuan Building Science, 2012, 38(1): 37-39. doi: 10.3969/j.issn.1008-1933.2012.01.009 [16] 禹争华,刘虹池. 风—车—人群联合作用下浔江特大桥振动性能与舒适性评价[J]. 铁道科学与工程学报,2023,20(4): 1425-1432.YU Zhenghua, LIU Hongchi. Vibration performance and comfort evaluation of Xunjiang cable-stayed bridges under combined action of wind-vehicle-pedestrian loadings[J]. Journal of Railway Science and Engineering, 2023, 20(4): 1425-1432. [17] 崔圣爱,刘品,曹艺缤,等. 多线铁路车桥耦合振动仿真研究[J]. 西南交通大学学报,2017,52(5): 835-843. doi: 10.3969/j.issn.0258-2724.2017.05.001CUI Sheng’ai, LIU Pin, CAO Yibin, et al. Simulation study on multiline vehicle-bridge coupled vibration[J]. Journal of Southwest Jiaotong University, 2017, 52(5): 835-843. doi: 10.3969/j.issn.0258-2724.2017.05.001 [18] 朱伟,戚铁,贾亮. 基于SIMPACK的钢桁梁斜拉桥车-桥系统动力性能分析[J]. 铁道标准设计,2014,58(7): 89-94.ZHU Wei, QI Tie, JIA Liang. Dynamic performance analysis of vehicle-bridge system for a cable-stayed bridge with steel truss girder based on SIMPACK[J]. Railway Standard Design, 2014, 58(7): 89-94. [19] YAN W, FISCHER F D. Applicability of the Hertz contact theory to rail-wheel contact problems[J]. Archive of Applied Mechanics, 2000, 70(4): 255-268. doi: 10.1007/s004199900035 [20] 陈果,翟婉明,左洪福. 仿真计算比较我国干线谱与国外典型轨道谱[J]. 铁道学报,2001,23(3): 82-87. doi: 10.3321/j.issn:1001-8360.2001.03.018CHEN Guo, ZHAI Wanming, ZUO Hongfu. Comparing track irregularities PSD of Chinese main lines with foreign typical lines by numerical simulation computation[J]. Journal of the China Railway Society, 2001, 23(3): 82-87. doi: 10.3321/j.issn:1001-8360.2001.03.018 [21] 张坤,段晓峰,韩峰,等. 轨道随机不平顺对高速铁路列车运行性能影响分析[J]. 铁道标准设计,2019,63(4): 28-33.ZHANG Kun, DUAN Xiaofeng, HAN Feng, et al. Analysis of the influence of random irregularity on high-speed railway train’s operation performance[J]. Railway Standard Design, 2019, 63(4): 28-33. [22] 马林. 国产1860级低松弛预应力钢绞线疲劳性能研究[J]. 铁道标准设计,2000,20(5): 21-23. doi: 10.3969/j.issn.1004-2954.2000.05.006MA Lin. Study on fatigue performance of domestic 1860-grade low relaxation prestressed steel strand[J]. Railway Standard Design, 2000, 20(5): 21-23. doi: 10.3969/j.issn.1004-2954.2000.05.006 -
下载:
点击查看大图
计量
- 文章访问数: 58
- HTML全文浏览量: 27
- PDF下载量: 12
- 被引次数: 0