双车道公路超车行为风险演化时间协变量建模

戢晓峰; 徐迎豪; 郝京京; 覃文文

doi:10.3969/j.issn.0258-2724.20230449

双车道公路超车行为风险演化时间协变量建模

doi: 10.3969/j.issn.0258-2724.20230449

戢晓峰^{1, 2,},
徐迎豪^{1, 2},
郝京京^{2, 3},
覃文文^{1, 2, ,}

1.
昆明理工大学交通工程学院，云南昆明 650504
2.
云南省现代物流工程研究中心，云南昆明 650604
3.
西南交通大学交通运输与物流学院，四川成都 611756

基金项目: 国家自然科学基金项目（52062024）；云南省交通运输厅科技创新及示范项目（2022-27（二））；云南省基础研究计划面上项目（202401AT070309）

详细信息

作者简介:
戢晓峰（1982—），男，教授，研究方向为交通规划与交通安全，E-mail：yiluxinshi@sina.com

通讯作者:
覃文文（1986—），男，讲师，研究方向为交通安全，E-mail： qinww@kust.edu.cn

中图分类号: U491.31
计量
- 文章访问数: 142
- HTML全文浏览量: 56
- PDF下载量: 46
- 被引次数: 0
出版历程
- 收稿日期: 2023-09-03
- 修回日期: 2024-03-17
- 网络出版日期: 2025-07-11
- 刊出日期: 2024-03-26

Time Covariate Modeling of Overtaking Risk Evolution on Two-Lane Highways

JI Xiaofeng^{1, 2
,},
XU Yinghao^{1, 2},
HAO Jingjing^{2, 3},
QIN Wenwen^{1, 2
, ,}

1.
Faculty of Transportation Engineering, Kunming University of Science and Technology, Kunming 650504, China
2.
Yunnan Modern Logistics Engineering Research Center, Kunming 650604, China
3.
School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China

摘要

摘要:
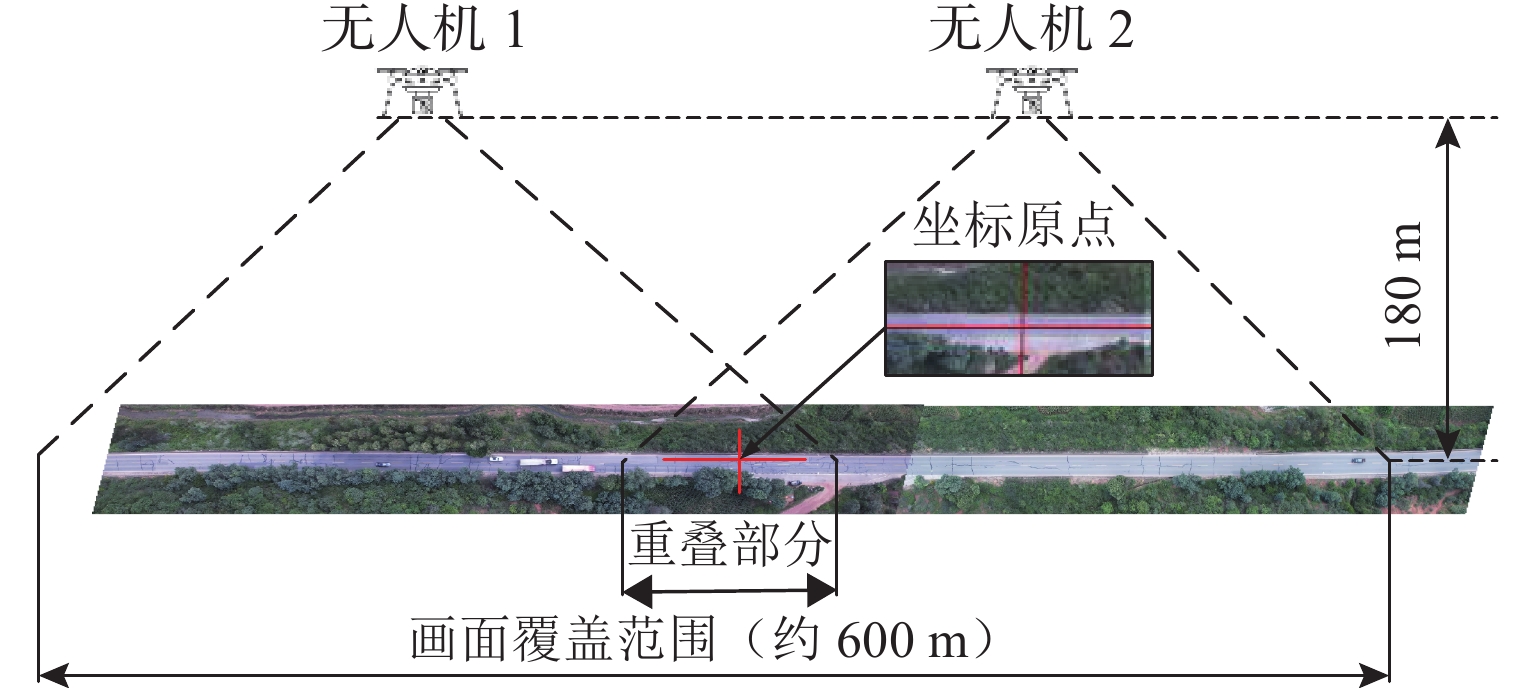
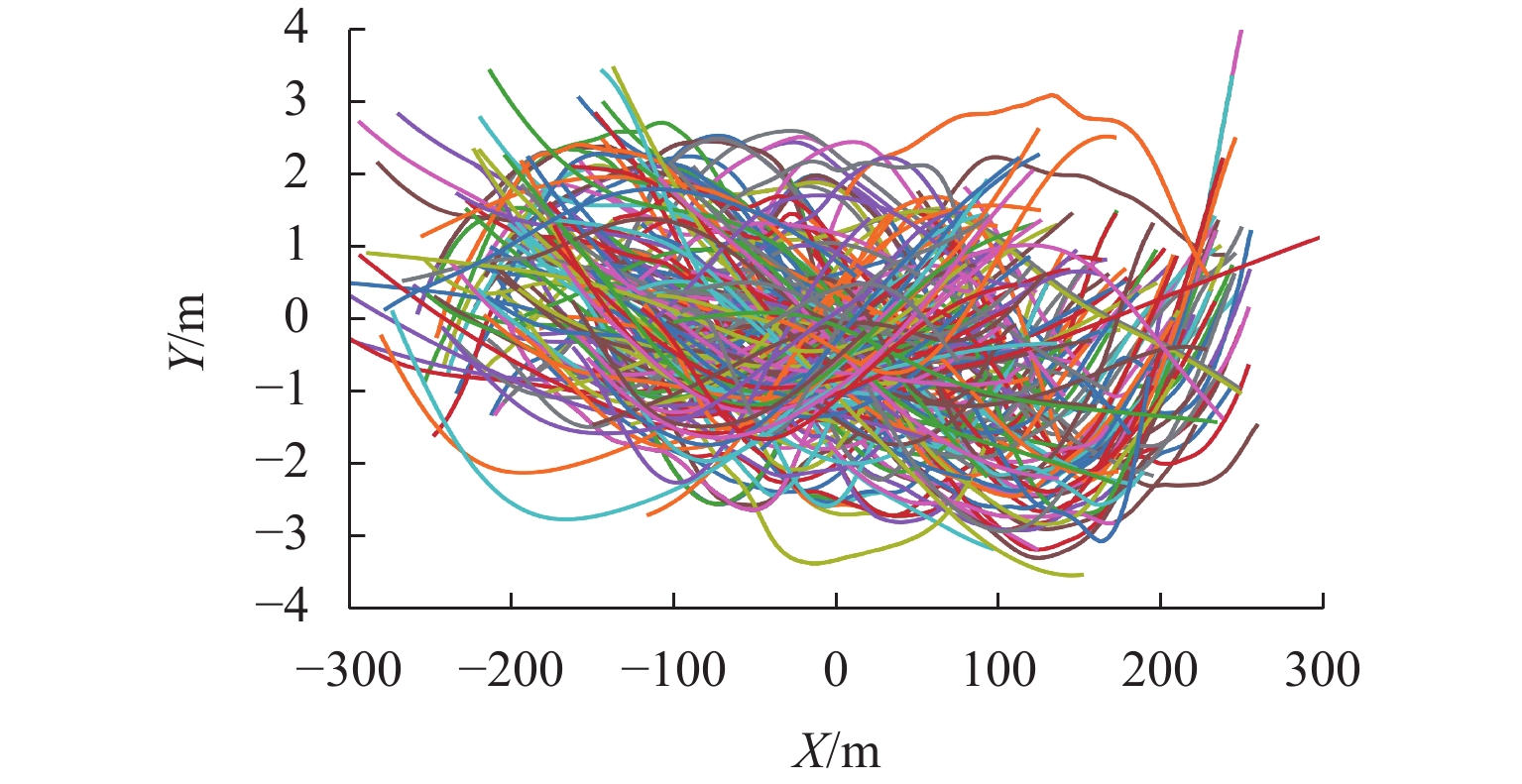
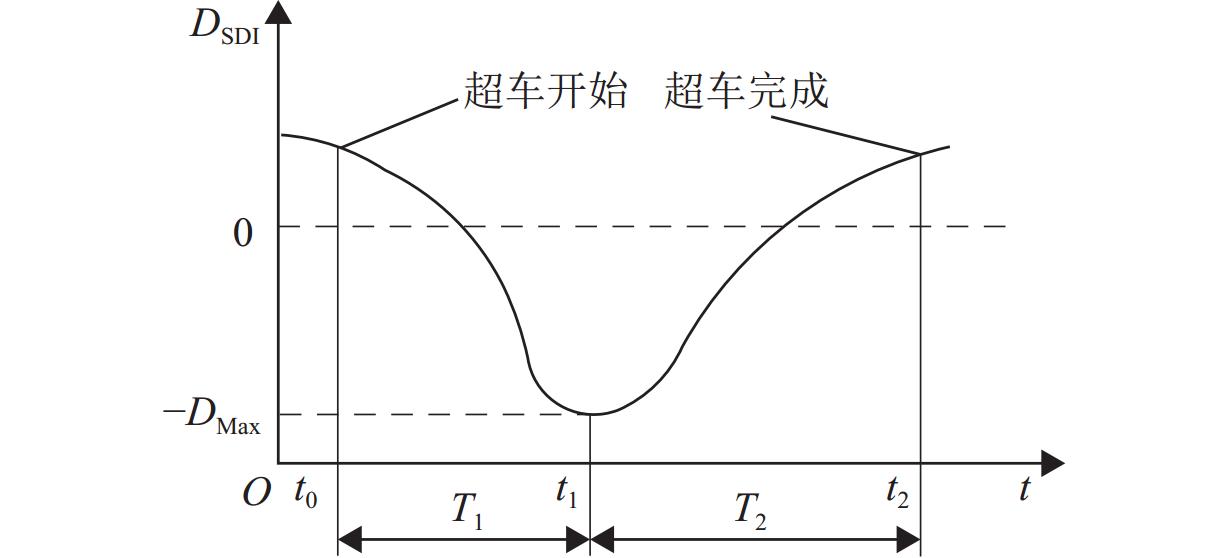
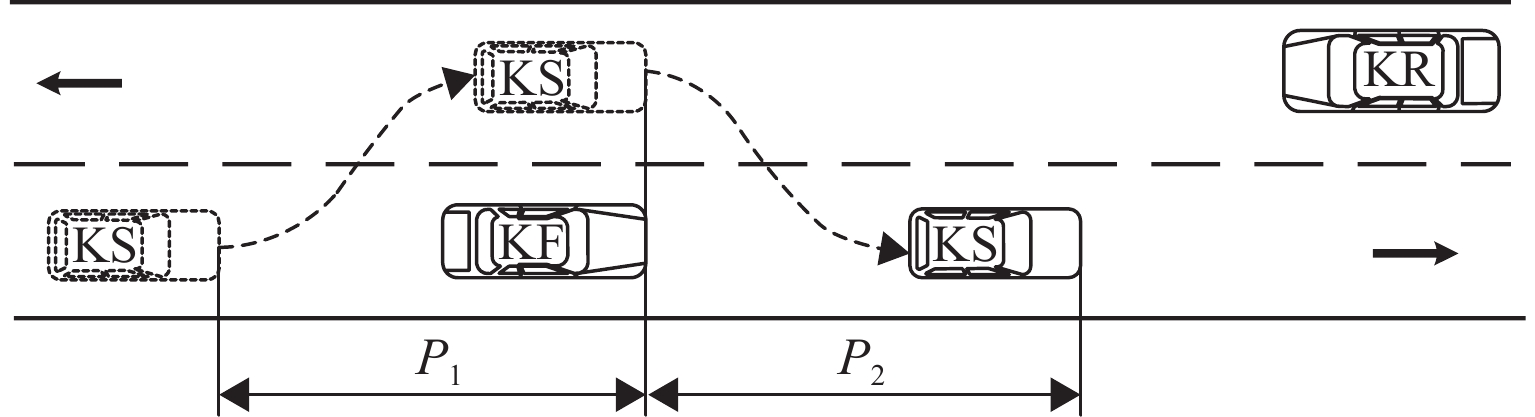
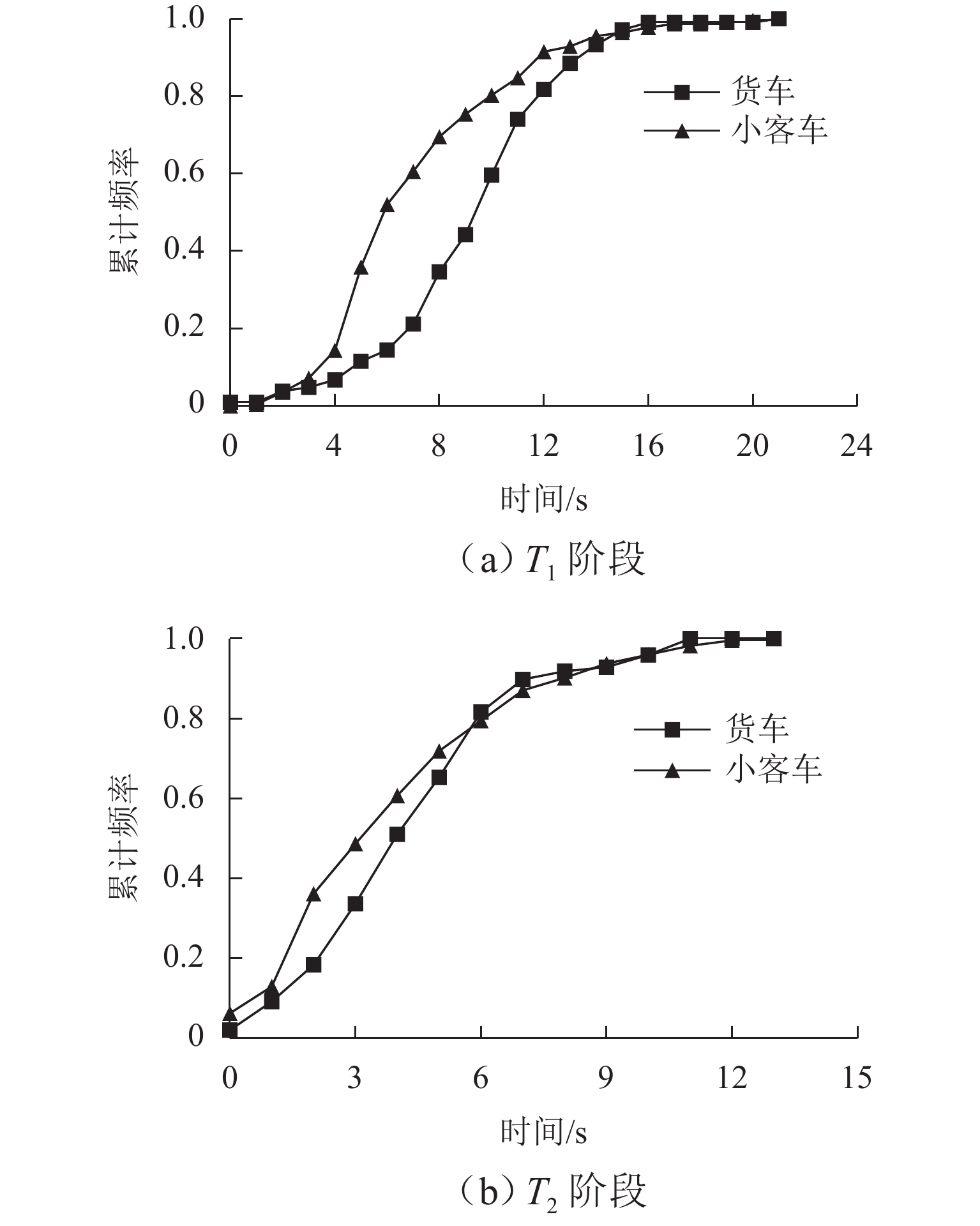
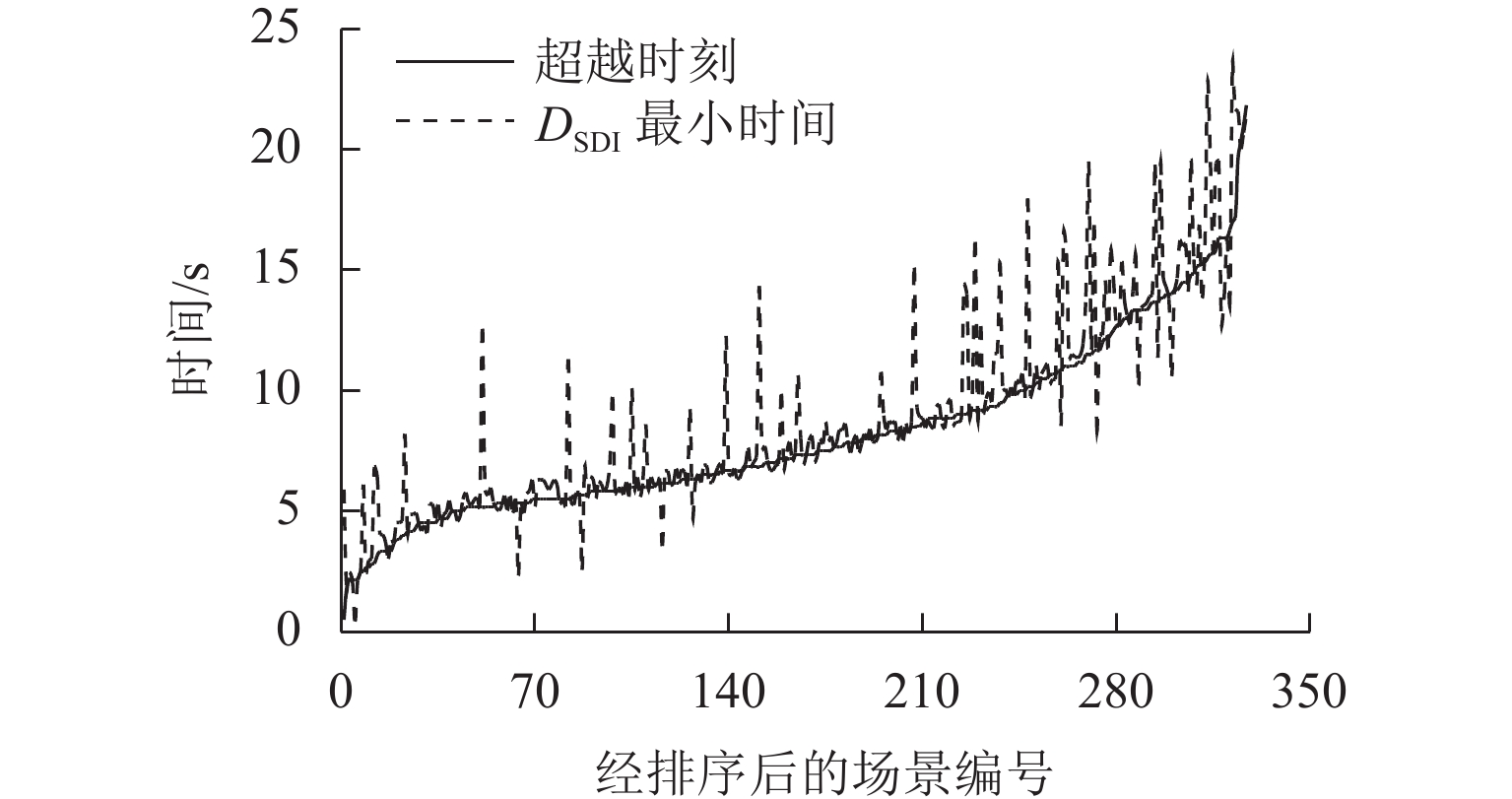
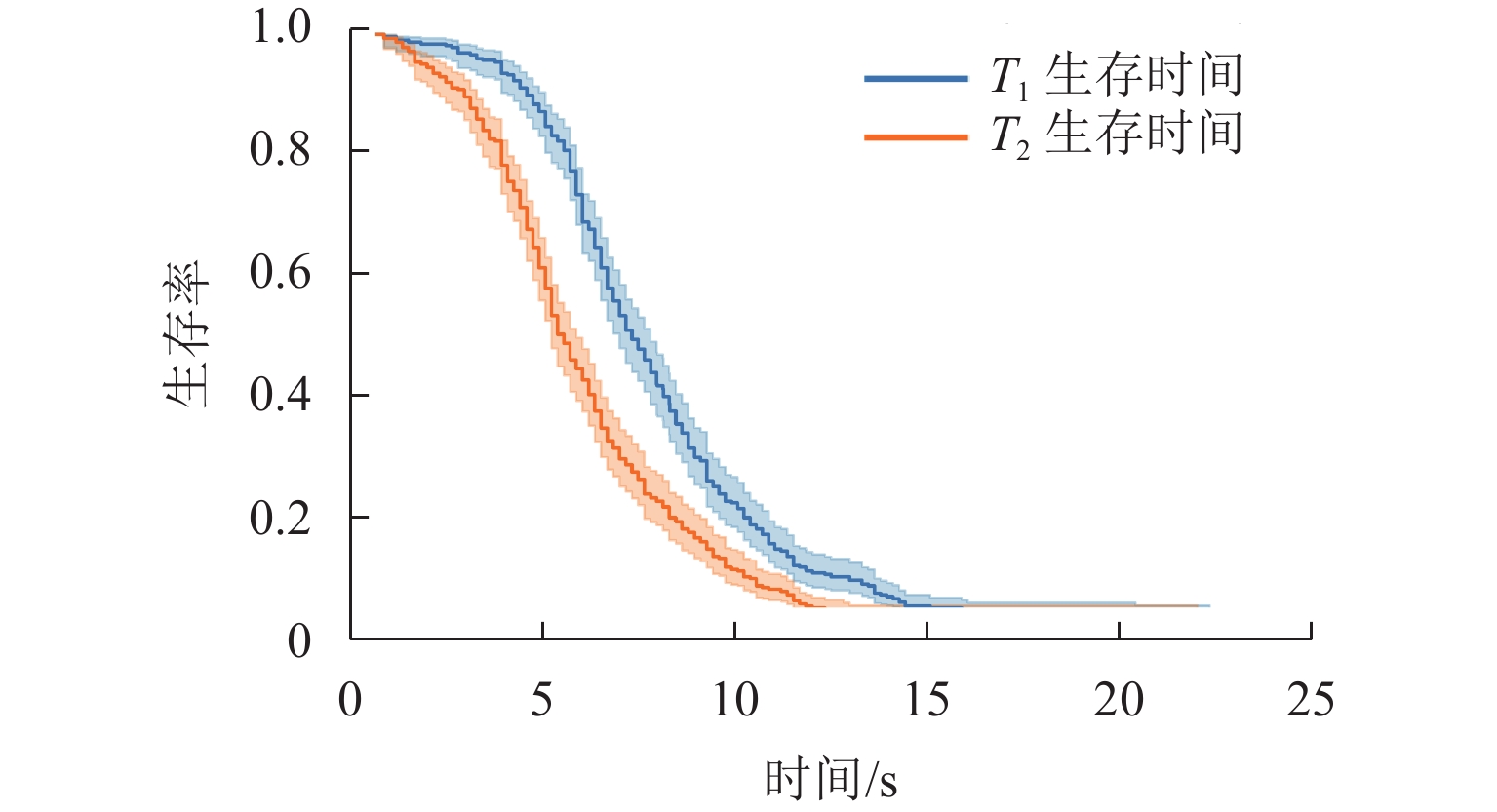
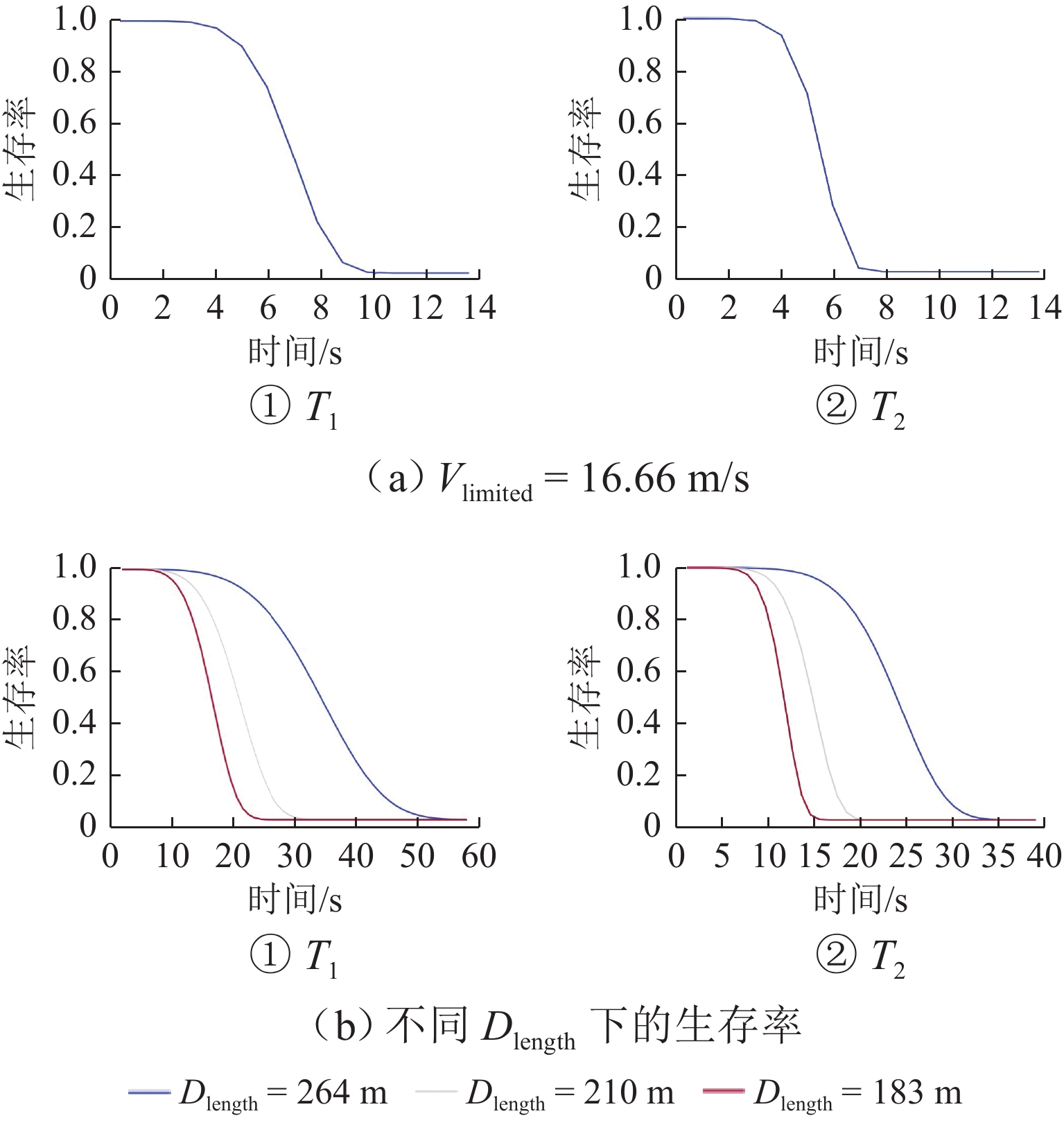
为获取双车道公路超车行为风险演化的时间特征，在利用超车风险视距指标分析超车风险演化特征的基础上，提出基于改进形状参数协变量建模方法的全参数AFT （accelerated failure time）模型预测路段期望超车时间，并通过无人机采集典型超车路段场景的328组完整超车轨迹数据进行实例分析和对比验证. 结果表明：超车风险演化时间包括风险递增（T₁）和风险递减（T₂）两阶段，平均超车距离分别为141.10、99.41 m，平均持续时间分别为8.18、5.61 s，超速超车现象严重；对向来车对T₁阶段有延长作用，超越货车对T₁阶段有缩短作用，场景异质性影响特征明显；全参数AFT模型在数据拟合度和异质性捕获能力方面更具优势，超车速度均值、超车距离和相对横向偏移标准差为模型关键协变量；预测得到在1%的生存率下3个研究场景的期望超车时间范围分别为18～93、18～50 s和18～39 s. 本文扩展了双车道公路超车持续时间建模方法，对于已建成路段超车安全管控和规划路段道路设计具有重要价值.
- 交通工程 /
- 超车行为风险演化 /
- 协变量建模 /
- 双车道公路 /
- 全参数AFT /
- 期望超车时间
Abstract:
In order to obtain the temporal characteristics of overtaking risk evolution on two-lane highways, a full-parameter accelerated failure time (AFT) model based on an improved shape parameter covariate modeling method was proposed to predict the expected overtaking time of the road section, which was carried out after introducing the overtaking risk sight distance index to analyze the evolution characteristics of overtaking risk. A total of 328 sets of complete overtaking trajectory data collected by UAVs in typical overtaking road sections were analyzed and compared. The results show that the overtaking risk evolution consists of two stages: a risk-increasing stage (T₁) and a risk-decreasing stage (T₂). The average overtaking distances for T₁ and T₂ are 141.10 and 99.41 m, respectively, and the average durations are 8.18 and 5.61 s, respectively, indicating a significant occurrence of speeding during overtaking. Oncoming vehicles can prolong T₁, while overtaking of trucks can shorten T₁, indicating a strong effect of scene heterogeneity. The full-parameter AFT model demonstrates better performance in terms of data fitting and heterogeneity capturing. The mean overtaking speed, overtaking distance, and standard deviation of relative lateral deviation were identified as key covariates of the model. Under a survival rate of 1%, the expected overtaking time ranges for the three studied scenarios are 18–93, 18–50 s, and 18–39 s, respectively. The research advances the overtaking duration modeling method for two-lane highways and provides valuable insights for the management of overtaking on existing road sections and the design of road sections under construction.
- traffic engineering /
- overtaking risk evolution /
- covariate modeling /
- two-lane highway /
- full parameter AFT /
- expected overtaking time

HTML全文

图 1 双车道公路数据采集场景

Figure 1. Two-lane highway data collection scenarios

下载: 全尺寸图片幻灯片

图 2 无人机同步交通流视频数据采集示意

Figure 2. Schematic diagram of UAV-synchronized traffic flow video data collection

下载: 全尺寸图片幻灯片

图 3 完整超车轨迹数据

Figure 3. Complete overtaking trajectory data

下载: 全尺寸图片幻灯片

图 4 超车风险演化趋势

Figure 4. Evolution trend of overtaking risk

下载: 全尺寸图片幻灯片

图 5 超车阶段定义示意

Figure 5. Schematic diagram of overtaking phase

下载: 全尺寸图片幻灯片

图 6 不同超越对象风险持续时间累计频率特征

Figure 6. Cumulative frequency characteristics of risk duration with different overtaken vehicles

下载: 全尺寸图片幻灯片

图 7 t₁与超越时刻相关性

Figure 7. Correlation between t₁ and overtaking moment

下载: 全尺寸图片幻灯片

图 8 T₁、T₂两阶段生存函数

Figure 8. Survival functions of T₁ and T₂

下载: 全尺寸图片幻灯片

图 9 协变量生存函数

Figure 9. Covariate-based survival functions

下载: 全尺寸图片幻灯片

图 10 路段期望超车时间生存函数曲线预测

Figure 10. Predicted survival curves of expected overtaking time for road sections

下载: 全尺寸图片幻灯片

表 1 特征变量

Table 1. Characteristic variables

变量类型	符号	说明
行为特征	V_Sm/（m•s⁻¹）	主车速度均值
	V_Fm/（m•s⁻¹）	被超越车速度均值
	A_Sm/（m•s⁻²）	主车加速度均值
	A_Fm/（m•s⁻²）	被超越车加速度均值
	V_Ssd/（m•s⁻¹）	主车速度标准差
	V_Fsd/（m•s⁻¹）	被超越车速度标准差
	A_Ssd/（m•s⁻²）	主车加速度标准差
	A_Fsd/（m•s⁻²）	被超越车加速度标准差
相对特征	V_m/（m•s⁻¹）	速度差均值
	H_m/m	相对偏移均值
	T_m/s	车头时距均值
	W_m/m	车头间距均值
	V_sd/（m•s⁻¹）	速度差标准差
	H_sd/m	相对偏移标准差
	T_sd/s	车头时距标准差
	W_sd/m	车头间距标准差
其他特征	T_time/s	超车总时间
	D_distance/m	超车总距离
	I	是否有对向来车（0：无，1：有）
	O_F	被超越车类型（0：乘用车，1：货车）

下载: 导出CSV

表 2 特征变量描述性统计

Table 2. Descriptive statistics of characteristic variables

阶段	类型	T_time	D_distance	V_Sm	A_Sm	V_Fm	A_Fm	V_Ssd	A_Ssd	V_Fsd	A_Fsd
T₁	均值	8.18 s	141.10 m	17.33 m/s	0.40 m/s²	14.85 m/s	0.08 m/s²	1.78 m/s	0.60 m/s²	0.73 m/s	0.41 m/s²
	方差	3.62 s²	51.24 m²	5.82 m²/s²	0.54 m²/s⁴	4.98 m²/s²	0.41 m²/s⁴	3.46 m²/s²	0.50 m²/s⁴	1.07 m²/s²	0.29 m²/s⁴
	最大值	21.84 s	306.18 m	31.60 m/s	1.98 m/s²	26.68 m/s	3.49 m/s²	59.51 m/s	4.92 m/s²	11.13 m/s	2.50 m/s²
	最小值	1.83 s	31.26 m	4.48 m/s	−2.41 m/s²	2.28 m/s	−1.54 m/s²	0.03 m/s	0.18 m/s²	0.03 m/s	0.07 m/s²
T₂	均值	5.61 s	99.41 m	19.95 m/s	0.24 m/s²	13.90 m/s	0.04 m/s²	0.97 m/s	0.58 m/s²	0.44 m/s	0.40 m/s²
	方差	2.91 s²	47.70 m²	7.10 m²/s²	0.74 m²/s⁴	4.93 m²/s²	0.39 m²/s⁴	2.12 m²/s²	0.59 m²/s⁴	0.62 m²/s²	0.41 m²/s⁴
	最大值	21.30 s	387.69 m	94.95 m/s	3.10 m/s²	47.77 m/s	2.52 m/s²	32.94 m/s	4.94 m/s²	8.11 m/s	3.50 m/s²
	最小值	1.00 s	12.19 m	4.02 m/s	−2.41 m/s²	3.11 m/s	−0.92 m/s²	0.02 m/s	0	0.03 m/s	0

阶段	类型	V_m	H_m	W_m	T_m	V_sd	H_sd	W_sd	T_sd	I	O_F
T₁	均值	3.48 m/s	1.90 m	5.89 m	8.93 s	1.77 m/s	1.01 m	3.85 m	5.45 s	0.23	0.32
	方差	2.83 m²/s²	1.50 m²	14.33 m²	9.70 s²	3.47 m²/s²	0.36 m²	7.45 m²	5.03 s²	0.42	0.47
	最大值	26.78 m/s	4.26 m	113.96 m	45.10 s	59.51 m/s	2.01 m	79.28 m	25.62 s	1.00	1.00
	最小值	−4.74 m/s	−3.48 m	−30.47 m	−33.67 s	0.03 m/s	0.03 m	0.09 m	0.19 s	0	0
T₂	均值	9.69 m/s	2.28 m	−3.64 m	−8.93 s	0.99 m/s	0.77 m	3.80 m	6.18 s	0.22	0.31
	方差	7.02 m²/s²	1.67 m²	9.45 m²	10.92 s²	2.11 m²/s²	0.40 m²	6.42 m²	5.36 s²	0.41	0.46
	最大值	94.95 m/s	5.88 m	27.52 m	16.28 s	32.94 m/s	2.34 m	58.51 m	24.49 s	1.00	1.00
	最小值	−2.73 m/s	−3.97 m	−67.89 m	−37.47 s	0.02 m/s	0.01 m	0.05 m	0.09 s	0	0

下载: 导出CSV

表 3 固定效应AFT参数估计（对$\lambda $建模）

Table 3. Parameter estimation of fixed effect AFT （for $\lambda $ modeling）

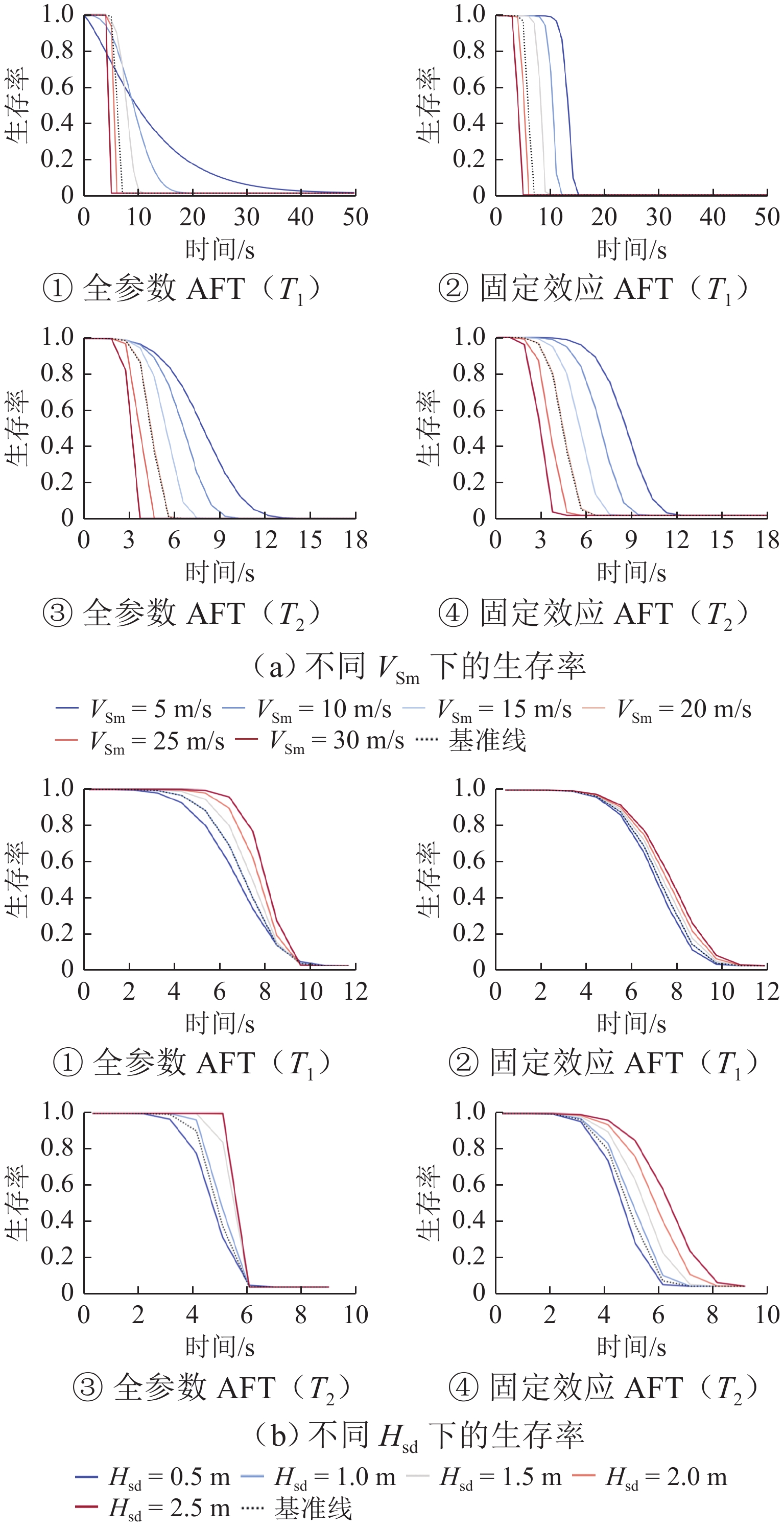
演化阶段	协变量	β	exp(β)	S_E	Z	P	C_I95(β)
演化阶段	协变量	β	exp(β)	S_E	Z	P	下限	上限
T₁	V_Sm	−0.047	0.954	0.002	−27.550	< 0.0005	−0.051	−0.044
	H_sd	0.045	1.046	0.030	1.509	0.1310	−0.014	0.104
	D_distance	0.007	1.007	0	24.858	< 0.0005	0.006	0.007
	I_β	1.852	6.370	0.047	39.027	< 0.0005	1.759	1.945
	对数似然值	331.422
	AIC	1111.154
T₂	V_Sm	−0.043	0.958	0.001	−41.027	< 0.0005	−0.045	−0.041
	H_sd	0.158	1.171	0.029	5.459	< 0.0005	0.101	0.215
	D_distance	0.009	1.010	0	35.353	< 0.0005	0.009	0.010
	I_β	1.453	4.277	0.026	55.405	< 0.0005	1.402	1.505
	对数似然值	483.496
	AIC	820.904
注：T₁阶段，$ \lambda ({\boldsymbol{x}})\text{=}\mathrm{exp}(1.852-0.047x_1 + 0.045x_2 + 0.007x_3)，\rho \text{=1}\text{.773} $；T₂阶段，$ \lambda ({\boldsymbol{x}})\text{=}\mathrm{exp}(1.453-0.043x_1 + 0.158x_2 + $$0.009x_3)， \rho \text{=1}\text{.892} $.

下载: 导出CSV

表 4 全参数AFT参数估计（对$\lambda $和$\rho $建模）

Table 4. Parameter estimation of full-parameter AFT （for$\lambda $ and $\rho $ modeling）

演化阶段	协变量	β	exp(β)	S_E	Z	P	C_I95(β)
演化阶段	协变量	β	exp(β)	S_E	Z	P	下限	上限
T₁	V_Sm	−0.046	0.955	0.002	−24.95	< 0.0005	−0.05	−0.043
	H_sd	0.067	1.069	0.030	2.249	0.0250	0.009	0.125
	D_distance	0.006	1.006	0	21.822	< 0.0005	0.006	0.007
	I_β	1.843	6.312	0.058	31.954	< 0.0005	1.730	1.956
	对数似然值	336.534
	AIC	1095.151
T₂	V_Sm	−0.036	0.964	0.001	−58.397	< 0.0005	−0.038	−0.035
	H_sd	0.097	1.102	0.015	6.367	< 0.0005	0.067	0.127
	D_distance	0.009	1.009	0	53.504	< 0.0005	0.008	0.009
	I_β	1.457	4.294	0.016	91.723	< 0.0005	1.426	1.488
	对数似然值	657.200
	AIC	568.960
注：T₁阶段，$ \lambda ({\boldsymbol{x}}){\text{ = }}\exp (1.843 - 0.046x_1 + 0.067x_2 + 0.006x_3) $，$\rho ({\boldsymbol{x}}){\text{ = }}\exp (1.011 + 0.013x_1 + 0.462x_2 + 0.001x_3) $；T₂阶段，$ \lambda ({\boldsymbol{x}}){\text{ = }}\exp (1.457 - 0.036x_1 + 0.097x_2 + 0.009x_3) $，$ \rho ({\boldsymbol{x}}){\text{ = }}\exp ( - 0.160 + 0.062x_1 + 1.324x_2 + 0.002x_3) $.

下载: 导出CSV

表 5 不同生存率下路段期望超车时间

Table 5. Expected overtaking time under different survival rates

生存率	路段	下限/s	上限/s
0.01	路段 1	17.969	93.303
	路段 2		50.365
	路段 3		39.314
0.05	路段 1	15.820	77.825
	路段 2		41.902
	路段 3		30.588
0.15	路段 1	14.859	70.610
	路段 2		38.256
	路段 3		27.873

下载: 导出CSV

参考文献(17)

[1]	徐进, 杨奎, 鲁工圆, 等. 基于自然驾驶的山区公路行驶舒适性研究[J]. 西南交通大学学报, 2017, 52(2): 309-318. doi: 10.3969/j.issn.0258-2724.2017.02.014 XU Jin, YANG Kui, LU Gongyuan, et al. Investigation on driving comfort of passenger cars on mountain roads based on naturalistic driving[J]. Journal of Southwest Jiaotong University, 2017, 52(2): 309-318. doi: 10.3969/j.issn.0258-2724.2017.02.014
[2]	WU Q, CHEN F, ZHANG G H, et al. Mixed logit model-based driver injury severity investigations in single- and multi-vehicle crashes on rural two-lane highways[J]. Accident Analysis & Prevention, 2014, 72: 105-115.
[3]	PAN J, SHEN Y J. Assessing driving risk at the second phase of overtaking on two-lane highways for young novice drivers based on driving simulation[J]. International Journal of Environmental Research and Public Health, 2022, 19(5): 2691.1-2691.13.
[4]	徐婷, 邓恺龙, 刘永涛, 等. 基于航测数据的不同风格换道轨迹规划[J]. 西南交通大学学报, 2024, 59(3): 720-728. doi: 10.3969/j.issn.0258-2724.20230392 XU Ting, DENG Kailong, LIU Yongtao, et al. Different style lane change trajectory planning based on aerial survey data[J]. Journal of Southwest Jiaotong University, 2024, 59(3): 720-728. doi: 10.3969/j.issn.0258-2724.20230392
[5]	吴德华, 彭锐, 陈荣峰. 异质流网联车的不同换道集聚策略[J]. 西南交通大学学报, 2023, 58(2): 348-356. WU Dehua, PENG Rui, CHEN Rongfeng. Different lane change agglomeration strategies of connected vehicles in heterogeneous flow networks[J]. Journal of Southwest Jiaotong University, 2023, 58(2): 348-356.
[6]	赵建东, 赵志敏, 屈云超, 等. 轨迹数据驱动的车辆换道意图识别研究[J]. 交通运输系统工程与信息, 2022, 22(4): 63-71. ZHAO Jiandong, ZHAO Zhimin, QU Yunchao, et al. Vehicle lane change intention recognition driven by trajectory data[J]. Journal of Transportation Systems Engineering and Information Technology, 2022, 22(4): 63-71.
[7]	SHANGGUAN Q Q, FU T, WANG J H, et al. A proactive lane-changing risk prediction framework considering driving intention recognition and different lane-changing patterns[J]. Accident Analysis & Prevention, 2022, 164: 106500.1-106500.14.
[8]	CHEN Q H, HUANG H L, LI Y, et al. Modeling accident risks in different lane-changing behavioral patterns[J]. Analytic Methods in Accident Research, 2021, 30: 100159.1-100159.20.
[9]	LI Y, GU R F, LEE J, et al. The dynamic tradeoff between safety and efficiency in discretionary lane-changing behavior: a random parameters logit approach with heterogeneity in means and variances[J]. Accident Analysis & Prevention, 2021, 153: 106036.1-106036.7.
[10]	YANG M M, WANG X S, QUDDUS M. Examining lane change gap acceptance, duration and impact using naturalistic driving data[J]. Transportation Research Part C: Emerging Technologies, 2019, 104: 317-331. doi: 10.1016/j.trc.2019.05.024
[11]	ALI Y, HAQUE M M, ZHENG Zuduo, et al. A hazard-based duration model to quantify the impact of connected driving environment on safety during mandatory lane-changing[J]. Transportation Research Part C: Emerging Technologies, 2019, 106: 113-131. doi: 10.1016/j.trc.2019.07.015
[12]	戢晓峰, 戴秉佑, 普永明, 等. 基于生存分析的山区双车道公路超车持续时间模型[J]. 交通运输系统工程与信息, 2022, 22(6): 183-190. JI Xiaofeng, DAI Bingyou, PU Yongming, et al. Overtaking duration model of two-lane mountainous highways based on survival analysis[J]. Journal of Transportation Systems Engineering and Information Technology, 2022, 22(6): 183-190.
[13]	PARK H, OH C, MOON J, et al. Development of a lane change risk index using vehicle trajectory data[J]. Accident Analysis & Prevention, 2018, 110: 1-8.
[14]	WILSON T, BEST W. Driving strategies in overtaking[J]. Accident Analysis & Prevention, 1982, 14(3): 179-185.
[15]	刘启远, 孙剑, 田野, 等. 机非交互路段非机动车越线超车行为建模与仿真[J]. 同济大学学报(自然科学版), 2019, 47(11): 1585-1592, 1599. LIU Qiyuan, SUN Jian, TIAN Ye, et al. Modeling and simulation of cross-line overtaking behavior of non-motorized vehicles at mixed flow road section[J]. Journal of Tongji University (Natural Science), 2019, 47(11): 1585-1592, 1599.
[16]	戢晓峰, 徐迎豪, 普永明, 等. 山区双车道公路货车移动遮断小客车跟驰风险预测模型[J]. 吉林大学学报 (工学版), 2024, 54(5): 1323-1331. JI Xiaofeng, XU Yinghao, PU Yongming, et al. Risk prediction model of passenger car following behavior under truck movement interruption of two-lane highway in mountainous area[J], Journal of Jilin University (Engineering and Technology Edition), 2024, 54(5): 1323-1331.
[17]	MANNERING F, BHAT C R, SHANKAR V, et al. Big data, traditional data and the tradeoffs between prediction and causality in highway-safety analysis[J]. Analytic Methods in Accident Research, 2020, 25: 100113.1-100113.9.