围岩蠕变作用下隧道支护结构的劣化特征

蓝日彦; 杨凯; 邱云辉; 崔耀中; 乔敏杰; 晏启祥

doi:10.3969/j.issn.0258-2724.20230442

围岩蠕变作用下隧道支护结构的劣化特征

doi: 10.3969/j.issn.0258-2724.20230442

蓝日彦^1,,
杨凯^{2, 3, 4, ,},
邱云辉²,
崔耀中²,
乔敏杰²,
晏启祥²

1.
广西新发展交通集团有限公司，广西南宁 530029
2.
西南交通大学交通隧道工程教育部重点实验室，四川成都 610031
3.
西华大学建筑与土木工程学院，四川成都 610039
4.
四川省公路规划勘察设计研究院有限公司，四川成都 610041

基金项目: 国家自然科学基金项目（U21A20152）；2020年度交通运输行业重点科技项目（2020-MS3-083）；广西科技计划项目（桂科AB20238036）

详细信息

作者简介:
蓝日彦（1976—），男，教授级高级工程师，博士，研究方向为岩土工程、公路建设与运营管理，Email：47573043@qq.com

通讯作者:
杨凯（1987—），男，讲师，博士，研究方向为隧道及地下工程，Email：87642189@qq.com

中图分类号: U45
计量
- 文章访问数: 36
- HTML全文浏览量: 10
- PDF下载量: 8
- 被引次数: 0
出版历程
- 收稿日期: 2023-08-31
- 修回日期: 2024-01-04
- 网络出版日期: 2025-05-20

Deterioration Characteristics of Tunnel Support Structures under Surrounding Rock Creep

LAN Riyan^1
,,
YANG Kai^{2, 3, 4
, ,},
QIU Yunhui²,
CUI Yaozhong²,
QIAO Minjie²,
YAN Qixiang²

1.
Guangxi Xinfazhan Communication Group Co., Ltd, Nanning 530029, China
2.
Key Laboratory of Transportation Tunnel Engineering, Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China
3.
School of Architecture and Civil Engineering, Xihua University, Chengdu 610039, China
4.
Sichuan Highway Planning, Survey, Design and Research Institute Ltd, Chengdu 610041, China

摘要

摘要:
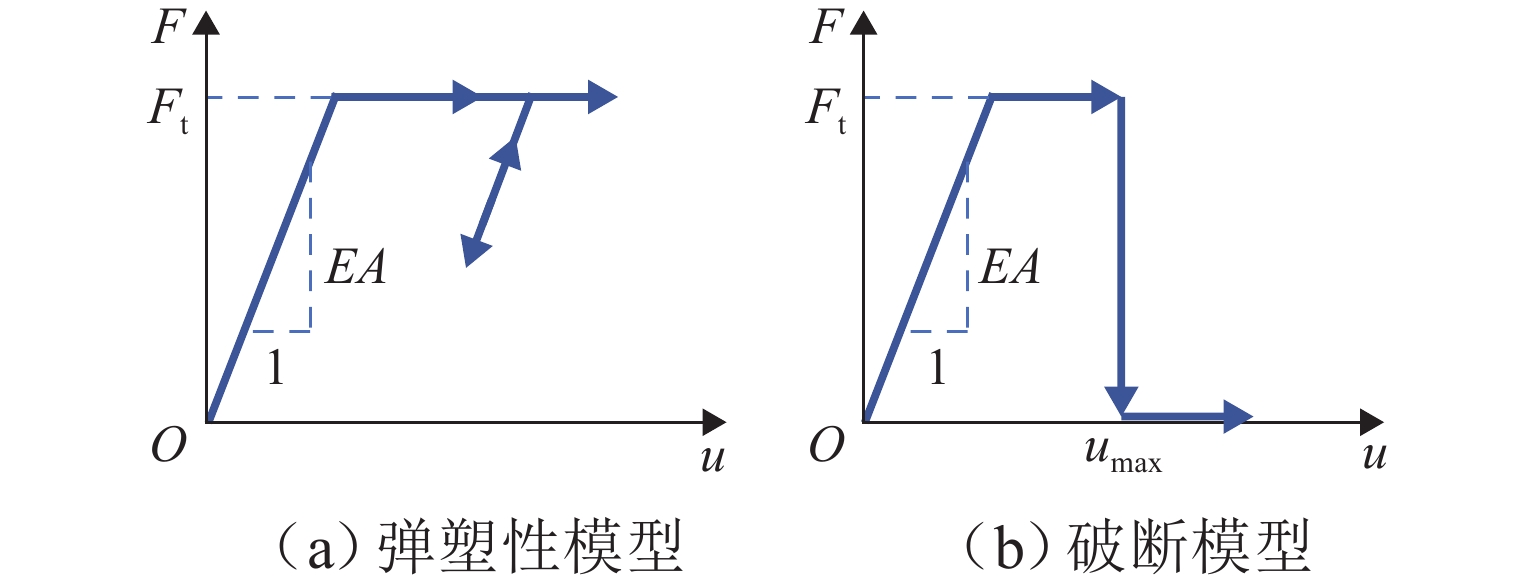
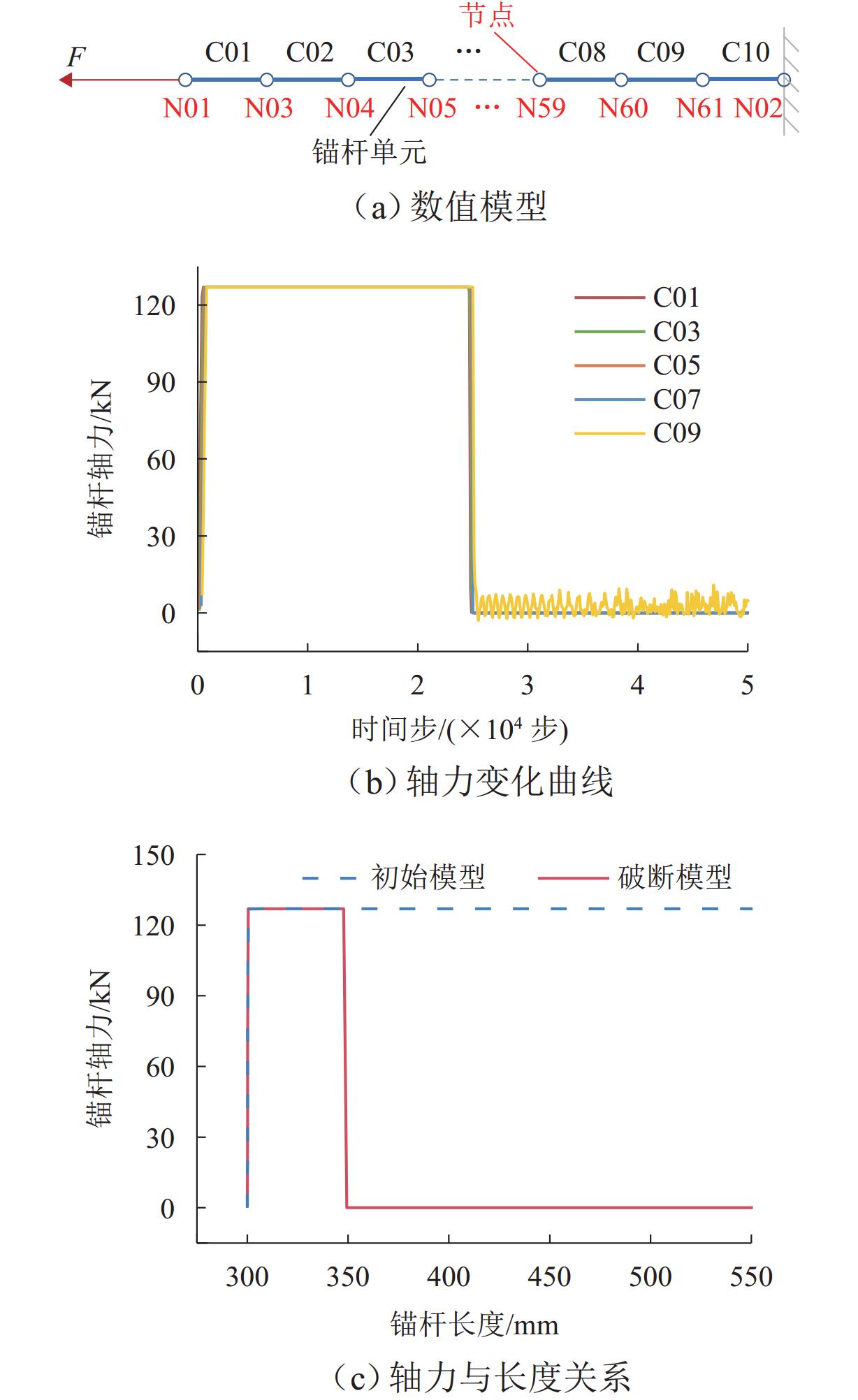
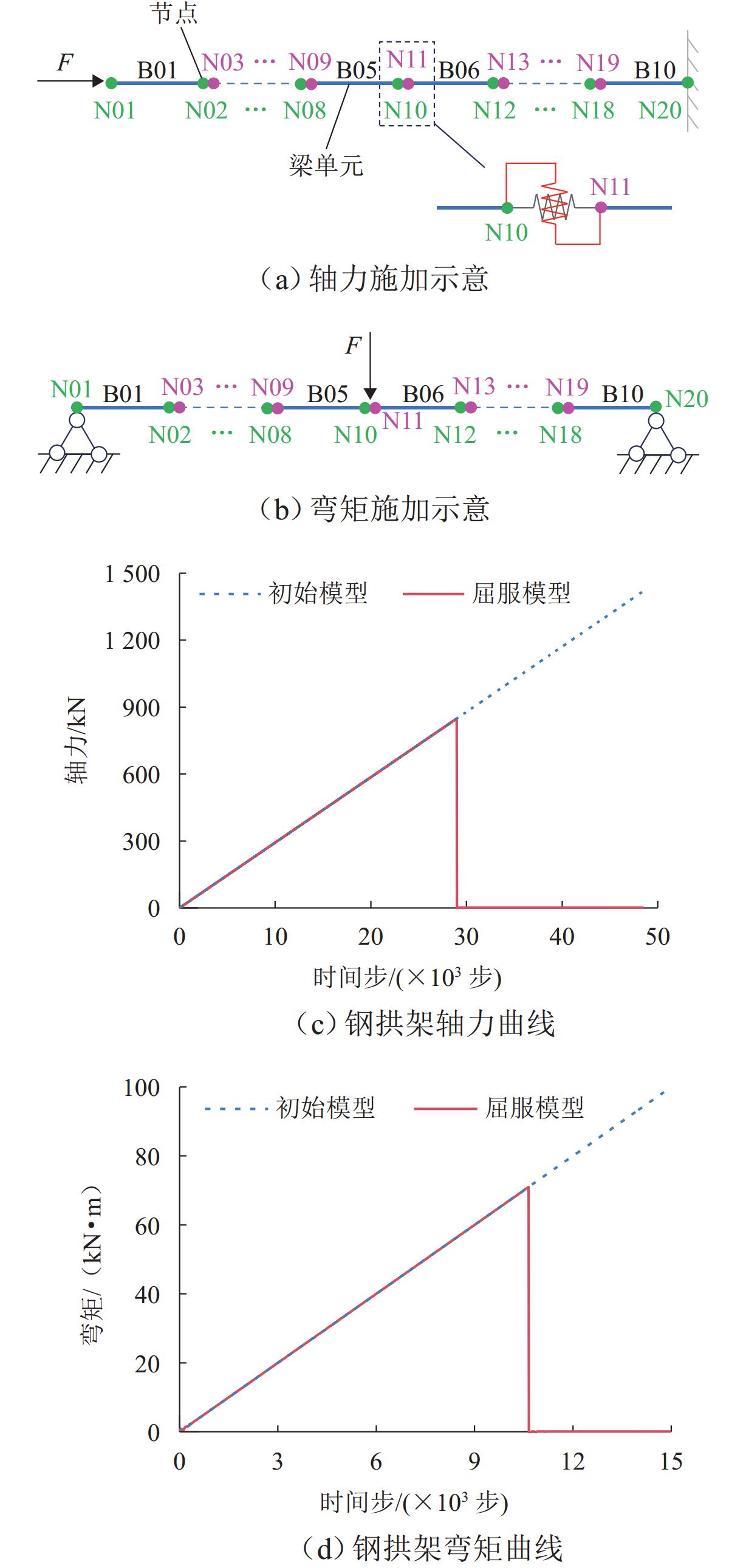
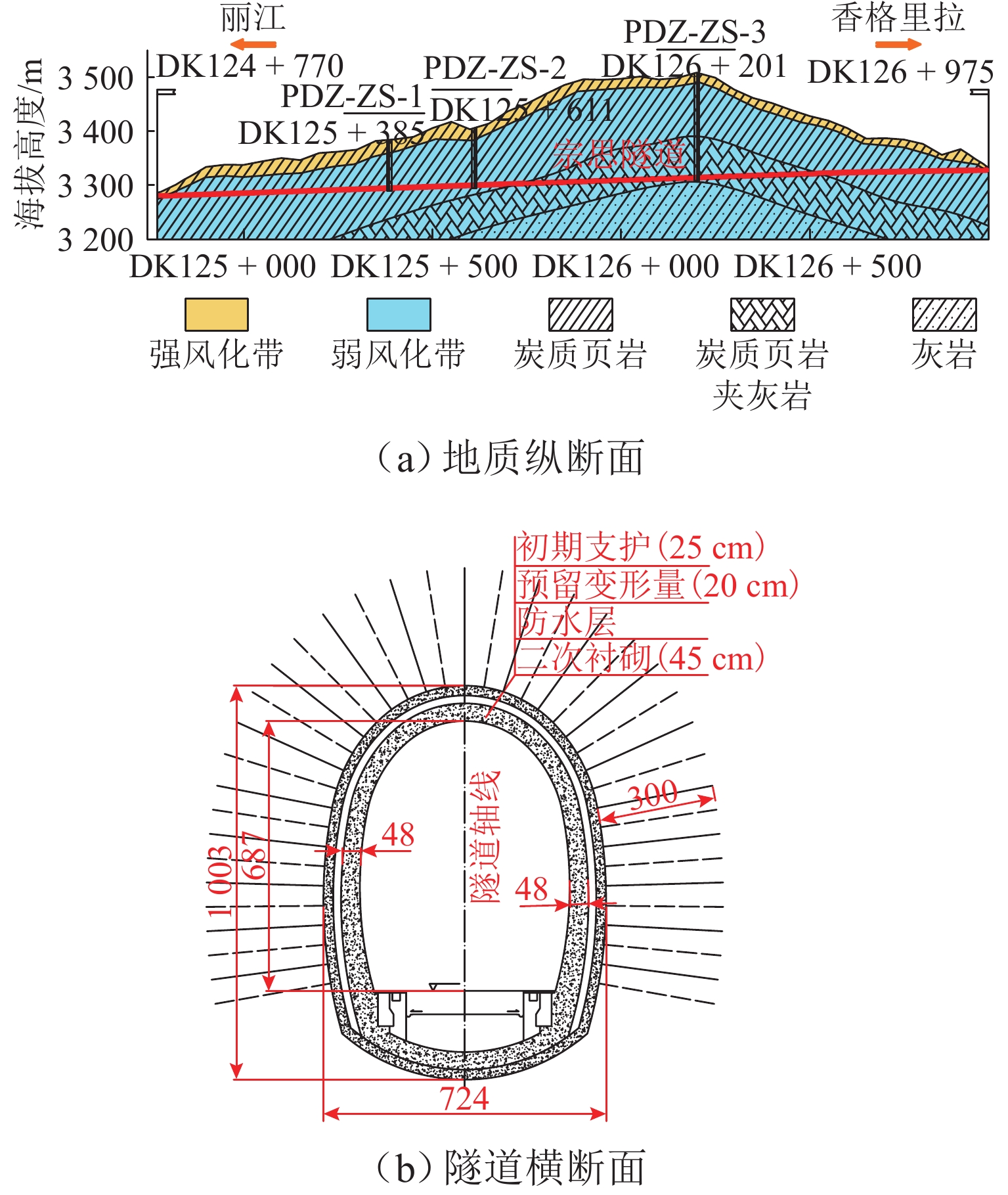
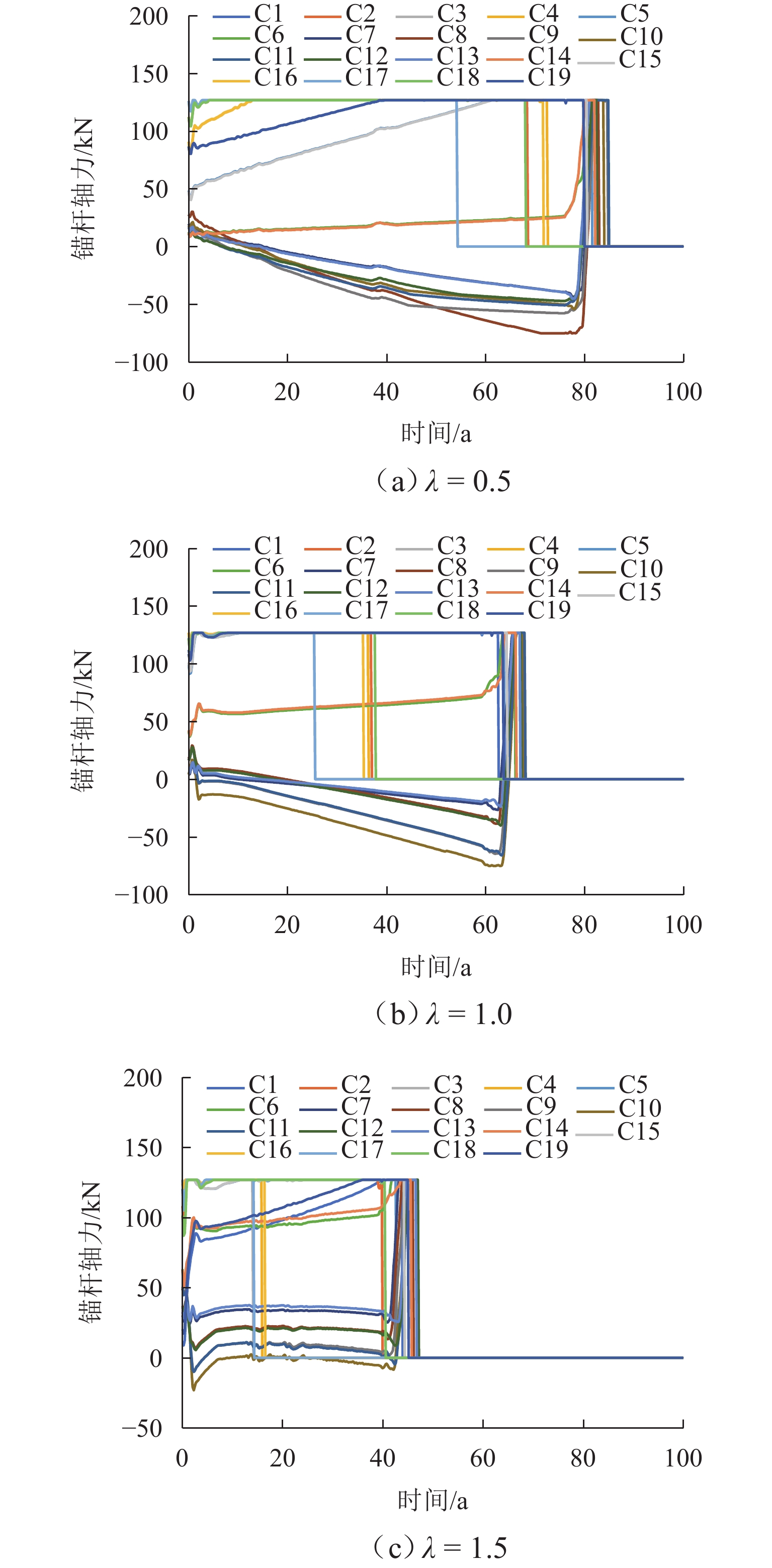
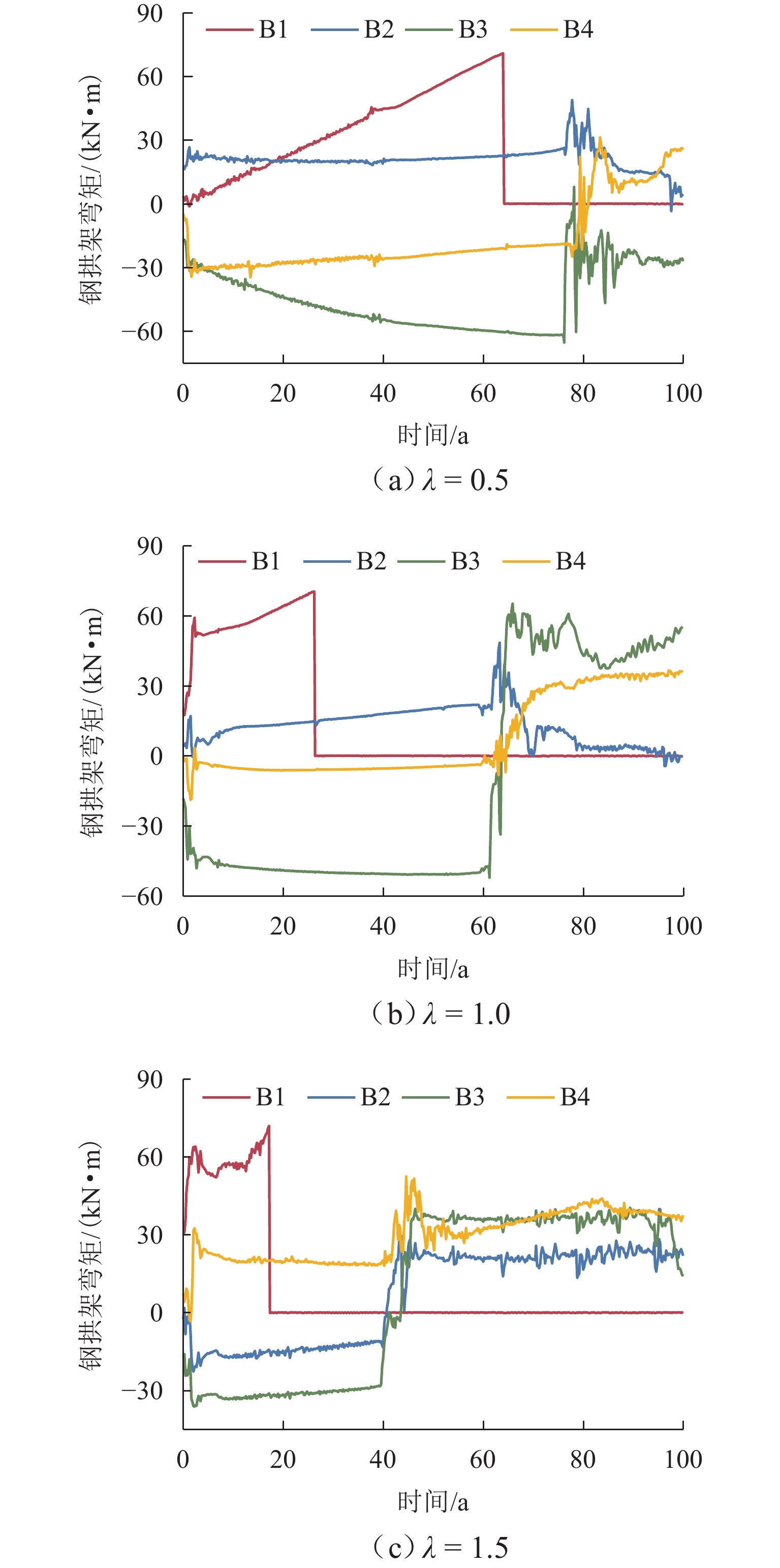
为探究蠕变效应下支护结构的长期劣化特性，针对隧道支护结构体系，建立锚杆破断、钢拱架屈服和混凝土塑性损伤力学模型，采用数值算例验证支护结构劣化力学模型的有效性，并探究竖向应力、静水压力和水平应力为主条件下锚杆破断、钢拱架屈服和衬砌损伤的劣化特性. 研究表明：破断首先发生在隧道边墙中部位置的锚杆，再沿隧道环向向两侧发展；钢拱架轴力呈先加速增长、后缓慢发展、最后急速降低的特征，轴力快速降低的同时伴随着弯矩的剧烈变化，部分测点弯矩出现由负变正的特征；受压损伤破坏区主要分布在隧道边墙和墙脚位置，受拉损伤首先出现在二次衬砌边墙中部的表面；侧压力系数越大，锚杆破断、钢拱架屈服、衬砌形成的贯通受压破坏区和受拉损伤达到最大值的时间越早.
- 蠕变 /
- 锚杆破断 /
- 钢拱架屈服 /
- 衬砌损伤 /
- 劣化特征
Abstract:
To investigate the long-term deterioration characteristics of tunnel support structures under creep effect, mechanical models of anchor bolt fracture, steel arch frame yielding, and concrete plastic damage were established for the tunnel support structure system. Numerical examples were used to verify the validity of the mechanical models for support structure deterioration. The deterioration characteristics of anchor bolt fracture, steel arch frame yielding, and lining damage were explored under conditions dominated by vertical stress, hydrostatic pressure, and horizontal stress. The results show that the fracture first occurs at the anchor bolt at mid-height of the tunnel sidewall and then develops circumferentially towards both sides. The axial force of the steel arch frame first increases rapidly, then develops slowly, and finally decreases significantly. The rapid decrease of axial force is accompanied by drastic changes in the bending moment, with some measuring points appearing a change of bending moment from negative to positive. The compressive damage zones are mainly distributed at the sidewall and wall foot positions of the tunnel, while tensile damage first appears on the surface of the secondary lining at the mid-height of the sidewall. As the lateral pressure coefficient increases, the anchor bolt fracture, the steel arch frame yielding, formation of a continuous compressive damage zone in the lining, and the maximum tensile damage appear earlier.
- creep /
- anchor bolt fracture /
- steel arch frame yielding /
- lining damage /
- deterioration characteristic

HTML全文

图 1 CVISC蠕变模型

Figure 1. CVISC creep model

下载: 全尺寸图片幻灯片

图 2 锚杆力学模型

Figure 2. Mechanical model of anchor bolt

下载: 全尺寸图片幻灯片

图 3 锚杆破断力学模型验证

Figure 3. Verification of mechanical model for anchor bolt fracture

下载: 全尺寸图片幻灯片

图 4 钢拱架屈服力学模型验证

Figure 4. Verification of mechanical model of steel arch frame yielding

下载: 全尺寸图片幻灯片

图 5 混凝土塑性损伤模型及其验证

Figure 5. Concrete plastic damage model and its verification

下载: 全尺寸图片幻灯片

图 6 宗思隧道（单位：cm）

Figure 6. Zongsi Tunnel (unit: cm)

下载: 全尺寸图片幻灯片

图 7 隧道支护结构劣化特征分析数值模型

Figure 7. Numerical model for deterioration characteristic analysis of tunnel support structures

下载: 全尺寸图片幻灯片

图 8 锚杆轴力监测结果

Figure 8. Axial force monitoring results of anchor bolt

下载: 全尺寸图片幻灯片

图 9 破断锚杆空间分布

Figure 9. Spatial distribution of anchor bolt fracture

下载: 全尺寸图片幻灯片

图 10 锚杆破断时间

Figure 10. Timing of anchor bolt fracture

下载: 全尺寸图片幻灯片

图 11 钢拱架轴力监测曲线

Figure 11. Monitoring curves of axial force in steel arch frame

下载: 全尺寸图片幻灯片

图 12 钢拱架弯矩监测曲线

Figure 12. Monitoring curves of bending moment in steel arch frame

下载: 全尺寸图片幻灯片

图 13 衬砌受压损伤分布

Figure 13. Distribution of compressive damage in lining

下载: 全尺寸图片幻灯片

图 14 受拉损伤分布

Figure 14. Distribution of tensile damage

下载: 全尺寸图片幻灯片

图 15 现场实测二衬裂纹分布

Figure 15. Measured crack distribution of secondary lining

下载: 全尺寸图片幻灯片

表 1 锚杆物理力学参数

Table 1. Physical and mechanical parameters of anchor bolt

E/GPa	F_t/MPa	延伸率/%	直径d/mm
200	335	16	22

下载: 导出CSV

表 2 钢拱架物理力学参数

Table 2. Physical and parameters of steel arch frame

钢拱架型号	E/GPa	泊松比v	N_u/kN	M_u/（kN•m）
I20a	200	0.3	849	71

下载: 导出CSV

表 3 混凝土力学参数

Table 3. Mechanical parameters of concrete

强度等级	弹性模量E/GPa	泊松比ν	内聚力c/MPa	内摩擦角φ/（°）	抗压强度σ_c/MP	抗拉强度σ_t/MPa
C25	28.0	0.2	3.0	50	16.7	1.78
C35	31.5	0.2	3.7	55	23.4	2.20

下载: 导出CSV

表 4 混凝土弹塑性损伤参数

Table 4. Elasto-plastic damage parameters of concrete

C25混凝土				C35混凝土
κ_s/ （ × 10⁻³）	D_s	κ_t/ （ × 10⁻³）	D_t	κ_s/ （ × 10⁻³）	D_s	κ_t/ （ × 10⁻³）	D_t
0	0	0	0	0	0	0	0
0.06	0.01	0.42	0.55	0.07	0.01	0.45	0.55
0.20	0.02	1.02	0.75	0.23	0.02	1.13	0.75
0.45	0.03	3.60	0.99	0.56	0.04	3.92	0.99
1.20	0.11			1.40	0.12
3.00	0.40			2.90	0.39
4.50	0.70			4.10	0.67
7.00	0.99			6.00	0.99

下载: 导出CSV

表 5 围岩蠕变力学参数

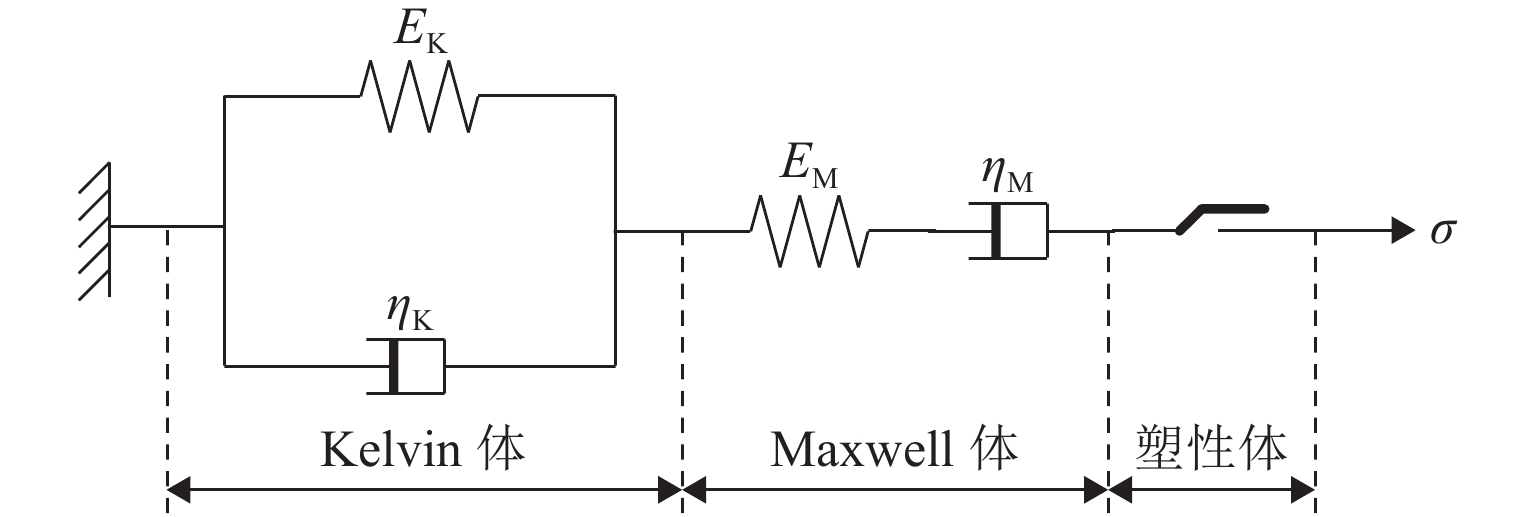
Table 5. Creep mechanical parameters of surrounding rock

K/ GPa	E_M/ GPa	E_K/ GPa	η_M/ GPa.a	η_K/ （GPa.a）	c/ MPa	φ/（°）	σ_t/ MPa
2	2.5	4	3	1.2	7	26	1

下载: 导出CSV

参考文献(34)

[1]	关宝树. 漫谈矿山法隧道技术第四讲:钢架[J]. 隧道建设,2016,36(2): 123-130. doi: 10.3973/j.issn.1672-741X.2016.02.001 GUAN Baoshu. Tunneling by mining method: lecture Ⅳ: steel arch[J]. Tunnel Construction, 2016, 36(2): 123-130. doi: 10.3973/j.issn.1672-741X.2016.02.001
[2]	李天胜,何川,方砚兵,等. 基于围岩变形失效的隧道结构可靠度设计方法[J]. 西南交通大学学报,2023,58(3): 613-621. doi: 10.3969/j.issn.0258-2724.20220137 LI Tiansheng, HE Chuan, FANG Yanbing, et al. Reliability-based design method of tunnel structures based on deformation failure of surrounding rock[J]. Journal of Southwest Jiaotong University, 2023, 58(3): 613-621. doi: 10.3969/j.issn.0258-2724.20220137
[3]	潘钦锋,张丙强,黄志斌. 隧道下穿诱发既有管道-土体非协调变形解析研究[J]. 西南交通大学学报,2024,59(3): 637-645. doi: 10.3969/j.issn.0258-2724.20230334 PAN Qinfeng, ZHANG Bingqiang, HUANG Zhibin. Analytical study for uncoordinated deformation of existing pipeline and soil induced by tunnel undercrossing[J]. Journal of Southwest Jiaotong University, 2024, 59(3): 637-645. doi: 10.3969/j.issn.0258-2724.20230334
[4]	中华人民共和国交通运输部. 公路隧道设计细则:JTG/T D70—2010[S]. 北京:人民交通出版社,2010.
[5]	国家铁路局. 铁路隧道设计规范:TB 10003—2016[S]. 北京:中国铁道出版社,2017.
[6]	周建,杨新安,蔡键,等. 深埋复合式衬砌隧道二衬分担比研究[J]. 公路交通科技,2020,37(5): 92-99.
[7]	王耀东,朱力强,余祖俊,等. 基于样本自动标注的隧道裂缝病害智能识别[J]. 西南交通大学学报,2023,58(5): 1001-1008,1036. doi: 10.3969/j.issn.0258-2724.20210092 WANG Yandong, ZHU Liqiang, YU Zujun, et al. Intelligent tunnel crack recognition based on automatic sample labeling[J]. Journal of Southwest Jiaotong University, 2023, 58(5): 1001-1008,1036. doi: 10.3969/j.issn.0258-2724.20210092
[8]	中华人民共和国交通运输部. 公路工程技术标准:JTG B01—2014[S]. 北京:人民交通出版社,2015.
[9]	陈志豪. 锈蚀加筋喷砼拱肋支护承载性能劣化与损伤评价[D]. 长沙:长沙理工大学,2021.
[10]	丁万涛,李术才. 锈蚀对海底隧道锚固支护结构加固性能的影响[J]. 华南理工大学学报(自然科学版),2013,41(6): 100-107,139. doi: 10.3969/j.issn.1000-565X.2013.06.016 DING Wantao, LI Shucai. Effect of corrosion on reinforcement performance of anchorage support structure of subsea tunnel[J]. Journal of South China University of Technology (Natural Science Edition), 2013, 41(6): 100-107,139. doi: 10.3969/j.issn.1000-565X.2013.06.016
[11]	杜建明,房倩,程荔琼,等. 围岩-支护结构时效性共同作用下运营隧道服役特性[J]. 中南大学学报(自然科学版),2022,53(10): 4001-4011. doi: 10.11817/j.issn.1672-7207.2022.10.020 DU Jianming, FANG Qian, CHENG Liqiong, et al. Service characteristics of operational tunnel under combined action of time effects of surrounding rock and supporting structure[J]. Journal of Central South University (Science and Technology), 2022, 53(10): 4001-4011. doi: 10.11817/j.issn.1672-7207.2022.10.020
[12]	席红兵,李柏生. 硫酸盐-冻融共同作用下隧道衬砌支护喷射混凝土劣化性能研究[J]. 隧道建设(中英文),2022,42(7): 1219-1226. XI Hongbing, LI Bosheng. Deterioration performance of tunnel lining support shotcrete under sulfate-freeze-thaw interaction[J]. Tunnel Construction, 2022, 42(7): 1219-1226.
[13]	杜学才,周辉,郭鹏云,等. 香炉山引水隧洞围岩的蠕变特性及模型研究[J]. 长江科学院院报,2022,39(12): 75-81. doi: 10.11988/ckyyb.20221011 DU Xuecai, ZHOU Hui, GUO Pengyun, et al. Creep characteristics and modelling of surrounding rock of Xianglushan water diversion tunnel[J]. Journal of Yangtze River Scientific Research Institute, 2022, 39(12): 75-81. doi: 10.11988/ckyyb.20221011
[14]	封坤,王胤丞,马文帅,等. 围岩蠕变对盾构隧道受荷特征影响研究[J]. 铁道标准设计,2022,66(8): 117-124,131. FENG Kun, WANG Yincheng, MA Wenshuai, et al. Influence of surrounding rock creep on loading characteristics of shield tunnel[J]. Railway Standard Design, 2022, 66(8): 117-124,131.
[15]	经纬,陈洪恩,杨仁树,等. 基于岩石蠕变及D-P准则的深部巷道围岩弹塑性分析[J]. 力学学报,2022,54(7): 1982-1993. doi: 10.6052/0459-1879-21-619 JING Wei, CHEN Hongen, YANG Renshu, et al. Elastoplastic analysis of surrounding rock of deep roadway based on rock creep and d-p criterion[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(7): 1982-1993. doi: 10.6052/0459-1879-21-619
[16]	路军富,肖铮,喻渝,等. 铁路隧道底鼓段围岩蠕变参数反演方法研究[J]. 铁道工程学报,2021,38(1): 66-71. doi: 10.3969/j.issn.1006-2106.2021.01.012 LU Junfu, XIAO Zheng, YU Yu, et al. Research on the back analysis method of creep parameters of surrounding rock at floor heave section of railway tunnel[J]. Journal of Railway Engineering Society, 2021, 38(1): 66-71. doi: 10.3969/j.issn.1006-2106.2021.01.012
[17]	张海洋,徐文杰,王永刚. 各向异性软岩隧道围岩蠕变特征及支护方案对比分析[J]. 铁道建筑,2018,58(8): 71-74. doi: 10.3969/j.issn.1003-1995.2018.08.18 ZHANG Haiyang, XU Wenjie, WANG Yonggang. Creep characteristics of surrounding rock in anisotropic soft rock tunnel and comparative analysis of supporting schemes[J]. Railway Engineering, 2018, 58(8): 71-74. doi: 10.3969/j.issn.1003-1995.2018.08.18
[18]	YANG K, YAN Q X, SHI Z D, et al. Numerical study on the mechanical behavior of shotcrete lining with yielding support in large deformation tunnel[J]. Rock Mechanics and Rock Engineering, 2023, 56(2): 1563-1584. doi: 10.1007/s00603-022-03126-w
[19]	XU G W, GUTIERREZ M. Study on the damage evolution in secondary tunnel lining under the combined actions of corrosion degradation of preliminary support and creep deformation of surrounding rock[J]. Transportation Geotechnics, 2021, 27: 100501. doi: 10.1016/j.trgeo.2020.100501
[20]	戴永浩,陈卫忠,于洪丹,等. 大坂膨胀性泥岩引水隧洞长期稳定性分析[J]. 岩石力学与工程学报,2010,29(增1): 3227-3234. DAI Yonghao, CHEN Weizhong, YU Hongdan, et al. Long-term stability analysis of daban diversion tunnel buried in swelling mudstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 3227-3234.
[21]	李建军,张志强. 岩石蠕变对隧道二次衬砌结构影响的研究[J]. 现代隧道技术,2011,48(6): 58-64,81. doi: 10.3969/j.issn.1009-6582.2011.06.012 LI Jianjun, ZHANG Zhiqiang. Study of the influence of rock creep on the structure of a tunnel’s secondary lining[J]. Modern Tunnelling Technology, 2011, 48(6): 58-64,81. doi: 10.3969/j.issn.1009-6582.2011.06.012
[22]	徐国文,何川,汪耀,等. 流变荷载作用下隧道裂损二次衬砌结构安全性能研究[J]. 土木工程学报,2016,49(12): 114-123. XU Guowen, HE Chuan, WANG Yao, et al. Study on the safety performance of cracked secondary lining under action of rheological load[J]. China Civil Engineering Journal, 2016, 49(12): 114-123.
[23]	王迎超,尚岳全,孙红月,等. 复合式衬砌在围岩蠕变过程中的受力规律研究[J]. 水文地质工程地质,2010,37(2): 49-54. doi: 10.3969/j.issn.1000-3665.2010.02.011 WANG Yingchao, SHANG Yuequan, SUN Hongyue, et al. Study on mechanical rules of double-lining in creeping surrounding rock[J]. Hydrogeology & Engineering Geology, 2010, 37(2): 49-54. doi: 10.3969/j.issn.1000-3665.2010.02.011
[24]	师亚龙,郑波,刘志强,等. 流变效应作用下高地应力铁路软岩隧道衬砌结构长期稳定性研究[J]. 铁道标准设计,2017,61(10): 95-99. SHI Yalong, ZHENG Bo, LIU Zhiqiang, et al. Study on long term stability of tunnel lining structure in high stress soft rock tunnel under the effect of rheology[J]. Railway Standard Design, 2017, 61(10): 95-99.
[25]	钱文喜,耿大新,梁国卿. 围岩蠕变对运营隧道衬砌安全性的影响[J]. 公路交通科技,2020,37(9): 90-96. doi: 10.3969/j.issn.1002-0268.2020.09.012
[26]	汪耀. 高地应力下围岩蠕变对隧道结构长期安全性的影响分析[D]. 成都:西南交通大学,2017.
[27]	Itasca Consulting Group Inc. Fast lagrangian analyses of continua in three-dimensions[CP/OL]. (2012-06-23)[2023-08-12]. https://www.itascacg.com/software/FLAC3D.
[28]	Hibbitt, Karlsson and Sorensen, Inc. Abaqus analysis user’s guide[CP/OL]. (2014-05-06)[2023-08-12]. https://www.3ds.com/products/simulia/abaqus.
[29]	Ansys. Mechanical 12.0 user’s guide & theory guide [CP/OL]. (2009-10-14)[2023-08-12]. https://www.ansys.com/.
[30]	徐国文. 层状千枚岩地层隧道稳定性分析[D]. 成都:西南交通大学,2017.
[31]	过镇海,时旭东. 钢筋混凝土原理和分析[M]. 北京:清华大学出版社,2003.
[32]	中华人民共和国建设部. 混凝土结构设计规范:GB 50010—2002[S]. 北京:中国建筑工业出版社,2004.
[33]	YANG K, YAN Q X, ZHANG C, et al. Study on mechanical properties and damage evolution of carbonaceous shale under triaxial compression with acoustic emission[J]. International Journal of Damage Mechanics, 2021, 30(6): 899-922. doi: 10.1177/1056789521991193
[34]	刘新喜,李盛南,徐泽沛,等. 冻融循环作用下炭质页岩蠕变模型研究[J]. 中国公路学报,2019,32(11): 137-145. LIU Xinxi, LI Shengnan, XU Zepei, et al. Research on creep model of carbonaceous shale under freeze-thaw cycle[J]. China Journal of Highway and Transport, 2019, 32(11): 137-145.