Collaborative Target Azimuth Perception Algorithm of Unmanned Aerial Vehicles Based on Spatial Spectrum Estimation
-
摘要:
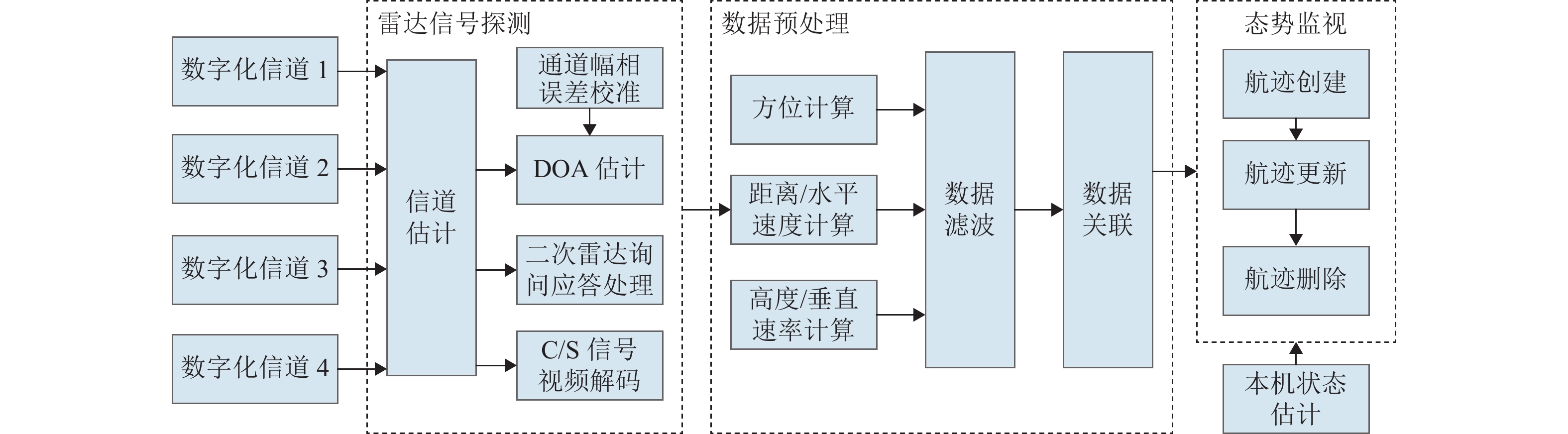
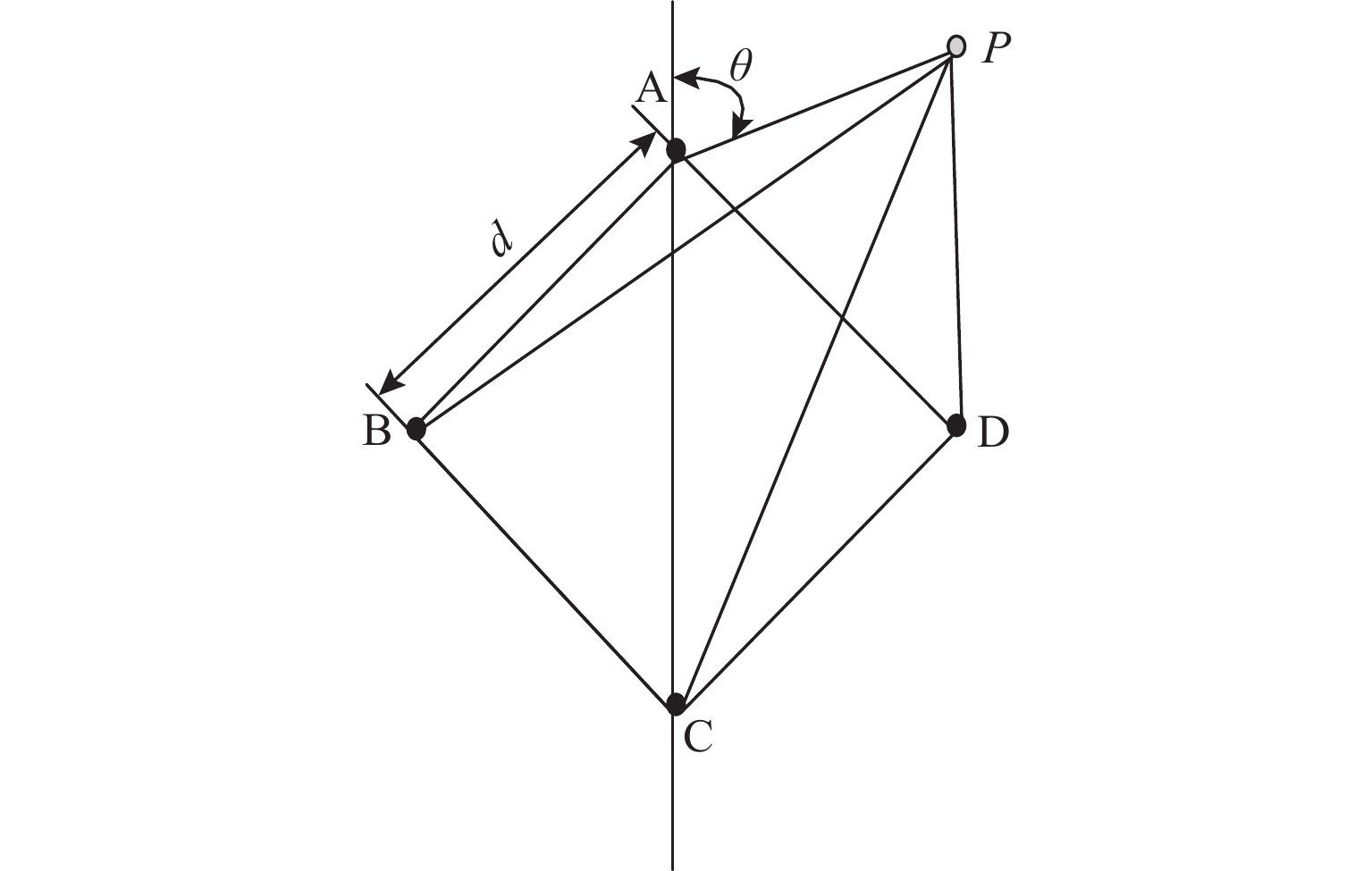
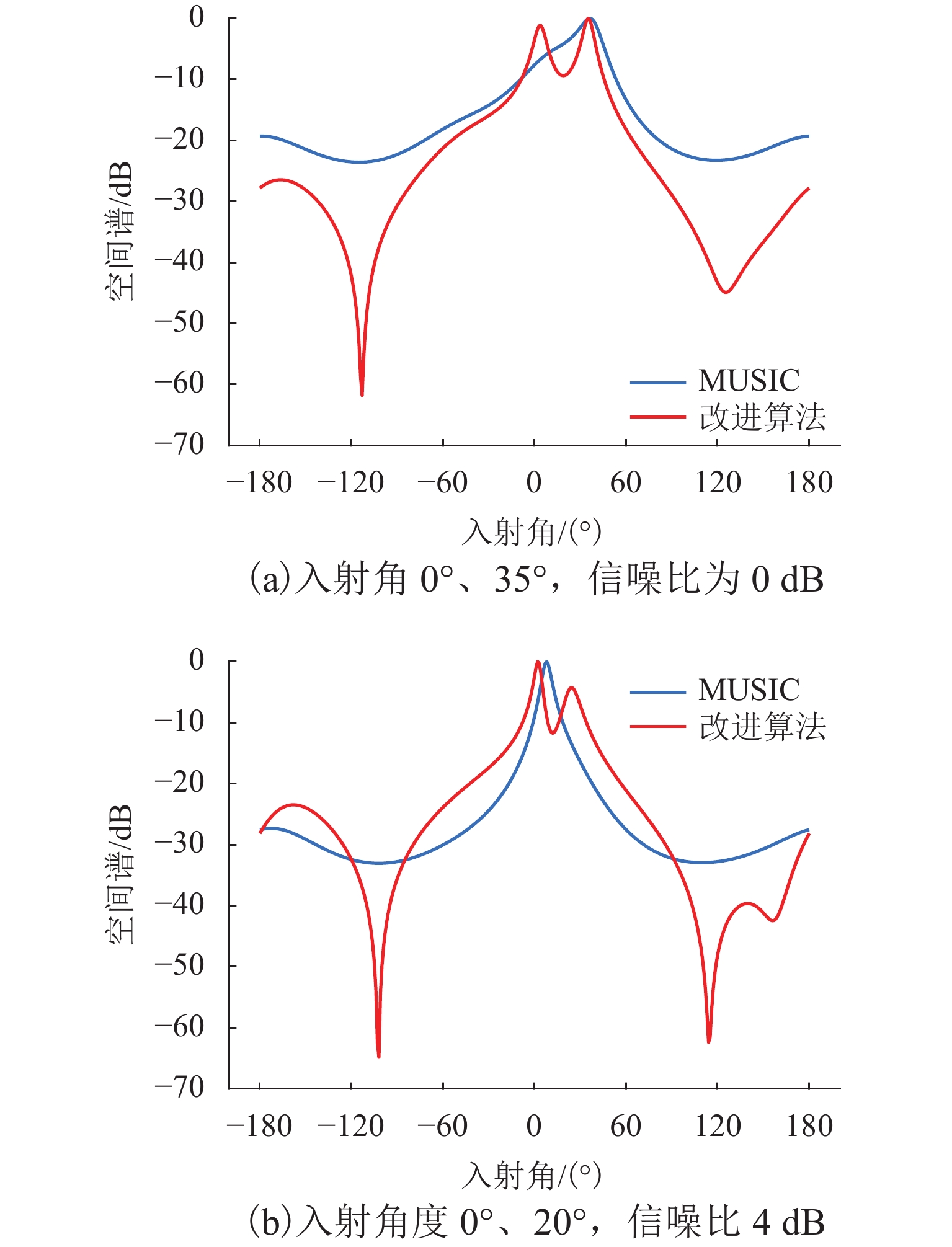
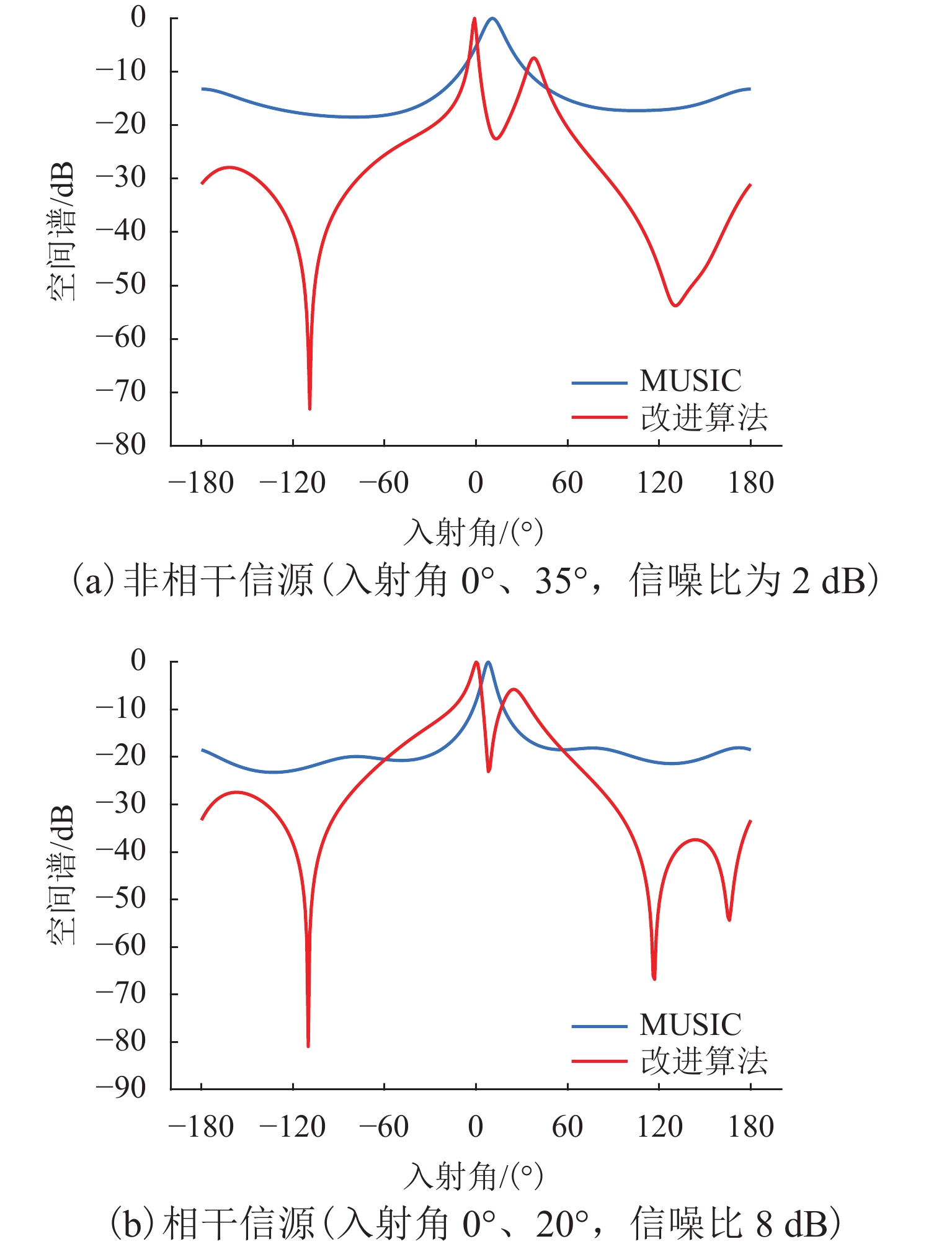
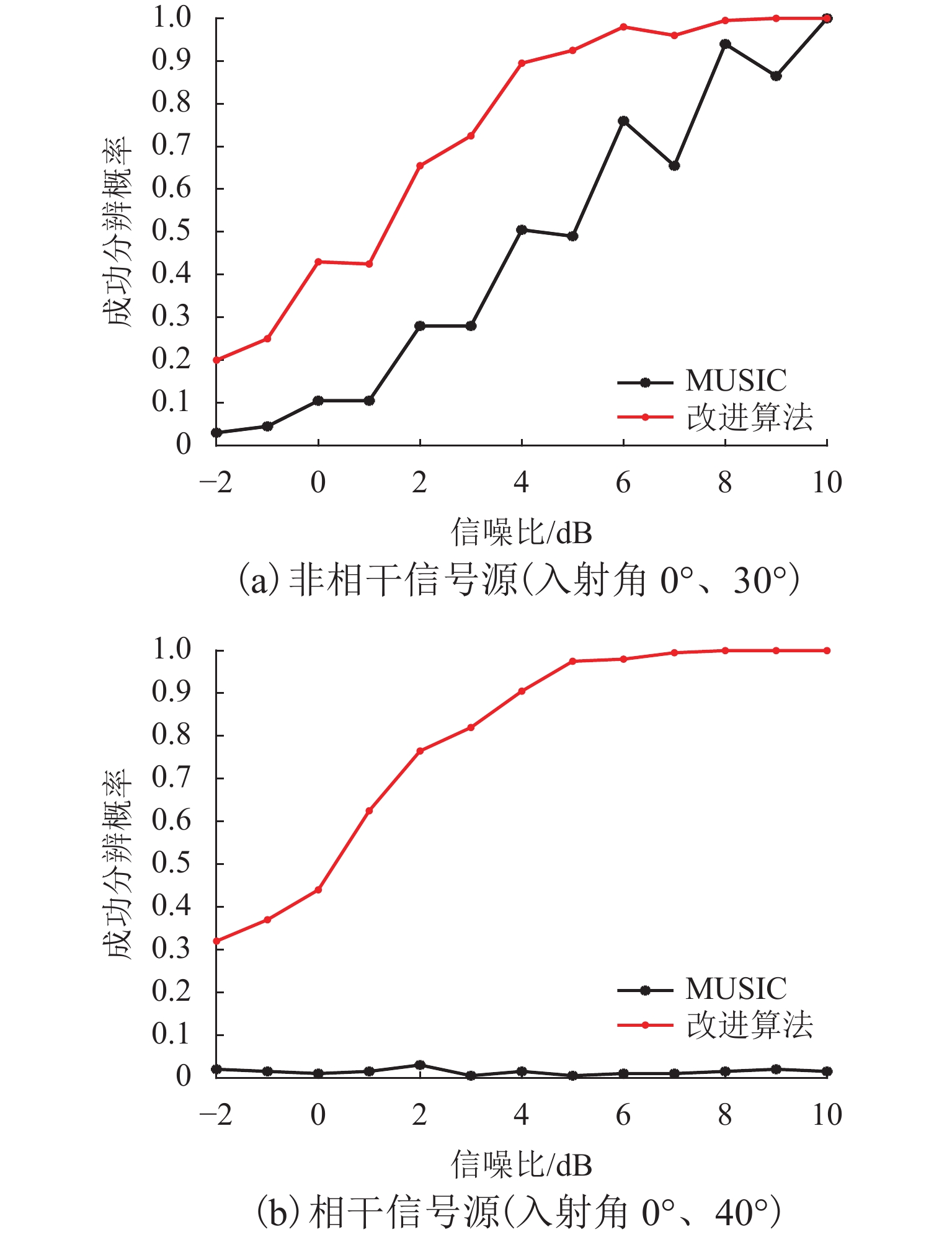
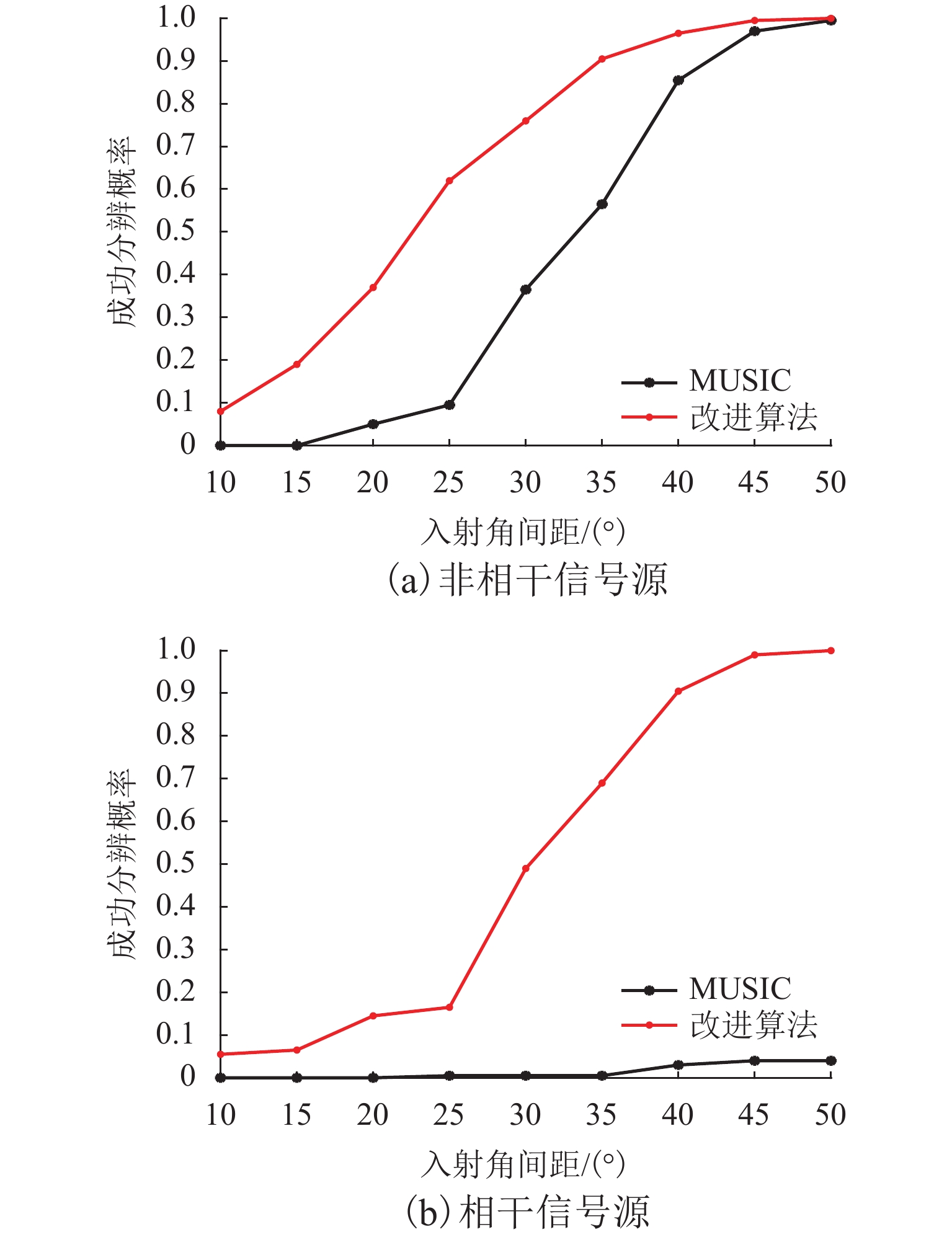
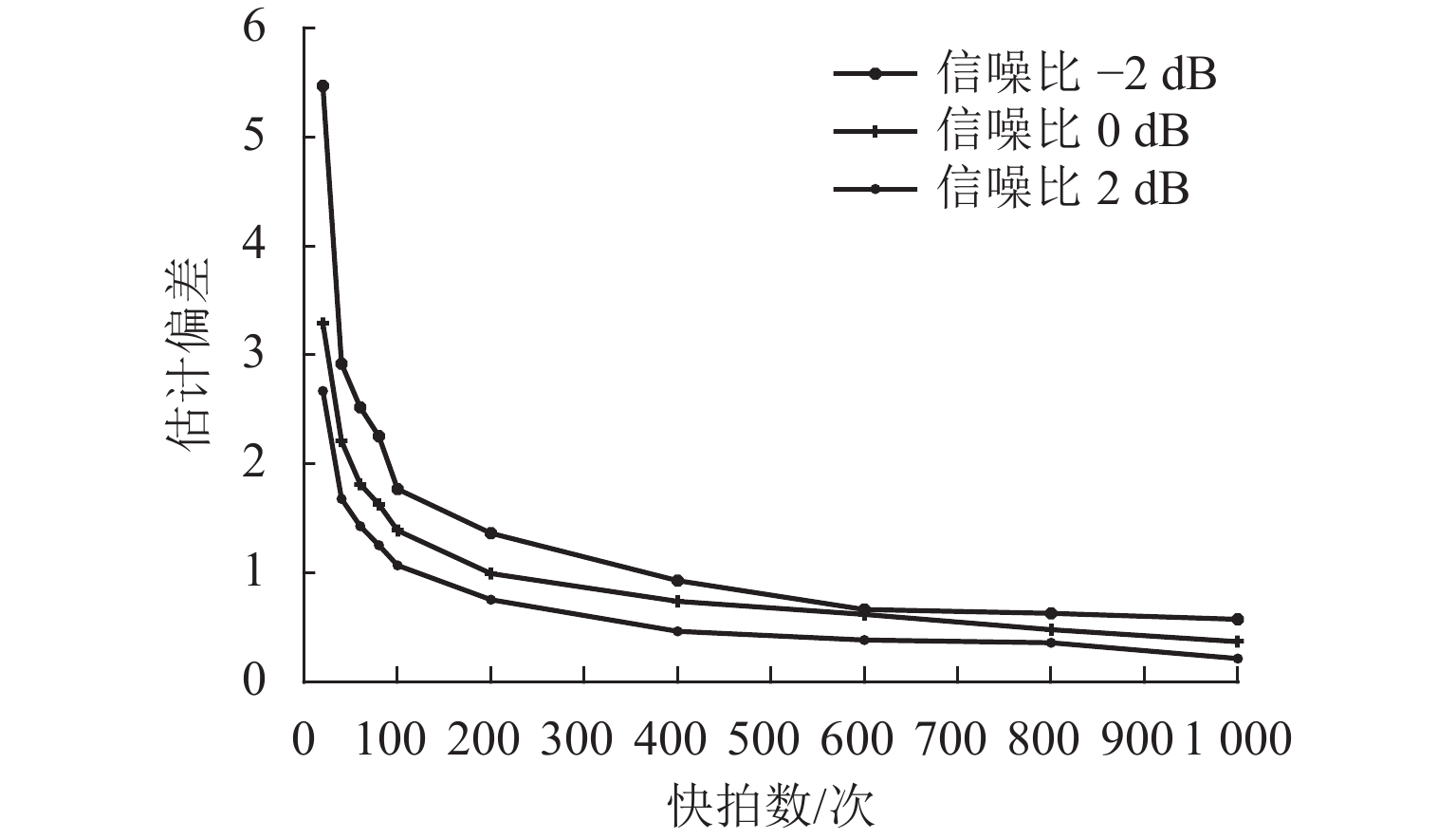
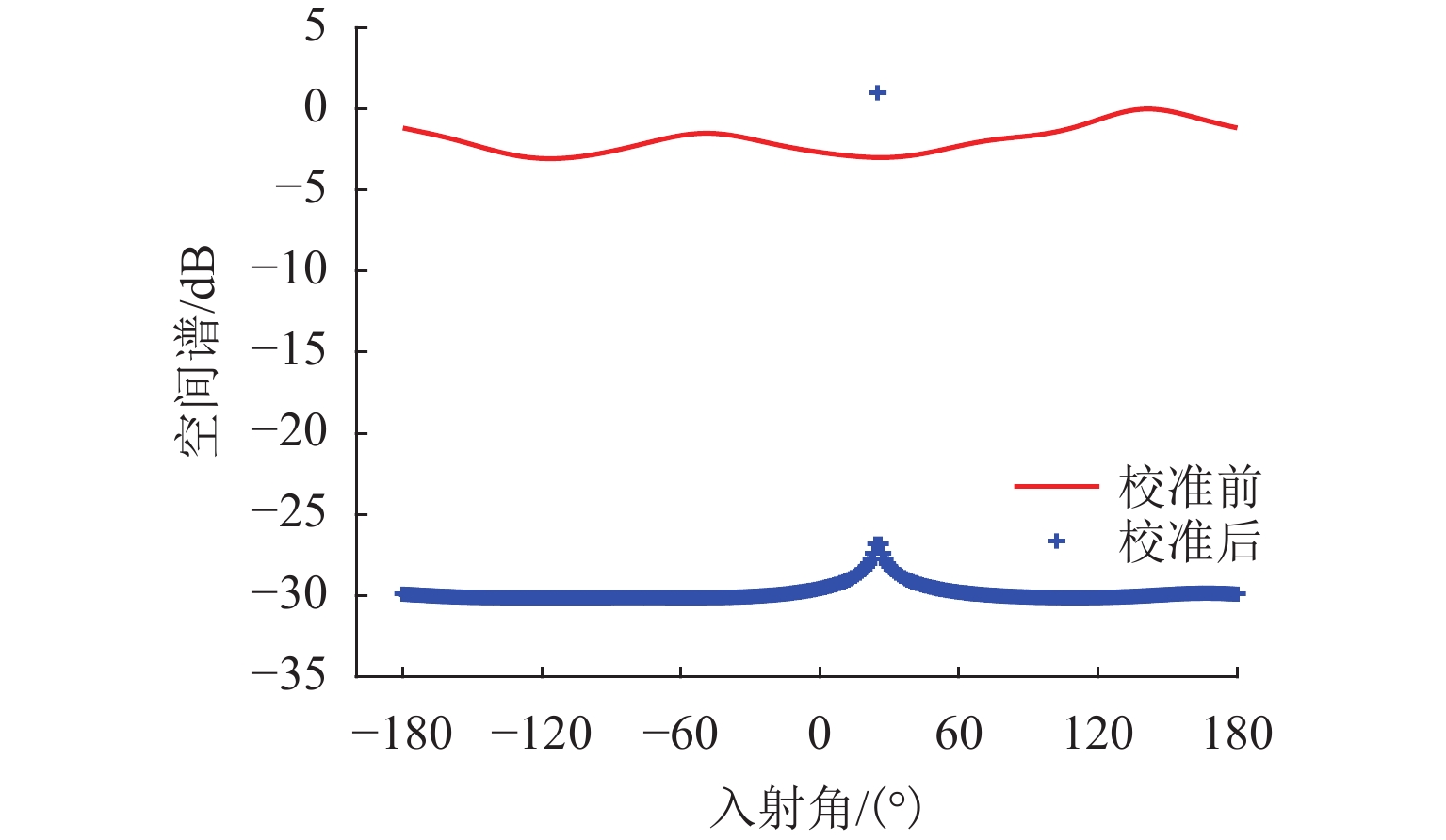
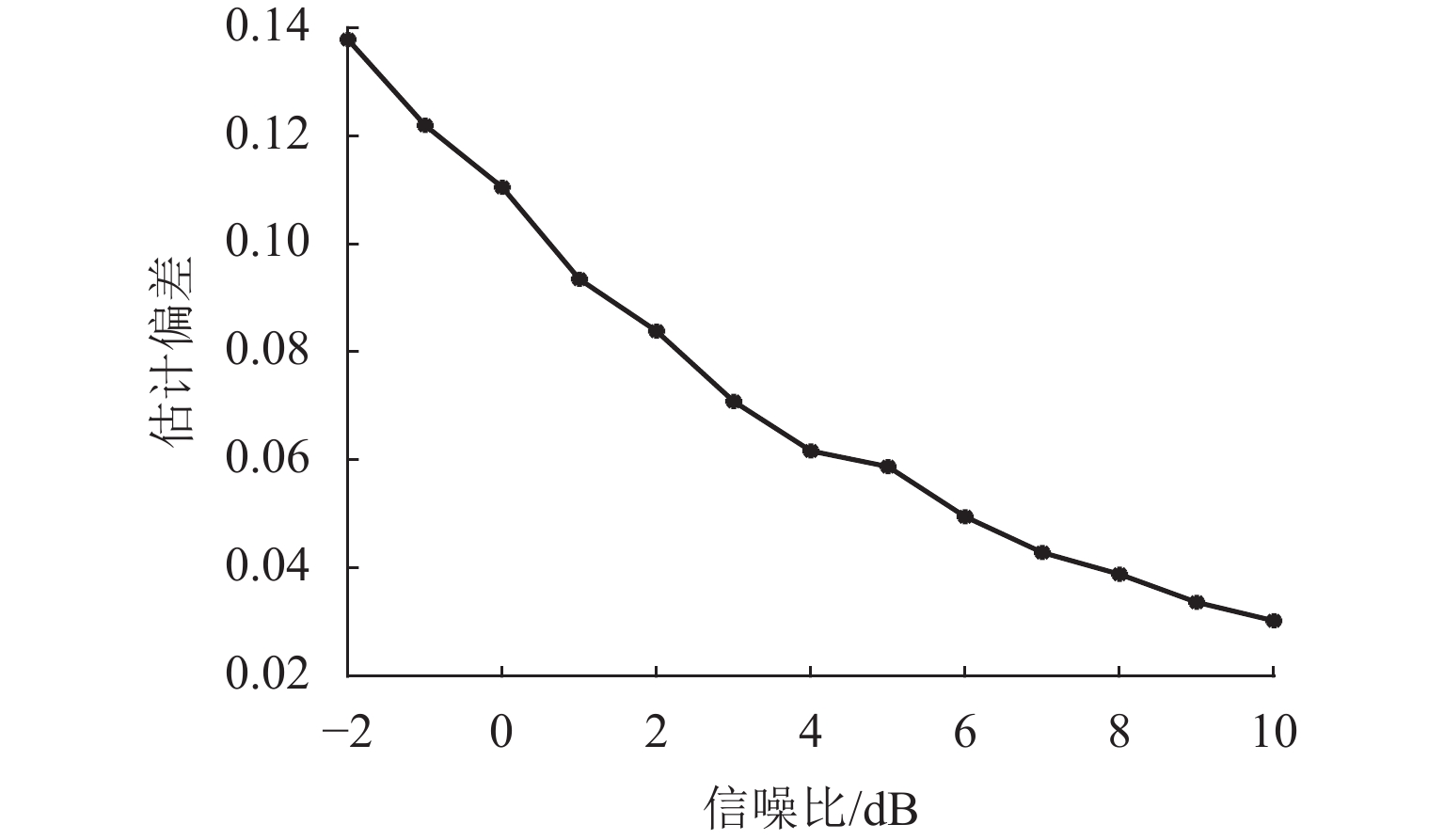
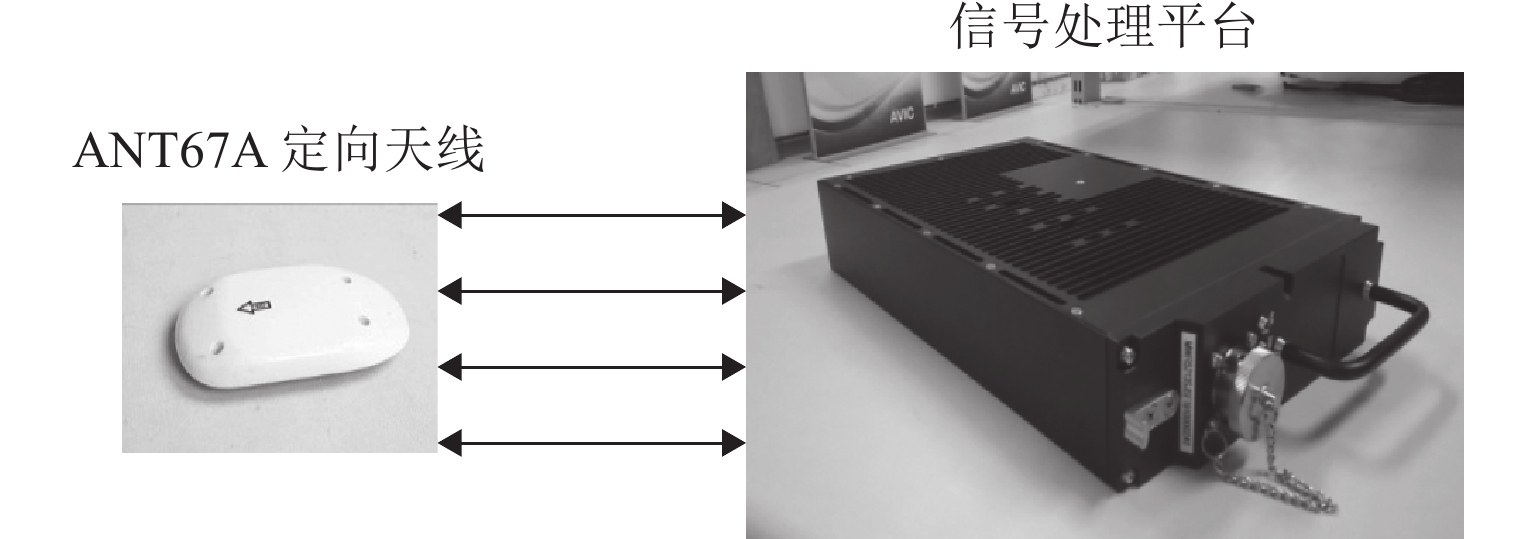
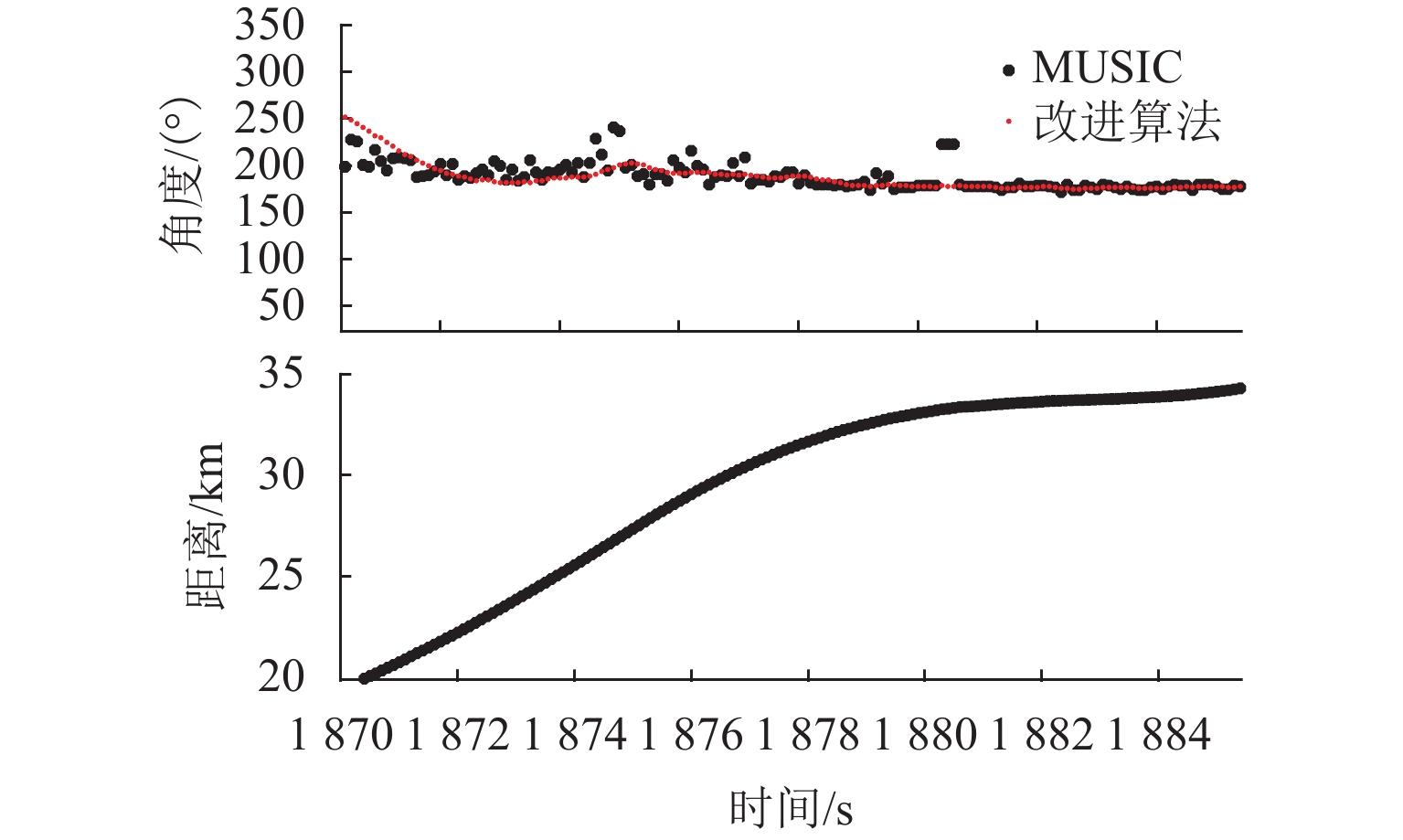
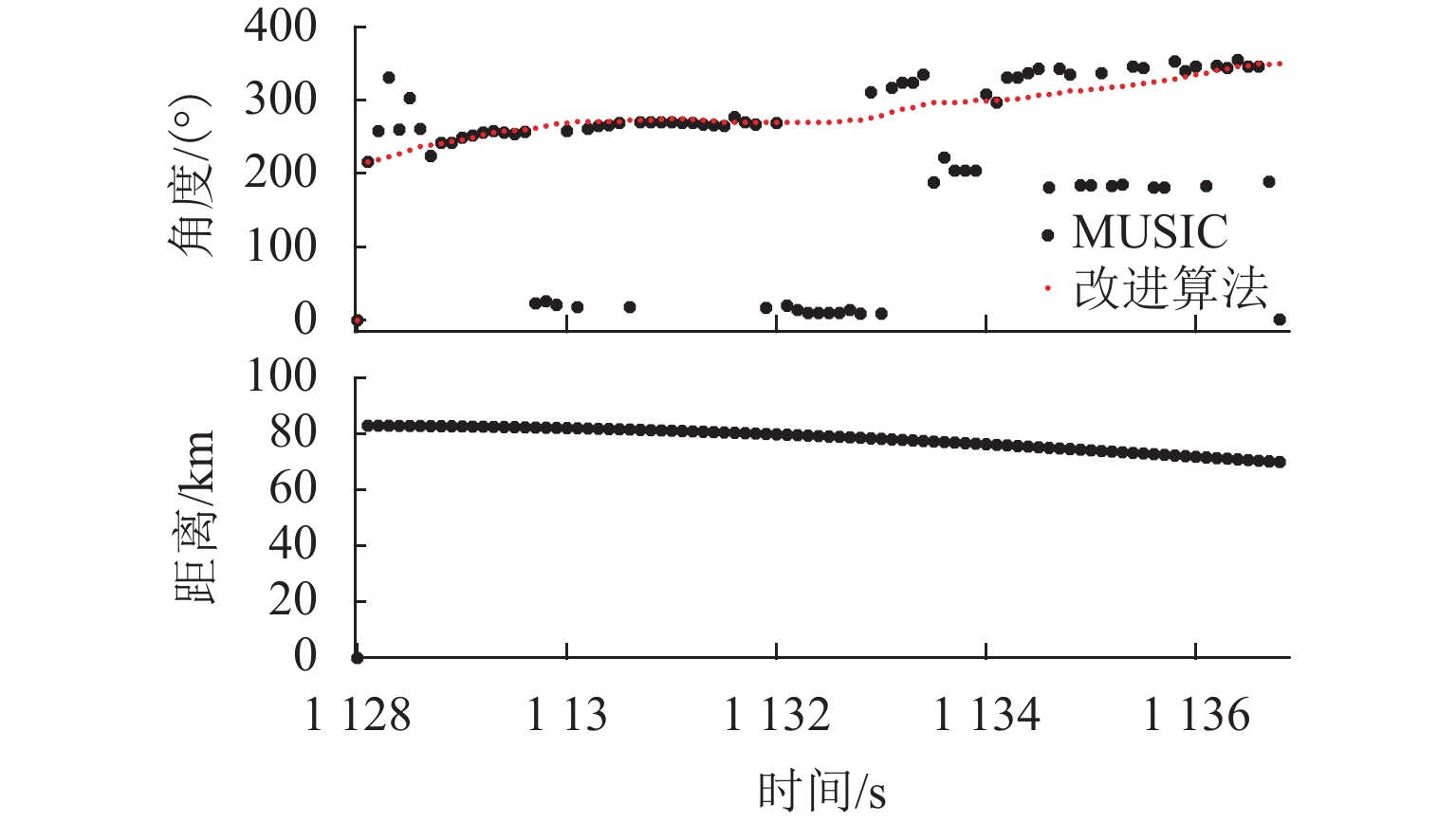
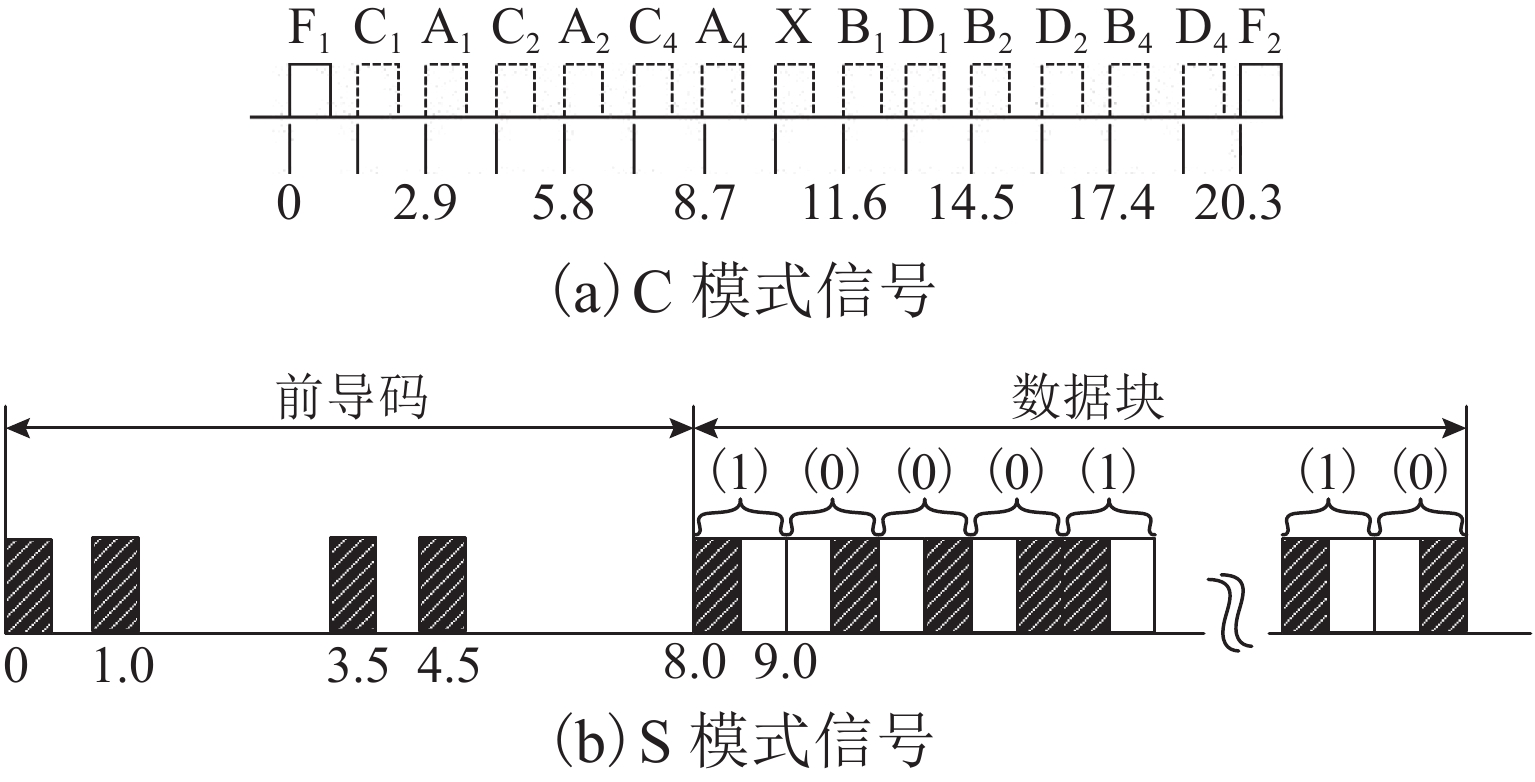
无人机协同目标感知技术是有人机无人机混合运行的重要安全保障. 针对复杂空域环境下的感知可靠性问题，分析大中型无人机的复杂融合空域运行场景，并确定无人机协同目标感知的精准性、高实时性、抗干扰性和低载荷性等需求，提出一种四单元阵列天线和数字化射频体制的无人机协同目标感知系统架构；同时，结合空管雷达信号特性和天线体制，设计方位感知算法，通过修正协方差矩阵、信号子空间加权和噪声子空间加权等方法，设计基于多信号分类（multiple signal classification，MUSIC）的空间谱估计算法，并提出基于子空间分解的幅相误差在线估计算法；最后，开展算法仿真试验和实际空域环境飞行试验. 研究结果表明：相比传统MUSIC算法，优化算法的方位感知高分辨性能提升23.3%，并改善了无人机协同目标方位感知的高实时性、抗干扰性和低载荷性.
Abstract:Collaborative target perception technology of unmanned aerial vehicles (UAVs) is an important security guarantee for the mixed operation of manned aerial vehicles and UAVs. In view of the perception reliability problem in complex airspace environments, the operation scenarios of large and medium-sized UAVs in complex mixed airspace were analyzed, and the needs of collaborative target perception of UAVs, such as precision, high real-time performance, anti-interference, and low load were determined. A collaborative target perception system architecture of UAVs combining a four-unit array antenna and digital radio frequency was proposed. At the same time, the signal characteristics and antenna system of air traffic control (ATC) radar were utilized to design an azimuth perception algorithm. By modifying the covariance matrix and weighting signal subspace and noise subspace, a spatial spectrum estimation algorithm based on multiple signal classification (MUSIC) was designed. In addition, an online amplitude-phase error estimation algorithm based on subspace decomposition was designed. Finally, the algorithm simulation test and flight test in a real airspace environment were carried out. The research results show that compared with the traditional MUSIC algorithm, the improved algorithm improves the high resolution performance of azimuth perception by 23.3% and enhances the high real-time performance, anti-interference, and low load of the collaborative target azimuth perception of UAVs.
-
近年来，随着无人机系统的飞速发展和在各领域的广泛应用，无人机大规模运行与有限空域资源的矛盾日益突出，而大中型无人机与有人机共享空域混合运行是行业内公认的有效解决手段. 在混合运行空域中，无人机必须对现存的有人机等协同目标具备感知能力，能够与协同目标实现协调的飞行环境感知、碰撞威胁估计与规避路径规划，以保障空域运行安全[1-6]. 无人机的协同目标感知能力相比有人机具有更高的技术难度和复杂度. 由于受无人机运行场景和机身平台等复杂环境影响，感知信息可能不精确，导致无人机对协同目标的态势监视不稳定，当存在交通冲突时，还会影响多机之间的安全间隔协调管理，制约有人、无人机的安全混合运行[7-12].
国内外对无人机协同目标感知进行了大量的研究试验. R3公司研制了无人机感知与规避系统，采用广播式自动相关监视（automatic dependent surveillance-broadcast，ADS-B）技术实现协同目标感知； GA-ASI公司采用ADS-B、机载防撞系统（traffic collision avoidance system，TCAS）、雷达等传感器数据进行多源异构信息融合，实现无人机的态势监视和避撞. 这些研究试验验证了无人机使用C/S数据链和ADS-B进行协同目标感知的可行性，但是没有考虑复杂空域环境对感知性能的影响[13]. 针对复杂环境下的信号探测技术，国内外也有深入研究，Miller等[14-15]提出了强干扰下相干多目标的识别算法和提高空间谱估计分辨率的超分辨率测向算法，但未考虑无人机协同目标感知信号的应用需求.
1. 无人机协同目标感知系统设计
1.1 需求分析
协同目标通过空管雷达C/S模式信号进行感知，信号格式如图1所示. C模式信号由一对框架脉冲（F1、F2）和代码脉冲（C1、A1、C2、A2、C4、A4、X、B1、D1、B2、D2、B4、D4）组成，脉冲宽度为0.45 μs，信号时长20.3 μs. S模式信号由4个前导模块（8.0 μs）和1个数据块（56.0 μs或112.0 μs）组成，脉冲宽度为0.50 μs，信号时长为64.0 μs或120.0 μs. 2种模式信号的时长均较短，需要在一组信号帧的时长内完成探测感知，同时考虑无人机的高速动态性. 因此，协同目标感知算法在精确性的基础上，还需具有高实时性.
与有人机相比，大中型无人机机体小、载重轻. 因此，协同目标感知系统载荷必须符合低功耗和轻量化的无人机装机要素要求，为兼顾感知性能的精确性和装机需求，本文选择沿用有人机的四单元阵列天线.
另外，由于混合运行场景的大交通流、复杂电磁环境等因素，以及空管雷达的询问应答体系的影响，协同信号可能存在非相干信源混叠、相干信源干扰、低信噪比等现象. 因此，协同目标感知算法应具备相应的抗干扰能力.
综上分析，无人机协同目标感知算法需要具有精准性、高实时性、抗干扰性和低载荷性.
1.2 系统架构设计
根据1.1节的需求分析，本文参考有人机感知流程和无人机运行场景[16-18]，提出的协同目标感知算法框架如图2所示. 通过对协同目标的探测和识别，计算获取交通态势信息，为任务决策和规划提供精确数据支持. 主要分为数字化射频信道、雷达信号探测、数据预处理和态势监视等主要步骤. 雷达信号探测单元接收4路数字化信道的射频信号，通过多信号分类（multiple signal classification，MUSIC）算法和波达方向定位技术（direction of arrival，DOA）估计计算来波方位，通过空管二次雷达的询问应答体制计算相对距离，通过C/S信号视频解码获取协议信息内容，从而得到协同目标的方位、距离和高度等航迹数据；数据预处理单元完成应答信号的大数据清洗、滤波和关联；态势监视单元通过航迹创建和维护实现无人机对协同目标的态势监视.
图 2 无人机协同目标感知系统架构Figure 2. Collaborative target perception system architecture of UAVs1.3 主要关键技术
1.3.1 方位感知算法
协同目标的方位信息是态势监视、交通冲突水平解脱和任务决策规划的主要参数. 方位感知性能是无人机协同目标感知的主要指标. 在考虑空管雷达信号特性和采用四单元阵列天线的技术体制下，本文采用基于空间谱估计的方位感知算法，通过改进MUSIC算法，实现基于子空间加权的超分辨率优化设计、相干信源的DOA优化设计，从而提高方位感知算法的精准性、高实时性、抗干扰性.
1.3.2 数字化射频信道
数字化射频信道是解决协同目标感知系统低功耗轻量化的重要技术路径. 一方面，通过基于子空间分解的幅相误差在线估计算法设计，实现多路收发通道的自动校准，从而去掉射频校准硬件网络和校准辐射源；另一方面，采取软件无线电技术直接实现射频信号数字化，去掉硬件混频和滤波电路，从而降低4路接收通道的硬件资源开销.
1.3.3 感知信息融合
感知信号融合实现航迹信息的清洗、滤波和关联，影响协同目标感知的整体性能，有人机采用了卡尔曼滤波估计来实现复杂背景下多传感器信息融合，有较好的工程应用效果，经分析能够满足无人机协同目标感知需求，本文不再累述.
2. 基于空间谱估计的方位感知算法
2.1 四单元阵列天线模型
方位感知算法沿用有人机交通监视系统的四单元阵列天线体制，四单元阵列天线所示，由4个无方向的全向阵元构成，A、B、C和D 阵元呈正方形图像排列，如图3所示. 图中：d为正方形边长，P为来波信号位置.
假设有M个窄带信号源，来波方向与阵元法线的夹角分别为$ {\mathrm{{\mathrm{\theta}} }}_{1} $,${\mathrm{\theta }}_{2}, \cdots, {\mathrm{\theta }}_{M}$，选取A阵元作为参考阵元，整个阵列在时刻t接收到的信号为
X(t)=AS(t)+N(t)， (1) 式中： ${\boldsymbol{A}} $为导向矢量，如式（2）所示，其中，λ为波长；${\boldsymbol{S}}(t) $为信号数据矢量；${\boldsymbol{N}}(t) $为噪声数据矢量.
A=[11⋯1ej(2πλd(sinθ1)−π4)ej(2πλd(sinθ2)−π4)⋯ej(2πλd(sinθM)−π4)ej(2πλd(sinθ1)+2πλd(cosθ1)−π4)ej(2πλd(sinθ2)+2πλd(cosθ2)−π4)⋯ej(2πλd(sinθM)+2πλd(cosθM)−π4)ej(2πλd(cosθ1)−π4)ej(2πλd(cosθ2)−π4)⋯ej(2πλd(cosθM)−π4)]. (2) 2.2 MUSIC算法原理
MUSIC算法作为阵列天线测角技术的经典算法，相比相干算法等具备更高精度和更好抗干扰性能，算法基本流程如下[19-21]：
步骤1 利用天线阵列对空间的来波信号进行多路数据接收，得到接收信号${\boldsymbol{X}} $(t).
步骤2 计算阵列接收数据的协方差矩阵$ {{\boldsymbol{R}}} $如式（3）所示. 根据信号与噪声的非相关性，数据协方差矩阵分解成信号部分（$ {{\boldsymbol{A}}}{{{\boldsymbol{R}}}}_{{\mathrm{S}}}{{{\boldsymbol{A}}}}^{{\mathrm{H}}} $）和噪声部分（$ {{{\boldsymbol{R}}}}_{{{\mathrm{N}}}} $）. 其中，$ {{{\boldsymbol{R}}}}_{{\mathrm{S}}} $为信号协方差矩阵.
R=E(XXH)=ARSAH+RN. (3) 步骤3 构造噪声子空间${{{\boldsymbol{E}}}}_{{\mathrm{N}}}$.
对$ {{\boldsymbol{R}}} $进行特征分解，得到M个特征值，从大到小排序为
\lambda_{1}\geqslant\lambda_{2}\geqslant \cdots \geqslant\lambda_{M}. (4) 在M个特征值中，D个特征值较大的信号特征值对应的特征向量组成信号子空间（根据接收端视频信号解码算法确定信源个数），M−D个噪声特征值对应的特征向量组成噪声子空间. 得到互相正交的信号子空间$ {{{\boldsymbol{E}}}}_{{{\mathrm{S}}}} $=(e1,e2,$\cdots $, eD)和噪声子空间$ {{{\boldsymbol{E}}}}_{{{\mathrm{N}}}} $=(e1+D,e2+D,$\cdots $, eM).
步骤4 计算空间谱函数$ {{{\boldsymbol{P}}}}_{{\mathrm{MUSI}}\mathit{C}}\left({\boldsymbol{\theta}} \right) $，如式（5）所示，θ=(θ1,θ2,$\cdots $, θM). 进行谱峰搜索，$ {{{\boldsymbol{a}}}}^{\mathbf{H}}\left({\boldsymbol{\theta}} \right) $为来波信源，由于信号子空间与噪声子空间的正交性，在来波方向上，$ {{\boldsymbol{a}}}^{{\mathrm{H}}}\left({\boldsymbol{\theta}} \right){{\boldsymbol{E}}}_{{\mathrm{N}}} $是一个趋近于0的矢量. 因此，估计波达方向即为极大值点对应的信号角度.
{{{\boldsymbol{P}}}}_{{\mathrm{MUSI}}\mathit{C}}\left({\boldsymbol{\theta}} \right)=\dfrac{\mathrm{I}}{{{\boldsymbol{a}}}^{{\mathrm{H}}}\left({\boldsymbol{\theta}} \right){{\boldsymbol{E}}}_{{\mathrm{N}}}{{\boldsymbol{E}}}_{{\mathrm{N}}}^{{\mathrm{H}}}{{\boldsymbol{a}}}\left({\boldsymbol{\theta}} \right)}. (5) 2.3 基于子空间加权的超分辨率优化设计
经典MUSIC算法性能受信噪比和快拍数影响较大. 当信噪低或者快拍数较少，或者2个来波信号方位接近时，空间谱函数的谱峰容易混叠，导致谱峰搜索不准确，MUSIC算法分辨性能下降. 而无人机协同目标感知受到天线阵元个数、信号脉冲宽度以及空管通信体制的约束，限制MUSIC算法的应用. 本文提出一种信号子空间和噪声子空间加权的超分辨率优化算法，旨在提高复杂信号环境下的空间谱函数分辨性能.
首先，构建加权的信号子空间. 根据信号子空间对非理想环境下的信噪比影响不敏感特性，通过信号特征值和信号特征向量构建信号子空间EIS，如式（6）所示.
{{{\boldsymbol{E}}}}_{\mathrm{I}\mathrm{S}}=({\lambda }_{1}^{-1}{e}_{1},{\lambda }_{2}^{-1}{e}_{2},\cdots ,{\lambda }_{D}^{-1}{e}_{D}) . (6) 采用信号子空间的主特征值倒数对特征向量进行加权，构建基于信号子空间的谱函数$ {{{\boldsymbol{P}}}}_{{{\mathrm{I}}}{{\mathrm{S}}}}\left({\boldsymbol{\theta}} \right) $，如式（7）所示，修正了最大特征向量方向上的权重，从而降低空间谱函数中最大特征值对应方位的幅度值，提高对来波方位相近目标的分辨能力.
{{{\boldsymbol{P}}}}_{{{\mathrm{IS}}}}\left({\boldsymbol{\theta}} \right)={{{\boldsymbol{E}}}}_{{{\mathrm{IS}}}}{{{\boldsymbol{E}}}}_{{\mathrm{IS}}}^{{\mathrm{H}}}=\sum _{i=1}^{D}{\mathrm{\lambda }}_{i}^{-1}\left|{{\boldsymbol{a}}}^{{\mathrm{H}}}\right.(\mathrm{{\boldsymbol{\theta}} }){e}_{i}{|}^{2} . (7) 然后，构建校正的噪声子空间. 利用噪声特征值对相应的特征向量进行校正处理，这种方法修正噪声子空间特征值的权重，控制信号发射程度，进而提高分辨率.
对噪声特征值进行校正：$ {\mathrm{\lambda }}_{i,{{c}}} $=$ {\mathrm{\lambda }}_{i}^{-1} $ + c （c为校正系数，满足$ \dfrac{{{\lambda}}_{D + 1} + {c}}{{{\lambda}}_{M} + {c}} $<1.5）. 改造后的噪声子空间为
{{{\boldsymbol{E}}}}_{{{\mathrm{I}}}{{\mathrm{N}}}} =( {\mathrm{\lambda }}_{D + 1,{{c}}} e_{D + 1}, {\mathrm{\lambda }}_{D + 2} e_{D + 2,{{c}}},\cdots, {\mathrm{\lambda }}_{M,c} e_{M}). (8) 基于噪声子空间的空间谱函数为
{{{{\boldsymbol{P}}}}_{{{\mathrm{I}}}{{\mathrm{N}}}}\left({{\boldsymbol{\theta}} }\right)={{\boldsymbol{E}}}}_{{{\mathrm{IN}}}}{{{\boldsymbol{E}}}}_{{{\mathrm{I}}}{{{{\mathrm{N}}}}}}^{{{\mathrm{H}}}}={1}\Bigg/{\displaystyle\sum\limits_{i=D + 1}^{M}{\mathrm{\lambda }}_{i,c}\left|{{\boldsymbol{a}}}^{{\mathrm{H}}}({{{{\boldsymbol{\theta}}}} }){e}_{i}\right|^{2}} . (9) 最后，构建超分辨率优化设计的空间谱函数. 根据加权信号子空间和校正噪声子空间的特性分析. 在信源方向上，$ {{{\boldsymbol{P}}}}_{{{\mathrm{I}}}{{{{\mathrm{S}}}}}}\left({\boldsymbol{\theta}} \right) $和$ {{{\boldsymbol{P}}}}_{{{\mathrm{I}}}{{\mathrm{N}}}}\left(\mathit{{\boldsymbol{\theta}} }\right) $均为极大值，$ \mathrm{而} {{{\boldsymbol{P}}}}_{{{\mathrm{I}}}{{\mathrm{S}}}}\left(\mathit{{\boldsymbol{\theta}} }\right) $、$ {{{\boldsymbol{P}}}}_{{{\mathrm{I}}}{{\mathrm{N}}}}\left(\mathit{{\boldsymbol{\theta}} }\right) $将呈现更加尖锐的谱峰. 为提高分辨率，定义优化后的空间谱函数为
\begin{split}& {{{\boldsymbol{P}}}}_{{{\mathrm{I}}}{{\mathrm{M}}}{{\mathrm{U}}}{{\mathrm{S}}}{{\mathrm{IN}}}}\left({\boldsymbol{\theta}} \right)={{{\boldsymbol{P}}}}_{{{\mathrm{IS}}}}\left(\mathit{{\boldsymbol{\theta}} }\right) {{{\boldsymbol{P}}}}_{\mathrm{IN}}\left(\mathit{{\boldsymbol{\theta}} }\right) = \\ &\quad {\displaystyle\sum\limits _{i=1}^{D}{\mathrm{\lambda }}_{i}^{-1}\left|{{\boldsymbol{a}}}^{{\mathrm{H}}}\right.(\mathrm{{\boldsymbol{\theta}} }){e}_{i}{|}^{2}}\Bigg/{\displaystyle\sum\limits _{i=D + 1}^{M}{\mathrm{\lambda }}_{i,c}\left|{{\boldsymbol{a}}}^{{\mathrm{H}}}\right.(\mathrm{{\boldsymbol{\theta}} }){e}_{i}{|}^{2}} .\end{split} (10) 2.4 相干信源的DOA优化设计
由于受到无人机机身、海面等反射产生的多径信号影响，无人机协同目标感知信号存在相干信源干扰，即入射到天线阵列的信号为主频信号和多径反射信号的矢量叠加. 由于主频信号和多径信号的相关性，两者之间只相差一个复衰落常系数. 这导致阵列接收数据的协方差矩秩损失，使得大特征值个数小于信号源数，进而造成信号子空间的维数不等于信号源数，破坏信号子空间与噪声子空间之间的正交性，严重影响了DOA 估计算法的效果. 为改善相干信源的空间谱估计性能，本文设计了一种针对相干信源的DOA优化算法.
空间平滑法是行业内常见并且有效的解相干算法，其主要原理是：如果天线阵列同时接收相干信源，那么所有阵列平滑后的协方差矩阵的大特征值的个数就不会减少. 根据平滑次数和子阵阵元数，最多能够分辨3M/2个相干源，该算法牺牲阵列的有效孔径，从而减低算法的分辨率，同时，多次平滑极大增加了算法的计算量.
考虑无人机协同目标感知的运行场景，主频信号经多次多径反射后，信号强度大幅衰落，对主频信号的干扰影响较小，相干信号的处理主要针对主频信号和一次多径反射信号. 同时，结合四单元阵列天线，对空间平滑算法进行改造，修正后的信源信号为
{{\boldsymbol{Y}}}\left(t\right)={{{\boldsymbol{J}}}}_{M}{{{\boldsymbol{X}}}}^{*}\left(\mathit{t}\right)， (11) 式中：$ {{{\boldsymbol{J}}}}_{M} $为M阶交换矩阵（反对角线元素为1，其余元素为0）.
${{\boldsymbol{Y}}}\left(t\right) $的协方差矩阵为
\begin{split}& {{{\boldsymbol{R}}}}_{{\mathrm{Y}}}={{{E}}}({{\boldsymbol{Y}}}{{{\boldsymbol{Y}}}}^{{\mathrm{H}}})={{\boldsymbol{J}}}_{M}{{{\boldsymbol{A}}}{{{\boldsymbol{R}}}}_{{\mathrm{S}}}{{\boldsymbol{A}}}}^{{\mathrm{H}}}{{{{\boldsymbol{J}}}}_{M}} + {{{\boldsymbol{R}}}}_{{\mathrm{N}}} = \\ &\quad {{{{\boldsymbol{J}}}}_{M}{{\boldsymbol{R}}}}^{*}{{{\boldsymbol{J}}}}_{M}. \end{split} (12) 重构后的解相干协方差矩阵为
{{{\boldsymbol{R}}}}_{{{\mathrm{I}}}}=({{{{\boldsymbol{R}}}}} + {{\boldsymbol{R}}}_{{\mathrm{Y}}})/2=({{\boldsymbol{R}}} + {{{{\boldsymbol{J}}}}_{M}{{\boldsymbol{R}}}}^{*}{{{\boldsymbol{J}}}}_{M})/2. (13) 解相干处理相当于在不损失阵元数量的前提下进行一个空间平滑，因此仅能估计2个相干信源. 同时，对于非相干信源的计算处理，由于$ {{{\boldsymbol{R}}}}_{{\mathrm{S}}} $为实对角阵，$ {{{\boldsymbol{R}}}}_{{\mathrm{Y}}} $与R相同，因此，本算法不影响对非相干信源的DOA估计.
2.5 方位感知算法结构
按照2.3、2.4节的分析，无人机协同目标方位感知算法的具体步骤如下：
步骤1 利用四单元阵列天线阵列对空间辐射源进行数据接收，得到阵列接收数据；
步骤2 对C/S模式信号进行同步，并根据C模式框架脉冲和S模式前导码脉冲锁定快拍数；
步骤3 使用式（13）计算优化的协方差矩阵$ {{\boldsymbol{R}}}_{{\mathrm{I}}} $，并进行特征分解，得到特征值和特征向量，组成信号子空间和噪声子空间；
步骤4 使用式（6）、（8）分别对信号子空间和噪声子空间进行加权处理；
步骤5 使用式（10）构造优化后的空间谱函数，进行谱峰搜索即完成波达方向估计.
步骤6 根据航迹方位的信息融合，得出协同目标方位态势.
3. 基于幅相误差在线估计的数字化射频信道
3.1 幅相误差影响分析
在协同目标方位感知算法设计中，阵列天线多通道的幅相一致性对DOA估计和波束成型的性能有很大影响，空管二次雷达的使用频率为L波段，射频收发通道中的放大器、混频器和滤波器等有源器件在不同温度下，其幅相特性存在非线性变化的现象. 同时，由于硬件加工误差等影响，每个阵元的通道增益和相移都会出现一定范围内的随机偏差，从而导致多个收发通道之间存在不一致性，影响DOA估计性能.
采用子空间类MUSIC算法进行来波DOA估计时，根据2.1节分析得到的信号模型，由式（14）可知，当阵元存在通道幅相误差时，
{\boldsymbol{X}}(t)= {{\boldsymbol{\varGamma }}} {\boldsymbol{AS}}(t) + {\boldsymbol{N}}(t)\text{，} (14) 式中：$ {{\boldsymbol{\varGamma}} } $=${ \left(1, {\mu }_{1}{{\mathrm{e}}}^{{\mathrm{j}}{\vartheta }_{1}},{\mu }_{2}{{\mathrm{e}}}^{{\mathrm{j}}{\vartheta }_{2}},{\mu }_{2}{{\mathrm{e}}}^{{\mathrm{j}}{\vartheta }_{2}}\right)}^{\mathrm{T}}$，为通道幅相误差矢量；$ {\mu }_{1} $～$ {\mu }_{3} $为通道间的幅度误差；$ {\vartheta }_{1} $～$ {\vartheta }_{3} $为通道间的相位误差.
考虑幅相误差的空间功率谱函数为
\begin{split}& {{{\boldsymbol{P}}}}_{{{\mathrm{c}}}}\left({\boldsymbol{\theta}} \right)=\dfrac{\boldsymbol{I}}{{{{\boldsymbol{a}}}}^{\mathrm{H}}\left({\boldsymbol{\theta}} \right){\widetilde{{{\boldsymbol{E}}}}}_{\mathrm{N}}{\widetilde{{{\boldsymbol{E}}}}}_{\mathrm{N}}^{\mathrm{H}}{{\boldsymbol{a}}}\left({\boldsymbol{\theta}} \right)}= \dfrac{{{\boldsymbol{I}}}}{{{{\boldsymbol{a}}}}^{\mathrm{{H}}}\left({\boldsymbol{\theta}} \right)({{\boldsymbol{I}}}-{\widetilde{{{\boldsymbol{E}}}}}_{\mathrm{S}}{\widetilde{{{\boldsymbol{E}}}}}_{\mathrm{S}}^{\mathrm{H}}){{\boldsymbol{a}}}\left({\boldsymbol{\theta}} \right)}， \end{split} (15) 式中：${\widetilde{{{\boldsymbol{E}}}}}_{\mathrm{N}}$、${\widetilde{{{\boldsymbol{E}}}}}_{\mathrm{S}}$分别为考虑幅相误差后噪声子空间、信号子空间.
经分析可知，当只存在幅度误差时，仅减少了谱峰值的幅度，不影响来波方位估计，当存在相位误差，谱峰搜索最大幅度对应的角度位置将产生偏差，因此，多个射频收发通道间的幅相误差将影响协同目标方位感知的性能.
3.2 基于子空间分解的幅相误差估计算法设计
根据3.1节的分析，射频多通道的幅相误差评估对于实现系统功能具有重要意义. 目前，Weiss等[22]提出的迭代自校准算法是处理多通道校准的主要算法之一. 该算法首先对来波方位角和阵列误差参数化，然后建立代价函数，并通过迭代法求最优解来联合估计来波方位和阵列误差参数. 然而，该算法要求阵元数大于4，并且信源数大于2，因此，不能适用于无人机协同目标感知算法所采用的四单元阵列天线体制[23-25].
本文结合系统应用特点，提出一种基于MUSIC子空间分解的改进子校准算法. 算法的具体步骤：
步骤1 根据信号强度、信号完整性和信噪比特性等选取一组接收到的ADS-B广播信号作为来波信源.
步骤2 根据主机经纬度信息和ADS-B报文携带的信源经纬度，进行信源的相对方位$ {{\boldsymbol{\theta}} }_{\mathrm{o}} $计算.
步骤3 参考Friedlander自校准算法，设计通道幅相误差矢量和信源方位的等式；利用导向矢量遵循与噪声子空间的正交关系，选取代价函数$ {\boldsymbol{Z}} $如式（16）所示.
\begin{split}&{{\boldsymbol{Z}}}={{{\boldsymbol{Q}}}^{\mathrm{H}}\left({{\boldsymbol{\theta}} }_{\mathrm{o}}\right)}{\boldsymbol{\varGamma }}^{\mathrm{H}}{\boldsymbol{E}}_{\mathrm{N}}{{\boldsymbol{E}}^{\mathrm{H}}_{\mathrm{N}}}\boldsymbol{\varGamma }\boldsymbol{Q}\left({{\boldsymbol{\theta}} }_{\mathrm{o}}\right)= \\ &\quad {\boldsymbol{\delta }}^{\mathrm{H}}\left(\boldsymbol{Q}^{\mathrm{H}}{\left({{\boldsymbol{\theta}} }_{\mathrm{o}}\right)}{\boldsymbol{E}}_{\mathrm{N}}{{\boldsymbol{E}}^{\mathrm{H}}_{\mathrm{N}}}\boldsymbol{Q}\left({{\boldsymbol{\theta}} }_{\mathrm{o}}\right)\right)\boldsymbol{\delta } ,\end{split} (16) 式中：$ {{\boldsymbol{\delta}} } $=diag $ \boldsymbol{\varGamma } $, $\boldsymbol{Q}\left({{\boldsymbol{\theta}} }_{\mathrm{o}}\right) $=diag$ \boldsymbol{a}\left({{\boldsymbol{\theta}} }_{\mathrm{o}}\right) $.
$ {\boldsymbol{Q}^{\mathrm{H}}\left({{\boldsymbol{\theta}} }_{\mathrm{o}}\right)}{\boldsymbol{E}}_{\mathrm{N}}{{\boldsymbol{E}}^{\mathrm{H}}_{\mathrm{N}}}\boldsymbol{Q}\left({{\boldsymbol{\theta}} }_{\mathrm{o}}\right) $是一个正定的Hermitan矩阵，则$ {\boldsymbol{\delta }}^{\mathrm{H}} $W=1，W=（1,0,0,0）T.
步骤4 将修正后的噪声子空间EIN代入式（16），可得传递变量为
{{{\boldsymbol{\delta }}}}_{\mathrm{c}}=\dfrac{{({{{\boldsymbol{Q}}}}^{\mathrm{H}}({{\boldsymbol{\theta}} }_{\mathrm{o}}){{{\boldsymbol{E}}}}_{\mathrm{I}\mathrm{N}}{{{\boldsymbol{E}}}}_{\mathrm{I}\mathrm{N}}^{\mathrm{H}}{{\boldsymbol{Q}}}({{\boldsymbol{\theta}} }_{\mathrm{o}}))}^{-1}{{\boldsymbol{W}}}}{{{{{\boldsymbol{W}}}}^{\mathrm{T}}({{{\boldsymbol{Q}}}}^{\mathrm{H}}({{\boldsymbol{\theta}} }_{\mathrm{o}}){{{\boldsymbol{E}}}}_{\mathrm{I}\mathrm{N}}{{{\boldsymbol{E}}}}_{\mathrm{I}\mathrm{N}}^{\mathrm{H}}{{\boldsymbol{Q}}}({{\boldsymbol{\theta}} }_{\mathrm{o}}))}^{-1}{{\boldsymbol{W}}}} . (17) 根据$ {\boldsymbol{\delta }}_{\mathrm{c}} $=diag $ {\boldsymbol{\varGamma }}_{\mathrm{c}} $，得到幅相误差矢量初估值$ {\boldsymbol{\varGamma }}_{\mathrm{c}} $.
步骤5 再根据初估值$ {\boldsymbol{\varGamma }}_{\mathrm{c}} $对空间谱修正后进行方位角估计$ {{\boldsymbol{\theta}} }_{\mathrm{o},\mathrm{c}} $，按照式（18）对$ {{\boldsymbol{\theta}} }_{\mathrm{o},\mathrm{c}}\;\mathrm{和}\;{{\boldsymbol{\theta}} }_{\mathrm{o}} $进行校验. 若两者的空间谱误差小于阈值门限，则估计完成，$ {\boldsymbol{\varGamma }}^{}= {\boldsymbol{\varGamma }}_{\mathrm{c}} $；若误差大于预设门限，则重复步骤1.
{\boldsymbol{P}}_{\mathrm{M}\mathrm{U}\mathrm{S}\mathrm{I}\mathrm{C}}\left({\boldsymbol{\theta}} \right)=\dfrac{\boldsymbol{I}}{{{\boldsymbol{a}}}^{\mathrm{H}}\left({{\boldsymbol{\theta}} }\right){{{\boldsymbol{\varGamma}} }}^{{\mathrm{H}}}{{{\boldsymbol{E}}}_{\mathrm{IN}}}{{{{\boldsymbol{E}}}^{{\mathrm{H}}}_{\mathrm{IN}}}}{{\boldsymbol{\varGamma}} }{{\boldsymbol{a}}}\left({{\boldsymbol{{\boldsymbol{\theta}}}} }\right)}. (18) 4. 仿真与试验
4.1 MUSIC改进算法仿真
从算法的可分辨性、信噪比影响和估计精度等维度对本文设计的改进算法和传统的MUSIC算法进行对比仿真分析. 基于四单元阵列天线模型和空管雷达C/S模式信号特征，设置2个天线阵元，按照实际天线位置进行布置，并进行了100次信号快拍.
4.1.1 算法可分辨性
试验1为非相干信源的方位感知性能对比试验，空间谱如图4所示. 试验2为相干信源的方位感知性能对比试验，多径信号幅度为主频信号的0.6倍，空间谱如图5所示.
由图4、5可知，改进算法能够有效地分辨2个角度相近的信号，方位感知准确，而MUSIC算法出现角度模糊，无法有效分辨.
4.1.2 信噪比对算法的影响
试验3为信噪比对算法分辨性能的影响试验. 入射信号信噪比2、0、2、4、6、8、10 dB，设置分辨成功的检测门限为15°，分别进行300次独立试验，仿真结果如图6所示. 由图可知，在非相干信号源条件下，改进算法的成功分辨概率相比MUSIC算法有较大的提升，在相干信号源条件下，改进算法的优势更加明显.
4.1.3 入射角间距对算法的影响
试验4考察了入射角间距对算法分辨性能的影响. 设计10°、15°、20°、25°、30°、35°、40°、45°、50° 角度间隔的入射信号信源，分辨成功的检测门限设置为5°，分别进行300次独立试验，信噪比为4 dB，仿真结果如图7所示. 由图可知，改进算法相比MUSIC算法分辨率有较大的提升.
4.1.4 快拍数对算法的影响
试验5考察快拍数对算法性能的影响. 信号源信噪比设置为 −2、0、2 dB，分别进行200次统计试验，计算得出不同快拍数条件下的方位感知性能误差，如图8所示. 当快拍数小于100次时，测向误差快速下降；当快拍数大于200次时，测向误差逐渐趋于平稳.
4.2 幅相误差估计算法仿真
首先，基于四单元阵列天线构造通道误差，对本文提出的幅相误差在线估计算法进行仿真，分析其校准性能. 进行试验6，设计天线阵元为4个，信号快拍数为100次，信噪比为5 dB, ADS-B信源入射角度为25°，通道1～4的幅相误差的设计值和估计值如表1所示，并根据估计结果进行幅相误差校准，校准前后的空间谱如图9所示.
表 1 幅相误差Table 1. Amplitude-phase error通道 设计值 估计值 1 1.0000 1.0000 2 0.2249 + 1.178 7i 0.1727 + 1.103 9i 3 −0.8229 − 1.132 6i −0.7198 − 1.012 8i 4 −1.5874 + 0.200 5i −1.3692 + 0.158 8i 然后，分析不同信噪比信源对估计误差的影响，进行试验7，设计信噪比 −2、0、2、4、6、8、10 dB的ADS-B信源，入射角度为70°，通道1～4的幅相误差分别为1.0000、0.6472 + 0.470 2i、−0.8090 + 0.587 8i、−0.3708 + 1.141 3i，各自进行300次独立试验. 仿真结果如图10所示.
图 10 不同信噪比条件下的算法估计偏差Figure 10. Estimation deviation under different signal-to-noise ratios由试验6、7可知，基于四单元阵列天线模型的幅相误差估计算法能够有效完成通道幅相校准，满足MUSIC空间谱估计，同时随着信噪比提高，算法的估计性能更准确，验证了算法的有效性.
4.3 无人机协同目标感知试验
依据4.1节和4.2节的仿真结果，开展无人机协同目标感知试验，验证实际空域环境下的无人机协同目标感知性能，搭建硬件验证平台如图11所示，四单元阵列天线选用Honeywell公司的ANT67A定向天线，信号处理平台选用ADR9024射频收发芯片和FMQL系列SOC的硬件架构，考虑到高实时性和并行计算力，感知算法通过采用FPGA程序实现并驻留于SOC平台. 根据C模式框架脉冲和S模式前导码脉冲的脉宽，设计数字化射频信道的抽取速率为120 MHz，满足4.1.4节分析快拍数大于100次的要求，从而实现一组信号帧时长的时间内完成包括方位、高度、距离等信息的航迹获取，提升感知算法的高实时性.
试验8，将硬件验证平台搭载在某型有人机，进行一个架次的飞行试验，通过对真实空域中的目标探测，验证感知算法对高动态协同目标的感知性能.
近距离、远距离协同目标的相对方位信息和相对距离信息如图12、13所示，数据更新周期为1 s. 由图12可知，该近距离协同目标的相对距离从20 km变化到35 km，相对方位从250° 变化到200°. 由图13可知，远距离协同目标的相对距离从83 km变化到70 km，相对方位从216° 变化到350°. 相比MUSIC算法，改进算法在方位感知的精确性和抗干扰性等方面表现出明显的优越性，特别是在处理远距离目标，即低信噪比的协同目标时，其优势更加显著.
飞行试验结果表明，本文提出的无人机协同目标方位感知算法能够在空域中实时感知高动态移动目标，实现了准确连续的态势信息. 在实际使用环境中，该算法展现出更优的精确性和抗干扰性，与仿真分析结果一致.
5. 结 论
经过仿真试验分析后发现，基于MUSIC改进的方位感知算法通过修正协方差矩阵、加权信号子空间和噪声子空间等优化设计，相较于传统的MUSIC算法在低信噪比、小入射角间隔等方面均表现出更好的角度分辨性能，尤其在处理相干信源时优势突出，提升了目标方位感知的高分辨性能和抗干扰能力. 此外，基于子空间分解的幅相误差在线估计算法，在不需要射频校准硬件网络和校准辐射源的情况下，能够实现多通道之间的幅相误差自动校准.
经过飞行试验验证，基于四单元阵列天线和数字化射频信道的无人机协同目标感知系统能够实现空域中高动态移动目标的实时感知，提升无人机协同目标感知的精准性、高实时性、抗干扰性和低载荷性.
本文的相关研究成果对无人机协同目标感知技术研究和应用具备一定参考价值. 提出的协同目标方位感知算法还需在多维相干信号处理、航迹感知的物理实验验证方面进行更深入的研究.
-
图 2 无人机协同目标感知系统架构
Figure 2. Collaborative target perception system architecture of UAVs
图 10 不同信噪比条件下的算法估计偏差
Figure 10. Estimation deviation under different signal-to-noise ratios
表 1 幅相误差
Table 1. Amplitude-phase error
通道 设计值 估计值 1 1.0000 1.0000 2 0.2249 + 1.178 7i 0.1727 + 1.103 9i 3 −0.8229 − 1.132 6i −0.7198 − 1.012 8i 4 −1.5874 + 0.200 5i −1.3692 + 0.158 8i 
下载: 导出CSV
-
[1] 李德仁,李明. 无人机遥感系统的研究进展与应用前景[J]. 武汉大学学报(信息科学版),2014,39(5): 505-513,540.LI Deren, LI Ming. Research advance and application prospect of unmanned aerial vehicle remote sensing system[J]. Geomatics and Information Science of Wuhan University, 2014, 39(5): 505-513,540. [2] 吕洋,康童娜,潘泉,等. 无人机感知与规避:概念、技术与系统[J]. 中国科学:信息科学,2019,49(5): 520-537. doi: 10.1360/N112018-00318LYU Yang, KANG Tongna, PAN Quan, et al. UAV sense and avoidance:concepts, technologies, and systems[J]. Scientia Sinica (Informationis), 2019, 49(5): 520-537. doi: 10.1360/N112018-00318 [3] 毕红哲,张洲宇,申功璋,等. 无人机感知与规避技术研究进展[J]. 电子测量与仪器学报,2016,30(5): 661-668.BI Hongzhe, ZHANG Zhouyu, SHEN Gongzhang, et al. Recent progress in UAV sense and avoid system[J]. Journal of Electronic Measurement and Instrumentation, 2016, 30(5): 661-668. [4] SAHAWNEH L R, DUFFIELD M O, BEARD R W, et al. Detect and avoid for small unmanned aircraft systems using ADS-B[J]. Air Traffic Control Quarterly, 2015, 23(2/3): 203-240. [5] LYU Y, PAN Q, ZHAO C H, et al. Autonomous stereo vision based collision avoid system for small UAV[C]//AIAA Information Systems−AIAA Infotech @ Aerospace. Virginia:AIAA,2017:1150.1-1150.12. [6] ACCARDO D, FASANO G, FORLENZA L, et al. Flight test of a radar-based tracking system for UAS sense and avoid[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1139-1160. doi: 10.1109/TAES.2013.6494404 [7] 何桂萍,徐亚军. ADS-B数据链的比较及特性研究[J]. 中国民航飞行学院学报,2010,21(4): 3-6. doi: 10.3969/j.issn.1009-4288.2010.04.001 [8] RTCA Inc. Minimum operational performance standards for 1090 MHz extended squitter automatic dependent surveillance—broadcast (ADS-B) and traffic information services—broadcast (TIS-B): RTCA DO-260[S]. Washington D. C.: RTCA,2020. [9] PETROCHILOS N, PIRACCI E G, GALATI G. Separation of multiple secondary surveillance radar sources in a real environment for the near-far case[C]//2007 IEEE Antennas and Propagation Society International Symposium. Honolulu: IEEE,2007: 3988-3991. [10] PETROCHILOS N, GALATI G, PIRACCI E. Separation of SSR signals by array processing in multilateration systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 965-982. doi: 10.1109/TAES.2009.5259177 [11] 李丞,张玉,唐波. 基于曼彻斯特编码算法的单通道二次雷达信号重构方法[J]. 探测与控制学报,2018,40(3): 66-69.LI Cheng, ZHANG Yu, TANG Bo. Secondary surveillance radar replies received in single channel based on Manchester decoding algorithm[J]. Journal of Detection & Control, 2018, 40(3): 66-69. [12] 张军. 空域监视技术的新进展及应用[J]. 航空学报,2011,32(1): 1-14.ZHANG Jun. New development and application of airspace surveillance technology[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(1): 1-14. [13] 吴振亚,王明辉,张瑞平,等. 一种基于ADS-B的雷达误差实时融合校正算法[J]. 西南交通大学学报,2013,48(1): 102-106,115. doi: 10.3969/j.issn.0258-2724.2013.01.016WU Zhenya, WANG Minghui, ZHANG Ruiping, et al. ADS-B-based algorithm for real-time optimal estimation of radar biases[J]. Journal of Southwest Jiaotong University, 2013, 48(1): 102-106,115. doi: 10.3969/j.issn.0258-2724.2013.01.016 [14] MILLER P C. General atomics successfully tests UAS sense-and-avoid system[EB/OL]. (2014-12-04)[2023-06-27]. https://uasmagazine.com/articles/889/. [15] 蓝晓宇. 提高空间谱估计分辨率的超分辨测向算法研究[D]. 哈尔滨: 哈尔滨工程大学,2012. [16] 田蕴琦. 强干扰下相干多目标的DOA估计算法研究[D]. 哈尔滨: 哈尔滨工程大学,2019. [17] RTCA. Minimum operational performance standards for traffic alert and collinsion avoidance system Ⅱ (TCAS Ⅱ): RTCA-DO-185[S]. Washington D. C.:RTCA, 2008. [18] RTCA Inc. Minimum operational performance standards for detect and avoid (DAA): RTCA-DO-365C[S]. Washington D. C.: RTCA, 2021. [19] 倪壮. 民机机载防撞系统算法研究与仿真[D]. 上海:上海交通大学,2015. [20] 田航. MUSIC算法性能研究综述[J]. 科技资讯,2019,17(27): 5-6. [21] 王永良,陈辉,彭应宁,等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社,2004: 18-52. [22] WEISS A J, FRIEDLANDER B. Eigenstructure methods for direction finding with sensor gain and phase uncertainties[J]. Circuits, Systems and Signal Processing, 1990, 9(3): 271-300. doi: 10.1007/BF01201215 [23] JIAO Y M, HUANG J G, HOU Y S. Multidimensional MUSIC DOA estimation using ant colony optimization algorithm[C]//IEEE 10th International Conference on Signal Processing Proceedings. Beijing:IEEE,2010:291-294. [24] 陈德莉. 波达方向估计中阵列误差校正技术研究[D]. 长沙: 国防科学技术大学,2008. [25] 周治宇,陈豪. 一种基于一维噪声子空间的幅相误差自校正方法[J]. 电子测量与仪器学报,2009,23(2): 58-62.ZHOU Zhiyu, CHEN Hao. A self-calibration method for gain and phase uncertainties based on one-dimension noise sub-space algorithm[J]. Journal of Electronic Measurement and Instrument, 2009, 23(2): 58-62. 期刊类型引用(1)
1. 马俊杰. 同频信号的空间谱直接定位方法研究. 中国无线电. 2025(01): 37-39 . 
百度学术其他类型引用(0)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 403
- HTML全文浏览量: 266
- PDF下载量: 125
- 被引次数: 1