管棚承载机制的理论分析

张建; 严松宏; 王文; 孙纬宇

doi:10.3969/j.issn.0258-2724.20230425

管棚承载机制的理论分析

doi: 10.3969/j.issn.0258-2724.20230425

张建^{1, 2,},
严松宏^{1, 3, ,},
王文²,
孙纬宇^{1, 3}

1.
兰州交通大学土木工程学院，甘肃兰州 730070
2.
甘肃省交通规划勘察设计院股份有限公司，甘肃兰州 730010
3.
兰州交通大学甘肃省道路桥梁与地下工程重点实验室，甘肃兰州 730070

基金项目: 国家自然科学基金项目（52208392，52068044）；甘肃省自然科学基金（21JR7RA309）；中国博士后科学基金（2021M693843）

详细信息

作者简介:
张建（1987—），男，博士研究生，研究方向为公路隧道设计方法，E-mail：16813698@qq.com

通讯作者:
严松宏（1966—），男，教授，研究方向为地下工程设计施工理论及其工程应用，E-mail：yansonghong@163.com

中图分类号: TU43；U451
计量
- 文章访问数: 173
- HTML全文浏览量: 67
- PDF下载量: 42
- 被引次数: 1
出版历程
- 收稿日期: 2023-08-23
- 修回日期: 2024-02-17
- 网络出版日期: 2024-07-25
- 刊出日期: 2024-03-02

Theoretical Analysis of Bearing Mechanism of Pipe Sheds

ZHANG Jian^{1, 2
,},
YAN Songhong^{1, 3
, ,},
WANG Wen²,
SUN Weiyu^{1, 3}

1.
School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China
2.
Gansu Provincial Transportation Planning Survey and Design Institute Co., Ltd., Lanzhou 730010, China
3.
Key Laboratory of Road & Bridge and Underground Engineering of Gansu Province, Lanzhou Jiaotong University, Lanzhou 730070, China

摘要

摘要:
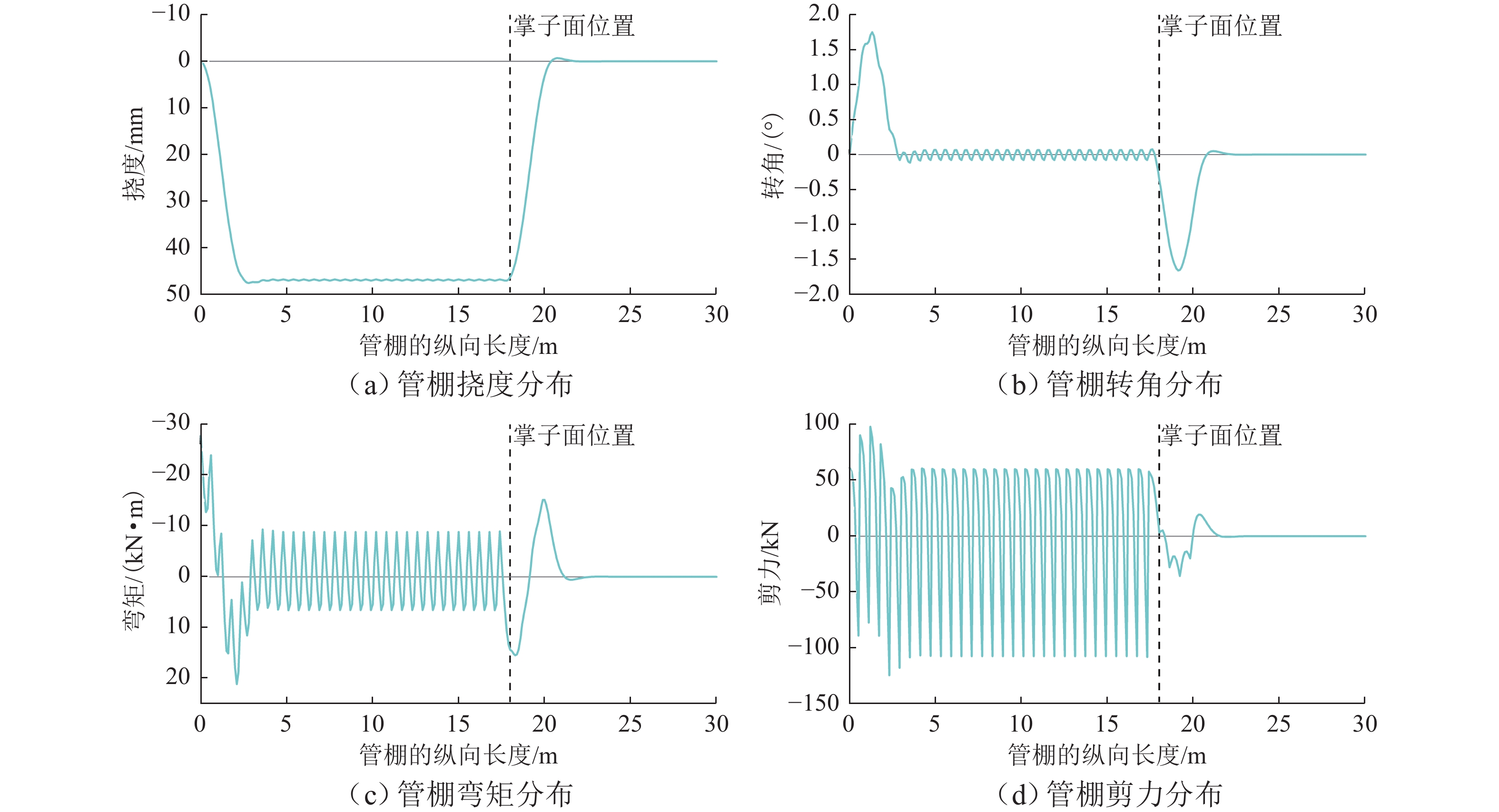
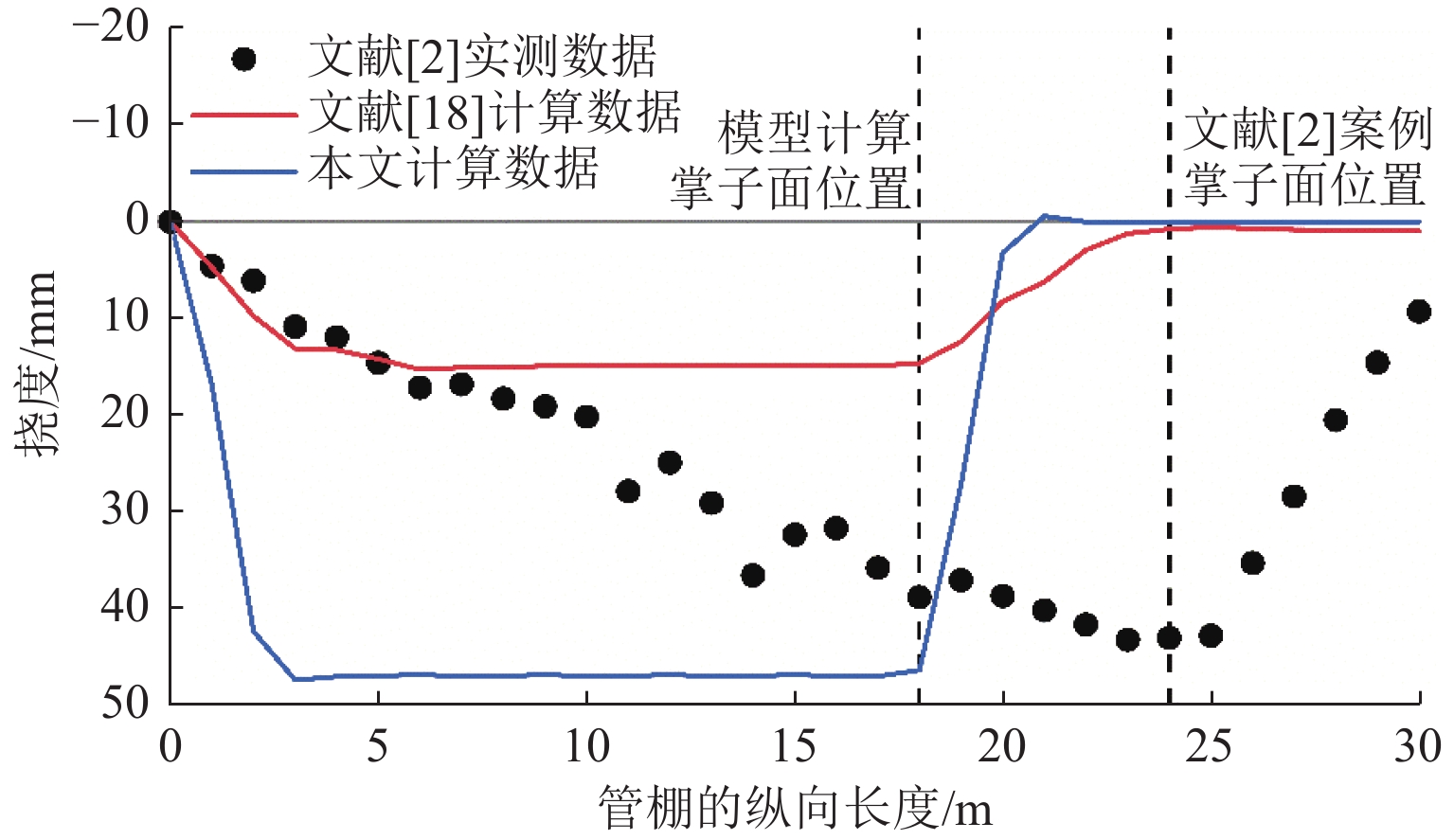
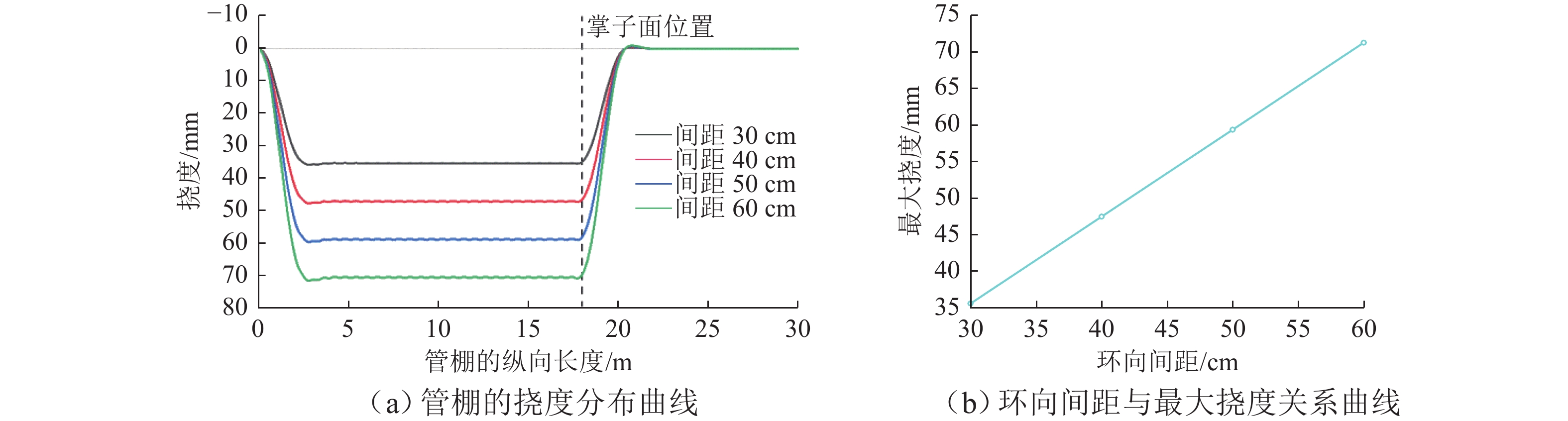
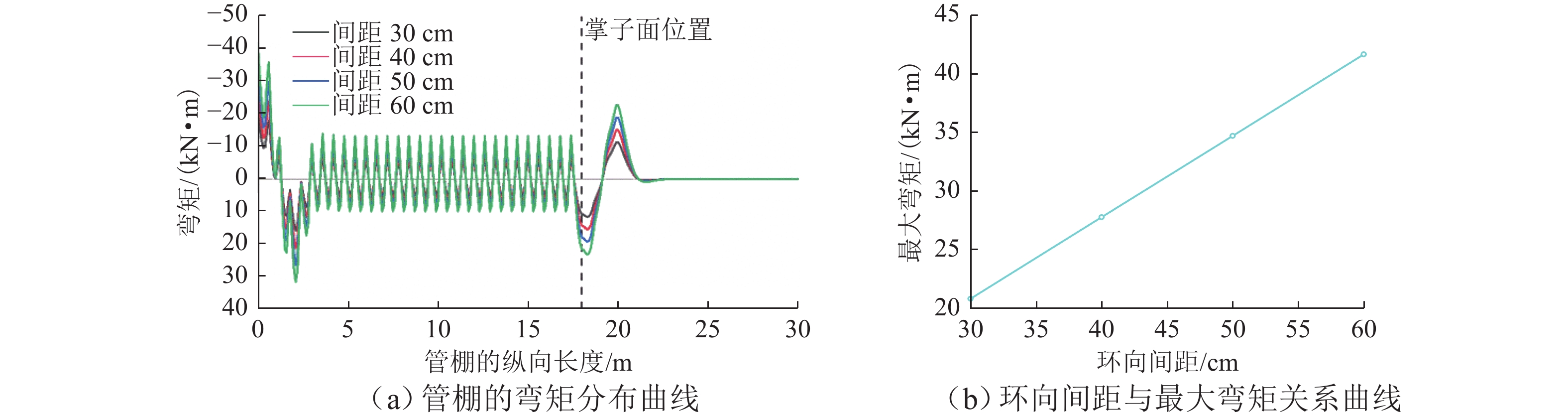
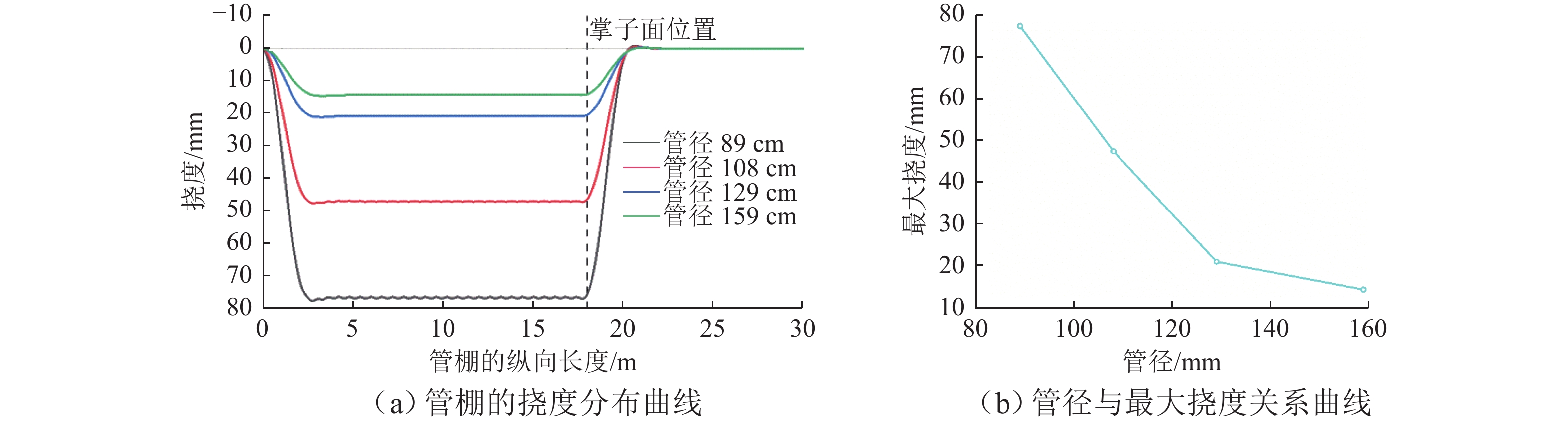
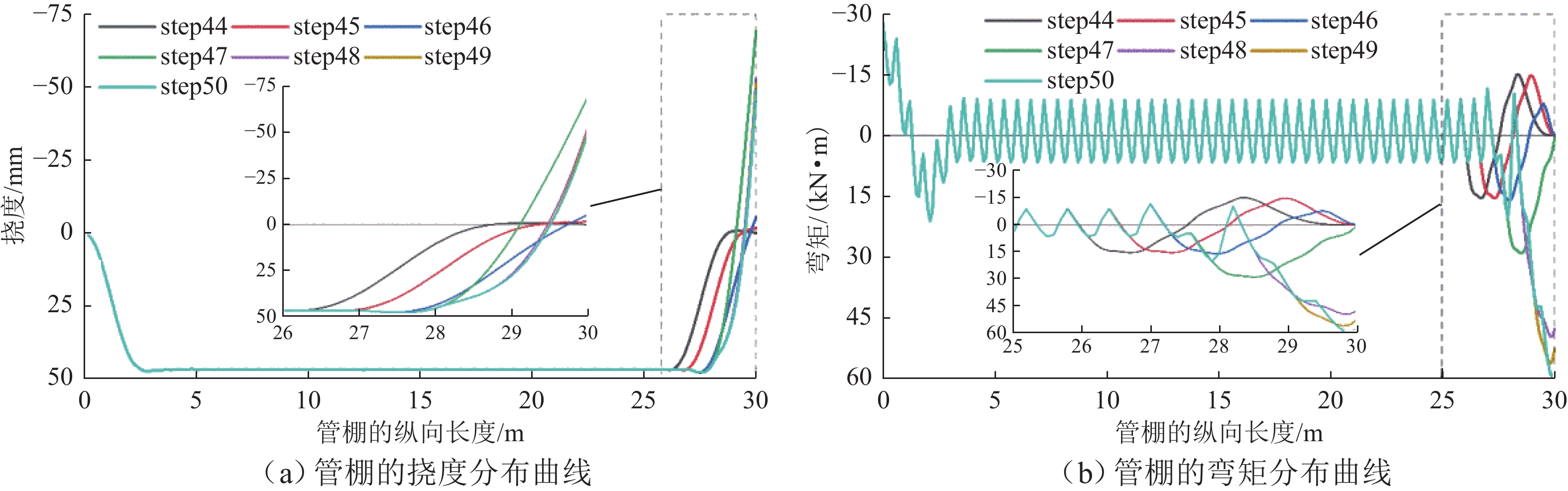
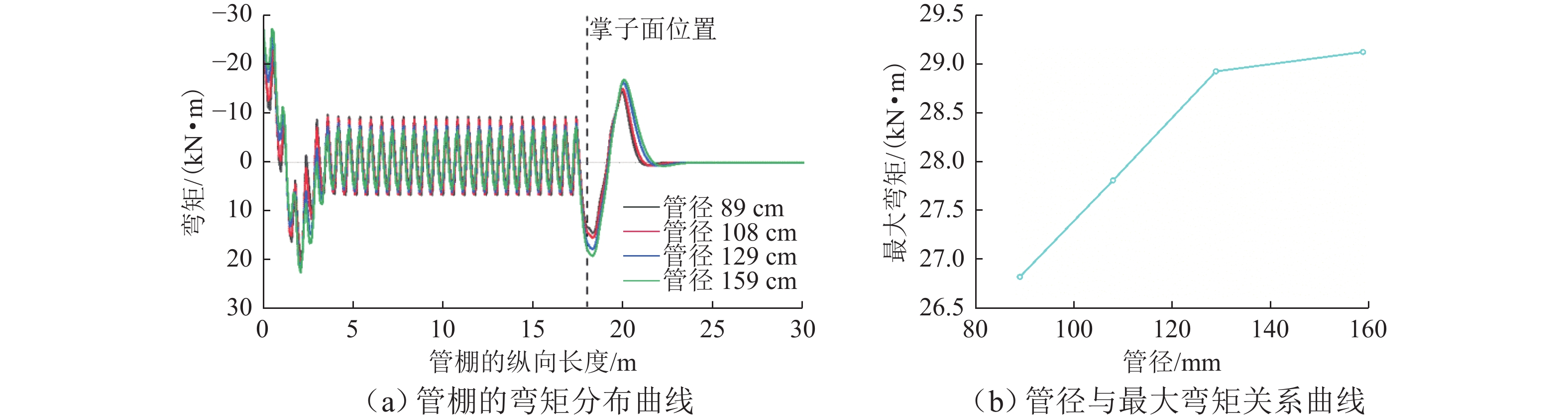
建立合理准确的管棚理论分析模型并对其进行求解，对推动管棚预支护技术的进一步发展具有重要意义. 本文在隧道开挖、支护的施工过程以及未开挖段由于掌子面扰动而导致管棚约束反力有所降低的基础上，建立了基于Euler-Bernoulli梁理论的管棚荷载结构模型，同时引入Pasternak弹性地基模型来确定初期支护及掌子面前方岩体对管棚的约束反力，推导出每一循环隧道开挖支护过程中管棚的受力和变形解析表达式，并通过叠加法求解掌子面掘进至任意位置时管棚的受力和变形分布；通过案例比对，验证了本文建立模型的合理性和有效性. 研究结果表明：管棚钢管环向间距越小、直径越大越有利于提升管棚的预加固能力；管棚合理搭接长度为1.8 m.
- 隧道工程 /
- 管棚 /
- 设计参数 /
- 解析解
Abstract:
Establishing a reasonable and accurate theoretical analysis model for pipe sheds and solving it are of great significance to promoting the development of pipe shed pre-support technology. By analyzing the construction process of tunnel excavation and support and the reduction of the restraining reaction force of the pipe shed due to the disturbance of the tunnel face in the unexcavated section, a load structure model of the pipe shed based on the Euler-Bernoulli beam theory was established. The Pasternak elastic foundation model was introduced to determine the initial support and the restraining reaction force of the rock mass in front of the tunnel face on the pipe shed, and the analytical expressions of the stress and deformation of the pipe shed during each cycle of tunnel excavation and support were derived. In addition, the superposition method was used to solve the stress and deformation distribution of the pipe shed when the tunnel face was tunneled to any position. Through case comparison, the rationality and effectiveness of the model were verified. The research results show that smaller circumferential spacing and larger diameter of the pipe shed steel pipes are helpful in improving the pre-reinforcement capacity of the pipe shed, and the reasonable lap length of the pipe shed is 1.8 m.
- tunnel engineering /
- pipe shed /
- design parameter /
- analytical solution

HTML全文

高层建筑作为典型的风敏结构，建筑上的风荷载与其气动外形密切相关^[1-2]. 随着建造技术的发展，越来越多的辅助构件，如阳台、外伸板、粗糙条^[3-4]等被安装在高层建筑外立面. 这些附属物的存在不仅影响建筑的气动外形，也会改变建筑表面风压分布、风荷载及周围风环境. 因此，弄清附属物对建筑风效应的影响十分必要.

部分学者通过风洞试验探索了附属物对风压和风荷载的影响. 阳台可以显著改变迎风面上部的平均和峰值风压分布^[5-6]，建筑物表面风压降低约30%^[7]. 不同布置形式的肋板对风荷载的影响不同^[8]，连续水平板会略微增加顺风向平均基底弯矩，而间隔水平板能降低横风向脉动基底弯矩^[9]. 迎风面边缘附近的竖向肋板会增加迎风角区域的吸力^[10]，同时，还会显著降低表面脉动风压，最大降幅约为57%^[11].

虽然试验证明了附属物能减弱结构上的风荷载，但其抗风工作机理尚不清楚. 因此，为阐明附属物的流场修正机理，一些学者尝试利用流动可视化技术（PIV）和LES （large eddy simulation）研究附属物对建筑周围流场特征的影响. Ai等^[12]发现带栏杆的水平阳台能显著抑制迎风面和背风面附近的竖向流，但同时增强了近壁湍流脉动. Zheng等^[13]认为相邻阳台间的局部旋涡是影响风速和风压分布的重要因素. 建筑边缘附近的阳台能有效抑制流动分离，并破坏涡脱过程^[14].

除水平附属物外，Liu等^[15]发现竖向肋板能显著降低侧风面附近湍流脉动，并将高湍流区推离侧风面；Liu等^[16-17]认为迎风角竖向肋板附近形成的局部涡旋可以明显改变模型周围的流场结构；Hui等^[18]发现不同位置的肋板对流场结构的影响明显不同，迎风面肋板抗风作用最明显，而侧风面和背风面肋板对流场结构的影响较弱.

尽管部分学者探究了外伸肋板的流场修正机理，但由于肋板布置的复杂性，水平肋板的抗风工作机理仍需进行系统的研究.

本文采用LES方法研究大气边界层来流（ABL）下水平肋板密度和布置形式对高层建筑流场和气动特性的影响，并详细分析肋板对风场特征的影响，如近壁流、涡结构和竖向流等，借助流场信息阐明肋板的抗风工作机理，为实际高层建筑外辅助构件的抗风设计和布置提供参考.

1. 数值方法

1.1 模型信息

以刚性模型为目标高层建筑，模型长、宽、高（D、B、H）的比例为1∶1∶4. 模型缩尺比为1∶200，模型高度和对应实际建筑高度分别为0.4 m和80 m. 外伸肋板安装在模型的外立面，如图1所示. 图中：d为外伸长度，b、h分别为2个相邻板间的水平和垂直距离, α为风向角. 模型1～3研究肋板密度的影响，模型2～5研究肋板布局的影响. 外伸肋板主要有3个参数， d固定为0.06D （实际尺寸为1.2 m），该尺寸与阳台的尺寸相似^[6]. 肋板的具体尺寸信息如表1所示.

图 1 模型示意

Figure 1. Sketch of models

下载: 全尺寸图片幻灯片

表 1 肋板尺寸信息

Table 1. Dimension information of ribs

模型编号	d/D/%	b/D//%	h/D//%
1	6		50.0
2	6		25.0
3	6		12.5
4	6	20	25.0
5	6	60	25.0

下载: 导出CSV

| 显示表格

1.2 控制方程及求解策略

本次模拟选择LES湍流模型，亚格子尺度模型为标准SGS （subgrid scale）模型，Smagorinsky常数C_s取值为0.13，C_s在0.10～0.14范围内模拟结果较好^[19]. 不可压缩流滤波后的N-S方程为

$\frac{{\partial {{\overline u }_i}}}{{\partial t}} + \frac{{\partial ({{\overline u }_i}{{\overline u }_j})}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial \overline p }}{{\partial {x_i}}} + \nu \frac{{{\partial ^2}{{\overline u }_i}}}{{\partial {x_j}\partial {x_j}}} - \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}}\;,$

(1)

${\tau _{ij}}{\text{ = }} - 2{\nu _{\mathrm{t}}}{\overline S _{ij}} + \frac{1}{3}{\tau _{kk}}{\delta _{ij}} ,$

(2)

${\overline S _{ij}}{\text{ = }}\frac{1}{2}\left( {\frac{{\partial {{\overline u }_i}}}{{\partial {x_j}}} + \frac{{\partial {{\overline u }_j}}}{{\partial {x_i}}}} \right)\;,$

(3)

$\frac{{\partial {{\overline u }_i}}}{{\partial {x_i}}} = {\text{0}}\;,$

(4)

式中：x_i （x_j）为笛卡尔坐标系中x、y、z 3个方向的坐标值， ${\overline u}_i\left(u_j\right)$ 为x、y、z 3个方向的速度， ${\overline p}$ 为滤波后的压力，ρ、ν分别为空气密度和运动黏度，τ_ij为SGS亚格子应力张量，ν_t为SGS涡黏性系数， ${\overline S}_{ij}$ 为滤波后的应变率张量，t为时间.

利用开源软件OpenFOAM进行瞬态模拟，求解器选择PimpleFoam. 在控制方程的求解中，数值模型离散格式选择如下：二阶后向差分方案用于时间离散，控制方程中的扩散项和对流项分别采用二阶中心差分格式和线性迎风稳定输运格式（LUST）. PIMPLE算法用于解决压力-速度耦合问题. 几何代数多重网格（GAMG）和预处理双共轭梯度（PBiCG）求解器用于计算迭代过程中的压力和速度^[20]. 本次模拟的时间步长设置为5 × 10⁻⁵，模拟中的平均库郎数（CFL）为0.008，最大库郎数小于1.200. 每个工况的总模拟时长为9 s.

1.3 网格信息和边界条件

计算域和网格信息如图2所示. 图中：①～④ 为加密区. 计算域入口处施加湍流来流（ABL），出口为自由流条件，侧壁和计算域顶部为滑移边界条件，建筑物表面和地面为无滑移边界条件，阻塞率为0.6%.

图 2 网格布局和计算域

Figure 2. Mesh configuration and computing domain

下载: 全尺寸图片幻灯片

利用网格生成工具snappyHexMesh生成网格系统. 本次模拟采用4个加密区实现网格的逐级加密（图2（a）、（b）），加密区 ①～④ 尺寸分别为9H × 3.5H × 2H、1.75H × 1.75H × 1.5H、0.75H × 0.75H × 1.1H、0.04H × 0.04H × 1.03H. 计算域内主要采用结构化网格，非结构化网格只出现在加密区的交界处. 3种不同的网格布局用于检查网格无关性，如表2所示. 网格2的近壁首层网格在水平方向上高度为1/125D. 建筑物附近竖直方向的网格尺寸远小于水平方向的网格尺寸，近地面的网格尺寸为1/600D，网格2的数量约为7百万.

表 2 网格信息

Table 2. Mesh information

网格	最小网格		最大网格		数量/百万
网格	x/y	z	x/y	z	数量/百万
网格 1	1/62.5D	1/300D	0.6D	1D	3.7
网格 2	1/125.0D	1/600D	0.6D	1D	7.2
网格 3	1/250.0D	1/1200D	0.6D	1D	13.6

下载: 导出CSV

| 显示表格

使用一致离散随机流生成（CDRFG）方法^[21]生成入口的脉动风速时程. 该方法基于速度功率谱的离散化和合成技术，可以很好地保持湍流能量和速度相干性，也可以准确评估作用在建筑物上的风荷载^[21]. 顺流向平均风速U、湍流强度I_u剖面^[22-23]及顺风向脉动风速功率谱如图3所示：速度剖面指数为1/6，建筑物屋顶处的顺风向平均风速U_H为8 m/s，对应的雷诺数Re=5.5 × 10⁴，建筑物高度处的湍流积分尺度L_uH为0.24 m. 目标建筑物处的风场特性决定结构上的风荷载. 由图3可知，平均风速和湍流强度剖面与已有文献^[22-23]结果吻合较好，但由于LES自身的数值耗散，模型位置处的湍流强度相比入口处有一定程度的减小；顺风向脉动风速谱也与von Karma谱^[20]一致，表明CDRFG方法生成的来流湍流是可靠的.

图 3 风场特征

Figure 3. Wind field characteristics

下载: 全尺寸图片幻灯片

1.4 气动力定义和结果验证

无量纲风压系数C_p、阻力系数C_d和升力系数C_l定义如下：

${C_{\mathrm{p}}} = \frac{{\Delta p}}{{{1 / 2}\rho U_{\mathrm{H}}^2}} \text{，}$

(5)

${C_{\mathrm{d}}} = \frac{{{F_{\mathrm{d}}}}}{{{1 / 2}\rho U_{\mathrm{H}}^2A}} ,$

(6)

${C_{\mathrm{l}}} = \frac{{{F_{\mathrm{l}}}}}{{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}\rho U_{\mathrm{H}}^2A}} \text{，}$

(7)

式中：Δp为压差，F_d、F_l分别为总阻力和总升力，A为投影面积.

大涡模拟的结果验证如图4^[22-23]和所示. 图中：a、b、c、d表示模型边缘. 表中：AR为高宽比， ${\overline C}_{\mathrm{d}}$ 、 ${C}_{{\mathrm{d}}1}$ 为阻力的时均值和均方根值，C_l1为升力的均方根值. 可以看出，本次LES得到的平均风压系数 ${\overline C}_{\mathrm{P}}$ 的分布与已有研究结果接近^[22-23]，但LES得到的脉动风压均方根 ${C}_{{\mathrm{p}}1}$ 与已有结果略微差异，可能因为湍流生成方法、数值方案和网格分辨率等方面的差异造成的. 风压的差异会导致模型上风荷载不同（如表3所示）. 与已有研究结果相比，本次模拟结果在合理范围内，表明本次模拟结果是可靠的. 网格1会高估脉动风压均方根，网格2、3的结果更接近已有研究结果. 因此，本研究采用网格2方案来平衡计算成本和结果精度.

图 4 方柱压力分布及验证^[22-23]

Figure 4. Pressure distribution on square column and verification

下载: 全尺寸图片幻灯片

表 3 参考方柱LES结果及验证

Table 3. LES results of square column and verification

方法	文献	R_e/10⁴	AR	${\overline C}_{\mathrm{d}}$	${C}_{{\mathrm{d}}1}$	${C}_{{\mathrm{l}}1}$	St
LES	网格 1	5.5	4	1.220	0.09	0.330	0.100
	网格 2	5.5	4	1.147	0.10	0.300	0.096
	网格 3	5.5	4	1.156	0.11	0.310	0.094
试验	文献 [22]	5.5	4	1.200		0.410	0.100
	文献 [23]	5.0	4	1.280	0.13	0.320	0.085
	文献 [24]	6.0	4	1.270	0.08	0.296	0.097
	文献 [25]	7.3	3	1.290			0.102
	文献 [11]	5.5	5	0.930		0.350	0.100
	文献 [10]	5.5	5	1.080

下载: 导出CSV

| 显示表格

2. 外伸板对流场结构的影响

2.1 平均流场结构

大气边界层来流下的建筑物周围会产生明显的三维流动结构，不同高度处的平均流场如图5所示. 可以看出：不同高度处的旋涡大小差异明显；相比模型1～3，在z=0.52H高度处，参考模型的尾涡相对较短，尺寸较小，表明肋板能拉长尾涡；模型顶部自由端效应导致建筑物屋顶附近尾涡缺失（z=0.95 H）.

图 5 不同高度处水平截面上的平均流线和平均流速

Figure 5. Mean streamlines and mean flow velocity on horizontal sections at different heights

下载: 全尺寸图片幻灯片

图6所示为竖直中心面（y=0D）上的顺风向平均风速和平均流线，以阐明水平肋板对竖向流动的影响. 对于参考模型，来流在迎风面0.73H高度附近停滞. 当模型上安装水平肋板时，迎风面上的驻点相比参考模型无明显变化，肋板附近形成小尺寸局部旋涡.

图 6 竖直截面上（y = 0D）的平均流线和平均流速

Figure 6. Mean streamlines and mean flow velocity on vertical sections （y = 0D）

下载: 全尺寸图片幻灯片

肋板密度会明显改变尾流区鞍点高度，鞍点高度随密度增加而减小，模型2、3的尾部鞍点高度分别为1.17D和1.23D（图6（c）、（d）），远低于参考模型的高度（1.50D）. 对比图6（c）、（d）的结果可以发现，沿建筑物高度的肋板密度较大时，肋板对尾部鞍点影响较小. 图6（c）中的点F表示流动再附点，局部旋涡再附在模型迎风面上.

另外，本节还研究了肋板水平间距（模型4和模型5）对平均流场的影响. 对比模型2、4、5的结果可以看出，随着水平间隙的增加，尾涡逐渐变小，尾部鞍点的高度明显变高（图6（c）、（e）～（f）），说明外伸板随着水平距离的增大，其对尾涡的影响逐渐变弱.

3. 外伸板对风压和风荷载的影响

3.1 外伸板密度影响

流场结构的变化会影响模型壁面风压分布（）. 由（a）可知，参考模型中心线上的 ${\overline C }_{\mathrm{P}}$ 沿竖向平滑变化， ${\overline C }_{\mathrm{P}}$ 最大值出现在0.8H左右. 当模型上安装外伸板时， ${\overline C }_{\mathrm{P}}$ 分布变化明显，模型1～3的 ${\overline C }_{\mathrm{P}}$ 呈“之”字形分布，肋板附近出现 ${\overline C }_{\mathrm{P}}$ 的局部最大值和最小值. Hui等^[9]也发现了迎风面和背风面 ${\overline C }_{\mathrm{P}}$ 的“之”字形模式. 这种结果可用图6所示的近壁流场来解释，因为肋板上、下形成的局部旋涡会导致局部压力的出现. 靠近模型自由端（0.8H～1.0H）或模型底部（0～0.3H）时，压力变化更显著（（a）），因为上、下部肋板附近形成的旋涡尺寸相对较大，大尺寸旋涡对 ${\overline C}_{\mathrm{P}}$ 的影响更大. ${\overline C }_{\mathrm{p}}$ 的变化幅度随着肋板密度的增加而减小，因为密集的肋板明显影响近壁流并减小肋板附近局部旋涡的尺寸（（b）～（d）中的区域L）. 较大的局部旋涡将导致模型1上出现较大 ${C}_{{\mathrm{p}}1}$ . 对于迎风面， ${C}_{{\mathrm{p}}1}$ 的变化也随着肋板密度的增加而减小，如图7（b）所示.

图 7 迎风面中心线上风压分布

Figure 7. Distribution of wind pressure on windward centerline

下载: 全尺寸图片幻灯片

在z=0.52H处，侧壁面上的风压分布如图8所示. 图中：A、B为侧风面边缘. 4个模型在0.52H处的风压系数在前缘和后缘处基本保持不变，（（a）），但模型边缘附近风压系数因流动分离和次级涡的影响而发生突变. 外伸板能明显降低侧壁面风压，相比参考模型，模型1～3在0.52H处的 ${\overline C }_{\mathrm{P}}$ 和 ${C}_{{\mathrm{p}}1}$ 小于参考模型， ${\overline C }_{\mathrm{P}}$ 和 ${C}_{{\mathrm{p}}1}$ 的最大降幅分别为20%和17%.

图 8 侧风面上风压分布

Figure 8. Distribution of wind pressure on sidewall

下载: 全尺寸图片幻灯片

带板和无板光面模型的平均阻力系数 ${\overline C}_{\mathrm{d}}$ 、 ${C}_{{\mathrm{d}}1}$ 和 ${C}_{{\mathrm{l}}1}$ 如所示，脉动力是荷载系数的标准差. 由表可知，外伸板虽然影响迎风面的压力分布，但其对阻力无明显影响，然而，带板模型1～3的 ${C}_{{\mathrm{l}}1}$ 明显较小，减幅约为27%，是因为模型1～3侧壁面风压较小（图8）.

表 4 参考方柱和模型1～3的风荷载系数

Table 4. Wind load coefficients for square column and models 1–3

名称	${\overline C}_{\mathrm{d}}$	${ C}_{{\mathrm{d}}1}$	${ C}_{{\mathrm{l}}1}$
方柱	1.147	0.100	0.300
模型 1	0.146	0.102	0.232
模型 2	0.149	0.102	0.219
模型 3	0.145	0.101	0.218

下载: 导出CSV

| 显示表格

3.2 外伸板布置形式的影响

为不同布置形式肋板模型的平均压力分布. 由图可知：连续和间断布置形式明显影响压力的分布；对于迎风面，肋板的存在使带板模型上的 ${\overline C}_{\mathrm{P}}$ 间断分布，模型4、5的 ${\overline C}_{\mathrm{P}}$ 表面压力分布特征逐渐消失；模型2中的连续肋板明显增加了模型迎风面顶部的 ${\overline C}_{\mathrm{P}}$ ；肋板显著降低整个侧壁面上的 ${\overline C}_{\mathrm{P}}$ ，尤其侧壁面底部，相比参考模型， ${\overline C}_{\mathrm{P}}$ 最大减小22%.

图 9 模型表面平均风压分布

Figure 9. Mean wind pressure distribution on model surface

下载: 全尺寸图片幻灯片

模型2、4、5的风荷载如表5所示. 由表可知，3个模型的阻力相似，但脉动升力从模型2到模型5逐渐增加，模型5的升力最大，这说明仅在模型角部布置水平板对升力影响较小.

表 5 模型2、4、5的风荷载

Table 5. Wind loads of models 2, 4, 5

名称	${\overline C}_{\mathrm{d}}$	${C}_{{\mathrm{d}}1}$	${C}_{{\mathrm{l}}1}$
模型 2	1.149	0.102	0.219
模型 4	1.156	0.106	0.229
模型 5	1.153	0.103	0.261

下载: 导出CSV

| 显示表格

4. 结　论

本文采用LES方法评估大气边界层流下外伸肋板对高层建筑气动特性的影响. 详细阐述了肋板密度和布置形式对模型流场特征的影响，如近壁流、涡结构和竖向流等，并借助流场信息阐明了壁面风压和整体风荷载的变化，以评估不同肋板的抗风性能，阐明湍流来流下外伸板的流场机理. 得到以下结论：

1）水平板明显影响尾涡尺寸和尾部鞍点，水平板能明显拉长尾涡. 尾部鞍点高度随着肋板密度的增加而减小，沿建筑物高度的肋板密度过大时，尾部鞍点无明显变化. 外伸板随着水平间距的增大，其对尾涡的影响逐渐变弱.

2）水平板可以有效抑制建筑立面附近的竖向流动，导致近壁流动形式明显变化. 连续竖直板明显影响近壁流，而间隔肋板对近壁流的影响相对较弱.

3）流场的变化会改变壁面风压分布. 水平板使迎风面的平均风压 ${\overline C}_{\mathrm{P}}$ 呈“之”字形分布. 水平板可以明显降低侧壁面上平均和脉动风压，最大降幅分别约为20%和17%.

4）水平板不改变模型的平均阻力 ${\overline C}_{\mathrm{d}}$ ，但会明显降低模型上的 ${ C}_{{\mathrm{l}}1}$ ，最大减幅为27%. 连续肋板相比间隔肋板能更明显的降低模型上的气动力.

5）连续布置且密度适中的水平肋板对高层建筑周围的流场结构和建筑上的风荷载影响更显著，因此，实际高层建筑外辅助构件的设计和布置时应采用连续水平肋板，肋板布置密度适中即可.

致谢：中国电建集团成都院科技项目（P49321，PA2202）

图 1 管棚在单个开挖循环进尺下的理论分析模型

Figure 1. Theoretical analysis model of pipe shed under an excavation cycle footage

下载: 全尺寸图片幻灯片

图 2 管棚的受力和变形分布（隧道开挖至第30个循环）

Figure 2. Stress and deformation distributions of pipe shed (tunnel excavation to the 30th cycle)

下载: 全尺寸图片幻灯片

图 3 管棚的受力和变形的分布变化

Figure 3. Distribution variations of stress and deformation of pipe shed

下载: 全尺寸图片幻灯片

图 4 管棚变形模型预测值与现场实测数据对比

Figure 4. Comparison between predicted values of pipe shed deformation model and on-site measured data

下载: 全尺寸图片幻灯片

图 5 环向间距与管棚变形的关系

Figure 5. Relationships between circumferential spacing and deformation of pipe shed

下载: 全尺寸图片幻灯片

图 6 环向间距与管棚内力的关系

Figure 6. Relationships between circumferential spacing and internal force of pipe shed

下载: 全尺寸图片幻灯片

图 7 管径与管棚变形的关系

Figure 7. Relationships between pipe diameter and deformation of pipe shed

下载: 全尺寸图片幻灯片

图 9 搭接长度对管棚受力和变形的影响

Figure 9. Influence of lap length on stress and deformation of pipe shed

下载: 全尺寸图片幻灯片

图 8 管径与管棚内力的关系

Figure 8. Relationship between pipe diameter and internal force of pipe shed

下载: 全尺寸图片幻灯片

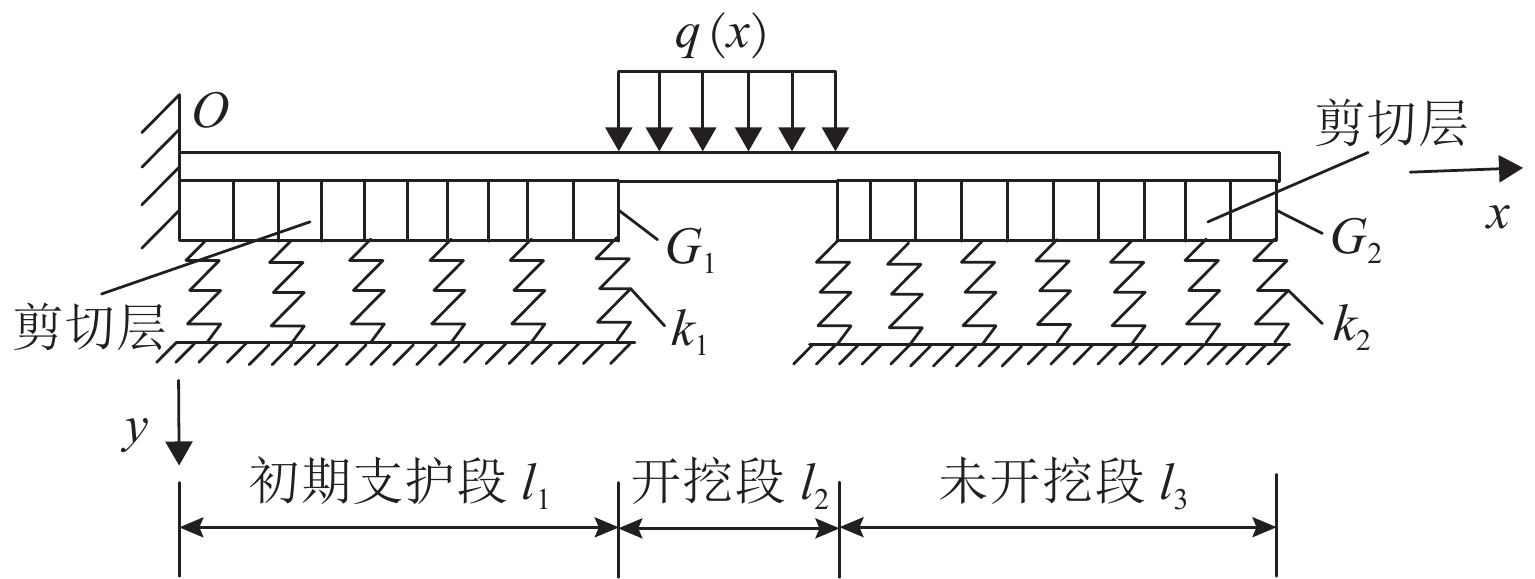
表 1 Pasternak弹性地基参数

Table 1. Pasternak elastic foundation parameters

项目基床系数/（kN·m⁻³）地基剪切模量/（kN·m⁻¹）

初期支护 7.84 × 10⁷ 9.51 × 10⁴

岩体 1.64 × 10⁵ 1.63 × 10³

下载: 导出CSV

参考文献(19)

[1]	师晓权. 软弱围岩隧道掌子面稳定性控制及预加固技术研究[D]. 成都:西南交通大学,2012.
[2]	王道远,袁金秀,李俊,等. 考虑施工特性的浅埋软弱洞口段管棚变形量预测及工程应用[J]. 岩石力学与工程学报,2017,36(3): 716-724. WANG Daoyuan, YUAN Jinxiu, LI Jun, et al. Deformation prediction of pipe roof in shallow soft portal section of tunnels considering construction feature[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(3): 716-724.
[3]	李化云,张志强,王志杰,等. 浅埋大跨隧道预加固措施相似模型试验研究[J]. 岩土力学,2012,33(增2):133-138. LI Huayun, ZHANG Zhiqiang, WANG Zhijie, et al. Similar model test study on pre-reinforcement measures of shallow-buried long-span tunnel[J]. Rock and Soil Mechanics, 2012, 33(S2):133-138.
[4]	HISATAKE M, OHNO S. Effects of pipe roof supports and the excavation method on the displacements above a tunnel face[J]. Tunnelling and Underground Space Technology, 2008, 23(2): 120-127. doi: 10.1016/j.tust.2007.02.002
[5]	SONG K I, CHO G C, CHANG S B, et al. Beam-spring structural analysis for the design of a tunnel pre-reinforcement support system[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 59: 139-150. doi: 10.1016/j.ijrmms.2012.12.017
[6]	周顺华. 软弱地层浅埋暗挖施工中管棚法的棚架原理[J]. 岩石力学与工程学报,2005,24(14): 2565-2570. ZHOU Shunhua. Principles of pipe roof applied to shallow-buried tunnels in soft ground[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(14): 2565-2570.
[7]	HOUNYEVOU KLOTOÉ C, BOURGEOIS E. Three dimensional finite element analysis of the influence of the umbrella arch on the settlements induced by shallow tunneling[J]. Computers and Geotechnics, 2019, 110: 114-121. doi: 10.1016/j.compgeo.2019.02.017
[8]	高文山,王立川,章慧健,等. 超前加固和初期支护对浅埋隧道地表沉降控制的贡献率分析[J]. 铁道科学与工程学报,2021,18(3): 720-727. GAO Wenshan, WANG Lichuan, ZHANG Huijian, et al. Analysis of the contribution of face support and primary support to the surface settlement control of shallow tunnel[J]. Journal of Railway Science and Engineering, 2021, 18(3): 720-727.
[9]	赵凯. 隧道洞口软岩段超前支护围岩变形控制及施工方法研究[D]. 西安:西安科技大学,2020.
[10]	MOROVATDAR A, PALASSI M, ASHTIANI R S. Effect of pipe characteristics in umbrella arch method on controlling tunneling-induced settlements in soft grounds[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2020, 12(5): 984-1000. doi: 10.1016/j.jrmge.2020.05.001
[11]	李沛莹. 管棚受力特性及其与后续工法配合效果分析[D]. 武汉:华中科技大学,2011.
[12]	BAGHERZADEH P, GOSHTASBI K, KASHEF M. Umbrella arch method performance, structural behavior and design elements utilizing in collapsing zones[J]. Environmental Earth Sciences, 2020, 79(23): 521.1-521.15. doi: 10.1007/s12665-020-09266-y
[13]	董新平,周顺华,胡新朋. 软弱地层管棚法施工中管棚作用空间分析[J]. 岩土工程学报,2006,28(7): 841-846. DONG Xinping, ZHOU Shunhua, HU Xinpeng. 3D analysis of function of piperoof applied in soft ground[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(7): 841-846.
[14]	宋战平,田小旭,周冠南,等. 隧道洞内管棚超前预支护力学行为的理论分析[J]. 中国公路学报,2020,33(4):89-98. SONG Zhanping, TIAN Xiaoxu, ZHOU Guannan, et al. Theoretical analysis of mechanical behavior of advanced pre-support of pipe-roof in tunnel[J]. China Journal of Highway and Transport, 2020, 33(4):89-98.
[15]	武松,汤华,罗红星,等. 浅埋软岩公路隧道超前管棚支护机制与工程应用研究[J]. 岩石力学与工程学报,2019,38(增1):3080-3091. WU Song, TANG Hua, LUO Hongxing, et al. Study on advanced pipe-shed support mechanism and engineering application of shallow-buried soft rock highway tunnel[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(S1):3080-3091.
[16]	黄华,巩江峰,邸成,等. 铁路隧道超前管棚变形规律及参数研究[J]. 铁道工程学报,2019,36(12): 65-70. HUANG Hua, GONG Jiangfeng, DI Cheng, et al. Research on the deformation law and parameters of advanced pipe shed for railway tunnel[J]. Journal of Railway Engineering Society, 2019, 36(12): 65-70.
[17]	王炳智. 软弱围岩隧道管棚超前预支护技术[D]. 重庆:重庆交通大学,2018.
[18]	ZHANG Z Q, LI H Y, LIU H Y, et al. Load transferring mechanism of pipe umbrella support in shallow-buried tunnels[J]. Tunnelling and Underground Space Technology, 2014, 43: 213-221. doi: 10.1016/j.tust.2014.05.018
[19]	卢新建. 基于变基床系数下双参数模型的管棚力学机理研究[J]. 福建建筑,2016(6): 58-62. LU Xinjian. Mechanical mechanism of piperoofs based on the Pasternak model with variable coefficient of subgrade reaction[J]. Fujian Architecture & Construction, 2016(6): 58-62.

施引文献

期刊类型引用(1)
1. 尹升. 浅埋区黄楼河隧道管棚加固效果探究. 中国公路. 2025(01): 98-100 . 百度学术
其他类型引用(0)

附加材料(0)

访问统计

点击查看大图

图(9) / 表(1)

计量

文章访问数: 173
HTML全文浏览量: 67
PDF下载量: 42
被引次数: 1

1. 数值方法
1.1 模型信息
1.2 控制方程及求解策略
1.3 网格信息和边界条件
1.4 气动力定义和结果验证
2. 外伸板对流场结构的影响
2.1 平均流场结构
3. 外伸板对风压和风荷载的影响
3.1 外伸板密度影响
3.2 外伸板布置形式的影响
4. 结　论

项目	基床系数/（kN·m⁻³）	地基剪切模量/（kN·m⁻¹）
初期支护	7.84 × 10⁷	9.51 × 10⁴
岩体	1.64 × 10⁵	1.63 × 10³

管棚承载机制的理论分析

doi: 10.3969/j.issn.0258-2724.20230425

作者简介: 张建（1987—），男，博士研究生，研究方向为公路隧道设计方法，E-mail：16813698@qq.com

通讯作者: 严松宏（1966—），男，教授，研究方向为地下工程设计施工理论及其工程应用，E-mail：yansonghong@163.com

计量

出版历程