路桥过渡段纵连轨道板纵向力分布特征与上拱机理分析

蔡小培; 王昌昌; 董博; 陈泽林; 张乾

doi:10.3969/j.issn.0258-2724.20230424

路桥过渡段纵连轨道板纵向力分布特征与上拱机理分析

doi: 10.3969/j.issn.0258-2724.20230424

北京交通大学土木建筑工程学院，北京 100044

基金项目: 国家自然科学基金项目（52178405）；京沪高速铁路股份有限公司科技研究项目（京沪科研-2020-13）；中国国家铁路集团有限公司科技研究开发计划（K2022G038）

详细信息

作者简介:
蔡小培（1982—），男，教授，博士，研究方向为铁路轨道结构与轨道动力学，E-mail：xpcai@bjtu.edu.cn

中图分类号: U213.21
计量
- 文章访问数: 85
- HTML全文浏览量: 39
- PDF下载量: 23
- 被引次数: 0
出版历程
- 收稿日期: 2023-08-22
- 录用日期: 2024-12-10
- 修回日期: 2023-11-24
- 网络出版日期: 2024-12-16

Analysis of Longitudinal Force Distribution Characteristics and Arching Mechanism of Longitudinally Connected Track Slabs in Bridge-Subgrade Transition Section

School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China

摘要

摘要:
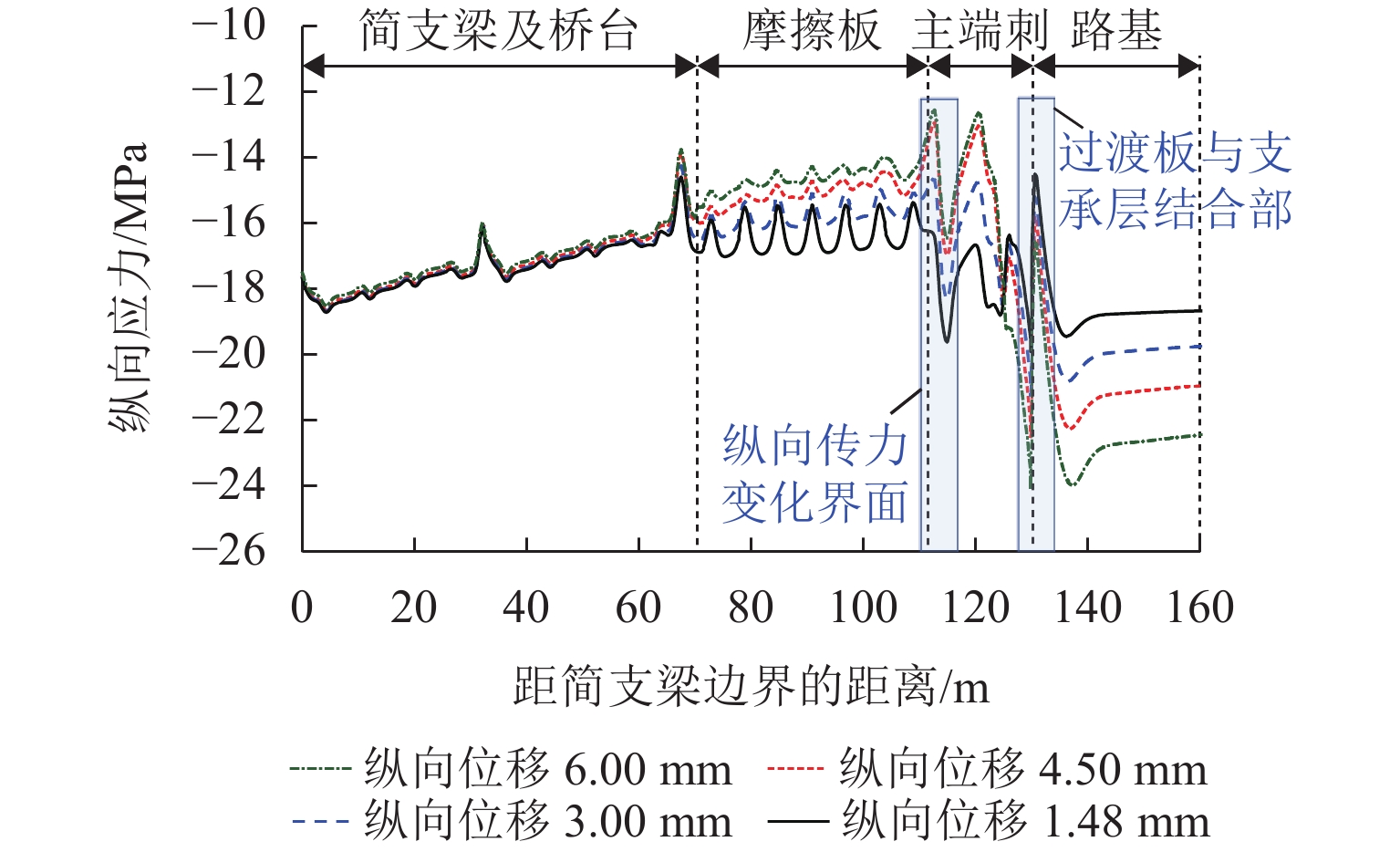
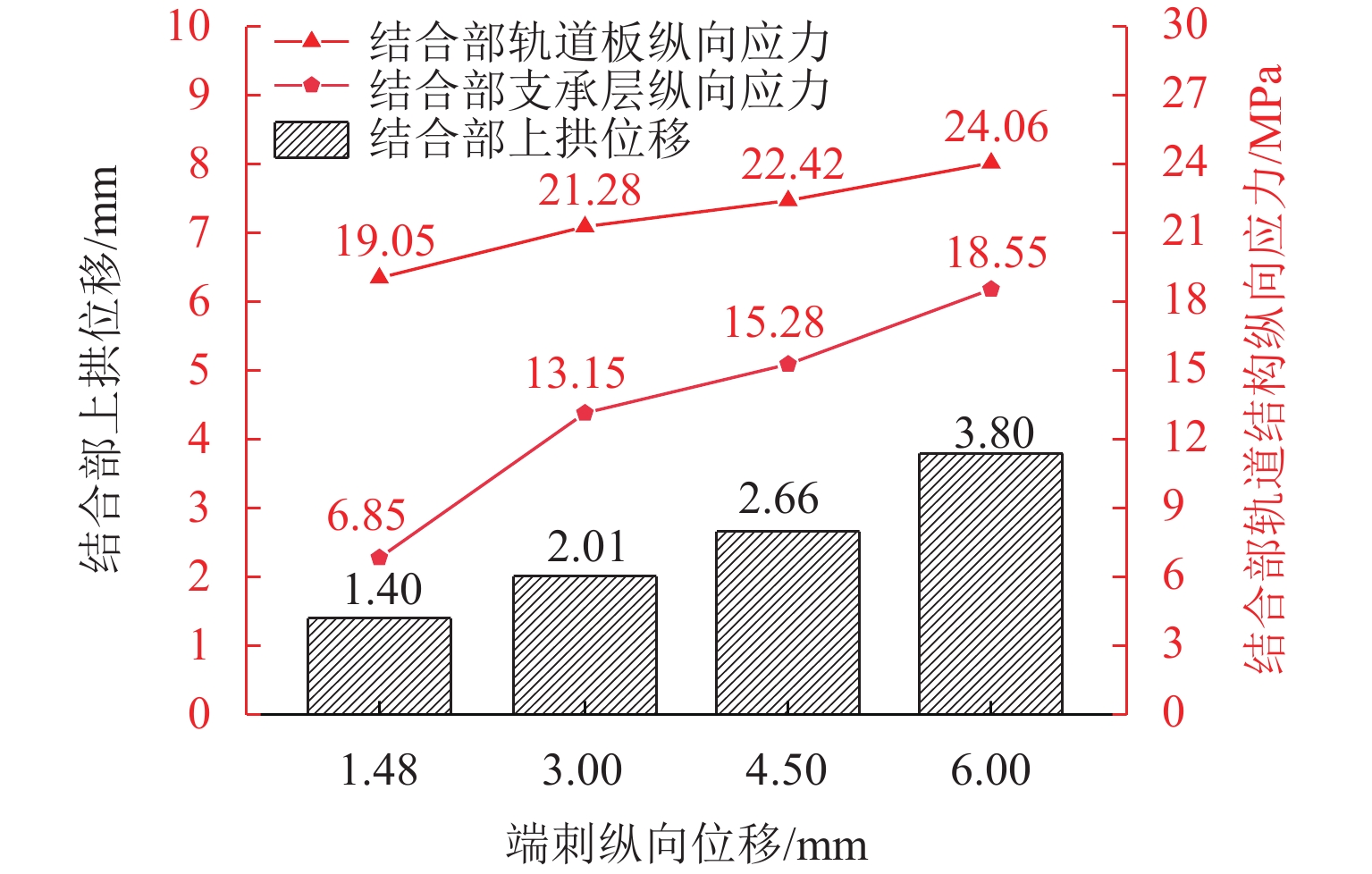
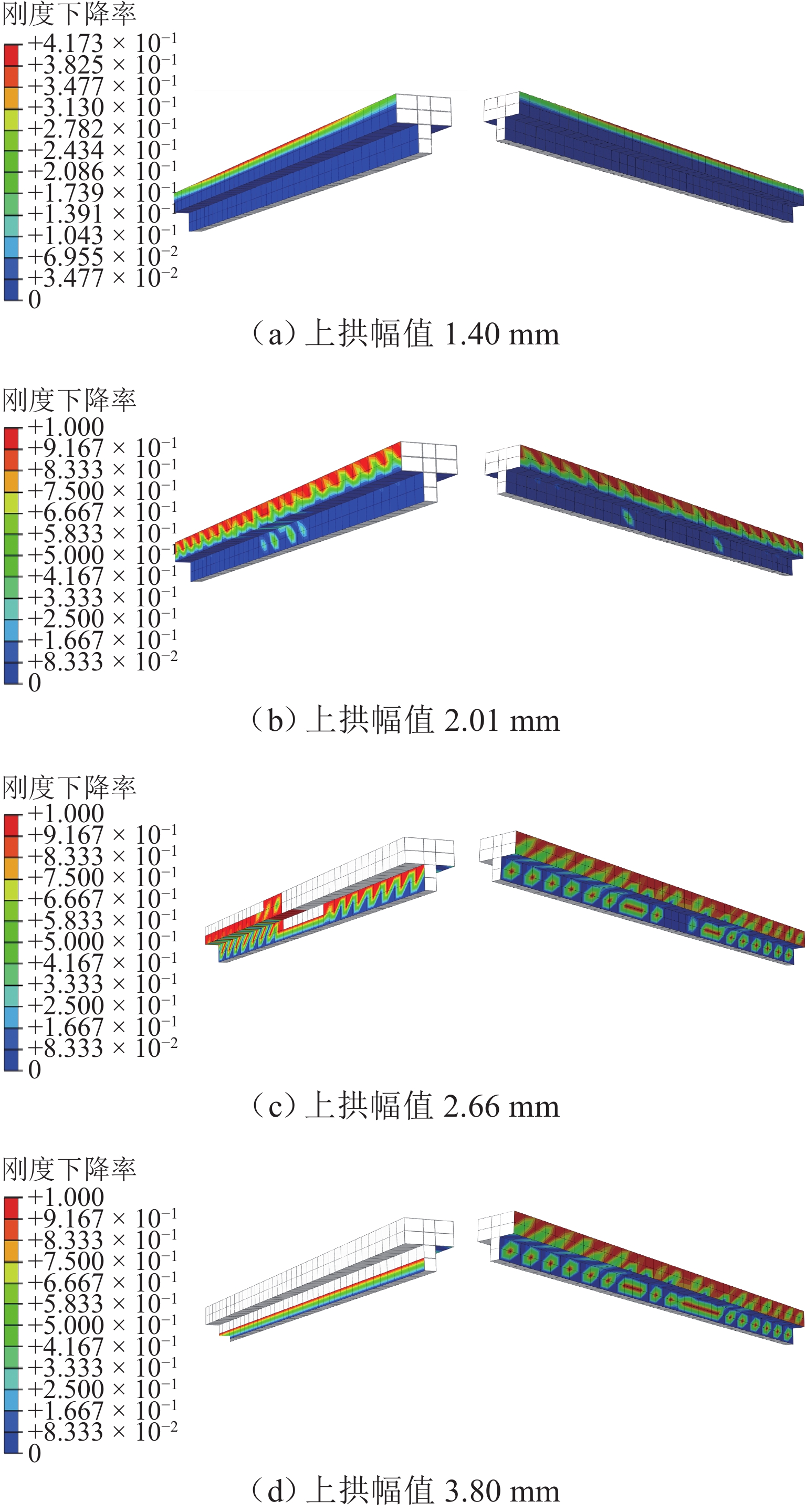
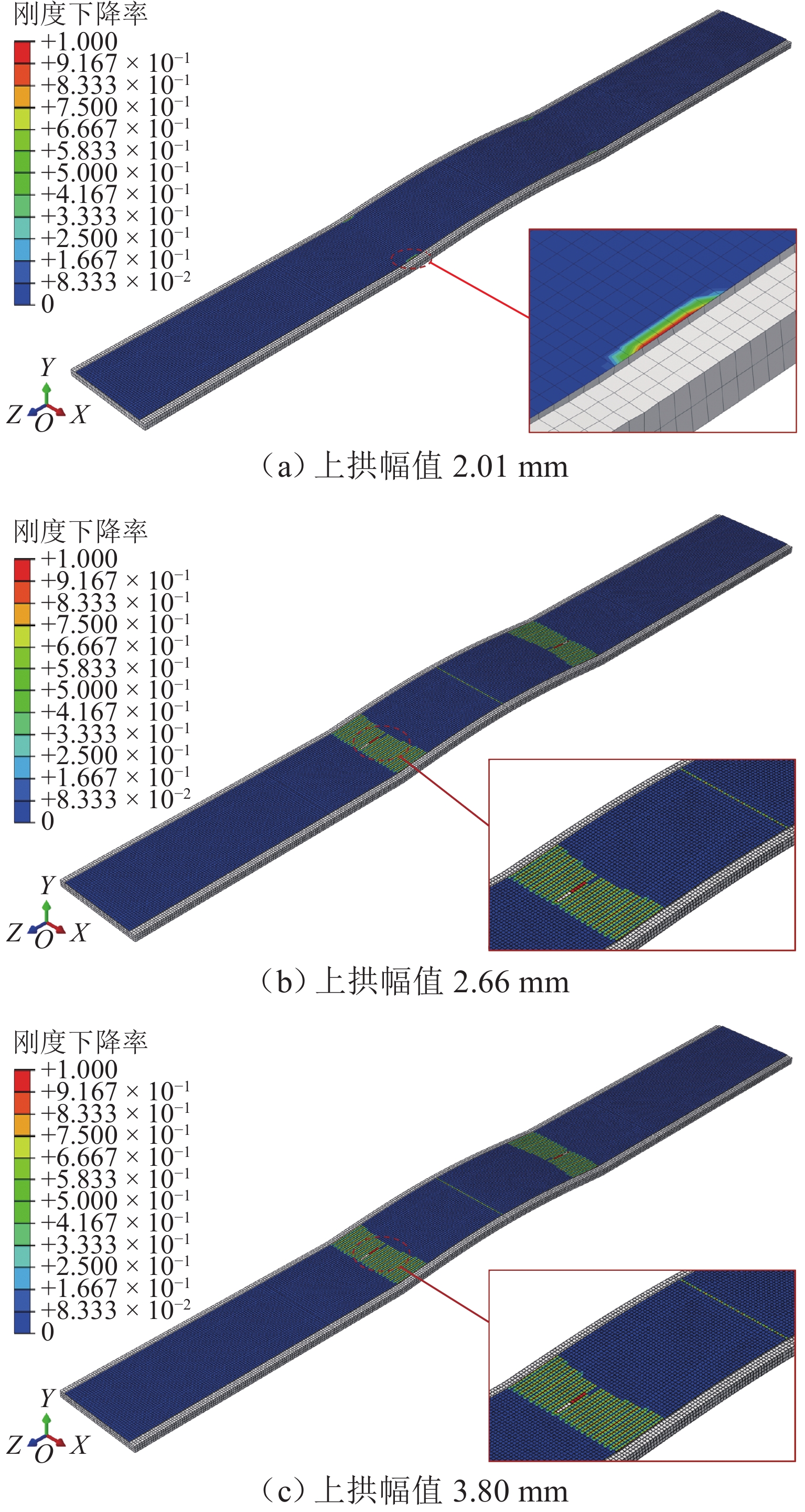
纵连板式无砟轨道在路桥过渡段区域力学行为复杂，且上拱病害频繁，以路桥过渡段 П 型端刺无砟轨道为研究对象，建立轨道-桥梁-端刺-路基一体化有限元模型；并引入双线性内聚力模型模拟板间及层间黏结关系，分析路桥过渡段纵连轨道板在不同温度荷载和端刺位移下的纵向力分布规律；并研究端刺应力敏感区域，即过渡段与支承层结合部的轨道板纵向应力特征以及结合部挤压变形与上拱变形的关系. 研究结果表明：在主端刺及过渡板与支承层结合部的轨道板纵向压应力水平最高，极端正温梯下的最大值为19.91 MPa，摩擦板及桥梁段较小，与端刺各结构组成的限位能力相对应；随着路基材料劣化脱空等病害发展，其纵向抵抗和层间摩阻不断降低，导致端刺纵向变形不断增加，端刺区轨道板的纵向应力降低，结合部支承层的纵向应力增加，当纵向变形达到6 mm时，结合部支承层的纵向压应力达到18.55 MPa，结构的压碎风险极高；结合部位的挤压上拱显著影响轨道结构板间和层间黏结状态，增加上拱病害的风险；研究成果可进一步优化和整治纵连板式无砟轨道过渡段病害，保障高铁安全平稳运行提供参考.
- CRTSⅡ型板式无砟轨道 /
- 内聚力模型 /
- 应力分析 /
- 损伤
Abstract:
The mechanical behavior of longitudinally connected ballastless track slabs in the transition section of subgrade and bridge is complex, and arching disease is frequent. The П-type end spine ballastless track in the transition section of subgrade and bridge was taken as the research object, and a track-bridge-end spine-subgrade integrated finite element model was established. The bilinear cohesive force model was introduced to simulate the bonding relationship between the slabs and the interlayers, and the longitudinal force distribution of the longitudinally connected track slabs in the transition section of subgrade and bridge under different temperature loads and end spine displacements was analyzed. The stress-sensitive area of the end spine, namely, the longitudinal stress characteristics of the track slabs at the junction of the transition section and the supporting layer and the relationship between the extrusion deformation of the junction and the arching deformation, were studied. The results show that the longitudinal compressive stress level of the track slabs at the main end spine and the junction of the transition plate and the supporting layer is the highest, and the maximum value under the extreme positive temperature gradient is 19.91 MPa. The friction plate and the bridge section are small, which corresponds to the limit capacity of each structure of the end spine. With the development of diseases such as deterioration and void of subgrade materials, the longitudinal resistance and interlayer friction decrease continuously, which leads to the increase in longitudinal deformation of the end spine, the decrease in longitudinal stress of the track slabs in the end spine area, and the increase in longitudinal stress of the supporting layer of the junction. When the longitudinal deformation reaches 6 mm, the longitudinal compressive stress of the supporting layer of the junction reaches 18.55 MPa, and the crushing risk of the structure is very high. The compressive arching of the junction greatly affects the bonding between the slabs and the layers of the track structure and increases the risk of arching disease. The research results can provide a reference for further optimizing and renovating the diseases of the transition section of the longitudinally connected ballastless track slabs and ensuring the safe and stable operation of high-speed railways.
- CRTSⅡ ballastless track slab /
- cohesive force model /
- stress analysis /
- damage

HTML全文

无砟轨道具备高平顺性、高稳定性等诸多优势，是我国高速铁路首选的轨道型式，其中，纵连式无砟轨道占比较大，具备竖向多层、纵向连续等结构特征. 纵连板式无砟轨道的连续式轨道板和底座受温度影响很大，使得轨道结构在面临复杂气候条件时的适应性较差^[1]，尤其是在路桥过渡段区域，端刺锚固结构会导致轨道结构受力及变形状况更加复杂. 据现场调研显示，CRTS Ⅱ型板式无砟轨道在路桥过渡段区域的上拱及层间离缝病害更加频繁，对线路平顺性造成较大破坏，严重影响了行车安全和稳定性. 因此，有必要针对路桥过渡段区域的结构受力及上拱特征进行研究.

目前，针对纵连板式无砟轨道纵向力及上拱问题开展了较多研究. 张鹏飞^[2]研发了CRTS Ⅱ型板式无砟轨道纵向力分析系统，对桥上无砟轨道无缝线路在复杂荷载作用下的纵向受力与变形规律进行分析；戴公连等^[3]通过实测获取的无砟轨道及桥梁温度数据施加荷载，分析大跨桥上无砟轨道纵向受力特征；徐庆元等^[4]研究高速铁路纵连板桥上无砟轨道纵向力学特性，并与单元板进行对比. Zhang等^[5]通过热流固耦合分析的方式，研究日照辐射下纵连板式无砟轨道温度场时空分布特征，以及轨道结构内力分布与结构变形特征；高亮等^[6]采用有限元内聚力单元模拟的方式，研究CRTSⅡ板式无砟轨道不同层间及板间内聚力参数对无砟轨道上拱变形的影响；周凌宇等^[7]通过制作的三跨无砟轨道-简支梁桥结构1/4缩尺模型，研究循环温度荷载作用下梁端位置的无砟轨道层间离缝发展规律；钟垚等^[8]研究CRTSⅡ型板式无砟轨道在持续高温作用下的层间离缝发展规律；赵国堂等^[9]建立了CRTSⅡ型板式无砟轨道全过程三维渐进损伤力学模型，发现层间界面离缝主要从主剪切型损伤区域开始，且损伤和离缝发展存在继承性.

综上所述，现有纵连板式无砟轨道纵向受力特征的研究主要关注桥梁基础上的钢轨及无砟轨道受力及变形规律，而针对结构及受力机理更加复杂的路桥过渡段区域的无砟轨道纵向力分布特征的研究仍存在不足. 除此之外，现有研究在分析纵连板式无砟轨道的上拱问题时，较少结合路桥过渡段锚固结构变形的影响. 因此，本文建立轨道-桥梁-端刺-路基一体化有限元模型，在纵连板式无砟轨道板间及层间建立基于双线性内聚力的黏结单元，对温度荷载作用下路桥过渡段纵连轨道板纵向力分布特征以及上拱机理进行研究.

1. 轨道-桥梁-端刺-路基空间耦合模型

1.1 有限元模型及参数

路桥过渡段纵连板式无砟轨道一体化有限元模型包括轨道结构、桥梁段、端刺锚固结构及路基等. 其中：轨道结构从上至下依次为钢轨、扣件、预制轨道板、宽窄接缝、水泥乳化沥青（CA）砂浆层、底座（路基段为支承层）；桥梁段包括 2跨32.6 m简支梁、桥台、桥墩、侧向挡块及剪力齿槽；端刺锚固结构包括摩擦板、主端刺及过渡板；路基分为2部分，过渡段端刺范围内靠近桥台侧路基采用掺水泥的级配碎石进行填筑，其后采用与普通路基段相同的AB组填料填筑. 纵连轨道结构底座与桥面之间设“两布一膜”滑动层，底座与端刺摩擦板之间设2层土工布，均采用面与面接触方式模拟，摩擦系数分别取0.35和0.70；端刺与路基土体之间同样采用面与面接触关系模拟，摩擦系数参考桩土接触分析取0.30^[2]. 模型轨道结构两端以及路基一侧采用对称约束，钢轨扣件、剪力齿槽、墩台刚度采用弹簧阻尼单元模拟，其余部件均采用实体单元模拟. 钢轨弹性模量为210 GPa，泊松比为0.3，线膨胀系数为1.18 × 10⁻⁵ ℃⁻¹. 轨道板及宽窄接缝、桥梁及墩台材料为C55混凝土，底座为C40混凝土，支承层及端刺为C30混凝土，弹性模量依次为35.5、32.5、30.0 GPa，密度、泊松比和线膨胀系数参数一致，分别取2500 kg/m³、0.20、1.0 × 10⁻⁵ ℃⁻¹. CA砂浆层密度为2400 kg/m³，弹性模量为8.5 GPa，泊松比为0.34，线膨胀系数为1.3 × 10⁻⁵ ℃⁻¹. 模型总体示意如图1所示. 路基土体材料^[2,10]的参数取值如表1所示.

图 1 纵连板式无砟轨道-桥梁-端刺-路基空间耦合模型

Figure 1. Spatial coupling model of longitudinally connected ballastless track slab-bridge-end spine-subgrade

下载: 全尺寸图片幻灯片

表 1 路基模型计算参数

Table 1. Calculation parameters of subgrade model

部件	密度/（kg•m⁻³）	弹性模量/MPa	泊松比	黏聚力/（kN•m⁻²）	剪切角/（°）	剪切膨胀角/（°）
级配碎石	2200	200	0.20	35	30	5
AB 组填料	2100	120	0.25	15	20	8

下载: 导出CSV

| 显示表格

1.2 双线性内聚力模型

为探究路桥过渡段区域纵连板式无砟轨道在温度荷载及下部锚固结构变形双重作用下的结构受力变形特征及上拱演化机理，在轨道板与宽窄接缝及CA砂浆层之间的接触界面采用双线性内聚力单元模型，以表征其损伤开裂关系.

1）内聚力损伤判定准则

本文模型计算选取二次名义应力准则（Quads）作为层间内聚力界面损伤萌生的判断条件，如式（1）.

${\left( {\frac{{\left\langle {{t_{\mathrm{n}}}} \right\rangle }}{{t_{{\mathrm{n}},0}^{}}}} \right)^2} + {\left( {\frac{{{t_{\mathrm{s}}}}}{{t_{{\mathrm{s}},0}^{}}}} \right)^2} + {\left( {\frac{{{t_{\mathrm{t}}}}}{{t_{{\mathrm{t}},0}^{}}}} \right)^2} = 1 ,$

(1)

式中：t_n,0、t_s,0、t_t,0分别为抗拉强度、第一剪切强度和第二抗剪强度；t_n为法向牵引力，〈t_n〉表示法向应力为负时内聚力黏结界面为受压状态，不发生损伤；t_s、t_t分别为切向的第一、第二切向牵引力.

2）损伤演化机理

基于弹塑性断裂力学理论^[11-14]，双线性内聚力模型定义黏结面之间法向和切向的牵引-分离作用关系^[15]如图2所示. 图中： t_τ为切向牵引力，点A_τ、A_m、A_n分别为切向、复合模型、法向的损伤起始点，点B表示界面完全损伤失效点，点B_τ、B_m、B_n分别为切向、复合模型、法向的界面完全损伤失效点，δ_τ,0、δ_m,0、δ_n,0分别为切向、有效相对位移、法向的损伤起始时的相对位移，t_τ,0、t_m,0、t_n,0为分别切向、有效相对应力、法向的极限强度，δ_τ,f、δ_m,f、δ_n,f分别为切向、有效相对位移、法向完全破坏时的相对位移，G_n,C、G_s,C为法向和切向2种断裂模式下的界面断裂能，G_C为临界断裂能.

图 2 双线性内聚力牵引-分离关系

Figure 2. Bilinear cohesive force traction-separation relationship

下载: 全尺寸图片幻灯片

图2中路径OA_n与OA_τ分别为黏结面法向张拉与切向剪切2种牵引-分离准则的初始阶段，此阶段黏结面损伤尚未产生，界面应力与应变关系为线弹性特征，牵引力-分离位移的关系如式（2）.

$\left[ {\begin{array}{*{20}{c}} {{t_{\mathrm{n}}}} \\ {{t_{\mathrm{s}}}} \\ {{t_{\mathrm{t}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{K_{{\mathrm{nn}}}}}&{{K_{{\mathrm{ns}}}}}&{{K_{{\mathrm{nt}}}}} \\ {{K_{{\mathrm{ns}}}}}&{{K_{{\mathrm{ss}}}}}&{{K_{{\mathrm{st}}}}} \\ {{K_{{\mathrm{nt}}}}}&{{K_{{\mathrm{st}}}}}&{{K_{{\mathrm{tt}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\delta _{\mathrm{n}}}} \\ {{\delta _{\mathrm{s}}}} \\ {{\delta _{\mathrm{t}}}} \end{array}} \right],$

(2)

式中：K_nn、K_ss、K_tt分别为法向、第一与第二切向的界面刚度，K_ns、K_nt、K_st均为0，δ_n、δ_s、δ_t分别为法向、第一与第二切向的相对位移.

图2中A_nB_n与A_τB_τ分别为黏结面法向与切向破坏的损伤演化阶段，点A表示损伤起始点，此时内聚力接触面开始萌生损伤裂纹，点B表示界面完全损伤失效. 引入损伤因子D（式（3））来评估界面损伤程度，D取值范围为0～1：当D=0时，表明界面没有伤损；当D=1时，表明界面完全伤损，层间脱黏.

$D = \frac{{\delta _{{\mathrm{m,f}}}^{}\left( {\delta _{{\mathrm{m}},\max }^{} - \delta _{{\mathrm{m}},0}^{}} \right)}}{{\delta _{{\mathrm{m}},\max }^{}\left( {\delta _{{\mathrm{m}},{\mathrm{f}}}^{} - \delta _{{\mathrm{m}},0}^{}} \right)}} ,$

(3)

式中：δ_m,max为加载过程中能达到的最大有效位移.

此时内聚力损伤演化阶段的牵引-相对位移关系可表示为

$\left\{ \begin{array}{cc} \text{ }{t}_{\text{n}}=(1-D){k}_{{\mathrm{n}}}{\delta }_{{\mathrm{n}}},& {\delta }_{{\mathrm{n}}}\geqslant0\\ {t}_{{\mathrm{s}}}=(1-D){k}_{{\mathrm{s}}}{\delta }_{{\mathrm{s}}},& \\ {t}_{{\mathrm{t}}}=(1-D){k}_{{\mathrm{t}}}{\delta }_{{\mathrm{t}}}.& \end{array} \right.$

(4)

损伤演化过程伴随着能量的释放，因此，本文采用基于能量（断裂能）的BK损伤演化准则来判定伤损演化后内聚力接触面是否脱黏. 断裂能数值上等于牵引力-相对位移曲线下所围成的面积. 临界断裂能^[16]为

${G_{\mathrm{C}}} = G_{{\mathrm{n,C}}}^{} + \left( {G_{{\mathrm{s,C}}}^{} - G_{{\mathrm{n,C}}}^{}} \right){\left( {\frac{{{G_{\mathrm{S}}}}}{{{G_{\mathrm{n}}+G_{\mathrm{s}}}}}} \right)^\eta } ,$

(5)

式中：η为混合系数，G_n为法向断裂模式下的界面断裂能，G_s为切向断裂模式下的界面断裂能.

本文在轨道板与宽窄接缝间以及轨道板与CA砂浆层间设置了双线性内聚力单元表征板间及层间接触界面的损伤状况，内聚力单元的参数取值^[17-19]如表2所示.

表 2 内聚力模型参数

Table 2. Cohesive force model parameters

黏结界面	法向抗拉强度/MPa	剪切强度/MPa	法向刚度/ （MPa•mm⁻¹）	切向刚度/ （MPa•mm⁻¹）	法向断裂能/（J•m²）	切向断裂能/（J•m²）
轨道板与宽窄接缝	1.700	1.600	500.0	150.0	35.00	15.20
轨道板与 CA 砂浆层	1.792	0.956	716.8	62.9	25.24	18.70

下载: 导出CSV

| 显示表格

1.3 模型验证

为确保本文模型计算结果的准确性和可靠性，将本模型计算结果与文献[2]和文献[20]计算结果对比，并进行模型验证. 选取与文献[2,20]相同的工况进行加载，提取轨道板及底座的最大纵向应力值进行对比. 在荷载为轨道结构正温梯90 ℃/m、桥梁结构整体升温40 ℃工况下，本模型计算得到的轨道板最大纵向应力为−19.05 MPa，底座板最大纵向应力为−11.98 MPa，与文献计算结果对比如表3所示.

表 3 模型验证计算结果对比

Table 3. Comparison of model verification and calculation results MPa

来源	轨道板最大纵向应力	底座最大纵向应力
文献[2]	−20.11	−12.04
文献[20]	−19.80	−10.80
本文计算结果	−19.05	−11.98
注：本文纵向应力负值表示压应力.

下载: 导出CSV

| 显示表格

由表3可知：本文模型计算得到轨道板与底座最大纵向应力数值与文献计算结果较为吻合，且应力最大值位置与文献保持一致. 因此，本文建立的模型正确、可靠.

2. 路桥过渡段轨道板纵向力分布特征

本文对轨道及桥梁分别施加温度梯度及整体温度荷载，研究路桥过渡段区域的纵连轨道的纵向力分布特征. 轨道板温度梯度的取值^[21-23]为95、85、75、65 ℃/m. 由于混凝土材料为不良导热材料^[24]，故不考虑CA砂浆层和底座/支承层间的温度差异，上述部件的荷载取值与正温梯下轨道板底面的温度值相同. 桥梁整体升温取为造成轨道板不同正梯度时相对应的环境温度升温荷载值. 不同温度梯度条件下轨道板的纵向力分布特征如图3所示.

图 3 不同温度梯度条件下轨道板纵向应力

Figure 3. Longitudinal stress of track slab under different temperature gradient conditions

下载: 全尺寸图片幻灯片

由图3可知：温度梯度大小对轨道板的受力有很大影响，温度梯度越大，轨道板的纵向压应力越大，正温梯为95、85、75、65 ℃/m时，轨道板的纵向压应力最大值分别为19.91、18.38、17.08、14.21 MPa，出现在过渡板末端与支承层结合位置处；根据纵向应力在路桥过渡段的分布特征可以看出，桥梁区段轨道板纵向应力水平总体最小，摩擦板区域稍大，主端刺区域最大. 轨道结构和桥面之间采用“两布一膜”滑动层，两者之间摩擦系数较小，轨道结构在纵向上变形相对自由，所以轨道板纵向应力总体水平较低. 轨道结构在过渡段端刺区域比较复杂，其传力机制如图4所示.

图 4 端刺与轨道结构受力

Figure 4. End spine and track structure force

下载: 全尺寸图片幻灯片

由图4可知：在纵向传力机制上，摩擦板与底座之间是摩擦状态，两者之间的摩擦系数较大，是桥梁与主端刺之间的过渡区域，轨道板纵向应力相比桥梁段稍大；到主端刺区域，轨道结构底座与主端刺共同浇筑，两者之间连结牢固，利用主端刺结构作为轨道结构纵向位移的主要限位装置，前部桥梁段和摩擦板段的纵向应力在此积聚，造成轨道板的纵向应力较大；4种工况下此界面轨道板的纵向力增幅都在21%左右.

由于纵向传力机制的变化，底座的纵向位移受到限制，但是轨道板、CA砂浆层、底座之间依靠黏结形成的3层结构往往会因为黏结力不足导致层间错动，产生轨道板与CA砂浆层之间的层间离缝. 在过渡板与支承层结合部位置处，轨道板的纵向应力出现了先增大后减小的状况，极端95 ℃/m温梯下从19.91 MPa减小至14.61 MPa，降幅达27.2%. 这是由于过渡板与支承层都受正温度梯度荷载的作用产生膨胀变形，两者相互挤压，同时过渡板一侧相对支承层一侧的纵向应力更大，支承层被过渡板挤压变形应力被释放了一部分，所以过渡板到支承层轨道板的纵向应力先增大后减小.

由以上分析可知，路桥过渡段区域的轨道板纵向应力分布复杂，纵向变形情况多变，尤其当路基土体劣化与端刺产生脱空状况下，土体的锚固能力大大下降，继而出现端刺纵向位移超过3 mm限值要求的情况. 端刺与路基接触部分的土体脱空劣化越严重，所导致的端刺纵向超限位移就越大. 本文选择端刺纵向位移限值3.00 mm、超限位移4.50、6.00 mm 3种工况在极端正温梯荷载作用下的轨道板纵向应力分布，与正常服役工况进行对比分析，如图5所示.

图 5 端刺超限位移下轨道板纵向应力分布

Figure 5. Longitudinal stress distribution of track slab under over-limit displacement of end spine

下载: 全尺寸图片幻灯片

从图5中可以看出：随着主端刺纵向位移逐渐增加，轨道板在端刺区域的纵向应力水平整体呈现下降的趋势，尤其是在主端刺区域，当位移超过3 mm后，纵向压应力下降较大，这表明端刺结构的限位能力大大下降；在结合部位置处，随着端刺位移增加，轨道板的纵向压应力最大值却在增加，如图6所示.

图 6 结合部变形与应力状况

Figure 6. Deformation and stress conditions of junction

下载: 全尺寸图片幻灯片

从图6可以看出，在纵向位移达到6.0 mm时，结合部轨道板纵向压应力为24.06 MPa，相对的下部支承层纵向压应力为18.55 MPa，接近支承层混凝土抗压强度标准值20.10 MPa，表明随着限位能力的降低，结合部支承层受到的挤压状况逐渐严重，混凝土结构挤碎掉块的风险逐渐增大.

图7所示为某一纵连板式无砟轨道路桥过渡段现场工点状况，展示了结合部位状况及主端刺区域轨道层间黏结状况.

图 7 路桥过渡段现场工点状况

Figure 7. Site condition of subgrade-bridge transition section

下载: 全尺寸图片幻灯片

由图7（a）可以看出：结合部位在纵向力的作用下混凝土产生较大的挤压掉块；上部宽窄接缝和层间离缝都有修补痕迹，表明板间及层间都产生因上拱导致的损伤. 从图7（b）可以看出：主端刺上方的轨道板与CA砂浆层之间出现层间离缝，在摩擦板区域轨道板与CA砂浆层之间黏结良好，并无层间离缝产生.

3. 路桥过渡段轨道板上拱机理

过渡板与支承层结合部位是路桥过渡段纵向应力及位移的敏感区域，最容易出现挤压破坏及上拱变形病害，从而影响上部轨道结构层间及板间的黏结状态. 而层间及板间良好的黏结是保证纵连板式无砟轨道纵向均匀传力，防止其上拱的重要条件. 因此，本文建立过渡板-支承层区段无砟轨道层间及板间设置内聚力黏结，分析结合部位挤压上拱对上部无砟轨道板间宽窄接缝黏结及层间黏结的影响.

3.1 结合部上拱对宽窄接缝黏结影响

由前文可知，极端温度荷载作用下，端刺结构在不同纵向位移下造成的结合部上拱幅值分别为1.40、2.01、2.66、3.80 mm. 4种工况下的结合部上拱位置上方宽窄接缝的板间黏结状态如图8所示. 图中：白色表示宽窄接缝混凝土，左右两侧彩色部分为内聚力黏结单元，黏结状态采用刚度下降率（取值0～1，意义与1.2节中的损伤因子相同，脱黏失效的单元会自动删除）表示^[25].

图 8 不同上拱幅值下宽窄接缝黏结损伤状况

Figure 8. Bonding damage status of wide and narrow joints under different arching amplitudes

下载: 全尺寸图片幻灯片

由图8可以看出：上拱位置的宽窄接缝损伤情况随上拱幅值的增加而增加，当上拱位移为1.40 mm时（端刺纵向位移小于3 mm），内聚力单元损伤较小，宽窄接缝板间的黏结状态较好；当上拱位移为2.01 mm时（端刺纵向位移刚好3 mm），内聚力单元损伤开始蔓延并出现较严重的损伤单元，宽接缝两侧相比窄接缝的损伤更大，呈现从上至下损伤逐渐减小的趋势；当上拱位移在2.66 mm和3.80 mm时（端刺纵向位移大于3 mm），宽窄接缝与相邻轨道板之间已经出现了部分区域脱黏的状况；宽窄接缝与过渡板一侧轨道板的黏结区域脱黏相对严重，另外一侧相对较小；从上往下宽接缝一侧的损伤脱黏最为严重，其次为宽窄交接的位置处，窄接缝的一侧的损伤脱黏出现最晚.

3.2 结合部上拱对层间黏结影响

结合部位上拱对层间黏结破坏位置的影响示意如图9所示，不同的上拱幅值下对层间黏结破坏状况如图10所示.

图 9 层间黏结破坏位置示意

Figure 9. Location of interlayer bonding damage

下载: 全尺寸图片幻灯片

图 10 不同上拱幅值下层间黏结损伤状况（变形放大100倍）

Figure 10. Bonding damage status between layers under different arching amplitudes （deformation magnified 100 times）

下载: 全尺寸图片幻灯片

从图9可以看出，过渡板支承层结合部上拱对砂浆层层间黏结的破坏主要集中在拱起范围的末端以及结合部位拱起峰值处. 当上拱幅值为1.40 mm时，层间黏结状态良好，并无损伤出现，故并未在图10中列出. 由图10（a）可知：当上拱幅值为2.01 mm时，拱起范围的末端板边位置开始出现黏结损伤，但是损伤的范围很小；结合部位拱起峰值处并无损伤出现. 由图10（c）可知：当上拱幅值为2.66 mm时，层间黏结损伤的区域开始扩大，拱起范围的末端已经产生了较大范围的黏结损伤，板中部分区域开始出现了脱黏失效；结合部宽窄接缝下部上拱峰值区域也开始出现黏结损伤；黏结损伤区域占整块板的18.4%，脱黏区域占0.3%. 由图10（d）可知，当上拱幅值达到3.80 mm时，拱起范围末端的黏结损伤区域以及黏结失效区域进一步扩大，黏结损伤区域占整块板的30.6%，脱黏区域占1.3%.

4. 结　论

1）轨道板纵向应力与温度呈正相关，其在主端刺区域及过渡板支承层结合部纵向应力水平最高，极端正温梯95 ℃/m下应力最大值为19.91 MPa；其次为摩擦板区域，桥梁段最小. 轨道板纵向应力分布特征与端刺锚固结构各组成的限位能力相对应.

2）随着端刺纵向位移的增加，轨道板在端刺区的纵向应力降低，结合部支承层的纵向应力随之增加，表明端刺的限位能力降低，结合部位挤压的状况愈发严重；当纵向位移达到6 mm时，结合部支承层的纵向压应力达到18.55 MPa，结构压坏风险极高.

3）随着端刺纵向位移增加，过渡板支承层结合部上拱逐步增大，其上方轨道结构板间及层间黏结状态不断降低，甚至出现了脱黏的状况，层间黏结损伤也在拱起范围的末端和上拱峰值处不断蔓延扩大，极大加剧了轨道上拱病害的风险.

图 1 纵连板式无砟轨道-桥梁-端刺-路基空间耦合模型

Figure 1. Spatial coupling model of longitudinally connected ballastless track slab-bridge-end spine-subgrade

下载: 全尺寸图片幻灯片

图 2 双线性内聚力牵引-分离关系

Figure 2. Bilinear cohesive force traction-separation relationship

下载: 全尺寸图片幻灯片

图 3 不同温度梯度条件下轨道板纵向应力

Figure 3. Longitudinal stress of track slab under different temperature gradient conditions

下载: 全尺寸图片幻灯片

图 4 端刺与轨道结构受力

Figure 4. End spine and track structure force

下载: 全尺寸图片幻灯片

图 5 端刺超限位移下轨道板纵向应力分布

Figure 5. Longitudinal stress distribution of track slab under over-limit displacement of end spine

下载: 全尺寸图片幻灯片

图 6 结合部变形与应力状况

Figure 6. Deformation and stress conditions of junction

下载: 全尺寸图片幻灯片

图 7 路桥过渡段现场工点状况

Figure 7. Site condition of subgrade-bridge transition section

下载: 全尺寸图片幻灯片

图 8 不同上拱幅值下宽窄接缝黏结损伤状况

Figure 8. Bonding damage status of wide and narrow joints under different arching amplitudes

下载: 全尺寸图片幻灯片

图 9 层间黏结破坏位置示意

Figure 9. Location of interlayer bonding damage

下载: 全尺寸图片幻灯片

图 10 不同上拱幅值下层间黏结损伤状况（变形放大100倍）

Figure 10. Bonding damage status between layers under different arching amplitudes （deformation magnified 100 times）

下载: 全尺寸图片幻灯片

表 1 路基模型计算参数

Table 1. Calculation parameters of subgrade model

部件	密度/（kg•m⁻³）	弹性模量/MPa	泊松比	黏聚力/（kN•m⁻²）	剪切角/（°）	剪切膨胀角/（°）
级配碎石	2200	200	0.20	35	30	5
AB 组填料	2100	120	0.25	15	20	8

下载: 导出CSV

表 2 内聚力模型参数

Table 2. Cohesive force model parameters

黏结界面	法向抗拉强度/MPa	剪切强度/MPa	法向刚度/ （MPa•mm⁻¹）	切向刚度/ （MPa•mm⁻¹）	法向断裂能/（J•m²）	切向断裂能/（J•m²）
轨道板与宽窄接缝	1.700	1.600	500.0	150.0	35.00	15.20
轨道板与 CA 砂浆层	1.792	0.956	716.8	62.9	25.24	18.70

下载: 导出CSV

表 3 模型验证计算结果对比

Table 3. Comparison of model verification and calculation results MPa

来源	轨道板最大纵向应力	底座最大纵向应力
文献[2]	−20.11	−12.04
文献[20]	−19.80	−10.80
本文计算结果	−19.05	−11.98
注：本文纵向应力负值表示压应力.

下载: 导出CSV

参考文献(25)

[1]	CAI X P, LUO B C, ZHONG Y L, et al. Arching mechanism of the slab joints in CRTS Ⅱ slab track under high temperature conditions[J]. Engineering Failure Analysis, 2019, 98: 95-108. doi: 10.1016/j.engfailanal.2019.01.076
[2]	张鹏飞. 复杂荷载条件下桥上CRTS Ⅱ型板式无砟轨道无缝线路纵向力研究[D]. 北京:北京交通大学,2018.
[3]	戴公连,葛浩,刘文硕,等. 实测温度下大跨度桥上纵连无砟轨道受力研究[J]. 铁道工程学报,2017,34(5): 26-31,93. DAI Gonglian, GE Hao, LIU Wenshuo, et al. Analysis of longitudinally connected ballastless track on the high-speed railway long-span bridge based on the actual measured temperature[J]. Journal of Railway Engineering Society, 2017, 34(5): 26-31,93.
[4]	徐庆元,张旭久. 高速铁路博格纵连板桥上无砟轨道纵向力学特性[J]. 中南大学学报(自然科学版),2009,40(2): 526-532. XU Qingyuan, ZHANG Xujiu. Longitudinal forces characteristic of Bogl longitudinal connected ballastless track on high-speed railway bridge[J]. Journal of Central South University (Science and Technology), 2009, 40(2): 526-532.
[5]	ZHANG Q, CAI X P, ZHONG Y L, et al. Temperature field and thermal effects of the longitudinal connected slab track based on the measurement data and thermal-fluid-structure coupling analysis[J]. Construction and Building Materials, 2022, 343: 128121.1-128121.14.
[6]	高亮,何宁,任西冲,等. 无砟轨道板端上拱变形影响规律研究[J]. 华中科技大学学报(自然科学版),2020,48(3): 92-97. GAO Liang, HE Ning, REN Xichong, et al. Research on effect law of arch deformation of ballastless track slab[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2020, 48(3): 92-97.
[7]	周凌宇,张广潮,余志武,等. 循环温度荷载下无砟轨道结构模型试验研究[J]. 铁道学报,2020,42(1): 82-88. ZHOU Lingyu, ZHANG Guangchao, YU Zhiwu, et al. Model experiments of ballastless track-bridge structure under cyclic temperature load[J]. Journal of the China Railway Society, 2020, 42(1): 82-88.
[8]	钟垚,何越磊,路宏遥,等. 持续高温作用下CRTSⅡ型无砟轨道层间离缝分析[J]. 铁道科学与工程学报,2018,15(5): 1128-1133. ZHONG Yao, HE Yuelei, LU Hongyao, et al. Analysis of interface seam of CRTSⅡ slab track under sustained high temperature[J]. Journal of Railway Science and Engineering, 2018, 15(5): 1128-1133.
[9]	赵国堂,刘钰. CRTSⅡ型板式无砟轨道结构层间离缝机理研究[J]. 铁道学报,2020,42(7): 117-126. ZHAO Guotang, LIU Yu. Mechanism analysis of delamination of CRTS II slab ballastless track structure[J]. Journal of the China Railway Society, 2020, 42(7): 117-126.
[10]	张乾,蔡小培,钟阳龙,等. 无砟轨道路基不均匀沉降区高速列车动力特性[J]. 西南交通大学学报,2023,58(1): 133-140. doi: 10.3969/j.issn.0258-2724.20210830 ZHANG Qian, CAI Xiaopei, ZHONG Yanglong, et al. Dynamic characteristics of high-speed trains in differential subgrade settlement zone of ballastless track[J]. Journal of Southwest Jiaotong University, 2023, 58(1): 133-140. doi: 10.3969/j.issn.0258-2724.20210830
[11]	刘笑凯,刘学毅,肖杰灵,等. 温升作用下CRTSⅡ型板宽窄接缝受力及损伤分析[J]. 西南交通大学学报,2024,58(1): 273-280. LIU Xiaokai, LIU Xueyi, XIAO Jieling, etal. Analysis of internal forces and damage of broad-narrow joint of CRTSⅡ slab track under temperature rise[J]. Journal of Southwest Jiaotong University, 2024, 58(1): 273-280.
[12]	张鹏飞,涂建,桂昊,等. 温梯荷载下桥上CRTSⅡ型板式无砟轨道的力学特性[J]. 西南交通大学学报,2021,56(5): 945-952. ZHANG Pengfei, TU Jian, GUI Hao, et al. Mechanical properties of CRTSⅡ slab ballastless track on bridge under temperature gradient loads[J]. Journal of Southwest Jiaotong University, 2021, 56(5): 945-952.
[13]	CUI X H, GUO G R, DU B W, et al. Effects of lateral differential settlement of the subgrade on deformation behavior and damage evolution of CRTS Ⅱ slab track[J]. Engineering Failure Analysis, 2021, 129: 105674.1-105674.18.
[14]	XU Y D, YAN D B, ZHU W J, et al. Study on the mechanical performance and interface damage of CRTS II slab track with debonding repairment[J]. Construction and Building Materials, 2020, 257: 119600.1-119600.16.
[15]	王军,卢朝辉,张玄一,等. CRTSⅡ型轨道板/CA砂浆界面内聚力模型研究[J]. 工程力学,2022,39(9): 72-80,109. doi: 10.6052/j.issn.1000-4750.2021.05.0336 WANG Jun, LU Chaohui, ZHANG Xuanyi, et al. Research on cohesive zone model of the interface between CRTS Ⅱ track slab and CA mortar[J]. Engineering Mechanics, 2022, 39(9): 72-80,109. doi: 10.6052/j.issn.1000-4750.2021.05.0336
[16]	LIU G Y, BAO H C, TANG K L. Damage prediction in notched fiber-reinforced composite laminates[J]. Composite Interfaces, 2016, 24(3): 279-290.
[17]	刘学毅,苏成光,刘丹,等. 轨道板与砂浆粘结试验及内聚力模型参数研究[J]. 铁道工程学报,2017,34(3): 22-28. doi: 10.3969/j.issn.1006-2106.2017.03.005 LIU Xueyi, SU Chengguang, LIU Dan, et al. Research on the bond properties between slab and CA mortar and the parameters study of cohesive model[J]. Journal of Railway Engineering Society, 2017, 34(3): 22-28. doi: 10.3969/j.issn.1006-2106.2017.03.005
[18]	ZHOU R, YUAN W H, LIU W B, et al. Thermal performance of CRTS Ⅱ slab track-bridge structure under extreme temperatures: numerical simulation[J]. Construction and Building Materials, 2023, 377: 131147.1-131147.13.
[19]	钟阳龙,高亮,王璞,等. 温度荷载下CRTSⅡ型轨道板与CA砂浆界面剪切破坏机理[J]. 工程力学,2018,35(2):230-238. ZHONG Yanglong, GAO Liang, WANG Pu, et al. Mechanism of interfacial shear failure between CRTS Ⅱ slab and ca mortar under temperature loading[J]. Engineering Mechanics, 2018, 35(2):230-238.
[20]	闫斌,程瑞琦,谢浩然,等. 极端温度作用下桥上CRTSⅡ型无砟轨道受力特性[J]. 铁道科学与工程学报,2021,18(4): 830-836. YAN Bin, CHENG Ruiqi, XIE Haoran, et al. Mechanical characteristics of CRTSⅡ ballastless track on bridge due to extreme temperature load[J]. Journal of Railway Science and Engineering, 2021, 18(4): 830-836.
[21]	国家铁路局. 高速铁路设计规范:TB 10621—2014[S]. 北京:中国铁道出版社,2015.
[22]	YAN D B, XU Y, ZHU W J. Effects of debonding repairment on interfacial damage and thermal deformation of CRTS Ⅱ slab ballastless track[J]. Construction and Building Materials, 2023, 389: 131793.1-131793.13.
[23]	ZHONG Y L, GAO L, ZHANG Y R. Effect of daily changing temperature on the curling behavior and interface stress of slab track in construction stage[J]. Construction and Building Materials, 2018, 185: 638-647. doi: 10.1016/j.conbuildmat.2018.06.224
[24]	朱永见,赵国堂,郑建. CRTS Ⅱ型板式无砟轨道层间离缝产生原因分析[J]. 铁道学报,2021,43(2): 111-117. doi: 10.3969/j.issn.1001-8360.2021.02.014 ZHU Yongjian, ZHAO Guotang, ZHENG Jian. Analysis on causes of gap under CRTS Ⅱ slab ballastless track[J]. Journal of the China Railway Society, 2021, 43(2): 111-117. doi: 10.3969/j.issn.1001-8360.2021.02.014
[25]	SONG L, LIU H B, CUI C X, et al. Thermal deformation and interfacial separation of a CRTS Ⅱ slab ballastless track multilayer structure used in high-speed railways based on meteorological data[J]. Construction and Building Materials, 2020, 237: 117528.1-117528.16.