Fractional-Order Sliding Mode Control for Maglev Rotary Table Based on Disturbance Compensation
-
摘要:
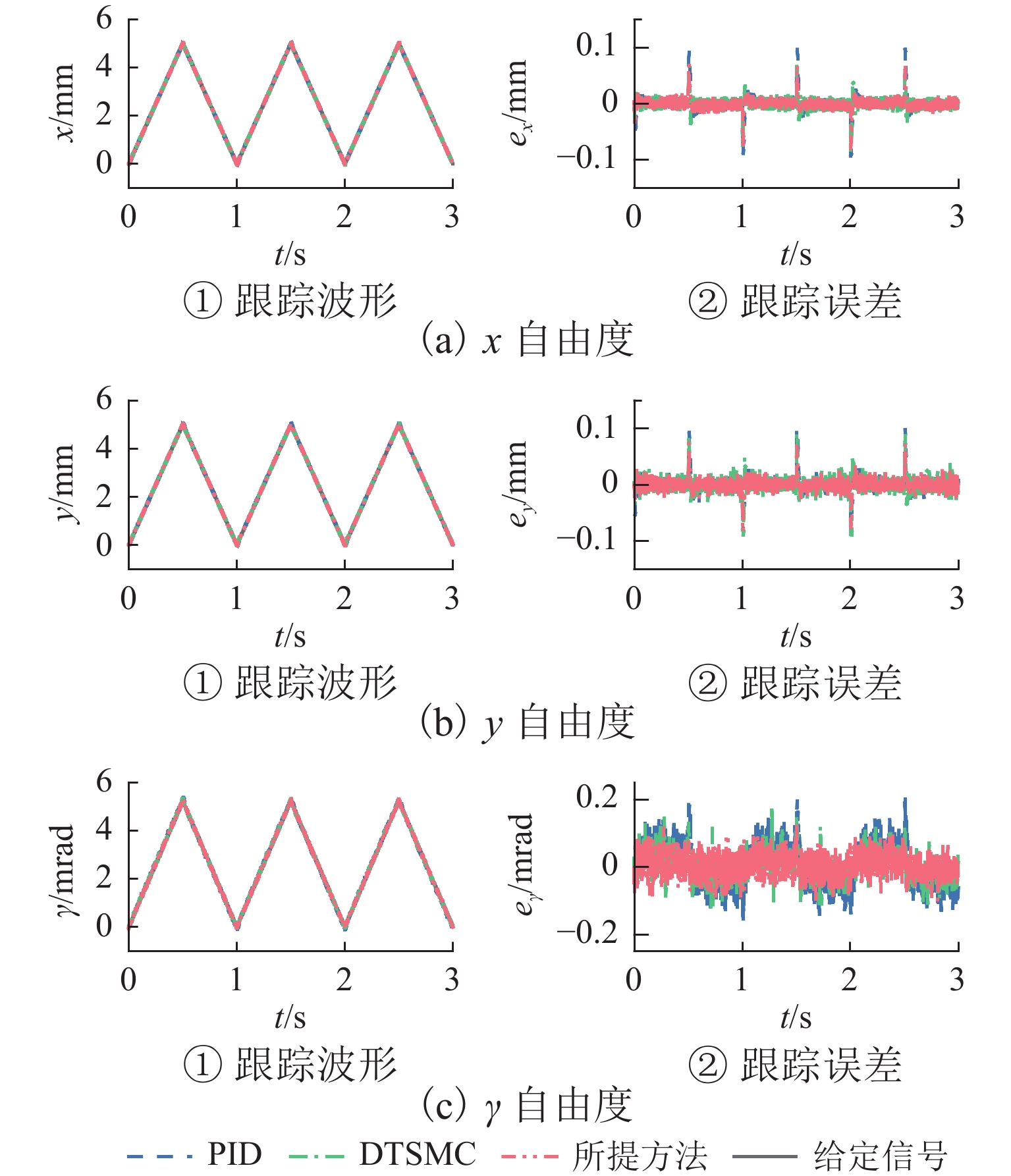
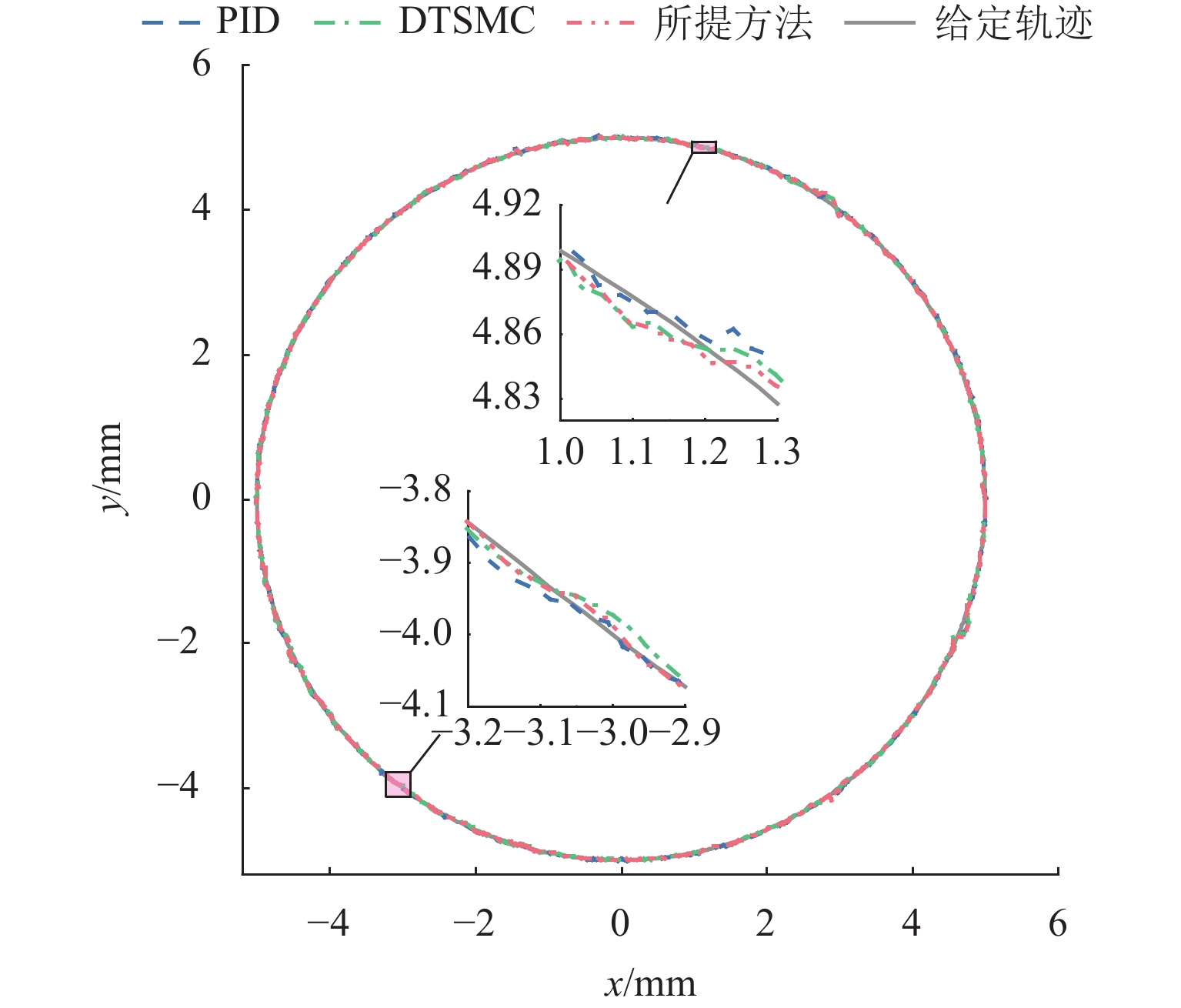
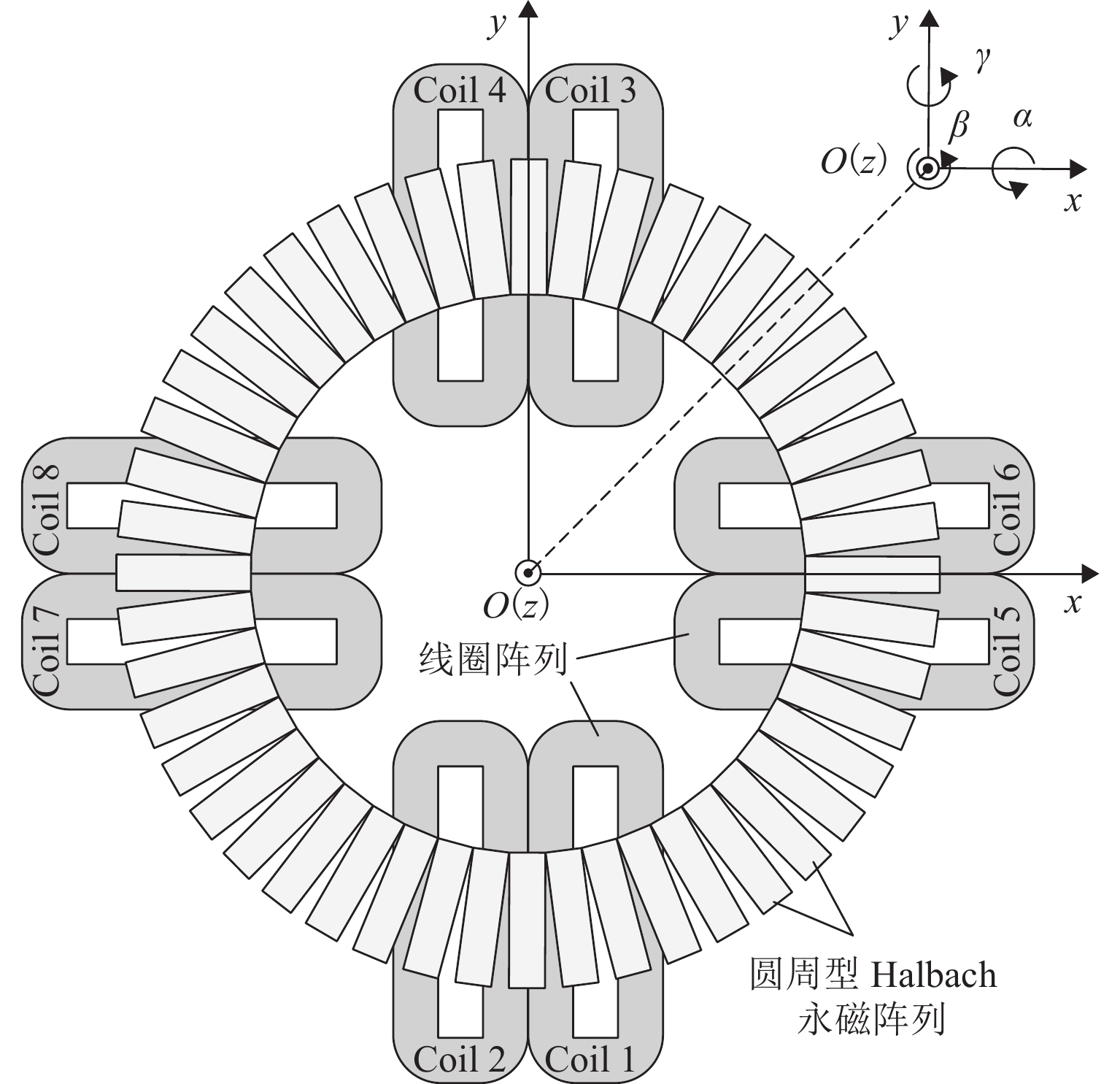
针对存在非线性、耦合性和不确定性的磁悬浮转台的高精度运动控制问题,提出一种基于非线性干扰观测器的分数阶滑模控制方法以提高跟踪精度. 首先,基于系统电磁力模型和动态解耦方法,构建六自由度磁悬浮转台系统动力学模型;其次,设计非线性干扰观测器,对包含系统误差、六自由度间耦合项和外界干扰的集总扰动进行估计,证明了估计误差有界且可调节到任意小;然后,在离散域提出了一种分数阶滑模面,采用分数幂函数替代传统符号函数来抑制抖振,引入分数阶微积分来减小跟踪误差;最后,设计有限时间收敛的分数阶滑模控制策略,并利用李雅普诺夫稳定性理论证明闭环系统稳定性. 实验结果表明:与整数阶滑模控制方法相比,采用所提方法,2个水平自由度和绕竖直方向旋转自由度对三角波的跟踪误差均方根分别减小了12.8%、16.8%和23.7%,最大跟踪误差分别减小9.26%、13.00%和33.20%;跟踪圆形轨迹时,2个水平自由度的跟踪误差均方值分别减小6.39%和12.40%,最大跟踪误差分别减小9.90%和12.10%.
Abstract:In view of the high-precision motion control problem of the maglev rotary table with nonlinearity, coupling, and uncertainty, a fractional-order sliding mode control method based on a nonlinear disturbance observer was proposed to improve the tracking accuracy. Firstly, based on the electromagnetic force model of the system and the dynamic decoupling method, the dynamical model of the six-degree-of-freedom maglev rotary table system was constructed. Secondly, a nonlinear disturbance observer was designed to estimate the lumped disturbance including system error, coupling term between six degrees of freedom, and external interference. It was proved that the estimation error was bounded and could be made arbitrarily small. Then, a fractional-order sliding surface was proposed in the discrete domain, where the fractional power function was used instead of the traditional symbolic function to suppress jitter, and the fractional calculus was introduced to reduce the tracking error. Finally, a fractional-order sliding mode control strategy with finite time convergence was designed, and the stability of the closed-loop system was proved by Lyapunov stability theory. The experimental results reveal that compared to the integer-order sliding mode control method, the proposed method reduces the root mean square of tracking error for triangular waves by 12.8%, 16.8%, and 23.7% for the two horizontal degrees of freedom and the rotational degree about the vertical axis, respectively, while the maximum tracking errors are reduced by 9.26%, 13.00%, and 33.20% respectively. When tracking a circular trajectory, the mean square values of tracking errors for two horizontal degrees of freedom are decreased by 6.39% and 12.40%, and the maximum tracking errors are reduced by 9.90% and 12.10%, respectively.
-
表 1 磁悬浮转台系统参数
Table 1. Systematic parameters of maglev rotary table
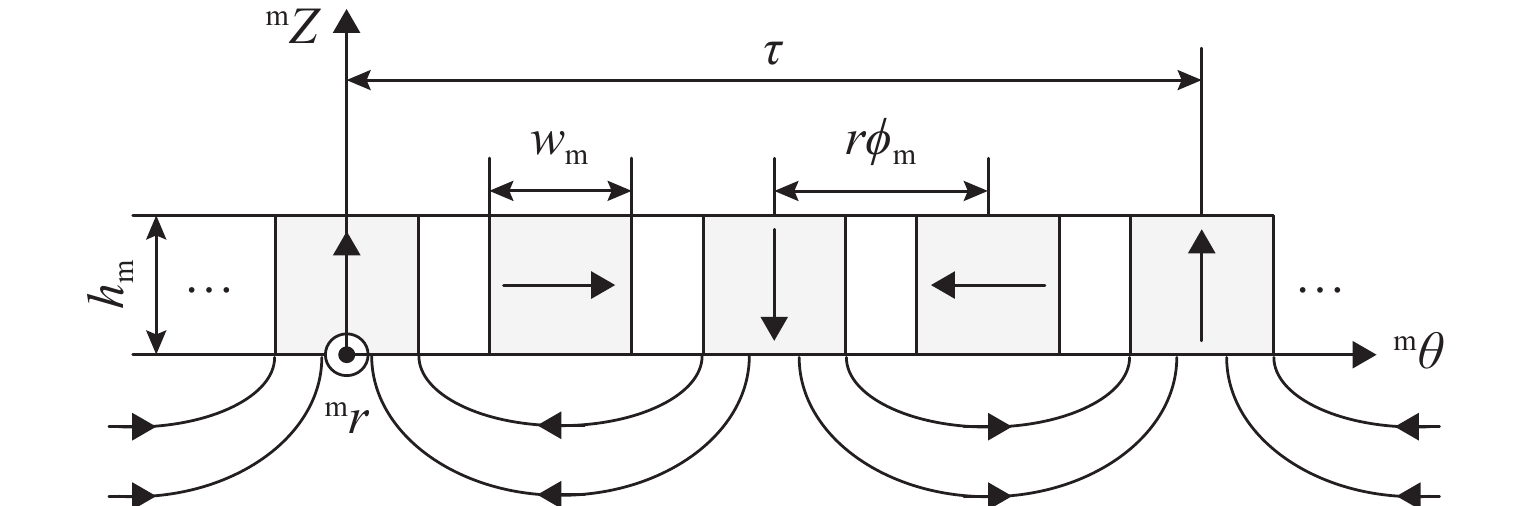
参数 数值 永磁体长(lm)、宽(wm)、高(hm)/mm 30、8、8 φm/(°) 7.5 r/mm 80 Br/T 1.2 线圈尺寸(lc、wc、hc、rc)/mm 60、10、10、10 线圈匝数 N/匝 300 m/kg 2.37 ${J_\alpha }$$({J_\beta })$、${J_\gamma }$/(kg·m2) 9.37×10−3 、1.87×10−2 采样间隔/ms 1 重力加速度/(m·s−2) 9.8 表 2 控制器参数
Table 2. Controller parameters
自由度 PID DTSMC 和所提方法 KPID k1 k2 l1 l2 x,y,z 0.124 1 19.3 8.84 21.4 α,β 4.90 × 10−4 3.95 × 10−3 0.0763 0.0348 0.0846 γ 9.78 × 10−4 7.89 × 10−3 0.152 0.0694 0.169 表 3 三角波跟踪误差
Table 3. Tracking errors of triangular wave
控制方法 x/mm y/mm γ/mrad eRMS eMAX eRMS eMAX eRMS eMAX PID 0.0148 0.0966 0.0155 0.0977 0.0706 0.212 DTSMC 0.0117 0.0875 0.0149 0.0953 0.0410 0.170 所提方法 0.0102 0.0794 0.0124 0.0829 0.0313 0.113 表 4 圆轨迹跟踪误差
Table 4. Tracking errors of circular trajectory
mm 控制方法 x y eRMS eMAX eRMS eMAX PID 0.0109 0.0686 0.0226 0.163 DTSMC 0.0101 0.0657 0.0251 0.158 所提方法 0.0091 0.0615 0.0220 0.138 -
[1] XU X Z, ZHENG C L, XU F Q. A real-time numerical decoupling method for multi-DoF magnetic levitation rotary table[J]. Applied Sciences, 2019, 9(16): 3263.1-3263.16. [2] ZHU H Y, TEO T J, PANG C K. Flexure-based magnetically levitated dual-stage system for high-bandwidth positioning[J]. IEEE Transactions on Industrial Informatics, 2019, 15(8): 4665-4675. doi: 10.1109/TII.2019.2890951 [3] LAHDO M, STRÖHLA T, KOVALEV S. Design and implementation of an new 6-DoF magnetic levitation positioning system[J]. IEEE Transactions on Magnetics, 2019, 55(12): 8107407.1-8107407.7. [4] SILVA-RIVAS J C, KIM W J. Multivariable control and optimization of a compact 6-DOF precision positioner with hybrid H2/H∞ and digital filtering[J]. IEEE Transactions on Control Systems Technology, 2013, 21(5): 1641-1651. doi: 10.1109/TCST.2012.2215035 [5] LI D F, GUTIERREZ H. Observer-based sliding mode control of a 6-DOF precision maglev positioning stage[C]//2008 34th Annual Conference of IEEE Industrial Electronics. Orlando: IEEE, 2008: 2562-2567. [6] 魏静波,罗浩,关子津. 基于干扰观测器的磁悬浮球系统全局快速终端滑模控制[J]. 西南交通大学学报,2023,58(4): 836-844.WEI Jingbo, LUO Hao, GUAN Zijin. Global fast terminal sliding mode control for maglev ball system based on disturbance observer[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 836-844. [7] DU H B, YU X H, LI S H. Dynamical behaviors of discrete-time fast terminal sliding mode control systems[M]//Recent Advances in Sliding Modes: From Control to Intelligent Mechatronics. Cham: Springer, 2015: 77-97. [8] ZHANG L, ZHANG Z, HUANG L. Hybrid non-linear differentiator design for a permanent-electro magnetic suspension maglev system[J]. IET Signal Processing, 2012, 6(6): 559-567. doi: 10.1049/iet-spr.2011.0264 [9] NGUYEN S D, LAM B D, NGO V H. Fractional-order sliding-mode controller for semi-active vehicle MRD suspensions[J]. Nonlinear Dynamics, 2020, 101(2): 795-821. doi: 10.1007/s11071-020-05818-w [10] SUN G H, MA Z Q, YU J Y. Discrete-time fractional order terminal sliding mode tracking control for linear motor[J]. IEEE Transactions on Industrial Electronics, 2018, 65(4): 3386-3394. doi: 10.1109/TIE.2017.2748045 [11] KUANG Z A, GAO H J, TOMIZUKA M. Precise linear-motor synchronization control via cross-coupled second-order discrete-time fractional-order sliding mode[J]. IEEE/ASME Transactions on Mechatronics, 2021, 26(1): 358-368. [12] HU C X, WANG Z, ZHU Y, et al. Performance-oriented precision LARC tracking motion control of a magnetically levitated planar motor with comparative experiments[J]. IEEE Transactions on Industrial Electronics, 2016, 63(9): 5763-5773. doi: 10.1109/TIE.2016.2538743 [13] JANSEN J W, VAN LIEROP C M M, LOMONOVA E A, et al. Magnetically levitated planar actuator with moving magnets[J]. IEEE Transactions on Industry Applications, 2008, 44(4): 1108-1115. doi: 10.1109/TIA.2008.926065 [14] DYCK M, LU X D, ALTINTAS Y. Magnetically levitated rotary table with six degrees of freedom[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(1): 530-540. doi: 10.1109/TMECH.2016.2621108 [15] YANG H L, DENG F, HE Y, et al. Robust nonlinear model predictive control for reference tracking of dynamic positioning ships based on nonlinear disturbance observer[J]. Ocean Engineering, 2020, 215: 107885.1-107885.7. [16] LU X, XU F Q, XU X Z, et al. Directed-driven 8-phase magnetically levitated rotary table based on an analytical-numerical model[J]. IEEE Access, 2020, 8: 31159-31170. doi: 10.1109/ACCESS.2020.2973223 -




 下载:
下载: