Flexural Bearing Performance of Prestressed Concrete Pipe Piles with Hybrid Reinforcement under Influence of Prestressed Control Level and Hybrid Reinforcement
-
摘要:
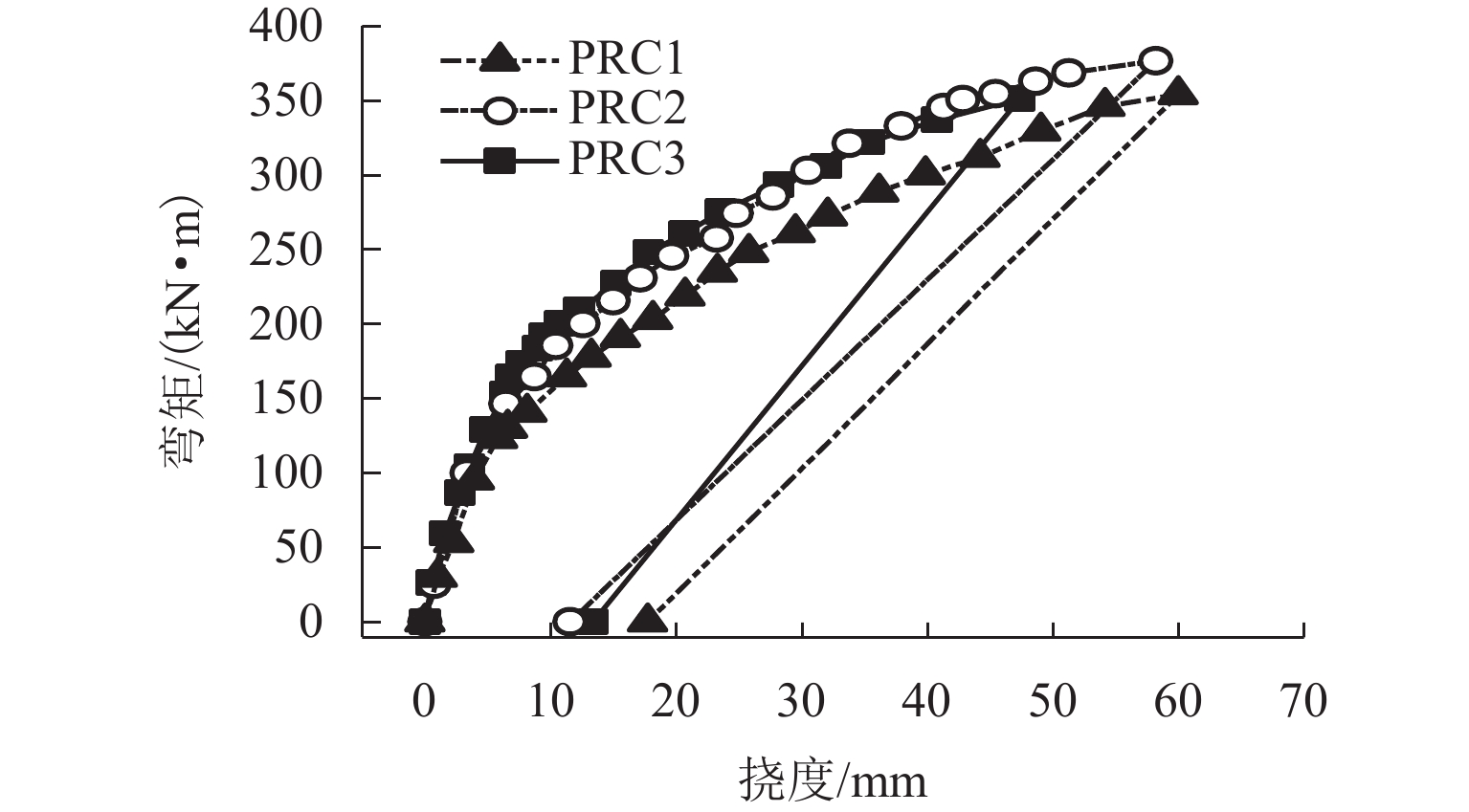
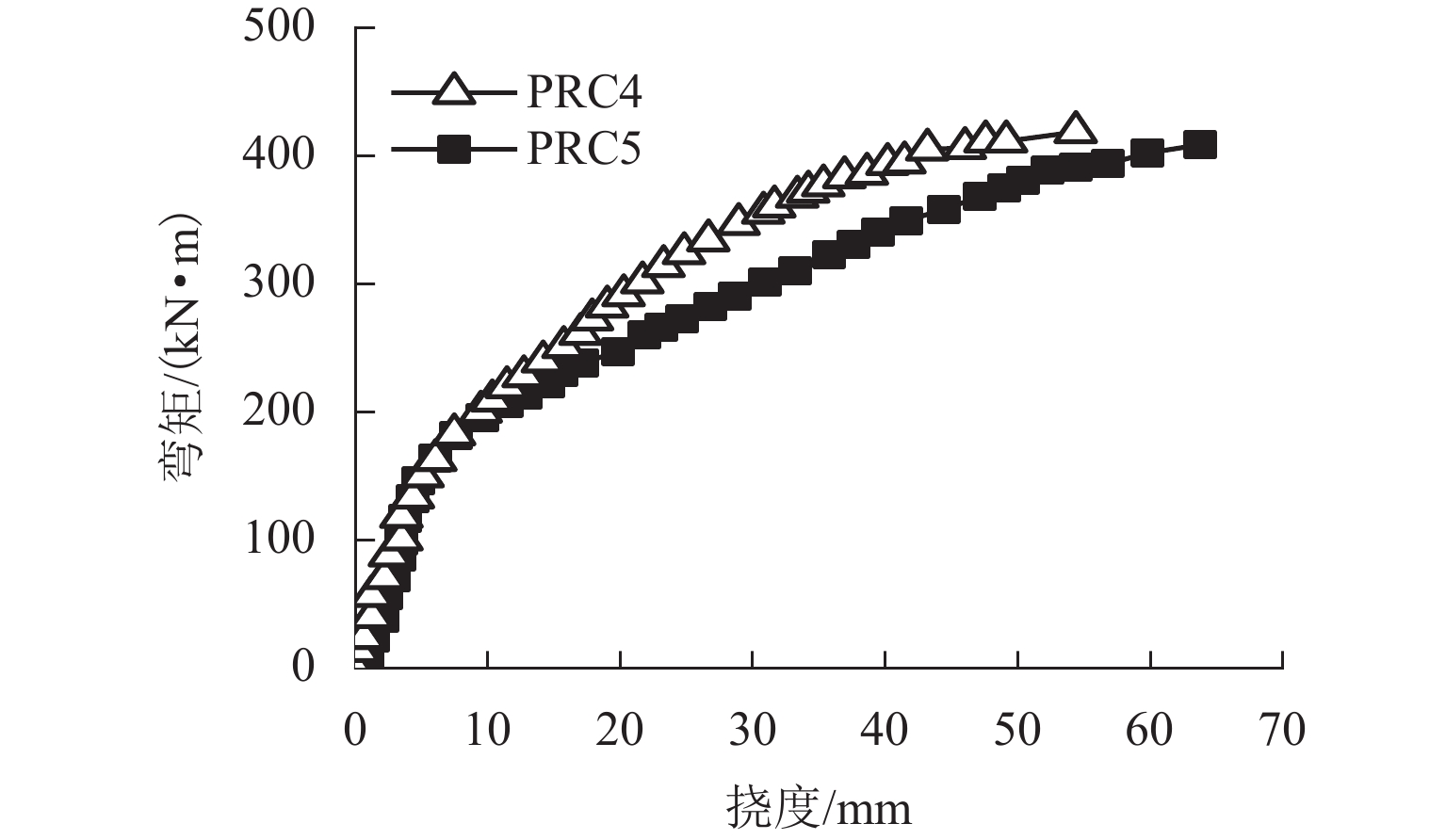
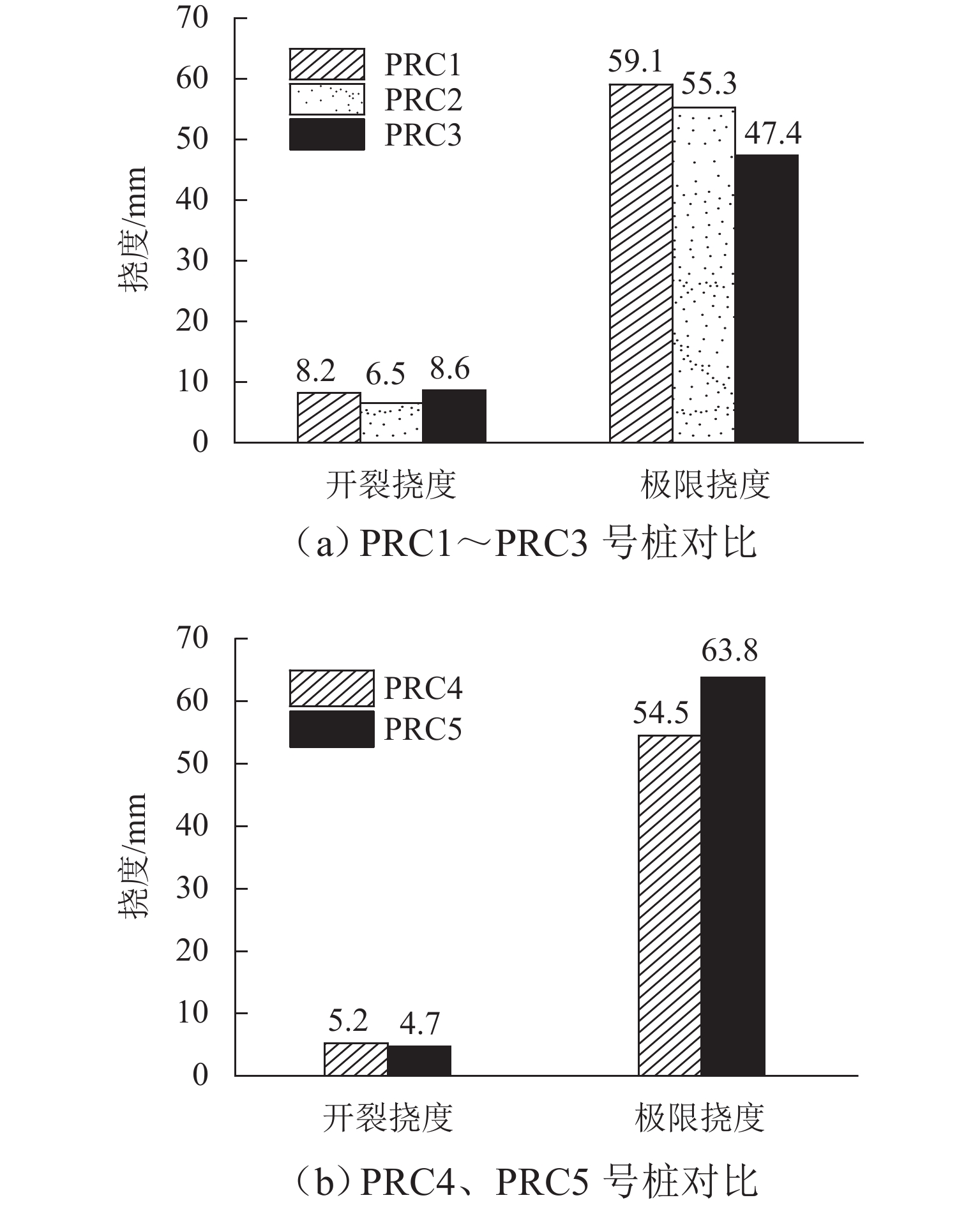
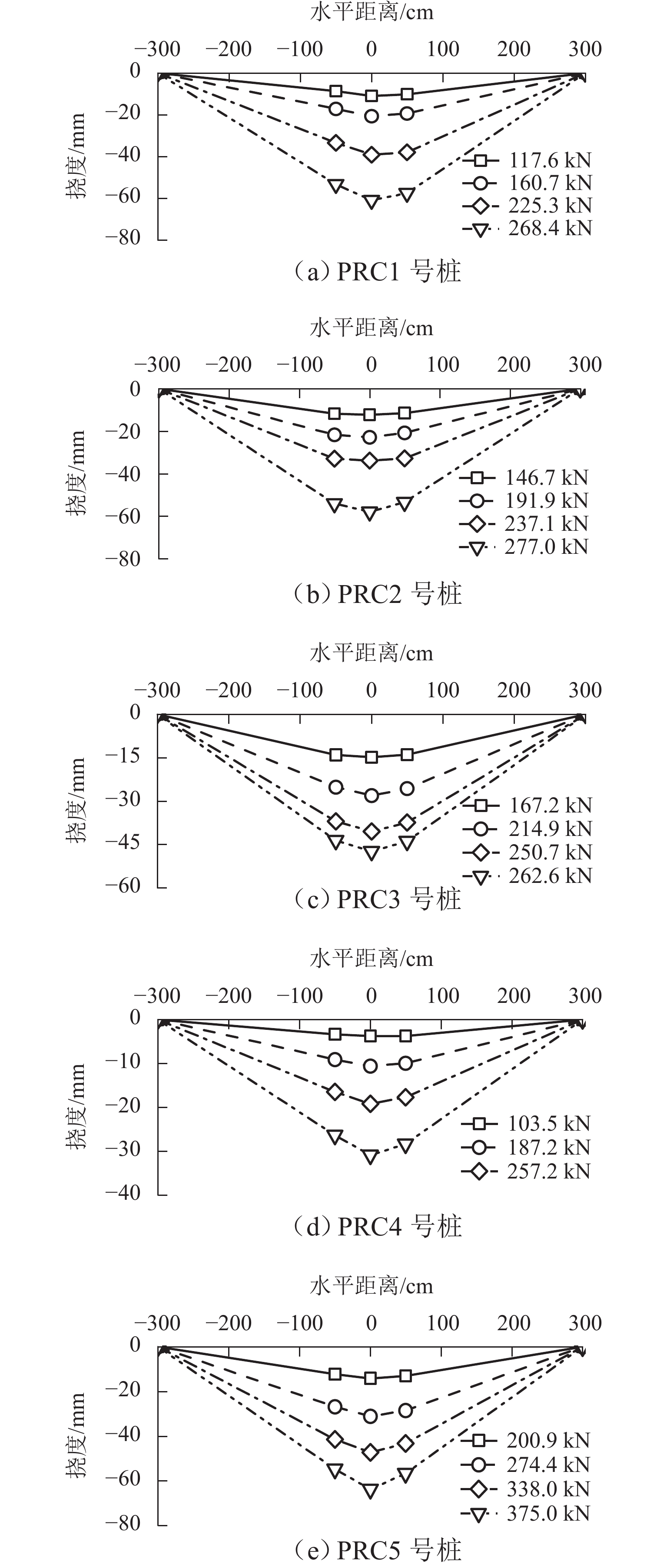
混合配筋预应力混凝土（PRC）管桩受预应力控制水平、混合配筋等因素影响，实际抗弯承载力与理论设计值存在偏差，致使其服役过程中存在桩身破坏或性能退化等潜在风险. 为研究PRC管桩实际抗弯承载性能表现，开展不同预应力水平、混合配筋情况下PRC管桩抗弯载荷试验研究. 荷载试验采用单调连续加载方式，记录不同PRC管桩桩身弯矩-挠度曲线，确定其抗弯载荷变化规律，最终对试验所得数据与现行标准中相关弯矩承载力理论计算值进行对比验证. 研究结果表明：混合配筋方式提高了桩身承载力及延性，初始预应力张拉控制比例越高，试件的弹性变形段越长、开裂弯矩越大、裂缝出现延后，初始预应力为0.5倍张拉力时试件的延性最好，弯曲变形延性大于10，最大挠度超过54 mm，裂缝宽度为1.05～1.50 mm；PC钢棒和螺纹钢同时张拉的构件变形相对趋缓，延性和韧性更好；非预应力钢棒参与预应力贡献时，极限弯矩提高约2.5%，弹性阶段结束时的开裂挠度更大；不同预应力PRC桩开裂弯矩实测值为设计理论值的1.25～1.50倍，极限弯矩实测值为理论值的0.96～1.07倍.
Abstract:The actual flexural bearing capacity of prestressed concrete pipe piles with hybrid reinforcement (PRC pipe piles) is different from the theoretical design value due to the influence of prestressed control level and hybrid reinforcement, which leads to the potential risk of pile body damage or performance degradation during its service. In order to study the actual flexural bearing capacity of PRC pipe piles, the flexural load test of PRC pipe piles under different prestressed levels and hybrid reinforcement was carried out. The monotone continuous loading method was adopted in the load test. The bending moment-deflection curves of different PRC pipe piles were recorded to determine the flexural load variation rule. Finally, the experimental data were compared with the theoretical calculation value of relevant bending moment bearing capacity in current standards. The results show that the deformation of the hybrid reinforcement method improves the bearing capacity and ductility of the pile body. A higher initial prestress-to-tension control ratio indicates a longer elastic deformation section of the specimen, a larger cracking moment, and a delay in crack occurrence. When the initial prestress is 0.5 times the tensile force, the ductility of the specimen is the best; the bending deformation ductility is greater than 10; the maximum deflection is more than 54 mm, and the crack width is 1.05–1.5 mm. The member deformation under simultaneous tension of steel bars for prestressed concrete (PC steel bar) and screw-thread steel is relatively slow, and ductility and toughness are better. When the non-prestressed steel bars contribute to the prestress, the ultimate bending moment is increased by about 2.5%, and the cracking deflection at the end of the elastic stage is larger. The measured cracking moment of different PRC pipe piles is 1.25–1.50 times the design theoretical value, and the measured ultimate bending moment is 0.96–1.07 times the theoretical value.
-
2004年，Donoho[1]提出了关于信号采样、压缩和重构的全新理论——压缩感知理论（compressive sensing，CS）. 在大规模机器类型通信（massive machine type communication，mMTC）下，即使是在高峰期，活跃用户的数量也不超过10%[2]，这使得压缩感知技术应用在大规模通信场景下成为可能. 压缩感知理论的研究主要集中在3个领域：信号的稀疏表示、高性能测量矩阵的构造以及信号的精准重构[3]. 其中，测量矩阵的构造将直接影响信号重构的误差大小，测量矩阵需要符合一定的条件，如有限等距性质[4]（restricted isometry property，RIP），这是保证原始信号不失真重建的必要条件.
学者们尝试通过相关性理论衡量并优化测量矩阵的性能[5]. 研究表明，减小稀疏基与测量矩阵的相关系数能提高压缩感知算法的重构性能. 目前，针对测量矩阵的研究成果不胜枚举. 曾祥洲[6]提出一种基于交替最小化的优化算法，最小化Gram矩阵与目标矩阵差值的傅里叶范数，建立最优测量矩阵，解决最小化单个指标易导致其他指标恶化的问题. Xu等[7]提出一种基于等角紧框架（equiangular tight frame，ETF）的迭代最小化算法，在不改变测量矩阵对应Gram矩阵属性的情况下修改奇异值，以减小Gram矩阵列向量之间的相关性. 宋儒瑛等[8]基于分块矩阵的思想构造新的测量矩阵，验证了测量矩阵的行列数相差不大时所构造的测量矩阵可以代替等角紧框架矩阵. 魏从静[9]对Gram矩阵进行Schmidt正交化，以此增强矩阵列向量之间的独立性，计算过程中的规范正交基能有效提高数值计算过程的稳定性. He等[10]提出一种基于伪随机序列的测量矩阵优化构造方法，将随机高斯矩阵与伪随机序列和Hadamard矩阵相结合，使得测量矩阵拥有更好的性能、较低复杂度和较好的应用价值.
本文对测量矩阵的性能优化算法进行研究，基于Gram矩阵，通过特征值分解降低测量矩阵与稀疏基之间的平均相关性. 再基于ETF理论与梯度缩减迭代算法，使得Gram矩阵向等角紧框架矩阵逼近，降低其非主对角线元素最大值，从而降低最大相关性，提高重构质量.
1. 压缩感知算法与测量矩阵相关性
1.1 压缩感知算法
假设一个长度为N的信号$ \boldsymbol{x}\in {\mathbb{C}}^{N\times 1} $经过一个$ M\times N $（M<N）的测量矩阵$\boldsymbol{\varPhi } $线性投影后，得到长度为M的测量值$ \boldsymbol{y}\in {\mathbb{C}}^{M\times 1} $，如式（1）所示.
y=Φx. (1) 压缩感知技术使用的前提是信号在某种变换基下具有稀疏性. 若x本身不稀疏，但在某个变换域上是稀疏的，式（1）可改写为
{y=Φx=Aθ,A=ΦΨ, (2) 式中：$ {\boldsymbol{\varPsi}}\mathrm{为}N\times N $的稀疏变换矩阵，称为稀疏基或稀疏字典；$ \boldsymbol{\theta } $为${\boldsymbol{x}} $在${\boldsymbol{\varPsi}} $上的投影；A为感知矩阵.
由式（2）可以看出，通过接收信号y来重构原始信号x，本质上是求解线性方程组. 由于$ M < N $，线性方程组有无穷多解. 但$ \boldsymbol{\theta } $是稀疏的，未知数的个数较少，使得重构信号成为可能.
在RIP准则基础上所构造的测量矩阵都能在一定程度上保留信号原本信息，保证重构精度[11]. 当矩阵$ \boldsymbol{A} $满足RIP准则时，测量矩阵的有限等距常数$ {\delta }_{K} $满足式（3）.
(1 - {\delta _K})||{\boldsymbol{x}}||_2^2 \leqslant ||{\boldsymbol{A x}}||_2^2 \leqslant (1 + {\delta _K})||{\boldsymbol{x}}||_2^2 , (3) 式中：K为信号的稀疏度.
RIP准则对测量矩阵进行了限制，使得经过投影后的压缩信号能够保留尽可能多的有用信息，用以在重构过程中更加精确地重构出信号.
当矩阵$ \boldsymbol{A} $满足RIP准则时，压缩感知算法就能通过求解如式（4）所示的L0范数最小问题，对原始信号进行重构.
\left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{\hat \theta }} = {\text{arg min}}\;||{\boldsymbol{\theta }}|{|_0}}, \\ {{\mathrm{s.t.}}\; {\boldsymbol{\varPhi \varPsi \theta }} = {\boldsymbol{y}},} \end{array}} \right. (4) 式中：$ \hat{\boldsymbol{\theta }} $为原始信号在${\boldsymbol{\varPsi}} $下的最稀疏系数向量.
得到$ \hat{\boldsymbol{\theta }} $后，即可利用稀疏反变换重构出原始信号，如式（5）所示.
{\boldsymbol{\hat x = \varPsi \hat \theta }}\text{，} (5) 式中：$ \hat{{\boldsymbol{x}}} $为重构所得的信号.
求解L0范数最小问题是一个NP-hard问题，Donoho等[12]提出，在一定条件下，对L0范数问题进行求解可等价于对L1范数问题进行求解，所求得的解是相同的，即式（4）等价于式（6）.
\left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{\hat \theta }} = {\text{arg}}\;{\text{min}}\;||{\boldsymbol{\theta }}|{|_1}} ,\\ {{\mathrm{s.t.}}\;\;{\boldsymbol{\varPhi \varPsi \theta }}{\text{ = }}{\boldsymbol{y}}}. \end{array}} \right. (6) 式（6）可以转化为线性规划问题进行求解. 常用的求解方法有贪婪类算法[13]、凸松弛算法[14]、贝叶斯类算法[15]等.
1.2 mMTC场景上行链路系统模型
在大规模通信场景中，基站端无法保证每个用户都能单独利用资源块，故不可避免地会产生冲突问题，而基站侧也很难得知哪些用户是处于活跃状态，因此活跃用户检测的问题需要得到解决.
假设一个社区用户数为N的蜂窝上行链路，在大规模随机接入的场景下，同一时间点中的设备大多为非活跃状态[16]. 以$ {a}_{n}\in \left\{\mathrm{0,1}\right\} $表示用户的活跃状态，0为非活跃状态，1为活跃状态，且$ 1\leqslant n\leqslant N $，则由$ {a}_{n} $构成的向量$ \boldsymbol{a}=({a}_{1},{a}_{2}, \cdots ,{a}_{{N}}) $中，大部分元素都为0，即$ {{\boldsymbol{a}}} $具备稀疏性，这使得压缩感知技术应用于大规模通信场景成为可能.
假设每个用户都由基站分配了1个长度为M的导频序列$ {\boldsymbol{\varphi }}_{n} $，则这N个用户的导频序列就能组成一个$ M\times N $的矩阵$ \boldsymbol{\varPhi } $，当矩阵$ \boldsymbol{\varPhi } $满足有限等距性质准则时，就可以应用压缩感知理论，基于接收信号y，通过重构算法对原始信号进行估计，进而对活跃用户的身份进行估计.
基站接收到的信号可以表示为
{\boldsymbol{y}} = \sum\nolimits_{n = 0}^N {{{\boldsymbol{\varphi }}_n}{a_n}{{{h}}_n}} = {\boldsymbol{\varPhi x}} \text{，} (7) 式中：$ {{h}}_{n} $为第$ n $个用户与基站之间的信道参数.
定义$ {{x}}_{n}={a}_{n}{{h}}_{n} $，$ \boldsymbol{x}=({{x}}_{1},{{x}}_{2},\cdots ,{{x}}_{\boldsymbol{N}})= ({a}_{1}{{h}}_{1}, {a}_{2}{{h}}_{2},\cdots , {a}_{N}{{h}}_{N}) $. 显然，$ \boldsymbol{x} $呈现为稀疏状态. 若第$ n $个用户为活跃状态，则$ {{x}}_{n} $等于真实的信道参数；若用户为非活跃状态，则$ {{x}}_{n} $为0. 综上可知，在mMTC场景中，活跃用户估计与信道估计可以联合实现.
1.3 测量矩阵列相关性与Welch下界
$ \boldsymbol{\varPhi } $的列相关性$\mu $可以表示为列向量之间内积的最大值，如式（8）所示[17].
\mu = \max \left| {\left\langle {{{\boldsymbol{\varphi }}_i},{{\boldsymbol{\varphi }}_j}} \right\rangle } \right| \text{，} (8) 式中：$ {\boldsymbol{\varphi }}_{i}、{\boldsymbol{\varphi }}_{j} $分别为矩阵$ \boldsymbol{\varPhi } $的第i、j列，$ 1\leqslant i, j\leqslant N， \mathrm{且}\;i\ne j $.
对于矩阵$ \boldsymbol{\varPhi } $，在其列向量单位化后，若$ N\leqslant M \times (M + 1)/2 $，则称矩阵$ \boldsymbol{\varPhi } $的列相关性存在下界，这个下界即Welch界，如式（9）所示.
\mu \geqslant \sqrt {\frac{{N - M}}{{(N - 1)M}}} . (9) 当式（9）取等号时，称该矩阵具备等角紧框架结构[18]. 特别地，若M$\ll $N，则下界将收敛至$ \sqrt{1/M} $. 通过使测量矩阵与稀疏基矩阵的互相关系数逼近Welch界，可以保证测量矩阵具有更好的压缩观测性能.
2. 基于矩阵分解与ETF理论的测量矩阵优化算法
测量矩阵$ \boldsymbol{\varPhi } $与稀疏基$ {\boldsymbol{\varPsi }} $之间的相关性是影响测量矩阵性能的因素之一. 2个矩阵之间的相关性定义为
\mu ({\boldsymbol{\varPhi }},{\boldsymbol{\varPsi }}) = \max \left| {\left\langle {{{\boldsymbol{\varphi }}_i},{{\boldsymbol{\gamma }}_{j}}} \right\rangle } \right| \text{，} (10) 式中：$ {\boldsymbol{\gamma }}_{j} $为矩阵$ {\boldsymbol{\varPsi }} $的第j列.
但仅依靠此定义很难得出两矩阵之间的具体联系. 为此，Elad[19]引入了Gram矩阵，从另一个角度对测量矩阵$ \boldsymbol{\varPhi } $和稀疏基$ {\boldsymbol{\varPsi }} $之间的相关性进行了定义，将最大相关系数定义为Gram矩阵中非对角线元素绝对值的最大值.
定义平均相关系数$ {\mu }_{\mathrm{a}\mathrm{v}\mathrm{g}} $为Gram矩阵中所有非主对角元素绝对值之和的平均值. 当 Gram 矩阵的非主对角元素中最大值较大而平均值较小时，如果仅依据最大值来判断，可能会误认为该矩阵性能不佳. 然而，由于其平均值相对较小，实际应用中的性能也相对良好. 因此，引入平均相关系数是为了避免因最大值与平均值差距过大而导致性能的误判.
首先，定义等价字典$ \boldsymbol{D} $，$ \boldsymbol{D}=\boldsymbol{\varPhi }{\boldsymbol{\varPsi }} $，假设$ {\boldsymbol{\vartheta }}_{i} $是矩阵$ \boldsymbol{D} $的第i列；然后，将等价字典$ \boldsymbol{D} $的每列进行单位化处理，得到单位化字典矩阵$ \tilde{\boldsymbol{D}}=[{\tilde{\boldsymbol{\vartheta }}}_{1}\;\;{\tilde{\boldsymbol{\vartheta }}}_{2}\;\;\cdots\;\; {\tilde{\boldsymbol{\vartheta }}}_{N}] $，并以此求出对应的Gram矩阵，如式（11）所示.
{\boldsymbol{G}} = {{{\tilde {\boldsymbol D}}}^{\mathrm{T}}}{{\tilde {\boldsymbol D}}} = \left[ {\begin{array}{*{20}{c}} 1&{{{\tilde {\boldsymbol{\vartheta}} }_1}{{\tilde {\boldsymbol{\vartheta}} }_2}}& \cdots &{{{\tilde {\boldsymbol{\vartheta}} }_1}{{\tilde {\boldsymbol{\vartheta}} }_N}} \\ {{{\tilde {\boldsymbol{\vartheta}} }_2}{{\tilde {\boldsymbol{\vartheta}} }_1}}&{\text{1}}& \cdots &{{{\tilde {\boldsymbol{\vartheta}} }_{\text{2}}}{{\tilde {\boldsymbol{\vartheta}} }_N}} \\ \vdots & \vdots &{}& \vdots \\ {{{\tilde {\boldsymbol{\vartheta}} }_N}{{\tilde {\boldsymbol{\vartheta}} }_1}}&{{{\tilde {\boldsymbol{\vartheta}} }_N}{{\tilde {\boldsymbol{\vartheta}} }_{\text{2}}}}& \cdots &1 \end{array}} \right] \text{.} (11) 2.1 基于特征值分解优化平均相关性
由上文可知，单位化后的等价字典$ \tilde{\boldsymbol{D}} $对应的Gram矩阵是一个主对角线元素全为1的N维半正定矩阵，其秩为M，假设其M个非零特征值为$ {\lambda }_{q}\;（q=1, 2, \cdots ,M） $，有$ {\lambda }_{q} > 0 $，由于矩阵所有特征值的和等于矩阵对角线上的元素之和，因此可以推出式（12）.
\sum\nolimits_{{{q}} = 1}^M {{\lambda _q} = N}. (12) 假设$ {\boldsymbol{l}}_{q} $是Gram矩阵$ \boldsymbol{G} $的某一特征向量，$ {{\lambda }}_{q} $是其对应的特征值，则有$ \boldsymbol{G}{\mathrm{\lambda }}_{q}={\boldsymbol{l}}_{q}{\mathrm{\lambda }}_{q} $. 又因为$ \boldsymbol{G} $为对称矩阵，则$ {\boldsymbol{G}}^{{\mathrm{T}}}\boldsymbol{Gl}_{q}=\boldsymbol{GG}{\boldsymbol{l}}_{q}=\boldsymbol{Gl}_{q}{\lambda }_{q}={\boldsymbol{l}}_{q}{\lambda }_{q}^{2} $，所以矩阵$ {\boldsymbol{G}}^{\mathrm{T}}\boldsymbol{G} $的特征值为$ \boldsymbol{G} $特征值的平方. 假设$ {g}_{i,j} $是Gram矩阵$ \boldsymbol{G} $中的第i行第j列的元素，则矩阵$ {\boldsymbol{G}}^{\mathrm{T}}\boldsymbol{G} $对角线上的元素之和为$ {\displaystyle\sum\nolimits _{i,j=1}^{N}}{{g}^{2}_{i,j}} $，于是推出式（13）.
\sum\nolimits_{{{q}} = 1}^M {{{{{\lambda}^2 _q}}} = \sum\nolimits_{i = j}^M {{{{{g}^2_{i,j}}}}} } . (13) 考虑到非主对角线元素绝对值之和与其平方的和具有相同的单调性，因此，可以通过最小化非主对角线元素平方的和来降低平均互相关系数$ {\mu }_{\mathrm{a}\mathrm{v}\mathrm{g}} $，实现平均相关性的优化，结合式（12），可将问题转化为式（14）所示的问题.
\left\{ {\begin{array}{*{20}{l}} {\text{min}}\;\displaystyle\sum\nolimits_{i \ne j} {{{{{g}^2_{i,j}}}} = \sum\nolimits_{{{q}} = 1}^M {{{{{\lambda}^2 _q}}} - \sum\nolimits_{{{i}} = 1}^M {{{{{g}^2_{i,{{i}}}}}}} } } , \\ {{\mathrm{s.t.}}\; \displaystyle\sum\nolimits_{{{q}} = 1}^M {{\lambda _q}{\text{ = }}N} .\;} \end{array}} \right. (14) 要在矩阵$ \boldsymbol{G} $的特征值之和保持不变的前提下，求出上述问题最优解，就需要尽可能减小矩阵$ \boldsymbol{G} $的特征值平方的和. 而矩阵$ \boldsymbol{G} $的特征值都大于0，因此，将所有特征值设置为平均值即可. 对Gram矩阵$ \boldsymbol{G} $进行特征值分解，如式（15）所示.
{\boldsymbol{G = P\varLambda }}{{\boldsymbol{P}}^{\mathrm{T}}}\text{，} (15) 式中：$ \boldsymbol{P} $为矩阵$ \boldsymbol{G} $的特征向量组成的矩阵，$ \boldsymbol{\varLambda } $为特征值组成的对角矩阵.
将对角矩阵$ \boldsymbol{\varLambda } $中的非零元素修改为$ M/N $，得到新的矩阵$ \hat{\boldsymbol{\varLambda }} $，再将对角矩阵$ \hat{\boldsymbol{\varLambda }} $进行分解，如式（16）所示.
{\boldsymbol{\hat \varLambda = }}{{\boldsymbol{L}}^{\mathrm{T}}}{\boldsymbol{L}}\text{，} (16) 式中：$ \boldsymbol{L} $为大小为$ M\times N $的矩阵.
${\boldsymbol{L}} $的主对角线中，对应$ \hat{\boldsymbol{\varLambda }} $中非零项的元素设为$ \sqrt{{N}/{M}} $，其余元素皆为0. 重新计算Gram矩阵，得到
{\boldsymbol{G = P}}{{\boldsymbol{L}}^{\mathrm{T}}}{\boldsymbol{L}}{{\boldsymbol{P}}^{\mathrm{T}}}. (17) 根据式（11），可以得到
{{\hat {\boldsymbol D} = {\boldsymbol{L}}}}{{\boldsymbol{P}}^{\mathrm{T}}}\text{，} (18) 式中：$ \hat{\boldsymbol{D}} $为更新后的字典矩阵.
2.2 基于ETF理论优化最大相关性
2.2.1 构造ETF矩阵
由于对字典矩阵$ \boldsymbol{D} $进行了列单位化处理，故得到的Gram矩阵中对角线元素全为1，且非对角线元素的值也都在1和 −1之间. 通过Gram矩阵减小测量矩阵$ \boldsymbol{\varPhi } $和稀疏基$ {\boldsymbol{\varPsi }} $之间的相关性，等价于减小Gram矩阵的非对角线元素. 当两矩阵之间不相关时，其所对应的Gram矩阵的非对角线元素也将全为0，此时，Gram矩阵等价于单位矩阵E. 所以，使Gram矩阵向$ {\boldsymbol{E}} $逼近，即可降低其最大相关性，如式（19）所示.
{\text{min}}\;\left\| {{\boldsymbol{G}} - {\boldsymbol{E}}} \right\|_2^2. (19) 要让2个矩阵相关性几乎为0，这在实际情况中是比较困难的[20]. 由于当矩阵满足等角紧框架理论时，其相关性呈最小状态[18]，同时，考虑到矩阵非对角线元素几乎都是一些接近0的小数，因此将条件放宽，即使非主对角线元素小于等于某一阈值$ \mu_0 $，使得矩阵$ \boldsymbol{G} $的非主对角线元素朝$ \mu_0 $逼近，$ \mu_0 $即为所期望的两矩阵之间的相关性. 假设与矩阵$ \boldsymbol{G} $维度相同的单位矩阵$ \boldsymbol{H}\;（\boldsymbol{H}=({H}_{i,j}),i\ne j） $，按照式（20）对矩阵$ \boldsymbol{H} $进行修改.
{{{H}}_{i,j}} = \left\{ {\begin{array}{*{20}{l}} {{{g}_{i,j}}},\quad{\left| {{{g}_{i,j}}} \right| < \mu_0 }, \\ {\mu_0{\mathrm{sgn}}\;{{g}_{i,j}} },\quad{\left| {{{g}_{i,j}}} \right| > \mu_0 } . \end{array}} \right. (20) 将阈值$ \mu_0 $设置为Welch界，可以让测量矩阵与稀疏基矩阵的相关系数逼近下界[21]，使得测量矩阵具有更好的性能.
对矩阵$ \boldsymbol{H} $进行更新后，就需要使得Gram矩阵$ \boldsymbol{G} $尽可能逼近矩阵$ \boldsymbol{H} $. 将关于矩阵$ \boldsymbol{G} $、$ \boldsymbol{H} $的表达式设为$ f $，如式（21）所示.
f = \left\| {{\boldsymbol{G}} - {\boldsymbol{H}}} \right\|_2^2. (21) 为使矩阵$ \boldsymbol{G} $尽可能逼近矩阵$ \boldsymbol{H} $，将问题转化为求函数f的最小值，将$ \boldsymbol{G}={\tilde{\boldsymbol{D}}}^{\rm{T}}\tilde{\boldsymbol{D}} $代入后，式（21）转化为式（22）.
f = \left\| {{{{{\tilde {\boldsymbol D}}}}^{\mathrm{T}}}{{\tilde {\boldsymbol D}}} - {\boldsymbol{H}}} \right\|_2^2. (22) 但是矩阵$ \boldsymbol{G} $的秩为$ M $，而修改后的矩阵$ \boldsymbol{H} $的秩为$ N $，因此，考虑对矩阵$ \boldsymbol{H} $降秩. 首先，进行特征值分解$ \boldsymbol{H}=\boldsymbol{P}{\boldsymbol{\varLambda }}_{{H}}{\boldsymbol{P}}^{{\mathrm{T}}} $，并修改其特征值，得到秩为$ M $的矩阵$ {\boldsymbol{H}}_{{M}} $，如式（23）所示，其中，$ {\boldsymbol{\varLambda }}_{{H}} $为特征值组成的对角矩阵，特征值由大到小排列.
{{\boldsymbol{H}}_{M}} = {\boldsymbol{PI}}{{\boldsymbol{\varLambda }}_{{H}}}{{\boldsymbol{P}}^{\mathrm{T}}}\text{，} (23) 式中：$ \boldsymbol{P} $为矩阵$ \boldsymbol{H} $的特征向量组成的矩阵；$ \boldsymbol{I}=\left[\begin{array}{cc}{\boldsymbol{E}}_{M}& {\boldsymbol{0}}\\ {\boldsymbol{0}}& {\boldsymbol{0}}\end{array}\right]\in {\mathbb{R}}^{N\times N} $，$ {\boldsymbol{E}}_{{M}} $为维度为$ {M} $的单位矩阵.
假设$ {{{\lambda}} }_{{{H}}_{{M}}}=({\lambda }_{{{H}}_{{M}},1},\;{\lambda }_{{{H}}_{{M}},2},\; \cdots ,\; {\lambda }_{{{{H}}}_{{M}},{M}},\;0,\; \cdots, 0) $，是矩阵$ {\boldsymbol{H}}_{{M}} $的特征值. 将所有特征值设为平均值，降低矩阵非主对角线的平方和，从而减少矩阵的平均相关性. 令$ {\hat{\lambda }}_{{{H}}_{{M}}}=\dfrac{1}{M}\displaystyle\sum _{p=1}^{M}{\lambda }_{{{H}}_{{M}},p} $，则修改后的特征值矩阵$ {\hat{\boldsymbol{\varLambda }}}_{{{H}}_{{M}}}={\mathrm{diag}}({\hat{\lambda }}_{{{H}}_{{M}}},{\hat{\lambda }}_{{{H}}_{{M}}}, \cdots ,{\hat{\lambda }}_{{{H}}_{{M}}},0,\cdots ,0) $. 优化后的矩阵为
{{\boldsymbol{H}}_{\rm{opt}}} = {\boldsymbol{P}}{\hat{\boldsymbol{\varLambda }}_{{{\boldsymbol{H}}_{M}}}}{{\boldsymbol{P}}^{\mathrm{T}}}. (24) 此时，所求问题变为式（25）所示问题.
{\text{min}}\;\left\| {{{{{\tilde {\boldsymbol D}}}}^{\mathrm{T}}}{{\tilde {\boldsymbol D}}} - {{\boldsymbol{H}}_{{{\mathrm{opt}}}}}} \right\|_2^2 . (25) 2.2.2 基于梯度缩减算法求最优解
最优测量矩阵$ \hat{\boldsymbol{\varPhi }} $存在解析解，可通过交替策略与奇异值分解[22]求出. 但其子问题的计算成本偏高，耗时较长. 因此，本文选择梯度缩减的思想对原问题求最优解.
由于矩阵$ {\boldsymbol{H}}_{\mathrm{o}\mathrm{p}\mathrm{t}} $为常量，f是一个关于字典矩阵$ \tilde{\boldsymbol{D}} $的函数，求f的最小值问题也就是求矩阵f关于字典矩阵$ \tilde{\boldsymbol{D}} $的梯度，由此需要找出目标函数关于字典矩阵$ \tilde{\boldsymbol{D}} $的下降方向，假设下降方向为k，如式（26）所示.
k = \frac{\partial }{{\partial{d_{i,j}}}}\left\| {{{{{\tilde {\boldsymbol D}}}}^{\mathrm{T}}}{{\tilde {\boldsymbol D}}} - {{\boldsymbol{H}}_{\rm{opt}}}} \right\|_2^2 \text{，} (26) 式中：$({d_{i,j}})={{\tilde {\boldsymbol D}}}. $
由矩阵分解规则变换为[23]
\begin{split} & k = \frac{\partial }{{\partial {d_{i,j}}}}{\mathrm{Tr}}\left\{ {({{{{\tilde {\boldsymbol D}}}}^{\mathrm{T}}}{{\tilde {\boldsymbol D}}} - {{\boldsymbol{H}}_{{{\mathrm{opt}}}}}){{({{{{\tilde {\boldsymbol D}}}}^{\mathrm{T}}}{{\tilde {\boldsymbol D}}} - {{\boldsymbol{H}}_{{{\mathrm{opt}}}}})}^{\mathrm{T}}}} \right\} = \\ &\quad 4{{\tilde {\boldsymbol D}}}({{{{\tilde {\boldsymbol D}}}}^{\mathrm{T}}}{{\tilde {\boldsymbol D}}} - {{\boldsymbol{H}}_{{{\mathrm{opt}}}}}) . \end{split} (27) 沿着下降方向迭代，逐渐迭代缩减目标值，如式（28）所示.
{{{\tilde {\boldsymbol D}}}_u} = {{{\tilde {\boldsymbol D}}}_{u - 1}} - 4\beta {{{\tilde {\boldsymbol D}}}_{u - 1}}({{\tilde {\boldsymbol D}}}_{u - 1}^{\mathrm{T}}{{{\tilde {\boldsymbol D}}}_{u - 1}} - {{\boldsymbol{H}}_{{{\mathrm{opt}}}}}) \text{，} (28) 式中：$u $为迭代次数；$ {\tilde{\boldsymbol{D}}}_{u} $为第$ u $次迭代后的字典矩阵；$ \beta $为每次缩减的步长，且$ \beta > 0 $，通常按照经验取较小的值.
经过多次迭代后，通过逆运算得到最终结果$ \hat{\boldsymbol{\varPhi }} $，如式（29）所示.
{{\hat {\boldsymbol \varPhi} }} = {{{\tilde {\boldsymbol D}}}_u}{{\boldsymbol{\varPsi }}^{ - 1}}. (29) 2.3 算法流程
首先，对Gram矩阵进行特征值分解，优化对角矩阵中的特征值，降低Gram矩阵非对角元素平均值；随后，构造出等角紧框架矩阵，并按照梯度缩减的策略使得Gram矩阵向等角紧框架矩阵逼近，减少其最大相关性，提高重构质量；最后，得到优化后的测量矩阵. 定义迭代终止参数$ {\sigma } $，当式（30）成立时，停止迭代，输出优化后的测量矩阵.
\left\| {{{\tilde {\boldsymbol D}}}_u^{\mathrm{T}}{{{{\tilde {\boldsymbol D}}}}_u} - {{\boldsymbol{H}}_{{{\mathrm{opt}}}}}} \right\|_2^2 < \sigma . (30) 基于矩阵分解与ETF理论的测量矩阵优化算法如下所示：
输入：测量矩阵$ \boldsymbol{\varPhi } $、测量矩阵$ \boldsymbol{\varPhi } $的行数M与列数N，稀疏基${\boldsymbol{\varPsi }}$、最大迭代次数t、缩减步长$ \beta $、Welch界$ \mu_0 $，迭代终止参数$ {\sigma } $；
输出：优化后的测量矩阵$ \hat{\mathit{\Phi }} $；
初始化：生成$ {N}\times {N} $的单位矩阵$ \boldsymbol{H} $，迭代次数$ u=1 $，计算字典矩阵$ \boldsymbol{D} $，并列标准化得到$ {\tilde{\boldsymbol{D}}}_{0} $；
1） 生成Gram矩阵：$ \boldsymbol{G}={\tilde{\boldsymbol{D}}}_{u-1}^{{\mathrm{T}}}{\tilde{\boldsymbol{D}}}_{u-1} $；
2） 对矩阵$ \boldsymbol{G} $进行特征值分解：$ \boldsymbol{G}={\boldsymbol{P}} {\boldsymbol{\varLambda }} {\boldsymbol{P}}^{{\mathrm{T}}} $；
3） 将矩阵$ {\boldsymbol{\varLambda }} $的对角线元素中的非零项设置为N/M，得到$ {\hat{\boldsymbol{\varLambda }}}_{{G}} $；
4） 重新计算Gram矩阵$ {\boldsymbol{G}}={\boldsymbol{P}} {\hat{\boldsymbol{\varLambda }}} {\boldsymbol{P}}^{{\mathrm{T}}} $；
5） 将矩阵$ {\hat{\boldsymbol{\varLambda }}} $进行分解，$ {\hat{\boldsymbol{\varLambda }}} ={\boldsymbol{L}}^{{\mathrm{T}}}\boldsymbol{L} $；
6） 代入$ {\boldsymbol{G}} $，计算$ {\boldsymbol{G}}={\boldsymbol{P}} {\boldsymbol{L}}^{{\mathrm{T}}}\boldsymbol{L}{\boldsymbol{P}}^{{\mathrm{T}}} $，令$ {\hat{\boldsymbol{D}}}_{i}=\boldsymbol{L}{\boldsymbol{P}}^{{\mathrm{T}}} $；
7） 若$ \left|{{g}}_{i,j}\right| \leqslant \mu_0 $，$ {\mathit{H}}_{i,j}={{g}}_{i,j} $，若$ \left|{{g}}_{i,j}\right| > \mu_0 $，$ {\mathit{H}}_{i,j}= \mu_0 \;{\mathrm{sgn}}\left({g}_{i,j}\right) $，对矩阵$ \boldsymbol{H} $进行修改；
8） 对矩阵$ {\boldsymbol{H}} $特征值分解$ ，\boldsymbol{H}={\boldsymbol{P}}{\boldsymbol{\varLambda }}_H{\boldsymbol{P}}^{{\mathrm{T}}} $；
9） 利用矩阵$ \boldsymbol{I}=\left[\begin{array}{cc}{\boldsymbol{E}}_{M}& {\boldsymbol{0}}\\ {\boldsymbol{0}}& {\boldsymbol{0}}\end{array}\right] $对矩阵$ \boldsymbol{H} $降秩，并重新计算$ {\boldsymbol{H}}_{M}={\boldsymbol{P}}_{{H}}\boldsymbol{I}{\boldsymbol{\varLambda }}_{{H}}{\boldsymbol{P}}_{{H}}^{{\mathrm{T}}} $；
10） 对$ {\boldsymbol{H}}_{M} $特征值分解，$ {\boldsymbol{H}}_{M}={\boldsymbol{P}}{\boldsymbol{\varLambda }}_{{{H}}_{M}}{\boldsymbol{P}}^{{\mathrm{T}}} $，$ {\boldsymbol{\varLambda }}_{{{H}}_{M}}= {\mathrm{diag}}({\lambda }_{{{H}}_{{M}},1}, {\lambda }_{{{H}}_{{M}},2}, \cdots , {\lambda }_{{{H}}_{{M}},M},0, \cdots ,0) $；
11） 令$ {\hat{\lambda }}_{{\boldsymbol{H}}_{\mathrm{M}}}=\displaystyle\frac{1}{M}\sum _{p=1}^{M}{\lambda }_{{\boldsymbol{H}}_{\mathrm{M}},p} $，修改特征值矩阵$ {\hat{\boldsymbol{\varLambda }}}_{{{H}}_{M}}= {\mathrm{diag}}({\hat{\lambda }}_{{{H}}_{{M}}},{\hat{\lambda }}_{{{H}}_{{M}}}, \cdots ,{\hat{\lambda }}_{{{H}}_{{M}}},0, \cdots ,0) $；
12） $ {\boldsymbol{H}}_{{\mathrm{opt}}}={\boldsymbol{P}}{\hat{\boldsymbol{\varLambda }}}_{{{H}}_{M}}{\boldsymbol{P}}^{{\mathrm{T}}} $；
13） $ {\tilde{\boldsymbol{D}}}_{u}={\tilde{\boldsymbol{D}}}_{u-1}-4\beta {\tilde{\boldsymbol{D}}}_{u-1}({\tilde{\boldsymbol{D}}}_{u-1}^{{\mathrm{T}}}{\tilde{\boldsymbol{D}}}_{u-1}-{\boldsymbol{H}}_{{\mathrm{opt}}}) $；
14） 若$ {\left|\right|{\tilde{\boldsymbol{D}}}_{u}^{{\mathrm{T}}}{\tilde{\boldsymbol{D}}}_{u}-{\boldsymbol{H}}_{{\mathrm{opt}}}\left|\right|}_{2}^{2} < \sigma $，进入16），否则进入15）；
15） 若$ u $<$ t $，则$ u=u + 1 $，返回1），否则进入16）；
16） 输出$ \hat{\boldsymbol{\varPhi }}={\tilde{\boldsymbol{D}}}_{u}{\boldsymbol{\varPsi }}^{-1} $.
3. 算法仿真
为验证本文优化算法的有效性，在MATLAB上进行仿真，以正交匹配追踪（orthogonal matching pursuit，OMP）作为重构算法，实验参数如表1所示.
表 1 参数表Table 1. Parameters参数名称 参数值 $ \boldsymbol{\varPhi } $ 随机导频矩阵 $ {\boldsymbol{\varPsi }}$ 单位矩阵 t/次 1000 $ \beta $ 0.01 信道类型 随机瑞利衰落 导频长度 100 信号长度 256 潜在用户数/人 30 图1比较了$ \boldsymbol{\varPhi } $与$ {\boldsymbol{\varPsi }} $的相关系数随观测维度M的变化趋势. 由图可见，经过基于矩阵分解与ETF理论的改进后，测量矩阵与稀疏基之间的相关性明显降低.
图 1 相关系数随观测维度M的变化Figure 1. Variation of correlation coefficient with observed dimension M图2比较了不同稀疏度的情况下不同算法错误估计活跃用户的数量. 从图中可以看出：信号稀疏度低于30时，各算法都能准确地估计活跃用户，但当稀疏度大于30以后，随着稀疏度不断增加，错误估计的活跃用户数量都在增加；本文提出的优化算法性能较好.
图 2 不同稀疏度下错误估计用户数比较Figure 2. Comparison of estimation errors of user number under different sparsity图3比较了不同稀疏度下，单次重构所消耗的时间. 文献[6-10]所提及的矩阵优化算法复杂度分别为$ {O}\left({{N}}^{2}\right){、}{O}\left({{N}}^{2}\right){、}{O}\left(1\right){、}{O}\left({N}\right){、}{O}\left({N}\right) $，本文所提出的算法复杂度为$ {O}\left({{N}}^{2}\right) $. 从图中可以看出，本文提出的算法所消耗的时间较多，是因为通过特征值分解优化了平均相关性，构造出ETF矩阵后又对其进行降秩与降低平均相关性的操作，计算流程较多，因此单次重构时间相对较长.
图 3 不同稀疏度下单次重构时间比较Figure 3. Comparison of single reconstruction time under different sparsity图4比较了不同信噪比（SNR）下信号稀疏度为30时，通过不同算法进行信道估计所得的均方误差（MSE）. 从结果可以看出，随着信噪比的增加，各算法均方误差都在降低，其中，本文提出的测量矩阵优化算法效果最好.
图5比较了在不同信噪比下信号稀疏度为30时不同算法所得的误码率（BER）. 由图可知，随着信噪比的增加，各个算法的误码率也逐渐下降，其中，本文提出的测量矩阵改进算法性能最好.
通过上述仿真实验可以看出，本文提出的基于矩阵分解和ETF理论的测量矩阵改进算法，虽然在时间复杂度上有所不足，但在重构性能、信道估计与活跃用户检测上有一定的优势.
4. 总 结
在大规模通信场景下，基于测量矩阵与稀疏基所构造出的Gram矩阵，提出一种矩阵分解与ETF理论相结合的优化算法. 主要结论如下：
1） 所提出的算法有效减小了测量矩阵与稀疏基之间的相关性，提高了信号重构的质量，优化了测量矩阵在信道估计与活跃用户检测中的性能.
2） 未来可对该算法时间复杂度进行优化，以提高重构的效率. 该算法单次重构时间相对较高，在后续研究中将尝试在保证算法性能的基础上，降低其时间复杂度.
-
图 3 不同初始预应力工况下PRC桩跨中弯矩-挠度曲线图
Figure 3. Bending moment-deflection curve in midspan of PRC pipe piles under initial prestress condition
图 4 PRC4及PRC5桩跨中弯矩-挠度曲线
Figure 4. Bending moment-deflection curves in midspan of PRC4 and PRC5 pipe piles
图 5 抗弯承载力与挠度关系曲线
Figure 5. Relationship between flexural bearing capacity and deflection
表 1 试件基本情况
Table 1. Specimen basic information
试件编号 外径/mm 壁厚/mm 长度/mm 张拉控制比例 非预应力钢筋贡献 PRC1 500 100 9 000 0.3 有 PRC2 0.5 PRC3 0.7 PRC4 500 100 9 000 0.5 无 PRC5 有 
下载: 导出CSV
表 2 桩身裂缝及弯曲延性情况统计
Table 2. Statistics of pile body cracks and ductility
桩身编号 裂缝数量/根 最大裂缝宽度/mm 延性系数μ PRC1 25 0.90 6.8 PRC2 22 0.95 8.5 PRC3 18 0.75 5.5 PRC4 27 1.05 10.6 PRC5 27 1.50 13.6
下载: 导出CSV
表 3 开裂弯矩理论与实测值对比结果
Table 3. Comparison of theoretical and measured cracking moments
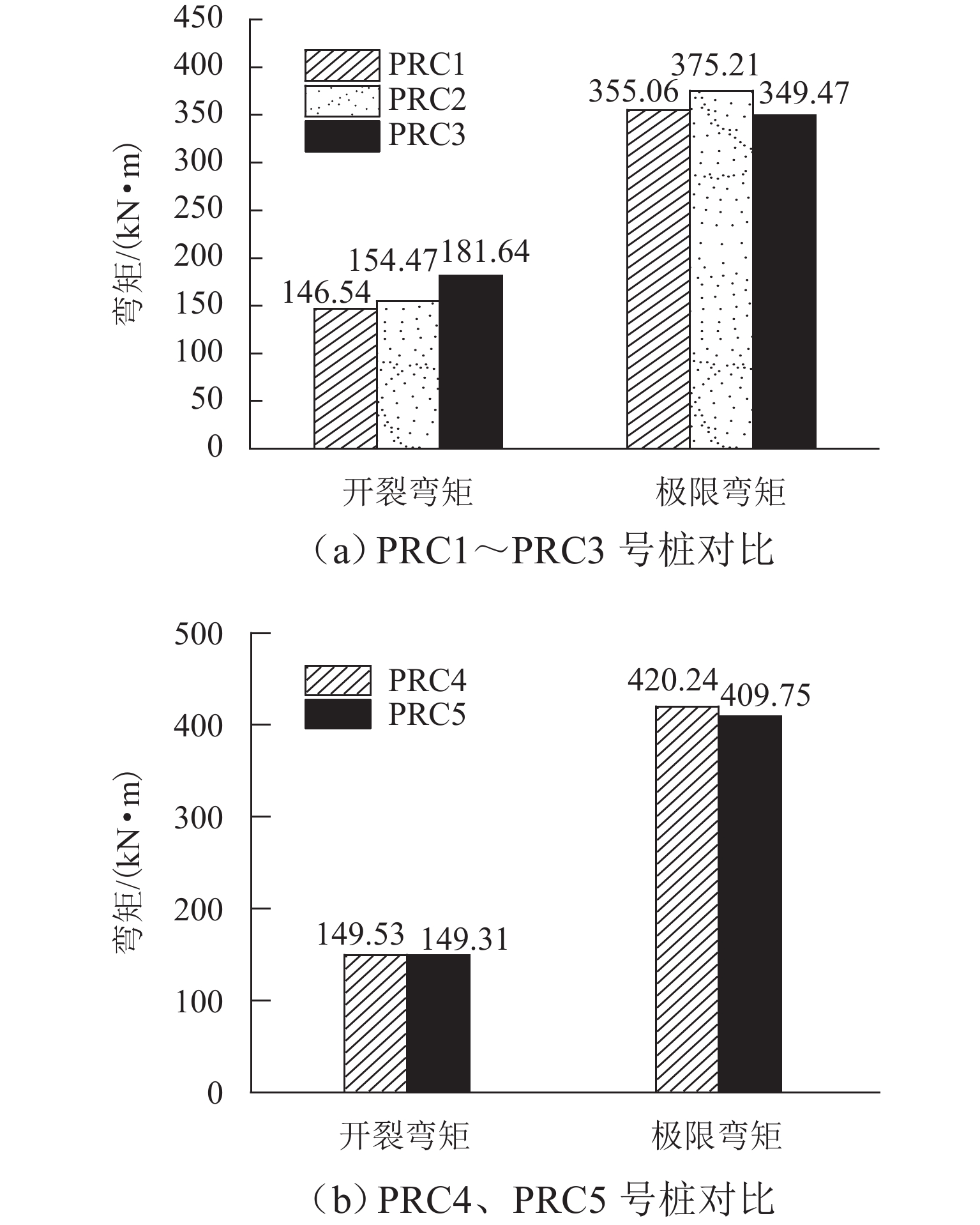
构件 初始预应力比例 理论值（KN·m） 实测值（KN·m） 实测值/计算值 PRC1 0.3 98.1 146.5 1.50 PRC2 0.5 121.6 154.5 1.28 PRC3 0.7 145.2 181.6 1.25 PRC4 0.5 119.3 149.3 1.39 PRC5 0.5 119.3 149.5 1.37
下载: 导出CSV
表 4 极限弯矩理论与实测比较
Table 4. Comparison of theoretical and measured ultimate bending moments
构件 初始预应力比例 实测值/
（KN·m）理论值1/
（KN·m）理论值2/
（KN·m）PRC1 0.3 355 310 354 PRC2 0.5 375 320 360 PRC3 0.7 349.5 330 363 PRC4 0.5 420.2 307 392 PRC5 0.5 409.8 307 392
下载: 导出CSV
-
[1] 赵升峰,黄广龙,马世强,等. 预制混凝土支护管桩在深基坑工程中的应用[J]. 岩土工程学报,2014,36(增1): 91-96.ZHAO Shengfeng, HUANG Guanglong, MA Shiqiang, et al. Application of precast concrete pipe piles in a deep excavation project[J]. Journal of Geotechnical Engineering, 2014, 36(S1): 91-96. [2] LIU H L, KONG G Q, DING X M, et al. Performances of large-diameter cast-in-place concrete pipe piles and pile groups under lateral loads[J]. Journal of Performance of Constructed Facilities, 2013, 27(2): 191-202. doi: 10.1061/(ASCE)CF.1943-5509.0000304 [3] 郭杨,吴平. 玻璃纤维筋与钢筋复合配筋预应力混凝土管桩承载性能试验研究[J]. 建筑结构学报,2018,39(2): 162-167.GUO Yang, WU Ping. Experimental study on bearing capacity of compositely reinforced with GFRP prestressed concrete pipe pile[J]. Journal of Building Structures, 2018, 39(2): 162-167. [4] 姚大立,贾金青,余芳. 有腹筋预应力超高强混凝土梁受剪承载力试验研究[J]. 湖南大学学报(自然科学版),2015,42(3): 23-30.YAO Dali, JIA Jinqing, YU Fang. Experimental study of the shear capacity of prestressed ultra-high reinforced concrete beams with stirrups[J]. Journal of Hunan University (Natural Sciences), 2015, 42(3): 23-30. [5] 王铁成,杨志坚,赵海龙,等. PHC管桩与承台连接节点试验研究与有限元分析[J]. 天津大学学报(自然科学与工程技术版),2015,48(6): 527-534.WANG Tiecheng, YANG Zhijian, ZHAO Hailong, et al. Experimental investigation and finite element analysis of prestressed high strength concrete pile-pile cap connections[J]. Journal of Tianjin University (Science and Technology), 2015, 48(6): 527-534. [6] IKEDA S. Ductility improvement of prestressed concrete piles[J]. Transactions of the Japan Concrete Institute, 1982, 4: 531-538. [7] YANG Z J, LI G C, WANG W J. Experimental investigation and nonlinear finite element analysis on seismic performance of PHC piles[J]. Structural Engineering International, 2018, 28(4): 475-488. doi: 10.1080/10168664.2018.1462672 [8] CARBONELL-MÁRQUEZ J F, GIL-MARTÍN L M, ALEJANDRO FERNÁNDEZ-RUÍZ M, et al. Effective area in tension stiffening of reinforced concrete piles subjected to flexure according to Eurocode 2[J]. Engineering Structures, 2014, 76: 62-74. doi: 10.1016/j.engstruct.2014.06.041 [9] 王新玲,高会宗,周同和,等. 新型混合配筋预应力混凝土管桩抗弯性能试验研究[J]. 工业建筑,2012,42(8): 64-68.WANG Xinling, GAO Huizong, ZHOU Tonghe, et al. Experimental studies of flexural behavior of new type prestressed concrete pipe pile with compound unprestressed reinforcement[J]. Industrial Construction, 2012, 42(8): 64-68. [10] 杜新喜,胡锐,袁焕鑫,等. 混合配筋预应力混凝土管桩抗弯承载性能研究[J]. 土木工程学报,2019,52(1): 44-52.DU Xinxi, HU Rui, YUAN Huanxin, et al. Study on flexural behavior of prestressed concrete pipe pile with hybrid reinforcement[J]. China Civil Engineering Journal, 2019, 52(1): 44-52. [11] 刘畅,孙雅楠,郑刚,等. 复合配筋管桩抗震性能试验研究[J]. 土木工程学报,2018,51(4): 77-86.LIU Chang, SUN Yanan, ZHENG Gang, et al. Experimental study on the seismic performance of the prestressed high-strength concrete pipe pile reinforced with non-prestressed steel bars[J]. China Civil Engineering Journal, 2018, 51(4): 77-86. [12] 徐金,窦远明. 混合配筋管桩拟静力试验研究[J]. 建筑结构,2019,49(14): 113-116,125.XU Jin, DOU Yuanming. Pseudo static test study on hybrid reinforced concrete pipe pile[J]. Building Structure, 2019, 49(14): 113-116,125. [13] 郭杨,吴平. 复合配筋预应力混凝土管桩受弯与受剪性能试验研究[J]. 施工技术,2021,50(2): 95-101.GUO Yang, WU Ping. Experimental study on flexural and shear behaviors of pre-stressed concrete pipe with hybrid reinforcement[J]. Construction Technology, 2021, 50(2): 95-101. [14] 张忠苗,刘俊伟,谢志专,等. 新型混凝土管桩抗弯剪性能试验研究[J]. 岩土工程学报,2011,33(增2): 271-277.ZHANG Zhongmiao, LIU Junwei, XIE Zhizhuan, et al. Experimental study on flexural and shearing properties of modified concrete pipe piles[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(S2): 271-277. [15] 朱俊涛,代天昊,李可. 变预应力度混合配筋混凝土管桩受弯性能[J]. 建筑结构学报,2024,45(1): 159-169.ZHU Juntao, DAI Tianhao, LI Ke. Flexural behavior of concrete pipe pile with various levels of prestress[J]. Journal of Building Structures, 2024, 45(1): 159-169. [16] 刘凯,马维尼. 混合配筋超高强混凝土管桩抗弯性能试验研究[J]. 水利与建筑工程学报,2022,20(6): 155-162. doi: 10.3969/j.issn.1672-1144.2022.06.023LIU Kai, MA Weini. Experimental study on flexural performance of ultra-high strength concrete PRC pipe pile[J]. Journal of Water Resources and Architectural Engineering, 2022, 20(6): 155-162. doi: 10.3969/j.issn.1672-1144.2022.06.023 [17] 刘永超,刘岩,李兵兵,等. 基于基坑支护工程的区段复式配筋预应力管桩抗弯试验及数值模拟[J]. 岩土工程学报,2024,46(2): 406-414. doi: 10.11779/CJGE20221359LIU Yongchao, LIU Yan, LI Bingbing, et al. Flexural tests and numerical simulations of prestressed concrete pipe piles with partial hybrid reinforcement based on support of foundation pits[J]. Chinese Journal of Geotechnical Engineering, 2024, 46(2): 406-414. doi: 10.11779/CJGE20221359 [18] 王新玲,杜琳,黄伟东. 混合配筋预应力混凝土管桩抗弯刚度模型研究[J]. 郑州大学学报(工学版),2013,34(6): 80-84. doi: 10.3969/j.issn.1671-6833.2013.06.020WANG Xinling, DU Lin, HUANG Weidong. Stiffness study of prestressed and reinforced concrete compounded pipe pile[J]. Journal of Zhengzhou University (Engineering Science), 2013, 34(6): 80-84. doi: 10.3969/j.issn.1671-6833.2013.06.020 [19] 郭杨,吴平,韩磊,等. 复合配筋预应力混凝土管桩抗弯性能试验和数值分析[J]. 地下空间与工程学报,2019,15(2): 481-488.GUO Yang, WU Ping, HAN Lei, et al. Experimental study and numerical analysis on bending capability of compositely reinforced (GFRP) prestressed concrete pipe pile[J]. Chinese Journal of Underground Space and Engineering, 2019, 15(2): 481-488. [20] 傅传国,商圣强,王玉镯,等. 火灾下预应力型钢混凝土梁抗弯承载力计算[J]. 西南交通大学学报,2013,48(4): 625-631,658. doi: 10.3969/j.issn.0258-2724.2013.04.006FU Chuanguo, SHANG Shengqiang, WANG Yuzhuo, et al. Bending bearing capacity calculation of prestressed steel reinforced concrete beam under fire[J]. Journal of Southwest Jiaotong University, 2013, 48(4): 625-631,658. doi: 10.3969/j.issn.0258-2724.2013.04.006 [21] 李福海,胡丁涵,余泳江,等. PP-ECC梁抗弯性能试验研究[J]. 西南交通大学学报,2021,56(2): 272-281.LI Fuhai, HU Dinghan, YU Yongjiang, et al. Experimental study on flexural capacity of PP-ECC beam[J]. Journal of Southwest Jiaotong University, 2021, 56(2): 272-281. [22] 中国建筑材料联合会. 先张法预应力混凝土管桩:GB/T 13476—2009 [S]. 北京:中国标准出版社,2010. [23] 河南省住房和城乡建设厅. 混合配筋预应力混凝土管桩:DBJT 19-34—2009 [S]. 郑州:河南科学技术出版社,2010. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 19
- HTML全文浏览量: 10
- PDF下载量: 4
- 被引次数: 0