Different Styles of Lane Changing Trajectory Planning Based on Aerial Survey Data
-
摘要:
不当的换道行为可能危及交通安全，导致交通事故和拥堵，因此有必要探索不同驾驶风格下在车道出口的换道轨迹. 本文利用中国高速公路和快速路拥堵场景数据集中的车辆轨迹数据，采用K-means算法将驾驶人分为谨慎型、普通型和激进型三类；通过聚类分析和换道时间预测，以最小化换道纵向位移和行驶稳定性加权值之和为优化目标，同时以舒适性和安全性评价指标为约束条件，采用五次多项式进行最优换道轨迹规划；随后，使用遗传算法解决轨迹规划问题，基于Prescan、CarSim、MATLAB/Simulink仿真平台建立横纵向联合控制二自由度车辆动力学模型；最后，设计自车前车、目标车道前车和目标车道后车三种典型换道场景，并通过仿真实验评价不同驾驶风格下的换道轨迹规划效果和车辆轨迹跟踪控制效果. 实验结果表明：在目标车道有车的场景下提出的融合驾驶风格的轨迹规划算法使得规划的换道轨迹增加了激进型驾驶风格的换道时长，同时减少了普通型和谨慎型驾驶风格司机的换道时长，进而能够确保换道过程的时效性、安全性和舒适性.
Abstract:Improper lane-changing may pose a threat to traffic safety, leading to traffic accidents and congestion. Therefore, it is necessary to explore lane-changing trajectories for different driving styles at lane exits. The trajectory data of vehicles from congested scenarios on Chinese highways and expressways was utilized, and drivers were categorized into cautious, normal, and aggressive types by using the K-means algorithm. According to cluster analysis and lane-changing time prediction, the minimum sum of lane-changing longitudinal displacement and weighted driving stability was pursued, and comfort and safety evaluation metrics were employed as constraints. A quintic polynomial was utilized for optimal lane-changing trajectory planning. Then, a genetic algorithm was employed to solve the trajectory planning problem. Based on the simulation platform comprising Prescan, CarSim, and MATLAB/Simulink, a two-degree-of-freedom vehicle dynamics model of joint longitudinal and lateral control was designed. Finally, three typical lane-changing scenarios, including the car in front of the vehicle, the car in front of the target lane, and the car behind the target lane were designed. The effects of lane-changing trajectory planning and vehicle trajectory tracking control under different driving styles were evaluated by simulation experiments. The experimental findings demonstrate that the proposed trajectory planning algorithm, incorporating driving styles, extends the lane-changing time for aggressive drivers in scenarios with vehicles in the target lane. In addition, it reduces the lane-changing time for normal and cautious drivers, ensuring timely, safe, and comfortable lane-changing maneuvers.
-
图 2 自车与周围6个位置的车辆的相关信息
Figure 2. Correlation information between studied vehicle and surrounding six vehicles in different positions
图 7 不同场景下不同驾驶风格车辆的轨迹跟踪效果对比
Figure 7. Comparison of trajectory tracking effect of vehicles with different driving styles in three scenarios
图 8 不同场景下不同驾驶风格车辆的方向盘转角对比
Figure 8. Comparison of steering wheel angle for vehicles with different driving styles in three scenarios
图 9 不同场景下不同驾驶风格的自车与周围车辆的距离对比
Figure 9. Comparison of distance between studied vehicle and surrounding vehicles with different driving styles in three scenarios
表 1 航拍摄像机参数
Table 1. Parameters of aerial filming camera
参数 取值 影像传感器 1/2.3英寸CMOS，有效像素1200万 镜头 视角 83°，等效焦距 24 mm，光圈f/2.8 数字变焦范围 4K：2倍，2.7K：3倍，FHD：4 倍 最长飞行时间 31 min（无风环境 17 km/h 匀速飞行） 最大信号有效
距离10 km （FCC），6 km （CE/SRRC/MIC） 录像分辨率 4K：3840 × 2160@24/25/自车fps
2.7K：2720 × 1530@24/25/30/48/50/60fps
FHD：1920 × 1080@24/25/30/48/50/60fps
下载: 导出CSV
表 2 评价指标的含义
Table 2. Meaning of evaluation indicators
符号 含义 符号 含义 vxmean/（m·s−1） 纵向速度均值 axstd/（m·s−2） 纵向加速度标准差 vxstd/（m·s−1） 纵向速度标准差 axmax/（m·s−2） 纵向加速度最大值 vxmax/（m·s−1） 纵向速度最大值 aymean/（m·s−2） 横向加速度均值 vymean/（m·s−1） 横向速度均值 aystd/（m·s−2） 横向加速度标准差 vystd/（m·s−2） 横向速度标准差 aymax/（m·s−2） 横向加速度最大值 vymax/（m·s−1） 横向速度最大值 dhw/m 最小跟车距离 axmean/（m·s−2） 纵向加速度均值 thw/（s·辆−1） 最小车头时距
下载: 导出CSV
表 3 总方差解释
Table 3. Explained total variance
公因子 特征值 方差/% 累计/% 1 4.464 31.886 31.886 2 3.057 21.836 53.722 3 2.870 20.503 74.225 4 2.184 15.601 89.826
下载: 导出CSV
表 4 聚类中心值和类别数
Table 4. Cluster center values and number of categories
类别 F1 F2 F3 F4 数目/辆 1 1.097 −0.453 0.143 −0.085 725 2 −0.102 −0.469 0.056 0.023 1391 3 −0.682 1.472 −0.347 0.019 932
下载: 导出CSV
表 5 各场景下遗传算法求得的最优换道距离与换道时长
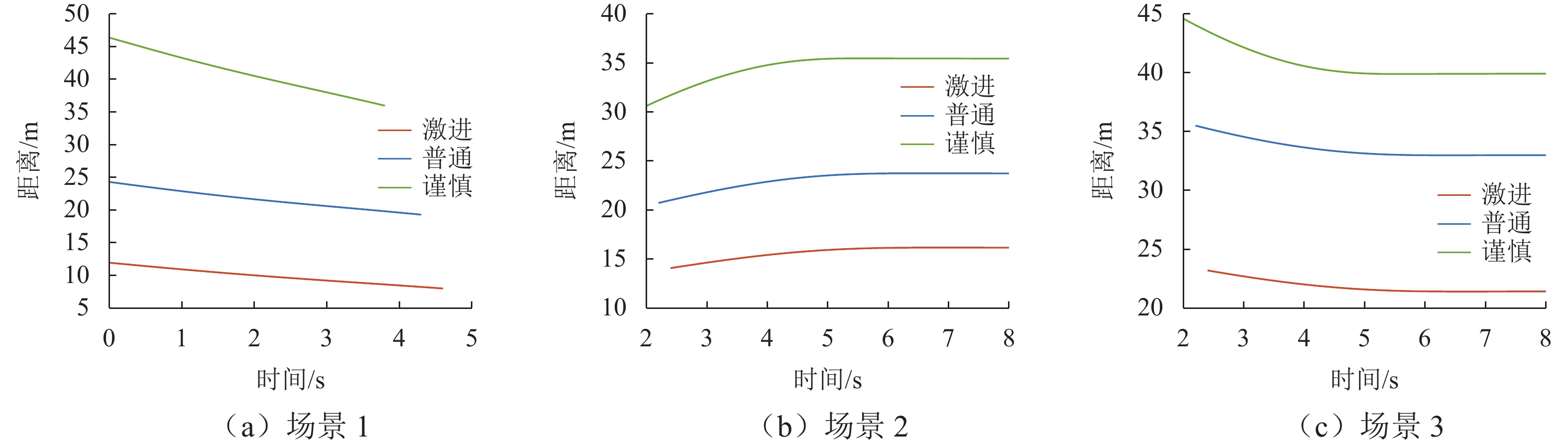
Table 5. Optimal lane-changing distance and lane-changing time by genetic algorithm in each scenario
场景 驾驶风格 换道距离/m 换道时长/s 1 激进型 35.02 6.92 普通型 46.34 6.55 谨慎型 88.88 5.72 2 激进型 38.23 6.84 普通型 50.52 6.46 谨慎型 97.18 5.67 3 激进型 38.16 6.77 普通型 50.66 6.40 谨慎型 97.76 5.69
下载: 导出CSV
-
[1] 吕思雨. 车辆换道意图识别及换道轨迹预测[D]. 广州: 广州大学,2022. [2] DO Q H, TEHRANI H, MITA S, et al. Human drivers based active-passive model for automated lane change[J]. IEEE Intelligent Transportation Systems Magazine, 2017, 9(1): 42-56. doi: 10.1109/MITS.2016.2613913 [3] LUO Y G, XIANG Y, CAO K, et al. A dynamic automated lane change maneuver based on vehicle-to-vehicle communication[J]. Transportation Research Part C: Emerging Technologies, 2016, 62: 87-102. doi: 10.1016/j.trc.2015.11.011 [4] 禹乐文,罗霞,刘仕焜. 复杂车路环境下自动驾驶车辆换道仿真研究[J]. 计算机仿真,2021,38(5): 146-152. doi: 10.3969/j.issn.1006-9348.2021.05.030YU Yuewen, LUO Xia, LIU Shikun. Research on simulation of lane-changing for autonomous vehicles under complex road conditions[J]. Computer Simulation, 2021, 38(5): 146-152. doi: 10.3969/j.issn.1006-9348.2021.05.030 [5] 邓召文,乔宝山,袁显举,等. 不同冲击度约束下智能汽车换道轨迹优化[J]. 机械设计与制造,2022(2): 17-20. doi: 10.3969/j.issn.1001-3997.2022.02.004DENG Zhaowen, QIAO Baoshan, YUAN Xianju, et al. Optimal design of the lane-change trajectory of intelligent vehicle under different jerking[J]. Machinery Design & Manufacture, 2022(2): 17-20. doi: 10.3969/j.issn.1001-3997.2022.02.004 [6] 李文礼,邱凡珂,廖达明,等. 基于深度强化学习的高速公路换道跟踪控制模型[J]. 汽车安全与节能学报,2022,13(4): 750-759. doi: 10.3969/j.issn.1674-8484.2022.04.016LI Wenli, QIU Fanke, LIAO Daming, et al. Highway lane change decision control model based on deep reinforcement learning[J]. Journal of Automotive Safety and Energy, 2022, 13(4): 750-759. doi: 10.3969/j.issn.1674-8484.2022.04.016 [7] 朱煦晗. 智能汽车换道决策与轨迹规划算法研究[D]. 长春: 吉林大学,2021. [8] 邱添,张志安,王海龙. 移动机器人的栅格概率路径图法路径规划[J]. 机床与液压,2022,50(21): 14-19. doi: 10.3969/j.issn.1001-3881.2022.21.003QIU Tian, ZHANG Zhian, WANG Hailong. Path planning of mobile robot based on grid probability path graph[J]. Machine Tool & Hydraulics, 2022, 50(21): 14-19. doi: 10.3969/j.issn.1001-3881.2022.21.003 [9] 郑奇. 智能驾驶中驾驶员风格识别及车辆行为预测研究[D]. 杭州: 浙江大学,2022. [10] 周波波. 基于深度学习的自动驾驶汽车主动换道决策与轨迹规划研究[D]. 重庆: 重庆大学,2021. [11] 王科银,杨亚会,王思山,等. 驾驶风格聚类与识别研究[J]. 湖北汽车工业学院学报,2021,35(3): 1-6,10. doi: 10.3969/j.issn.1008-5483.2021.03.001WANG Keyin, YANG Yahui, WANG Sishan, et al. Research of clustering and recognition for driving style[J]. Journal of Hubei University of Automotive Technology, 2021, 35(3): 1-6,10. doi: 10.3969/j.issn.1008-5483.2021.03.001 [12] 胡春燕,曲大义,赵梓旭,等. 考虑前车驾驶风格的改进自适应巡航控制跟驰模型及仿真[J]. 济南大学学报(自然科学版),2023,37(3): 331-338.HU Chunyan, QU Dayi, ZHAO Zixu, et al. Improved adaptive cruise control car-following model and simulation considering driving styles of leading car[J]. Journal of University of Jinan (Science and Technology), 2023, 37(3): 331-338. [13] 马依宁,姜为,吴靖宇,等. 基于不同风格行驶模型的自动驾驶仿真测试自演绎场景研究[J]. 中国公路学报,2023,36(2): 216-228. doi: 10.3969/j.issn.1001-7372.2023.02.018MA Yining, JIANG Wei, WU Jingyu, et al. Self-evolution scenarios for simulation tests of autonomous vehicles based on different models of driving styles[J]. China Journal of Highway and Transport, 2023, 36(2): 216-228. doi: 10.3969/j.issn.1001-7372.2023.02.018 [14] HAN S F, XIAO L. An improved adaptive genetic algorithm[J]. SHS Web of Conferences, 2022, 140: 01044.1-01044.6. [15] 郑金. 有关科氏加速度的疑难问题探究[J]. 物理通报,2021(11): 12-14. doi: 10.3969/j.issn.0509-4038.2021.11.004 -
下载:
点击查看大图
计量
- 文章访问数: 271
- HTML全文浏览量: 51
- PDF下载量: 28
- 被引次数: 0