Periodic Motion Transition and Driving Characteristics of Collision and Stick-Slip Vibration-Driven System
-
摘要:
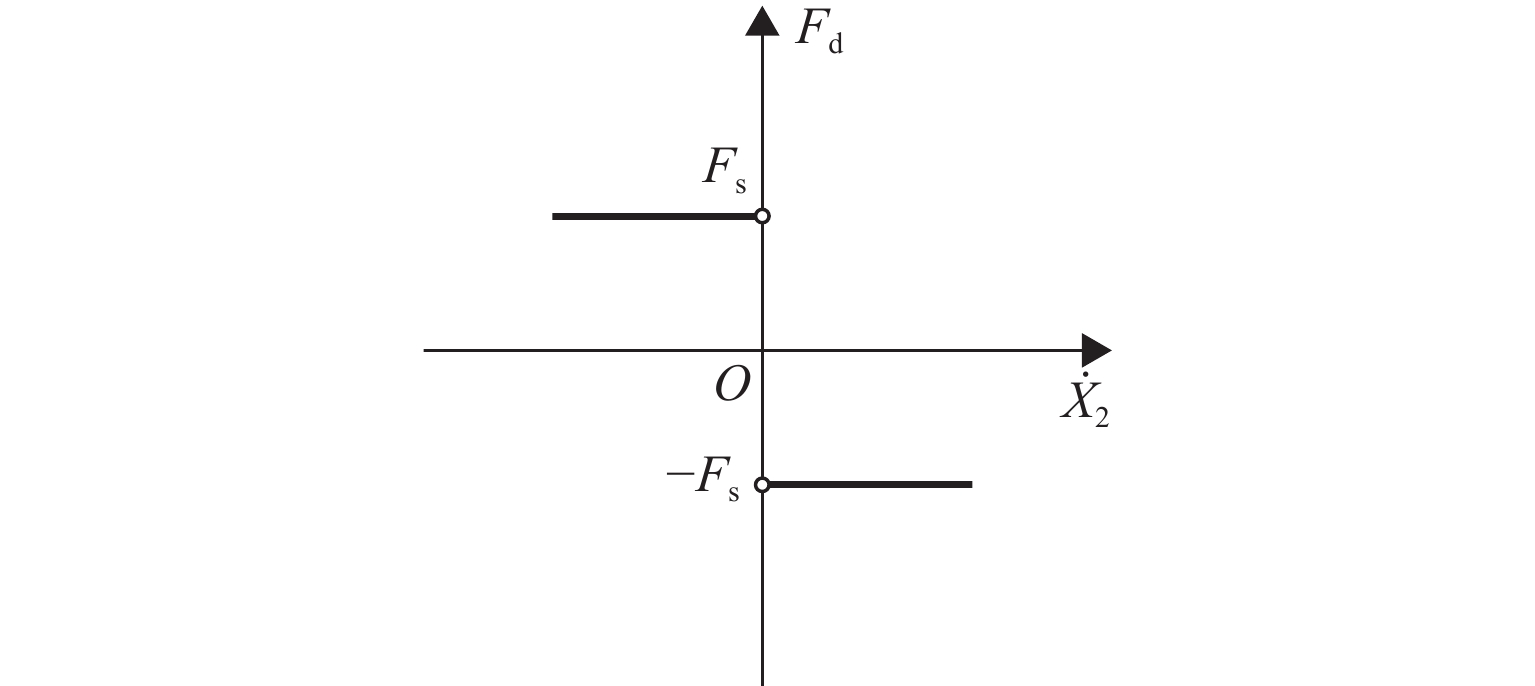
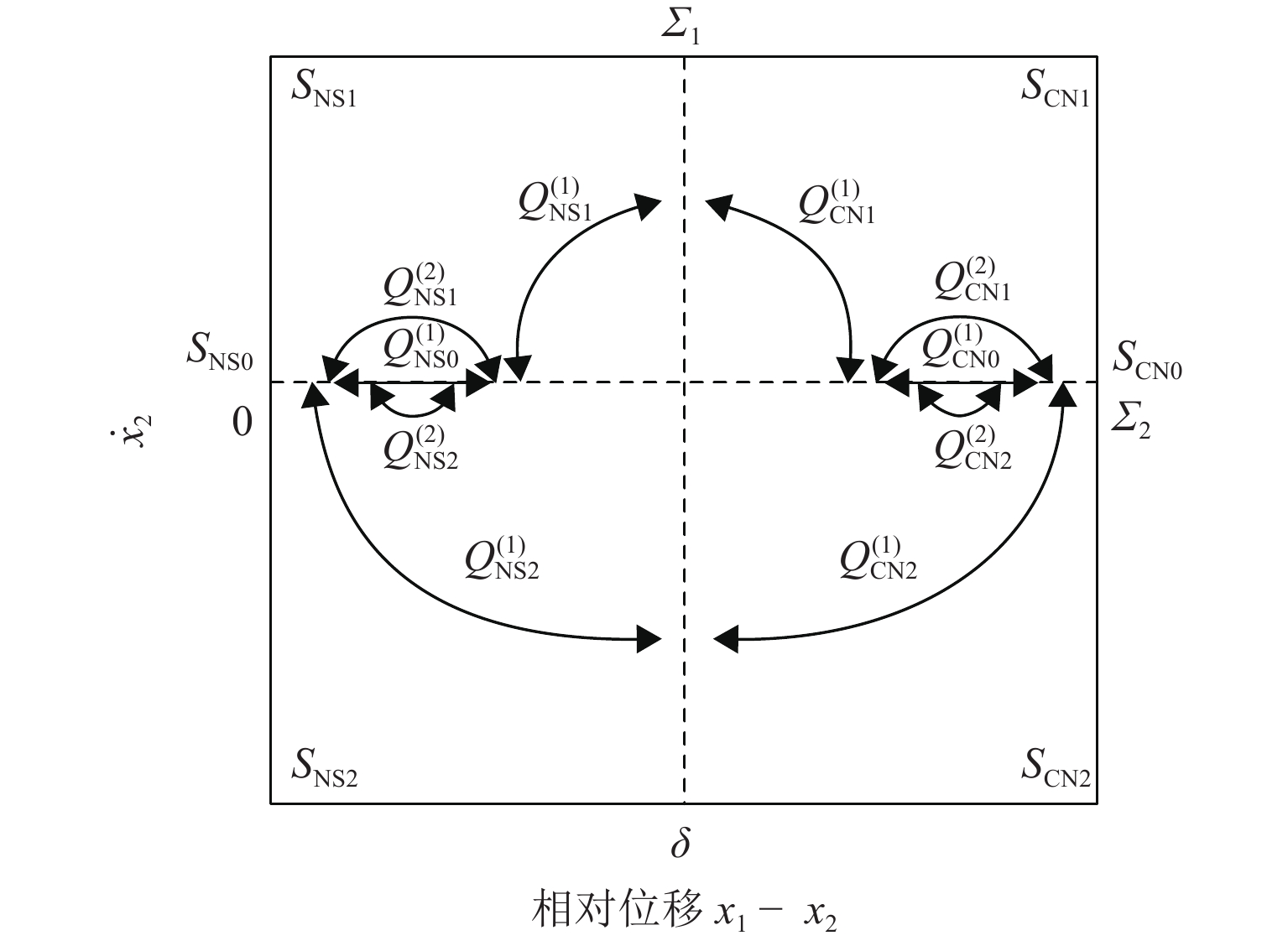
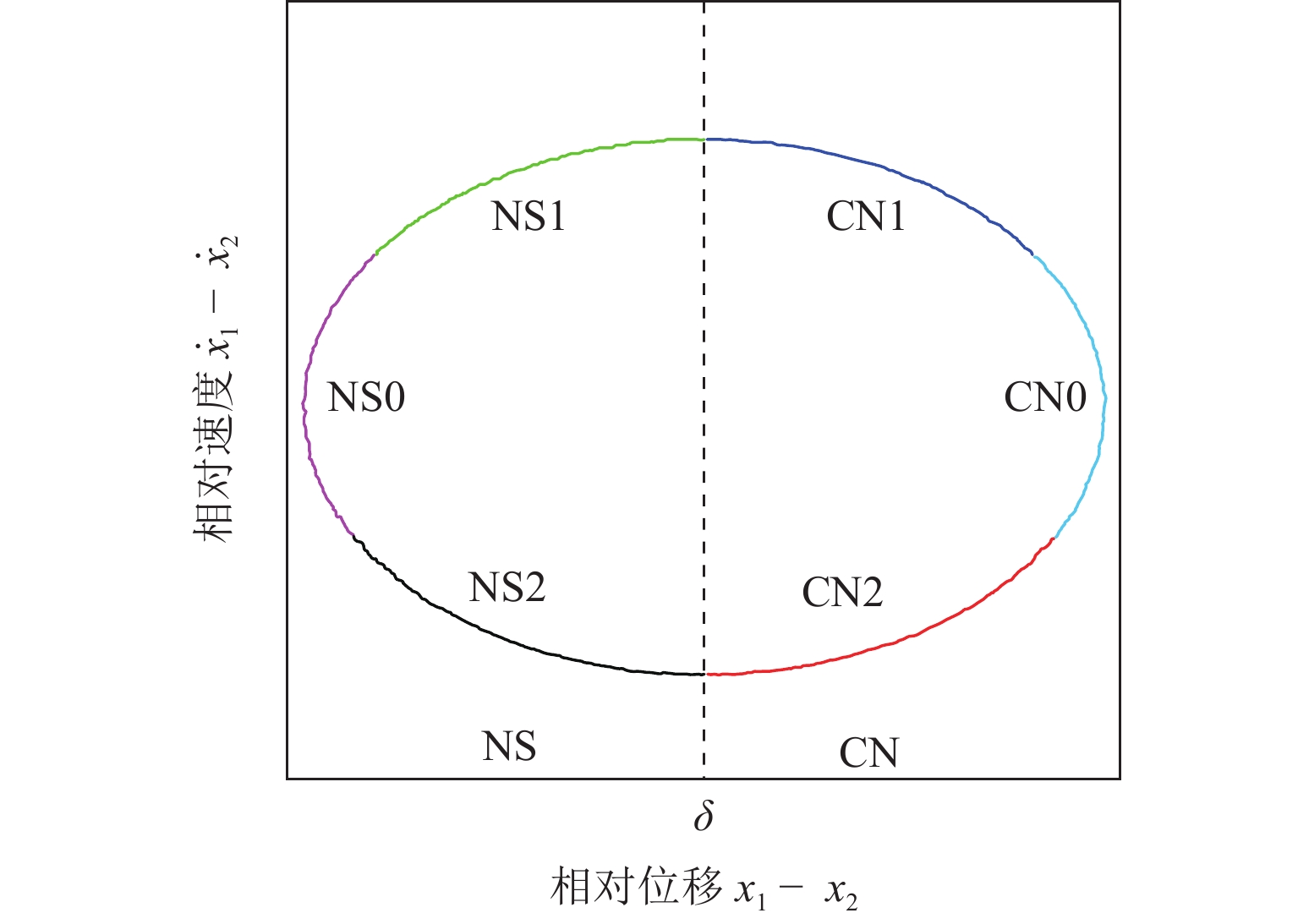
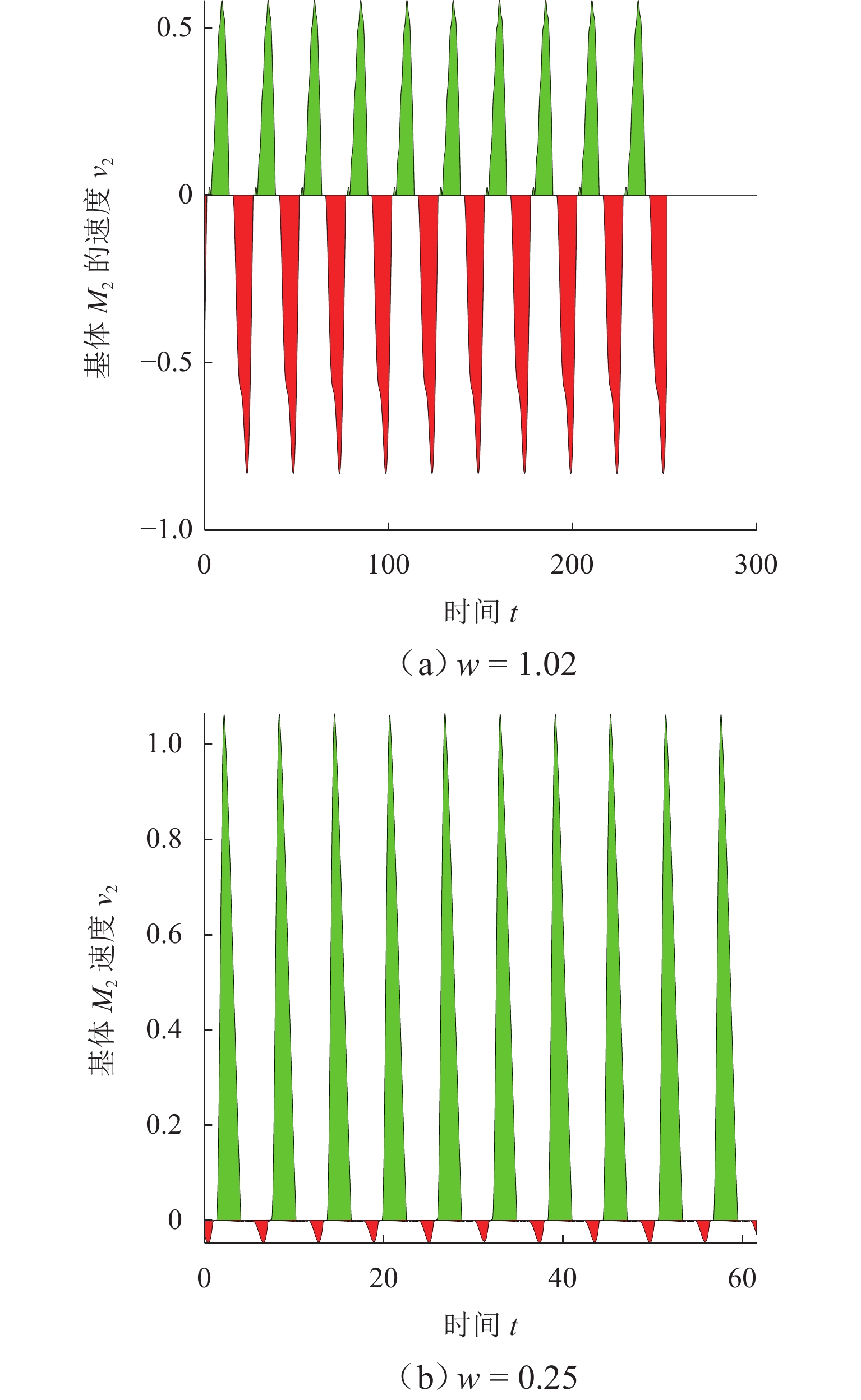
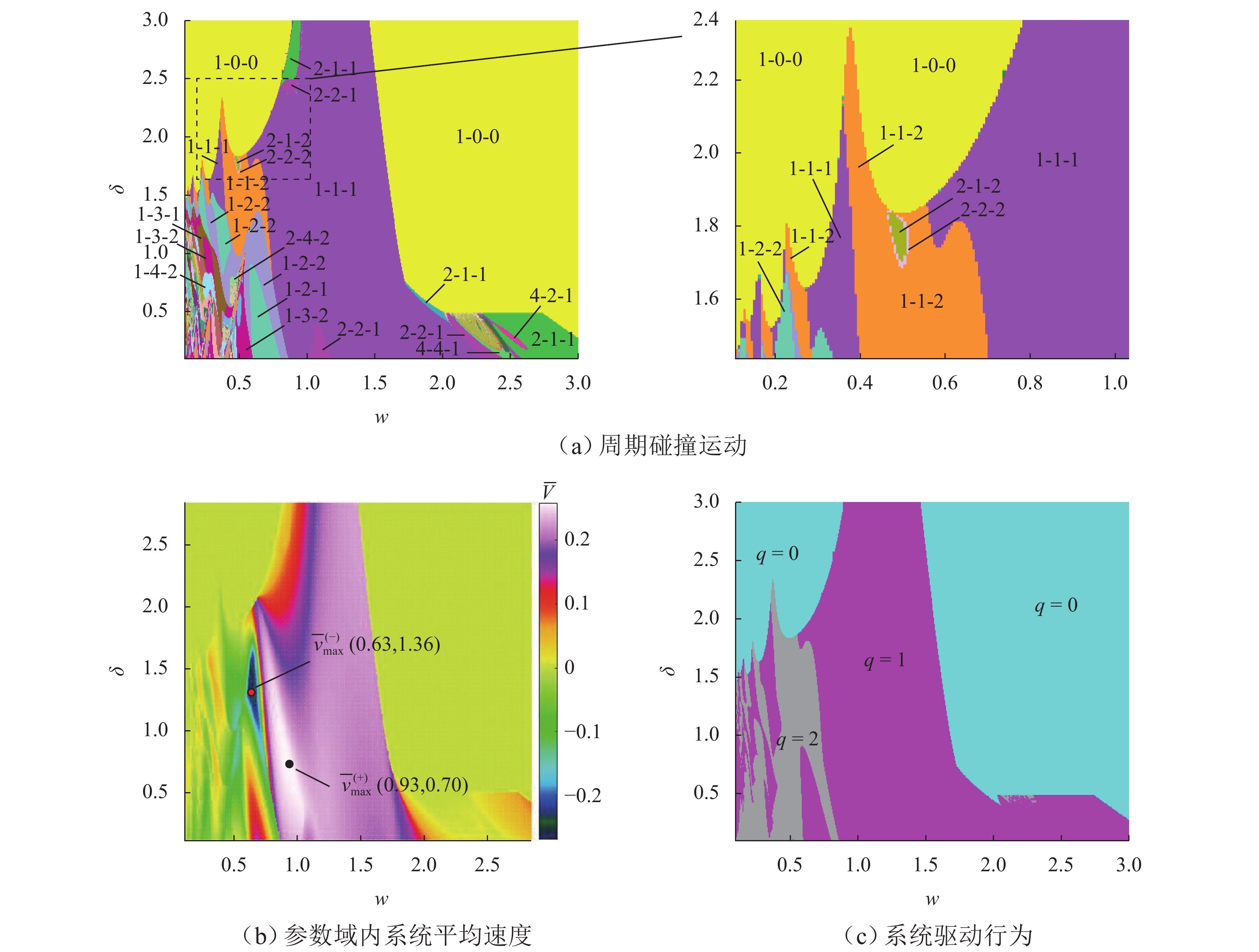
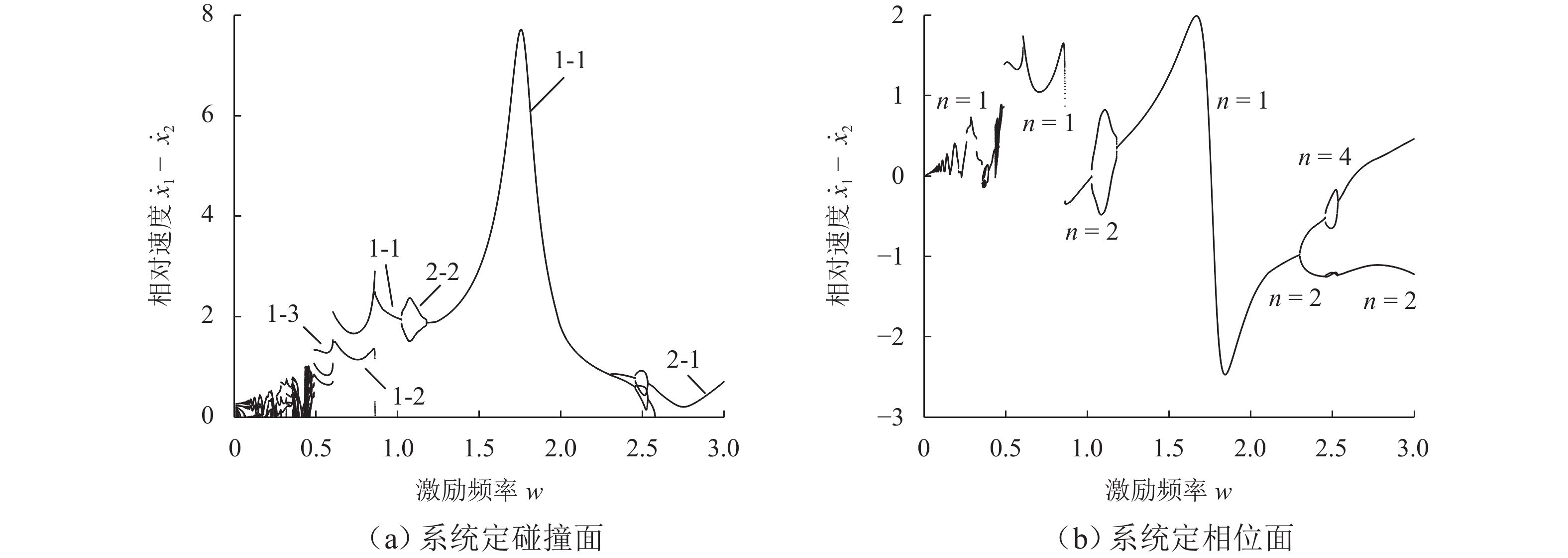
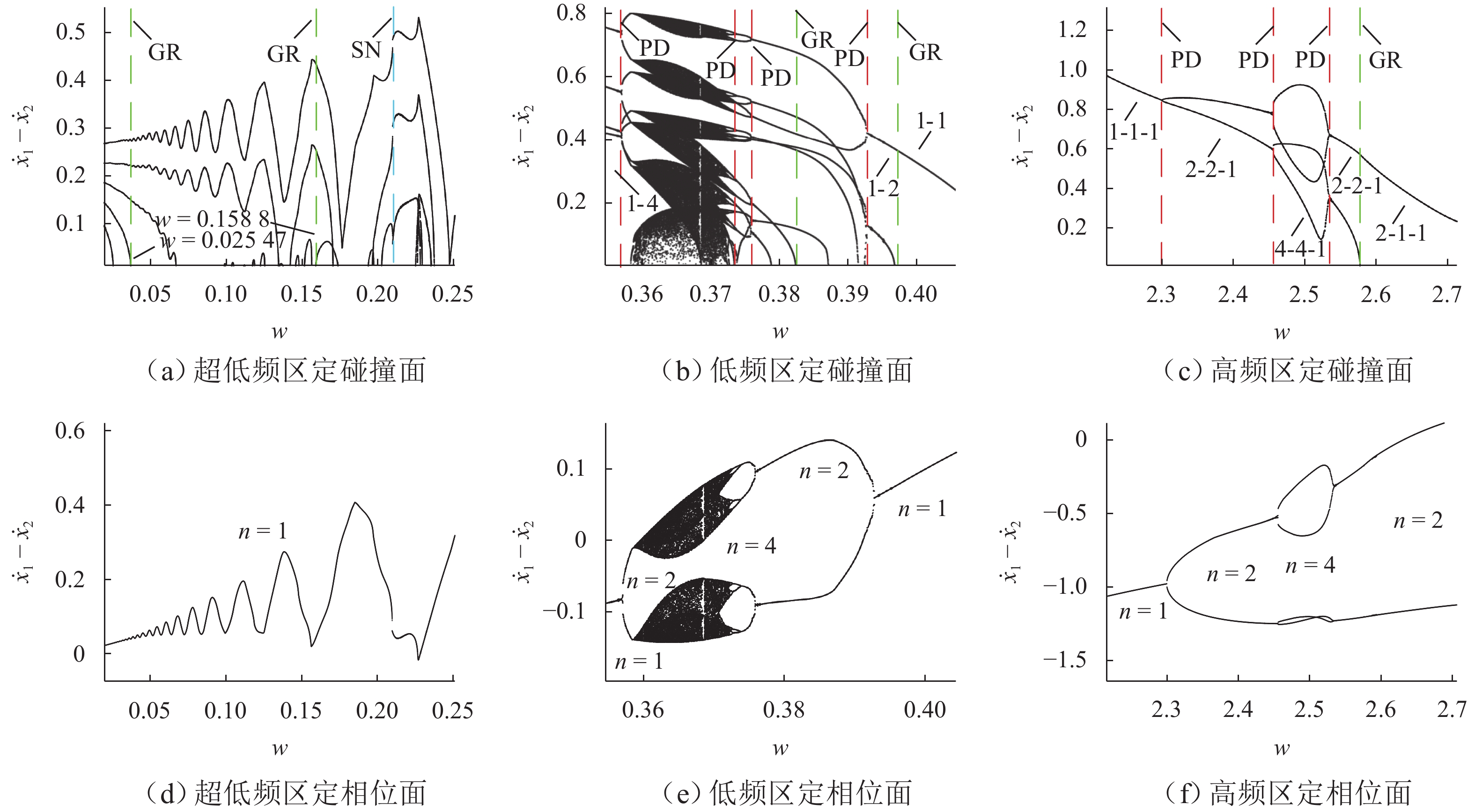
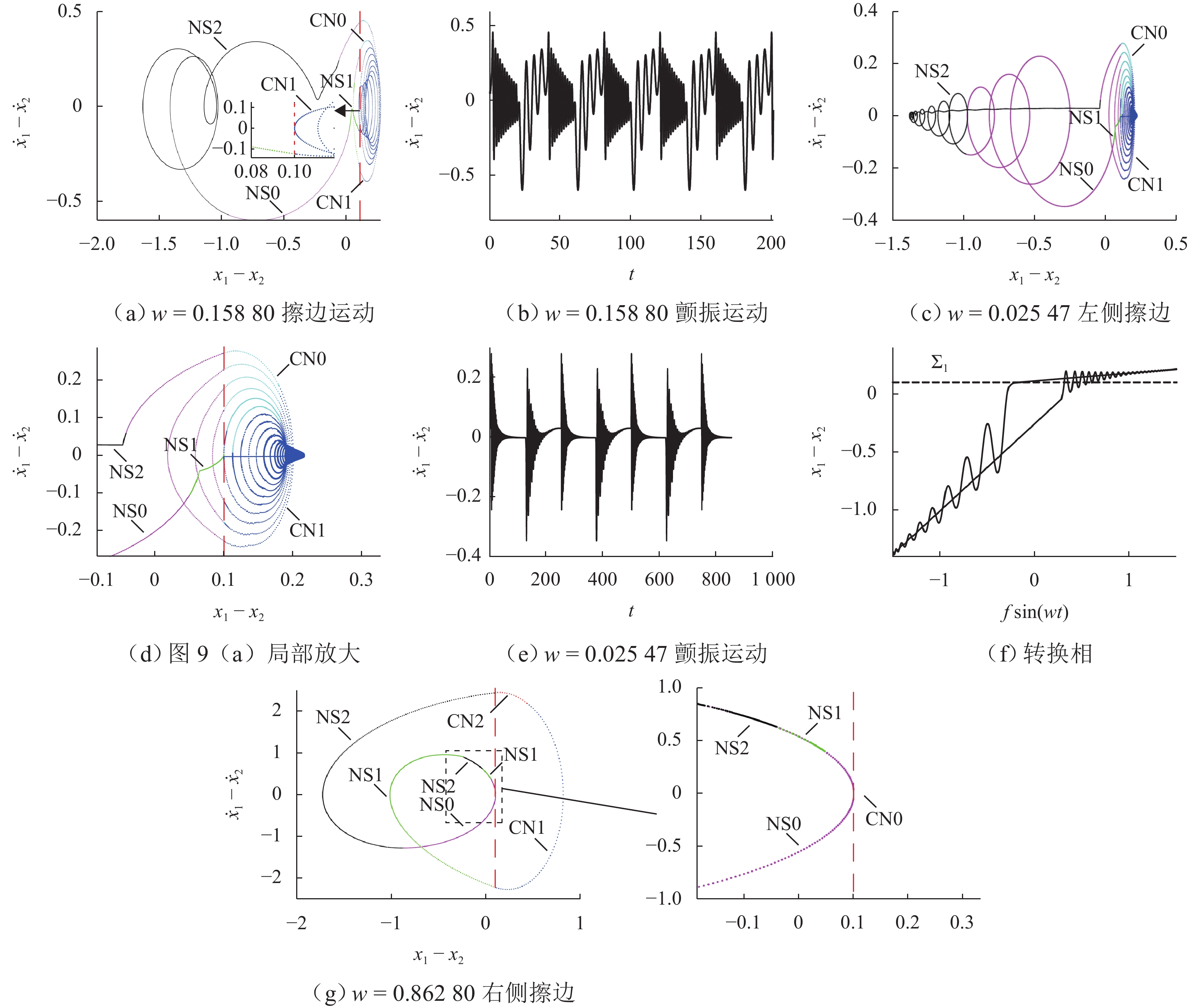
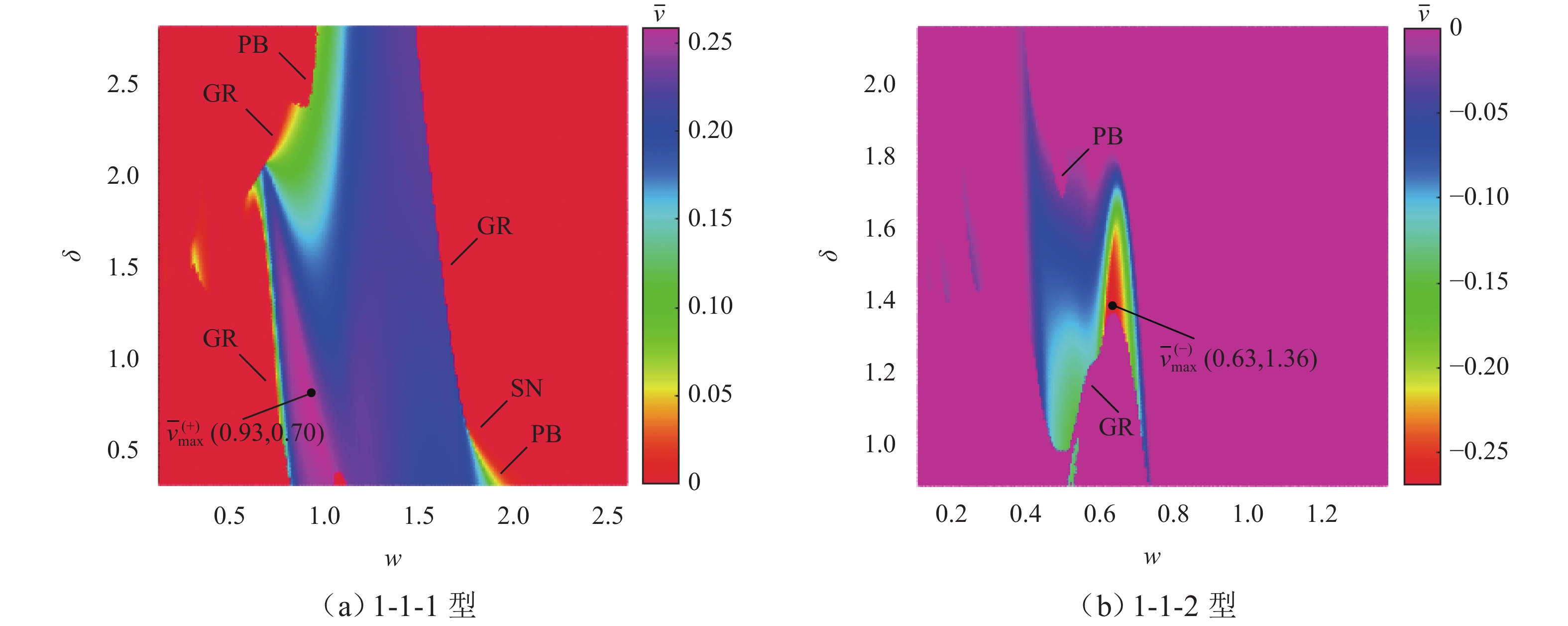
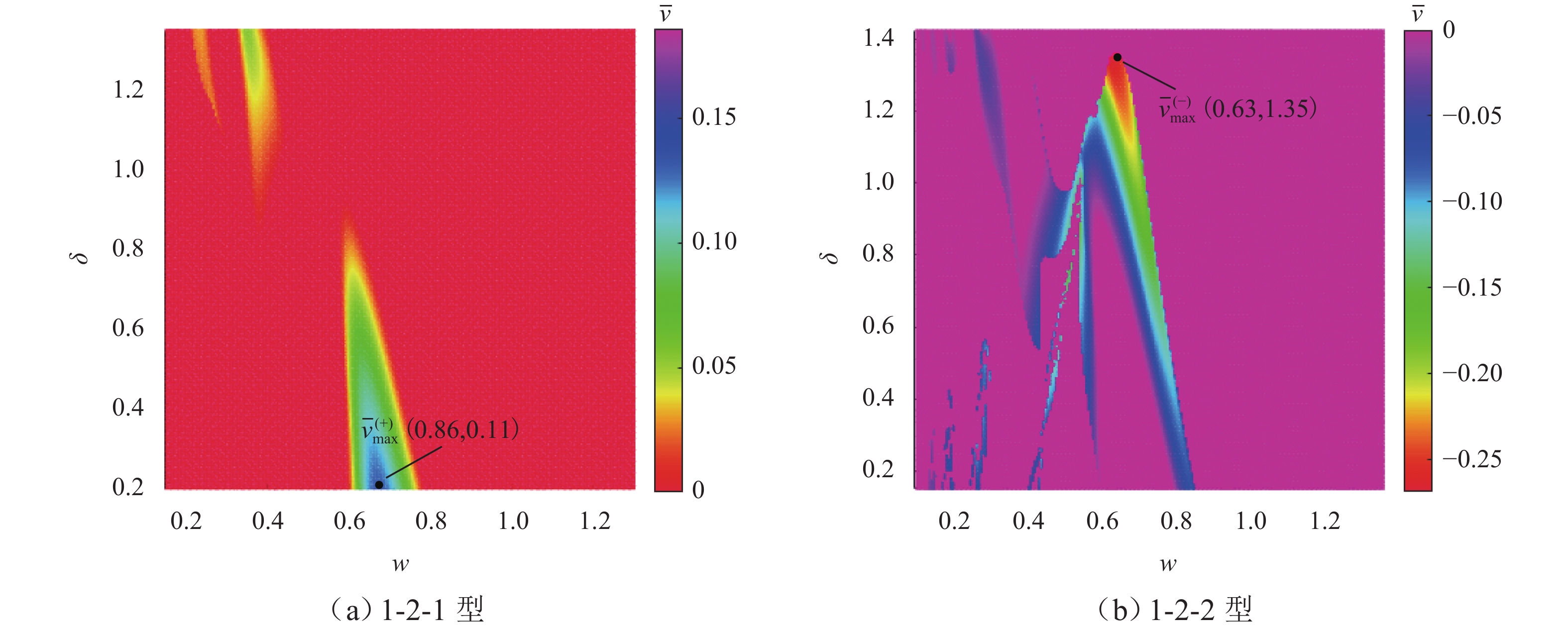
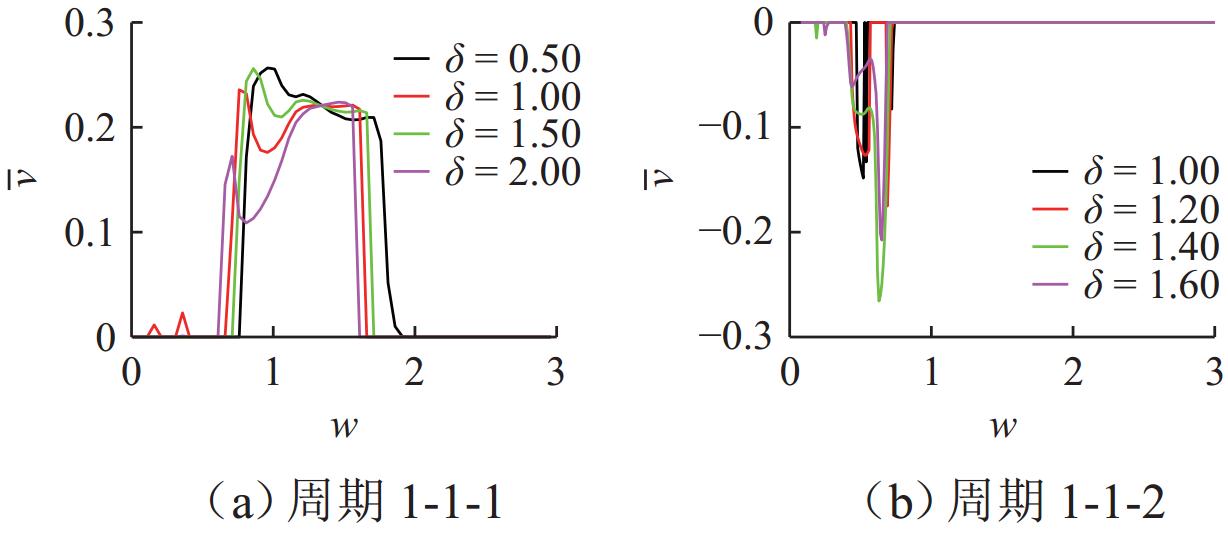
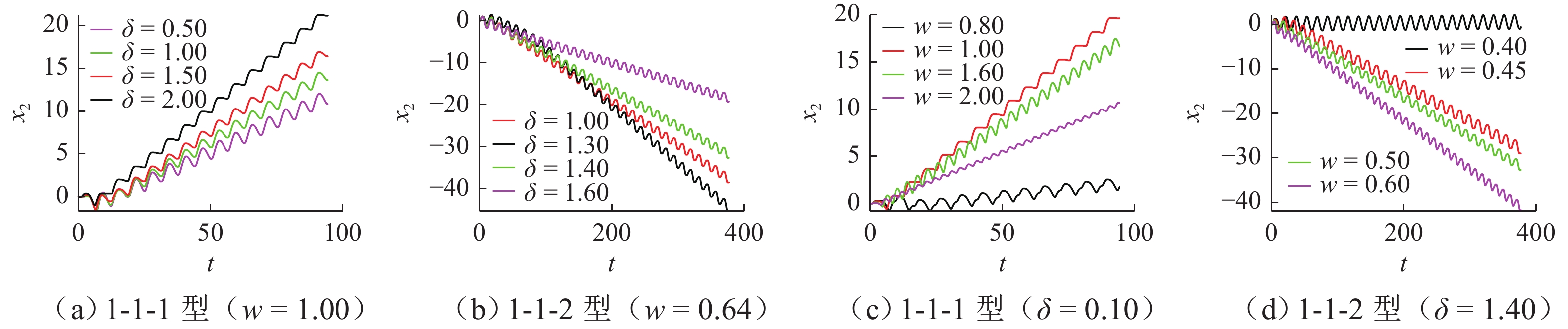
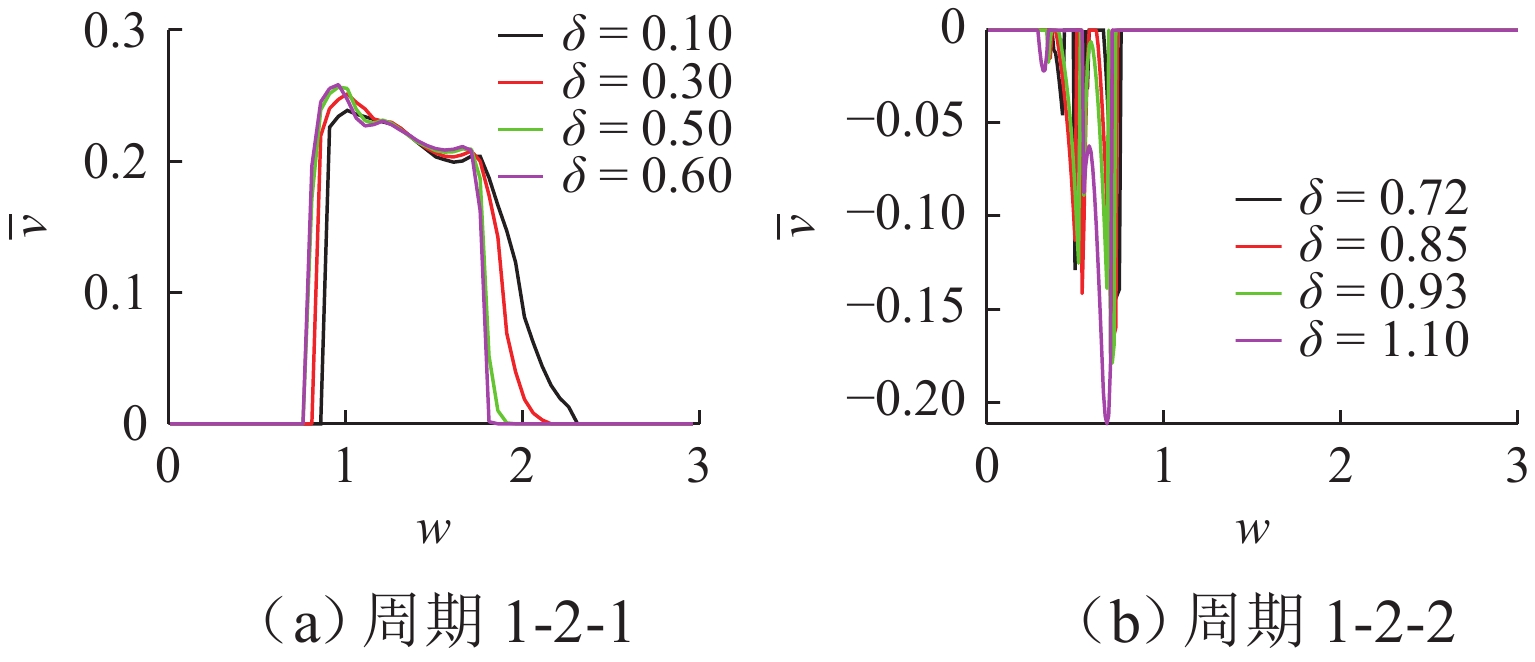
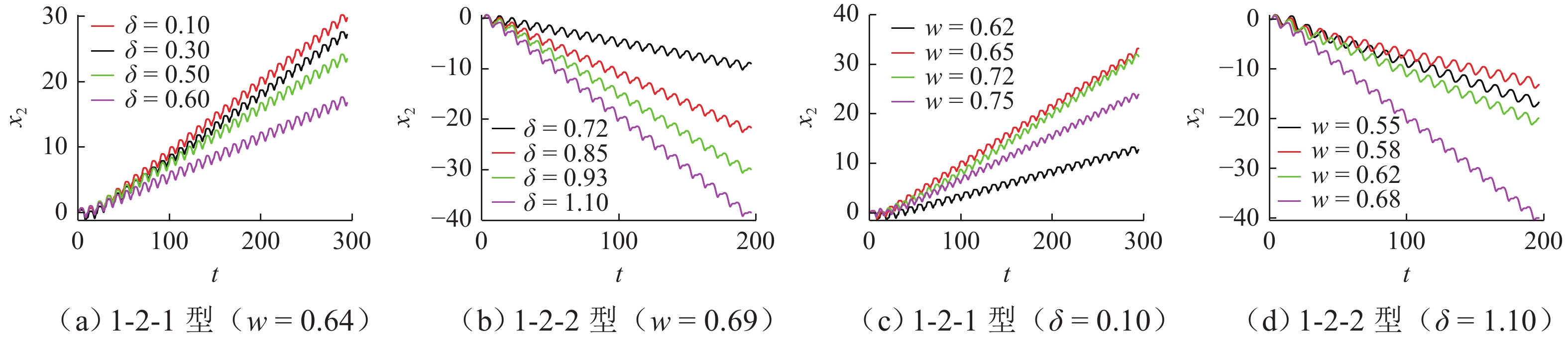
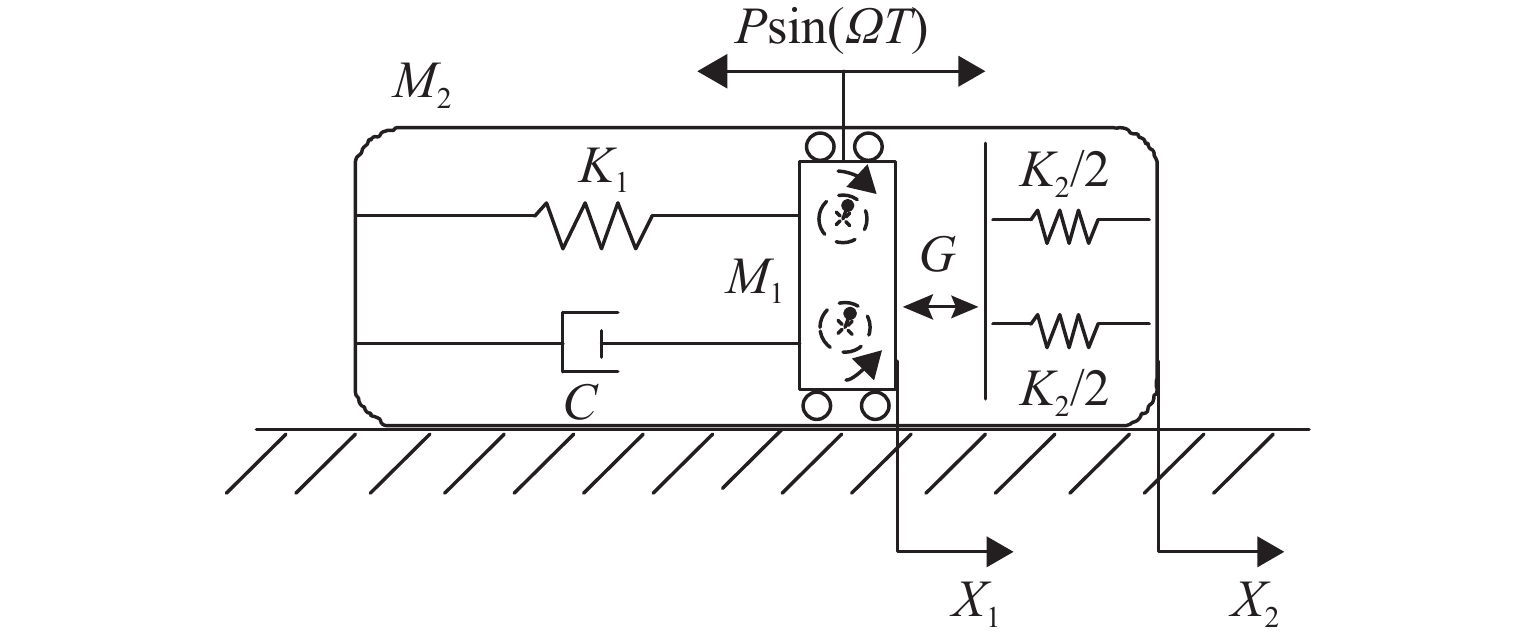
为研究碰撞振动系统的动力学演化规律和驱动性能，首先，考虑外部环境不连续力与内部非光滑碰撞，建立一类碰撞与黏滑振动驱动系统；其次，基于不连续动力系统的流转换理论与映射动力学理论，刻画系统相空间内的不连续边界和子区域映射关系，采用分段分析法描绘系统相空间运行轨迹；最后，通过数值协同仿真研究参数域内系统周期运动分布转迁机理和平均速度分布规律. 研究表明：在激励频率 、间隙双参数平面内，系统正反向最大平均驱动速度集中于主共振区，呈现周期1-1-1（或1-1-2）运动类型；结合参数域内系统驱动方向和驱动速度与系统参数的关联关系，可通过调控系统参数与外激励频率实现宽速驱动；低频小间隙区存在2种序列擦边分岔，一种在低频区随着激励频率减小，右侧擦边分岔诱导系统碰撞次数依次增加，另一种在超低频区围绕碰撞子空间内的平衡点衍生出序列相轨迹，泛延过程中出现左侧擦边分岔，系统呈现出簇发振荡的现象.
Abstract:To study the dynamic evolution laws and driving performance of collision vibration-driven systems, firstly, Considering the discontinuous resistance of the external environment and the internal non-smooth collision were considered, and a type of mobile system driven by collision and stick-slip vibration-driven system is was established. The evolution law of system dynamics and driving performance are two key issues in the study of vibration-driven system. This article first considers external environmental discontinuous forces and internal non-smooth collisions, and establishes a type of collision and stick-slip vibration-driven system. Secondly, based on the flow conversion theory and mapping dynamics theory of discontinuous dynamical systems, the mapping relationship between discontinuous boundaries and subregions in the phase space of the system is was characterized, and the segmented analysis method is was used to depict the motion trajectory of the system's system’s phase space operation. The segmented analysis method is used to describe the trajectory of the system in the phase space. Study the mechanism of periodic motion distribution transition and average velocity distribution in the parameter domain were studied through numerical collaborative simulation. Research has shown that in the two-parameter plane of excitation frequency w and gap δ, the maximum average driving velocityspeed of the system in the forward and reverse directions is concentrated in the main resonance region, exhibiting a period of 1-1-1 (or 1-1-2) motion type. By combining the correlation between the driving direction and velocityspeed of the system within the parameter domain and the system parameters, widely velocityspeed driving can be achieved by adjusting the system parameters and external excitation frequency. There are two types of sequence edge scraping bifurcations in the low-frequency small gap region. One is that in the low-frequency region, as the excitation frequency decreases, the right edge scraping bifurcation induces an increase in the number of collisions in the system. Another method is to derive sequence phase trajectories around equilibrium points in the collision subspace in the ultra-low frequency region. During the generalization process, there is a left edge scraping bifurcation, and the system exhibits a phenomenon of cluster oscillation.
-
图 3 碰撞与黏滑振动驱动系统映射关系
Figure 3. Mapping relationship between collision and stick-slip vibration-driven system
图 10 1-1最大平均驱动速度颜色编码像素
Figure 10. Color coded pixel map of maximum average driving velocity for 1-1 system
图 11 1-2型系统平均驱动速度颜色编码像素图
Figure 11. Color coded pixel map of average driving velocity for 1-2 system
图 12 周期1-1下$ w {\text{-}}v $分布
Figure 12. Distribution of$ w {\text{-}}v $under cycle 1-1
-
[1] 魏巍, 丁维高, 谢进. 带仿生躯干的被动行走机器人步态特性[J]. 西南交通大学学报, 2024, 59(2): 477-484.WEI Wei, DING Weigao, XIE Jin. Gait properties of passive walking robots with bionic torso[J]. Journal of Southwest Jiaotong University, 2024, 59(2): 477-484. [2] 窦汝桐, 于慎波, 孙凤, 等. 7自由度仿人机械臂工作空间求解的降密蒙特卡洛法[J]. 西南交通大学学报, 2023, 58(6): 1328-1338. doi: 10.3969/j.issn.0258-2724.20220777DOU Rutong, YU Shenbo, SUN Feng, et al. Density-reducing monte carlo method for 7 degrees of freedom humanoid robot arm workspace solution[J]. Journal of Southwest Jiaotong University, 2023, 58(6): 1328-1338. doi: 10.3969/j.issn.0258-2724.20220777 [3] 张敏, 徐鉴. 振动驱动移动系统平面避障运动分析[J]. 力学学报, 2017, 49(2): 397-409. doi: 10.6052/0459-1879-16-367ZHANG Min, XU Jian. Analysis on planar obstacle avoidance locomotion of vibration-driven system[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(2): 397-409. doi: 10.6052/0459-1879-16-367 [4] YIN S, YAN Y, PÁEZ CHÁVEZ J, et al. Bifurcation analysis of a vibro-impacting capsule robot in contact with a circular fold[J]. Physica D: Nonlinear Phenomena, 2022, 442: 133524.1-133524.18. [5] 郭瑞, 朱清东, 郭俞良, 等. 小内径管道检测用振动驱动机器人的设计与试验[J]. 动力学与控制学报, 2023, 21(1): 89-96.GUO Rui, ZHU Qingdong, GUO Yuliang, et al. Design and experiment of vibration driven robot for inspection of small inner diameter pipes[J]. Journal of Dynamics and Control, 2023, 21(1): 89-96. [6] BI Z H, ZHOU Q Y, FANG H B. A worm-snake-inspired metameric robot for multi-modal locomotion: design, modeling, and unified gait control[J]. International Journal of Mechanical Sciences, 2023, 254: 108436.1-108436.18. [7] PAVLOVSKAIA E, WIERCIGROCH M. Periodic solution finder for an impact oscillator with a drift[J]. Journal of Sound and Vibration, 2003, 267(4): 893-911. doi: 10.1016/S0022-460X(03)00193-7 [8] CHERNOUS’KO F L. Analysis and optimization of the motion of a body controlled by means of a movable internal mass[J]. Journal of Applied Mathematics and Mechanics, 2006, 70(6): 819-842. doi: 10.1016/j.jappmathmech.2007.01.003 [9] CHERNOUS’KO F L. The optimal periodic motions of a two-mass system in a resistant medium[J]. Journal of Applied Mathematics and Mechanics, 2008, 72(2): 116-125. doi: 10.1016/j.jappmathmech.2008.04.014 [10] LIU Y, WIERCIGROCH M, PAVLOVSKAIA E, et al. Modelling of a vibro-impact capsule system[J]. International Journal of Mechanical Sciences, 2013, 66: 2-11. doi: 10.1016/j.ijmecsci.2012.09.012 [11] DEN HARTOG J P. LXXIII. Forced vibrations with combined viscous and coulomb damping[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1930, 9(59): 801-817. doi: 10.1080/14786443008565051 [12] 李国芳, 俞力洋, 丁旺才, 等. 一类无足自驱动系统的运动特性分析[J]. 振动与冲击, 2020, 39(14): 9-16.LI Guofang, YU Liyang, DING Wangcai, et al. Motion characteristics analysis of a wheel-free self-driving system[J]. Journal of Vibration and Shock, 2020, 39(14): 9-16. [13] 王二虎, 丁旺才, 李国芳, 等. 小型电磁振动驱动器的设计与参数匹配分析[J]. 机械科学与技术, 2018, 37(7): 1022-1026.WANG Erhu, DING Wangcai, LI Guofang, et al. Designing and analyzing parameter matching of a small electromagnetic vibration-driving system[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(7): 1022-1026. [14] LIU Y, PAVLOVSKAIA E, WIERCIGROCH M, et al. Forward and backward motion control of a vibro-impact capsule system[J]. International Journal of Non-linear Mechanics, 2015, 70: 30-46. doi: 10.1016/j.ijnonlinmec.2014.10.009 [15] TIAN J Y, AFEBU K O, WANG Z P, et al. Dynamic analysis of a soft capsule robot self-propelling in the small intestine via finite element method[J]. Nonlinear Dynamics, 2023, 111(11): 9777-9798. doi: 10.1007/s11071-023-08376-z [16] 薛珊. 一类碰撞振动系统中的不连续动力学行为分析[D]. 济南: 山东师范大学, 2018. [17] GUO B Y, LIU Y. Three-dimensional map for a piecewise-linear capsule system with bidirectional drifts[J]. Physica D: Nonlinear Phenomena, 2019, 399: 95-107. doi: 10.1016/j.physd.2019.04.008 [18] 张正娣, 彭淼, 曲子芳, 等. 频域两尺度下非光滑Duffing系统的簇发振荡及其机理分析[J]. 中国科学: 物理学 力学 天文学, 2018, 48(11): 22-33.ZHANG Zhengdi, PENG Miao, QU Zifang, et al. Bursting oscillations and mechanism analysis in a non-smooth Duffing system with frequency domain of two time scales[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2018, 48(11): 22-33. [19] 马新东, 姜文安, 张晓芳, 等. 一类三维非线性系统的复杂簇发振荡行为及其机理[J]. 力学学报, 2020, 52(6): 1789-1799. doi: 10.6052/0459-1879-20-231MA Xindong, JIANG Wenan, ZHANG Xiaofang, et al. Complicated bursting behaviors as well as the mechanism of a three dimensional nonlinear system[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(6): 1789-1799. doi: 10.6052/0459-1879-20-231 [20] SHAW S W, HOLMES P J. A periodically forced piecewise linear oscillator[J]. Journal of Sound and Vibration, 1983, 90(1): 129-155. doi: 10.1016/0022-460X(83)90407-8 [21] 吕小红, 罗冠炜. 冲击渐进振动系统的双参数分岔分析[J]. 振动与冲击, 2019, 38(7): 50-56, 76.LV Xiaohong, LUO Guanwei. Two-parameter bifurcation analysis for an impact progressive vibration system[J]. Journal of Vibration and Shock, 2019, 38(7): 50-56, 76. [22] 吴鑫, 李高磊, 乐源. 单自由度碰撞振动系统的奇异非混沌动力学和多稳态共存[J]. 振动与冲击, 2022, 41(2): 45-52, 86.WU Xin, LI Gaolei, LE Yuan. Strange nonchaotic dynamics and multistable coexistence phenomena of a single-degree-of-freedom vibro-impact system[J]. Journal of Vibration and Shock, 2022, 41(2): 45-52, 86. [23] 李得洋, 丁旺才, 卫晓娟, 等. 单自由度含干摩擦碰振系统相邻周期运动转迁规律分析[J]. 振动与冲击, 2020, 39(22): 50-59.LI Deyang, DING Wangcai, WEI Xiaojuan, et al. Analysis on the transition of adjacent periodic motion in a 1DOF vibro-impact system with dry friction[J]. Journal of Vibration and Shock, 2020, 39(22): 50-59. [24] 丁杰, 王超, 丁旺才, 等. 双侧不同约束碰振系统的周期运动转迁规律[J]. 华中科技大学学报(自然科学版), 2021, 49(1): 6-11.DING Jie, WANG Chao, DING Wangcai, et al. The transition law of periodic motions of the vibro-impact system with different constraints on both sides[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2021, 49(1): 6-11. [25] ZHAO H X, SHNEIDERMAN B. Colour-coded pixel-based highly interactive Web mapping for georeferenced data exploration[J]. International Journal of Geographical Information Science, 2005, 19(4): 413-428. doi: 10.1080/1365881051233125120 -
下载:
点击查看大图
计量
- 文章访问数: 89
- HTML全文浏览量: 68
- PDF下载量: 25
- 被引次数: 0