采用高强钢棒的混凝土短肢剪力墙抗震性能

袁维光; 赵华; 马兰; 肖强; 魏丞瑾

doi:10.3969/j.issn.0258-2724.20230376

采用高强钢棒的混凝土短肢剪力墙抗震性能

doi: 10.3969/j.issn.0258-2724.20230376

袁维光^{1, 3,},
赵华^{1, 3, ,},
马兰²,
肖强²,
魏丞瑾²

1.
成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川成都 610059
2.
成都理工大学环境与土木工程学院，四川成都 610059
3.
自然资源部丘陵山地质灾害防治重点实验室，福州 350002

基金项目: 西藏自治区自然资源厅项目（藏财采20200890-1）

详细信息

作者简介:
袁维光（1986—），男，讲师，博士，研究方向结构工程抗震，E-mail：906579475@qq.com

通讯作者:
赵华（1976—），女，副教授，博士，研究方向结构工程抗震，E-mail：zhaohua@cdut.edu.cn

计量
- 文章访问数: 8
- HTML全文浏览量: 7
- PDF下载量: 0
- 被引次数: 0
出版历程
- 收稿日期: 2023-08-09
- 修回日期: 2024-01-08
- 网络出版日期: 2025-07-05

Investigation on Seismic Performance of Concrete Short-Leg Shear Wall with High-Strength Steel Bars

YUAN Weiguang^{1, 3
,},
ZHAO Hua^{1, 3
, ,},
MA Lan²,
XIAO Qiang²,
WEI Chengjin²

1.
State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology, Chengdu 610059, China
2.
College of Environment and Civil Engineering, Chengdu University of Technology, Chengdu 610059, China
3.
Key Laboratory of Geohazard Prevention of Hilly Mountains, Ministry of Natural Resources of China, Fuzhou 350002, China

摘要

摘要:
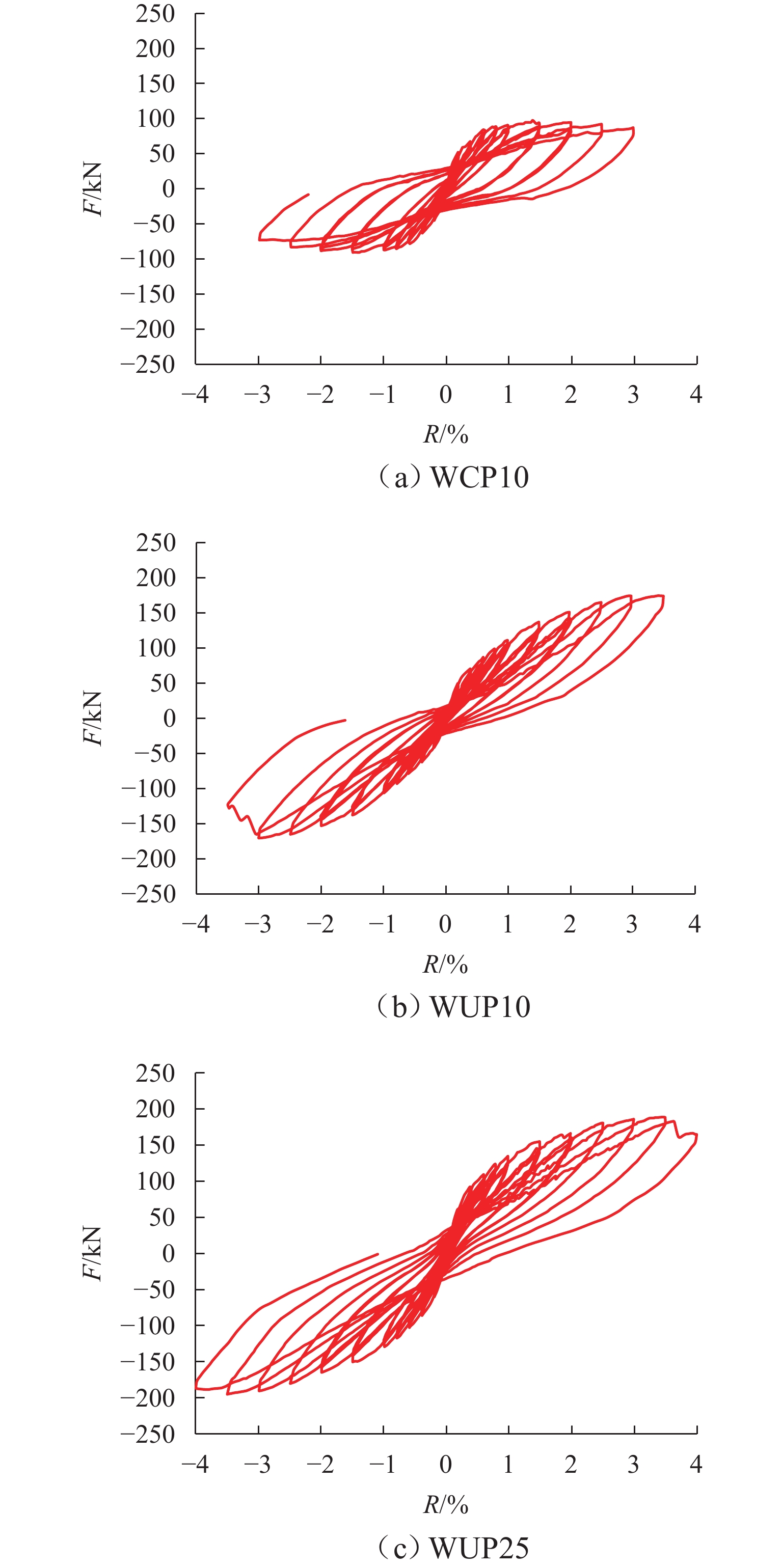
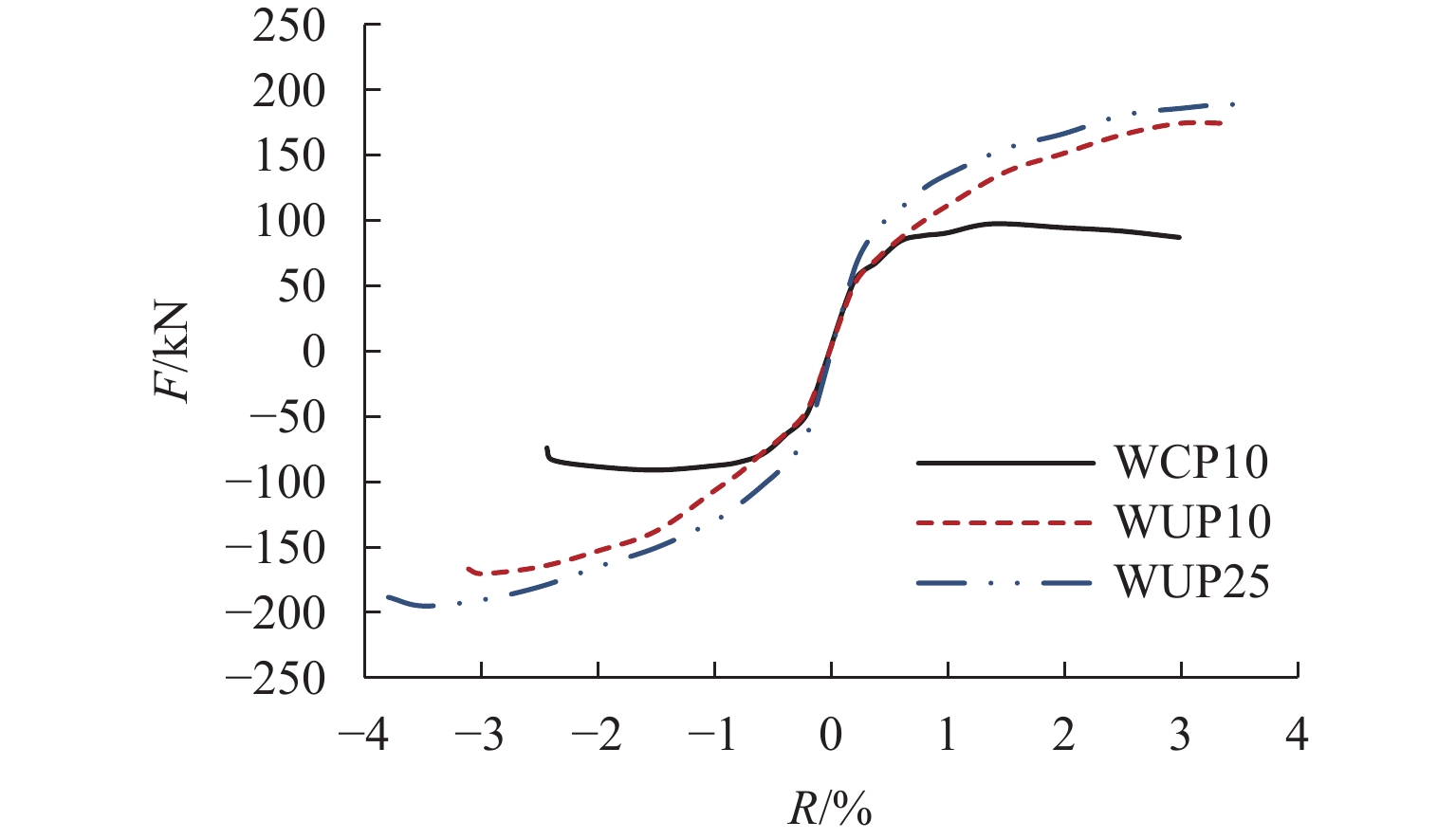
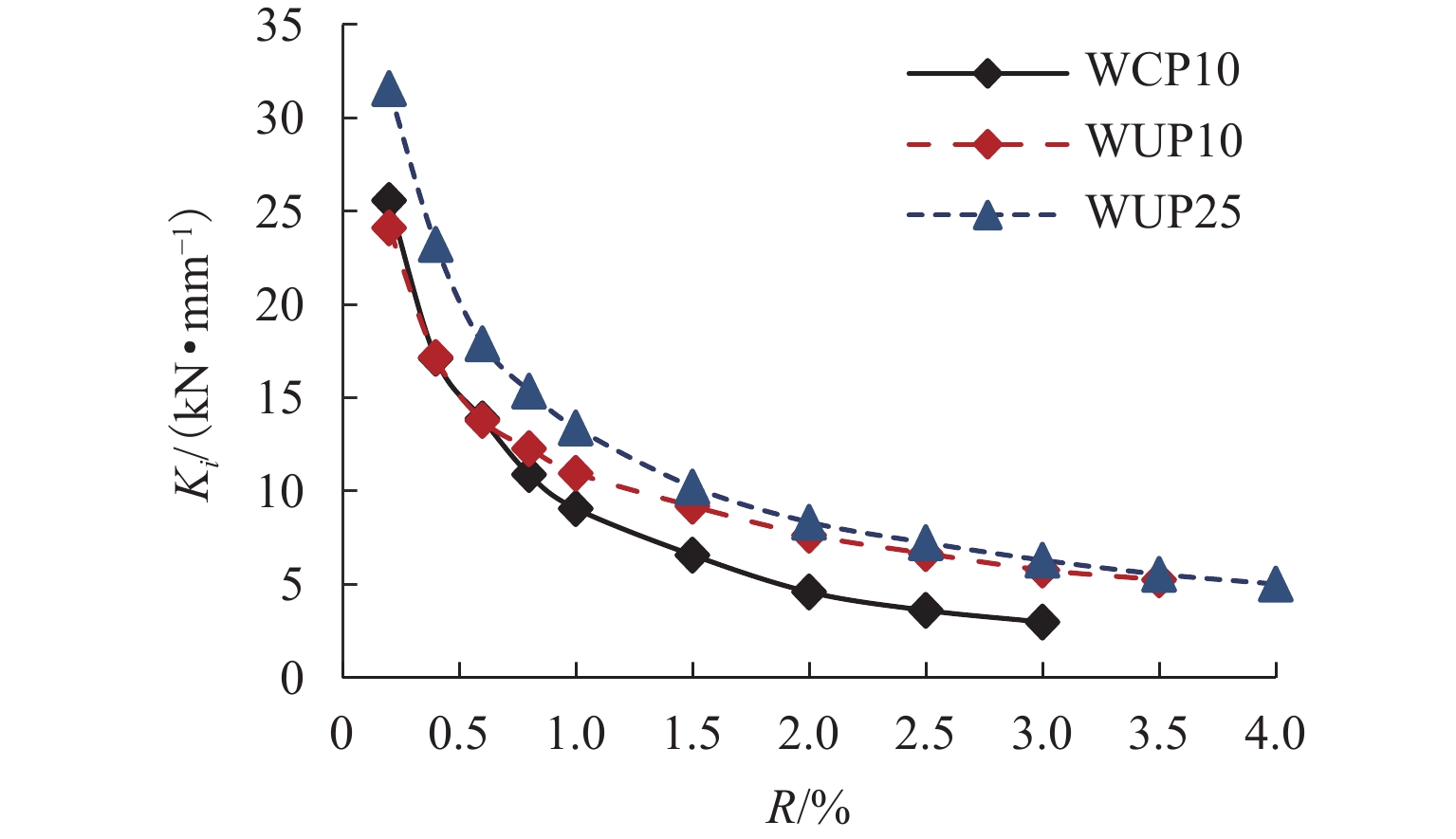
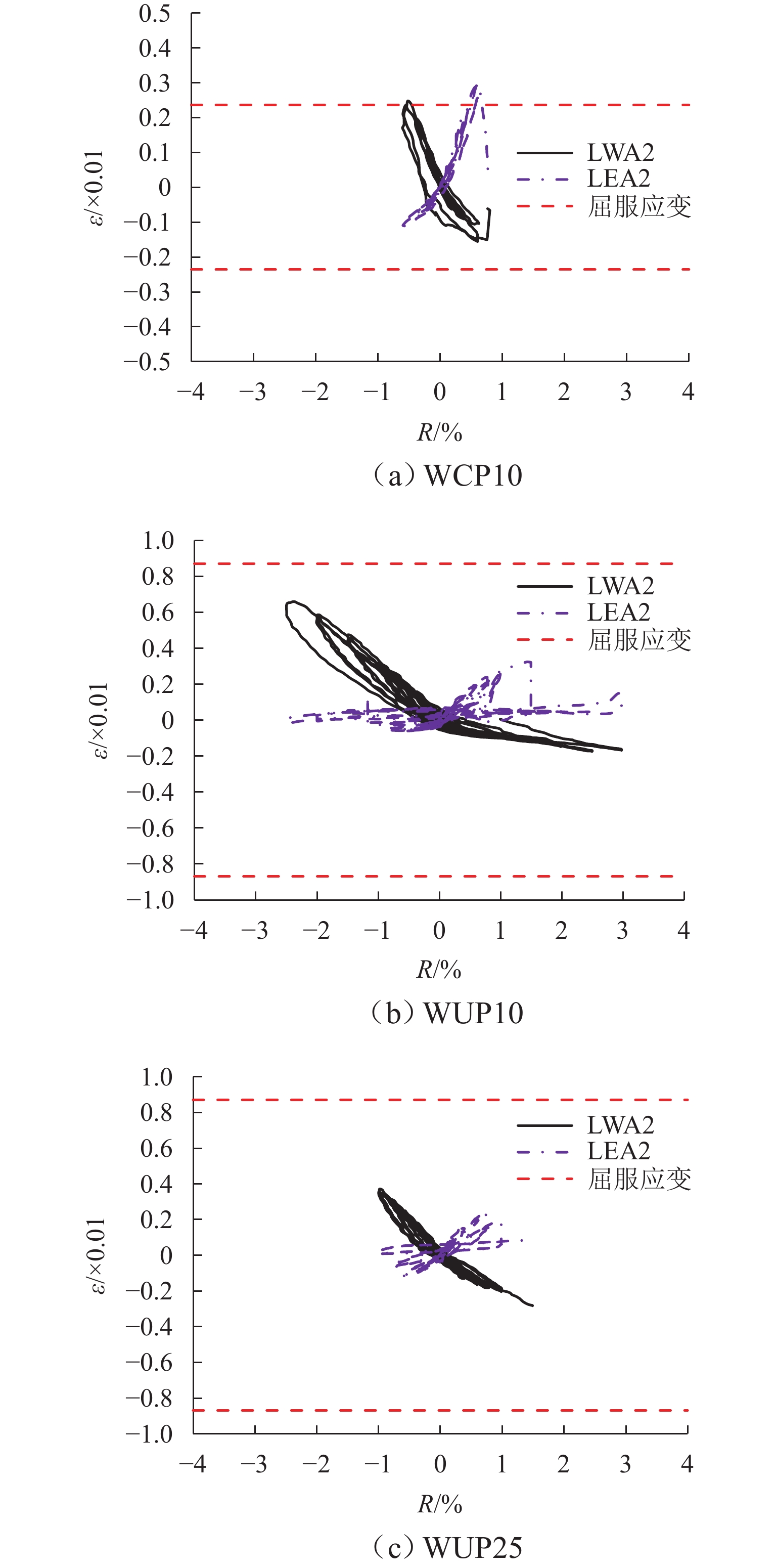
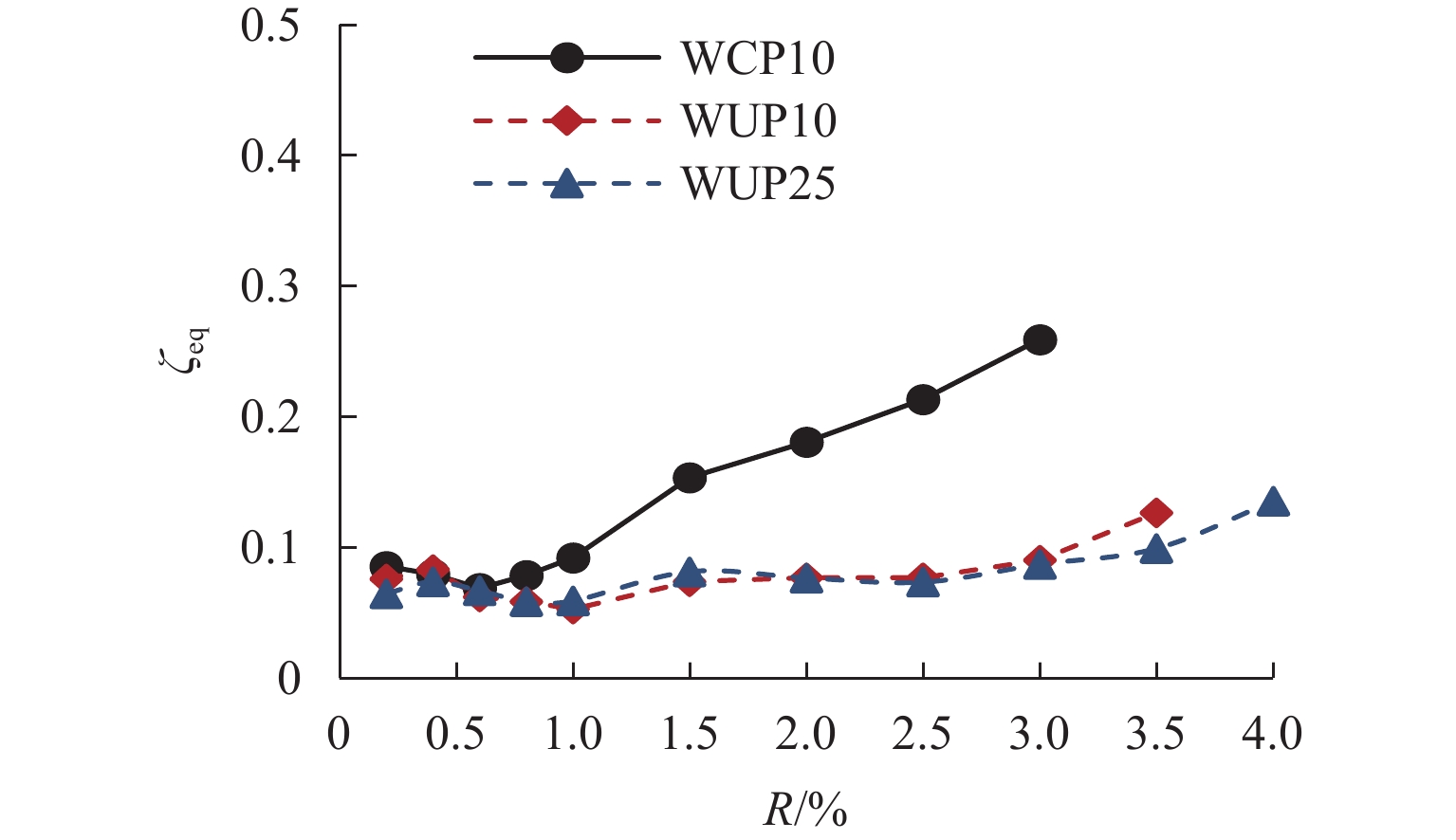
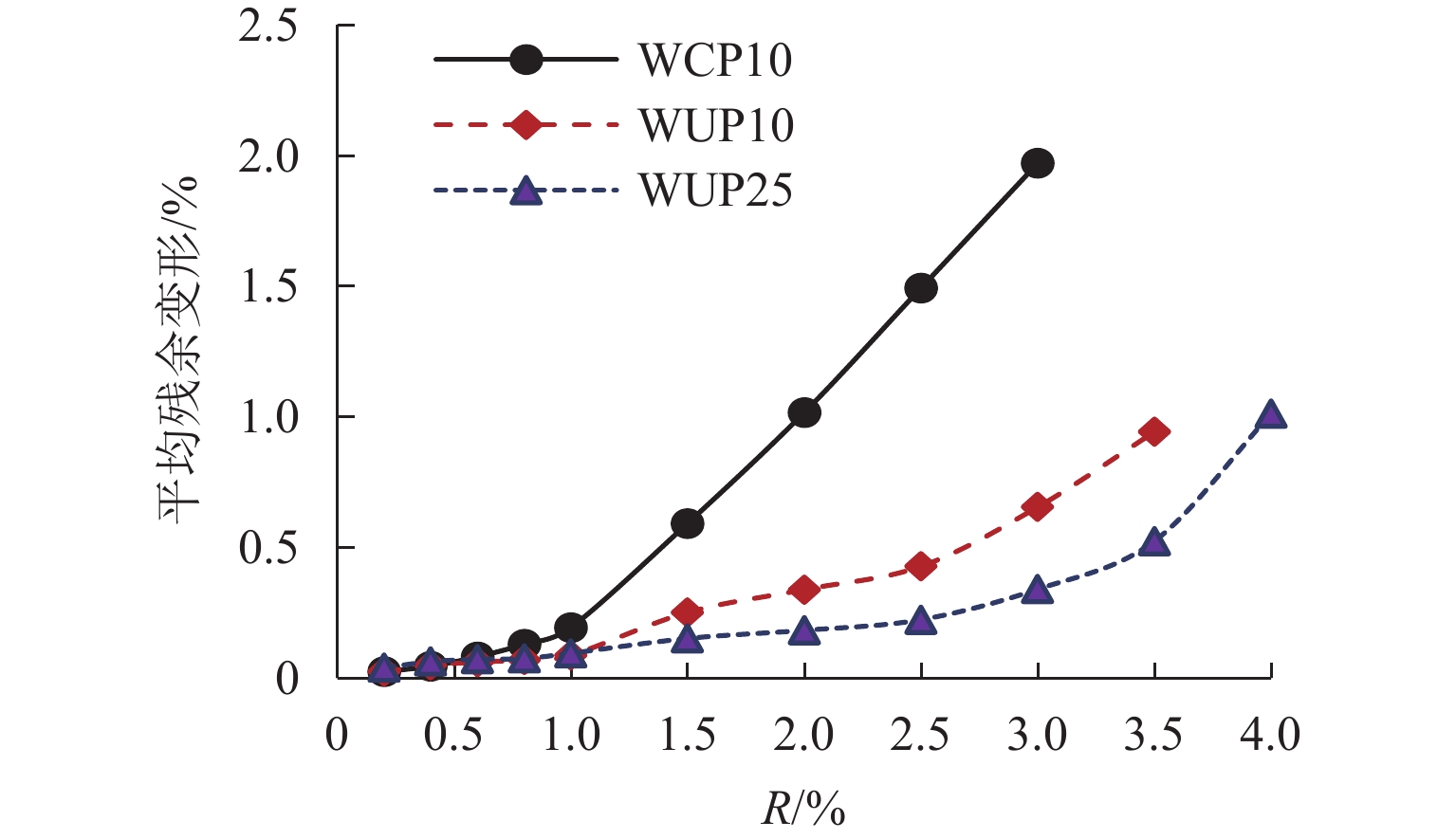
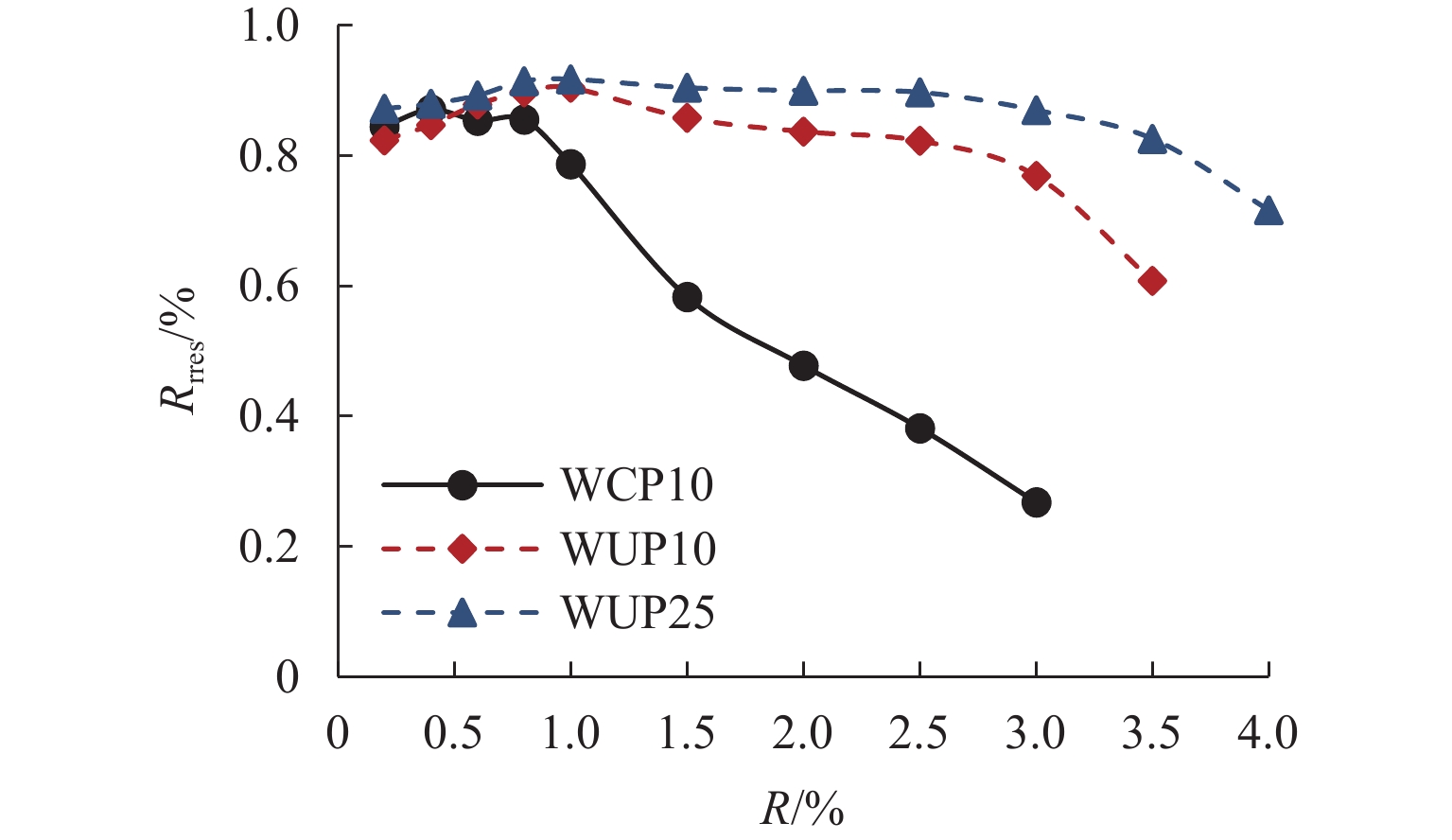
为满足震后建筑结构快速修复的需求，提出一种以高强钢棒（HG钢棒）作为暗柱纵筋的短肢剪力墙，即采用高强钢棒的混凝土短肢剪力墙，预制3个1/3缩尺的钢筋混凝土短肢剪力墙构件，通过拟静力试验，分析暗柱纵筋类型和轴压比对试件抗震性能及自复位能力的影响. 试验结果表明，与普通混凝土短肢剪力墙相比，在大变形时，高强钢棒-混凝土短肢剪力墙构件表现出良好的位移-硬化效应和自复位性，滞回曲线整体呈S形，极限承载力提高83%；其残余变形较小，在位移角3.0%时，残余变形为0.65%；在高轴压比（限值）作用下，高强钢棒-混凝土短肢剪力墙构件的极限承载能力提高11%，在位移角3.5%时，残余变形为0.50%.
- 高强钢棒 /
- 短肢剪力墙 /
- 轴压比 /
- 抗震性能 /
- 自复位能力
Abstract:
To meet the demand for rapid repair of building structures after earthquakes, a short-leg shear wall with high-strength steel bars (HG bars) as longitudinal reinforcement of the concealed column, namely short-leg shear wall with high-strength steel bars was proposed. Three prefabricated 1/3-scale reinforced concrete short-leg shear wall components were constructed, and quasi-static tests were conducted to analyze the effects of longitudinal reinforcement types of the concealed column and axial compression ratio on the seismic performance and self-restoring capability of the components. The test results show that compared to the ordinary concrete short-leg shear walls, the short-leg shear wall components with HG steel bars demonstrate a good displacement-hardening effect and self-restoring capability under large deformations and develop an overall S-shaped hysteresis curve and an 83% increase in the ultimate bearing capacity. While the residual deformation is relatively small, a residual deformation of 0.65% occurs at a displacement angle of 3.0%. In addition, under the high axial compression ratio (limit value), the ultimate bearing capacity of short-leg shear wall components with HG steel bars increases by 11%, and the residual deformation is 0.50% at a displacement angle of 3.5%.
- high-strength steel bar /
- short-leg shear wall /
- axial compression ratio /
- seismic performance /
- self-restoring ability

HTML全文

图 1 构件尺寸及配筋

Figure 1. Component dimensions and reinforcement

下载: 全尺寸图片幻灯片

图 2 测量装置布置

Figure 2. Layout of measuring device

下载: 全尺寸图片幻灯片

图 3 加载装置

Figure 3. Loading device

下载: 全尺寸图片幻灯片

图 4 加载制度

Figure 4. Loading system

下载: 全尺寸图片幻灯片

图 5 构件最终破坏形态及裂缝

Figure 5. Final failure pattern and fracture of components

下载: 全尺寸图片幻灯片

图 6 荷载-位移角滞回曲线

Figure 6. Load–displacement hysteresis curves

下载: 全尺寸图片幻灯片

图 7 骨架曲线

Figure 7. Skeleton curves

下载: 全尺寸图片幻灯片

图 8 刚度退化曲线

Figure 8. Stiffness degradation curves

下载: 全尺寸图片幻灯片

图 9 纵筋应变

Figure 9. Longitudinal reinforcement strain

下载: 全尺寸图片幻灯片

图 10 等效黏滞阻尼系数

Figure 10. Equivalent viscous damping coefficient

下载: 全尺寸图片幻灯片

图 11 残余变形

Figure 11. Residual deformation

下载: 全尺寸图片幻灯片

图 12 相对残余变形

Figure 12. Relative residual deformation

下载: 全尺寸图片幻灯片

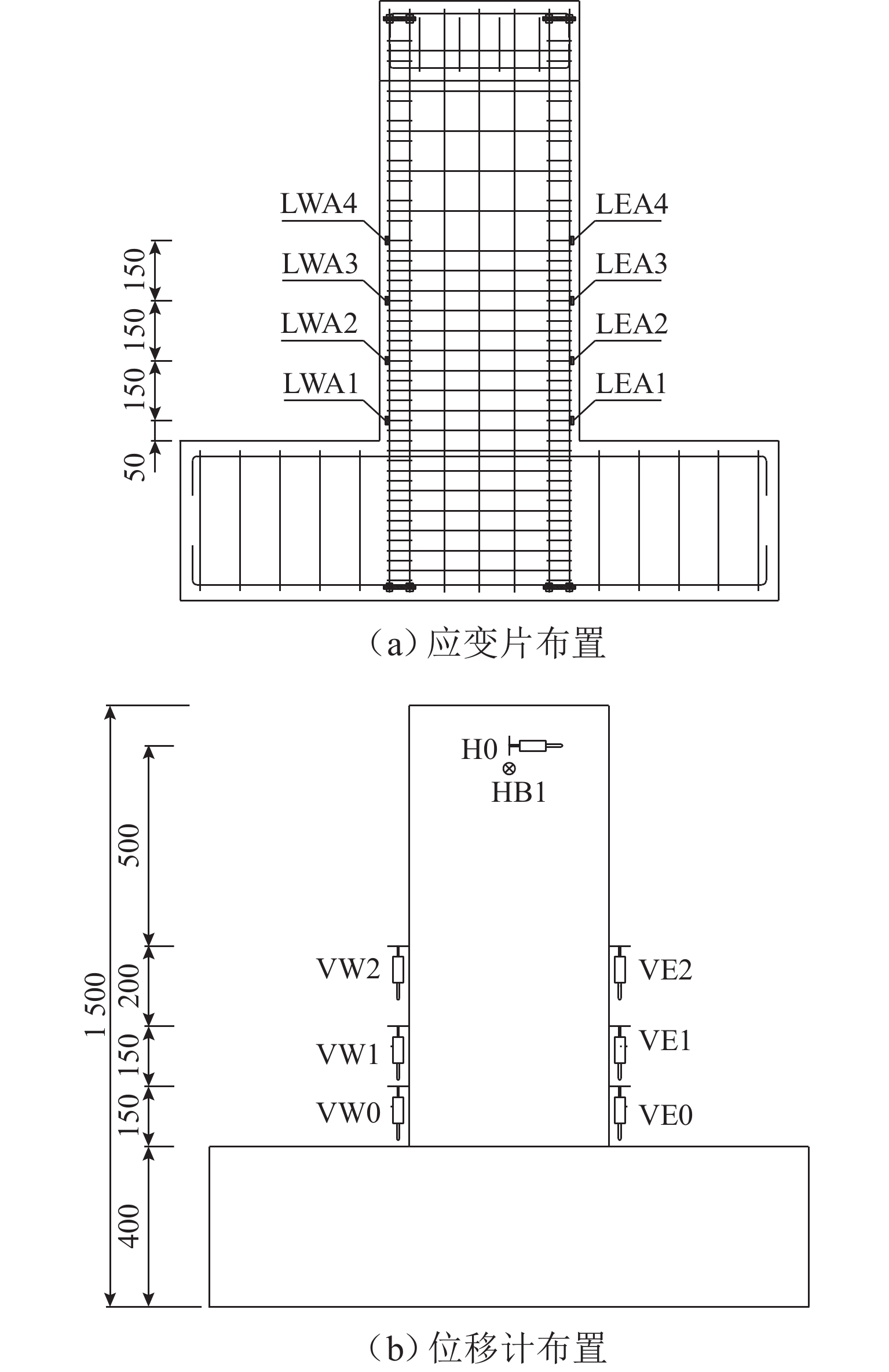
表 1 构件基本参数

Table 1. Basic parameters of components

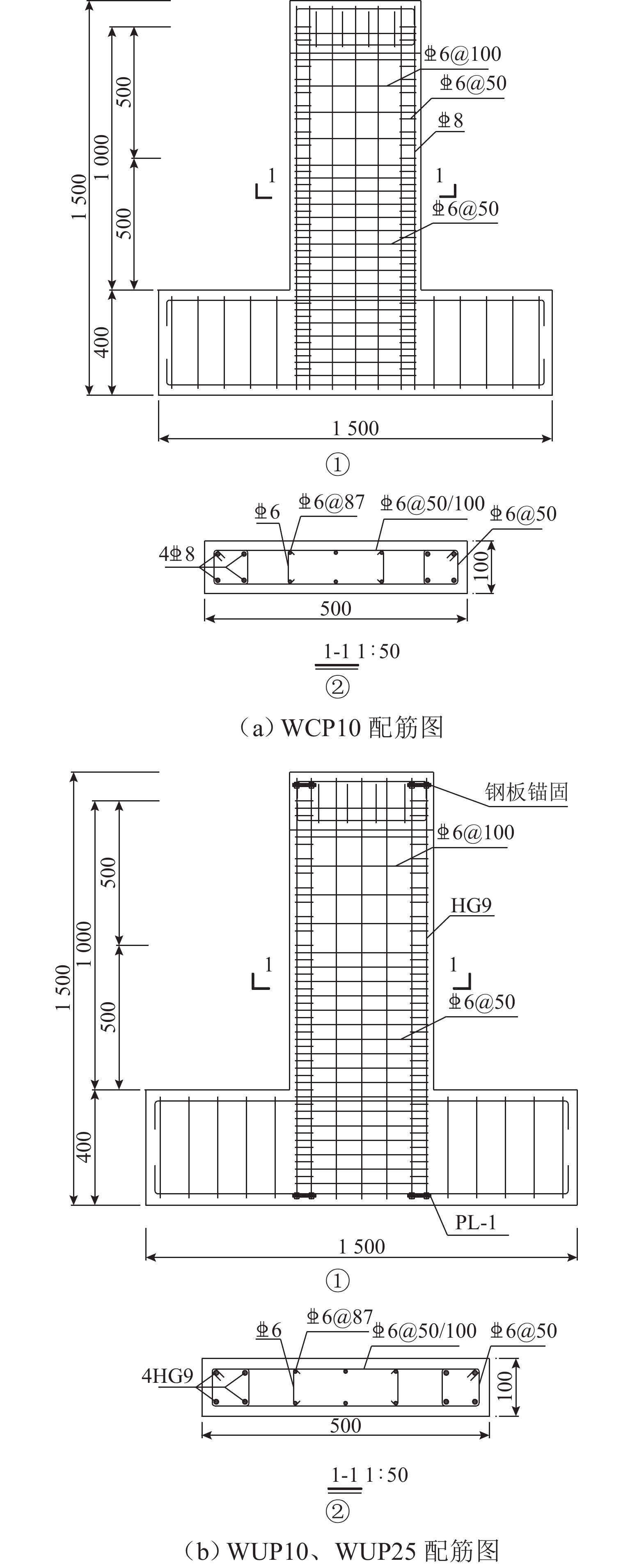
试件编号	宽厚比	剪跨比	轴压比	纵筋配筋率/%	暗柱纵筋配筋率/%	横筋配筋率/%
WCP10	5	2	0.10	0.65 （6@87）	2.01 （48）	1.13 （6@50/ 100）
WUP10			0.10		2.54 （4HG9）
WUP25			0.25		2.54 （4HG9）
注：4HG9表示4根直径为9的高强钢棒，48表示4根直径为8的HRB400的钢筋.

下载: 导出CSV

表 2 钢材的力学性能

Table 2. Mechanical properties of steel

材料类型	屈服强度/MPa	屈服应变/%	极限强度/MPa	弹性模量/GPa
HG9	1386.00	0.87	1437.84	206
8	383.85	0.23	444.92	208

下载: 导出CSV

表 3 混凝土材料性能

Table 3. Properties of concrete materials

名称	强度等级	立方体抗压强度/MPa	轴心抗压强度/MPa	弹性模量/GPa
取值	C40	44.36	35.31	3.46

下载: 导出CSV

参考文献(22)

[1]	陈炜. 高层结构设计中短肢剪力墙的运用[J]. 工程建设与设计,2023(4): 19-21. CHEN Wei. Application of short limb shear walls in the design of high-rise structures[J]. Construction & Design for Engineering, 2023(4): 19-21.
[2]	张智吉. 高强钢筋高强混凝土短肢剪力墙抗震性能研究[D]. 昆明:昆明理工大学,2022.
[3]	吴金源. 短肢剪力墙在民用建筑结构设计中的运用分析[J]. 新型工业化,2022,12(2): 70-73. WU Jinyuan. Application analysis of short-leg shear wall in civil building structure design[J]. The Journal of New Industrialization, 2022, 12(2): 70-73.
[4]	袁维光. 可恢复功能混凝土剪力墙的抗震性能与评估方法[D]. 成都:西南交通大学,2019.
[5]	赵军,袁维光,孙玉平,等. 钢绞线-钢筋混凝土剪力墙抗震性能试验研究[J]. 建筑结构学报,2020,41(9): 68-76. ZHAO Jun, YUAN Weiguang, SUN Yuping, et al. Experimental study on seismic behavior of shear wall reinforced by steel strands and steel bars[J]. Journal of Building Structures, 2020, 41(9): 68-76.
[6]	肖水晶,徐龙河,卢啸. 具有复位功能的钢筋混凝土剪力墙设计与性能研究[J]. 工程力学,2018,35(8): 130-137. doi: 10.6052/j.issn.1000-4750.2017.04.0296 XIAO Shuijing, XU Longhe, LU Xiao. Design and behavior study on reinforced concrete shear walls with self-centering capability[J]. Engineering Mechanics, 2018, 35(8): 130-137. doi: 10.6052/j.issn.1000-4750.2017.04.0296
[7]	王威,任英子,苏三庆,等. 高层剪力墙抗震理论发展:从高强高刚到震后可恢复设计[J]. 西安建筑科技大学学报(自然科学版),2019,51(4): 493-502. WANG Wei, REN Yingzi, SU Sanqing, et al. Seismic theory development of shear walls in tall buildings: from high strength and high rigidity to resilient design after earthquake[J]. Journal of Xi’an University of Architecture & Technology (Natural Science Edition), 2019, 51(4): 493-502.
[8]	邱灿星,杜修力. 自复位结构的研究进展和应用现状[J]. 土木工程学报,2021,54(11): 11-26. QIU Canxing, DU Xiuli. A state-of-the-art review on the research and application of self-centering structures[J]. China Civil Engineering Journal, 2021, 54(11): 11-26.
[9]	KURAMA Y, SAUSE R, PESSIKI S, et al. Lateral load behavior and seismic design of unbonded post-tensioned precast concrete walls[J]. Journal of Structural Engineering, 1999, 125(4): 419-428.
[10]	DOLCE M, CARDONE D, MARNETTO R. Implementation and testing of passive control devices based on shape memory alloys[J]. Earthquake Engineering & Structural Dynamics, 2000, 29(7): 945-968.
[11]	SATYARNO I. Concrete columns incorporating mixed ultra high and normal strength longitudinal reinforcement[D]. Christchurch: University of Canterbury, 1993.
[12]	PANDEY G R, MUTSUYOSHI H. Seismic performance of reinforced concrete piers with bond-controlled reinforcements[J]. ACI Structural Journal, 2005, 102(2): 295-304.
[13]	SUN Y, TAKEUCHI T, FUNATO Y, et al. Earthquake-resisting properties and evaluation of high-performance concrete columns with low residual deformation[C]// 15th World Conference on Earthquake Engineering. Lisbon: 2021: 24-30.
[14]	船戸佑樹,孫玉平,竹内崇,等. スパイラル溝を有する超高強度鉄筋の付着特性のモデル化と柱部材の履歴解析への応用[J]. コンクリート工学年次論文集,2012(3): 157-162. FUNATO Y, SUN Y, TAKEUCHI T, et al. Modeling of bonding properties of ultra-high strength reinforcement with spiral ribs and its application to historical analysis of column members[J]. Proceedings of Concrete Engineering Annual Meeting, 2012(3): 157-162.
[15]	細居清剛,市来隆志,中塚佶. PC鋼より線とグラウトとの付着特性に関する研究[J]. プレストレストコンクリートの発展に関するシンポジウム論文集,2003,12:77-80. HOSOI K, ICHIKI T, NAKATSUKA T. Study on bonding properties between PC steel strand and grout[J]. Proceedings of Symposium on the Development of Prestressed Concrete, 2003, 12: 77-80.
[16]	刘志华. 采用低黏结超高强筋的可恢复性混凝土圆柱的抗震性能研究[D]. 成都:西南交通大学,2020.
[17]	中华人民共和国住房和城乡建设部. 高层建筑混凝土结构技术规程:JGJ3—2010[M]. 北京:中国建筑工业出版社,2011.
[18]	中华人民共和国建设部. 混凝土结构设计规范:GB 50011—2010[S]. 北京:中国建筑工业出版社,2010.
[19]	中国钢铁工业协会. 金属材料拉伸试验第一部分:温室试验方法:GB /T 228.1—2021[S]. 北京:中国标准出版社,2021.
[20]	中华人民共和国住房和城乡建设部. 混凝土物理力学性能试验方法标准:GB/T 50081—2019[S]. 北京:中国建筑工业出版社,2019.
[21]	中国建筑科学研究院. 建筑抗震试验规程:JGJ/T 101—2015[M]. 北京:中国建筑工业出版社,2015.
[22]	谢剑,孙文笑,徐福泉,等. 钢筋混凝土自复位剪力墙抗震性能试验研究[J]. 建筑结构学报,2019,40(2): 108-116. XIE Jian, SUN Wenxiao, XU Fuquan, et al. Experimental study on seismic behavior of self-centering RC shear walls[J]. Journal of Building Structures, 2019, 40(2): 108-116.