Optimal Feeder Flex-route Transit Schedule Design of Urban Rail Transit
-
摘要:
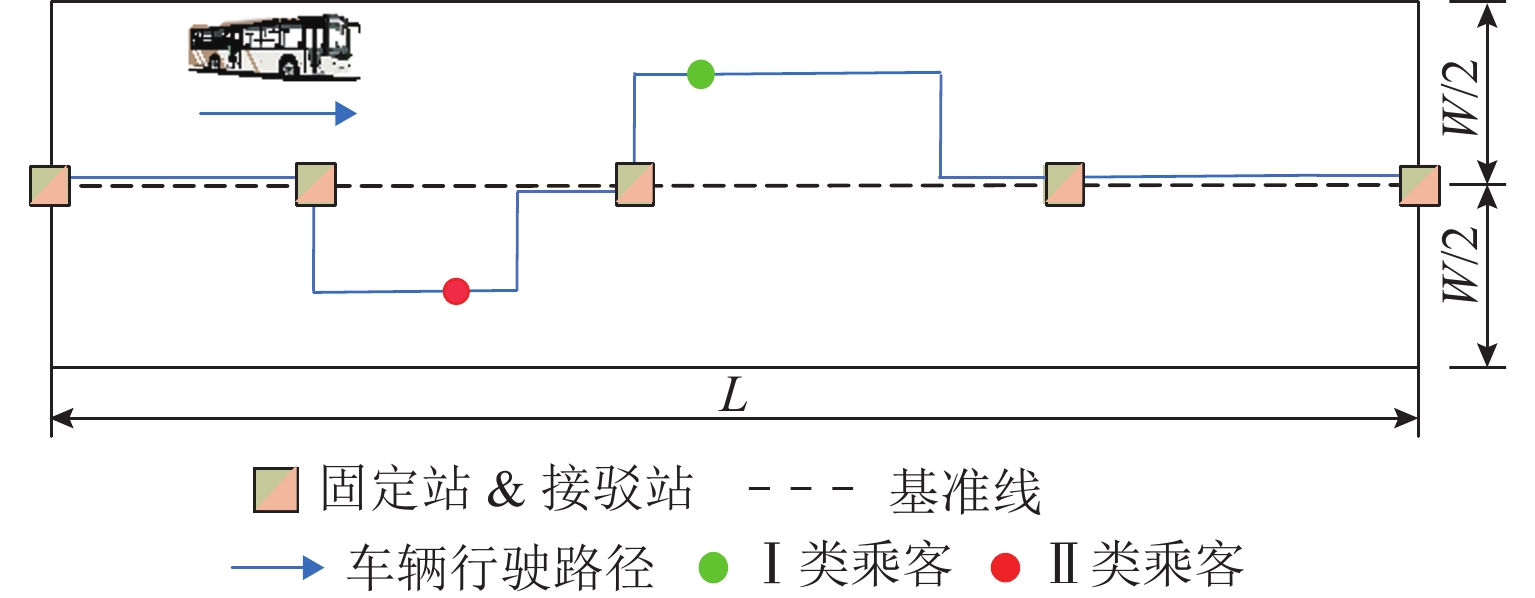
为尽可能满足乘客出行需求，制定科学合理的公交运行时刻表能够保持公交稳定运行的同时降低运行成本. 首先，针对可变线路公交区别于常规定点定线公交的运行特征，提出一种将常规公交转变为可变线路公交接驳地铁的策略，在无需开设新接驳线路的前提下服务原有公交车出行需求乘客和短途出行需求的地铁乘客；然后，通过分析乘客出行行为的规律与特点，根据可变线路公交和地铁的时空信息以及乘客换乘行为的时空参数，利用混合整数非线性规划构建可变线路公交接驳地铁的路径、时间、调度协同优化模型和算法；最后，结合案例，分析车辆运行速度与出行需求水平以及不同时间成本侧重情况对发车间隔、车辆运行时间、运行成本等系统各项指标的影响. 研究表明：在运行周期内适当增加发车频率可以有效降低乘客出行时间成本，且不会增加系统总成本；为可变线路公交接驳地铁的时刻表构建提供了基本理论和自动化编制方法，提高了公交运行效率和服务质量.
Abstract:A scientific schedule should be able to meet the needs of most passengers, maintain stable operation, and reduce operating costs. Aiming at the operation characteristics of the flex-route transit different from the traditional fixed-route transit, a method of making the schedule of the feeder flex-route transit of urban rail transit is proposed. A strategy of traditional fixed-route transit into flex-route transit to connect urban rail transit is proposed, which can serve the original traditional fixed-route passengers and urban rail transit passengers with short-distance travel demand at the same time without the need to open new feeder routes. The rules and characteristics of passenger travel behavior are analyzed. According to the space-time parameters of transfer behavior of passengers and the space-time information of flex-route transit and urban rail transit, the mixed integer nonlinear programming is used to construct the path, time, and scheduling collaborative optimization model and algorithm of the feeder flex-route transit of urban rail transit. Combined with the case analysis, the influence of vehicle driving speed and travel demand level and different time cost emphasis on the system indicators such as departure interval, vehicle running time, and operation cost are analyzed. The results indicate that increasing the departure frequency appropriately during the operating cycle can effectively reduce the travel time cost of passengers without increasing the total system cost. It provides basic theory and automatic compilation method for the feeder flex-route transit schedule design of urban rail transit, reduces the travel cost and improves the operation efficiency and service quality.
-
Key words:
- Flex-route transit /
- Urban rail transit /
- Schedule /
- Transfer analysis /
- Operations coordination
-
现行电气化铁路采用换相（异相）单边供电[1-2]，以减少负序对三相电网的影响[3]，进而降低电能质量问题中的三相电压不平衡[4]. 为此，需要在接触网的各供电分区之间增设电分相以进行隔离. 然而，电分相[5]的设置导致了无电区，给铁路运行带来诸多问题[6-10]. 同相供电可以同时解决牵引变电所的负序问题及其出口处的电分相问题. 在文献[11]提出同相供电方案之后，研究者们基于无功型对称补偿技术[12-17]进一步开发了牵引变电所有功型同相供电方法[18-19]. 该方法能以最小补偿容量使三相电压不平衡度达标[20]，同时消除变电所出口处的电分相. 为进一步消除分区所处和全线的电分相和无电区，不仅需要实现两个牵引变电所间的双边供电和更大范围的贯通供电[18,21-22]，还需应对铁路贯通供电可能对电网带来的新问题.
1. 贯通供电
贯通供电是两个及以上牵引变电所同相供电和分区所双边供电的结合，能够确保现代交直交列车的牵引和（电）制动都需要的牵引网不间断供电. 最简单的贯通供电是采用单相牵引变压器的牵引变电所同相供电和分区所双边供电的结合，如图1所示. 图中，分区所纵向断路器K需要合闸才能实现贯通供电，否则，仅为牵引变电所的同相供电，属于单边供电. 电网中，将分区所断路器K合闸的操作称为合环，合环需满足电网规定的条件，否则无法进行贯通供电.
图 1 同相单边供电和贯通供电空载示意Figure 1. Co-phase single-end power supply and interconnected power supply under no-load condition虽然俄罗斯、乌克兰等前苏联国家[2]及韩国的电气化铁路一直采用双边供电，但其牵引变电所仍然采用异相供电，即换相接入电网，并不属于本文定义的贯通供电.
图1（a）所示的同相单边供电牵引网通过单个牵引变电所与电网的单个公共连接点连接后向列车供电. 而图1（b）所示的贯通供电牵引网则通过多个牵引变电所与电网的多个公共连接点连接后向列车供电，此时，牵引网成为电网中的连接支路，牵引供电系统和电网的拓扑结构发生变化. 以牵引网空载情况为例，双边供电的牵引变电所和牵引网串联后在电网不同公共连接点之间又增生了一条新的支路，形成新的电流分量，称为均衡电流或环路电流，或者说增生了一个新的功率分量，称为穿越功率. 与贯通供电相比，由于同相单边供电分区所（SP）的纵向断路器K分闸，牵引网不贯通，空载工况下不会产生穿越功率.
图2为同相单边和贯通供电的列车牵引用电和再生发电工况示意. 从图中可见，同相单边供电时，不同牵引变电所的列车牵引用电功率和列车再生发电功率在贯通供电时得以叠加，虽然列车的用电和发电总量不变，但贯通供电后，从电网用电或向电网发电的最大功率会减小，对应的负序最大值也会减小. 从这个意义上说，贯通供电优于单边供电.
图 2 同相单边和贯通供电运行工况示意Figure 2. Operation under co-phase single-end power supply and interconnected power supply但与同相单边供电相比，贯通供电给电网带来新的问题，即能否合环以及合环后的穿越功率问题. 本文讨论电网的正常状态，关于故障状态和对应的继电保护技术，可参见文献[18]、[23-24].
2. 贯通供电合环
以图1（b）中选择两个牵引变电所构成的双边供电合环情形加以讨论，如图3所示. 假设实施双边供电的两个变电所SS1、SS2的电源分别来自有（等效）电气连接的电网公共连接点PCC1、PCC2，当牵引变电所SS1、SS2之间分区所的纵向断路器K合闸，就构成双边供电.
实现双边供电必须在同一电网内进行. 电气化铁路的双边供电与电网的电磁合环有所不同：电网电磁合环为三相合环，而双边供电是单相合环；电网电磁合环的开关是常开的，而双边供电的纵向开关是常闭的. 尽管如此，由于双边供电和电网的电磁合环都将改变电网的拓扑结构和运行方式，因此，必须满足电网规定的合环条件.
《青海省电力系统调度规程》[25]规定了电网的解合环操作，其中合环操作：“必须相位相同，电压差一般允许在20%之内，相角差一般不超过20°，以确保合环时不因环路电流过大引起潮流的变化而超过继电保护、系统稳定和设备容量等方面的限额. 合环后应当及时通知有关调度及厂站. 对于较复杂环网的操作，应当先进行模拟计算. ”
《中国南方电网电力调度管理规程》[26]解合环操作规定：1） 必须确保相序相位正确才能合环；2） 解、合环操作必须确保解、合环后潮流不超过稳定极限、设备不过负荷、电压在正常范围内，不引起继电保护和安全自动装置误动；3） 具备条件时，合环操作应使用同期装置；4） 500 kV合环时电压差一般不应超过额定电压10%，220 kV不应超过额定电压20%；500 kV系统合环一般应检同期合环，有困难时应启用合环开关的同期装置检查相角差；500 kV合环时相角差一般不应超过20°，220 kV一般不应超过25°.
图3中PCC1和PCC2之间的电压差和相角差可以于K合闸之前在分区所测得，也可以在已知PCC1和PCC2之间的电气连接关系时通过潮流计算得到[3].
实际电网中，图3所示PCC1和PCC2之间的电气连接方式多种多样，作为举例，这里考虑220 kV输电线路对铁路两个牵引变电所的专用线供电方式，则三相等值电路可由图4描述. 图中，ZA、ZB和ZC为输电线的三相阻抗，L为牵引变电所之间的距离.
首先，分析分区所纵向断路器K合闸之前PCC1和PCC2之间的电压差和相角差是否满足合环规程的规定.
当末端负荷电流˙I通过电阻为R、电抗为X，即阻抗为Z=R+jX的线路时，首端电压˙Uf与末端电压˙Ue的电压降Δ˙U、电压差ΔU和相位差θ的相量图如图5所示[1,15]. ΔU和θ分别为[1,27]
ΔU=|˙Uf|−|˙Ue|=√(Ue+XIsinφ+RIcosφ)2+(XIcosφ−RIsinφ)2−Ue≈XIsinφ+RIcosφ, (1) θ=arctanXIcosφ−RIsinφXIsinφ+RIcosφ, (2) 式中：φ为电流˙I的功率因数角，以滞后为正.
220 kV输电线路最大输送功率为500 MV•A[3]. 计算中，输电线采用2 × LGJQ-500二分裂导线，取单位长阻抗z0=
0.0312 + j0.3052 Ω/km，PCC2处的输送功率分别取200、300、500 MV•A. 考虑相邻牵引变电所的间距L与输电线匹配，L分别取50、60、70、80 km，输送功率的功率因数分别取0.95和0.90，ΔU和θ的计算结果分别列于表1和表2. 其中，ΔU的百分值以额定电压220 kV为基准.表 1 功率因数为0.95（滞后）时的电压差ΔU和相角差θTable 1. Voltage difference (ΔU) and phase angle difference (θ) at a power factor of 0.95 (lagging)L/km 传输功率 200 MV•A 传输功率 300 MV•A 传输功率 500 MV•A ΔU/kV ΔU/% θ/（o） ΔU/kV ΔU/% θ/（o） ΔU/kV ΔU/% θ/（o） 50 3.49 2.74 3.23 5.38 4.23 4.78 9.44 7.43 7.74 60 4.23 3.33 3.85 6.56 5.16 5.69 11.60 9.13 9.16 70 4.99 3.93 4.47 7.77 6.12 6.58 13.85 10.90 10.53 80 5.77 4.54 5.08 9.02 7.10 7.45 16.17 12.73 11.85 表 2 功率因数为0.90（滞后）时的电压差ΔU和相角差θTable 2. Voltage difference (ΔU) and phase angle difference (θ) at a power factor of 0.90 (lagging)L/km 传输功率 200 MV•A 传输功率 300 MV•A 传输功率 500 MV•A ΔU/kV ΔU/% θ/（o） ΔU/kV ΔU/% θ/（o） ΔU/kV ΔU/% θ/（o） 50 4.41 3.47 2.99 6.74 5.30 4.41 11.63 9.16 7.10 60 5.33 4.20 3.56 8.17 6.44 5.23 14.19 11.17 8.37 70 6.26 4.93 4.13 9.64 7.59 6.04 16.81 13.24 9.60 80 7.21 5.68 4.68 11.13 8.76 6.84 19.50 15.35 10.78 从图5和表1、2可见，输送（视在）功率的功率因数越高，电压差越小，但相角差越大. 总的看：在牵引变电所间距不超过80 km下（通常如此），双边供电时分区所的合环电压差不大于16.00%，相角差不大于12.00°，低于合环规程的规定值，符合要求.
实践中，双边供电除了仿真计算之外，在合环前应选择牵引网处于空载状态，并检测分区所两侧接触网的电压差和相角差，在允许的电压差和相角差范围内，才能令纵向断路器K合闸.
双边供电一旦合环就可长期运行.
3. 穿越功率分析与计算
牵引供电系统的正常状态可分为牵引、再生和空载3种工况. 其中，空载工况下，双边供电与单边供电才有本质区别，双边供电的牵引供电系统与电网（等效）输电线并联，造成均衡电流或者穿越功率. 从图6可见，空载工况下，双边供电的穿越功率在一个变电所（如SS1）表现为用电状态，在另一个变电所（如SS2）则表现为发电状态，更多牵引变电所贯通供电时，穿越功率可能穿越得更远.
3.1 等效电路与均衡电流计算
对应图1和图4，将归算到电网侧的三相等效电路示于图7. 图中，Zd为三相输电线的相阻抗，即ZA=ZB=ZC=Zd；ZJ1和ZJ2为牵引变电所SS1和SS2的进线相阻抗；ZT1,e和ZT2,e为归算到电网侧的单相牵引变压器阻抗；Zq,e为归算到电网侧的牵引网阻抗；LC为电力机车.
考虑牵引网空载工况，选择A相或B相可得计算均衡电流的单相等效电路，如图8所示. 图中，用Zd、Zq分别表示电网输电线与牵引供电系统（包括进线相阻抗）的归算阻抗. 设总电流为˙I，通过电网输电线的电流为˙Id，通过牵引供电系统的电流为˙Iq，则有支路电压方程如式（3）所示.
˙IqZq=Zd˙Id. (3) 设ZJ1=ZJ2=ZJ，则求得均衡电流Iq为
˙Iq=ZdZq˙Id=Zd2ZJ+(ZT+12Zq,e)k2T˙Id, (4) 式中：kT为牵引变压器变比，即电网进线的线电压与牵引母线额定电压的比值.
定义分流比为η，即均衡电流与电网输电线中的电流之比，则由式（4）得
η=|˙Iq˙Id|=|ZdZq|=|Zd2ZJ+(ZT+12Zq,e)k2T|. (5) 精确计算需要掌握具体数据. 假设电网PCC1和PCC2之间220 kV输电线的长度为50 km，PCC1（PCC2）到牵引变电所SS1（SS2）的进线长度为10 km，输电线单位长阻抗同前，牵引变压器均为单相变压器，额定容量均为31.5 MV•A，短路电压百分比为10.5%，则求得归算到牵引侧的漏抗ZT=
0.2134 + j2.52 Ω，相邻牵引变电所间距50 km，直供方式牵引网空载电压为27.5 kV，变比kT=8，单线铁路、单链型悬挂牵引网单位长阻抗z=0.232 + j0.515 Ω/km，代入式（5）可得η=1.44%. 工程上，可以用η≈1k2T, (6) 进行估算，计算得η=1/64≈1.56%，接近且略大于精确计算值.
3.2 穿越功率计算与测量
设电网输电线的额定电压为UN，由式（3）得到穿越功率Sq为
Sq=UNIq=ZdZqUNId, (7) 或者已知电网输电线三相功率S时，由式（8）估算得牵引网（单相）穿越功率.
Sq≈S√3k2T. (8) 一般110 kV输电线最大输送功率为50 MV•A，则直供方式时，变比kT=4，由式（8）估算得双边供电最大穿越功率为1.8 MV•A，占比3.6%；220 kV输电线最大输送功率为500 MV•A，则直供方式时，kT=8，由式（8）估算得双边供电穿最大越功率为4.6 MV•A，占比1.8%.
上述定义和讨论的均衡电流和穿越功率均沿线路传输，故称为纵向分量. 穿越功率可进一步分为有功分量和无功分量（一般为感性），都属于纵向分量. 因此，如果穿越功率存在，则在牵引变电所进线、牵引馈线以及牵引网的任何方便的部位都能测量得到. 还有一个像负荷一样的横向分量，这就是线路的容性无功功率，也叫充电功率. 穿越功率取决于电网对牵引供电系统的供电方式和电网潮流，充电功率则沿输电线和牵引网分布，取决于其长度和电压等级. 线路充电功率在分区所纵向断路器合闸前后的总量不变，但合闸后将在系统中重新分配，此时也存在一个分流点. 当分流点与分区所不重合时，分区所会测到这个分量不是0，而当分流点与分区所重合时，分区所的这个分量就是0.
要判断分区所合环后是否存在穿越功率，则应在牵引网空载时测量牵引网的有功分量，才能准确反映穿越功率情况：若检测到的有功分量为0，则穿越功率中的（纵向）无功分量亦为0，穿越功率即为0；而此时若检测到的无功分量不为0，只能说明存在充电功率（横向分量），不是穿越功率. 下面会看到，当电网对铁路牵引变电所进行树形供电时，理论上穿越功率为0.
4. 穿越功率解决方案
正常运行状态下，双边供电与单边供电在潮流分布上的唯一区别就是穿越功率问题. 由上分析可知，穿越功率占比很小，不会对电网潮流造成大的影响. 但是，为不产生穿越功率或不向电网发电（分量），仅达到与单边供电相同或更好的效果，必须关注并解决穿越功率的问题.
1） 树形供电
电网的变电站用同一（分段）母线公共连接点（PCC）为多个铁路变电所供电，这种供电方式称为树形供电[19,22,28]，如图9所示. 此时，对应图3，可认为PCC1与PCC2合并，电网输电线长度为0，即令式（6）中Zd=0，得η=0. 因此，铁路实施树形双边供电不会产生均衡电流和穿越功率，而负序等电能质量影响与铁路单边供电的处理方式相同.
我国西北地区地广人稀，电网对铁路牵引变电所多进行树形供电，为开展和实施树形双边供电提供了得天独厚的条件. 国铁集团于2020年在科技研究开发计划中立项开展“电气化铁路牵引变电所双边供电试验”研究，通过综合比选，考虑电网电源条件，试验段选取在海拔约
3000 m、线路坡度16‰的格库铁路（青海段）东柴山至花土沟车站区段，长度约75 km. 格库铁路为国铁Ⅰ级客货共线的单线双向电气化铁路，设计速度120 km/h，使用HXD1C系列电力机车. 2021年7月试验取得圆满成功，仿真和试验证明在树形供电方式下，双边供电不产生穿越功率，具备投运条件.交通运输部国家“交通强国”试点中的“巴准铁路贯通式同相供电工程化”项目也是在电网树形供电下的铁路贯通供电应用实例[26]. 该铁路位于内蒙古鄂尔多斯市，为国铁Ⅰ级复线电气化重载运煤铁路，东起点岱沟站，向西经海勒斯壕南站与包神铁路在巴图塔站接轨，全长128 km. 改造前设有4座牵引变电所，贯通供电改造后由电网的川掌变电站树形供电至保留的四道柳和纳林川两个牵引变电所，牵引变电所均采用组合式同相供电方案[11]：主变更换为不等边Scott接线，其M座额定容量为40 MV•A，T座同相供电装置采用5 MV•A运行 + 5 MV•A备用方式，2014年6月25日8时58分四道柳和纳林川变电所之间的分区所合环成功，2024年9月实现全线贯通，这是世界首条取消全部电分相和无电区的贯通供电线路.
2） 合建所
将牵引变电所与电力（动照）变电所合建在一起，牵引变压器和电力（动照）变压器接入同一进线母线，如图10的SS2所示. 假设穿越功率由变电所SS1流向SS2，只要电力变压器的电力负荷大于穿越功率，则穿越功率就被“淹没”，合建所总体对电网表现为用电状态，而不会向电网发电. 由于穿越功率通常较小，只需电力负荷大于该值，即可解决穿越功率向电网发电的问题.
3） 穿越功率利用
首先识别穿越功率，例如通过光纤实时传递双边供电两端牵引馈线的有功功率，设流向牵引网为正，当该功率非0且两者之和为0时，则判定该功率为穿越功率，再在穿越功率末端的牵引变电所牵引母线上将穿越功率通过交/直/交（AC/DC/AC）装置将穿越功率转移到三相电力用电母线上，供电力负荷利用，或者通过交/直（AC/DC）装置与储能装置（ES）连接进行储能利用，为了更好利用和控制储能装置容量，一般串接直/直（DC/DC）变换装置，如图11所示. 图中，TT为牵引变压器，PTa为电压互感器，CTa为电流互感器.
多数情况下，电网对铁路的供电方式是非树形的，这时就有穿越功率产生[12-14]，例如，广州地铁18号和22号线采用同相供电，在陇枕变电所和陈头岗变电所进行了贯通供电试验，试验测试显示，穿越功率最大为2.2 MV•A.
5. 多功能的智能牵引变电所
与单边供电相比，贯通供电仍会产生负序功率和再生发电功率，但其最大值通常较小. 此外，贯通供电可能还会产生穿越功率. 由于再生发电功率和穿越功率的发电分量可以在牵引变电所进行统一处理，因此应提出一种多功能的牵引变电所供电方案，如图12所示. 图中：TSB为牵引母线；部分功率直流变换器（TPC）和三端口变换器（TPC）均为单相变流器，两者串联构成同相供电装置；DPC为三相交直变流器构成的能量转换装置，与TPC配合向铁路三相用电系统送电；ES为储能装置；RES为新能源发电装置；HPF为高通滤波器；PT为电压互感器；CT1和CT2为电流互感器；A、B、C为牵引变电所进行三相母线；a、b、c则为铁路三相用电系统的母线.
该方案借助单相组合式同相供电方案，仍然以Scott牵引变压器的M座牵引绕组为供电主通道，通过共用直流母线，增加新的潮流调节通道，最大程度复用变流器，减低变流器容量，增加性价比，使全寿命周期成本降至最低. 由于这种多功能供电方案可以根据供电需求进行灵活配置，同时实现牵引供电系统状态数据离线和在线智慧预测与监测，故亦可称为智能牵引变电所.
智能牵引变电所按照需要可以配置以下几个部分：1） M座牵引绕组构成单相牵引变压器，为供电主通道，简单、经济、可靠；2） 同相供电装置，由TPC、PPC串联构成，按需配置，使负序达标；3） 发电功率及穿越功率发电分量利用通道由TPC和DPC或ES构成，联通铁路三相用电或融入储能系统，能源高效融合利用，按需配置；4） 新能源发电通道，按需配置，接入地点可在变电所或车站，实现铁路沿线新能源消纳；5） 高通滤波通道，按需配置，消除高次谐波和谐振.
一般同相供电装置的容量仅占M座牵引绕组（主变）容量1/4甚至更小，穿越和再生功率利用通道容量也在5 MV•A及以下，可有效减少设备重复与投资.
智能牵引变电所具有故障导向安全特性，即使图12中的②～⑤通道退出运行，也能够保持牵引供电.
此外，借助单相组合式同相供电方案，还可以构造共用交流牵引母线的智能牵引变电所方案.
智能牵引变电所具有以下多种功能：1） 可以补偿负序，使三相电压不平衡达标，不对电网造成影响；2） 可以补偿无功功率，提高功率因数，提高和稳定网压；3） 可以消除高次谐波和谐振；4） 可以调控系统潮流，将剩余再生发电功率和穿越功率发电分量转变为用电功率，不向电网发电，不影响电网发电潮流调度；5） 可以促进铁路沿线新能源消纳等.
以上功能可以根据工程实际需要进行灵活组合.
6. 结 论
1） 在一般牵引变电所间距（不超过80 km）下，双边供电时分区所的合环电压差不大于16.00%，相角差不大于12.00°，符合电网合环规定.
2） 与单边供电相比，双边供电和贯通供电可能会产生穿越功率. 该穿越功率可以通过计算和测量获得. 以110 kV输电线为例，其最大输送功率为50 MV•A，采用直供方式时，牵引网的最大穿越功率为1.8 MV•A，占电网输送功率的3.6%；而220 kV输电线的最大输送功率为500 MV•A，直供方式下牵引网的最大穿越功率为4.6 MV•A，占比为1.8%.
3） 消除穿越功率向电网发电的影响，可以采取电网树形供电、合建变电所和穿越功率利用等方案加以解决.
4） 可以进一步发展多功能的智能牵引变电所，根据实际需求进行灵活配置，综合解决负序、再生发电和穿越功率等对电网的影响问题，从而实现电气化铁路的更大范围贯通供电，推动电网和铁路的双赢发展.
致谢：黄小红、王辉、张戬、王帅博士参加了相关研究工作，在此表示感谢.
-
图 1 可变线路公交接驳地铁短途出行乘客示意图
Figure 1. Schematic of FRT picking up/dropping off urban rail transit short-distance passengers
图 2 地铁与接驳可变线路公交换乘时空图
Figure 2. Transfer time-space of urban rail transit and feeder FRT
图 3 南京市地铁2号线和公交5路运行线路图
Figure 3. Operation route of metro line 2 and bus line 5 of Nanjing
图 5 车辆行驶速度和乘客出行需求水平随时间段变化情况
Figure 5. Change trend of bus driving speed and passenger travel demand level with time period
图 7 运行周期内平均车辆运行时间变化
Figure 7. Changes of average vehicle running time during the operating cycle
表 1 发车间隔设置算法设计
Table 1. Algorithm design of departure interval setting
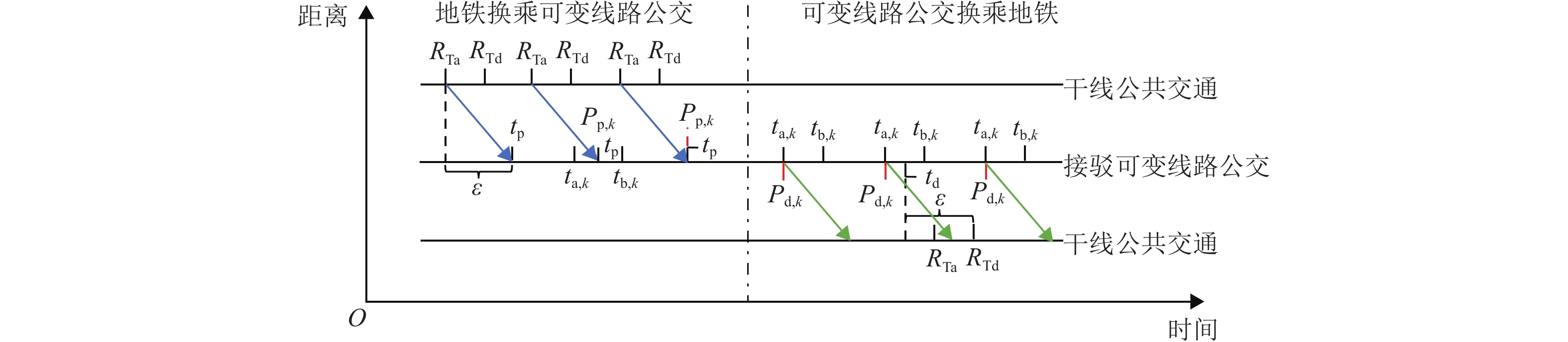
步骤 指令 输入 发车间隔下限Hmin，发车间隔上限Hmax，发车间隔Hν，其中：Hν = Hmin,⋯, Hmax，ν = 1, 2, ⋯, n 步骤 取初始H1 = Hmin，令H* = H1，计算当前U（H1），令U*（H*） = U（H1） 循环 当ν < n时，执行步骤1、2 步骤1 在上述基础上，获取新的Hν + 1，判断是否满足约束，若Hν + 1不满足约束，则重复步骤1 步骤2 计算Hν + 1下的U（Hν + 1），若U（Hν + 1） < U*（H*），则接受Hν + 1作为新的最优发车间隔，H* = Hν + 1，否则保留原来的H* 步骤3 若满足终止条件Hn = Hmax，则输出H*和U*（H*），结束程序，否则返回步骤1. 输出 最优发车间隔H*，最优系统成本U*（H*） 
下载: 导出CSV
表 2 班次设置算法设计
Table 2. Algorithm design of shift setting
步骤 指令 输入 种群规模，交叉概率，变异概率，最大迭代数Imax 步骤0 输入运营参数，设置种群数量、交叉、变异概率，最大迭代次数Imax，初始化种群迭代次数In = 0 循环 当In < Imax时，执行步骤1～8 步骤1 编码：染色体采用由0-1变量构成的矩阵体现乘客分配和班次设置的二维关系，并假设存在一个新的虚拟班次存放被拒绝的乘客 步骤2 适应度函数：当完成运营周期内一次完整班次设置之后，计算染色体对应的适应度 步骤3 染色体更新：1） 在每个乘客和班次完成分配和设置后，将被拒绝乘客的信息反馈给染色体，对相应的基因进行更改，实现染色体的更新；2） 尝试将被拒绝的乘客重新安排回接驳可变线路公交中，提高染色体质量，跳出局部最优 步骤4 选择：精英保留策略和锦标赛法 步骤5 交叉：选用单点交叉方式 步骤6 变异：选用单点变异方式 步骤7 种群适应度更新并记录最优解 步骤8 迭代次数更新，In = In + 1 步骤9 算法终止条件：In ≥ Imax 输出 最优解u，最优系统成本U
下载: 导出CSV
表 3 发车时间设置算法设计
Table 3. Algorithm design of departure time setting
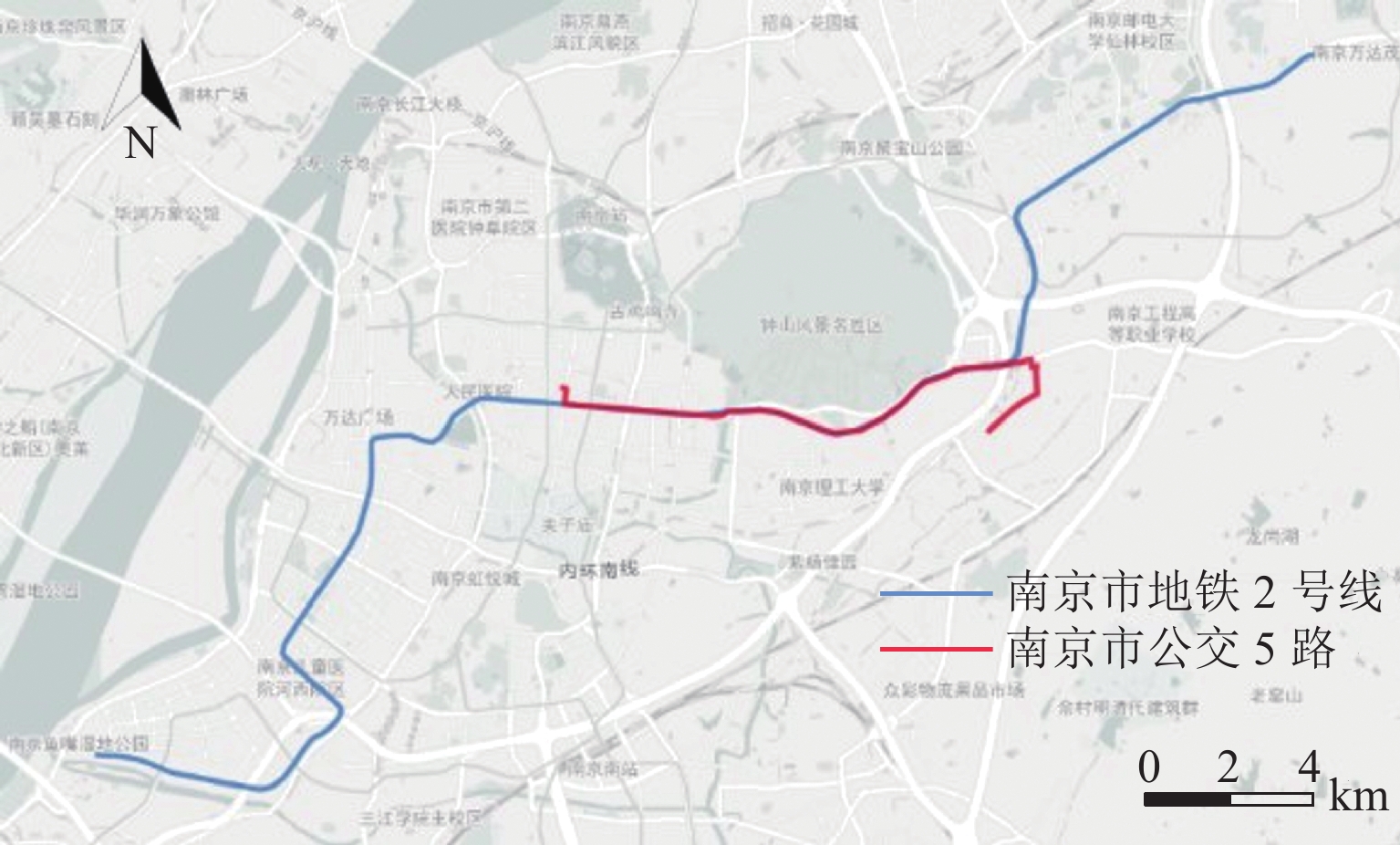
步骤 指令 输入 初始运行站点、线路，出行需求信息，乘客分配情况，车辆班次情况，初始车辆状态 步骤0 输入出行需求行程时间分布和接驳可变线路公交线路运营各项参数 步骤1 将乘客起终点在各分配的车辆班次中依次插入 步骤2 判断约束，若乘客起点或终点的插入会导致可变线路公交违背接驳站的时间约束，则拒绝请求 步骤3 被拒绝乘客重新安排，明确班次的选择顺序，分别将乘客实际上、下车时间与预计/预约上、下车时间比较，时间成本越小，班次排序越靠前，乘客优先尝试插入到该班次中，不再尝试安排到其他班次； 步骤4 计算得到各班次的运行周期时间，松弛时间和固定站点发车时间； 步骤5 编制接驳地铁的可变线路公交时刻表. 输出 最优各班次车辆运行路径，运行周期时间，松弛时间，接驳站发车时间
下载: 导出CSV
表 4 固定站点地铁运行时刻表
Table 4. Urban rail transit running timetable data of fixed stations
编号 接驳站
（地铁-公交）固定站点
相对位置始发
时间末班
时间r1 新街口（东） 0 06：11 23：33 r2 大行宫（东） 1.00 06：13 23：35 r3 西安门•浦发银行 2.00 06：15 23：37 r4 明故宫（东） 3.40 06：17 23：40 r5 下马坊-小卫街 6.20 06：21 23：44 r6 孝陵卫 7.20 06：23 23：46 r7 钟灵街 8.30 06：25 23：48 r8 马群 11.00 06：00 23：52
下载: 导出CSV
表 5 不同需求水平下不同车速所对应的最优发车间隔
Table 5. Optimal departure interval corresponding to different driving speeds under different demand levels
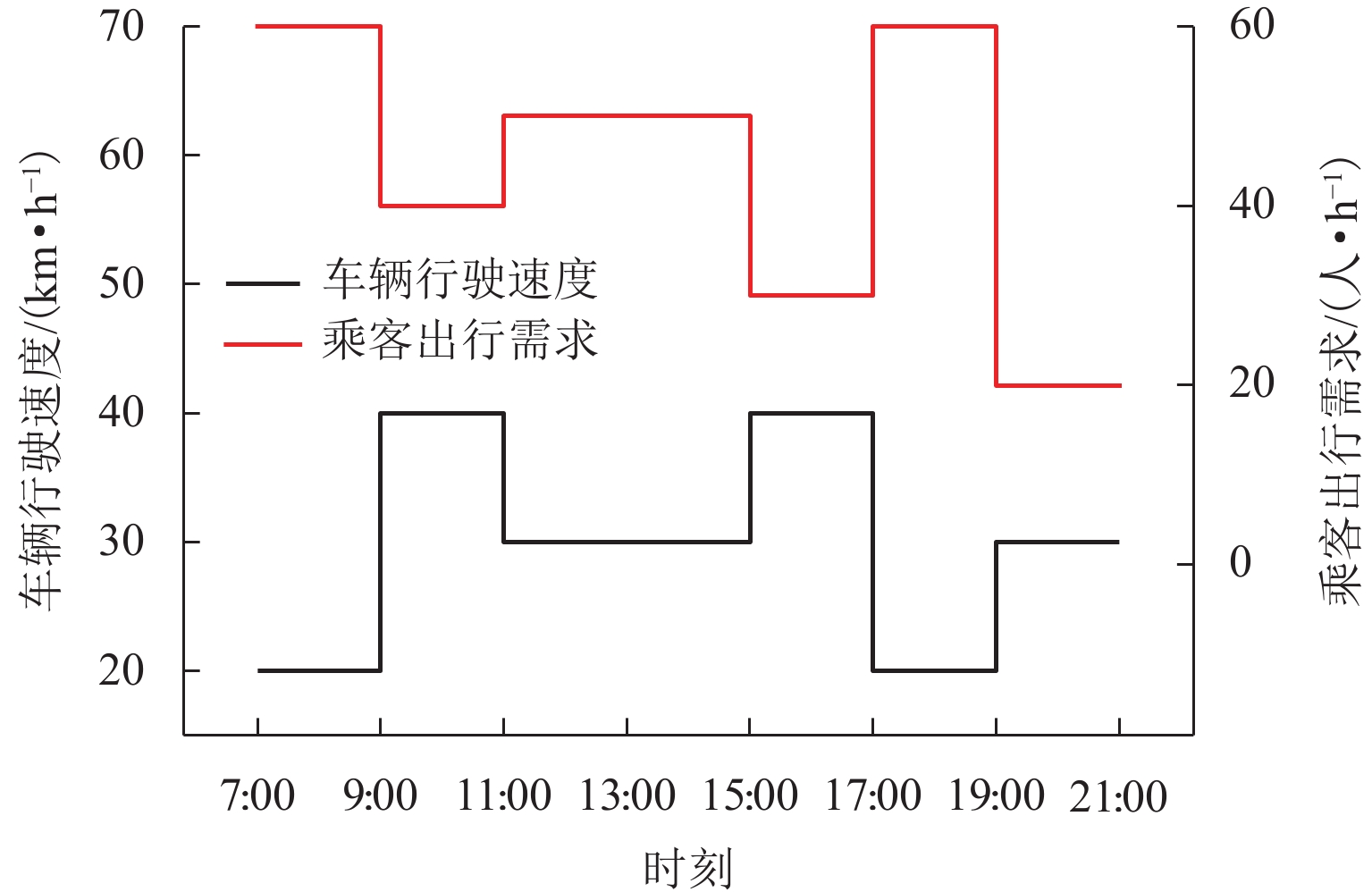
需求/（人·h−1） 发车间隔H/（分钟） v=20千米/
小时v=30千米/
小时v=40千米/
小时10 30 30 30 20 30 30 30 30 20 20 30 40 15 20 20 50 12 15 15 60 10 12 15
下载: 导出CSV
表 6 不同时段下接驳地铁可变线路公交发车时间间隔
Table 6. Departure time interval of feeder FRT at different periods
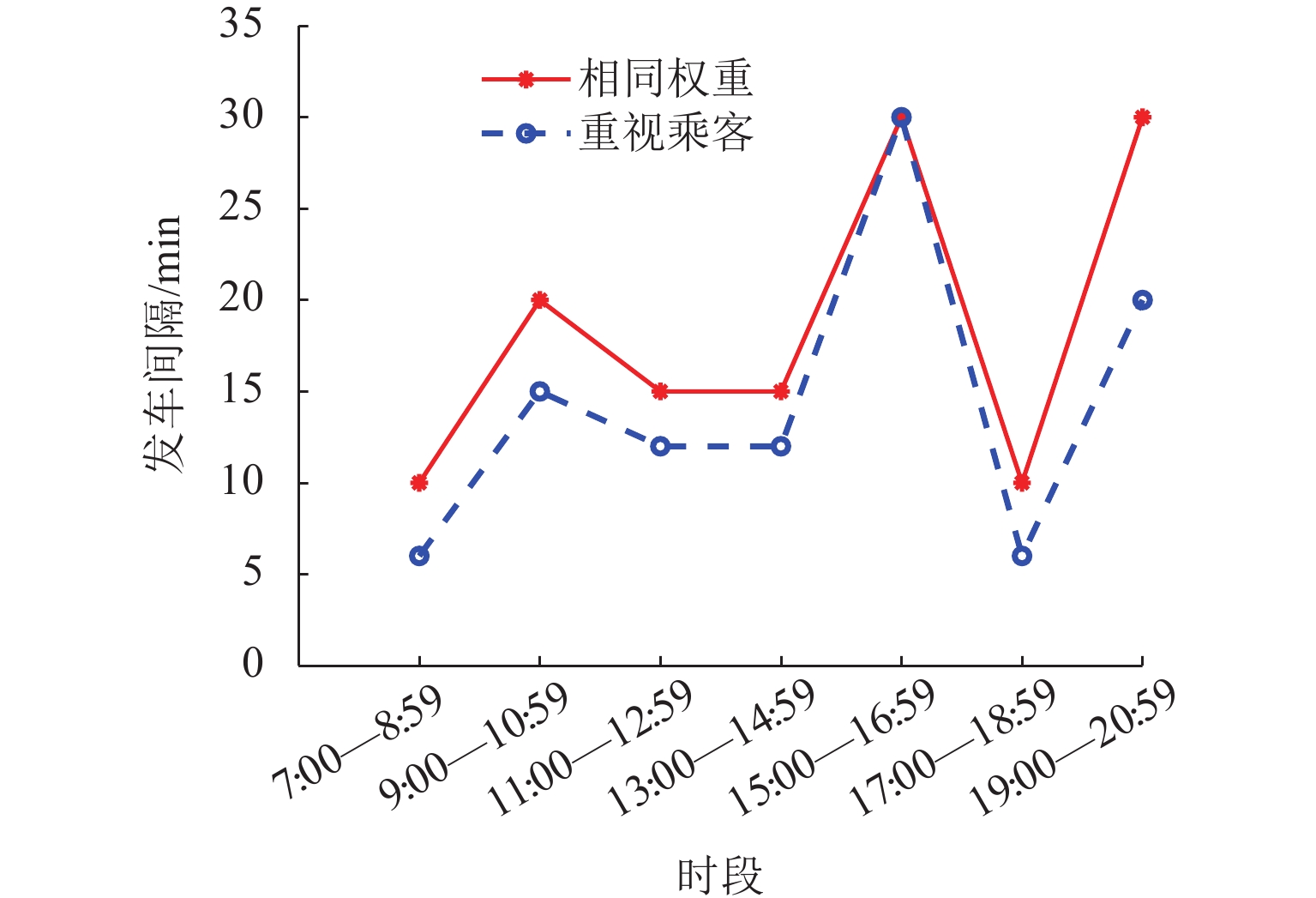
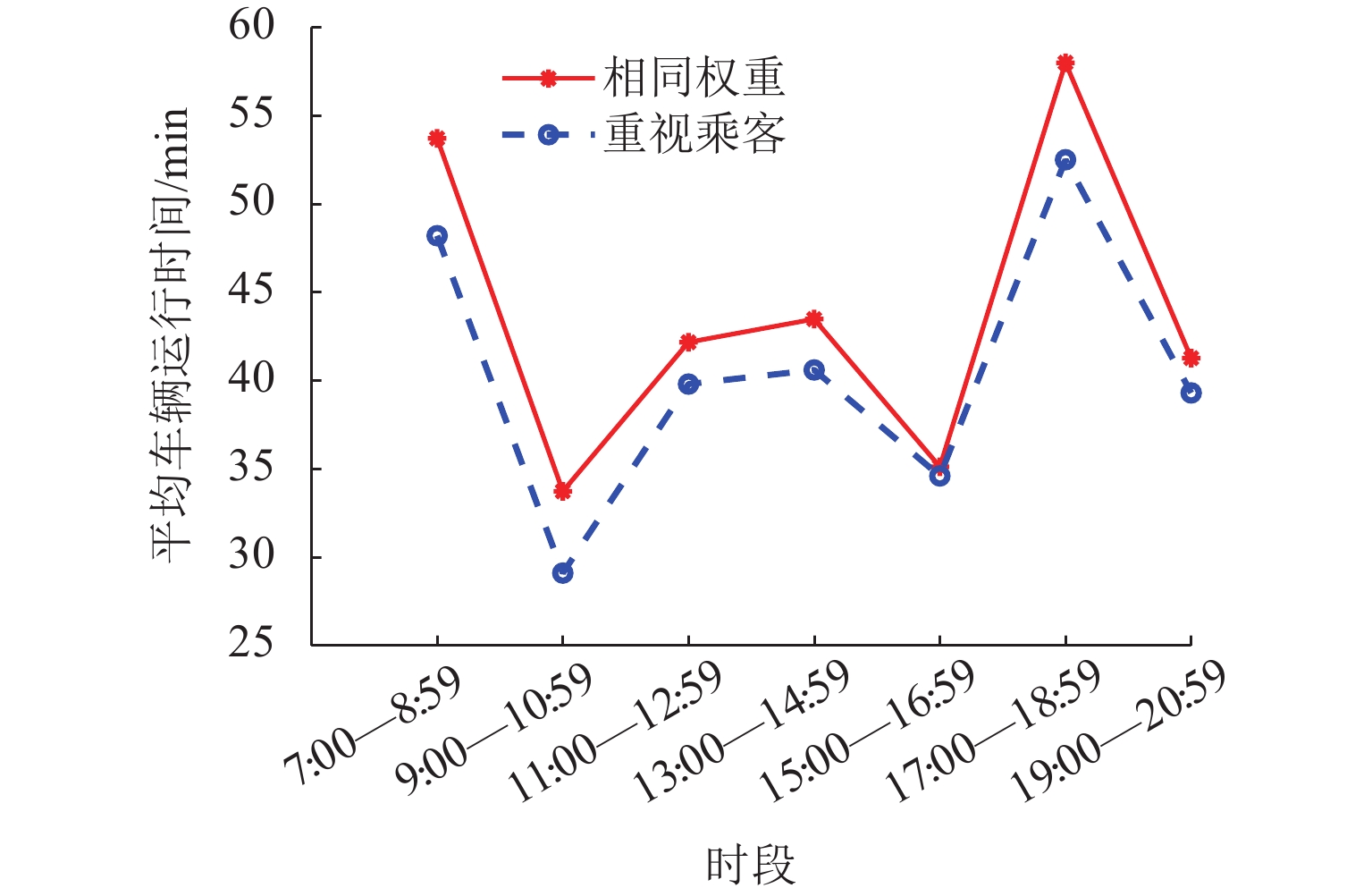
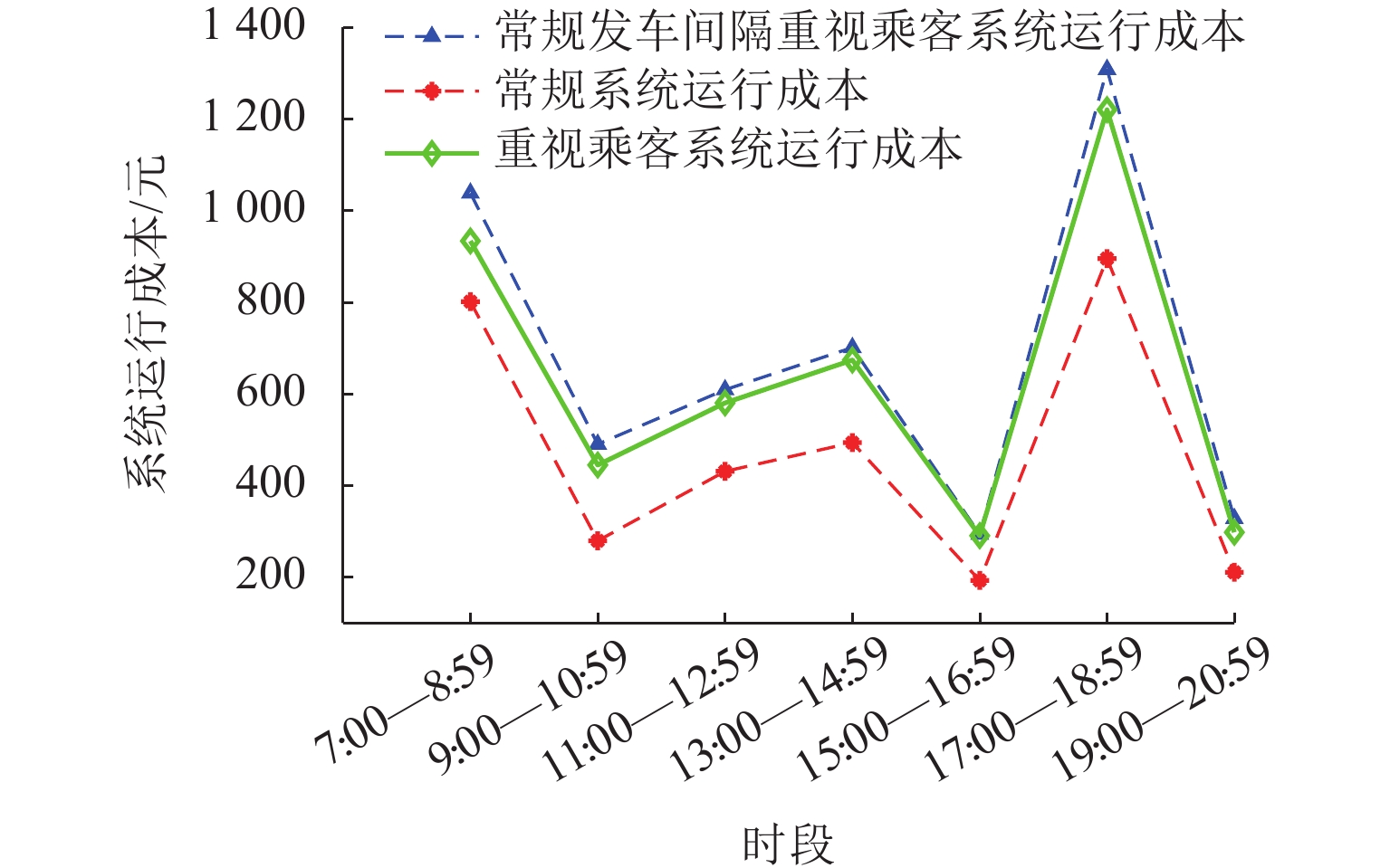
时段 V/（km·h−1） 需求/（人·h−1） H /min 7：00-8：59 20 60 10 9：00-10：59 40 40 20 11：00-12：59 30 50 15 13：00-14：59 30 50 15 15：00-16：59 40 30 30 17：00-18：59 20 60 10 19：00-20：59 30 20 30
下载: 导出CSV
表 7 系统各运行时段的仿真结果
Table 7. Simulation results of each operating period of system
时段 H/min U/元 平均ςk/min 发车次数
/次车辆数
/辆7：00-8：59 10 801.22 53.71 12 11 9：00-10：59 20 279.18 33.73 6 4 11：00-12：59 15 430.76 42.17 8 6 13：00-14：59 15 493.44 43.48 8 6 15：00-16：59 30 192.75 35.12 4 3 17：00-18：59 10 895.30 57.99 12 11 19：00-20：59 30 210.46 41.27 4 3
下载: 导出CSV
-
[1] 夏亮,江欣国,范英飞. 基于均值-方差理论的多阶段公交走廊设计[J]. 西南交通大学学报,2023,58(6): 1294-1302. doi: 10.3969/j.issn.0258-2724.20210874XIA Liang, JIANG Xinguo, FAN Yingfei. Phased transit service design based on mean-variance theory[J]. Journal of Southwest Jiaotong University, 2023, 58(6): 1294-1302. doi: 10.3969/j.issn.0258-2724.20210874 [2] 蒋阳升,李衍,李皓,等. 基于模块化仿真的共享汽车联合调度优化[J]. 西南交通大学学报,2023,58(1): 74-82. doi: 10.3969/j.issn.0258-2724.20210083JIANG Yangsheng, LI Yan, LI Hao, et al. Optimization for joint relocation of carsharing based on modular simulation[J]. Journal of Southwest Jiaotong University, 2023, 58(1): 74-82. doi: 10.3969/j.issn.0258-2724.20210083 [3] 胡路,梁志梅,蒋阳升. 拥挤传播对汽车共享系统运行影响的仿真分析[J]. 西南交通大学学报,2023,58(3): 499-510. doi: 10.3969/j.issn.0258-2724.20220231HU Lu, LIANG Zhimei, JIANG Yangsheng. Simulation analysis on influence of congestion propagation on operation of carsharing systems[J]. Journal of Southwest Jiaotong University, 2023, 58(3): 499-510. doi: 10.3969/j.issn.0258-2724.20220231 [4] WANG J D, YUAN Z Z, CAO Z C, et al. Optimal bus bridging schedule with transfer passenger demand during disruptions of urban rail transit[J]. Journal of Transportation Engineering, Part A: Systems, 2021, 147(10): 04021071.1-04021071.12. [5] 窦雪萍,董冉,李同飞,等. 考虑乘客排队行为的接驳公交行车计划优化[J]. 系统科学与数学,2022,42(12): 3355-3367. doi: 10.12341/jssms22368DOU Xueping, DONG Ran, LI Tongfei, et al. Feeder bus schedule optimization considering passenger queuing behavior[J]. Journal of Systems Science and Mathematical Sciences, 2022, 42(12): 3355-3367. doi: 10.12341/jssms22368 [6] XIONG J, HE Z B, GUAN W, et al. Optimal timetable development for community shuttle network with metro stations[J]. Transportation Research Part C: Emerging Technologies, 2015, 60: 540-565. doi: 10.1016/j.trc.2015.10.007 [7] LIU J R, WU X Y. Research of emergency feeder bus scheme for urban rail transit under unexpected incident[J]. IOP Conference Series: Materials Science and Engineering, 2019, 688(4): 044040.1-044040.7. [8] CHEN Y, AN K. Integrated optimization of bus bridging routes and timetables for rail disruptions[J]. European Journal of Operational Research, 2021, 295(2): 484-498. doi: 10.1016/j.ejor.2021.03.014 [9] 邱丰,李文权,沈金星. 可变线路式公交的两阶段车辆调度模型[J]. 东南大学学报(自然科学版),2014(5): 1078-1084.QIU Feng, LI Wenquan, SHEN Jinxing. Two-stage model for flex-route transit scheduling[J]. Journal of Southeast University (Natural Science Edition), 2014(5): 1078-1084. [10] 赵展轮. 可变线路公交运行时刻表编制方法研究[D]. 南京:东南大学,2019. [11] 姚尹杰. 通道型需求响应公交的调度优化研究[D]. 广州:华南理工大学,2021. [12] SHANG H Y, HUANG H J, WU W X. Bus timetabling considering passenger satisfaction: an empirical study in Beijing[J]. Computers & Industrial Engineering, 2019, 135: 1155-1166. [13] Associates I. TRB’s Transit Cooperative Research Program (TCRP) report 100: transit capacity and quality of service manual, second edition[M]. Washington, D. C. : TRB, 2003. [14] 美国交通运输研究委员会. 公共交通通行能力和服务质量手册[M]. 北京:中国建筑工业出版社,2010. [15] Avishai C. 公共交通规划与运营──理论、建模及应用[M]. 北京:清华大学出版社,2010. [16] ZHENG Y, LI W Q, QIU F. A slack arrival strategy to promote flex-route transit services[J]. Transportation Research Part C: Emerging Technologies, 2018, 92: 442-455. doi: 10.1016/j.trc.2018.05.015 [17] 茧敏,王卓,陈哲轩,等. 基于时空路径推算的城轨网络客流分配方法[J]. 西南交通大学学报,2023,58(5): 1117-1125. doi: 10.3969/j.issn.0258-2724.20220545JIAN Min, WANG Zhuo, CHEN Zhexuan, et al. Passenger flow assignment method for urban rail transit networks based on inference of spatiotemporal path[J]. Journal of Southwest Jiaotong University, 2023, 58(5): 1117-1125. doi: 10.3969/j.issn.0258-2724.20220545 [18] QUADRIFOGLIO L, DESSOUKY M M, PALMER K. An insertion heuristic for scheduling Mobility Allowance Shuttle Transit (MAST) services[J]. Journal of Scheduling, 2007, 10(1): 25-40. doi: 10.1007/s10951-006-0324-6 [19] ZHENG Y, LI W Q, QIU F, et al. The benefits of introducing meeting points into flex-route transit services[J]. Transportation Research Part C: Emerging Technologies, 2019, 106: 98-112. doi: 10.1016/j.trc.2019.07.012 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 24
- HTML全文浏览量: 16
- PDF下载量: 7
- 被引次数: 0