Finite Element Model Updating for Bridges Based on Adaptive Nested Sampling and Bayesian Theory
-
摘要:
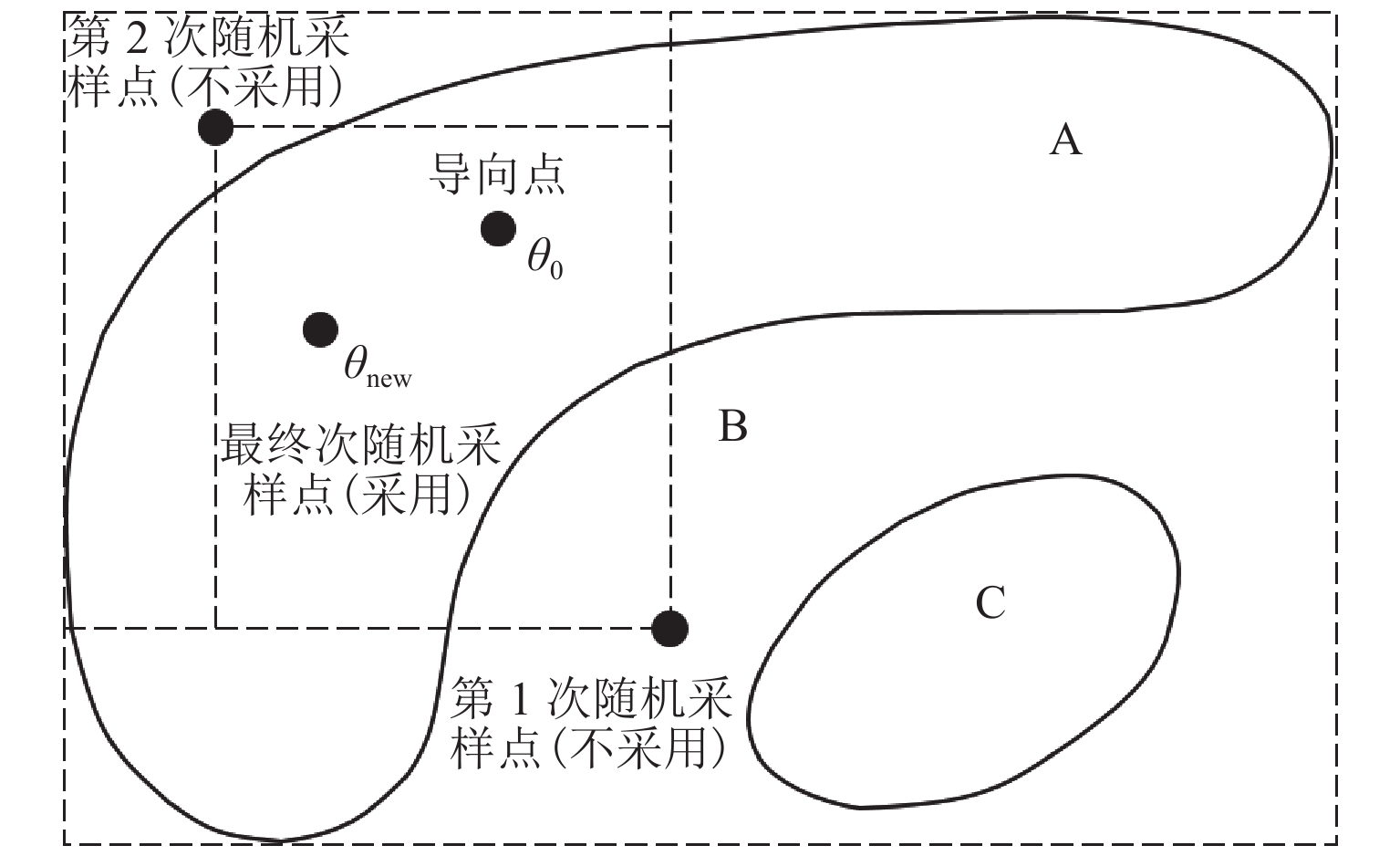
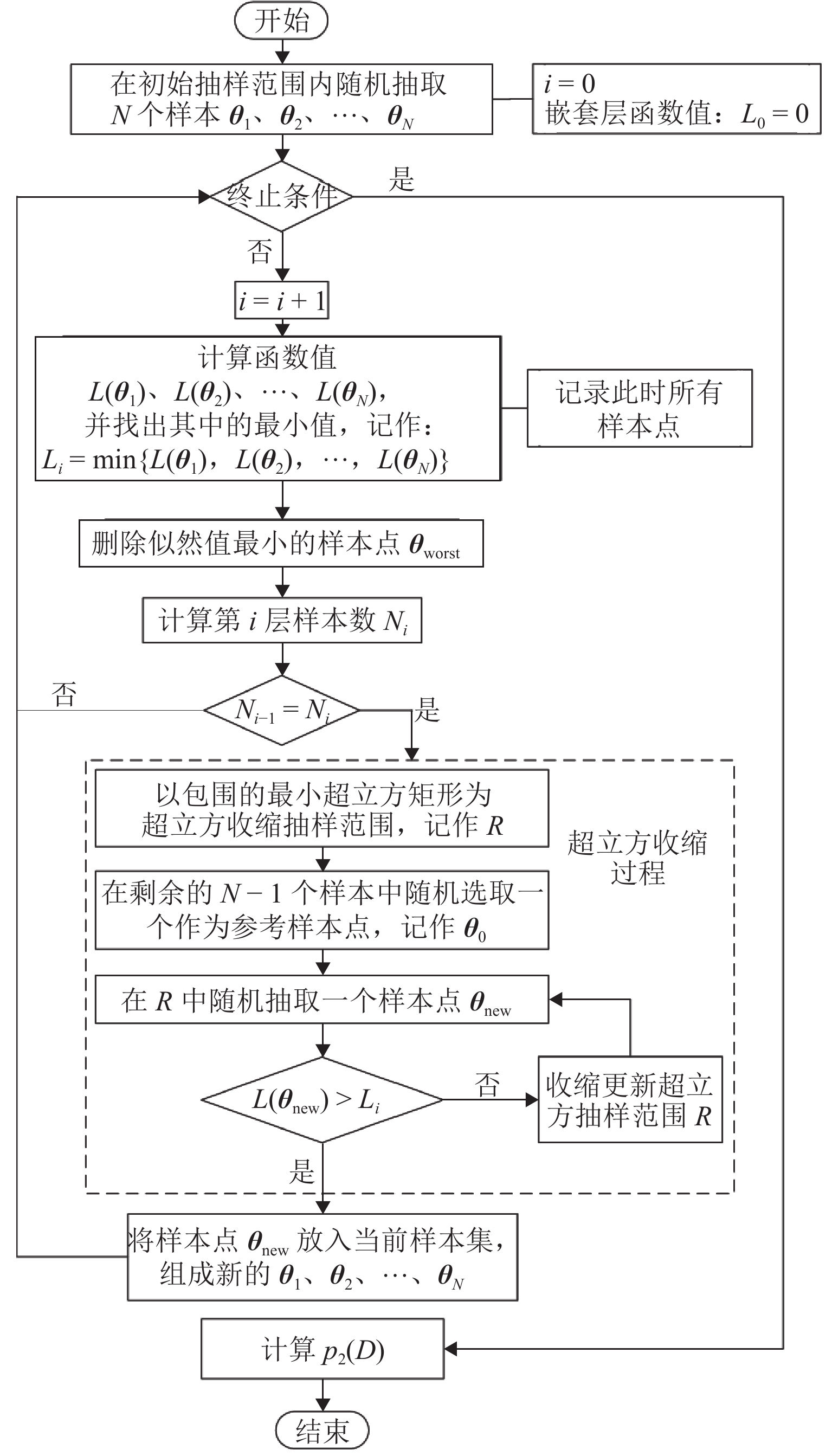
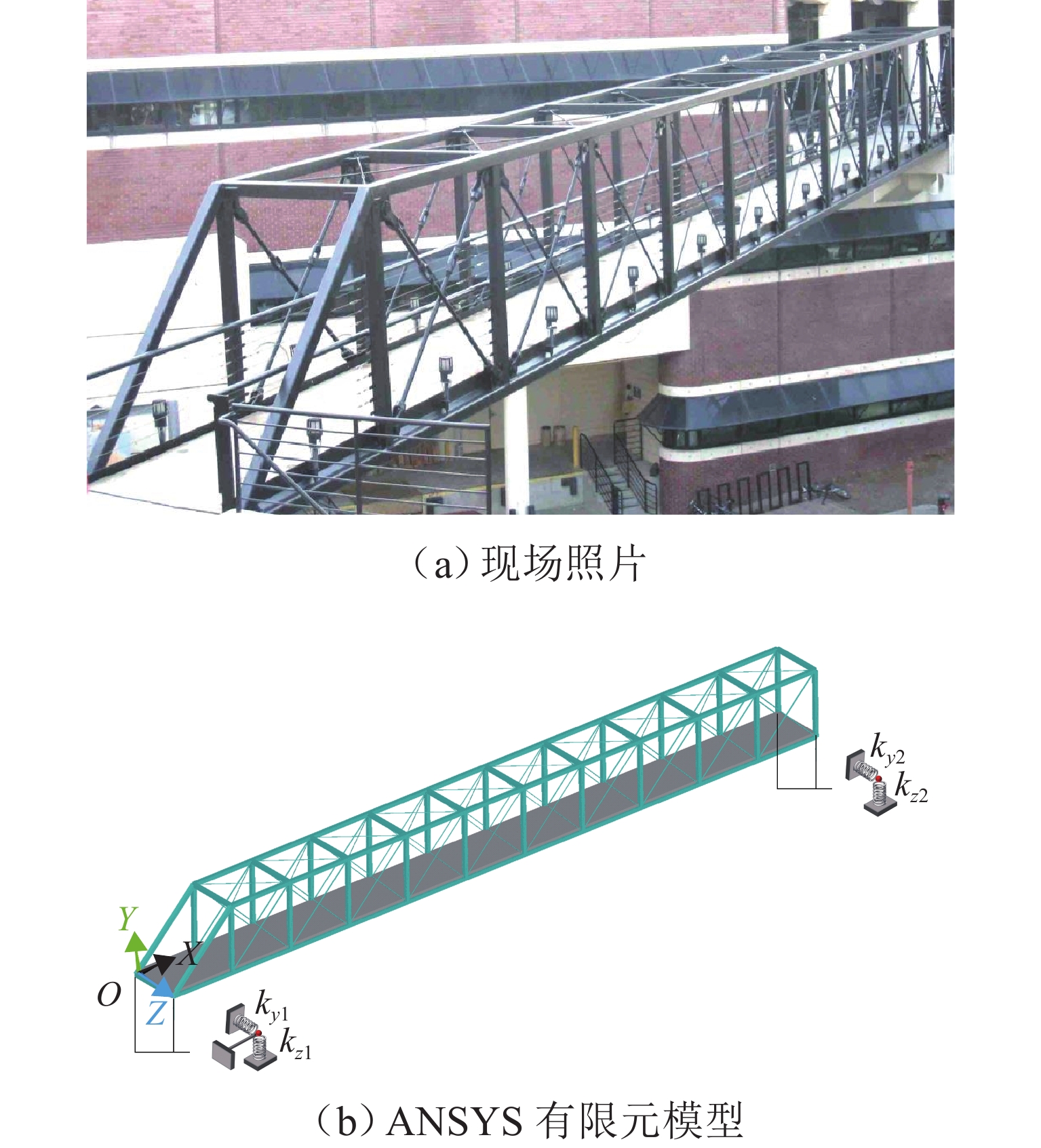
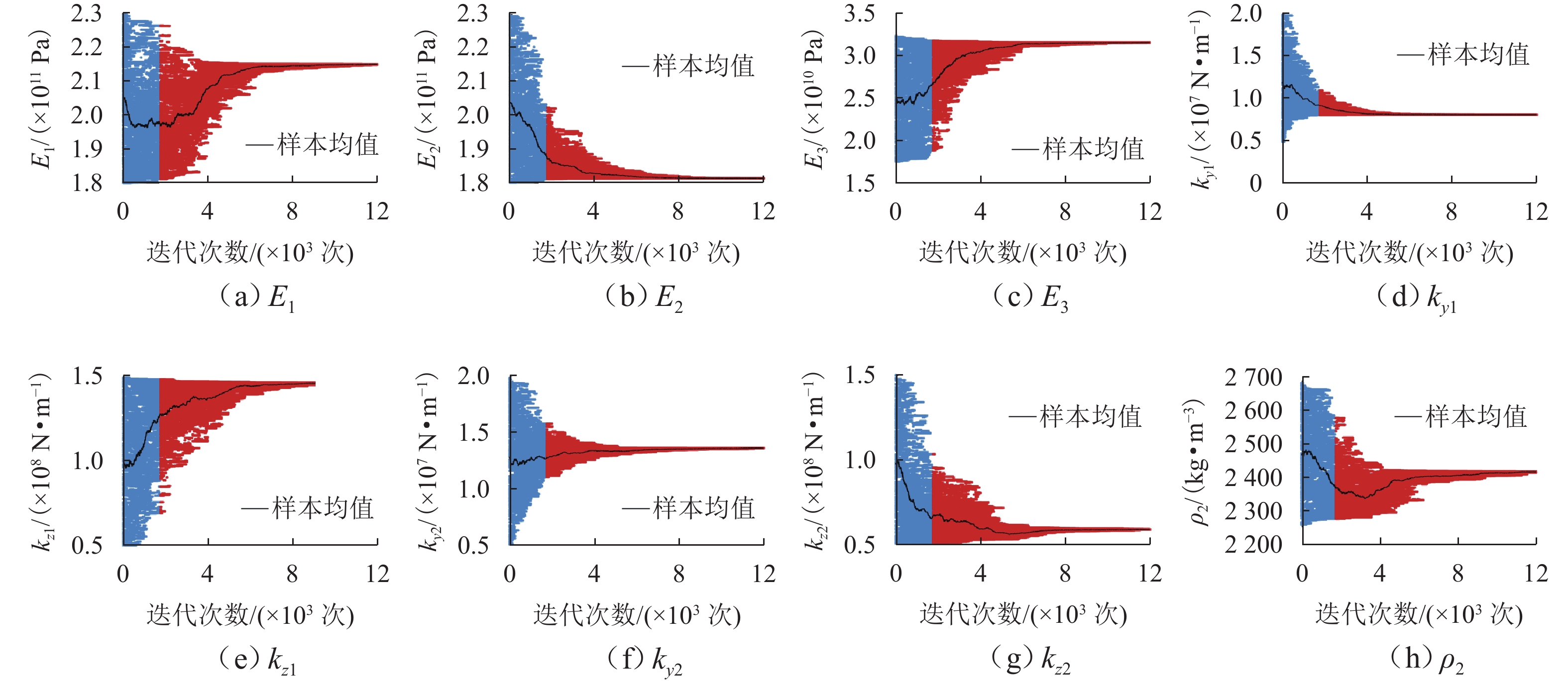
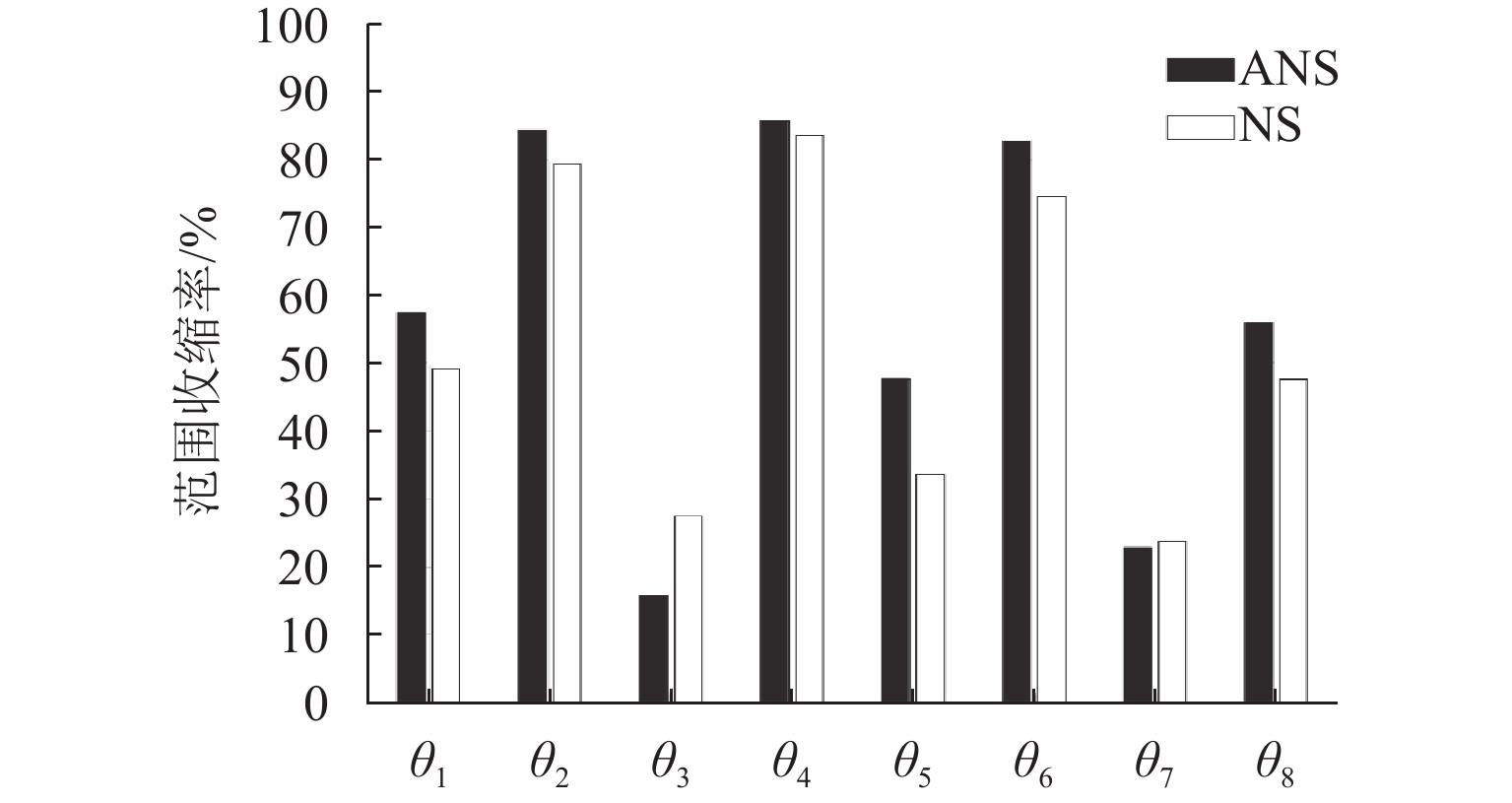
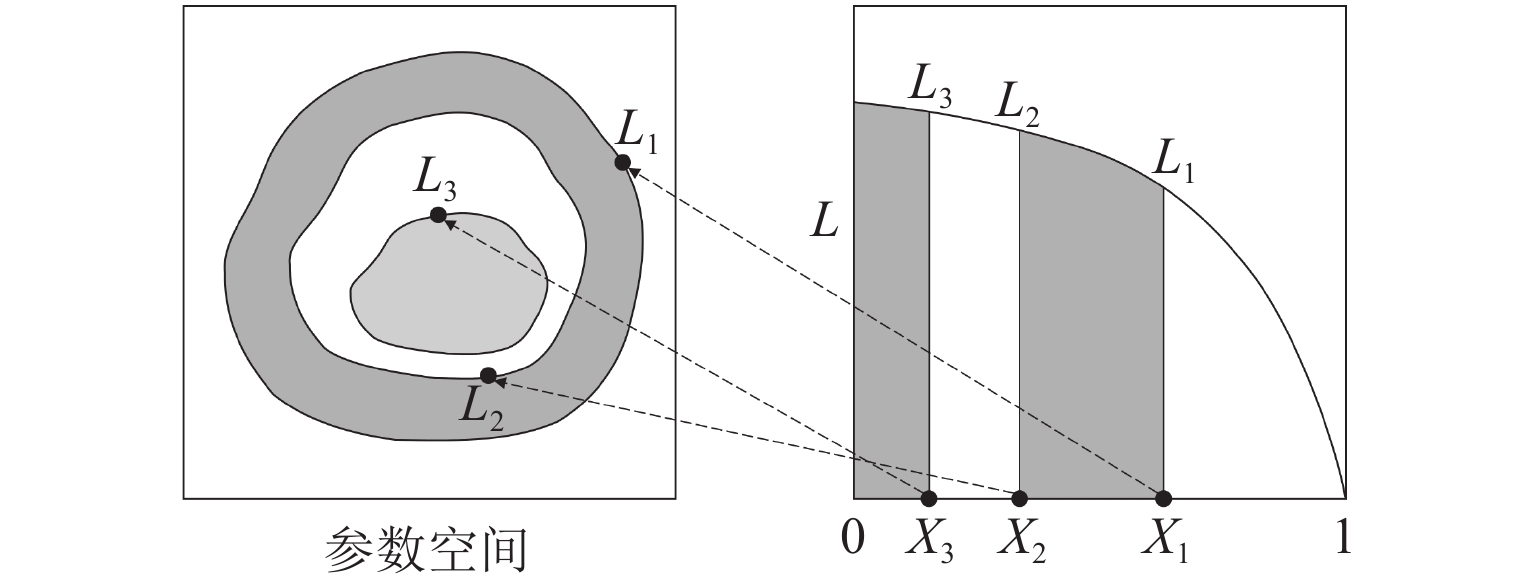
在基于有限元模型的桥梁健康监测中，贝叶斯模型修正技术通常被用于量化有限元模型中重要参数的不确定性，以解决模型修正中由于测量误差、建模误差、计算误差等造成的非唯一解问题. 为解决由于大量调用有限元模拟运算，导致修正效率低下的问题，基于自适应嵌套抽样（ANS）算法，提出一种贝叶斯模型修正方法. 该方法利用模态参数构建概率目标函数，并采用 ANS 算法对其进行逼近，ANS 保留了嵌套抽样（NS）的性质，通过逐层缩小抽样范围，使得样本最终逼近最优参数；通过逐层近似，将高维积分问题转化为简单的一维积分问题，简化了证据值和后验概率密度值的计算过程；在此基础上，ANS 算法在迭代过程中通过自适应地调整样本数量，减少对有限元模型的调用；最后，对一座人行桁架桥进行了贝叶斯有限元模型修正试验. 结果表明：在相同算法参数设置下，ANS 算法相比传统 NS 算法降低了约 84% 的有限元模拟调用次数，节省了约 86% 计算时间，并能获得同等精度的不确定性修正结果.
Abstract:In bridge health monitoring based on finite element models, Bayesian model updating techniques are commonly used to quantify the uncertainties of important parameters in the finite element models, so as to address the issue of non-uniqueness in model updating caused by measurement errors, modeling errors, computational errors, etc. To resolve the problem of low efficiency in model updating due to the large number of finite element simulations required, a Bayesian model updating method based on an adaptive nested sampling (ANS) algorithm was proposed. The method used the modal parameters to construct the probability objective function and adopted the ANS algorithm to approximate it. ANS retained the nature of nested sampling (NS), which made the samples ultimately approximate the optimal parameters by narrowing the sampling range layer by layer, and it simplified the computation process of the evidence value and the a posteriori probability density value by transforming the high-dimensional integration problem into a simple one-dimensional integration problem through layer-by-layer approximation. On this basis, the ANS algorithm could also reduce the call of the finite element model by adaptively adjusting the number of samples during the iteration process. Finally, a pedestrian truss bridge was used as a case study for Bayesian finite element model updating experiments. The results demonstrate that under the same algorithm parameter settings, the ANS algorithm reduces the number of finite element simulation calls by approximately 84% compared to the traditional NS algorithm. This leads to approximately 86% computational time savings while obtaining uncertainty updating results with equal accuracy.
-
图 5 修正参数各分量的收敛过程
Figure 5. Convergence processes of each component of updated parameters
图 6 修正参数各分量的收敛过程
Figure 6. Convergence processes of each component of updated parameters
表 1 模态参数识别结果
Table 1. Modal parameter identification results
序号 方向 模态阶数 频率/Hz 振型 1 横向弯曲 测试结果 4.140 
初始 ANSYS
模型模拟结果4.484 
2 竖向弯曲 测试结果 4.620 
初始 ANSYS
模型模拟结果4.552 
3 横向剪切 测试结果 6.895 
初始 ANSYS
模型模拟结果7.093 
4 纵向扭转 测试结果 8.598 
初始 ANSYS
模型模拟结果9.307 
5 竖向弯曲 测试结果 10.448 
初始 ANSYS
模型模拟结果10.709 
下载: 导出CSV
表 2 修正参数初始值及取值范围
Table 2. Initial values and range of updated parameters
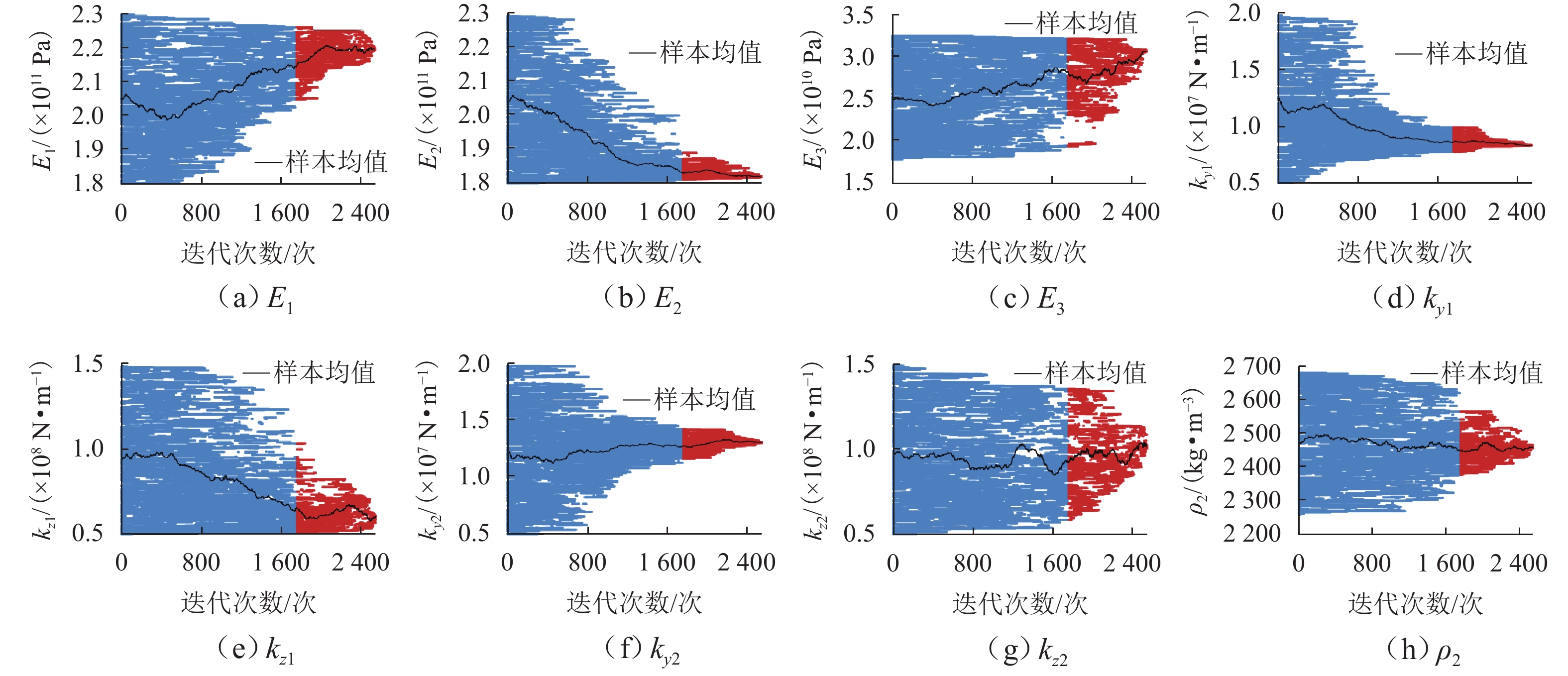
参数 初始值 下限 上限 数值 θ 值 数值 θ 值 数值 θ 值 E1/Pa 2.00 × 1011 1.00 1.80 × 1011 0.90 2.30 × 1011 1.15 E2/Pa 2.00 × 1011 1.00 1.80 × 1011 0.90 2.30 × 1011 1.15 E3/Pa 2.00 × 1010 1.00 1.75 × 1010 0.88 3.25 × 1010 1.63 ky1/（N·m−1） 1.50 × 107 1.00 4.95 × 106 0.33 2.00 × 107 1.33 kz1/（N·m−1） 1.00 × 108 1.00 5.00 × 107 0.50 1.50 × 108 1.50 ky2/（N·m−1） 1.50 × 107 1.00 4.95 × 106 0.33 2.00 × 107 1.33 kz2/（N·m−1） 1.00 × 108 1.00 5.00 × 107 0.50 1.50 × 108 1.50 ρ2/（kg·m−3） 2.48 × 103 1.00 2.26 × 103 0.91 2.68 × 103 1.08
下载: 导出CSV
表 3 ANS修正结果
Table 3. Updated results of ANS method
参数 最大后验概率参数 90% 置信下限 90% 置信上限 数值 θ 值 变化率/% 数值 θ 值 数值 θ 值 E1/Pa 2.19 × 1011 1.10 +10 2.04 × 1011 1.02 2.26 × 1011 1.13 E2/Pa 1.82 × 1011 0.91 −9 1.81 × 1011 0.91 1.89 × 1011 0.95 E3/Pa 3.06 × 1010 1.53 +53 1.94 × 1010 0.97 3.21 × 1010 1.60 ky1/（N·m−1） 0.84 × 107 0.56 −44 0.79 × 107 0.52 1.00 × 107 0.67 kz1/（N·m−1） 0.61 × 108 0.61 −39 0.51 × 108 0.51 1.04 × 108 1.04 ky2/（N·m−1） 1.32 × 107 0.88 −12 1.17 × 107 0.78 1.44 × 107 0.96 kz2/（N·m−1） 1.02 × 108 1.02 +2 0.59 × 108 0.59 1.36 × 108 1.36 ρ2/（kg·m−3） 2.46 × 103 0.99 −1 2.38 × 103 0.96 2.56 × 103 1.03
下载: 导出CSV
表 4 NS修正结果
Table 4. Updated results of NS method
参数 最大后验概率参数 90% 置信下限 90% 置信上限 数值 θ 值 变化率/% 数值 θ 值 数值 θ 值 E1/Pa 2.14 × 1011 1.07 +7 2.06 × 1011 1.03 2.14 × 1011 1.14 E2/Pa 1.82 × 1011 0.91 −9 1.82 × 1011 0.91 1.97 × 1011 0.99 E3/Pa 3.20 × 1010 1.60 +60 2.19 × 1010 1.10 3.20 × 1010 1.61 ky1/（N·m−1） 0.83 × 107 0.55 −45 0.81 × 107 0.54 0.97 × 107 0.65 kz1/（N·m−1） 0.62 × 108 0.62 −38 0.53 × 108 0.53 1.03 × 108 1.03 ky2/（N·m−1） 1.32 × 107 0.88 −12 1.22 × 107 0.81 1.53 × 107 1.02 kz2/（N·m−1） 1.06 × 108 1.06 +6 0.61 × 108 0.61 1.38 × 108 1.38 ρ2/（kg·m−3） 2.42 × 103 0.98 −2 2.38 × 103 0.96 2.60 × 103 1.05
下载: 导出CSV
表 5 修正后模态频率对比
Table 5. Comparison of updated modal frequencies
模态频率/Hz 测试值/Hz 初始值/Hz 初始误差/% NS 修正值/Hz NS 误差/% ANS 修正值/Hz ANS 误差/% 1 4.140 4.484 8.30 4.162 0.53 4.159 0.47 2 4.620 4.552 −1.47 4.627 0.15 4.617 −0.06 3 6.895 7.093 2.87 6.930 0.51 6.938 0.63 4 8.598 9.307 8.24 8.580 −0.21 8.552 −0.54 5 10.448 10.709 2.50 10.492 0.42 10.463 0.15 注：相对误差＝（修正值−测试值）/测试值.
下载: 导出CSV
-
[1] MEI Z, WU B, BURSI O S, et al. Hybrid simulation with online model updating: application to a reinforced concrete bridge endowed with tall piers[J]. Mechanical Systems and Signal Processing, 2019, 123: 533-553. doi: 10.1016/j.ymssp.2019.01.009 [2] CHEN Z, SUN H. Sparse representation for damage identification of structural systems[J]. Structural Health Monitoring, 2020, 20(4): 1644-1656. [3] MO J, WANG L, GU K X. A two-step interval structural damage identification approach based on model updating and set-membership technique[J]. Measurement, 2021, 182: 109464.1-109464.19. [4] PU Q H, HONG Y, CHEN L J, et al. Model updating-based damage detection of a concrete beam utilizing experimental damped frequency response functions[J]. Advances in Structural Engineering, 2019, 22(4): 935-947. doi: 10.1177/1369433218789556 [5] ZENG J C, KIM Y H. Identification of structural stiffness and mass using bayesian model updating approach with known added mass: numerical investigation[J]. International Journal of Structural Stability and Dynamics, 2020, 20(11): 2050123.1-2050123.31. [6] ASTROZA R, ALESSANDRI A, CONTE J P. A dual adaptive filtering approach for nonlinear finite element model updating accounting for modeling uncertainty[J]. Mechanical Systems and Signal Processing, 2019, 115: 782-800. doi: 10.1016/j.ymssp.2018.06.014 [7] 万华平,任伟新,黄天立. 基于贝叶斯推理的随机模型修正方法[J]. 中国公路学报,2016,29(4): 67-76,95. doi: 10.3969/j.issn.1001-7372.2016.04.009WAN Huaping, REN Weixin, HUANG Tianli. Stochastic model updating approach by using Bayesian inference[J]. China Journal of Highway and Transport, 2016, 29(4): 67-76,95. doi: 10.3969/j.issn.1001-7372.2016.04.009 [8] JOUBERT D J, MARWALA T. Monte Carlo dynamically weighted importance sampling for finite element model updating[M]//Conference Proceedings of the Society for Experimental Mechanics Series. Cham: Springer International Publishing,2016: 303-312. [9] 彭珍瑞,郑捷,白钰,等. 一种基于改进MCMC算法的模型修正方法[J]. 振动与冲击,2020,39(4): 236-245.PENG Zhenrui, ZHENG Jie, BAI Yu, et al. A model updating method based on an improved MCMC algorithm[J]. Journal of Vibration and Shock, 2020, 39(4): 236-245. [10] 秦世强,廖思鹏,黄春雷,等. 基于自适应Kriging模型的人行斜拉桥有限元模型修正[J]. 中山大学学报(自然科学版)(中英文),2021,60(6): 43-53.QIN Shiqiang, LIAO Sipeng, HUANG Chunlei, et al. Adaptive Kriging model based finite element model updating of a cable-stayed pedestrian bridge[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2021, 60(6): 43-53. [11] 王其昂,王腾,倪一清. 基于卷积神经网络的高铁车轮损伤识别方法研究[J]. 中国矿业大学学报,2020,49(4):781-787.WANG Qi’ang, WANG Teng, NI Yiqing. Damage detection of wheels for high-speed rail based on convolutional neural network[J]. Journal of China University of Mining & Technology, 2020, 49(4):781-787. [12] SKILLING J. Nested sampling for general Bayesian computation [J]. Bayesian Analysis, 2006, 1:833-859. [13] HANDLEY W J, HOBSON M P, LASENBY A N. Polychord: next-generation nested sampling[J]. Monthly Notices of the Royal Astronomical Society, 2015, 453(4):4384-4398. [14] CAO T T, ZENG X K, WU J C, et al. Integrating MT-DREAMzs and nested sampling algorithms to estimate marginal likelihood and comparison with several other methods[J]. Journal of Hydrology, 2018, 563: 750-765. doi: 10.1016/j.jhydrol.2018.06.055 [15] HIGSON E, HANDLEY W J, HOBSON M P, et al. Dynamic nested sampling: an improved algorithm for parameter estimation and evidence calculation[J]. Statistics and Computing, 2019, 29(5): 891-913. doi: 10.1007/s11222-018-9844-0 [16] TRASSINELLI M, CICCODICOLA P. Mean shift cluster recognition method implementation in the nested sampling algorithm[J]. Entropy, 2020, 22(2): 185. doi: 10.3390/e22020185 [17] QIAN F, ZHENG W. An evolutionary nested sampling algorithm for Bayesian model updating and model selection using modal measurement[J]. Engineering Structures, 2017, 140: 298-307. doi: 10.1016/j.engstruct.2017.02.048 [18] XU X K, HONG Y, CHEN L J, et al. Hybrid nested sampling method for identifying the uncertainty of the high-dimensional updating parameters in Bayesian structural model updating[J]. Advances in Structural Engineering, 2022, 25(8): 1730-1744. doi: 10.1177/13694332211069511 [19] 王坤阳,公茂盛,左占宣. 基于贝叶斯理论嵌套抽样的结构物理参数识别研究[J]. 振动与冲击,2022,41(7): 74-80.WANG Kunyang, GONG Maosheng, ZUO Zhanxuan. Structural physical parameter identification based on Bayesian theory and nested sampling[J]. Journal of Vibration and Shock, 2022, 41(7): 74-80. [20] 杨朋超,薛松涛,谢丽宇. 消能减震建筑结构的贝叶斯有限元模型修正[J]. 土木工程学报,2021(S01): 13-19,47.YANG Pengchao, XUE Songtao, XIE Liyu. Bayesian finite-element model updating of passively controlled building structures[J]. China Civil Engineering Journal, 2021(S01): 13-19,47. [21] NEAL R M. Slice sampling[J]. The Annals of Statistics, 2003, 31(3): 705-767. [22] DONG X J, WANG Y. A comparative study of frequency-domain finite element updating approaches using different optimization procedures[C]//8th European Workshop on Structural Health Monitoring (EWSHM 2016). Bilbao: [s.n.],2016: 1-10. [23] 洪彧. 基于振动信号的桥梁结构模态参数识别与模型修正研究[D]. 成都:西南交通大学,2019. -
下载:
点击查看大图
计量
- 文章访问数: 128
- HTML全文浏览量: 56
- PDF下载量: 9
- 被引次数: 0