Determination Method of Rock Strength Based on Digital Drilling Parameters
-
摘要:
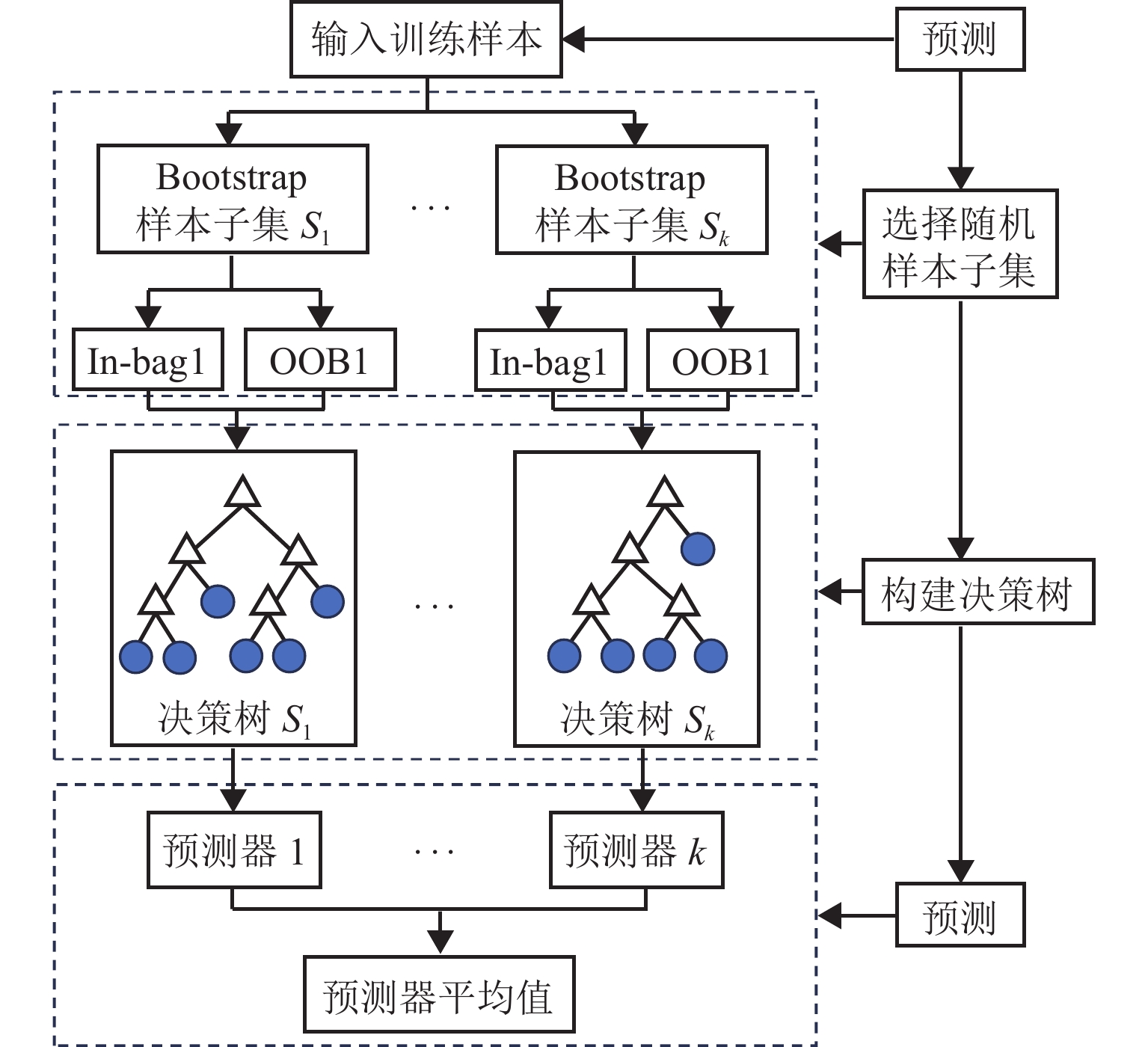
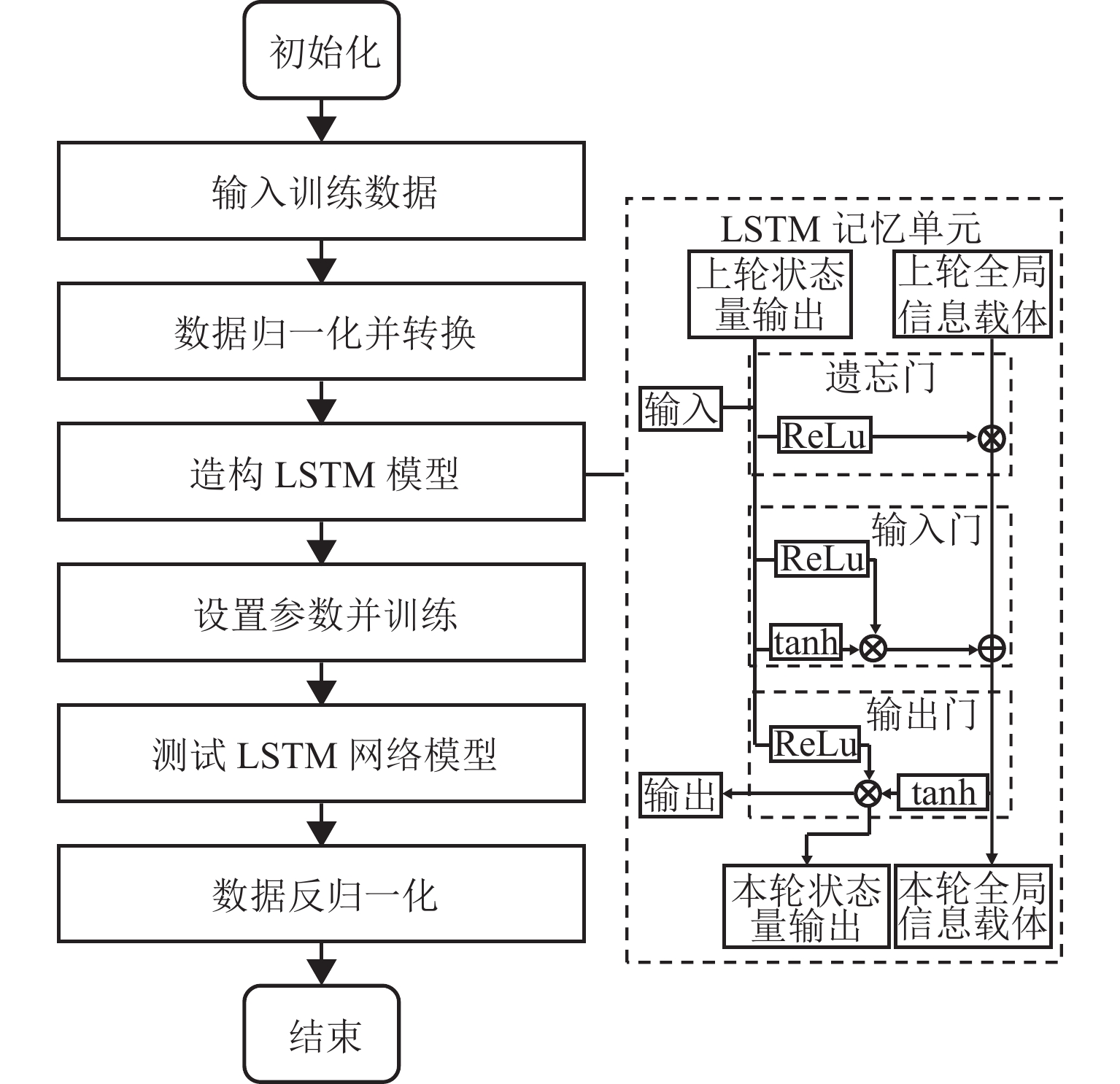
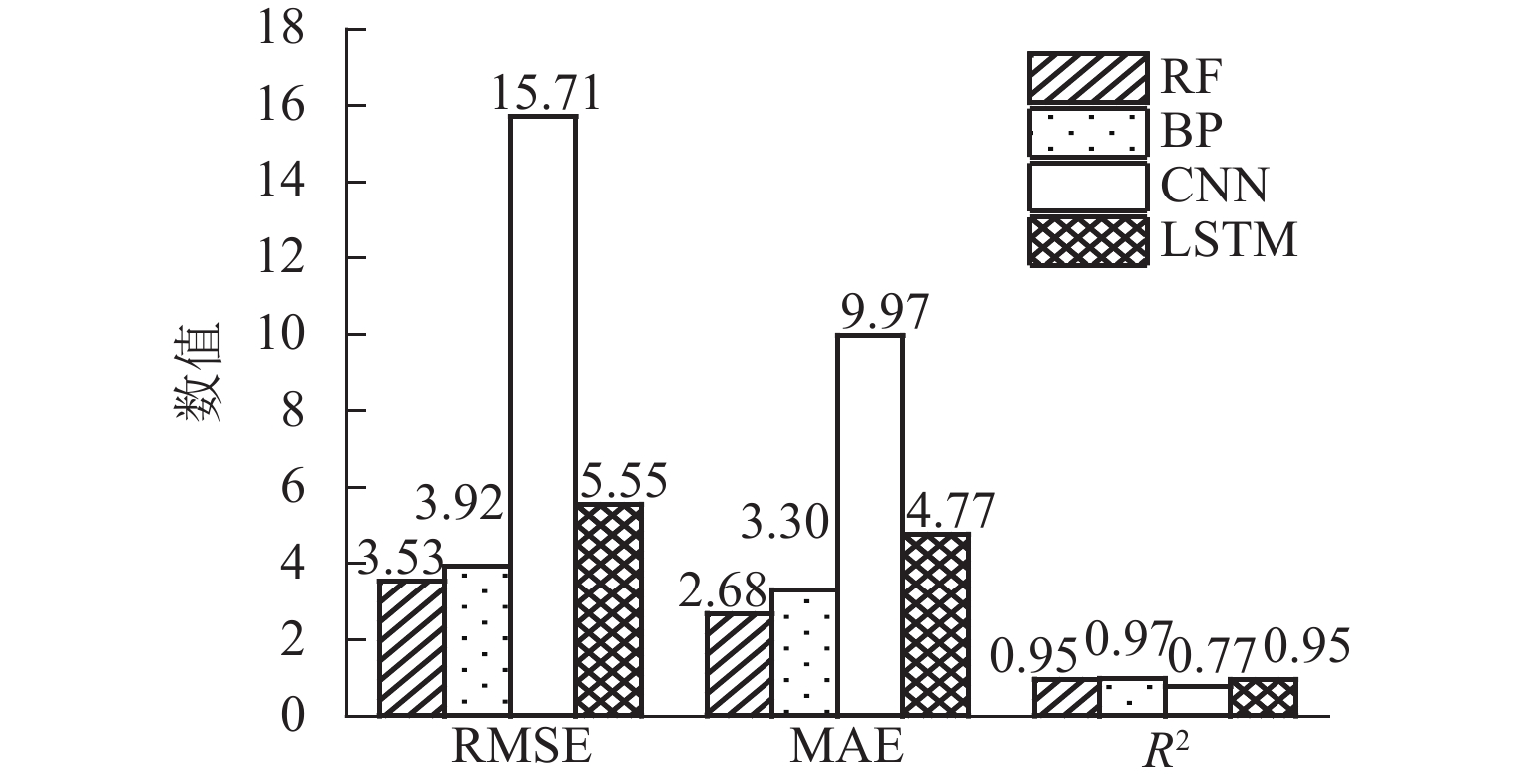
岩石强度是衡量岩石稳定性和安全性的关键参数，而高效准确地预测岩石强度可以有效指导隧道的开挖和支护工作. 本文收集分析源于不同设备的数字钻进参数和岩石力学性质相关数据，基于钻进过程中的能量传递分析建立数字钻进参数与单轴抗压强度的定量关系；采用机器学习方法建立基于钻进参数的岩石强度预测模型，选择BP神经网络、随机森林、卷积神经网络和长短期记忆网络4种算法比较不同算法的预测效果，最终确定最优模型. 结果显示：相对于理论公式和其他3种机器学习算法，BP神经网络算法在岩石强度预测中表现优秀，其预测结果的均方根误差为5.794，平均绝对误差为4.129，相关系数为
0.9749 .Abstract:Rock strength is a critical parameter for assessing rock stability and safety. Efficient and accurate prediction of rock strength can effectively guide tunnel excavation and support. Digital drilling parameters and mechanical property data of rock were collected from various devices. By analyzing energy transfer during the drilling process, a quantitative relationship between digital drilling parameters and uniaxial compressive strength (UCS) was established. Meanwhile, machine learning methods were employed to develop a rock strength prediction model based on drilling parameters. Four algorithms, including a back-propagation (BP) neural network, random forest, convolutional neural network (CNN), and long short-term memory network were chosen to compare their prediction effects and identify the optimal model. The results indicate that compared to the theoretical formulas and the other three machine learning algorithms, the BP neural network algorithm excels in rock strength prediction, with a root mean square error of 5.794, a mean absolute error of 4.129, and a correlation coefficient of
0.9749 .-
Key words:
- drilling parameters /
- energy method /
- compressive strength /
- neural networks /
- random forests
-
有限元模型修正是通过实测信息获取结构的高可信度有限元模型的一种技术手段，常用于工程领域中的结构检测监测[1-2]、损伤识别[3-4]、结构参数识别[5]等方面. 其中，贝叶斯模型修正是一种不确定性有限元模型修正技术[6]，考虑多种不确定性因素（测量误差、建模误差、计算误差等），主要具有以下优点：1） 模型修正目标函数为概率密度函数，其结果能方便地量化修正参数的不确定性，同时能够利用统计量（均值、方差、置信区间等）来表示非唯一解；2） 基于贝叶斯推断能够很好地结合先验知识（主观经验、试验数据规律等），提高推断的精度和效率；3） 通过正向模型计算代替复杂的逆向计算（梯度计算、病态矩阵、非唯一解等）.
然而，贝叶斯模型修正问题的求解往往需要进行高维复杂积分，通常采用随机模拟的方法（也称蒙特卡罗模拟）来进行替代，主要包括：接受-拒绝抽样[7]、重要性抽样[8]、马尔科夫链蒙特卡洛抽样（ MCMC）[9]等. 以上方法虽然大幅提升了贝叶斯模型修正的求解效率，但存在需要采集大量样本、收敛性难以确定的缺点. 除此之外，在真实结构的模型修正问题中，有限元模型计算造成每单个样本就需要消耗大量计算时间. 为降低对有限元模型的调用，学者们提出基于代理模型或神经网络的有限元模型修正法[10- 11]. 该方法通过调用计算代价较低的代理模型代替有限元模型，从而达到提高模型修正效率的目的. 但是，在模型修正前，代理模型通常也需要通过大量的有限元模型计算来进行训练，并且由于代理模型本身为新引入的模型，也存在不准确和误差引入的问题. 因此，若能在模型修正过程中减少对有限元模型的调用，将对贝叶斯有限元模型修正的应用具有重要意义.
嵌套抽样（NS）[12]是一种近年才发展出来的贝叶斯问题求解方法，其特点在于收敛性明确，且能够在不进行额外计算的情况下，同时计算贝叶斯证据因子，并获得后验分布样本集. NS 方法的核心思想是通过层层缩小先验样本范围，从而逐步逼近目标分布，并收敛于全局最优值附近，并通过建立层间先验质量的比例关系，将高维的复杂积分转化为一维的简单积分，从而直接估计出贝叶斯证据因子. 由于标准 NS 方法要求在每层抽样中所有选取的新样本都要满足在上一层样本集所围成的范围内，并且在本层中均匀分布，因此，如何高效的完成每层样本抽取就成为改进 NS 研究的重点及难点之一. 近年来，也出现了很多 NS 的改进研究，例如：Handley 等[13]提出一种 PolyChord 算法，该算法在 NS 的基础上，利用切片采样生成似然约束内的新样本； Cao等[14]将 MT-DREAMzs （multi-try differential evolution adaptive metropolis with z-scores）算法融入 NS，提高搜索复杂概率空间的效率； Higson 等[15]提出动态 NS 算法，通过动态设置活样本的数量来提高后验概率的精度； Trassinelli 等[16]提出基于均值移位聚类的 NS 算法，提高样本空间搜索效率. 另外，NS 方法在贝叶斯结构模型修正领域的研究还处于探索阶段：Qian 等[17]将基于遗传算法的 NS 方法应用于钢桁架结构的贝叶斯模型修正中；Xu 等[18]提出混合 NS 方法并应用于多层框剪结构的贝叶斯模型修正； 王坤阳等[19]通过修改先验概率和似然函数的方法改进了 NS 算法，并通过 RC 框架结构振动台试验进行验证. 以上方法都在一定程度上提高了贝叶斯模型修正效率，但大多属于空间搜索层面的效率提升. 由于实际工程中的贝叶斯模型修正通常会涉及大型的有限元模型计算，如果所需样本数量过大，则会令贝叶斯模型修正的计算量陡增. 因此，急需一种改进的 NS 方法来调控迭代过程中所需的样本数量，以适应工程中的贝叶斯模型修正.
本文提出一种自适应嵌套抽样（ ANS）方法来进行贝叶斯模型修正问题的求解，该方法根据迭代过程中样本边界的收缩率来实现自适应的样本数调控，在保证修正结果的基础上，达到降低有限元模型调用次数的目的，从而提高具有复杂有限元模型的贝叶斯模型修正效率.
1. 贝叶斯模型修正理论
1.1 结构模型修正理论
结构模型修正的基本方法是通过调整待修正的模型参数（也称修正参数），来最小化有限元模型的预测数据与对应的实际结构测试数据之间的误差，从而得到最优的模型参数，即修正结果，其表达式为
argminθe(θ,M)=argminθ∑tαt|yt(θ,M)−ˆytˆyt|, (1) 式中：θ为修正参数，记 θ=(θ1,θ2, ⋯ ,θn)T；M 为待修正的有限元模型；e(θ,M)为总误差值；ˆyt为所考察的第 t 个指标的测试数据；yt(θ,M) 为第t个指标的预测数据； αt 为第 t 个指标的权重值.
本文采用基于动力学响应的模型修正方法，因此，yt(θ,M) 与 ˆyt 为动力学指标，主要包含固有频率 ω 和模态振型 ϕ=(φ1,φ2,⋯,φs)T（s 为布置的测点数）. 考虑到测量精度和参数识别能力有限，仅使用前 r 阶的固有频率和模态振型.
在实际测试中，测试数据往往是不确定的，因此，有必要对测试数据的不确定性进行量化. 本文将引入基于贝叶斯推断的不确定性模型修正理论来求解问题.
1.2 贝叶斯推断
贝叶斯模型修正理论最基本的贝叶斯定理公式为
p(θ,M|D)=p0(D|θ,M)p1(θ,M)p2(D), (2) 式中：p(θ,M|D) 为后验概率，指在数据集 D 的条件下，有限元模型 M 中修正参数为θ出现的概率；p0(D|θ,M) 为似然函数，指当有限元模型 M 中修正参数为θ时，测得数据集为 D 的概率；p1(θ,M) 为先验概率，指有限元模型 M 中修正参数为θ的概率，通常由经验或前期采样试验给出；p2(D) 为证据因子，是保证后验概率为 0～1 的控制常数，可由式（3）计算得到.
p2(D)=∫Θp0(D|θ,M)p1(θ,M)dθ, (3) 式中：Θ为修正参数为θ的样本集.
在式（2）的基础上，利用式（1）就可以构造贝叶斯模型修正目标函数. 假设误差呈正态分布，即e(θ,M)～N(μ,σ2)，其中均值 μ = 0. 则似然函数[20]为
p(D|θ,M)=∏D1σ√2πexp(−(e(θ,M))22σ2). (4) 若数据集 D 包含多组测试，则似然函数是通过各组误差的似然函数的联合概率得出.
将式（3）、（4）代入式（2）即可得到关于修正参数θ的后验概率表达式.
2. 改进的自适应嵌套抽样方法
2.1 标准嵌套抽样
假设 p1(θ,M) 为均匀分布，记作 ρ(θ)；定义 L(X)=min{L(θ)}=min{p0(D|θ,M)}，表示似然值大于p0(D|θ,M)区域最小似然值；dX=ρ(θ)dθ为分布质量X(λ)（λ为理论的最小似然值）的微元. 其中：L(θ)、(L(x)) 分别为样本θ （边缘上样本点）的 p0(D|θ,M)值，dθ为参数空间的微元. 则原本的高维积分问题就可以被转化为关于分布质量 X 的一维积分问题[17]. 定义
X(λ)=∫L(θ)>λρ(θ)dθ. (5) X(λ) 将随着 λ 的增大，逐渐从 1 减小到 0. 则式（3）可以转化为
p2(D)≈12m−1∑i=1(Xi−1−Xi)(Li−1+Li), (6) 式中：X、L分别为测点的分布质量和对应的函数，将分布质量 X(λ) 从 1 到 0 离散化，则有 0<Xm<⋯<X2<X1<X0=1，对应的区域最小似然值为 Lm>⋯>L2>L1>L0=0；下标 i 为嵌套的层数，即第 i 次迭代对应的层数；m 为最大层数.
通过以上推导，整个问题的关键是对分布质量 Xi 以及对应的函数 Li 的估计. 此时，可经过层层嵌套抽样的方法来确定每层的 Xi 和 Li，最终利用式（6）计算出 p2(D). 如图1 所示，当参数空间只有3个维度时，似然值 L1、L2、L3 所围成的曲线可以视作各嵌套层的等高线，X1、X2、X3 可以视作对应层的面积，则左侧的高维复杂积分就能被简化为右侧的一维简单积分.
在参数空间中，通过各层的 Li 即可确定对应的样本分布范围，而每层样本都对应了各自的分布质量 Xi. 根据等比例缩小原则，Xi 可以通过式（7）计算得到.
Xi=(NN+1)i≈e−iN, (7) 式中：N为初始样本数.
2.2 自适应嵌套抽样
在实际使用当中，NS 方法还存在一些缺陷. 特别是随着嵌套层数的增大，随机抽样的范围会收缩到很小. 此时如果要在初始条件下随机抽到满足L(θ)大于Li要求的样本点的概率会非常小，从而导致计算效率急剧下降，甚至无法工作. 因此，需要改进每层中嵌套范围内获取均匀分布样本的抽样方法. 本文采用超立方收缩法予以解决. 超立方收缩法在原理上与切片抽样（Slice Sampling）方法[21]类似. 该方法是在参数空间中，以超立方矩形的形式逐渐收缩抽样范围，并在收缩后的抽样范围内进一步采取均匀抽样策略，从而提高抽样效率. 以二维参数空间为例，如图2 所示，其中：实线内部（A、C）为目标区域、B为非目标区域；矩形虚线内部为抽样范围，随着嵌套层数的增加，该范围会逐渐缩小，并使样本点最终落入目标区域中.
此外，在有限元模型修正问题中，涉及到土木结构的有限元模型计算，因此，相比于其他应用场景，往往单次的计算量就具有相当大的规模. 所以，合理地缩小样本集将极大的提高模型修正效率. 本文提出自适应嵌套抽样（ANS）算法，根据每层边界总长度的变化，自适应地匹配样本数量，从而达到减少有限元模型计算量的目的.
与标准 NS 算法不同的是，ANS 算法在每一层抽样之前，需要先进行样本数量判定. 本算法根据超立方边界总长度收缩率来实现自适应的样本点数调控，判定规则如式（8）所示.
Ni=ceil(Nn∑j=1|Bi,j−Si,j|n∑j=1|B0,j−S0,j|), (8) 式中：Ni 为第i层的样本数；Bi,j和Si,j分别为第i层的样本集在第j个维度上的最大值和最小值，j=1,2,⋯,n；B0,j和S0,j分别为初始样本集在第j个维度上的最大值和最小值；ceil(•)为向上取整函数.
在第i层中，样本集为 {θ1,θ2,⋯,θNi}，对应的似然值集合为{L(θ1),L(θ2),⋯,L(θNi)}. 令其中似然值最小的样本为θworst，则Li=L(θworst). 在迭代过程中，当 Ni−1>Ni 时，删去样本 θworst，且不抽取新的样本点； 当 Ni−1=Ni 时，则与标准 NS 流程相同. 为保证 Ni 不至于缩减到0，设置最小样本数 Nmin； 当 Ni<Nmin 时，Ni=Nmin.
由于样本数随嵌套层数过程发生改变，因此，Xi 的计算需要进行式（9）的调整，
Xi=∏iNiNi−1+1, (9) 式中：N0=N.
为防止模型修正无限制的进行下去，采取以下终止条件：
1） 当嵌套层数超过预设最大值时.
2） 当样本集在各个维度上的集中程度均达到阈值时. 集中程度通过样本集在各个维度上的最大值Bi,j与最小值Si,j来评价，如式（10）所示，当 ∑nj=1f(j)=n 时，终止迭代.
f(j)={1，|Bi,j−Si,j|⩽ (10) 式中： {\varepsilon _j} 为样本集在第 j 个维度上极差的阈值.
自适应嵌套抽样算法流程如图3所示.
该方法的主要流程大致可以分为样本数自适应调整过程、嵌套抽样过程及超立方收缩过程. 其中，样本数自适应调整过程基于超立方边界总长度收缩公式，对样本数进行合理的配置，大大降低了有限元计算的调用频率；嵌套抽样过程包括样本采样、样本筛选和剔除，对参数空间进行高效而合理的探索；超立方收缩过程大大提高了样本的筛选与剔除的效率.
3. 人行桁架桥试验
3.1 结构概况与有限元模拟
本文以一座位于美国佐治亚理工校园内的在役人行桥为研究对象（如图4 (a)）. 由于该桥已过长期服役，又处于人流量较多的通行要道，因此，通过模型修正的办法定期获取其结构参数的变化情况，能够有效帮助我们发现桥梁的缺陷，从而避免潜在的安全隐患，确保桥梁的安全性.
该桥为钢桁架简支梁桥，共由 11 个节段组成，全桥总长 30.18 m、宽 2.13 m、高 2.74 m. 主弦杆采用3种不同截面尺寸的 Q345 方形空心钢管，材料设计参数为：密度 7.78 × 103 kg/m3、弹性模量 2.00 × 1011 N/m2. 斜撑杆采用6种不同截面尺寸的 Q345 实心圆钢管，材料设计参数与主弦杆相同. 桥面铺装为 C20 混凝土，材料设计参数为：密度 2.48 × 103 kg/m3、弹性模量 2.00 × 1010 N/m2. 两端支座采用橡胶支座，设计参数为：竖向刚度 1.00 × 108 N/m、横向刚度 1.50 × 107 N/m. 该桥更详细的描述可参考文献[22]. 通过ANSYS软件建立该桥的基准有限元模型. 其中，主弦杆采用梁单元（BEAM188），斜撑杆采用杆单元（LINK180），桥面板采用壳单元（SHELL181），桥底的橡胶支座采用弹簧单元（COMBIN14）来模拟. 整个模型共含有 298 个节点和 466 个单元（如图4 （b））. 图4（b）中：ky1、kz1为左端支座横向和竖向弹簧刚度，ky2、kz1为右端支座横向弹簧刚度 、右端支座竖向弹簧刚度.
3.2 锤击试验
在进行有限元模型修正之前，需提前获取该桥的模态参数信息. 本文采取人行桥锤击试验法，获取其前 5 阶模态参数. 试验中，在结构周身杆件连接处共布置了 46 个测点，试验采集了每个测点的横向和竖向加速度，加速度传感器为Silicon Designs2260-010，冲击力锤采用PCB Model 086D20，详细试验过程参考团队前期研究[23]. 模态参数识别结果见表1（表中结果为多次测量后的平均值）.
表 1 模态参数识别结果Table 1. Modal parameter identification results序号 方向 模态阶数 频率/Hz 振型 1 横向弯曲 测试结果 4.140 
初始 ANSYS
模型模拟结果4.484 
2 竖向弯曲 测试结果 4.620 
初始 ANSYS
模型模拟结果4.552 
3 横向剪切 测试结果 6.895 
初始 ANSYS
模型模拟结果7.093 
4 纵向扭转 测试结果 8.598 
初始 ANSYS
模型模拟结果9.307 
5 竖向弯曲 测试结果 10.448 
初始 ANSYS
模型模拟结果10.709 
3.3 贝叶斯模型修正
在进行桁架桥有限元模型修正之前，首先需要选取待修正的模型参数. 需要注意的是，初始有限元模型中其实存在大量可调节的模型参数，但如果选择过多修正参数，可能导致计算量过大，而无法完成. 相反，如果选择的修正参数过少，有可能达不到模型修正的目的. 在本案例中，未发现明显的局部损伤迹象，因此，初选取的修正参数均为整体范围的材料参数，包括：主弦杆弹性模量 E1、斜撑杆弹性模量 E2、混凝土弹性模量 E3、左端支座横向弹簧刚度 ky1、左端支座竖向弹簧刚度 kz1、右端支座横向弹簧刚度 ky2、右端支座竖向弹簧刚度 kz2、钢材密度 ρ1、混凝土板密度 ρ2. 为避免在模型修正过程中发生同向耦合变化的现象，本文假设钢材密度参数 ρ1 保持不变. 因此，最终选定8个修正参数为E1、E2、E3、ky1、kz1、ky2、kz2、ρ2为方便表示，分别将修正参数归一化（与设计值之比），并记作θ. 考虑到修正参数的变化过大是不合理的，因此，根据经验设定了修正参数的取值范围，如表2 所示. 其中，在材料参数方面，主要考虑均匀性与稳定性的影响，因此除混凝土刚度以外均设置了较小的可修正范围. 由于支座的不确定因素较多，因此适当扩大了修正范围.
表 2 修正参数初始值及取值范围Table 2. Initial values and range of updated parameters参数 初始值 下限 上限 数值 θ 值 数值 θ 值 数值 θ 值 E1/Pa 2.00 × 1011 1.00 1.80 × 1011 0.90 2.30 × 1011 1.15 E2/Pa 2.00 × 1011 1.00 1.80 × 1011 0.90 2.30 × 1011 1.15 E3/Pa 2.00 × 1010 1.00 1.75 × 1010 0.88 3.25 × 1010 1.63 ky1/（N·m−1） 1.50 × 107 1.00 4.95 × 106 0.33 2.00 × 107 1.33 kz1/（N·m−1） 1.00 × 108 1.00 5.00 × 107 0.50 1.50 × 108 1.50 ky2/（N·m−1） 1.50 × 107 1.00 4.95 × 106 0.33 2.00 × 107 1.33 kz2/（N·m−1） 1.00 × 108 1.00 5.00 × 107 0.50 1.50 × 108 1.50 ρ2/（kg·m−3） 2.48 × 103 1.00 2.26 × 103 0.91 2.68 × 103 1.08 3.3.1 自适应嵌套抽样（ANS）结果
设好修正参数后，基于初始有限元模型及模态测试数据即可进行贝叶斯模型修正. 本次模型修正采用ANS算法. 假设先验分布为均匀分布，目标函数的标准差为0.002. 并按如下设置超参数：最大嵌套层数为
12000 层，初始活样本个数为 200 个，集中程度阈值为 0.03. 通过 MATLAB 的 MATLABrunANSYS函数进行有限元模型调用，并通过编程完成该人行桥的贝叶斯模型修正，总共进行了2 545 次迭代，调用有限元模拟12 508 次，在硬件配置为 Intel（R） Core（TM） i7-6800K CPU @ 3.40GHZ 3.10 GHz 的条件下，用时约 4.43 h. 得到修正参数分布及其收敛过程，如表3 和图5 所示. 计算得出证据因子 ln p2(D) 约为 −269.8755 ，并在其基础上绘制了 90% 置信区间（即置信度CI大于 90% 的区间），如图5 中红色范围所示.表 3 ANS修正结果Table 3. Updated results of ANS method参数 最大后验概率参数 90% 置信下限 90% 置信上限 数值 θ 值 变化率/% 数值 θ 值 数值 θ 值 E1/Pa 2.19 × 1011 1.10 +10 2.04 × 1011 1.02 2.26 × 1011 1.13 E2/Pa 1.82 × 1011 0.91 −9 1.81 × 1011 0.91 1.89 × 1011 0.95 E3/Pa 3.06 × 1010 1.53 +53 1.94 × 1010 0.97 3.21 × 1010 1.60 ky1/（N·m−1） 0.84 × 107 0.56 −44 0.79 × 107 0.52 1.00 × 107 0.67 kz1/（N·m−1） 0.61 × 108 0.61 −39 0.51 × 108 0.51 1.04 × 108 1.04 ky2/（N·m−1） 1.32 × 107 0.88 −12 1.17 × 107 0.78 1.44 × 107 0.96 kz2/（N·m−1） 1.02 × 108 1.02 +2 0.59 × 108 0.59 1.36 × 108 1.36 ρ2/（kg·m−3） 2.46 × 103 0.99 −1 2.38 × 103 0.96 2.56 × 103 1.03 
图 5 修正参数各分量的收敛过程Figure 5. Convergence processes of each component of updated parameters3.3.2 与普通嵌套抽样（NS）结果对比
为研究 ANS 算法性能，在保持各项算法配置、终止条件及硬件配置不变的条件下采用普通的嵌套抽样（NS）算法对该座人行桥进行贝叶斯模型修正. 运算总共迭代了
11 729 次，调用有限元模拟79 936 次，用时 32.70 h. 其修正参数分布及其收敛过程如表4 和图6 所示. 证据因子 ln p2（D） 约为 −280.3563.表 4 NS修正结果Table 4. Updated results of NS method参数 最大后验概率参数 90% 置信下限 90% 置信上限 数值 θ 值 变化率/% 数值 θ 值 数值 θ 值 E1/Pa 2.14 × 1011 1.07 +7 2.06 × 1011 1.03 2.14 × 1011 1.14 E2/Pa 1.82 × 1011 0.91 −9 1.82 × 1011 0.91 1.97 × 1011 0.99 E3/Pa 3.20 × 1010 1.60 +60 2.19 × 1010 1.10 3.20 × 1010 1.61 ky1/（N·m−1） 0.83 × 107 0.55 −45 0.81 × 107 0.54 0.97 × 107 0.65 kz1/（N·m−1） 0.62 × 108 0.62 −38 0.53 × 108 0.53 1.03 × 108 1.03 ky2/（N·m−1） 1.32 × 107 0.88 −12 1.22 × 107 0.81 1.53 × 107 1.02 kz2/（N·m−1） 1.06 × 108 1.06 +6 0.61 × 108 0.61 1.38 × 108 1.38 ρ2/（kg·m−3） 2.42 × 103 0.98 −2 2.38 × 103 0.96 2.60 × 103 1.05 
图 6 修正参数各分量的收敛过程Figure 6. Convergence processes of each component of updated parameters在算法效率方面，ANS的迭代次数仅为 NS 的21.7%，有限元模拟次数仅为15.6%，节省了86.4% 的运算时间. 可以看出， ANS算法极大程度的减少了抽样次数和有限元模拟次数，从而极大地提高了贝叶斯模型修正的效率. 在算法准确性方面，通过对比表3 和表4 的修正结果可以发现，ANS与NS算法得出的结果具有较高的一致性. 因此，ANS算法虽然牺牲了大量的抽样样本，但在计算准确度方面依然保持良好. 此外，从p2（D） 的计算结果来看，ANS依然保留了NS能快速计算p2（D） 值的特性. 总的来说，ANS算法通过自适应的动态调整每个嵌套层活性样本数量的方式，在保持结果可靠性的前提下，成功实现了NS算法在运算效率方面的大幅提升. 在实际工程场景下，对所用方法的灵活性和时效性都具有较高的要求，NS算法虽然无需预训练，能满足灵活性需求，但由于实际工程中的有限元模型通常较为复杂，造成其在时效性上依然存在较大缺陷，因此，尽量避免大量调用有限元模型是在实际工程应用中提高效率的核心解决方案. 所以，相较于传统的NS算法，ANS更能适应实际工程场景下的贝叶斯模型修正.
3.4 修正结果分析
如表5 所示，初始有限元模型的模态频率与测试值之间的最大误差为 8.30%，通过模型修正后，最大误差下降到了 0.63%，即修正后的有限元模型相对于初始模型而言，更加贴近真实结构. 此外，NS、ANS 算法的最大误差分别为 0.53%、0.63%，表明 ANS 算法依旧保持了 NS 算法原有的修正精度.
表 5 修正后模态频率对比Table 5. Comparison of updated modal frequencies模态频率/Hz 测试值/Hz 初始值/Hz 初始误差/% NS 修正值/Hz NS 误差/% ANS 修正值/Hz ANS 误差/% 1 4.140 4.484 8.30 4.162 0.53 4.159 0.47 2 4.620 4.552 −1.47 4.627 0.15 4.617 −0.06 3 6.895 7.093 2.87 6.930 0.51 6.938 0.63 4 8.598 9.307 8.24 8.580 −0.21 8.552 −0.54 5 10.448 10.709 2.50 10.492 0.42 10.463 0.15 注：相对误差＝（修正值−测试值）/测试值. 如图5 、6 所示，通过贝叶斯模型修正，最终能够得到各修正参数的 90% 置信区间范围，即修正结果具有 90% 的概率落在该范围内. 该范围区间越小，代表修正结果的不确定性越低. 如图7 所示，绘制了各修正参数的 90% 置信区间范围相对于初始区间范围收缩率R图像，范围收缩率如式（11）所示. 收缩率越大，则对应不确定性越低.
R=1-\frac{|{B}_{i,j}-{S}_{i,j}|}{|{B}_{0,j}-{S}_{0,j}|}, (11) 式中：i取置信度为 90% 时的嵌套层数.
针对不同确定性的修正结果，对确定性高的结果分配更多资源并做更详细的解决方案，而对确定性低的结果保持更怀疑的态度并做针对性的策略调整. 据此，我们将修正参数分为以下 3 类（确定性低、中性、确定性高，以 30% 与 60% 为划分）来进行分析.
1） 收缩率超过 60% 的修正参数有 E2、ky1、ky2. 结合最大后验概率参数的变化量来看，E2、ky2 的变化率小于 15%，考虑测量误差的影响，可以判定 E2、ky2 参数变化不明显，属于安全合理范围. 而 ky1 的削减量则达到了 40% 以上，可能存在桥底橡胶支座老化问题，建议进行局部排查，以规避安全隐患.
2） 相对而言，收缩率在 30%～60% 的修正参数有 E1、kz1、ρ2. 虽然 kz1 存在较大的变化，但是由于修正结果存在较大的不确定性，所以暂不能通过目前的测试数据对其进行较确定性的评判. 因此，建议通过增加测试次数、提高测试精度、增加测试节点、提升测试的模态阶数等手段来进一步提高修正结果的确定性.
3） 此外，收缩率不足 30% 的修正参数有 E3、kz2. 由于其确定性过低，认为该2项参数对测试数据的敏感度极低，不适用于本识别方法. 因此，建议通过现场排查或其他检测手段来识别可能的潜在风险.
4. 结 论
贝叶斯有限元模型修正对桥梁健康监测、损伤识别等具有重要意义，抽样算法又是解决贝叶斯推断问题的关键技术. 本文改进了传统的 NS 算法，构造一种自适应嵌套抽样算法，即 ANS 算法. 并通过一座人行桥现场试验，证明基于 ANS 算法的贝叶斯模型修正是高效准确的.
1） 该方法通过在迭代过程中自适应地调整样本数量，极大程度地提高了嵌套抽样算法的运算效率. 与传统 NS 算法相比，在贝叶斯模型修正中，ANS 算法减少了 84.4% 的有限元模型调用，节省了约 86.4% 的运算时间.
2） 根据模型修正结果，ANS 相比于传统 NS 算法，在大幅提升计算效率的同时，依旧保持了较高的计算精度，修正后模态频率的相对误差最大不超过 0.63%，且保持了 NS 算法能直接计算证据因子的特性.
3） 本研究通过实际的人行桥试验，验证了基于 ANS 算法的贝叶斯模型修正方法在实际工程中的可行性，并体现了其在不确定性量化计算中的效率优势.
-
表 1 232组数字钻进样本
Table 1. 232 groups of digital drilling samples
组数 来源 强度/MPa 岩石类型 30 组 文献[9] 49.80～61.91 较硬砂岩 1.90～30.81 砂浆试件 45 组 文献[10] 1.98～116.09 砂岩 51 组 文献[11] 2.50～9.00 砂浆试件 36 组 文献[12] 49.80～61.91 较硬砂岩 1.90～35.21 砂浆试件 24 组 文献[13] 48.35～55.68 较硬砂岩 1.56～36.05 砂浆试件 6 组 文献[14] 81.90/69.20/
49.80/49.20完整花岗岩/灰岩/
粉砂岩/砂岩9.40 破碎砂岩 28.10 注浆砂岩 15 组 文献[15] 58.29/约10.89/19.98 完整/破碎/注浆砂岩 75.23/约13.44/21.23 完整/破碎/注浆灰岩 约9.11/约33.45/18.99 完整/破碎/注浆泥岩 1.59～16.49 砂浆试件 25 组 文献[16-17] 1.63～20.80 砂浆试件 
下载: 导出CSV
表 2 部分样本数据
Table 2. Part of sample data
序号 V/
（ mm·min−1）N/
（r·min−1）M/
（N·m）F/
kN岩石强
度/MPa1 105.70 100.00 6.19 0.03 3.29 2 87.94 100.00 7.30 0.02 2.58 3 138.95 100.00 8.38 0.05 3.22 4 124.80 50.00 17.01 0.03 2.37 5 118.08 100.00 21.44 2.07 10.60 6 132.05 100.00 22.34 2.15 10.54 7 83.85 50.00 28.77 2.79 10.23 8 85.18 99.71 48.25 3.86 28.10
下载: 导出CSV
表 3 数据集样本参数统计
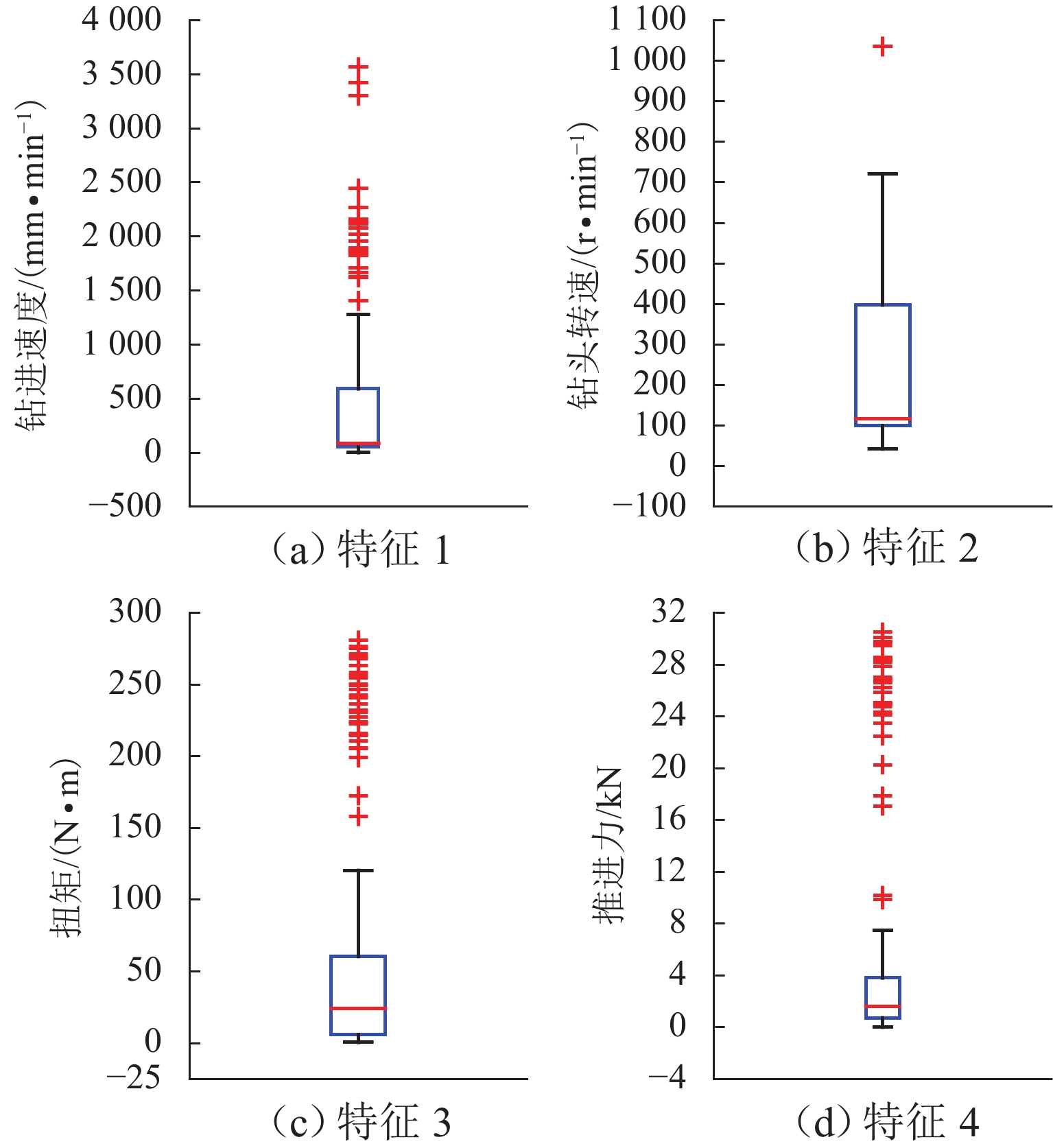
Table 3. Dataset sample parameters
取值类型 F/kN M/（N·m） V/
（mm·min−1）N/
（r·min−1）UCS/
MPa最小值 0.01 0.42 0.19 41.92 1.59 最大值 30.51 280.95 3566.00 1035.00 194.58 中位值 1.49 22.34 85.66 100.32 16.24 平均值 6.34 63.40 468.23 222.84 30.69 标准差 9.96 88.01 757.52 192.39 37.30
下载: 导出CSV
表 4 岩石强度计算结果
Table 4. Results of rock strength calculation
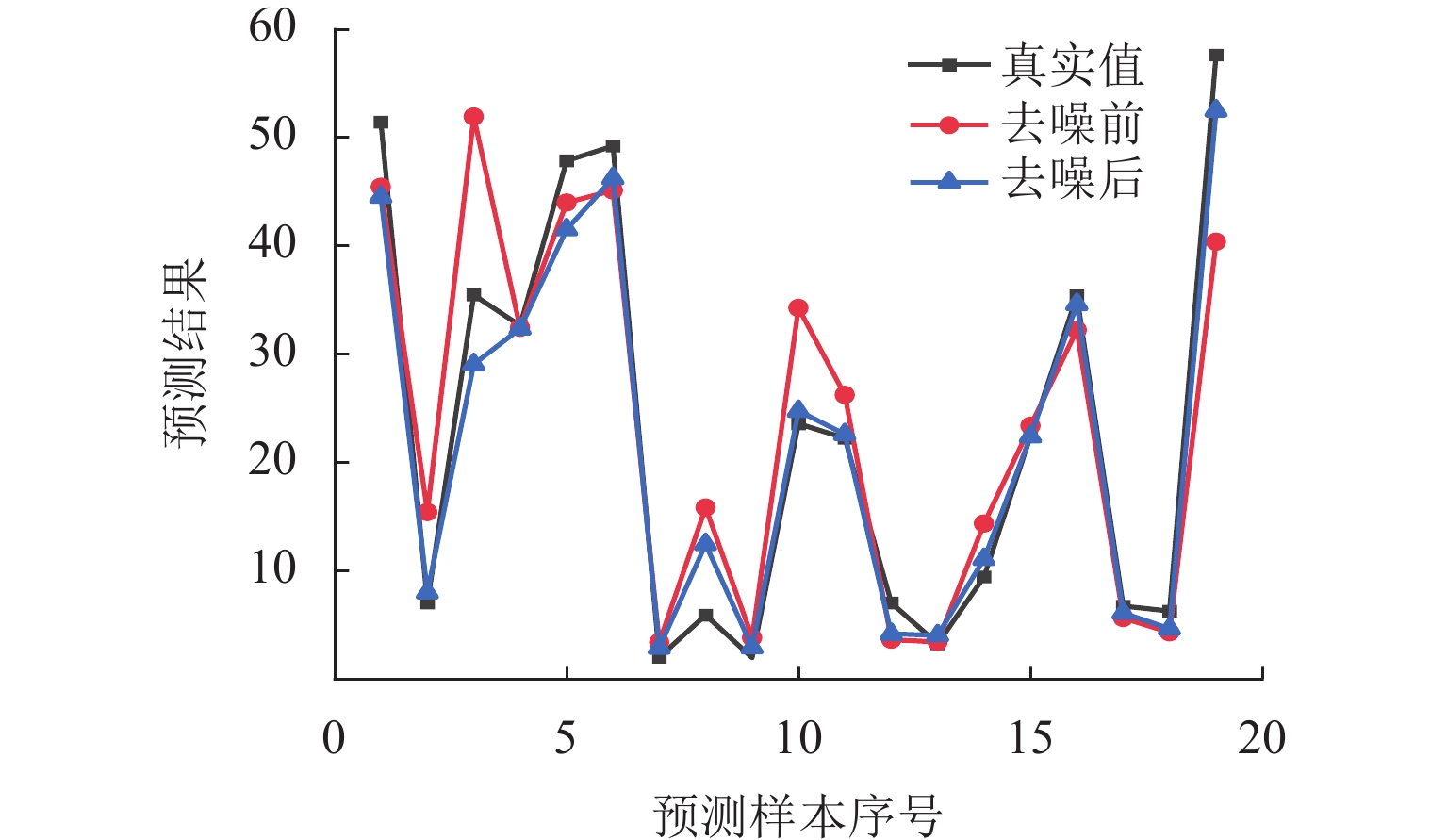
序号 真实值/MPa 计算值/MPa 相对误差/% 1 3.29 2.61 10.10 2 2.58 3.14 21.80 3 3.22 2.29 28.93 4 2.37 15.89 24.81 5 10.60 2.21 32.76 6 10.54 4.27 38.98 7 10.23 1.97 30.54 8 28.10 1.07 31.62
下载: 导出CSV
表 5 预测结果对比
Table 5. Comparison of prediction results
序号 真实值/
MPa理论计算
值/MPaBP预测
值/MPa理论计算
误差/%机器学习
误差/%1 3.29 2.23 4.58 32.20 8.93 2 2.58 3.15 5.11 22.27 20.60 3 3.22 2.32 5.06 27.99 5.04 4 2.37 2.63 1.95 10.86 17.52 5 10.60 7.30 11.89 31.18 12.19 6 10.54 7.21 12.33 31.60 16.96 7 10.23 8.40 7.45 17.93 17.40 8 28.10 19.81 34.35 29.51 22.24
下载: 导出CSV
-
[1] 王玉杰,佘磊,赵宇飞,等. 基于数字钻进技术的岩石强度参数测定试验研究[J]. 岩土工程学报,2020,42(9): 1669-1678.WANG Yujie, SHE Lei, ZHAO Yufei, et al. Experimental study on measurement of rock strength parameters based on digital drilling technology[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(9): 1669-1678. [2] 佘磊. 岩石强度与耐磨性参数的数字钻进测定技术研究[D]. 西安:西安理工大学,2019. [3] 谭卓英. 金刚石钻进能量在风化花岗岩地层中的变化特征[J]. 岩土工程学报,2007,29(9): 1303-1306.TAN Zhuoying. Variation characteristics of penetrating energy for diamond drilling in weathered granite formation[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(9): 1303-1306. [4] 田昊,李术才,薛翊国,等. 基于钻进能量理论的隧道凝灰岩地层界面识别及围岩分级方法[J]. 岩土力学,2012,33(8): 2457-2464.TIAN Hao, LI Shucai, XUE Yiguo, et al. Identification of interface of tuff stratum and classfication of surrounding rock of tunnel using drilling energy theory[J]. Rock and Soil Mechanics, 2012, 33(8): 2457-2464. [5] MUNOZ H, TAHERI A, CHANDA E K. Rock drilling performance evaluation by an energy dissipation based rock brittleness index[J]. Rock Mechanics and Rock Engineering, 2016, 49(8): 3343-3355. doi: 10.1007/s00603-016-0986-0 [6] 王琦,孙会彬,江贝,等. 基于数字钻探和支持向量机预测岩体单轴抗压强度的方法[J]. 岩土力学,2019,40(3): 1221-1228.WANG Qi, SUN Huibin, JIANG Bei, et al. A method for predicting uniaxial compressive strength of rock mass based on digital drilling test technology and support vector machine[J]. Rock and Soil Mechanics, 2019, 40(3): 1221-1228. [7] 陈庆贺. 岩石力学参数随钻预测实验研究[D]. 徐州:中国矿业大学,2022. [8] 宋超,赵腾远,许领. 基于贝叶斯高斯过程回归与模型选择的岩石单轴抗压强度估计方法[J]. 岩土工程学报,2023,45(8): 1664-1673.SONG Chao, ZHAO Tengyuan, XU Ling. Estimation of uniaxial compressive strength based on fully Bayesian Gaussian process regression and model class selection[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(8): 1664-1673. [9] 江贝,马凤林,王琦,等. 基于切削理论的数字钻探参数与岩石单轴抗压强度关系研究[J]. 中南大学学报(自然科学版),2021,52(5): 1601-1609.JIANG Bei, MA Fenglin, WANG Qi, et al. Study on the relationship between digital drilling parameters and uniaxial compressive strength of rock based on cutting theory[J]. Journal of Central South University (Science and Technology), 2021, 52(5): 1601-1609. [10] 何明明. 基于旋切触探技术的岩体力学参数预报研究[D]. 西安:西安理工大学,2017. [11] 牛钢钢. 基于钻机响应特征的岩体质量评价理论与应用[D]. 徐州:中国矿业大学,2022. [12] 高松. 岩石力学参数数字钻探快速预测技术研究[D]. 济南:山东大学,2018. [13] GAO H K, WANG Q, JIANG B, et al. Relationship between rock uniaxial compressive strength and digital core drilling parameters and its forecast method[J]. International Journal of Coal Science & Technology, 2021, 8(4): 605-613. [14] 王琦,高红科,蒋振华,等. 地下工程围岩数字钻探测试系统研发与应用[J]. 岩石力学与工程学报,2020,39(2): 301-310.WANG Qi, GAO Hongke, JIANG Zhenhua, et al. Development and application of a surrounding rock digital drilling test system of underground engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(2): 301-310. [15] WANG Q, GAO H K, YU H C, et al. Method for measuring rock mass characteristics and evaluating the grouting-reinforced effect based on digital drilling[J]. Rock Mechanics and Rock Engineering, 2019, 52(3): 841-851. doi: 10.1007/s00603-018-1624-9 [16] 孙鑫,张少华,程敬义,等. 基于MLR-RBF的岩石强度智能随钻识别实验研究[J]. 采矿与安全工程学报,2022,39(5): 981-991. [17] 孙鑫. 基于锚固孔随钻参数的岩石强度量化识别研究[D]. 徐州:中国矿业大学,2021. [18] 李田军. PDC钻头破碎岩石的力学分析与机理研究[D]. 武汉:中国地质大学,2012. [19] 李骞. 岩石的切削强度特性及岩体力学参数的旋切触探试验研究[D]. 西安:西安理工大学,2016. [20] INABA T, NISHIDA M, KANEKO K, et al. Static rock breaker using shape memory alloy[J]. 7th ISRM Congress, 1991, 2: 1005-1008 [21] 谭卓英,岳中琦,蔡美峰. 风化花岗岩地层旋转钻进中的能量分析[J]. 岩石力学与工程学报,2007,26(3): 478-483.TAN Zhuoying, YUE Zhongqi, CAI Meifeng. Analysis of energy for rotary drilling in weathered granite formation[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 478-483. [22] GOWIDA A, ELKATATNY S, GAMAL H. Unconfined compressive strength (UCS) prediction in real-time while drilling using artificial intelligence tools[J]. Neural Computing and Applications, 2021, 33(13): 8043-8054. doi: 10.1007/s00521-020-05546-7 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 161
- HTML全文浏览量: 120
- PDF下载量: 26
- 被引次数: 0