基于核磁共振技术的硬石膏岩孔隙结构冻融损伤特性

候超; 靳晓光; 何杰; 方智远

doi:10.3969/j.issn.0258-2724.20230314

基于核磁共振技术的硬石膏岩孔隙结构冻融损伤特性

doi: 10.3969/j.issn.0258-2724.20230314

候超^1,,
靳晓光^{2, 3, 4, ,},
何杰²,
方智远¹

1.
河南科技大学土木建筑学院，河南洛阳 471000
2.
重庆大学土木工程学院，重庆 400044
3.
重庆大学山地城镇建设与新技术教育部重点实验室，重庆 400044
4.
重庆大学煤矿灾害动力学与控制国家重点实验室，重庆 400044

基金项目: 国家重点研发计划（2021YFB3901402）；重庆市交通科技项目（2022-05）

详细信息

作者简介:
候超（1990—），男，讲师，博士，研究方向为寒区岩石损伤力学，E-mail：chaohou@haust.edu.cn

通讯作者:
靳晓光（1967—），男，教授，博士生导师，研究方向为隧道及地下空间工程，E-mail： jinxiaoguang@cqu.edu.cn

中图分类号: TU45
计量
- 文章访问数: 34
- HTML全文浏览量: 22
- PDF下载量: 4
- 被引次数: 0
出版历程
- 收稿日期: 2023-06-30
- 修回日期: 2023-09-20
- 网络出版日期: 2024-11-21

Freeze-Thaw Damage Characteristics of Anhydrite Rock Pore Structures Based on Nuclear Magnetic Resonance Technology

HOU Chao^1
,,
JIN Xiaoguang^{2, 3, 4
, ,},
HE Jie²,
FANG Zhiyuan¹

1.
School of Civil Engineering and Architecture, Henan University of Science and Technology, Luoyang 471000, China
2.
School of Civil Engineering, Chongqing University, Chongqing 400044, China
3.
Key Laboratory of New Technology for Construction of Cities in Mountain Area, Chongqing 400045, China
4.
State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400044, China

摘要

摘要:
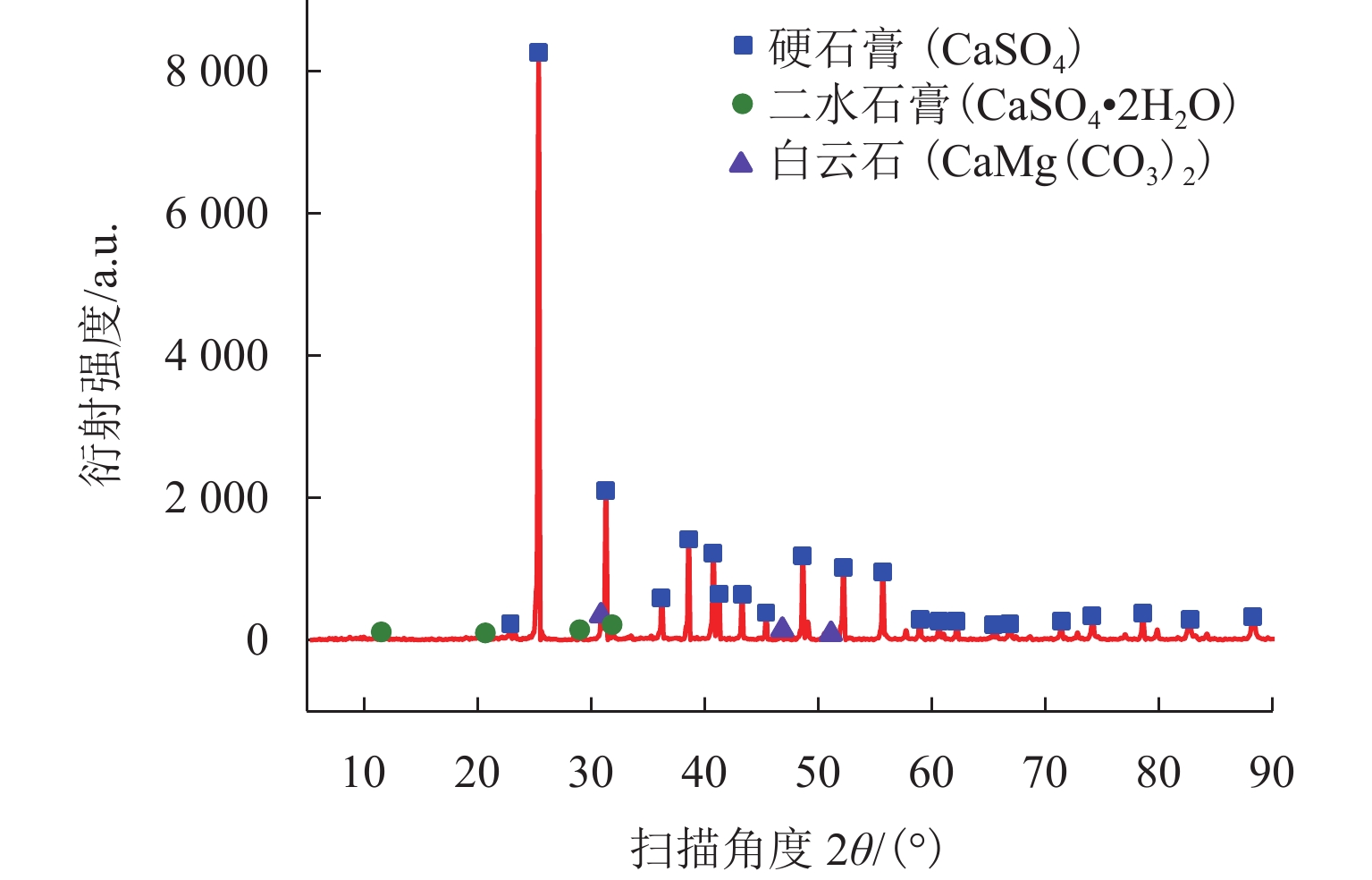
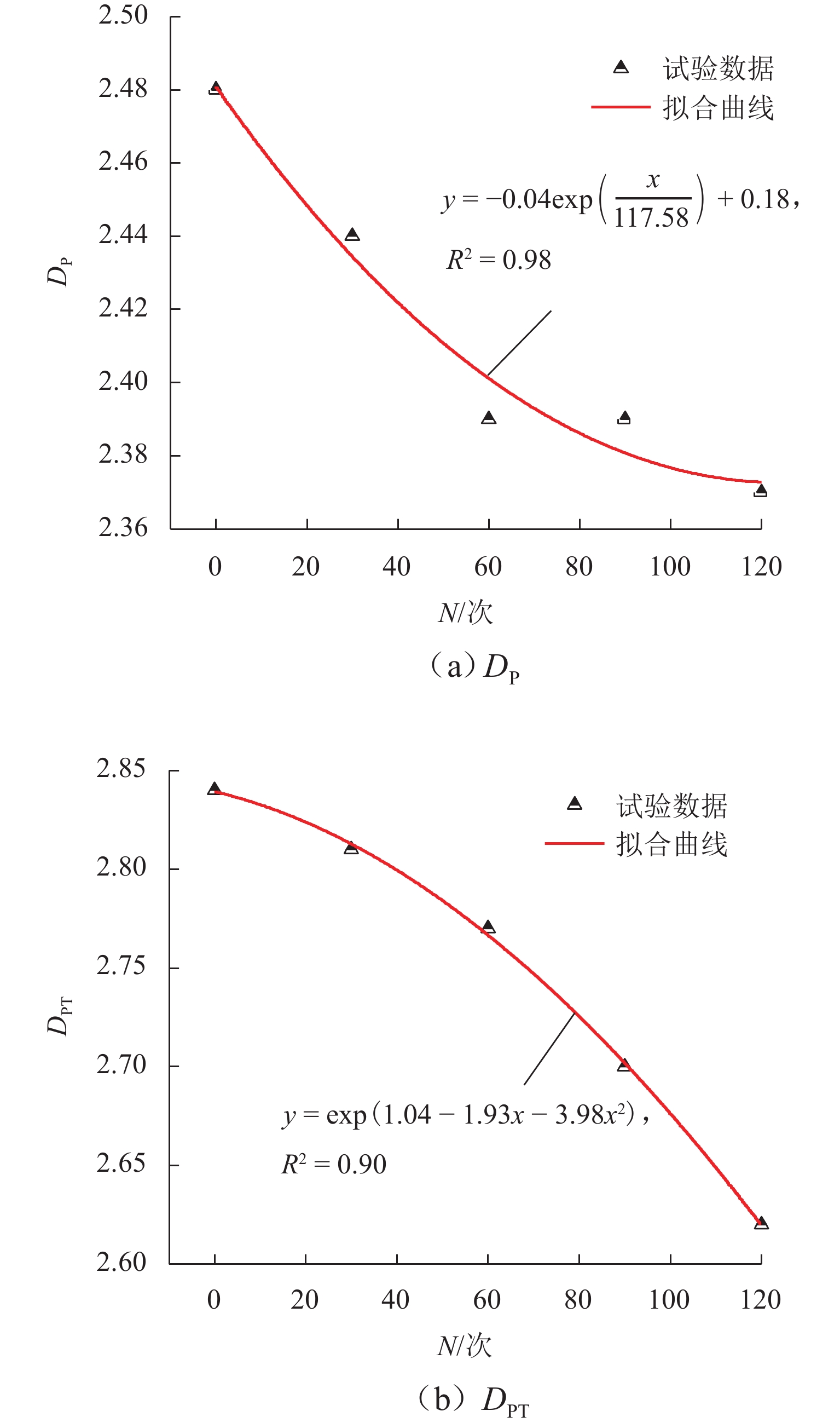
为研究寒区遭受冻融作用的石膏质岩石的细观和微观孔隙结构损伤特性，以硬石膏岩为研究对象，基于核磁共振试验，获得硬石膏岩在冻融循环作用下的孔隙度、孔径和孔喉分布特征；结合分形理论，推导岩石孔径和孔喉分形维数的计算式，探讨冻融循环作用对硬石膏岩孔隙结构分形维数的影响规律；建立不同孔隙结构及孔隙分形维数与孔隙度之间的关系，并指出对孔隙度影响程度较大的孔隙结构类型. 结果表明：冻融循环作用下,硬石膏岩的孔径呈“三峰”型分布，随着冻融次数增加，硬石膏岩微孔(孔径r ≤ 0.100 μm)、PT-Ⅰ (r∈(0，0.100] μm)孔喉、孔隙分形维数($ {{D}}_{\text{P}} $)和孔喉分形维数($ {{D}}_{\text{PT}} $)呈指数型递减，而中孔(r∈(0.100，1.000) μm)、大孔(r≥1.000 μm)、PT-Ⅱ (r∈(0.100，4.000] μm)孔喉和孔隙度则呈指数型递增，规模较大的孔隙、规模较小的孔喉以及孔喉分形维数对硬石膏岩孔隙度的影响程度较大.
- 核磁共振 /
- 硬石膏岩 /
- 孔隙结构 /
- 冻融循环 /
- 损伤特性
Abstract:
In order to study the damage characteristics of meso and micro pore structures of gypsum rock subjected to freeze-thaw cycles in cold regions, anhydrite rock was taken as the research object, and the porosity, pore size, and pore throat distribution characteristics of anhydrite rock were obtained based on nuclear magnetic resonance (NMR) experiments. According to fractal theory, the calculation formulas of the fractal dimension of pore size and pore throat of rock were derived, and the influence of freeze-thaw cycles on the fractal dimension of pore structures of anhydrite rock was discussed. The relationship among different pore structures, fractal dimensions of pores, and porosity was established, and the pore structure types that had a greater impact on porosity were revealed. The results show that the pore size of anhydrite rock under freeze-thaw cycles presents a “three-peak” distribution. 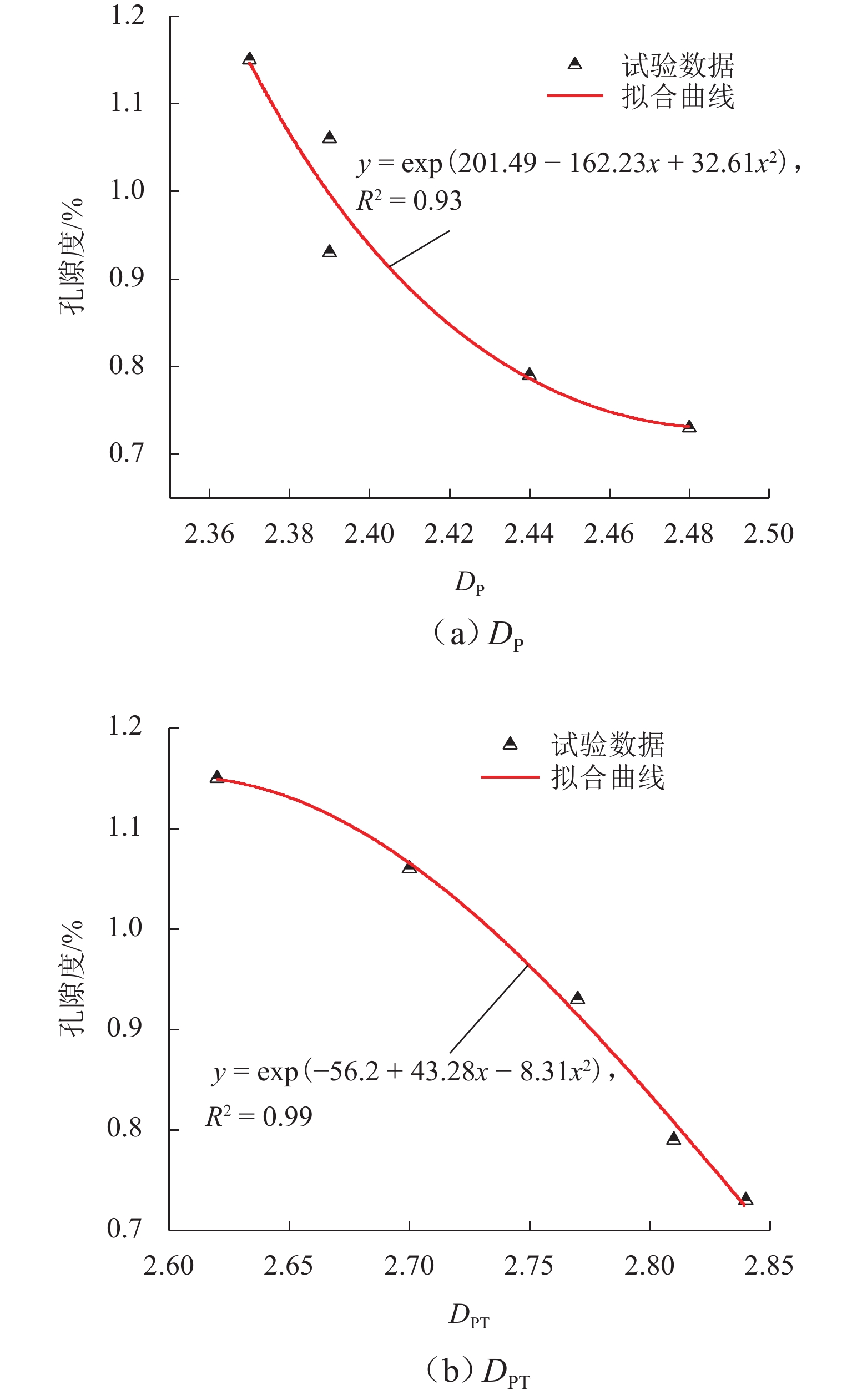With the increase in freeze-thaw cycles, the micropore (r ≤ 0.100 μm), PT-Ⅰ (r∈(0, 0.100) μm) of pore throat, fractal dimension of pore (D_P), and fractal dimension of pore throat (D_PT) decrease exponentially. While, the mesopores (r∈(0.100, 1.00) μm), macropores (r ≥ 1.000 μm), PT-Ⅱ(r∈(0.100, 4.00] μm) of pore throats, and porosity increase exponentially. It can be concluded that larger pores, as well as smaller pore throats and fractal dimension of pore throats, have a greater influence on the porosity of anhydrite rock.
- nuclear magnetic resonance /
- anhydrite rock /
- pore structure /
- freeze-thaw cycle /
- damage characteristic

HTML全文

图 1 X射线衍射图谱

Figure 1. X-ray diffraction pattern

下载: 全尺寸图片幻灯片

图 2 试验装置

Figure 2. Test device

下载: 全尺寸图片幻灯片

图 3 冻融循环作用下硬石膏岩孔径分布演化曲线

Figure 3. Pore size distribution evolution curves of anhydrite rock under freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 4 冻融作用下N₂试样不同类型孔隙对应的曲线面积演化规律

Figure 4. Curve area evolution law for different types of pores of N₂ sample under freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 5 冻融循环作用下硬石膏岩孔喉分布演化

Figure 5. Pore throat distribution evolution of anhydrite rock under freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 6 冻融循环作用下N2试样不同类型孔喉占比演化规律

Figure 6. Evolution law of different types of pore throats in N2 sample under freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 7 冻融循环作用下N2试样孔隙结构分形维数演化规律

Figure 7. Fractal dimension evolution law of pore structures for N2 sample under freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 8 冻融作用下N2试样各类孔隙分布曲线面积与孔隙度关系

Figure 8. Relationship between various pore size distribution curve area and porosity of N2 sample under freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 9 冻融作用下 N2试样各类孔喉占比与孔隙度关系

Figure 9. Relationship between various pore throat proportion and porosity of N2 sample under freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 10 N2试样孔隙结构分形维数与孔隙度关系

Figure 10. Relationship between fractal dimension of pore structure and porosity of N2 sample

下载: 全尺寸图片幻灯片

表 1 不同冻融循环次数下硬石膏岩孔隙度

Table 1. Porosity of anhydrite under different freeze-thaw cycles %

试样编号	0	30 次	60 次	90 次	120 次
N1	0.64	0.78	0.91	1.03	1.12
N2	0.73	0.79	0.93	1.06	1.15
N3	0.70	0.81	0.92	0.98

下载: 导出CSV

表 2 不同类型孔隙对应的曲线面积

Table 2. Curve area for different types of pores

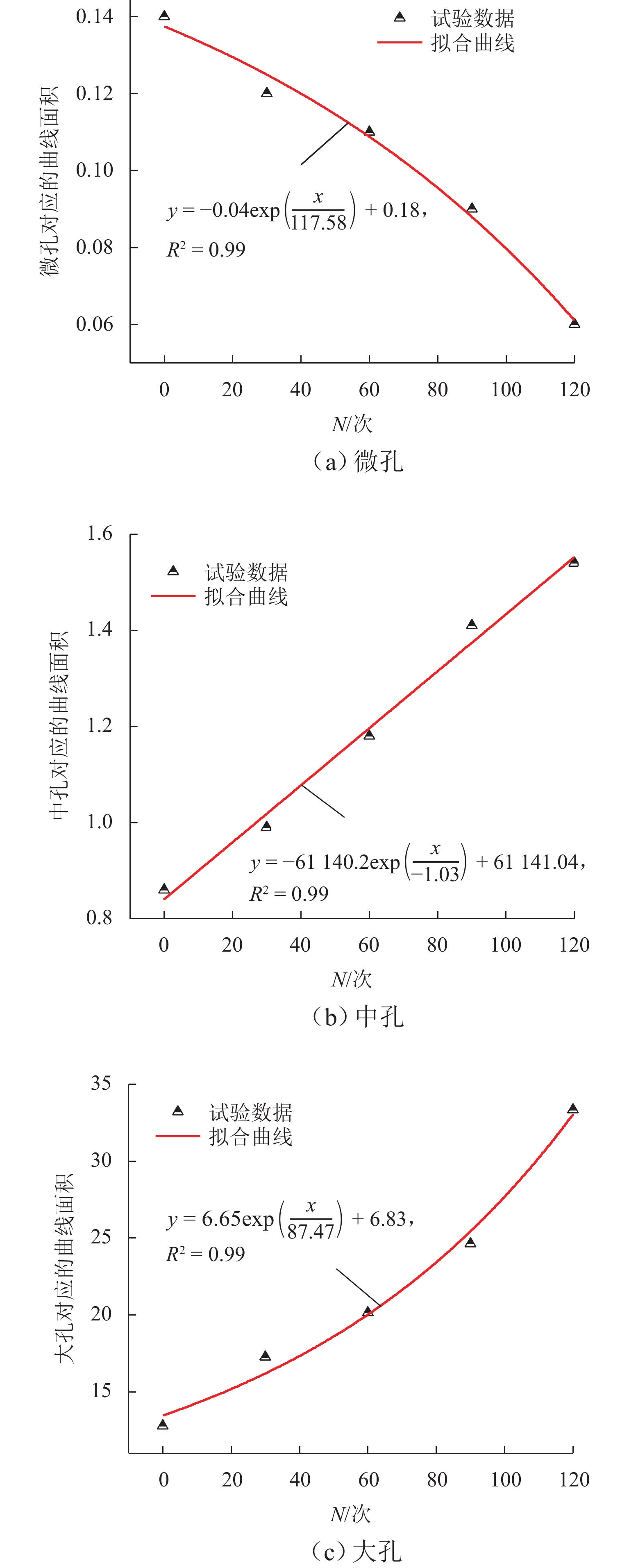
试样编号	孔隙类型	0	30 次	60 次	90 次	120 次
N1	微孔	0.17	0.11	0.14	0.10	0.06
	中孔	0.94	1.51	1.67	2.12	1.61
	大孔	17.38	19.86	21.28	25.08	37.77
N2	微孔	0.14	0.12	0.11	0.09	0.06
	中孔	0.86	0.99	1.18	1.41	1.54
	大孔	12.79	17.26	20.15	24.63	33.34
N3	微孔	0.12	0.09	0.08	0.05
	中孔	1.21	1.50	1.67	2.22
	大孔	13.96	19.11	20.18	24.06

下载: 导出CSV

表 3 冻融循环作用下硬石膏岩不同类型孔喉占比

Table 3. Proportion of different types of pore throats for anhydrite rock under freeze-thaw cycles %

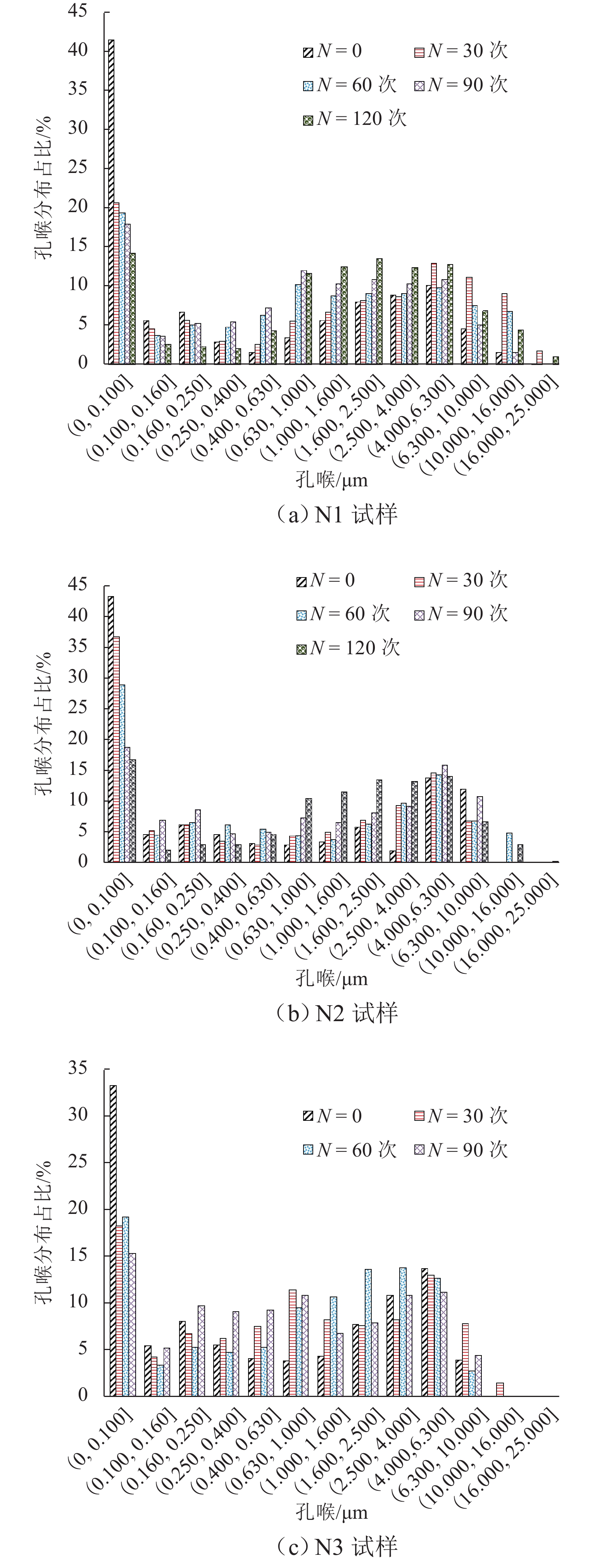
试样编号	孔喉类型	0	30 次	60 次	90 次	120 次
N1	PT-Ⅰ	41.39	20.64	19.27	17.86	14.12
	PT-Ⅱ	42.41	44.61	56.77	64.77	61.03
	PT-Ⅲ	16.08	34.75	23.96	17.37	24.85
N2	PT-Ⅰ	43.14	36.64	28.83	18.62	16.58
	PT-Ⅱ	31.37	42.14	45.65	55.07	59.90
	PT-Ⅲ	25.50	21.22	25.52	26.30	23.31
N3	PT-Ⅰ	33.14	18.19	19.15	15.24
	PT-Ⅱ	49.37	59.68	65.63	69.26
	PT-Ⅲ	17.50	22.13	15.22	15.50

下载: 导出CSV

参考文献(22)

[1]	LI M, LIU X S. Experimental and numerical investigation of the failure mechanism and permeability evolution of sandstone based on hydro-mechanical coupling[J]. Journal of Natural Gas Science and Engineering, 2021, 95: 104240.1-104240.22.
[2]	ZHANG Y F, ZHAO Y, YANG H Q, et al. A semianalytical solution for a Griffith crack nonuniformly pressurized by internal fluid[J]. Rock Mechanics and Rock Engineering, 2020, 53(6): 2439-2460.
[3]	ZHAO Y, ZHANG Y F, YANG H Q, et al. Experimental study on relationship between fracture propagation and pumping parameters under constant pressure injection conditions[J]. Fuel, 2022, 307: 121789.1-121789.19.
[4]	李玉成,陈有亮,孙浩程,等. 寒区花岗岩冻融损伤破坏的试验研究[J]. 工业建筑,2019,49(7): 83-88,107. LI Yucheng, CHEN Youliang, SUN Haocheng, etal. An experimental study of granite’s damage caused by freeze-thaw cycles in cold region[J]. Industrial Construction, 2019, 49(7): 83-88,107.
[5]	张德,刘恩龙,刘星炎,等. 基于修正Mohr-Coulomb屈服准则的冻结砂土损伤本构模型[J]. 岩石力学与工程学报,2018,37(4): 978-986. ZHANG De, LIU Enlong, LIU Xingyan, et al. A damage constitutive model for frozen sandy soils based on modified Mohr-Coulomb yield criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(4): 978-986.
[6]	徐拴海,李宁,王晓东,等. 露天煤矿冻岩边坡饱和砂岩冻融损伤试验与劣化模型研究[J]. 岩石力学与工程学报,2016,35(12): 2561-2571. XU Shuanhai, LI Ning, WANG Xiaodong, et al. Damage test and degradation model of saturated sandstone due to cyclic freezing and thawing of rock slopes of open-pit coal mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(12): 2561-2571.
[7]	倪骁慧,沈晓梅,华昕若,等. 冻融循环后砂岩卸荷过程应变能转化特征研究[J]. 水力发电学报,2019,38(4): 246-255. doi: 10.11660/slfdxb.20190423 NI Xiaohui, SHEN Xiaomei, HUA Xinruo, et al. Strain energy conversion behaviors of sandstone after freeze-thaw cycles under triaxial confining pressure unloading[J]. Journal of Hydroelectric Engineering, 2019, 38(4): 246-255. doi: 10.11660/slfdxb.20190423
[8]	JUMASSULTAN A, SAGIDULLINA N, KIM J R, et al. Performance of cement-stabilized sand subjected to freeze-thaw cycles[J]. Geomechanics and Engineering, 2021, 25(1): 41-48.
[9]	宋勇军,张磊涛,任建喜,等. 基于核磁共振技术的弱胶结砂岩干湿循环损伤特性研究[J]. 岩石力学与工程学报,2019,38(4): 825-831. SONG Yongjun, ZHANG Leitao, REN Jianxi, et al. Study on damage characteristics of weak cementation sandstone under drying-wetting cycles based on nuclear magnetic resonance technique[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(4): 825-831.
[10]	谢凯楠,姜德义,孙中光,等. 基于低场核磁共振的干湿循环对泥质砂岩微观结构劣化特性的影响[J]. 岩土力学,2019,40(2): 653-659,667. XIE Kainan, JIANG Deyi, SUN Zhongguang, et al. Influence of drying-wetting cycles on microstructure degradation of argillaceous sandstone using low field nuclear magnetic resonance[J]. Rock and Soil Mechanics, 2019, 40(2): 653-659,667.
[11]	李杰林,刘汉文,周科平,等. 冻融作用下岩石细观结构损伤的低场核磁共振研究[J]. 西安科技大学学报,2018,38(2): 266-272. LI Jielin, LIU Hanwen, ZHOU Keping, et al. An LF-NMR study of the micro-structural deterioration of rocks under the effect of freeze-thaw cycles[J]. Journal of Xi’an University of Science and Technology, 2018, 38(2): 266-272.
[12]	姜德义,张水林,陈结,等. 砂岩循环冻融损伤的低场核磁共振与声发射概率密度研究[J]. 岩土力学,2019,40(2): 436-444. JIANG Deyi, ZHANG Shuilin, CHEN Jie, et al. Low filed NMR and acoustic emission probability density study of freezing and thawing cycles damage for sandstone[J]. Rock and Soil Mechanics, 2019, 40(2): 436-444.
[13]	SHEN Y J, WANG Y Z, WEI X, et al. Investigation on meso-debonding process of the sandstone–concrete interface induced by freeze-thaw cycles using NMR technology[J]. Construction and Building Materials, 2020, 252: 118962.1-118962.11.
[14]	ZHOU X P, LI C Q, ZHOU L S. The effect of microstructural evolution on the permeability of sandstone under freeze-thaw cycles[J]. Cold Regions Science and Technology, 2020, 177: 103119.1-103119.18.
[15]	SERAFEIMIDIS K, ANAGNOSTOU G. The solubilities and thermodynamic equilibrium of anhydrite and gypsum[J]. Rock Mechanics and Rock Engineering, 2015, 48(1): 15-31. doi: 10.1007/s00603-014-0557-1
[16]	牛键,张彬,王汉勋,等. 深部高内压环境下硬石膏质储气库围岩稳定性分析[C]//2018年全国工程地质学术年会论文集. 西安:[出版社不详],2018:534-540.
[17]	许崇帮,秦幼林,高晓静,等. 硬石膏岩膨胀力学试验研究进展及展望[J]. 公路交通科技,2021,38(6): 1-10. doi: 10.3969/j.issn.1002-0268.2021.06.001 XU Chongbang, QIN Youlin, GAO Xiaojing, etal. Study progress and prospect of swelling mechanical test on anhydrite rock[J]. Journal of Highway and Transportation Research and Development, 2021, 38(6): 1-10. doi: 10.3969/j.issn.1002-0268.2021.06.001
[18]	ZAREI M M, HOSSEINI M, MOHAMMADI A H, et al. Model development for estimating calcium sulfate dihydrate, hemihydrate, and anhydrite solubilities in multicomponent acid and salt containing aqueous solutions over wide temperature ranges[J]. Journal of Molecular Liquids, 2021, 328: 115473.1-115473.15.
[19]	中华人民共和国国家发展和改革委员会. 水电水利工程岩石试验规程:DL/T 5368—2007[S]. 北京:中国电力出版社,2007.
[20]	LI J L, KAUNDA R B, ZHOU K P. Experimental investigations on the effects of ambient freeze-thaw cycling on dynamic properties and rock pore structure deterioration of sandstone[J]. Cold Regions Science and Technology, 2018, 154: 133-141. doi: 10.1016/j.coldregions.2018.06.015
[21]	张峰瑞,姜谙男,江宗斌,等. 化学腐蚀-冻融综合作用下岩石损伤蠕变特性试验研究[J]. 岩土力学,2019,40(10): 3879-3888. ZHANG Fengrui, JIANG Annan, JIANG Zongbin, et al. Experimental study of damage and creep property of rock under coupled chemical corrosion and freeze-thaw cycle[J]. Rock and Soil Mechanics, 2019, 40(10): 3879-3888.
[22]	ZHANG Z Y, ZHOU J T, YANG J, et al. Understanding of the deterioration characteristic of concrete exposed to external sulfate attack: insight into mesoscopic pore structures[J]. Construction and Building Materials, 2020, 260: 119932.1-119932.13.