Fluctuation Characteristics of Wavy Vortex Field Within Annular Gap in Taylor-Couette
-
摘要:
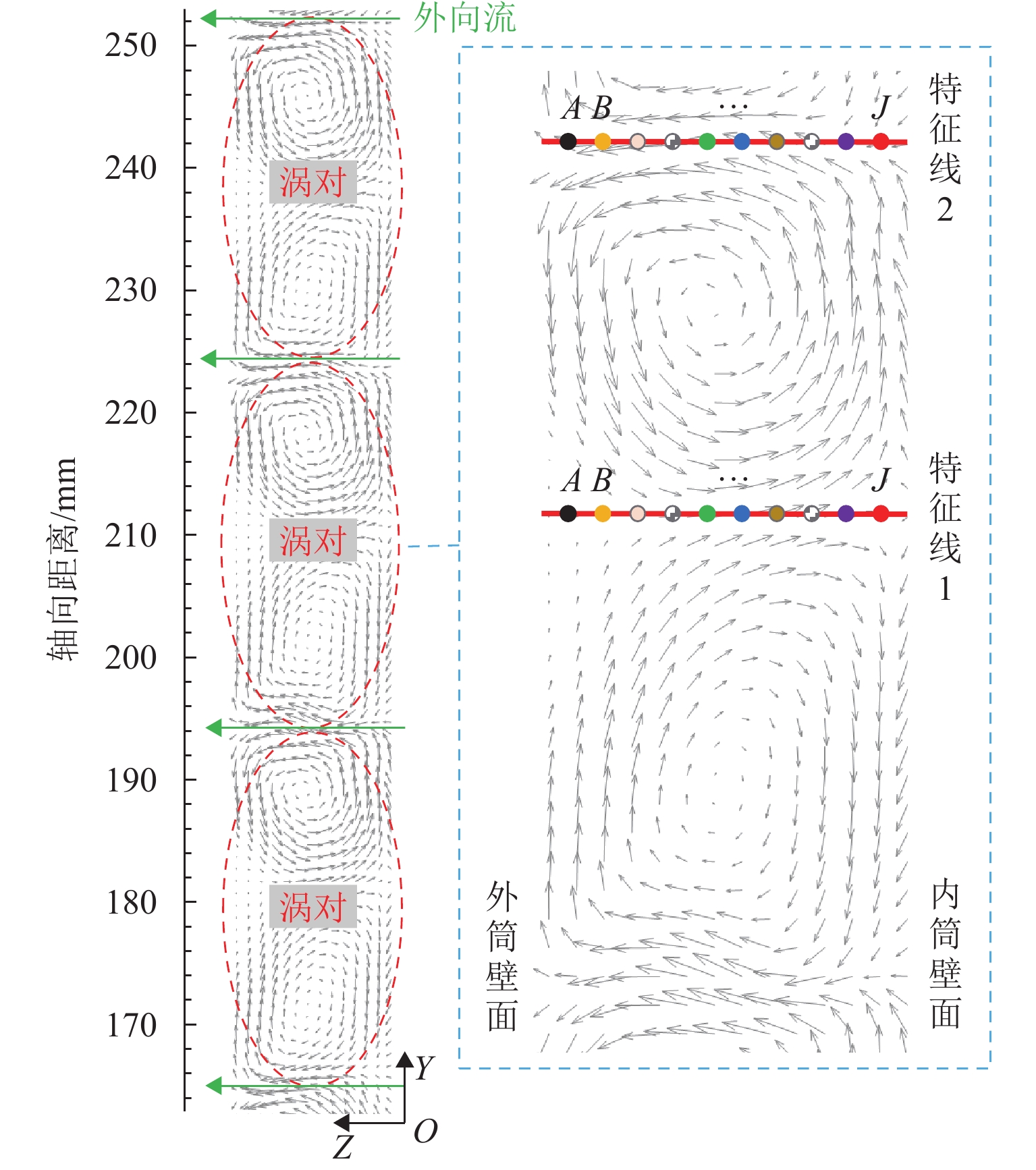
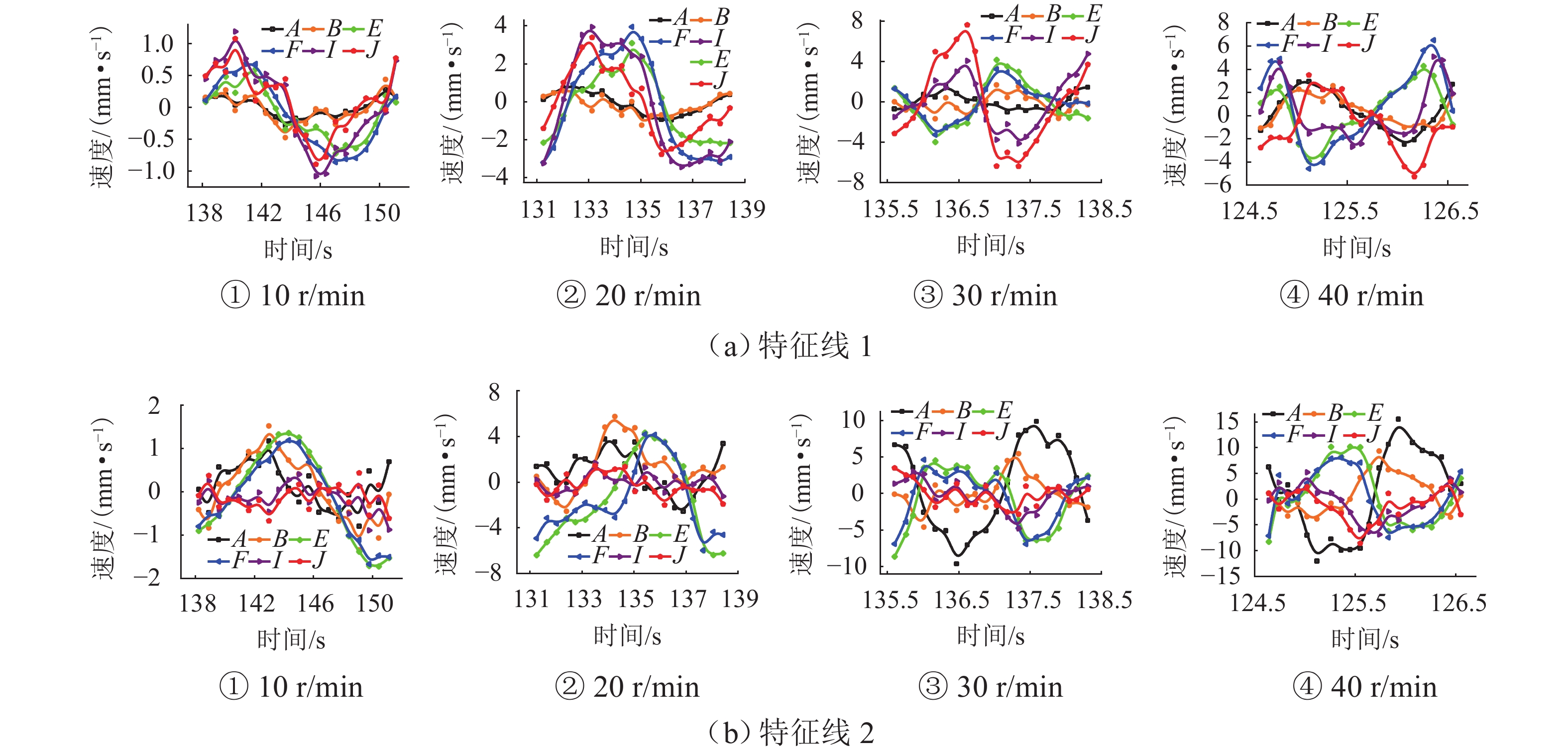
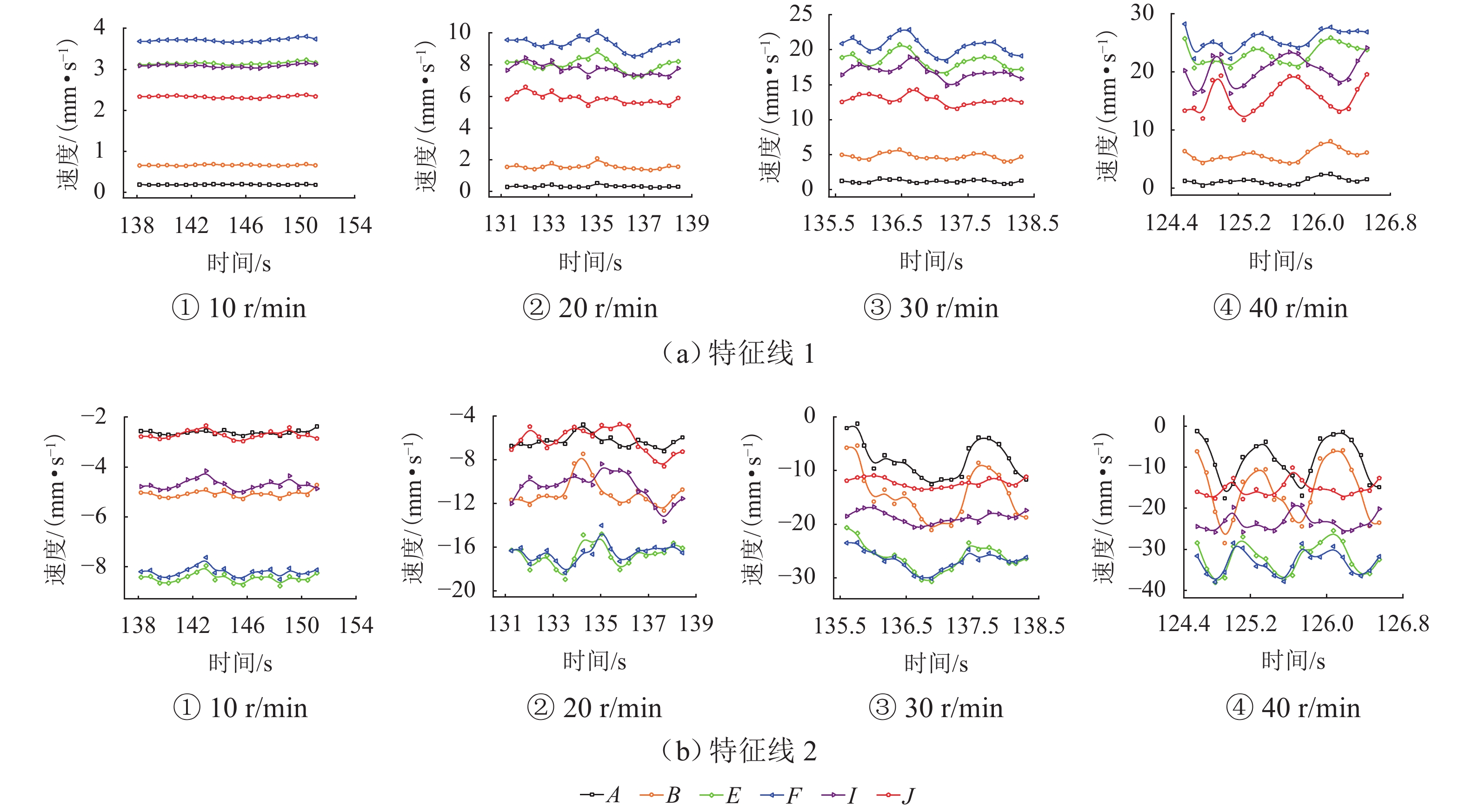
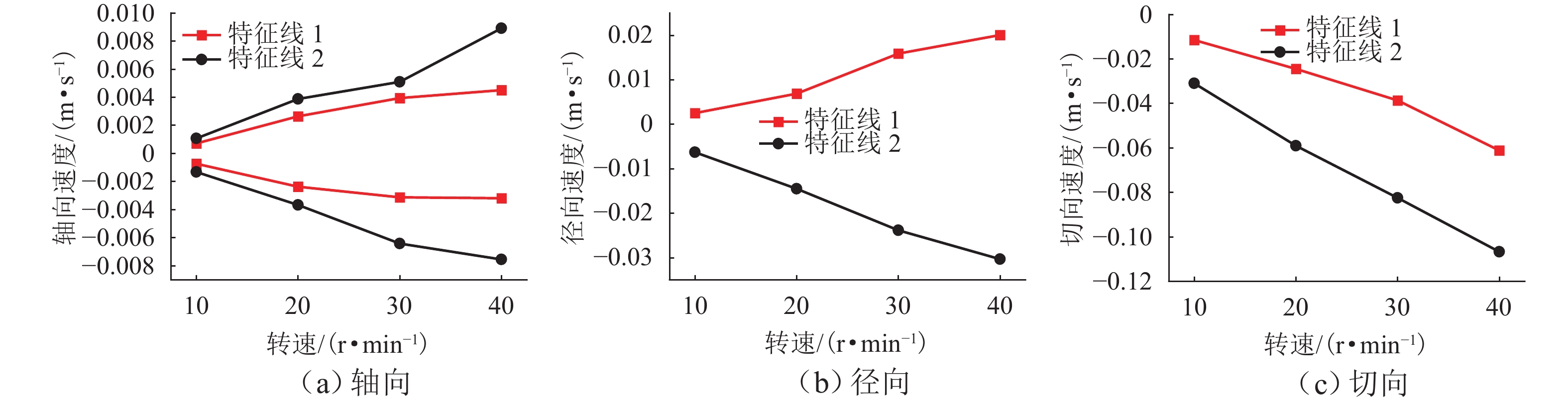
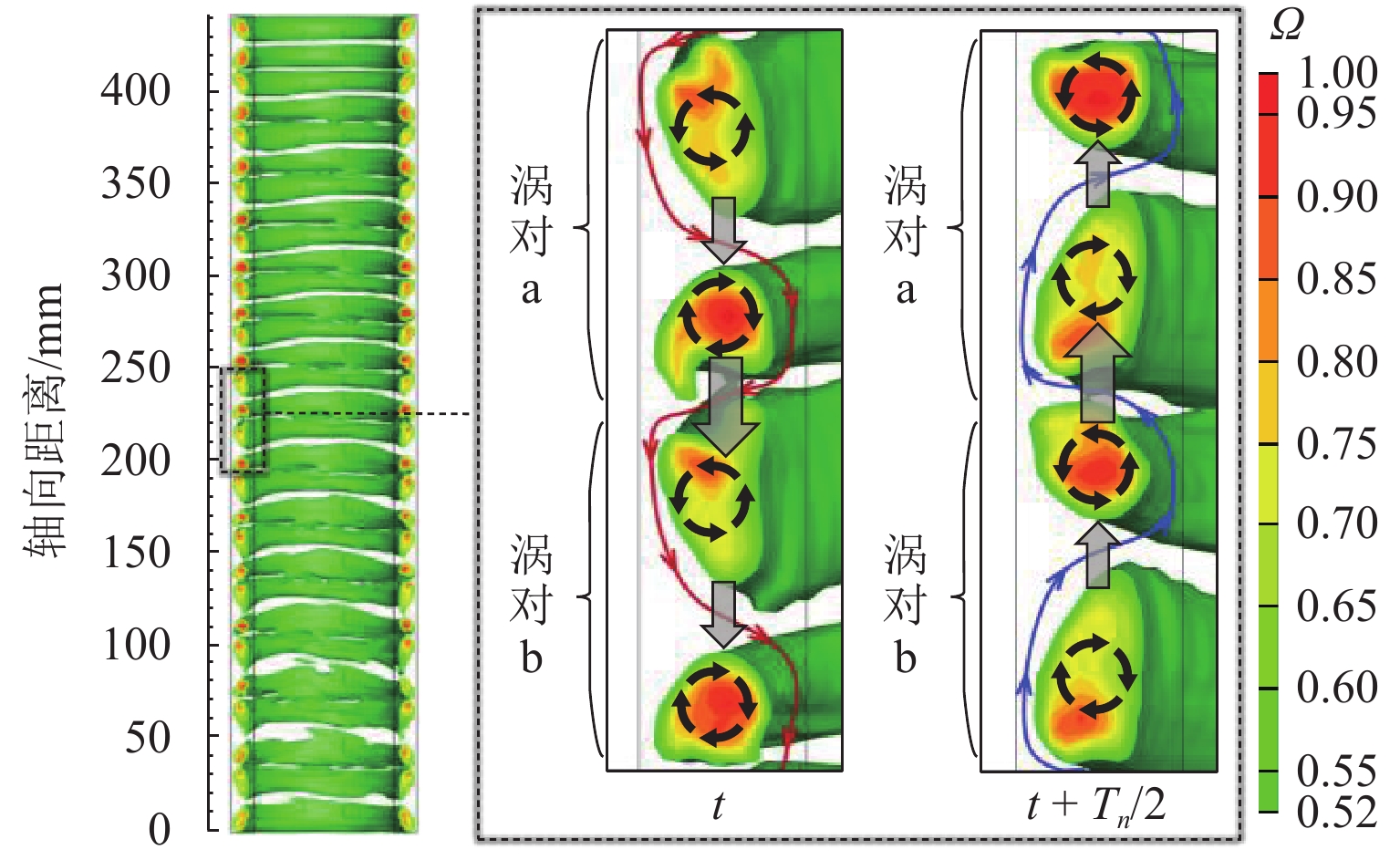
为研究Taylor-Couette环隙流场波状涡涡间的波动变化情况，采用大涡模拟（LES）方法对Taylor-Couette波状涡流场进行瞬态数值模拟，并从二维和三维的角度对环隙间波状涡流场进行分析. 结果表明：波状涡流场中二维环隙子午面速度矢量场存在周期性波动变化特征，在周期始末时刻速度矢量场基本保持一致；涡交界位置处的轴向速度方向在不断发生周期性变化，径向和切向速度方向保持不变；涡对间各向速度值均大于涡对内的涡间，主流液体传递主要发生在外向流的涡对间；另一方面，三维波状涡流场涡旋周期波动现象明显，也具有周期特征，各工况（10、20、30、40 r/min）的周期分别为12.94、6.80、1.93、1.49 s；随着旋转雷诺数增大，涡旋波动幅度大幅减小，波动周期也缩短；环隙间主流液体在涡间的周期性流动带动流体微团在环隙间绕内筒做螺旋偶合涡旋转运动.
-
关键词:
- Taylor-Couette /
- 波状涡 /
- 速度矢量场 /
- 环隙 /
- 波动特征
Abstract:The large eddy simulation (LES) method was applied to transiently simulate the wavy vortex field within the annular gap in Taylor-Couette and investigate the variation of fluctuations between wavy vortices. The wavy vortex field within the annulus gap was investigated from both two-dimensional and three-dimensional perspectives. The results indicate that the velocity vector field on the meridian plane of the two-dimensional wavy vortex field within the annular gap exhibits periodic fluctuation characteristics. The velocity vector field remains essentially the same at the beginning and end moments of the cycle. The axial velocity direction at the vortex junction changes constantly and periodically, while the radial and tangential velocity directions remain constant. The velocity values of the vortex pairs are greater than those of the vortex pairs inside the vortex, and the mainstream liquid transfer mainly occurs between the vortex pairs in the outward flow. Additionally, the fluctuation phenomenon of the three-dimensional wavy vortex field is clearly evident and exhibits periodic characteristics. The cycles for each working condition (10, 20, 30, and 40 r/min) are 12.94 seconds, 6.80 seconds, 1.93 seconds, and 1.49 seconds, respectively. With the increase in rotational Reynolds number, there is a significant decrease in vortex fluctuation amplitude and a reduction in the duration of fluctuations. The periodic flow transport of the mainstream liquid between vortices within the annulus gap propels fluid microclusters to perform a spiral-coupled vortex rotation around the inner cylinder within the annulus gap.
-
Key words:
- Taylor-Couette /
- wavy vortex /
- velocity vector field /
- annular gap /
- fluctuation characteristic
-
藏羌民居通常以黄泥和不规则片石块作为建筑材料，因就地取材、生态环保、砌筑工艺简单、造价低廉且具有浓厚的地域民族文化等特点一直沿用至今. 这类建筑广泛分布在我国西部经济欠发达的少数民族村镇地区，由于缺乏正规的抗震设计和有效抗震构造措施，村镇一直是抗震薄弱地区，容易出现“中震大灾”的现象. 同时，四川村镇约80%为丘陵和山地地区，在地震作用下可能发生山体落石、滑坡等次生灾害，对村镇建筑造成二次伤害[1].
国内外学者对不同类型的石墙进行相关试验研究和理论分析，许浒等[2]设计毛石-黏土砌体墙的无轴压条件下的水平抗剪试验来研究墙体的水平抗剪强度；郭子雄等[3]对条石的抗剪强度和抗震性能进行试验研究，并对其力学性能进行分析；王春萍等[4]在单轴压缩条件下对花岗岩石的力学性能及破坏特征进行了试验研究；徐明等[5-6]分别对细料石和粗料石墙体进行低周往复荷载试验，分析其抗震性能和受剪承载力；潘毅等[7-8]分别对藏族石木结构民居在马尔康6.0级地震震害情况和片石砌体在尼泊尔8.1级地震中震害情况进行了调查和分析；Milosevic等[9]对毛石砌体墙进行抗剪强度参数的试验评估；Abdulla等[10]对石砌体的抗剪性能进行试验评估. 同时，也有不少学者提出片毛石墙体的加固措施：黄辉等[11]提出玄武岩纤维增强复合材料（BFRP）网格改良毛石墙体的受力性能；冯一博[12]提出在转角处墙体内外两侧增加木构造柱来增加土石墙体的抗震性能；徐天航等[13]提出利用钢筋网片改性砂浆加固石砌体；Maio等[14]提出一套共6种加固方案对传统石建筑进行改造. 然而，在保证藏羌民居石墙原有风貌不被破坏的前提下，通过增设抗震构造措施来增加片石墙体抗震性能的研究成果较少.
藏羌民居因石墙体具有墙体加厚、墙体收分且砌筑杂乱无序等特点，使得如设置扶壁柱、构造柱等[15-17]传统的抗震措施，因存在破坏藏羌民居传统风貌、当地施工困难等原因，不适用于藏羌民居石墙体的抗震.
本研究为保护藏羌民居传统风貌、提高石墙抗震性能，针对藏羌地区常见的片石墙，提出增设钢筋骨架系统来加强传统藏羌石木结构的整体性和抗震性能的方案，并开展水平低周往复试验，和有限元数值模拟进行对比分析，研究钢筋骨架系统对石墙抗震性能的影响，为提高藏羌民居的抗震性能提出有效的构造措施.
1. 试验概况
1.1 试件设计
结合调研情况，选中理县一典型石木结构的墙体为原型，确定墙体平面尺寸为
4000 mm （长） ×2800 mm （高） × 600 mm （厚），该墙体用片石和黄泥砌筑. 考虑到实验室加载条件的限制，采用“墙体长度缩尺、砌块足尺”[18]的缩尺模型设计并制作了两面墙体，编号为W-1与W-2. 两面试验石墙长度、高度、厚度为实际尺寸的1/2，即2000 mm ×1400 mm × 300 mm，砌筑材料为黄泥、片石、钢筋和水泥砂浆，砌筑砂浆基本含水量控制在30%～40%，灰缝厚度控制在20～30 mm. 本文所采用的试验材料均采于藏羌民居原聚居地的阿坝藏族羌族自治州理县，且设计的所有试件均由同一批工人砌筑完成.W-1主要设定参数：不采用任何抗震措施，整面石墙采用片石与黄泥砌筑. W-2主要设定参数：采用钢筋骨架系统约束片石墙体，该墙体钢筋骨架系统由水平钢筋网、竖向钢筋骨架和拉结筋组成，钢筋骨架系统中钢筋使用量参照《四川省藏羌石木结构房屋建造图册》[19]选取. 钢筋骨架抗震系统如图1所示，两面墙体的具体参数如表1所示. 水平钢筋网：2层，上下层间距120 mm；通长钢筋采用3根直径为10 mm的HRB400钢筋，间距100 mm；横向短筋采用直径为6 mm的HPB300钢筋，间距300 mm；水平钢筋网上下各200 mm范围内的墙体采用M10的水泥砂浆砌筑. 竖向钢筋骨架：骨架尺寸为200 mm × 200 mm；纵向通长钢筋采用4根直径为12 mm的HRB400钢筋；箍筋采用直径为6 mm的HPB300钢筋，间距300 mm；竖向钢筋骨架周围200 mm墙体内采用强度为M10的水泥砂浆砌筑. 拉结筋：墙体中部设置2根直径为6 mm的水平拉结筋，每边伸入墙体500 mm；拉结筋上绑扎直径为6 mm的横向短筋，间距300 mm.
表 1 试件设计参数Table 1. Design parameters of specimens编号 长/高/厚/mm 抗震设计 W-1 2000 /1400 /300无 W-2 2000 /1400 /300钢筋骨架系统：包含水平钢筋网、竖向钢筋骨架和拉结筋 W-2试件中竖向钢筋骨架的纵筋上部应从水平钢筋网内侧穿过并做弯钩处理，弯钩长度为15倍竖向钢筋直径，下部应伸入基础内部. 本文选用钢筋混凝土基础模拟实际中的石墙基础，将竖向钢筋骨架的纵筋伸入石墙底梁内部，实际工程中底梁即地圈梁. 底梁设计如图2所示. 底梁截面尺寸为400 mm（宽） × 300 mm （高）. 箍筋直径8 mm，间距200 mm，而二级钢筋架立筋和底部纵筋各设直径16 mm的三级钢筋.
1.2 材料性能
1.2.1 钢筋力学性能试验
为检验试验中钢筋的性能是否符合要求，通过现场取样，对公称直径d0=10，12 mm的HRB400钢筋进行钢筋拉伸试验，每种型号钢筋的取样数量为2，标定原始标距L0分别为100 mm和120 mm. 试验在四川农业大学微机屏显液压式万能试验机（WEW-2000B）上完成，得到钢筋下屈服力Fel、下屈服强度Rel、最大力Fm和抗拉强度Rm的值见表2.
表 2 钢筋试验结果Table 2. Reinforcement test resultsd0/mm L0/mm Fel/
kNRel/MPa Fm/
kNRm/MPa 10 100 35.7 455 48.7 623 36.4 464 49.1 12 120 50.3 445 69.9 610 49.3 436 68.1 1.2.2 石砌体轴心抗压试验
《砌体基本力学性能试验方法标准》GB/T
50129 —2011中4.1.4条规定[20]，片石的标准砌体抗压试件厚度为400 mm，宽度为700～800 mm，试件的高度按高厚比3～5确定. 最终确定片石砌体抗压试件的尺寸为1200 mm（高） × 700 mm（宽） × 400 mm（厚），一组3个试件，编号分别为SM-1、SM-2、SM-3，片石砌体试件制作过程如图3所示.石砌体砌筑完毕后，根据《砌体结构工程施工质量验收规范》GB 50203—2011[21]的相关规定对石砌体进行养护. 石砌体轴心抗压试验在四川农业大学工程结构与力学试验中心电液伺服长柱试验机（WAW-J10000）下完成. 表3给出了试件SM-1、SM-2、SM-3的抗压强度和平均抗压强度，表中：F为试验最终荷载，Xm为最大位移，A为受压面积，f为抗压强度.
表 3 石砌体抗压强度Table 3. Compressive strength of stone masonry试件编号 F/kN Xm/mm A/（×105 mm2） f /（N·mm−2） 单个 平均值 SM-1 122.2 27.7 2.8 0.436 0.598 SM-2 205.0 45.8 2.8 0.732 SM-3 175.0 52.5 2.8 0.625 1.2.3 黏结材料性能试验
根据《建筑砂浆基本性能试验方法标准》（JGJ/T70—2009）[22]中立方体抗压强度规定，在砌筑石墙的同时制备砂浆小砌块. 黄泥砂浆的黄泥和水的配合比为3∶1，M10水泥砂浆的配合比为1.16∶1.00∶5.20 （水：水泥：砂）. 砂浆试件与石墙在同等标准养护条件下养护28 d，加载过程如图4所示. 表4给出了试验测得的黄泥砂浆（HNSJ1～HNSJ3）和水泥砂浆（SNSJ1～SNSJ3）抗压强度. 表中：Nu为试件破坏荷载；fm,cu为试件抗压强度；f2为试件抗压强度平均值.
经材料性能试验和文献[23]可得到片石材轴心抗压强度为67.920 MPa，片石砌体抗压强度为0.598 MPa、弹性模量为46.24 MPa，泊松比为0.2，黄泥砂浆抗压强度为2.376 MPa，水泥砂浆抗压强度值为18.702 MPa. 钢筋材料性能如表5所示. 表中：fy为钢筋的屈服强度；fu为钢筋的抗拉强度；εy为屈服应变；Es为弹性模量.
表 4 砂浆立方体抗压强度试验结果Table 4. Compressive strength test results of mortar cube试件编号 A/mm2 Nu/N fm,cu/MPa f2/MPa HNSJ1 4998.32 8364.69 1.674 1.828 HNSJ2 4998.32 9075.95 1.816 HNSJ3 4998.32 9960.65 1.993 SNSJ1 4998.32 71869.84 14.379 14.386 SNSJ2 4998.32 71276.04 14.260 SNSJ3 4998.32 72569.61 14.519 表 5 钢筋材料性能Table 5. Material property of reinforcementd0/mm fy/MPa εy/10−3 fu/MPa Es/5GPa 10 460 2.300 623 200 12 441 2.205 610 200 1.3 试件制作
W-1墙体的砌筑采用传统的铺浆法，未加入抗震构造措施. 砌筑墙体选用的石材应质地坚硬、无裂纹、无风化作用，黄泥砂浆在拌和过程中应将含水率控制在30%～40%. W-1墙体制作过程如图5所示.
W-2墙体嵌入钢筋骨架系统进行约束，该墙体施工流程如下：绑扎底梁钢筋、浇筑钢筋混凝土底梁、确定好竖向钢筋骨架的位置后砌筑石墙、石墙砌筑接近墙体顶部时绑扎水平钢筋网后再砌筑墙体. W-2墙的上部墙体砌筑工艺与W-1一致，但在其砌筑过程中应注意：钢筋四周各200 mm范围内的墙体采用M10的水泥砂浆砌筑；竖向钢筋骨架处，石块应伸入竖向钢筋骨架内，且距离不小于100 mm. W-2墙体制作过程如图6所示.
1.4 加载制度及测点布置
1.4.1 竖向荷载确定
根据选中建筑的实际情况，选取阿嘎土不上人屋面、黄泥楼面等相关信息计算竖向荷载. 阿嘎土屋面从内到外做法为：次梁、劈柴、树枝层、50 mm厚粗土、卷材、100 mm厚阿嘎土拍实. 原型为四面
4000 mm （长） ×2800 mm （高） × 600 mm （厚）的墙体围建而成的房屋，计算选取阿嘎土体容重为15 kN/m3、粗土容重为15 kN/m3、墙体容重为22 kN/m3、不上人屋面活载0.5 kN/m2，计算得到1∶2缩尺模型单面墙体竖向荷载为23.57 kN. 试验中竖向荷载采用砝码堆载一次性施加.1.4.2 水平荷载确定
2个墙体试件的水平荷载均采用位移控制，加载位移幅值由层间位移角变化计算得到. 位移加载幅值为：1.40、1.75、2.80、5.60、7.00、9.30、14.00、20.00、28.00、35.00、46.70 mm. 前两级采用双循环加载，之后各级采用三级循环加载；每级荷载施加完成后持荷1 min，加载速率全程保持一致，均为0.2 kN/s；当石墙发生严重倾斜时停止加载.
1.4.3 测点布置及加载
本次试验重点研究W-2墙体在低周往复荷载下的破坏形式以及墙体中钢筋骨架系统的受力情况，测点位置布置如图7所示.
加载系统由水平加载系统和竖向加载系统组成. 水平推拉力采用位移变化范围为±200 mm、最大推力为500 kN的50 T电液伺服作动器施加，竖向加载系统由矩形钢与砝码组成，加载装置如图8所示.
2. 试验结果及分析
2.1 试验的破坏特征
有钢筋骨架系统约束的片石墙体破坏过程与未加抗震构造的普通石墙类似，按照裂缝的出现、发展和构件的最终破坏，大致可以分为以下3个阶段：
1） 弹性受力阶段：试件在前三级加载过程中，未能观察到明显裂缝，该阶段荷载-位移曲线基本呈线性变化，墙体受力均匀，残余变形小.
2） 裂缝萌生及扩展阶段：该阶段从墙身剪切裂缝出现，直到出现贯通裂缝为止，对于W-1墙，加载阶段出现明显斜裂缝，在墙体的底部和顶部出现多条斜裂缝，随荷载增加后，裂缝进一步开展并形成通缝，最后整片墙体呈明显的X型裂缝. W-2墙体在此加载阶段，随着位移的增大裂缝持续开展，形成多斜向贯通裂缝，只有用黄泥的部位出现明显的X型裂缝，且每级卸载后都有较大的残余变形.
3） 破坏阶段：W-1在此阶段斜向裂缝宽度增大并形成明显通缝，砂浆及腻子大片脱落，墙体变形明显，受力较上一级不增反降. W-2在此阶段砂浆脱落明显，竖向钢筋骨架处片石开始脱落，并与黄泥砌筑部分产生竖向通缝，黄泥部分裂缝较多且集中形成X型裂缝，墙体侧面能明显观察到片石向外挤压.
试验观察到的相似点：增设W-1墙与W-2墙的破坏过程和最终破坏相似. 不同点：W-1墙体在试验过程中裂缝一旦产生便迅速延伸，最终形成X型交叉斜裂缝；W-2墙在整个加载过程中墙身的斜向裂缝发展较缓慢，裂缝数量较少，且承载能力相较于普通片石墙体增长显著. W-1、W-2墙体最终破坏如图9所示.
2.2 滞回曲线
试验所得的滞回曲线如图10所示，分析上述曲线可知：
1） 在加载初期，W-2墙体比W-1墙体的水平承载力高，初始刚度高. 2个试件滞回曲线呈近似直线变化，滞回环面积较小，循环加载后无明显残余变形，墙体处于弹性工作阶段，试件耗能较少.
2） 墙体开裂后，由于墙体中黄泥砂浆的黏结能力较低，使试件产生一定程度的滑移，W-1墙体曲线斜率逐渐减小，滞回环所包围面积增大，具有捏缩现象， W-2墙体的切线刚度较加载初期明显变缓，由于墙体在约束作用下导致裂缝开展相对缓慢，滞回环数量增多，捏缩现象更加明显，但W-2墙体较W-1墙体弹塑性受力阶段明显.
3） 加载后期，W-2墙体各级加载循环下滞回环形状与面积变化较W-1墙体滞回环形状与面积变化小，表明钢筋骨架系统的加入让墙体在塑性破坏阶段耗能性能更加稳定.
2.3 骨架曲线
试验所得荷载-位移骨架曲线如图11. 表6给出了W-1墙体和W-2墙体各阶段荷载及位移，表中：Pcr、Py、Pm、Pu分别为试件开裂、屈服、极限、破坏状态下对应的水平荷载；Δcr、Δy、Δm、Δu分别为试件开裂、屈服、极限、破坏状态下对应的水平位移；μy为试件的延性系数，即Δu 与Δy之比；$ {\theta }_{\mathrm{u}} $为极限位移，即Δu 与试件高度H之比. 分析表6可知：W-2试件的延性系数较W-1试件的延性系数较低，原因是增设钢筋骨架系统对试件W-2的屈服位移提高幅度大于破坏位移的提高幅度；W-2试件比W-1试件从开裂到破坏的变形空间明显增大，破坏位移提高了1.67倍，表明了W-2试件的延性较W-1试件好.
由图11、表6分析可知：1） 骨架曲线均呈反S型，表明试件经历了弹性变形、裂缝萌生及发展阶段和破坏阶段3个典型受力阶段，与试验现象一致. 2）比较2个试件的极限承载力及极限位移可知，试件W-2的极限承载力63.33 KN明显高于试件W-1的极限承载力19.49 KN，提高了3.25倍，试件W-2的破坏位移值46.7 mm是试件W-1破坏位移值28.0 mm的1.67倍，表明有钢筋骨架系统约束的墙体抗剪能力和变形能力均较无任何构造措施的片石墙好. 3） W-2在达到极限承载力后其抗剪刚度退化较W-1缓慢，这主要由于在下降阶段钢筋骨架系统有效的抑制了斜向剪切裂缝的开展，表明增设钢筋骨架的效果明显.
表 6 各阶段荷载及位移Table 6. Load and displacement at each stage试件编号 Pcr/kN Δcr/mm Py/kN Δy/mm Pm/kN Δm/mm Pu/kN Δu/mm μy θu W-1 10.07 1.75 13.48 2.80 19.49 20.00 18.19 28.00 10.00 1/55 W-2 23.85 2.80 38.70 5.60 63.33 20.00 62.56 46.70 8.34 1/33 2.4 刚度退化
试件等效刚度可定义为每次循环滞回曲线定点割线刚度来表示，其表达式为
Ki=|Pi|+|−Pi||Δi|+|−Δi|, (1) 式中：±Pi、±Δi分别为第i次循环滞回曲线的峰值荷载和峰值位移.
基于式（1）得出试件W-1与试件W-2的割线刚度和位移关系如图12示，由图可知：1） 2个试件刚度退化规律大致相同，在加载初期刚度退化较快，后期刚度退化相对较缓；2） 在整个加载过程中，W-1墙体在裂缝萌生及扩展阶段的刚度退化较快，W-2墙体的刚度随着位移的增大逐渐下降；3） 在整个加载过程中，相同的水平位移情况下，试件W-2的抗侧刚度均大于试件W-1的抗侧刚度，初始刚度较试件W-1提高了1.22倍，表明增设钢筋骨架系统可以显著改善石墙的抗侧刚度.
图 12 W-1、W-2刚度退化曲线对比Figure 12. Comparison of stiffness degradation curves of W-1 and W-22.5 钢筋应变分析
试件W-2中钢筋骨架系统中的纵、横向钢筋测点应变如图13、14所示，测点16因损坏而无数据显示. 由图可知：1） 纵向钢筋应变随位移的增加而增大，表明所有的纵向钢筋在整个加载过程中均发挥作用，且受力明显，拉压应变基本对称；2） 纵向钢筋上部应变小于钢筋下部应变，表明墙体下部受力大于上部受力；3） 水平钢筋与竖向钢筋形成整体作用，上层水平钢筋应变明显大于下层水平钢筋的应变，表明上层钢筋的受力大于下层钢筋的受力.
图 14 水平钢筋上、下层测点应变对比Figure 14. Comparison of strains at upper and lower measuring points of horizontal reinforcement2.6 耗能能力
耗能能力是衡量结构或构件抵抗地震作用的重要指标，其大小反应了试件在地震反复作用下吸收的能量值. 通过累积滞回耗能系数$ {E}_{{\mathrm{u}}} $和等效黏滞阻尼系数ζeq对藏羌石墙的耗能性能进行分析，计算结果见表7.
表 7 不同阶段受力Eu试验结果Table 7. Stress Eu test results at different stages编号 开裂 极限 破坏 Eu ζeq Eu ζeq Eu ζeq W-1 0.034 0.119 0.538 0.200 0.843 0.242 W-2 0.109 0.086 0.890 0.114 2.383 0.200 由表7可知：1） 随着位移幅值的增加，$ {\xi }_{{\mathrm{eq}}} $和$ {E}_{{\mathrm{u}}} $呈递增趋势，墙体耗能能力不断提高；2） W-2累积滞回耗能系数始终高于试件W-1的，W-2耗能性能是W-1的2.83倍，表明试件W-2的钢筋骨架系统有效地吸收地震能量，能更好地抵抗地震作用.
3. 有限元分析
3.1 计算模型
基于ABAQUS有限元分析软件，建立普通片石墙体和加入钢筋骨架系统约束的片石墙体有限元模型. 钢筋骨架系统采用桁架单元T3D2来模拟，片石墙体采用C3D8R单元进行模拟. 墙体采用修正后的混凝土受拉本构关系，受压本构模型采用杨卫忠[24]提出的砌体受压本构关系. 钢筋材料属性设置密度为7.8 g/cm3，杨氏模量为
210000 MPa，泊松比为0.3，屈服应力为300、400 MPa. 水泥砂浆砌筑墙体材料属性设置密度为2.55 g/cm³，杨氏模量为2462.56 MPa，泊松比为0.2；黄泥砂浆砌筑墙体材料属性设置密度为2.49 g/cm3，杨氏模量为46.24 MPa，泊松比为0.2. 为验证试验可靠性并进行2类墙体在拟静力作用下的对比，2类墙体加载制度相同. 模型计算设置步数为2的静力通用分析步，在step1中施加竖向荷载，step2中传递step1中荷载. 边界条件设置为约束模型底部各项自由度，在step2中设置指定位移约束，位移变化与试验中一致.3.2 砌体力学模型
3.2.1 砌体受压本构模型
本文采用杨卫忠[24]提出的受压本构关系，其受压本构关系为
σfm=η1+(η−1)(ε1/εm)η/(η−1)ε1εm, (2) 式中：$\sigma $为砌体压应力，fm为砌体轴心受压强度平均值，$\varepsilon_1 $、$\varepsilon_{\mathrm{m}} $分别为砌体压应变及fu对应的应变，η为初始切线模量与峰值割线模量的比值.
依据砌体试块试验结果，将εm取值0.035代入式（2）即可得到受压本构模型.
3.2.2 砌体受拉本构模型
砌体材料受拉破坏形式与混凝土受拉破坏形式相近，故采用修正后的混凝土受拉本构模型，其表达式[25]为
{σ2ftm=ε2εtm, ε2εtm⩽1,σ2ftm=ε2/εtm2(ε2εtm−1)1.7+ε2/εtm, ε2εtm>1, (3) 式中：$\sigma_2 $为砌体拉应力；ftm，$\varepsilon_2 $、$\varepsilon_{\mathrm{tm}} $分别为砌体峰值拉应力、砌体拉应变及ftm对应的应变.
3.3 计算结果分析
W-1墙体Mises应力云图、W-2墙体Mises应力云图和等效塑性应变云图如图15所示. 1）W-1墙体承受竖向荷载以及水平往复力作用，使得结构出现斜向应力，近似45°角由左下角延伸至右上角，右下角延伸至左上角，试件的斜对角出现应力集中，说明裂缝比较密集，破坏较为严重，与试验“X”型裂缝破坏情况相似. 2）W-2墙体承受竖向荷载和水平往复周期荷载作用，钢筋骨架系统的水平钢筋网和竖向钢筋网连接节点出现较大应力，连接处钢筋发生屈服，墙体出现塑性应变并向四周挤压变形，墙身出现裂缝并伴随砂浆脱落和部分块石脱落，模拟结果与试验现象相似.
图 15 W-1墙体应力、W-2墙体应力和等效塑性应变云图Figure 15. Stresses and equivalent plastic strain cloud maps of W-1 and W-23.4 试验结果对比分析
将数值计算所得的骨架曲线、滞回曲线与试验结果进行对比，结果如图16、17所示.
图 16 W-1、W-2墙体试验与模拟骨架曲线对比Figure 16. Comparison between test and simulated skeleton curves of W-1 and W-21） 由图16可知：W-1墙体和W-2墙体模拟结果和试验所得曲线的发展趋势相近，均为S形；试件在开裂前期，正向加载和反向加载试验值微大于模拟值，开裂后正向加载和反向加载模拟值大于试验值，原因在于实验时材料具有极强的脆性，在很小的位移条件下即开裂，在开裂后其承载力和刚度均降低.
2） 由图17可知：W-1墙体模拟滞回曲线近似为梭形又不够饱满，滞回环面积均较大于试验结果，原因在于石墙在砌筑过程中受石材摆放和砌筑工艺影响较大，石墙的整体性较差，与模拟中理想的砌体受拉和修正后混凝土受拉本构关系存在差距；W-2墙体由于钢筋骨架系统的加入，模拟得到墙体的滞回曲线为梭形，滞回环形状饱满，墙体的塑性变形能力较好；在各级循环加载位移控制为0时曲线有细微的内凹，但相比试验得到的反S形滞回曲线捏缩现象较弱，原因在于W-2墙体在加载卸载过程中受到剪力作用，并且与钢筋的粘结产生了滑移，试验中由于钢筋与石块和水泥砂浆之间存在孔隙从而导致滑移现象更加明显.
图 17 W-1、W-2墙体试验与模拟滞回曲线对比Figure 17. Comparison between test and simulated hysteretic curves of W-1 and W-23） 将２个试件的极限荷载实验值和模拟值进行对比，W-1墙体位移控制为28.00 mm时，试验得到极限荷载为19.49 KN，模拟得到极限荷载为21.62 KN，相对误差为9.9%；W-2墙体位移控制为46.70 mm时，试验测得极限荷载为63.33 KN，模拟测得极限荷载78.04 KN,相对误差为18.8%；模拟和试验相对误差均保持在20%以内，说明所采用的有限元计算模型较为合理.
4. 结 论
通过对普通片石墙体和加入钢筋骨架约束的片石墙进行拟静力试验与数值模拟，分析墙体的破坏特征、滞回特性、骨架曲线、刚度特性、耗能性能等，比较两面墙体的破坏形式以及受力情况，具体结论如下：
1） 藏羌石砌体呈脆性破坏. 因片石是刚性材料，黄泥砂浆的黏结性能较差，藏羌石木结构的石砌体在受压过程中体现出明显的脆性，易发生局部脱落和倒塌破坏，抗压强度低.
2） 藏羌民居石墙呈X型斜向剪切破坏. 通过石墙的低周反复加载试验，发现2面石墙在低周反复荷载作用下主要经历3个阶段：弹性阶段、裂缝萌生及发展阶段、破坏阶段，最终均呈现典型的X型斜向剪切破坏.
3） 钢筋骨架系统约束的片石墙抗震性能优异. 对比分析抗震性能，发现有钢筋骨架系统的墙体弹性阶段、裂缝萌生及发展阶段历时更长，且极限承载力、抗侧刚度、耗能性能均有提升，其中，极限承载力提升了225%，耗能性能提升了183%. 极限位移提高了67%，证明了钢筋骨架系统对石墙抗震性能提高的有效性，该措施有助于四川省藏羌地区新建石木结构的抗震应用.
4） 试验和数值模拟得到W-1、W-2墙体的破坏特征、滞回特性基本一致. 骨架曲线数值略有误差，但单一曲线变化趋势一致且均为S形，滞回曲线形状不同，但W-2墙体滞回性能、抗震性能均优于W-1墙体的.
5） 钢筋骨架系统可适用于藏羌民居片石墙体. 通过试验发现，钢筋骨架系统约束的石墙具有抗震可行、施工易行、无需模板、缩短工期、成本低廉、不破坏片石墙特色风貌等优点，对实际工程建造有一定的指导意义.
-
图 1 Taylor-Couette反应器几何模型及网格划分示意
Figure 1. Geometry model and meshing for Taylor-Couette reactor
图 2 大涡模拟与PIV测量环隙子午面速度矢量图对比
Figure 2. Comparison between LES and PIV measurement of velocity vector on meridian plane
图 4 各转速工况下速度矢量图周期变化过程
Figure 4. Periodic variations in velocity vector diagram at different rotational velocities
图 5 各转速工况特征线上一个周期内轴向速度随时间的变化
Figure 5. Variation of axial velocity with time along characteristic line at different rotational velocities within a cycle
图 6 各转速工况特征线上一个周期内径向速度随时间的变化
Figure 6. Variation of radial velocity with time along characteristic line at different rotational velocities within a cycle
图 7 各转速工况特征线上一个周期内切向速度随时间的变化
Figure 7. Variation of tangential velocity with time along characteristic line at different rotational velocities within a cycle
图 8 各工况特征线上各向最大速度对比
Figure 8. Comparison of maximum velocities along characteristic line under various working conditions
图 9 各工况三维涡旋等值面周期内变化
Figure 9. Variation of three-dimensional vortex isosurface within a cycle under various working conditions
-
[1] SCHRIMPF M, ESTEBAN J, WARMELING H, et al. Taylor-Couette reactor: principles, design, and applications[J]. AIChE Journal, 2021, 67(5): e17228.1-e17228.24. doi: 10.1002/aic.17228 [2] KÁDÁR R, BALAN C. Transient dynamics of the wavy regime in Taylor-Couette geometry[J]. European Journal of Mechanics: B/Fluids, 2012, 31: 158-167. doi: 10.1016/j.euromechflu.2011.07.003 [3] MAO Y H, CHANG Q, ZENG L Y, et al. Velocity field structure and flocculation efficiency in Taylor–Couette flow[J]. Separation Science and Technology, 2013, 48(4): 659-663. doi: 10.1080/01496395.2012.692420 [4] DASH A, ANANTHARAMAN A, POELMA C. Particle-laden Taylor-Couette flows: higher-order transitions and evidence for azimuthally localized wavy vortices[J]. Journal of Fluid Mechanics, 2020, 903: A20.1-A20.35. [5] CHOUIPPE A, CLIMENT É, LEGENDRE D, et al. Numerical simulation of bubble dispersion in turbulent Taylor–Couette flow[J]. Physics of Fluids, 2014, 26(4): 043304.1-043304.22. [6] TENG H, LIU N, LU X, et al. Direct numerical simulation of Taylor-Couette flow subjected to a radial temperature gradient[J]. Physics of Fluids, 2015, 27(12): 125101.1-125101.21. [7] BAROUDI L, MAJJI M V, PELUSO S, et al. Taylor-Couette flow of hard-sphere suspensions: overview of current understanding[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2023, 381(2243): 20220125.1-20220125.20. doi: 10.1098/rsta.2022.0125 [8] RUDMAN M, METCALFE G, GRAHAM L J W. Nonmixing vortex cores in wavy Taylor vortex flow[J]. Physics of Fluids, 2008, 20(6): 063602.1-063602.6. [9] 郑云,刘志祥,余志祥,等. 基于PIV试验的积雪平屋面风场特性研究[J]. 西南交通大学学报,2023,58(2):430-437,461.ZHENG Yun, LIU Zhixiang, YU Zhixiagn, et al. Wind field characteristics of snow-covered low-rise building roof based on PIV experiments[J]. Journal of Southwest Jiaotong University, 2023, 58(2):430-437,461. [10] LUO G H, YAO Z Q, SHEN H. A new hybrid turbulence model applied to highly turbulent Taylor-Couette flow[J]. Physics of Fluids, 2018, 30(6): 065103.1-065103.12. [11] CHENG W, PULLIN D I, SAMTANEY R. Large-eddy simulation and modelling of Taylor-Couette flow[J]. Journal of Fluid Mechanics, 2020, 890: A17.1-A17.31. doi: 10.1017/jfm.2020.101 [12] YANG Z Y. Large-eddy simulation: past, present and the future[J]. Chinese Journal of Aeronautics, 2015, 28(1): 11-24. doi: 10.1016/j.cja.2014.12.007 [13] 康啊真,殷瑞涛,祝兵,等. 基于 LES 的跨海桥梁施工期围堰波流力数值模拟[J]. 西南交通大学学报,2020,55(3):537-544, 587.KANG Azhen, YIN Ruitao, ZHU Bing, LI Xin, ZHANG Jiawei. Numerical simulation of wave-current forces acting on cofferdam for sea-crossing bridge based on large eddy simulation[J]. Journal of Southwest Jiaotong University, 2020, 55(3): 537-544, 587. [14] 刘超群. Liutex-涡定义和第三代涡识别方法[J]. 空气动力学学报,2020,38(3): 413-431,478.LIU Chaoqun. Liutex-third generation of vortex definition and identification methods[J]. Acta Aerodynamica Sinica, 2020, 38(3): 413-431,478. [15] DONG X R, WANG Y Q, CHEN X P, et al. Determination of epsilon for Omega vortex identification method[J]. Journal of Hydrodynamics, 2018, 30(4): 541-548. doi: 10.1007/s42241-018-0066-x -
下载:
下载:
点击查看大图
计量
- 文章访问数: 73
- HTML全文浏览量: 32
- PDF下载量: 3
- 被引次数: 0