Nonlinear Buckling Analysis of Suspended Domes Considering Initial Curvature of Members
-
摘要:
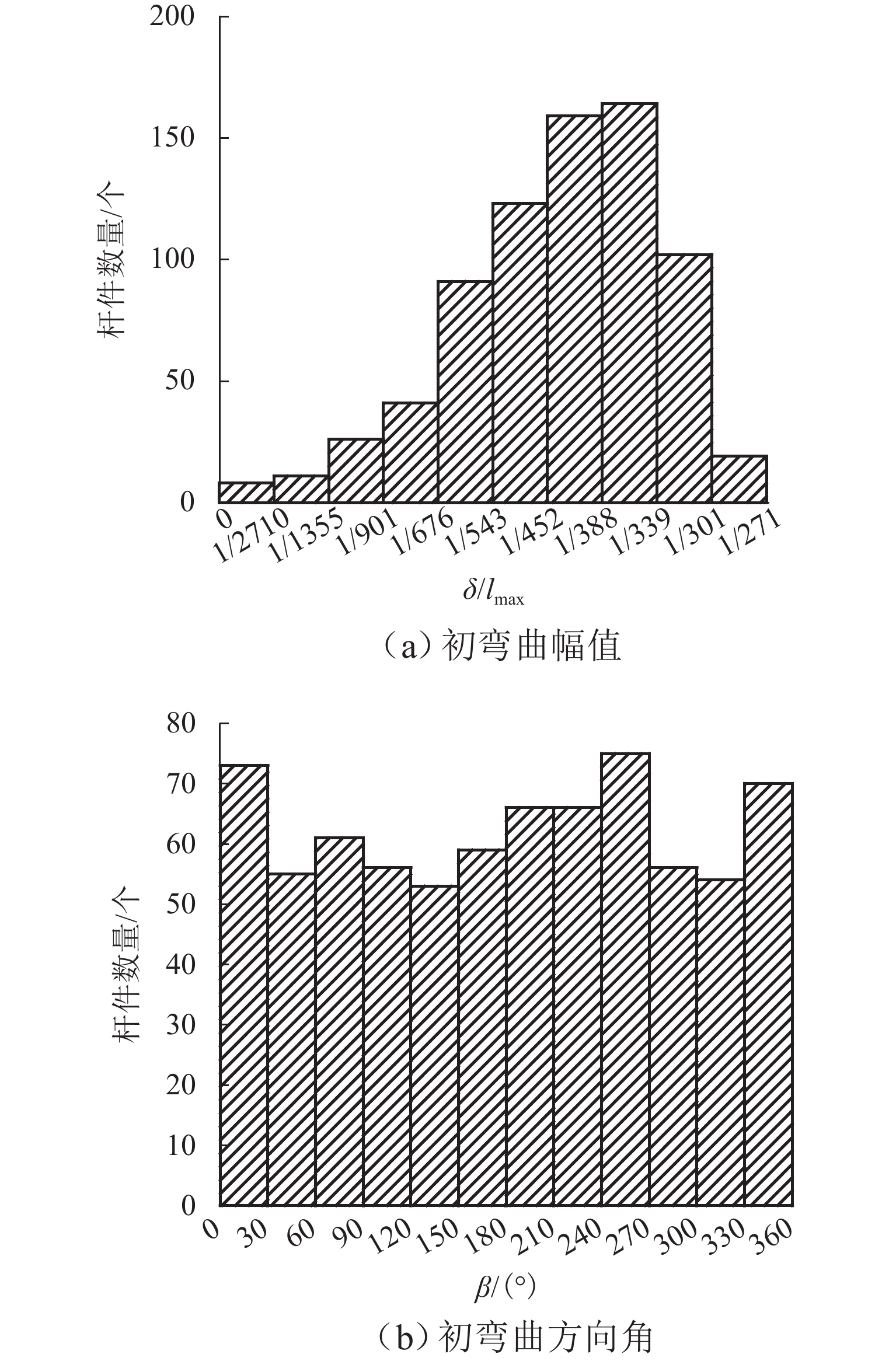
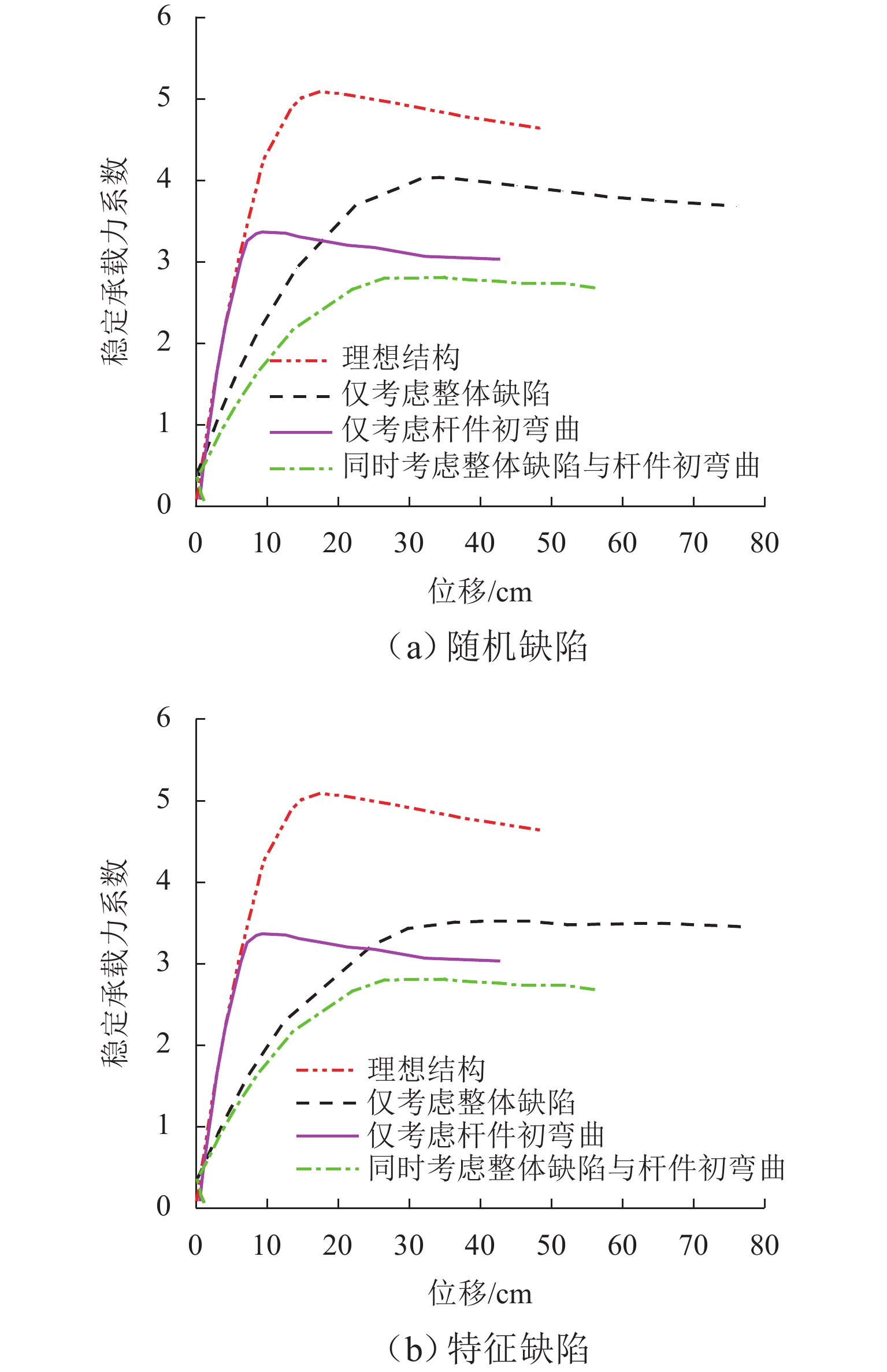
为揭示杆件初弯曲对弦支穹顶结构稳定承载力的影响规律，以多段直梁法模拟杆件初弯曲，采用随机缺陷模态法引入不同形状及幅值的杆件初弯曲，对弦支穹顶结构进行非线性屈曲分析；引入整体缺陷与杆件初弯曲，考察2种缺陷的共同施加对结构稳定性能的影响. 结果表明：仅考虑杆件初弯曲时，弦支穹顶结构的稳定承载力系数平均值显著降低（最大降幅为33.84%），该结构对杆件初弯曲较为敏感；相比于正弦全波，以正弦半波为初弯曲形状来引入杆件初弯曲，对结构的稳定性更为不利；相比于理想结构，同时考虑整体缺陷与杆件初弯曲时，结构的稳定承载力系数进一步降低（最大降幅为44.80%），但其降幅小于两者分别引入的降幅之和，2种缺陷的同时施加，对结构的稳定承载力存在耦合影响，一定程度上削弱了两者单独引入时的不利影响.
Abstract:In order to reveal the influence laws of the initial curvature of members on the stability bearing capacity of suspended domes, a nonlinear buckling analysis of suspended domes was carried out by applying the multi-beam method to simulate the initial curvature of members and the random imperfection mode method to introduce the initial curvature of members with different shapes and amplitudes. The overall imperfection and the initial curvature of members were introduced to investigate the effect of the two kinds of imperfections imposed jointly on the structural stability behaviors. The results show that the mean coefficients of stability bearing capacity of suspended domes are significantly reduced when only the initial curvature of members is considered, and the maximum reduction is 33.84%, which indicates that the structure is sensitive to the initial curvature of members. Compared with the sinusoidal full-wave, the sinusoidal half-wave as the shape of initial curvature is more unfavorable to the structural stability. When the overall imperfection and the initial curvature of members are both considered, the coefficients of stability bearing capacity are further reduced for the suspended domes compared with the perfect structure, with the maximum reduction being 44.80%, but the reductions are smaller than the sums of reductions when the two kinds of imperfections are introduced separately. The joint action of the two kinds of imperfections has coupling effects on the structural stability bearing capacity, which weakens the adverse effects when the two kinds of imperfections are introduced separately to some extent.
-
图 4 一次模拟所得的初弯曲幅值及方向角分布直方图
Figure 4. Distribution histograms of amplitudes and direction angles of initial curvature from one simulation
图 5 理想结构引入杆件初弯曲分布（放大50倍）
Figure 5. Distributions of initial curvature of members introduced in perfect structure （enlarged by 50 times）
图 6 稳定承载力系数分布直方图
Figure 6. Distribution histograms of coefficients of stability bearing capacity
图 7 仅考虑杆件初弯曲的稳定承载力系数平均值对比
Figure 7. Comparison of mean coefficients of stability bearing capacity considering initial curvature of members only
图 8 整体缺陷结构引入杆件初弯曲分布（放大50倍）
Figure 8. Distributions of initial curvature of members introduced in structures with overall imperfection （enlarged by 50 times）
图 9 同时考虑2种缺陷的稳定承载力系数平均值对比
Figure 9. Comparison of mean coefficients of stability bearing capacity considering both kinds of imperfections
图 10 不同模型对应的荷载-位移曲线对比
Figure 10. Comparison of load-displacement curves corresponding to different models
表 1 构件和材料规格
Table 1. Specifications of members and materials
结构部位 构件 材质 规格 上部单层
网壳凯威特
部分径向杆 Q355B ϕ219 × 12 环向杆 Q355B ϕ219 × 12 斜杆 Q355B ϕ203 × 10 联方
部分环向杆 Q355B ϕ203 × 10 斜杆 Q355B ϕ194 × 10 撑杆 Q355B ϕ168 × 8 下部索杆
体系环向索 内圈 平行钢丝
束，1670 级ϕ5 × 61 中圈 平行钢丝
束，1670 级ϕ5 × 91 外圈 平行钢丝
束，1670 级ϕ5 × 139 径向索 平行钢丝
束，1670 级ϕ5 × 55 
下载: 导出CSV
表 2 仅考虑杆件初弯曲的稳定承载力系数
Table 2. Coefficients of stability bearing capacity considering initial curvature of members only
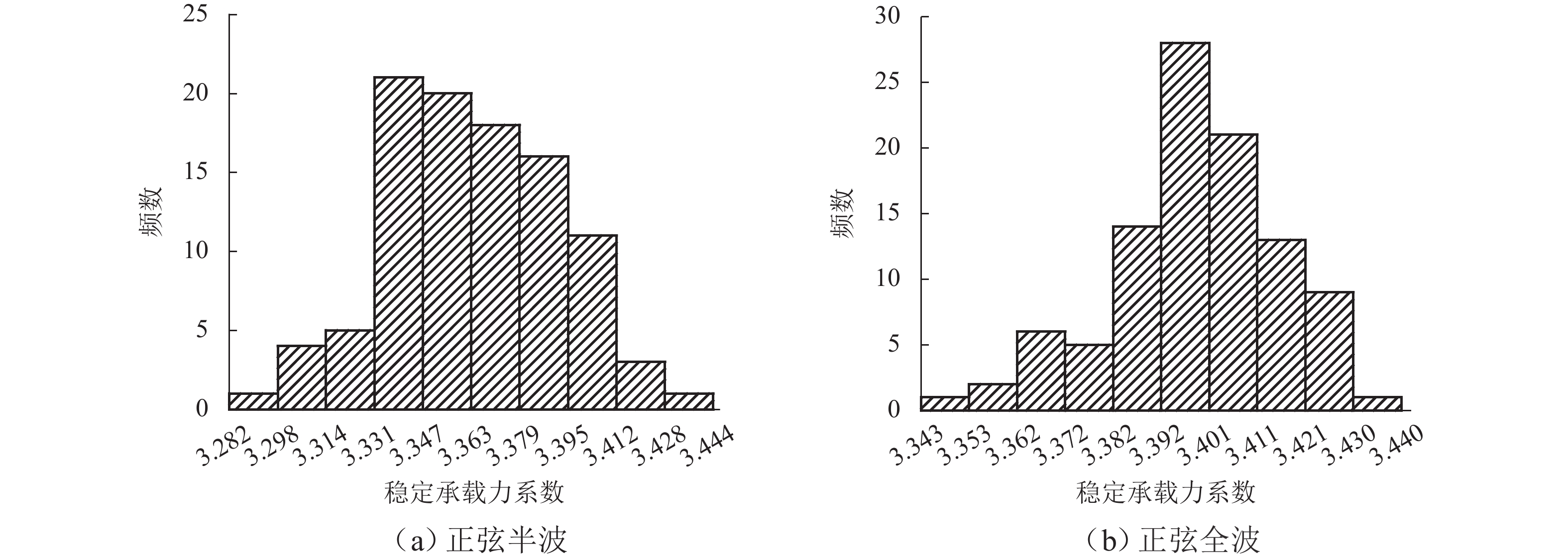
初弯曲形状 稳定承载力系数 正弦半波 3.361，3.328，3.382，3.390，3.391，3.398，
3.377，3.345，3.338，3.355，3.343，3.367，
3.324，3.401，3.344，3.368，3.371，3.353，
3.375，3.350，3.387，3.379，3.340，3.389，
3.389，3.340，3.320，3.313，3.378，3.401，
3.282，3.378，3.404，3.369，3.370，3.331，
3.444，3.371，3.333，3.342，3.310，3.361，
3.394，3.402，3.338，3.314，3.377，3.348，
3.337，3.359，3.383，3.405，3.358，3.351，
3.360，3.383，3.391，3.329，3.349，3.421，
3.365，3.414，3.346，3.386，3.354，3.339，
3.357，3.393，3.418，3.364，3.339，3.361，
3.364，3.339，3.362，3.345，3.384，3.348，
3.346，3.336，3.356，3.403，3.346，3.350，
3.409，3.375，3.379，3.393，3.377，3.326，
3.355，3.312，3.336，3.397，3.382，3.351，
3.332，3.404，3.397，3.385$ {K_{\min }} = 3.282 $，$ {K_{\max }} = 3.444 $，$ \mu = 3.3642 $，$ {\sigma } = 0.028\;8 $ 正弦全波 3.424，3.416，3.406，3.416，3.395，3.387，
3.409，3.357，3.400，3.415，3.410，3.392，
3.406，3.395，3.370，3.369，3.390，3.409，
3.380，3.399，3.370，3.400，3.413，3.422，
3.398，3.385，3.405，3.422，3.424，3.423，
3.377，3.401，3.392，3.403，3.421，3.360，
3.408，3.393，3.407，3.411，3.397，3.440，
3.406，3.390，3.392，3.410，3.381，3.391，
3.411，3.397，3.388，3.397，3.409，3.419，
3.388，3.409，3.403，3.366，3.372，3.388，
3.410，3.399，3.367，3.386，3.427，3.412，
3.394，3.401，3.411，3.402，3.383，3.393，
3.400，3.415，3.392，3.427，3.398，3.421，
3.393，3.373，3.387，3.390，3.409，3.395，
3.384，3.395，3.406，3.414，3.401，3.416，
3.343，3.413，3.376，3.406，3.395，3.394，
3.400，3.410，3.387，3.410$ {K_{\min }} = 3.343 $，$ {K_{\max }} = 3.440 $，$ \mu = 3.3987 $，$ {\sigma } = 0.017\;0 $
下载: 导出CSV
表 3 仅考虑杆件初弯曲的稳定承载力系数对比
Table 3. Comparison of coefficients of stability bearing capacity considering initial curvature of members only
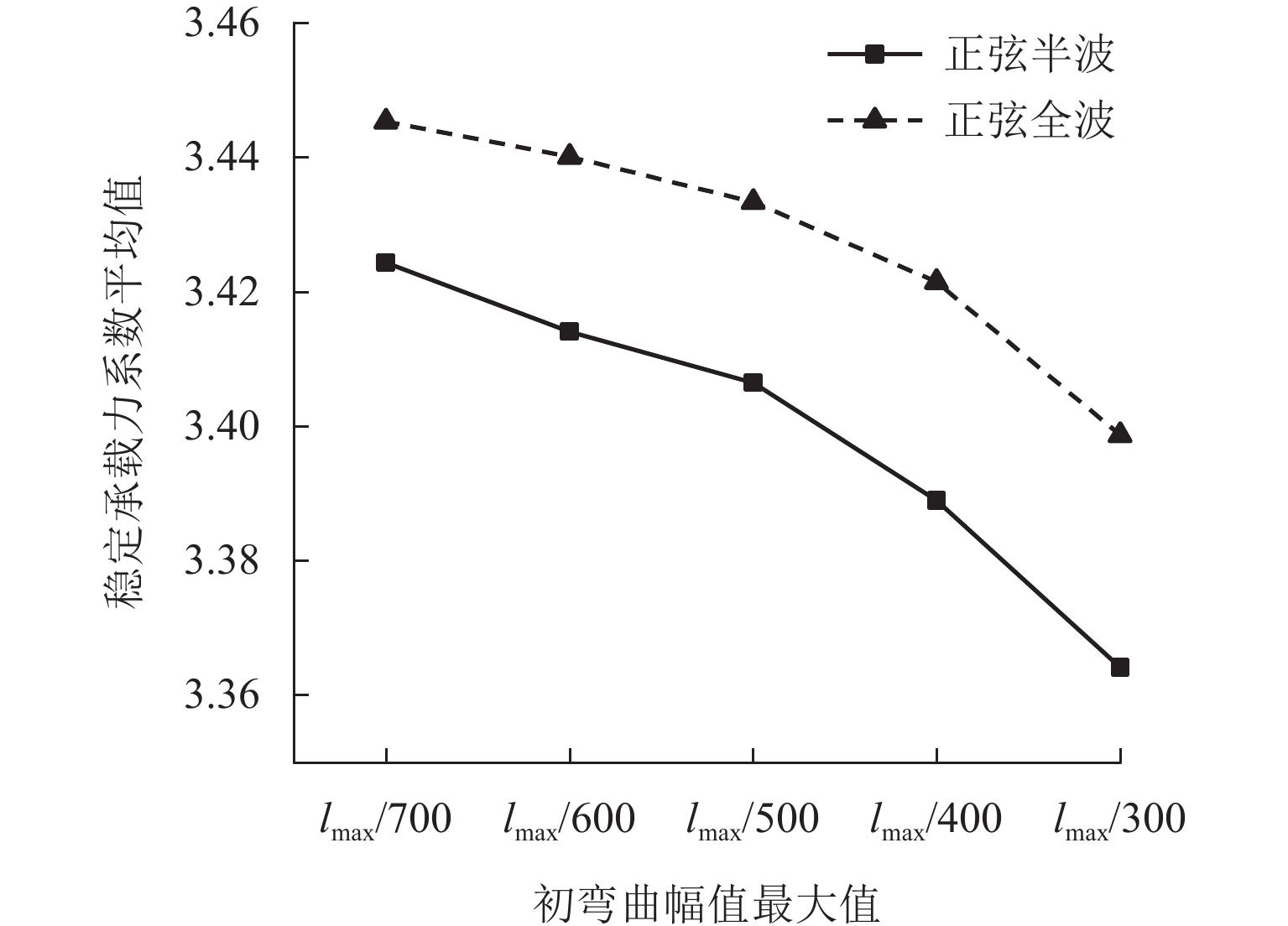
初弯曲幅值最大值 初弯曲形状 Kmin Kmax $ \mu $ $ \sigma $ 是否满足 χ2 检验 $ \mu - 3\sigma $ lmax/700 正弦半波 3.365 3.482 3.4243 0.0178 否 正弦全波 3.424 3.473 3.4453 0.0092 是 3.4177 lmax/600 正弦半波 3.344 3.469 3.4141 0.0216 是 3.3493 正弦全波 3.400 3.465 3.4401 0.0102 是 3.4095 lmax/500 正弦半波 3.356 3.461 3.4065 0.0192 是 3.3489 正弦全波 3.401 3.459 3.4334 0.0109 是 3.4007 lmax/400 正弦半波 3.305 3.476 3.3890 0.0305 是 3.2975 正弦全波 3.369 3.443 3.4215 0.0120 是 3.3855 lmax/300 正弦半波 3.282 3.444 3.3642 0.0288 是 3.2778 正弦全波 3.343 3.440 3.3987 0.0170 是 3.3477
下载: 导出CSV
表 4 同时考虑2种缺陷的稳定承载力系数对比
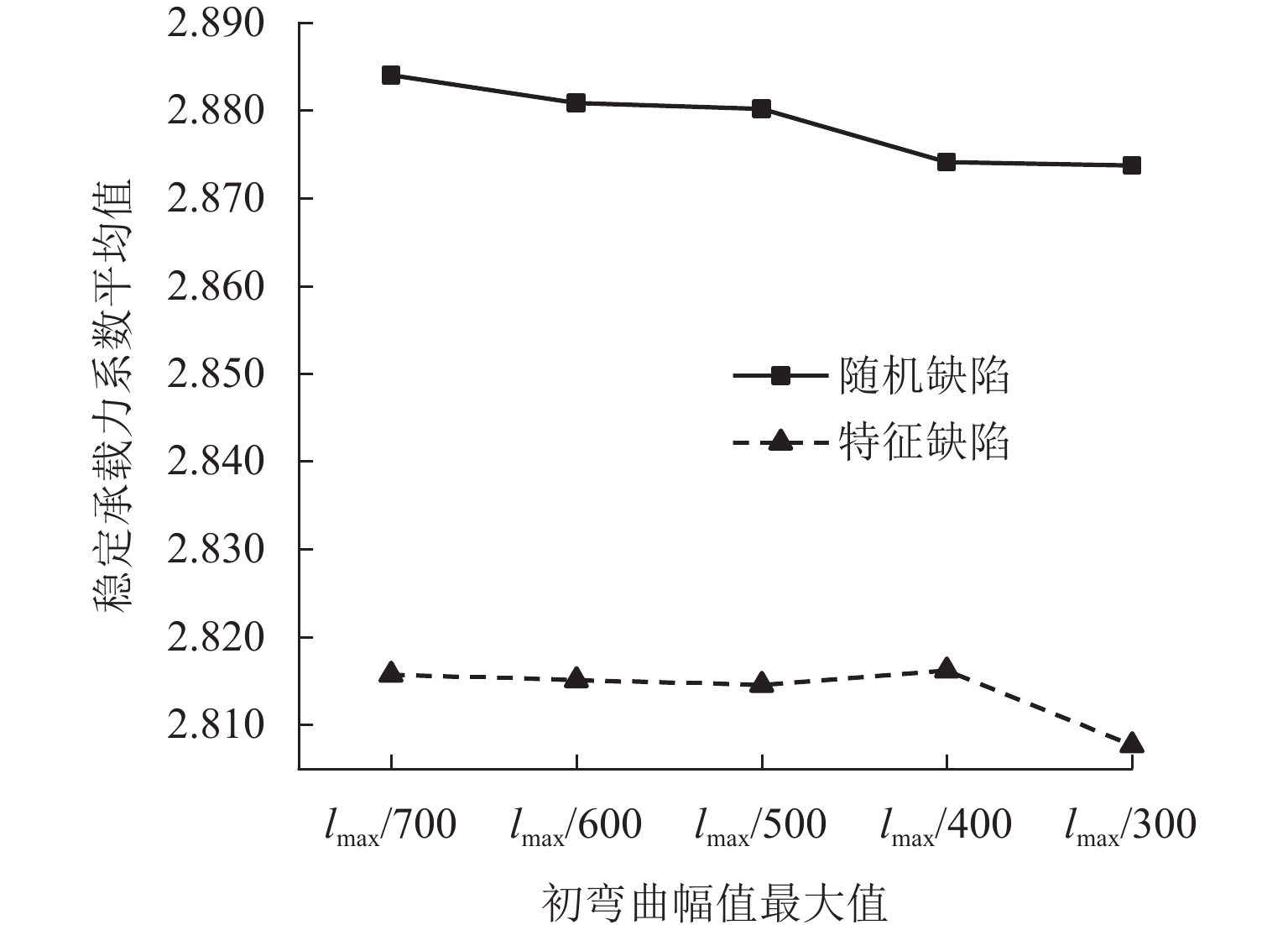
Table 4. Comparison of coefficients of stability bearing capacity considering both kinds of imperfections
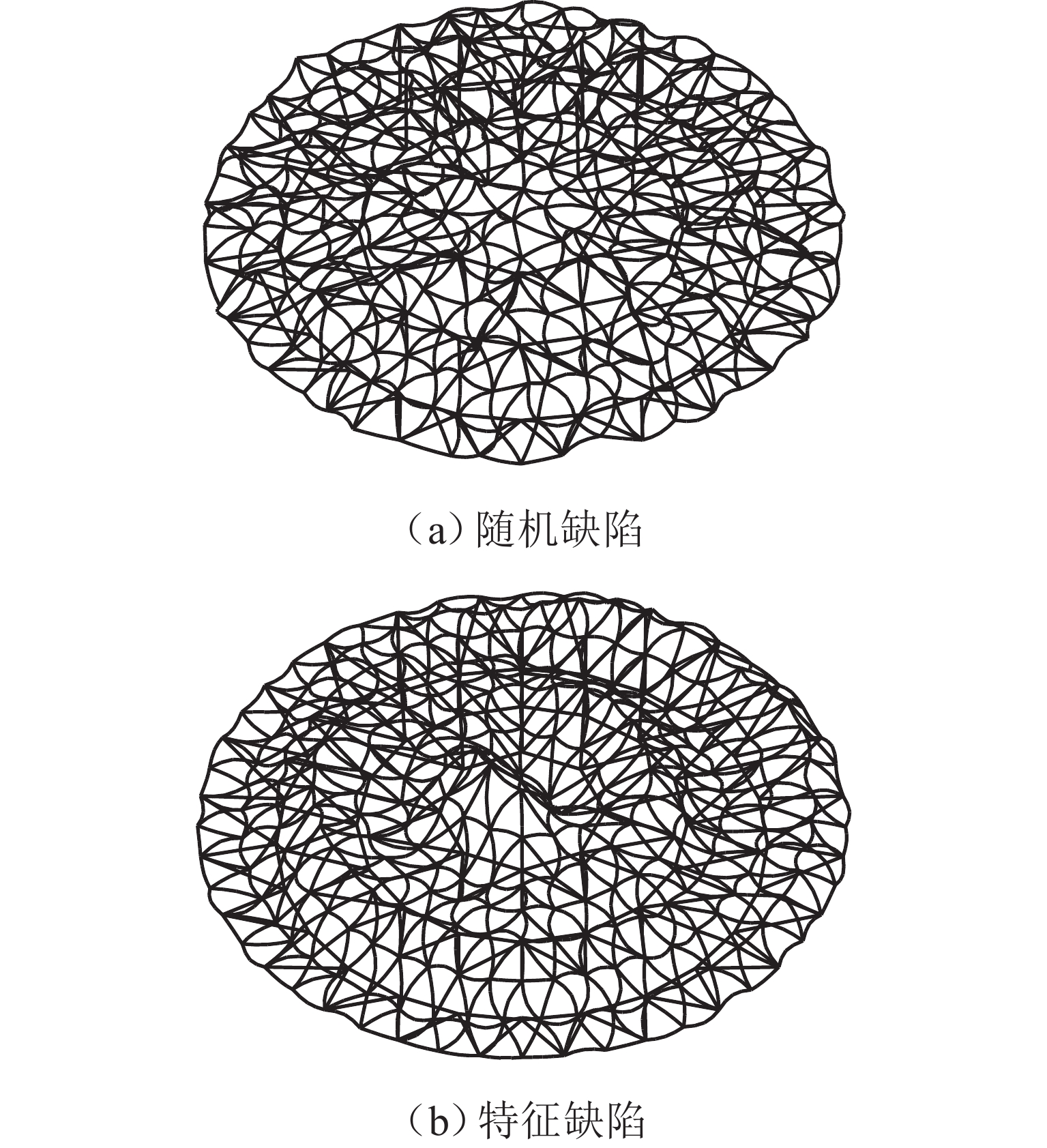
整体缺陷分布模式 初弯曲幅值最大值 Kmin Kmax $ \mu $ $ \sigma $ 是否满足 χ2 检验 $ \mu - 3\sigma $ 随机缺陷 lmax/700 2.845 2.916 2.8840 0.0142 否 lmax/600 2.841 2.914 2.8809 0.0125 是 2.8434 lmax/500 2.843 2.940 2.8802 0.0137 是 2.8391 lmax/400 2.841 2.913 2.8741 0.0164 是 2.8249 lmax/300 2.833 2.912 2.8737 0.0153 是 2.8278 特征缺陷 lmax/700 2.773 2.848 2.8157 0.0129 否 lmax/600 2.770 2.862 2.8151 0.0157 否 lmax/500 2.769 2.859 2.8146 0.0186 否 lmax/400 2.775 2.899 2.8162 0.0198 是 2.7568 lmax/300 2.759 2.878 2.8077 0.0197 否
下载: 导出CSV
-
[1] KAWAGUCHI M, ABE M, TATEMICHI I. Design, tests and realization of “suspen-dome” system[J]. Journal of the International Association for Shell and Spatial Structures, 1999, 40(3): 179-192. [2] 陈丰,潘睿,王四清. 张家界大成俄罗斯马戏城主馆屋盖结构的稳定性、抗连续倒塌及施工模拟分析[J]. 建筑结构,2020,50(20): 54-58.CHEN Feng, PAN Rui, WANG Siqing. Analysis on the stability, progressive collapse resistance and construction simulation of the roof structure of Dacheng Russian Circus City main pavilion in Zhangjiajie[J]. Building Structure, 2020, 50(20): 54-58. [3] 李璐. 张弦结构在景德镇游泳馆中的应用[J]. 建筑结构,2021,51(增2): 335-339.LI Lu. Application of string structure in Jingdezhen swimming center[J]. Building Structure, 2021, 51(S2): 335-339. [4] 葛家琪,张国军,王树,等. 2008奥运会羽毛球馆弦支穹顶结构整体稳定性能分析研究[J]. 建筑结构学报,2007,28(6): 22-30,44. doi: 10.3321/j.issn:1000-6869.2007.06.003GE Jiaqi, ZHANG Guojun, WANG Shu, et al. The overall stability analysis of the suspend-dome structure system of the badminton gymnasium for 2008 Olympic Games[J]. Journal of Building Structures, 2007, 28(6): 22-30,44. doi: 10.3321/j.issn:1000-6869.2007.06.003 [5] 刘静,赵若旭,陈宗学,等. 河北北方学院体育馆弦支穹顶屋盖稳定性能分析[J]. 建筑结构,2020,50(5): 82-87.LIU Jing, ZHAO Ruoxu, CHEN Zongxue, et al. Stability analysis on the suspend-dome structure roof of Hebei North University gymnasium[J]. Building Structure, 2020, 50(5): 82-87. [6] 陈前吉. 800 m凯威特巨型网格弦支穹顶静力及稳定性研究[D]. 哈尔滨:哈尔滨工业大学,2018. [7] 姜正荣,王仕统,石开荣,等. 厚街体育馆大跨度椭圆抛物面弦支穹顶结构的非线性屈曲分析[J]. 土木工程学报,2013,46(9): 21-28.JIANG Zhengrong, WANG Shitong, SHI Kairong, et al. Nonlinear buckling analysis of long-span elliptic paraboloid suspended dome structure for Houjie Gymnasium[J]. China Civil Engineering Journal, 2013, 46(9): 21-28. [8] LIU X C, ZHAN X X, ZHANG A L, et al. Random imperfection method for stability analysis of a suspended dome[J]. International Journal of Steel Structures, 2017, 17(1): 91-103. doi: 10.1007/s13296-015-1234-3 [9] 于敬海,胡相宜,陈彦,等. 弦支穹顶初始几何缺陷分布及稳定安全系数取值研究[J]. 空间结构,2017,23(3): 3-10,20.YU Jinghai, HU Xiangyi, CHEN Yan, et al. Research on initial geometric imperfection distribution and stability safety factor of suspen-dome[J]. Spatial Structures, 2017, 23(3): 3-10,20. [10] 王琼,邓华,黄莉. 杆件初弯曲对弦支穹顶静动力承载力的影响[J]. 空间结构,2013,19(4): 18-24,33. doi: 10.3969/j.issn.1006-6578.2013.04.003WANG Qiong, DENG Hua, HUANG Li. Effect of member’s initial curvature on the static and dynamic bearing capacity of suspended dome[J]. Spatial Structures, 2013, 19(4): 18-24,33. doi: 10.3969/j.issn.1006-6578.2013.04.003 [11] DING Y, ZHANG T L. Research on influence of member initial curvature on stability of single-layer spherical reticulated domes[J]. Advanced Steel Construction, 2019, 15(1): 9-15. [12] ZHAO Z W, LIU H Q, LIANG B, et al. Influence of random geometrical imperfection on the stability of single-layer reticulated domes with semi-rigid connection[J]. Advanced Steel Construction, 2019, 15(1): 93-99. [13] 闫翔宇,巩昊,陈志华,等. H型钢弦支穹顶结构弹塑性稳定性分析[J]. 空间结构,2022,28(3): 39-48.YAN Xiangyu, GONG Hao, CHEN Zhihua, et al. Elastic-plastic stability analysis of H-beam suspendome[J]. Spatial Structures, 2022, 28(3): 39-48. [14] 严佳川. 考虑杆件初弯曲的网壳结构耦合失稳机理研究[D]. 哈尔滨:哈尔滨工业大学,2012. [15] 陈惠发,ATSUTA T. 梁-柱分析与设计[M]. 北京:人民交通出版社,1997. [16] 邱俊明. 弦支穹顶结构的预应力多目标优化及静力稳定性分析[D]. 广州:华南理工大学,2022. [17] 李冬村. 凯威特-联方型单层网壳结构的静力稳定性及局部破坏敏感性分析[D]. 广州:华南理工大学,2019. [18] 刘红亮. 大跨度弦支穹顶结构的缺陷敏感区域及动力稳定性研究[D]. 广州:华南理工大学,2015. [19] 中华人民共和国住房和城乡建设部. 空间网格结构技术规程:JGJ 7—2010[S]. 北京:中国建筑工业出版社,2011. -
下载:
点击查看大图
计量
- 文章访问数: 72
- HTML全文浏览量: 38
- PDF下载量: 1
- 被引次数: 0