Comparison of Stress-Dilatancy Rules and Research on Stress-Dilatancy Rule for Rocks
-
摘要:
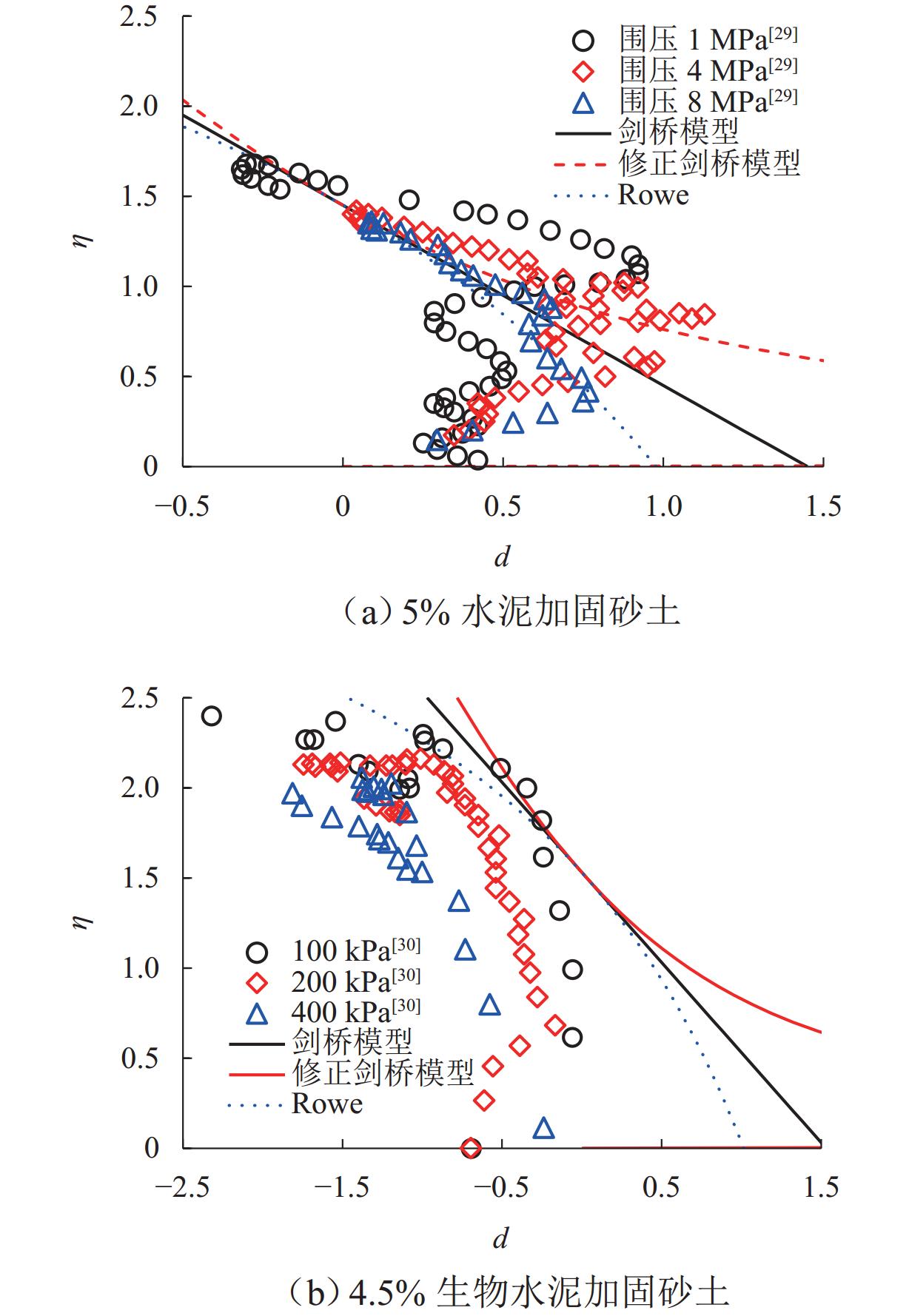
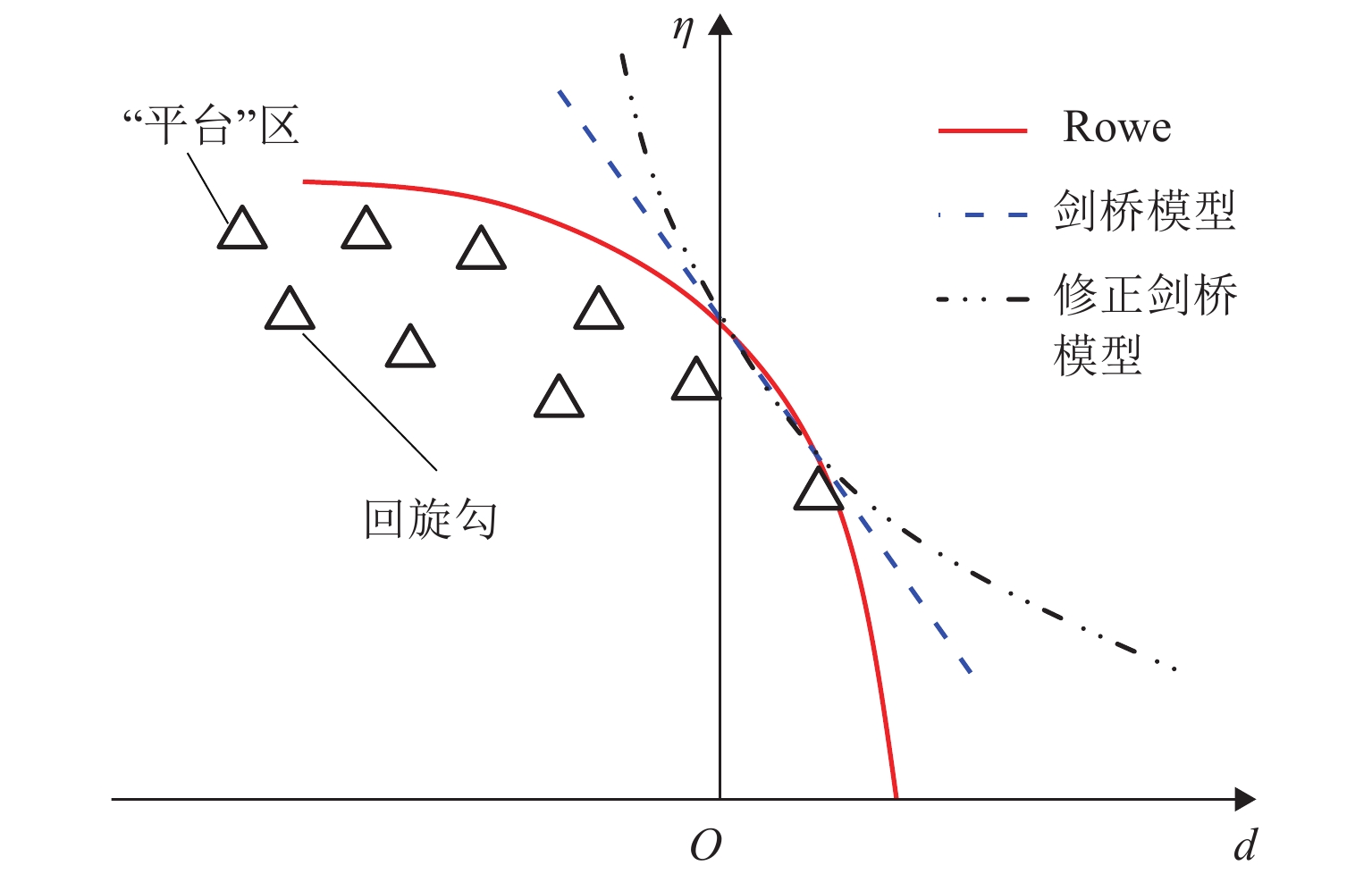
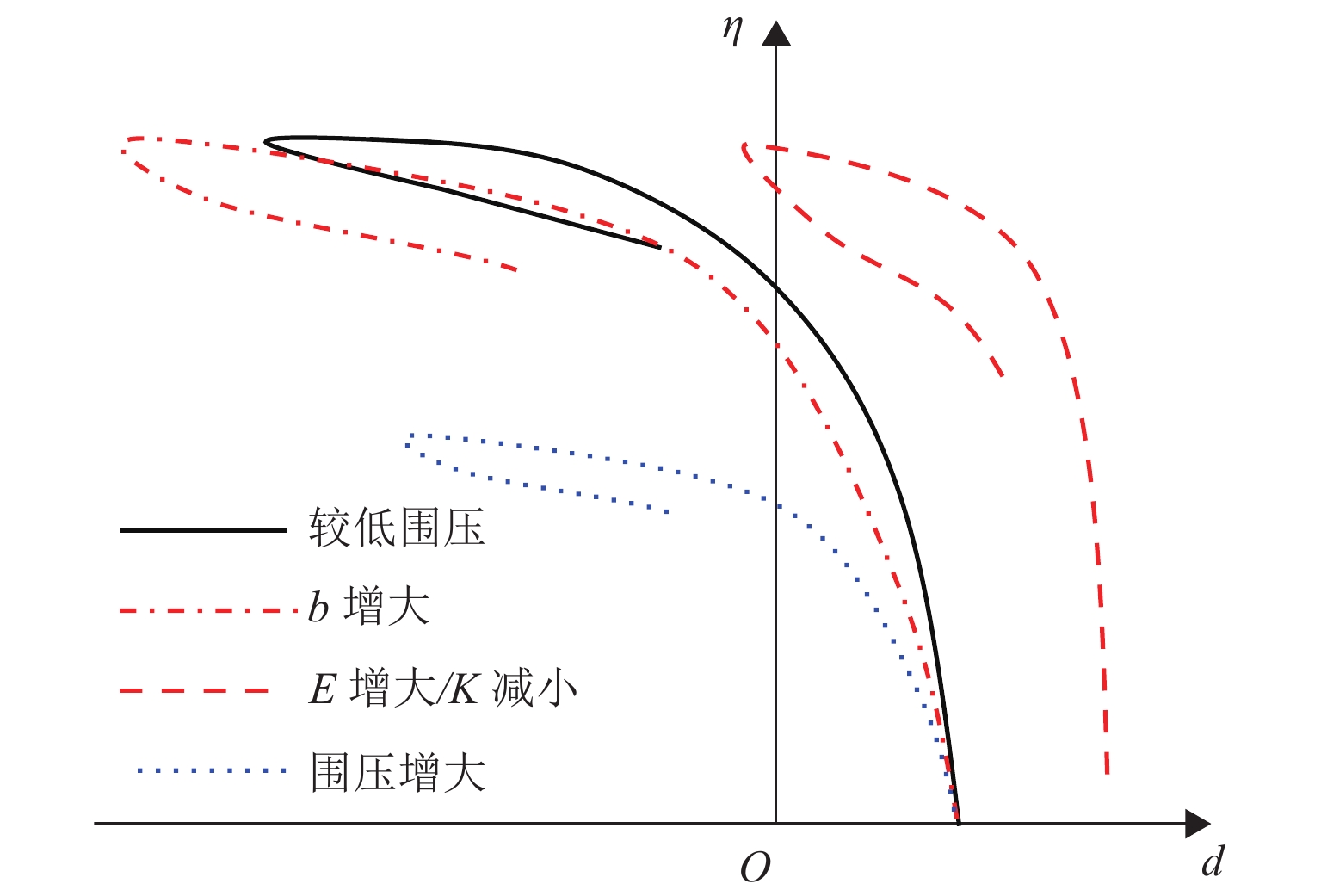
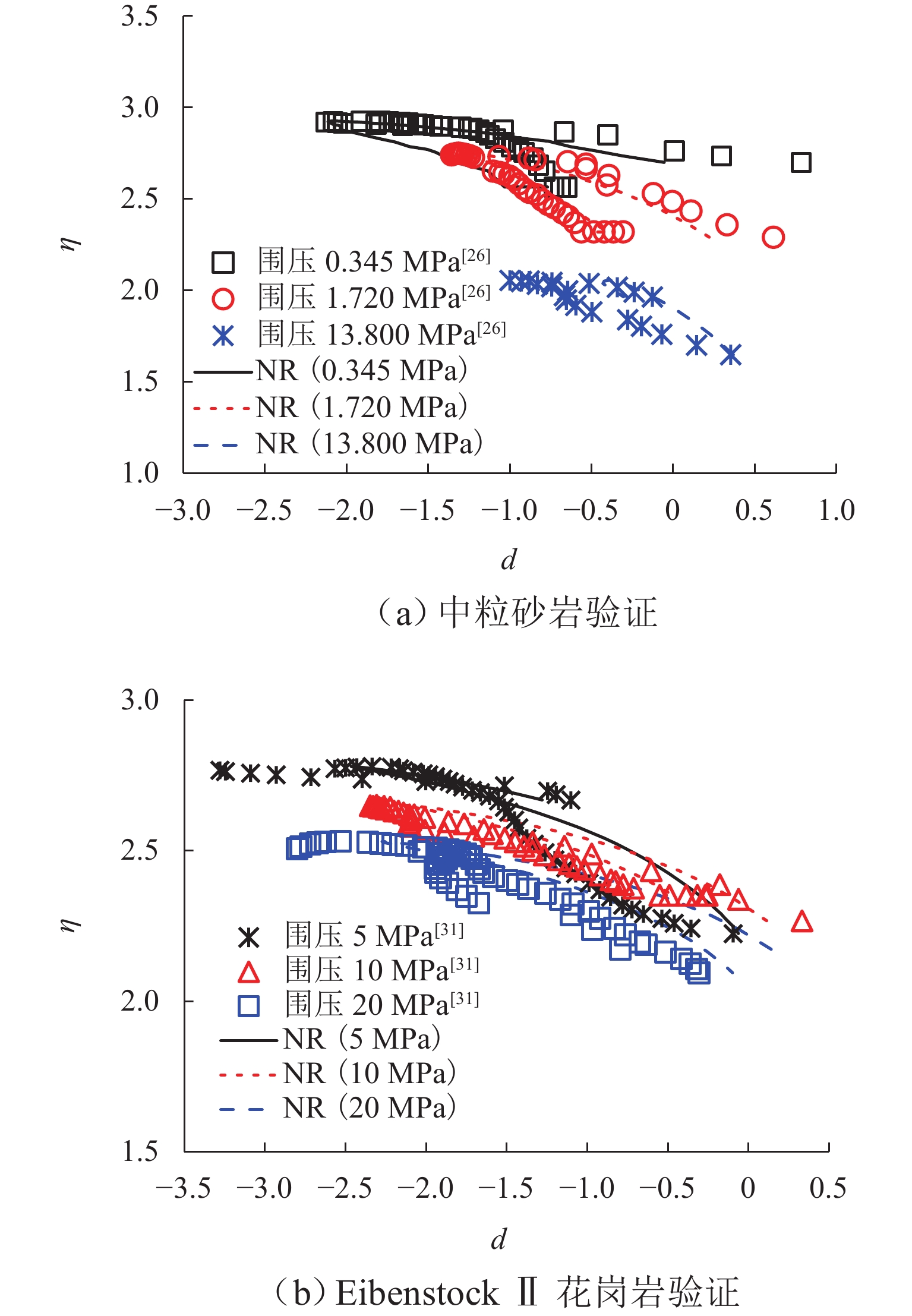
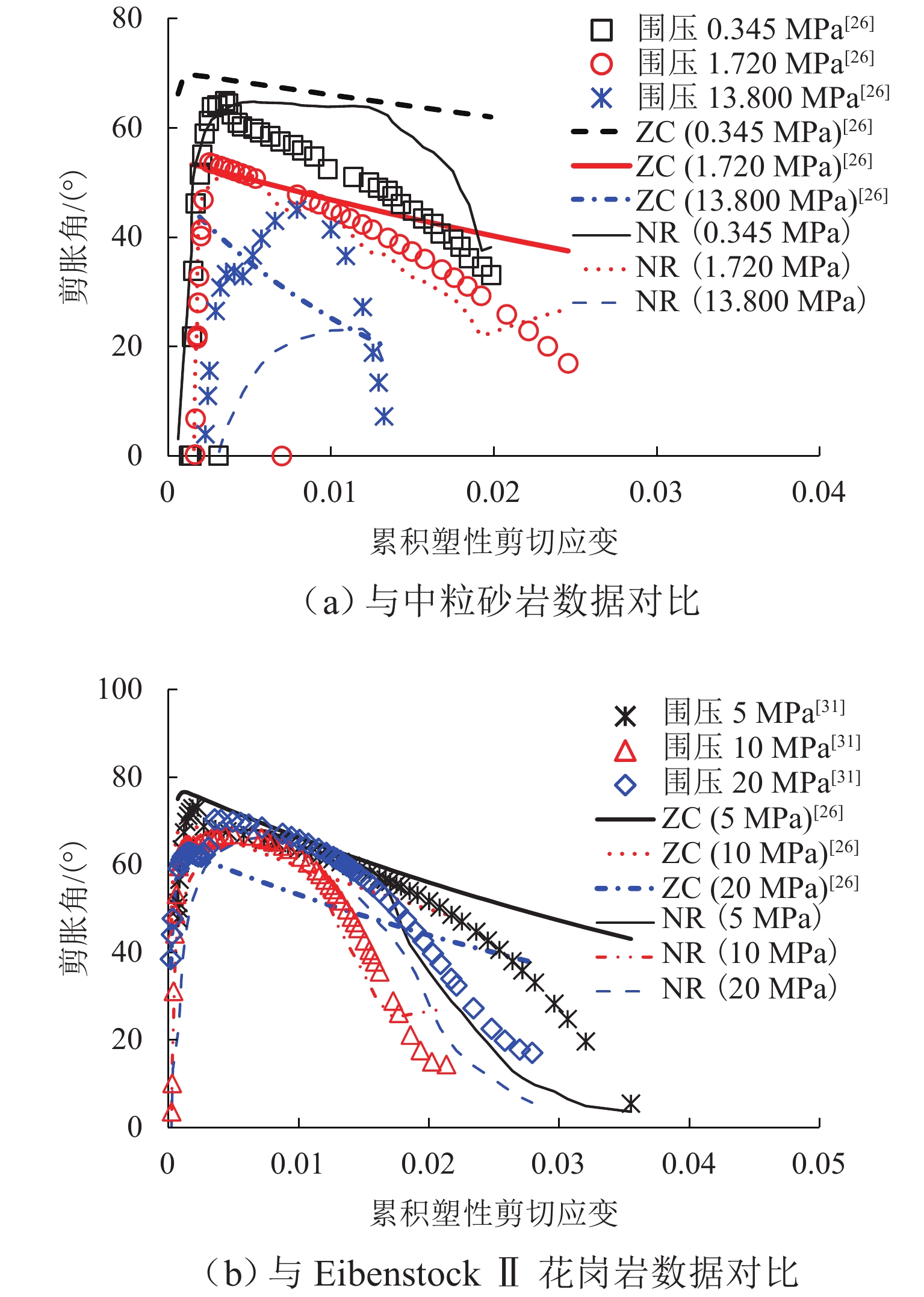
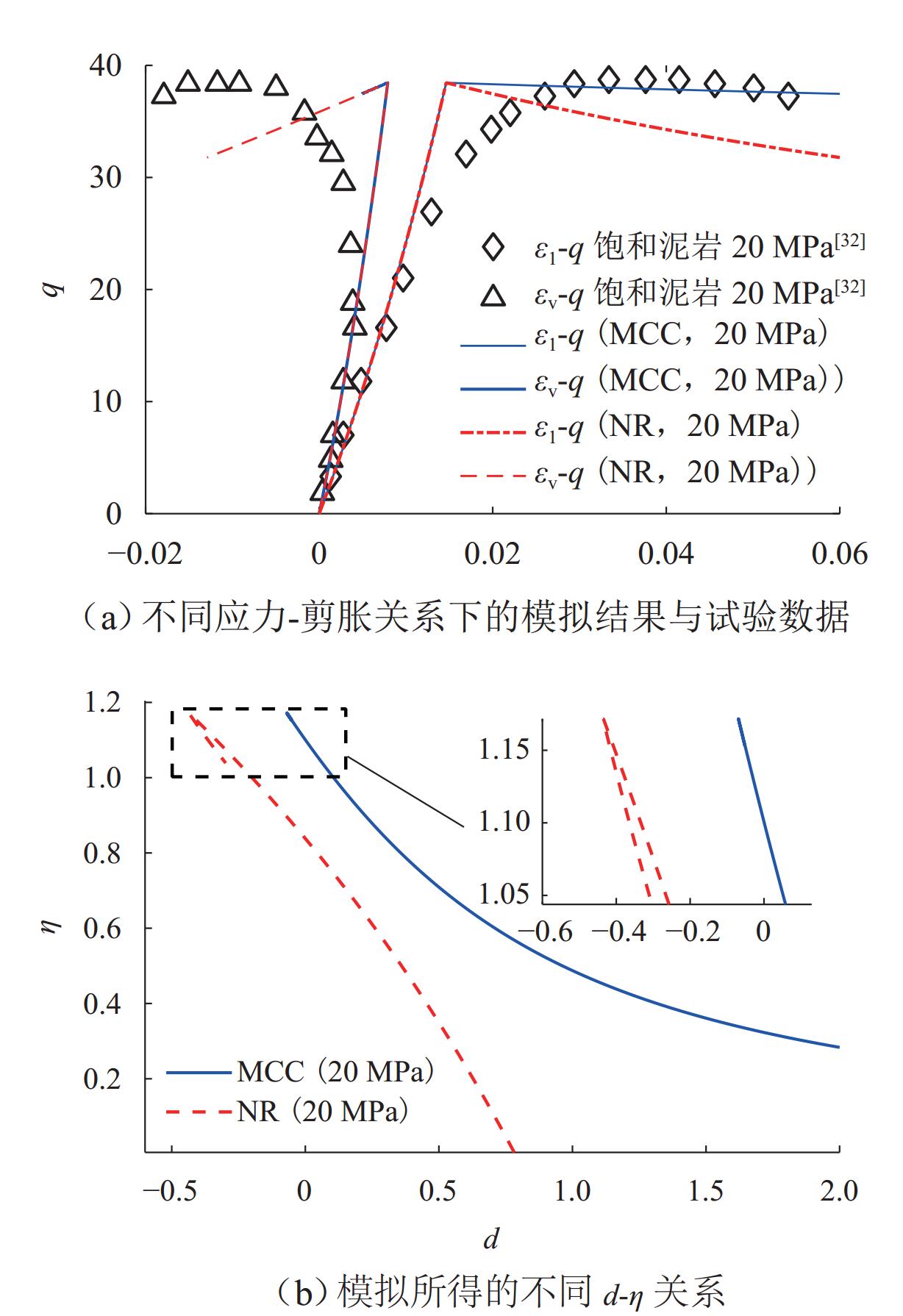
为研究典型应力-剪胀关系对常见岩土材料力学响应的预测效果，构建适合岩石材料的应力-剪胀关系，提升本构模型的准确性，本文结合试验数据对典型应力-剪胀关系展开对比分析，并构建适用于岩石的应力剪胀关系模型. 首先，基于热动力学框架和能量守恒方程，梳理出3种典型的应力-剪胀关系模型，并将多种岩土材料的应力-剪胀数据与典型应力-剪胀关系进行对比；随后，以Rowe剪胀关系模型为基本框架，考虑多种因素影响，提出适用于岩石的改进Rowe应力-剪胀关系模型，分析了其对试验数据的拟合效果，并对比所提模型和变剪胀角模型对加载过程剪胀角演化的模拟效果；最后，将修正Rowe剪胀关系与修正剑桥模型耦合，与经典的修正剑桥模型的模拟结果和试验数据进行对比校验. 研究结果表明：由于黏聚力的影响，基于纯摩擦假设推导的经典应力-剪胀关系无法准确描述含黏聚力岩土材料的应力-剪胀响应；修正Rowe剪胀关系模型可以有效反映岩石的应力-剪胀响应，并能模拟数据中的“回旋勾”现象；本文提出的应力-剪胀关系模型不仅形式简洁，且参数数量较变剪胀角模型少；应用所提修正Rowe剪胀关系模型可以提升本构模型在变形预测方面的准确性.
Abstract:In order to evaluate the prediction accuracy of typical stress-dilatancy rules on the mechanical response of common geomaterials, propose a stress-dilatancy rule suitable for rocks, and improve the accuracy of the constitutive model, typical stress-dilatancy rules derived from experiment data were compared to propose a stress-dilatancy model suitable for rocks. Firstly, based on the thermodynamic framework and the energy conservation equation, three typical stress-dilatancy models were sorted out, and the stress-dilatancy data of various geomaterials were compared with the typical stress-dilatancy rules. Then, by taking the Rowe dilatancy model as the basic framework and considering the influence of many factors, an improved Rowe stress-dilatancy model suitable for rocks was proposed, and its fitting effect on the test data was analyzed. The simulation effect of the proposed model and the variable dilatancy angle model on the evolution of dilatancy angle during loading was compared. Finally, the modified Rowe dilatancy rule was coupled with the modified Cambridge model, and the simulation results and test data of the classical modified Cambridge model were compared and verified. The results show that the classical stress-dilatancy rule based on the pure friction hypothesis cannot accurately describe the stress-dilatancy response of geomaterials with cohesive force due to the influence of cohesive force. The modified Rowe dilatancy model can effectively reflect the stress-dilatancy response of rock and simulate the “turning hook” phenomenon in the data. Furthermore, the proposed stress-dilatancy model is not only simple in form but also has fewer parameters than the variable dilatancy angle model. The proposed modified Rowe dilatancy model can improve the accuracy of the constitutive model in deformation prediction.
-
Key words:
- stress-dilatancy rule /
- rocks /
- cohesive force /
- dilatancy angle /
- models
-
图 1 砂土/大坝堆填料的应力-剪胀关系对比
Figure 1. Comparison of stress-dilatancy rules for sand and dam fill
图 2 水泥/生物水泥加固砂土的应力-剪胀关系对比
Figure 2. Comparison of stress-dilatancy rules for cement-enhanced and biocement-enhanced sands
图 3 软岩/硬岩的应力-剪胀关系对比
Figure 3. Comparison of stress-dilatancy rules for a soft rock and a hard rock
图 4 含黏聚力材料的应力-剪胀特性
Figure 4. Stress-dilatancy characteristics of materials with cohesive force
图 5 改进Rowe应力-剪胀关系特征
Figure 5. Characteristics of modified Rowe’s stress-dilatancy rule
图 6 改进Rowe关系与数据对比
Figure 6. Comparison between modified Rowe rule and experimental data
图 7 不同模型预测剪胀角与试验数据对比
Figure 7. Comparison between dilatancy angle predicted by different models and experimental data
图 8 修正应力-剪胀关系校验及应用
Figure 8. Validation and application of modified stress-dilatancy rule
表 1 3种典型应力-剪胀关系
Table 1. Three classical stress-dilatancy rules
典型应力-剪胀关系 $ {{{W}}_e} $形式 $ {{\varPhi }} $形式 $ {{\varPsi }} $形式 应力-剪胀关系形式 剑桥模型[8] $p{\mathrm{d}}\varepsilon _{{{v}}}^{{\mathrm{p}}} + q{\mathrm{d}}\varepsilon _{{\gamma } }^{{\mathrm{p}}}$ $Mp{\mathrm{d}}\varepsilon _{{\text{γ} } }^{{\mathrm{p}}}$ 无 $d = M - \eta $ 修正剑桥模型[10] $\dfrac{1}{2}{p_{{\mathrm{c}}}}\sqrt {{{\left( {{\mathrm{d}}\varepsilon _{{{v}}}^{{\mathrm{p}}}} \right)}^2} + {{\left( {M{\mathrm{d}}\varepsilon _{{\gamma } }^{{\mathrm{p}}}} \right)}^2}} $ $ \dfrac{1}{2}{p_{{\mathrm{c}}}}{\mathrm{d}}\varepsilon _{{\mathrm{v}}}^{{\mathrm{p}}} $ $d = \dfrac{{{M^2} - {\eta ^2}}}{{2\eta }}$ Rowe[6] $Mp{\mathrm{d}}\varepsilon _{{\gamma } }^{{\mathrm{p}}} + \dfrac{{2q - 3p}}{9}M{\mathrm{d}}\varepsilon _{{{v}}}^{{\mathrm{p}}}$ 无 $d = \dfrac{{9\left( {M - \eta } \right)}}{{9 + 3M - 2M\eta }}$ 
下载: 导出CSV
表 2 改进Rowe准则参数
Table 2. Parameters of modified Rowe rule
岩石 $E$ $b$ $ \xi $ $ \omega $ 中粒砂岩 30 0.30 6 0.10 Eibenstock II花岗岩 50 0.10 4.80 0.20
下载: 导出CSV
表 3 模拟所用参数
Table 3. Parameters for simulation
$\mu $ $\kappa $ $\lambda $ $M$ ${p_{{{\mathrm{c}}0}}}$/MPa ${v_0}$ $ \xi $ $\omega $ $E$ $b$ 0.23 0.015 0.15 1.10 70 1.258 4 0.15 0.05 20
下载: 导出CSV
-
[1] 梁明纯,苗胜军,蔡美峰,等. 考虑剪胀特性和峰后形态的岩石损伤本构模型[J]. 岩石力学与工程学报,2021,40(12): 2392-2401.LIANG Mingchun, MIAO Shengjun, CAI Meifeng, et al. A damage constitutive model of rock with consideration of dilatation and postpeak shape of the stress-strain curve[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(12): 2392-2401. [2] 陈静,高睿,刘洋泽鹏,等. 黏土脏污对道砟集料的应力-剪胀关系影响[J]. 西南交通大学学报,2022,57(6): 1201-1207.CHEN Jing, GAO Rui, LIU Yangzepeng, et al. Effect of clay contamination on stress-dilatancy relationships of ballast aggregate[J]. Journal of Southwest Jiaotong University, 2022, 57(6): 1201-1207. [3] 高彦芳,任战利,姜海龙,等. 考虑剪胀性和应变软化的油砂非线性弹性模型[J]. 地下空间与工程学报,2023,19(1): 43-50.GAO Yanfang, REN Zhanli, JIANG Hailong, et al. A nonlinear elastic model for oil sands considering shear dilation and strain softening[J]. Chinese Journal of Underground Space and Engineering, 2023, 19(1): 43-50. [4] 寇昊,何川,蒙伟等. 考虑残余强度的层状岩体损伤演化规律[J/OL]. 西南交通大学学报:1-8.KOU Hao, HE Chuan, MENG Wei, et al. Damage evolution law of layered rock mass considering residual strength[J/OL]. Journal of Southwest Jiaotong University: 1-8. [5] 李修磊,陈洪凯,张金浩. 考虑初始空隙压密的岩石变形全过程本构模型[J]. 西南交通大学学报,2022,57(2): 314-321.LI Xiulei, CHEN Hongkai, ZHANG Jinhao. Statistical damage model for whole deformation and failure process of rock considering initial void closure[J]. Journal of Southwest Jiaotong University, 2022, 57(2): 314-321. [6] ROWE P W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1962, 269(1339): 500-527. [7] ZHANG J, SALGADO R. Stress–dilatancy relation for Mohr–Coulomb soils following a non-associated flow rule[J]. Géotechnique, 2010, 60(3): 223-226. [8] ROSCOE K H, SCHOFIELD A N. Mechanical behaviour of an idealized'wet'clay[C]//Proc 3rd Eur Conf Soil Mech. Wiesbaden: [s. n. ]. 1963: 47-54. [9] TAYLOR D W. Fundamentals of soil mechanics[M]. New York: J. Wiley, 1948. [10] MUIR WOOD D. Soil behaviour and critical state soil mechanics[M]. Cambridge: Cambridge University Press, 1990. [11] TSEGAYE A B, BENZ T. Plastic flow and state-dilatancy for geomaterials[J]. Acta Geotechnica, 2014, 9(2): 329-342. doi: 10.1007/s11440-013-0290-z [12] TSEGAYE A B. A new stress-dilatancy framework for the modelling of rocks and rock masses[J]. IOP Conference Series: Earth and Environmental Science, 2021, 727(1): 012014.1-012014.10. [13] JEFFERIES M. Plastic work and isotropic softening in unloading[J]. Géotechnique, 1997, 47(5): 1037-1042. [14] NOVA R. A constitutive model under monotonic and cyclicloading[C]// Soil mechanics—transient and cyclic loads. New York: John Wiley & Sons Ltd, 1982: 343-373. [15] XIAO Y, LIU H L, ZHU J G, et al. Dilatancy equation of rockfill material under the true triaxial stress condition[J]. Science China Technological Sciences, 2011, 54(1): 175-184. doi: 10.1007/s11431-010-4201-3 [16] 石北啸,刘赛朝,吴鑫磊,等. 考虑颗粒破碎的堆石料剪胀特性研究[J]. 岩土工程学报,2021,43(7): 1360-1366.SHI Beixiao, LIU Saichao, WU Xinlei, et al. Dilatancy behaviors of rockfill materials considering particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(7): 1360-1366. [17] 郭万里,朱俊高,彭文明. 粗粒土的剪胀方程及广义塑性本构模型研究[J]. 岩土工程学报,2018,40(6): 1103-1110.GUO Wanli, ZHU Jungao, PENG Wenming. Dilatancy equation and generalized plastic constitutive model for coarse-grained soils[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(6): 1103-1110. [18] 郭万里,朱俊高,彭文明. 粗粒土的剪胀方程及广义塑性本构模型研究[J]. 岩土工程学报,2018,40(6): 1103-1110.GUO Wanli, ZHU Jungao, PENG Wenming. Dilatancy equation and generalized plastic constitutive model for coarse-grained soils[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(6): 1103-1110. [19] GUO W L, ZHU J G. Particle breakage energy and stress dilatancy in drained shear of rockfills[J]. Géotechnique Letters, 2017, 7(4): 304-308. [20] JIN W F, TAO Y, CHEN R Z. Capturing the turning hook of stress-dilatancy curve of crushable calcareous sand[J]. Journal of Marine Science and Engineering, 2022, 10(9): 1269.1-1269.19. [21] ALEJANO L R, ALONSO E. Considerations of the dilatancy angle in rocks and rock masses[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(4): 481-507. doi: 10.1016/j.ijrmms.2005.01.003 [22] WALTON G, ARZÚA J, ALEJANO L R, et al. A laboratory-testing-based study on the strength, deformability, and dilatancy of carbonate rocks at low confinement[J]. Rock Mechanics and Rock Engineering, 2015, 48(3): 941-958. doi: 10.1007/s00603-014-0631-8 [23] ZHAO R, LI C G. A new dilation angle model for rocks[J]. Rock Mechanics and Rock Engineering, 2022, 55(9): 5345-5354. doi: 10.1007/s00603-022-02835-6 [24] MAS D, CHEMENDA A I. Dilatancy factor constrained from the experimental data for rocks and rock-type material[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 67: 136-144. doi: 10.1016/j.ijrmms.2013.12.014 [25] RAHJOO M, EBERHARDT E. Development of a 3-D confinement-dependent dilation model for brittle rocks; Part 1, derivation of a Cartesian plastic strain increments ratios approach for non-potential flow rules[J]. International Journal of Rock Mechanics and Mining Sciences, 2021, 145: 104668.1-104668.27. [26] RAHJOO M, EBERHARDT E. Development of a 3-D confinement-dependent dilation model for brittle rocks; part 2, formulation and parameterization based on the Cartesian plastic strain increments ratios approach[J]. International Journal of Rock Mechanics and Mining Sciences, 2021, 148: 104773.1-104773.30. [27] ZHAO X G, CAI M. A mobilized dilation angle model for rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(3): 368-384. doi: 10.1016/j.ijrmms.2009.12.007 [28] CHANG C S, DENG Y B. Energy equation and stress–dilatancy relationship for sand[J]. Acta Geotechnica, 2022, 17(7): 2675-2696. doi: 10.1007/s11440-021-01389-1 [29] LIU J M, ZOU D G, KONG X J, et al. Stress-dilatancy of Zipingpu gravel in triaxial compression tests[J]. Science China Technological Sciences, 2016, 59(2): 214-224. doi: 10.1007/s11431-015-5919-8 [30] SZYPCIO Z, DOŁŻYK-SZYPCIO K. The stress-dilatancy behaviour of artificially bonded soils[J]. Materials, 2022, 15(20): 7068.1-7068.13. [31] WU S F, LI B, CHU J. Stress-dilatancy behavior of MICP-treated sand[J]. International Journal of Geomechanics, 2021, 21(3): 04020264.1-04020264.12. [32] TAN X, KONIETZKY H, FRÜHWIRT T. Numerical simulation of triaxial compression test for brittle rock sample using a modified constitutive law considering degradation and dilation behavior[J]. Journal of Central South University, 2015, 22(8): 3097-3107. doi: 10.1007/s11771-015-2846-6 [33] HU D W, ZHANG F, SHAO J F. Experimental study of poromechanical behavior of saturated claystone under triaxial compression[J]. Acta Geotechnica, 2014, 9(2): 207-214. doi: 10.1007/s11440-013-0259-y -
下载:
点击查看大图
计量
- 文章访问数: 42
- HTML全文浏览量: 13
- PDF下载量: 8
- 被引次数: 0