Influence of Stress-Free Temperature Difference on Force Characteristics of Seamless Turnouts in Plateau Areas
-
摘要:
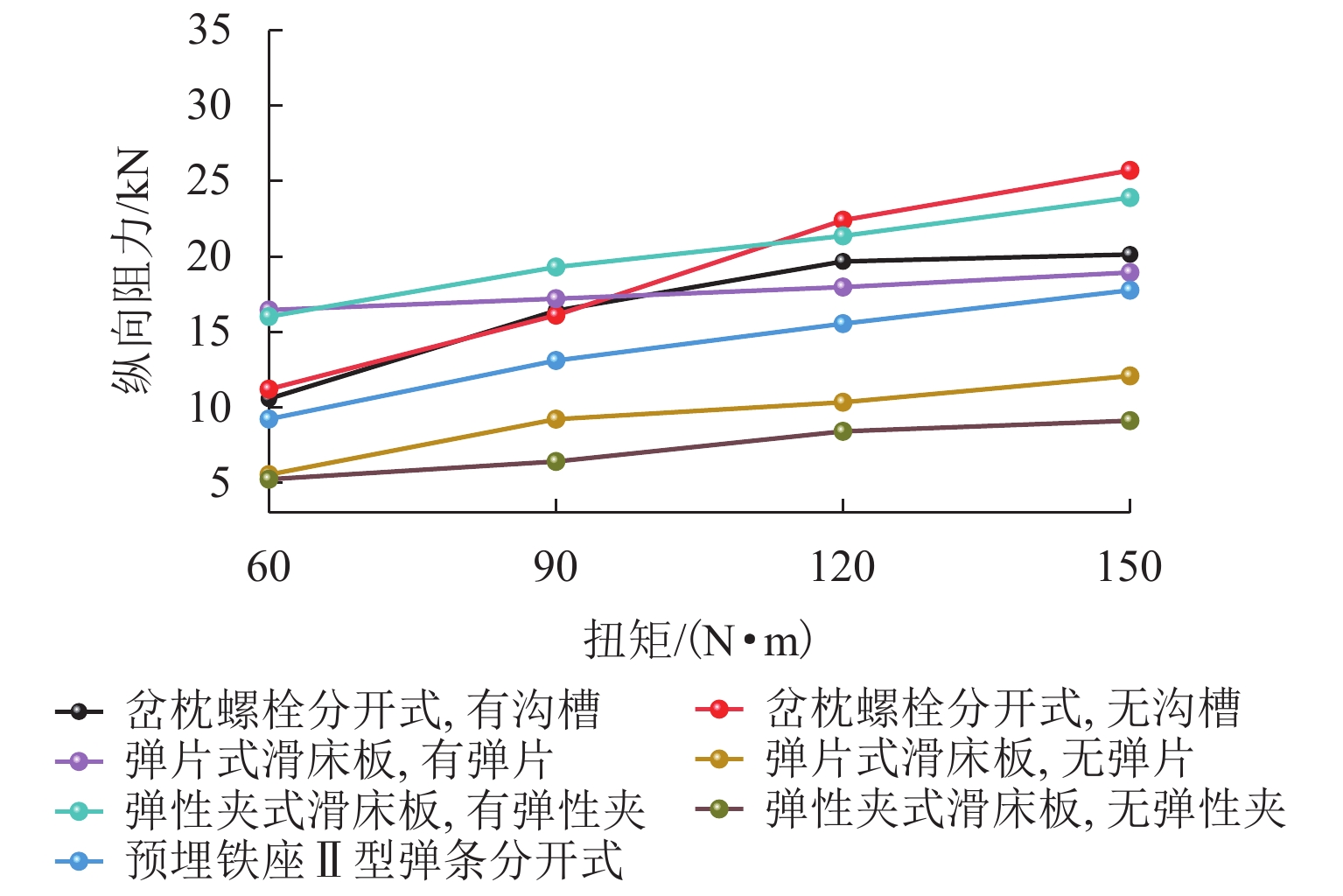
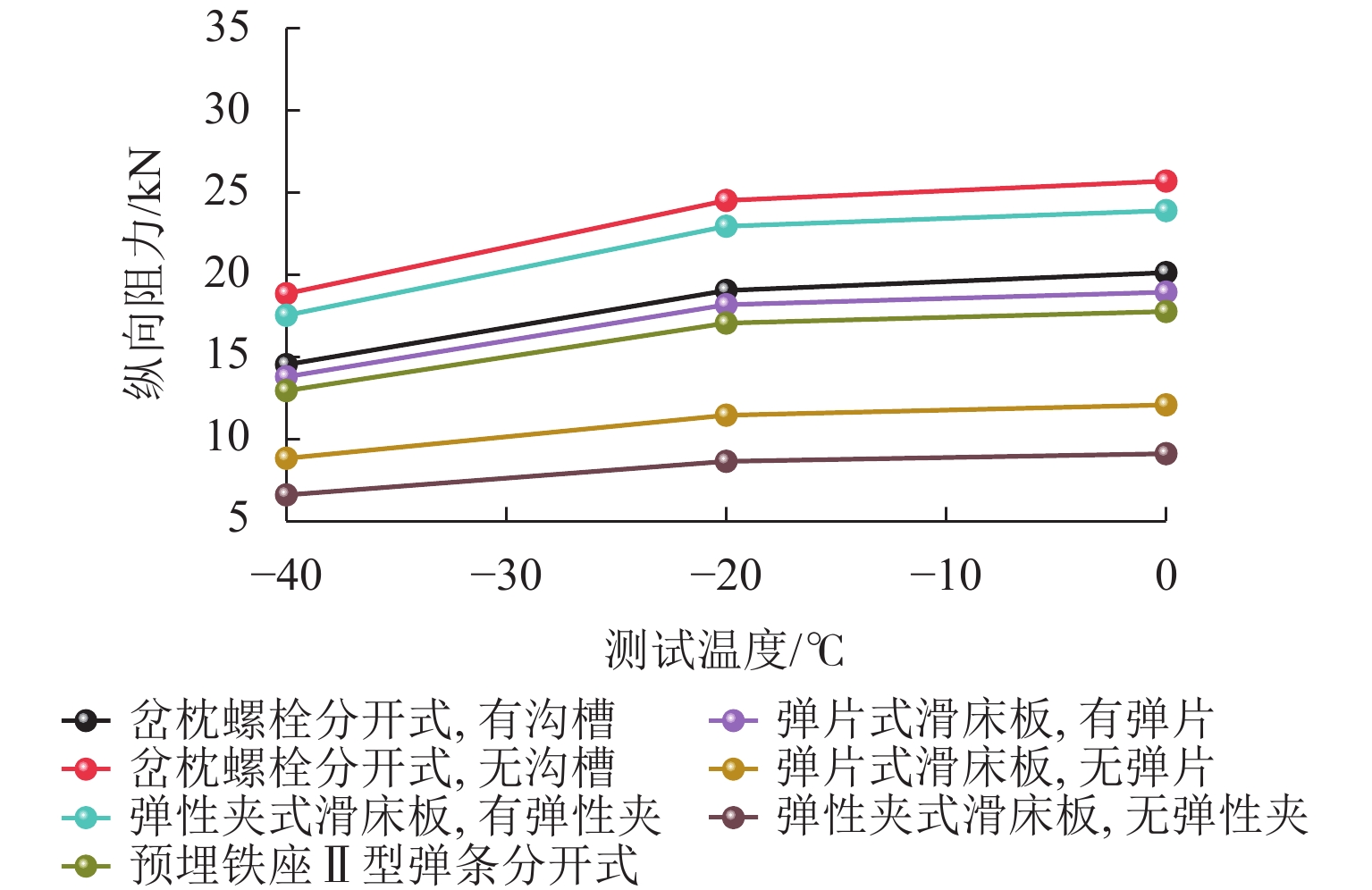
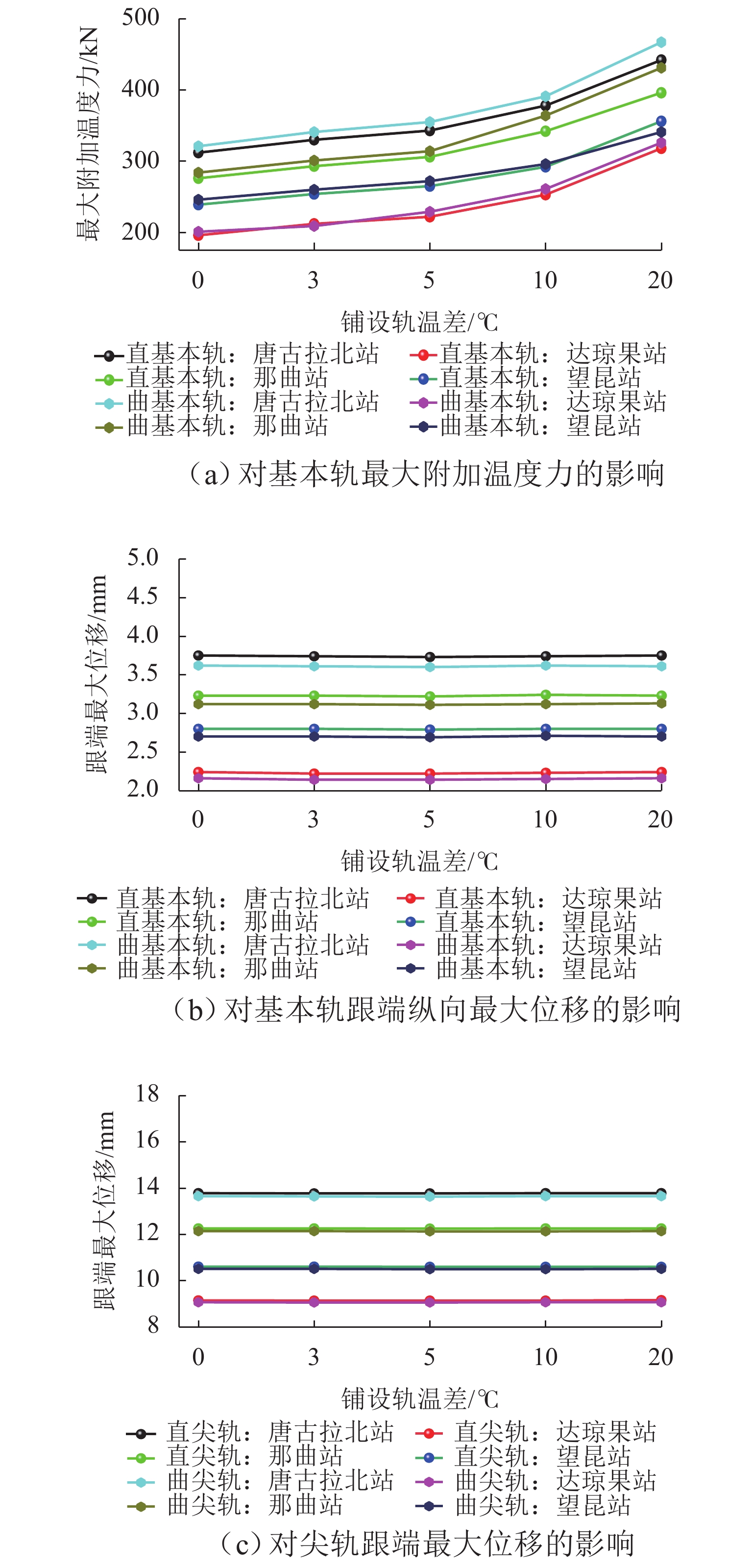
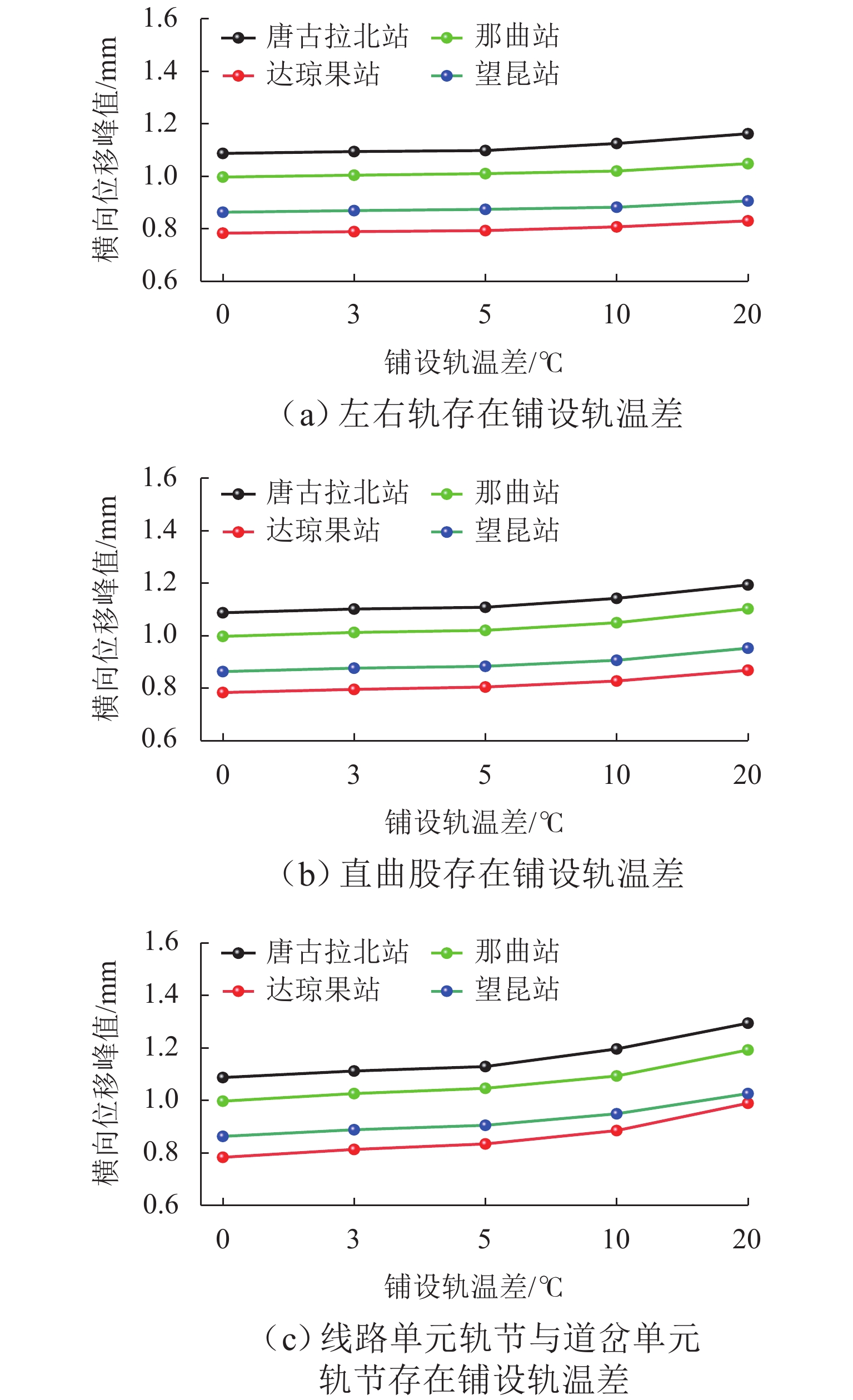
为研究高原地区铺设无缝道岔的可行性与高原气候环境对跨区间无缝线路稳定性的影响，探讨了不同气候、不同海拔和不同结构型式道岔实现无缝化时，铺设锁定轨温差对无缝道岔力学特性的影响. 首先，基于高原铁路自然地理环境与线路运营条件，选取青藏线升级改造过程中实现无缝化的典型道岔作为研究对象；其次，结合不同结构形式下的道岔关键传力部件力学特性开展室内参数测试，掌握高原气候低温环境对扣件、道床等阻力的影响；最后，构建考虑多场耦合和塑性阻力的无缝道岔计算模型，揭示铺设轨温差与无缝道岔受力变形的关系. 研究结果表明：当线路所处温差越大，铺设锁定轨温差引起的基本轨温度附加力增加速率从4.5 kN/℃（达琼果站）增加到6 kN/℃（唐古拉北站）；无缝道岔与相邻线路或相邻道岔间的铺设锁定轨温差对无缝道岔受力与变形影响较大，而线路轨节/道岔轨节铺设锁定轨温差引起的横向位移增加速率从0.010 mm/℃（达琼果站）增加到0.011 mm/℃（唐古拉北站），左右轨与直侧轨铺设轨温差对道岔失稳影响较小；考虑到高原道岔涉及多股钢轨锁定，易造成锁定轨温差相差较大，为提高安全冗余，铺设锁定轨温差应控制在±3 ℃，相邻轨节锁定轨温差不超过5 ℃.
Abstract:To investigate the feasibility of laying seamless turnouts in plateau areas and the influence of plateau climate on the stability of seamless turnouts across areas, the effect of stress-free temperature difference on the force characteristics of seamless turnouts under different climates, elevations, and structural types was analyzed. First, based on the physic-geographical environment and operating conditions of railways in plateau areas, the typical seamless turnouts of the Qinghai−Xizang line during upgrading were selected as research objects, and then the parameter tests of key force transmission components with force characteristics in turnouts under different structural types were conducted, clarifying the influence of the low temperature of plateau climate on resistance force of fasteners and ballast beds. At last, the calculation model of seamless turnouts considering the multi-field coupling effect and plastic resistance force was established, and the relationship between stress-free temperature difference and stress deformation of seamless turnouts was revealed. The results show that when the temperature difference is high, the growth rate of temperature additional force induced by stress-free temperature difference increases from 4.5 kN/℃ (Daqiongguo Station) to 6 kN/℃ (Tanggulabei Station); the stress-free temperature difference between seamless turnouts and adjacent lines or adjacent turnouts has great impact on stress formation of seamless turnouts, and the growth rate of lateral displacement caused by the stress-free temperature difference of the line/turnout rail section increases from 0.010 mm/℃ (Daqiongguo Station) to 0.011 mm/℃ (Tanggulabei Station). The impact of the stress-free temperature difference between left/right or straight/side rails on turnout stability is small. In plateau areas, the turnout involves the locking of multiple strands of rail, which is easy to cause a large stress-free temperature difference. To increase safety redundancy, the stress-free temperature difference should be controlled within ±3 ℃, while that of the adjacent rail section should be no more than 5 ℃.
-
图 7 直线和曲线工况下的道床阻力
Figure 7. Ballast bed resistance under straight and curve line conditions
图 9 铺设锁定轨温差对无缝道岔受力与变形的影响
Figure 9. Influence of stress-free temperature difference on force formation of seamless turnout
图 10 铺设锁定轨温差对无缝道岔稳定性的影响
Figure 10. Influence of stress-free temperature difference on stability of seamless turnout
表 1 典型试验车站
Table 1. Typical experiment stations
站名 海拔/m 纬度/（°） 线路条件 唐古拉北 4955 34.2 最低温、最高海拔车站 那曲 4500 31.6 西藏段、较高海拔 达琼果 4375 30.5 低纬度、较高海拔，类似川藏条件 望昆 4484 35.7 青海段、高纬度、较高海拔 
下载: 导出CSV
表 2 典型车站轨温预测
Table 2. Prediction of rail temperature in typical stations
站名 年气温/℃ 预测轨温/℃ 验证数据 R 值 唐古拉北 −45.23～24.75 −45.22～35.84 0.9498 那曲 −38.02～27.28 −37.26～42.18 0.9652 达琼果 −10.04～31.06 −6.84～49.68 0.9857 望昆 −26.52～35.58 −24.32～54.63 0.9728
下载: 导出CSV
表 3 限位器和间隔铁阻力测试
Table 3. Resistance test of limiting stopper and filler
对象 螺母扭矩/（N·m） 最大滑移荷载/kN 限位器 800 345 1000 462 间隔铁 800 364 1000 486
下载: 导出CSV
表 4 接头阻力测试
Table 4. Resistance test of joints
接头 夹板扭矩/（N·m） 最大荷载/kN 胶接冻结接头 800 799 1100 1110 普通接头 800 307 1100 442
下载: 导出CSV
-
[1] 卢耀荣. 无缝线路研究与应用[M]. 2版. 北京:中国铁道出版社,2010:1-94. [2] 叶军. 寒冷地区小半径曲线无缝线路设计研究[D]. 北京:北京交通大学. [3] 李媛. 青藏铁路多年冻土区无缝道岔力学特性研究[D]. 兰州:兰州交通大学,2021. [4] 王平,肖杰录,陈嵘. 高速铁路桥上无缝线路技术[M]. 北京:中国铁道出版社,2016. [5] AN R, LUO Y Y, LEE L. Analysis of relationship between lateral stability and dynamic characteristic of continuous welded rail track[J]. Applied Mechanics and Materials, 2014, 488/489: 1027-1030. doi: 10.4028/www.scientific.net/AMM.488-489.1027 [6] BANI M M, MANJUNATH D Y M, NANDY M P P. Effect of temperature gradient on continuous PSC bridge for straight and curved profile[J]. International Journal of Engineering Research and, 2017, V6(5): 362-371. [7] SHU D, GUO L, YIN L A, et al. Research on global and local stability of continuous welded rail based on finite element analysis and discrete short-time Fourier transform[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2016, 230(4): 1351-1362. doi: 10.1177/0954409715596193 [8] KISH A, ATEN J. A “smart systems” approach for better managing cwr thermal forces at extreme temperature[C]//Rail: the core of integrated transport, conference on railway engineering. Perth: IEEE, 2012: 71-79. [9] ZHAO G Y, CAI X P, LIU W L, et al. Mechanical properties and structural optimization of continuous welded rail on super-long-span suspension bridges for high-speed railway[J]. Applied Sciences, 2021, 12(1): 305. doi: 10.3390/app12010305 [10] 刘浩,谢铠泽,王平,等. 道床阻力区域分布及退化对钢轨纵向力的影响[J]. 西南交通大学学报,2017,52(1): 98-105. doi: 10.3969/j.issn.0258-2724.2017.01.014LIU Hao, XIE Kaize, WANG Ping, et al. Effect of regional distribution and degradation of ballast resistance on longitudinal force of rail[J]. Journal of Southwest Jiaotong University, 2017, 52(1): 98-105. doi: 10.3969/j.issn.0258-2724.2017.01.014 [11] 高亮,张雅楠,吕宝磊,等. 千米级以上超大跨径桥上无缝线路梁轨相互作用分析及应用[J]. 北京交通大学学报,2021,45(4): 9-18. doi: 10.11860/j.issn.1673-0291.20210111GAO Liang, ZHANG Yanan, LYU Baolei, et al. Analysis and application of continuous welded rail’s beam-track interaction on ultra-large span bridges above one kilometer[J]. Journal of Beijing Jiaotong University, 2021, 45(4): 9-18. doi: 10.11860/j.issn.1673-0291.20210111 [12] 徐浩,林红松,田春香,等. 100m简支钢桁梁桥无缝线路伸缩力影响因素研究[J]. 铁道工程学报,2022,39(2): 46-51. doi: 10.3969/j.issn.1006-2106.2022.02.009XU Hao, LIN Hongsong, TIAN Chunxiang, et al. Research on the influence factors of expansion and contraction force of CWR on 100 m simply supported steel truss bridge[J]. Journal of Railway Engineering Society, 2022, 39(2): 46-51. doi: 10.3969/j.issn.1006-2106.2022.02.009 [13] RUGE P, BIRK C. Longitudinal forces in continuously welded rails on bridgedecks due to nonlinear track-bridge interaction[J]. Computers & Structures, 2007, 85(7/8): 458-475. [14] 王平,陈嵘,徐井芒,等. 高速铁路道岔系统理论与工程实践研究综述[J]. 西南交通大学学报,2016,51(2): 357-372. doi: 10.3969/j.issn.0258-2724.2016.02.015WANG Ping, CHEN Rong, XU Jingmang, et al. Theories and engineering practices of high-speed railway turnout system: survey and review[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 357-372. doi: 10.3969/j.issn.0258-2724.2016.02.015 [15] Ren J J, LI X Y. Occasional forces and displacements of longitudinally coupled ballastless jointless turnout on bridges[J]. Science Journal of Transportation, 2010(2): 38-46. [16] 王树国,高原,杨东升. 高原铁路铺设跨区间无缝线路可行性研究与试验方案[J]. 中国铁路,2022(8): 22-28.WANG Shuguo, GAO Yuan, YANG Dongsheng. Feasibility study and test scheme of trans-section CWR track laid on plateau railway[J]. China Railway, 2022(8): 22-28. [17] 郭云龙,王新雨,廉栋,等. 摩擦型轨枕道床的横向阻力研究[J]. 西南交通大学学报,2022,57(2): 301-305,368. doi: 10.3969/j.issn.0258-2724.20200464GUO Yunlong, WANG Xinyu, LIAN Dong, et al. Lateral resistance of frictional sleeper ballast bed[J]. Journal of Southwest Jiaotong University, 2022, 57(2): 301-305,368. doi: 10.3969/j.issn.0258-2724.20200464 [18] 陈政,郭春,谌桂舟,等. 基于MEC-BP高海拔隧道供氧浓度与劳动强度规律[J]. 西南交通大学学报,2023,58(3): 622-629. doi: 10.3969/j.issn.0258-2724.20210669CHEN Zheng, GUO Chun, CHEN Guizhou, et al. Oxygen supply concentration and labor intensity of high altitude tunnel based on MEC-BP[J]. Journal of Southwest Jiaotong University, 2023, 58(3): 622-629. doi: 10.3969/j.issn.0258-2724.20210669 [19] 张晓阳,王树国. 客货共线铁路60 kg/m钢轨9号与12号道岔统型与结构优化[J]. 铁道建筑,2022,62(10): 1-7,16.ZHANG Xiaoyang, WANG Shuguo. System type and structure optimization of 60 kg/m rail No. 9 and No. 12 turnout on passenger-freight common railway[J]. Railway Engineering, 2022, 62(10): 1-7,16. [20] 杨东升. 高原铁路道岔无缝化关键技术研究[R]. 北京:中国铁道科学研究院集团有限公司,2022. -
下载:
点击查看大图
计量
- 文章访问数: 101
- HTML全文浏览量: 54
- PDF下载量: 15
- 被引次数: 0