城市轨道交通土建工程造价非线性预测与反演

孟春成; 亐道远; 段晓晨

doi:10.3969/j.issn.0258-2724.20230209

城市轨道交通土建工程造价非线性预测与反演

doi: 10.3969/j.issn.0258-2724.20230209

1.
石家庄铁道大学管理学院，河北石家庄 050043
2.
石家庄铁道大学经济与法律学院，河北石家庄 050043

基金项目: 国家自然科学基金项目（72071133）

详细信息

作者简介:
孟春成（1996—），男，博士研究生，研究方向为工程管理，E-mail：2202203001@student.stdu.edu.cn

通讯作者:
段晓晨（1962—），男，教授，博士生导师，研究方向为工程经济与造价管理，E-mail：duanxch888@sohu.com

中图分类号: U121
计量
- 文章访问数: 214
- HTML全文浏览量: 56
- PDF下载量: 41
- 被引次数: 0
出版历程
- 收稿日期: 2023-05-04
- 修回日期: 2023-11-27
- 网络出版日期: 2024-07-25
- 刊出日期: 2023-12-05

Nonlinear Prediction and Inversion of Civil Engineering Cost of Urban Rail Transit

1.
School of Management, Shijiazhuang Tiedao University, Shijiazhuang 050043, China
2.
School of Economics and Law, Shijiazhuang Tiedao University, Shijiazhuang 050043, China

摘要

摘要:
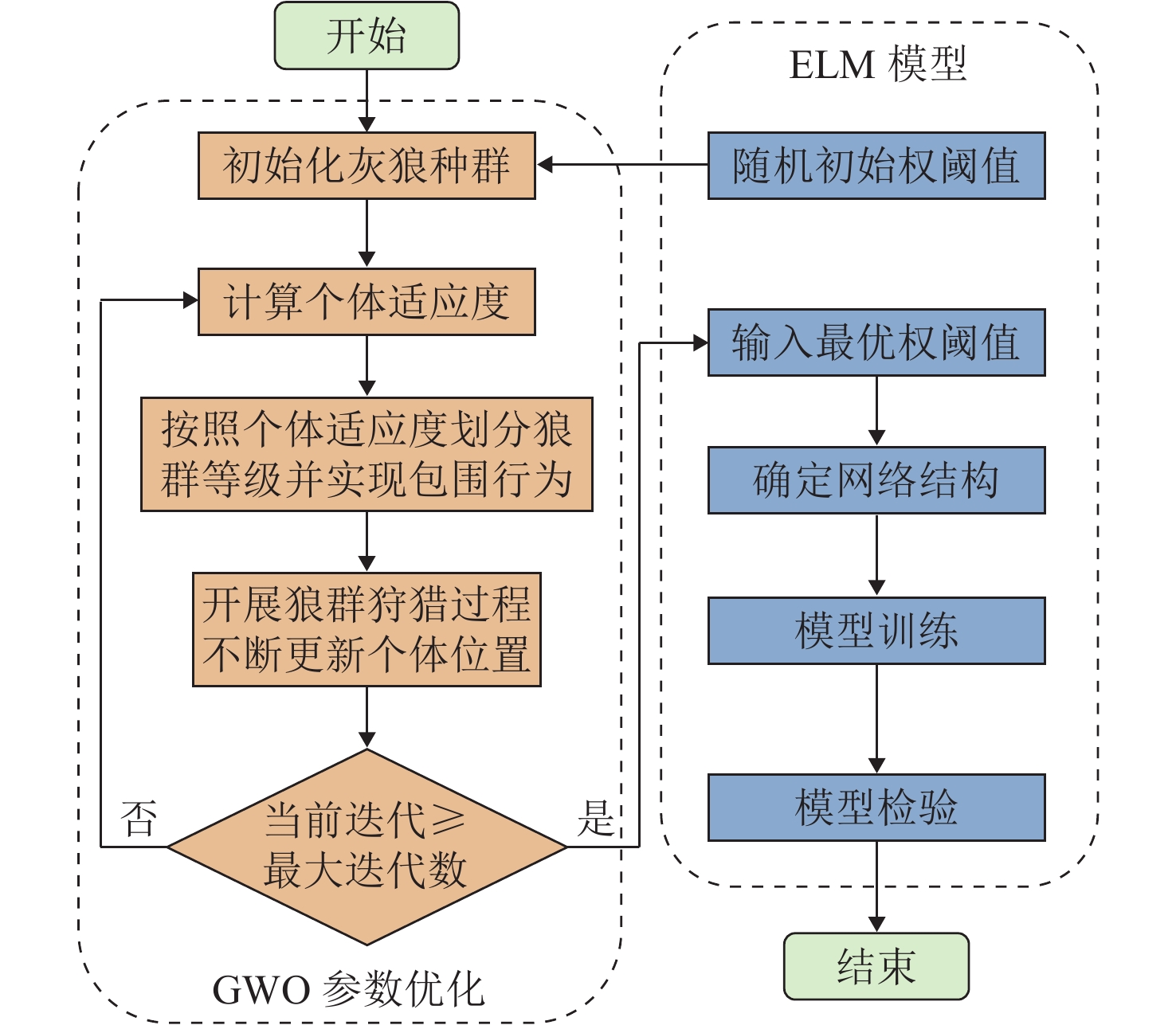
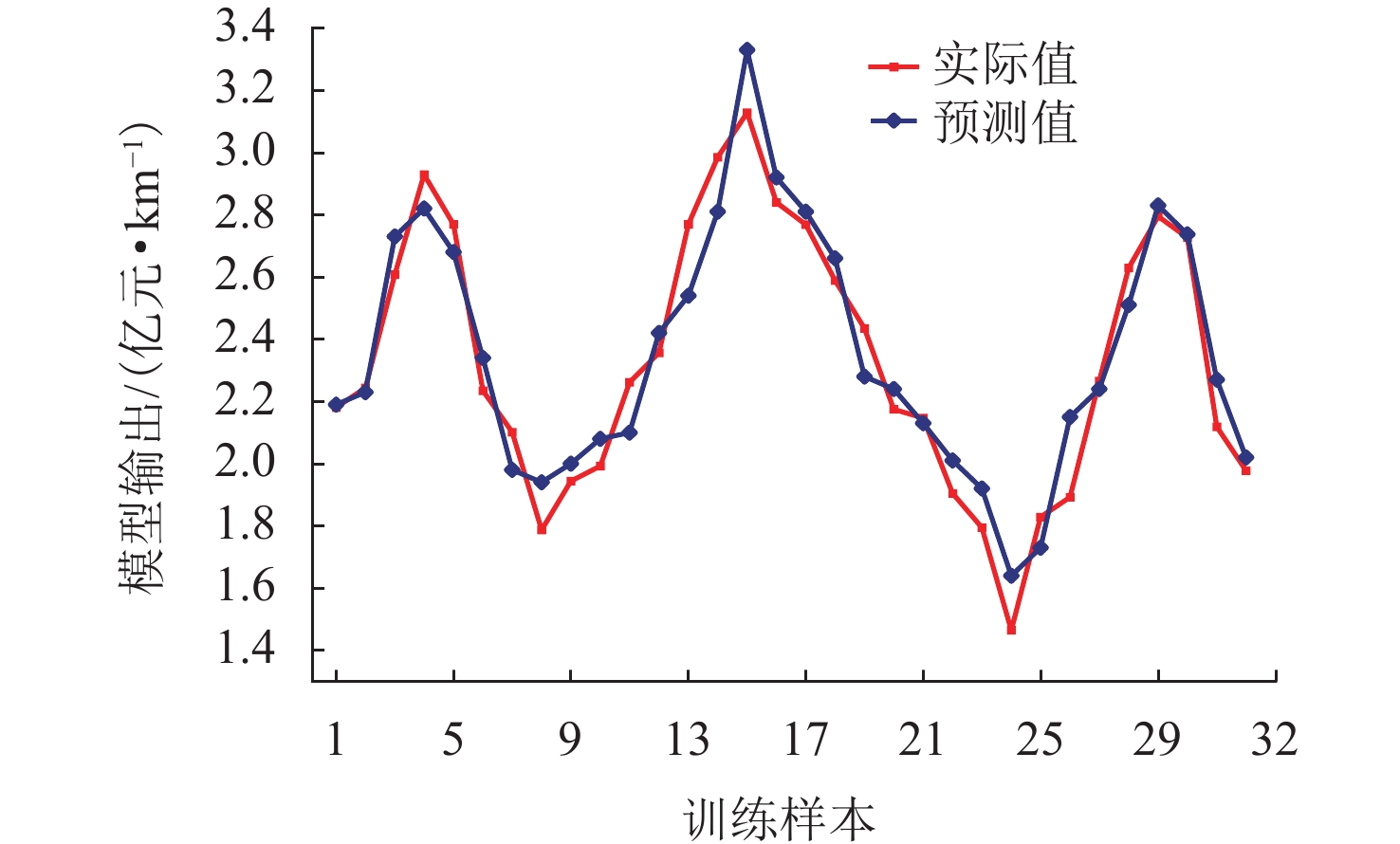
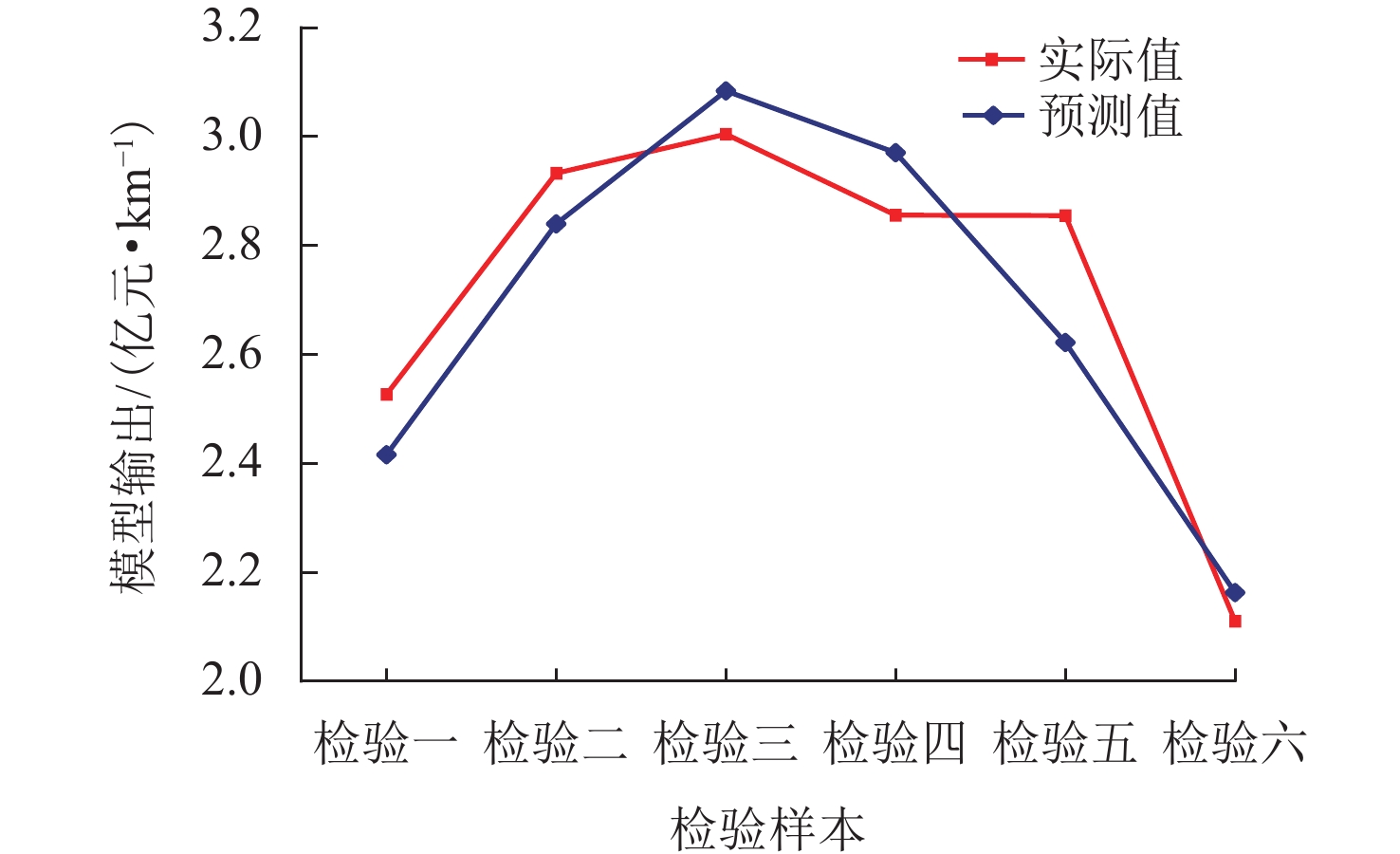
为解决城市轨道交通土建工程传统造价预测模型缺乏决策信服力的问题，首先，运用特征选择与知识判断方法提取城市轨道交通土建工程造价关键影响因素并建立工程案例数据库；然后，通过粒子群优化（PSO）聚类算法筛选相似案例，采用基于灰狼优化算法（GWO）的极限学习机（ELM）建立土建工程造价非线性预测模型并设计双环境对比实验；最后，将Sobol’ 全局敏感性分析和Curve Fitting分析用于模型解释性反演，并以成都市轨道交通10号线1期工程为例验证模型优越性. 研究结果表明：模型平均绝对误差与均方根误差分别为0.113 9和0.127 4，平均绝对百分比误差为4.14%，非线性造价预测模型预测效果优于线性模型，同时采用因素优化与案例聚类方法所得预测效果更好；全局敏感性分析发现，地下线长度和地下车站数的总敏感度明显高于其他因素，可作为方案优化重点调节因素；采用Curve Fitting分析提高了机器学习智能预测模型作用机理“黑箱”效应33.70%～64.52%的解释性.
- 城市轨道交通 /
- 土建工程 /
- 造价预测 /
- GWO-ELM模型 /
- 反分析
Abstract:
The traditional prediction model for the civil engineering cost of urban rail transit lacks decision-making credibility. To address this issue, First, critical factors affecting the civil engineering cost of urban rail transit were retrieved utilizing the feature selection and knowledge judgment methods, and an engineering case database was created. Then, similar cases were screened using the particle swarm optimization (PSO) clustering algorithm, and a nonlinear prediction model of civil engineering cost was established using the extreme learning machine (ELM) based on gray wolf optimizer (GWO), followed by a dual environment comparison experiment. Finally, Sobol’s global sensitivity analysis and curve fitting analysis were conducted to invert the model and validate its superiority by using the Chengdu Rail Transit Line 10 Phase 1 Project as an example. The results show that the prediction model’s mean absolute error and root mean square error are 0.113 9 and 0.127 4, respectively, and the mean absolute percentage error is 4.14%. The prediction effect of the nonlinear cost prediction model is better than that of the linear model, and the better prediction effect is obtained by simultaneously using the factor optimization and case clustering methods. The global sensitivity study reveals that the total sensitivity of the subterranean line length and the number of underground stations is much larger than the other factors, making them the major factors to be adjusted for the scheme optimization. The “black box” effect of intelligent predictive modeling mechanism based on machine learning is better understood by 33.70%–64.52% when curve fitting analysis is used.
- urban rail transit /
- civil engineering /
- cost prediction /
- GWO-ELM model /
- anti-analysis

HTML全文

磁悬浮铣削电主轴是以磁悬浮轴承为支承的高速机床主轴部件，其将磁悬浮轴承的主动可控性、无摩擦、免润滑、低噪声、长寿命等优点与电主轴零传动、超高速的特点结合在一起，满足了高速切削加工的要求^[1-2]. 但由于磁悬浮铣削电主轴在高速切削时，切屑会沿着容屑槽进入刀具一起旋转，进而改变“主轴-刀具”系统的质量大小及分布，并由此引发“主轴-刀具”系统的惯性特性、模态参数以及系统动态响应随时间的非线性变化, 进而影响铣削加工的质量. 因此，进行磁悬浮铣削电主轴变质量系统的旋转特性与动态响应研究，以提高铣削加工的质量，具有重要的理论和应用价值.

现有国内外对磁悬浮转子系统动力学建模方法的研究，主要将磁悬浮轴承视为约束，将转子等效为盘-轴模型的Jeffcott转子，或是将其简化为质量不变且连续分布的梁-轴模型，如欧拉-伯努利梁、瑞利梁、铁木辛科梁等. 在具体研究时，针对细长轴，通常基于欧拉-伯努利梁理论进行建模；对于非细长轴，若同时考虑梁的剪切变形和梁弯曲变形所引起的转动惯量，则采用铁木辛科梁理论进行建模；若只考虑梁弯曲变形所引起的转动惯量，则基于瑞利梁理论进行建模. 主要研究成果有：钟志贤等^[3]为研究以主动磁悬浮轴承支承的高速转子的裂纹故障特征，依据Jeffcott转子理论建立系统的运动微分方程；吴超等^[4]以磁悬浮汽轮机多盘转子系统为研究对象，利用基于欧拉-伯努利梁理论的有限单元法，建立考虑盘轴耦合特性的磁悬浮转子系统的运动微分方程；Lei等^[5]利用基于瑞利梁振动理论的有限单元法，并考虑陀螺力矩的激励效应，建立磁悬浮柔性转子的运动微分方程；KUNG等^[6]基于欧拉-伯努利梁理论，利用Hamilton原理和Galerkin理论推导出由磁悬浮轴承支承的裂纹主轴系统的运动方程；Bouaziz等^[7]采用基于铁木辛科梁理论的有限单元法，建立磁悬浮铣削电主轴系统的运动微分方程等.

另外，有部分学者在磁悬浮转子动力学模型的基础上，围绕外部激励对系统动态响应的影响进行了深入研究. 如：Zhang等^[8]通过Newmark积分法求解磁悬浮柔性转子的运动微分方程，研究磁悬浮转子在移动载体上工作时，其基底运动激励引起转子振动的动态变化规律；陈小安等^[9-10]基于电磁学和机械系统动力学基本理论，建立各种偏心状态下高速电主轴的广义不平衡力表达式，分析了高速电主轴转子在电磁不平衡拉力与离心力作用下，系统在偏心状态下振动的幅值及频率特性；宋春生等^[11]针对磁悬浮柔性转子的解耦控制问题，利用有限元法建立磁悬浮柔性转子的动力学模型; 王艺宇等^[12]针对磁悬浮叶轮机械，采用有限元方法，基于铁木辛科梁单元模型建立考虑界面接触影响的磁悬浮轴承转子动力学模型.

上述研究成果都是以质量不变的转子系统为研究对象，而对质量时变转子系统的动力学建模与动态特性研究，目前国内外的成果主要集中在纺织机械和机床加工主轴领域. 如：彭超英等^[13-14]建立纺织机械变质量转子的动力学模型，并采用龙格库塔法进行求解，以分析变质量效应对转子振动响应的影响；袁龙翔等^[15]针对车削过程中工件质量时变导致工件的质量矩阵、陀螺矩阵、刚度矩阵同步时变的现象，采用转子动力学有限单元法，建立工件的时变动力学模型，并引入动态切削力，分析工件质量时变对工件系统的临界转速、车削加工稳定性区域的影响；Cao等^[16]针对磁悬浮车削电主轴在加工过程中由于工件材料的去除导致系统质量时变的现象，以车削加工三维移动切削力、切屑流失造成的反推力以及振动量变化引起的时变电磁力为激励，基于瑞利连续梁振动理论，利用假设模态法和拉格朗日方程建立磁悬浮车削电主轴系统动力学方程，分析质量时变对系统动态特性的影响；欧阳智海等^[17]针对磁悬浮铣削电主轴在切削过程中因切屑不断进入和离开刀具容屑槽中而导致“刀具-主轴”系统质量变化的现象，通过建立“切屑-刀具-主轴”系统的变质量动力学方程，分析不平衡磁拉力、惯性力等对系统动态特性的影响. 但这些研究成果都没有考虑当系统质量改变时，主轴系统在高速旋转下惯性载荷的非线性变化规律，以及由此所引起的系统新的动态特性.

基于此，本文首先利用连续梁振动理论的有限单元法建立磁悬浮铣削电主轴变质量系统的动力学模型，分析切屑从进入到离开容屑槽的整个过程，时变切屑质量对系统临界转速的影响规律；然后探索由时变切屑质量所引起的旋转惯性载荷，并以初始不平衡离心力、切削力、磁悬浮轴承电磁力以及由切屑质量引起的旋转惯性载荷等为激励，利用MATLAB求解系统的振动响应，探索由时变切屑质量所引起的系统旋转惯性载荷对变质量系统动态特性的影响规律，进而为类似质量时变系统的动力学建模与动态分析提供理论支撑与方法借鉴.

1. 磁悬浮铣削电主轴变质量系统动力学建模

以磁悬浮铣削电主轴系统的整体结构为依据，忽略系统前后保护轴承和传感器的分布位置，获得“磁悬浮轴承-主轴-刀具”系统的结构简图如图1（a）所示. 图中：1为径向磁悬浮轴承，2为电机转子，3为径向磁悬浮轴承，4为铣刀，5为切屑 6为工件.

图 1 磁悬浮铣削电主轴系统模型示意

Figure 1. System model of motorized spindle for magnetic suspension milling

下载: 全尺寸图片幻灯片

图1（a）中：F_Ax、F_Ay、F_Bx、F_By分别为上、下2个径向磁轴承在 $x$ ， $y$ 方向的电磁力；F_cx、F_cy分别为切屑旋转产生的旋转惯性力在在 $xO{\textit{z}}$ 平面和 $yO{\textit{z}}$ 平面内的投影；F_q为铣削力.

当磁悬浮铣削电主轴加工时，切屑会不断进入铣刀容屑槽，并随主轴同步旋转，由此引发2个后果：一是“主轴-刀具”系统的质量随着切屑的不断进入和离开而不断发生变化，使系统质量具有时变特性；二是随着切屑的不断进入，会使系统不平衡质量的大小和位置非线性变化，并在高速下产生旋转惯性载荷，从而引发系统新的动态特性. 为分析高速旋转下质量时变系统的非线性动态过程，探索系统动力学模型的构建，是进行动态分析的前提.

1.1 “主轴-刀具”变质量系统有限元模型的构建

采用有限元方法建立“主轴-刀具”系统质量随切屑进入和流出而不断变化的转子动力学模型. 在建模过程中，假设刀具与主轴为刚性连接的整体，将切屑视为一形状不变的刚性质量块并随铣刀同频旋转，忽略主轴切削过程中剪切变形的影响. 将“主轴-刀具-切屑”系统沿轴线划分为由“弹性轴 + 刚性圆盘”组成的等效单元，各单元之间通过节点联结，使系统简化为具有 $N$ 个节点的模型，并且将切屑等效到最后一个节点上，如图1（b）所示.

建模时，以电主轴转子的末端中心为坐标原点，主轴轴心线为z轴，如（a）所示的O-xyz坐标系；将主动磁悬浮轴承的支承特性以电磁力的形式施加在主轴转子的相应节点上；铣削产生的切削力和由切屑所导致的旋转惯性载荷作用在最后一个节点上，以及将切屑等效为在最后一个节点上的圆盘. 每个节点有 $x$ 、 $y$ 方向上的2个平移自由度和2个转动自由度，因此，对于具有 $N - 1$ 个轴段、 $N$ 个节点联结而成的“主轴-刀具”系统的x、y方向位移向量分别表示为

$\left\{ \begin{gathered} {{\bf{U}}_1} = {\left[ {{x_1},{\theta _{y1}},{x_2},{\theta _{y2}}, \cdots ,{x_N},{\theta _{yN}}} \right]^{\mathrm{T}}}, \\ {{\bf{U}}_2} = {\left[ {{y_1}, - {\theta _{x1}},{y_2}, - {\theta _{x2}}, \cdots ,{y_N}, - {\theta _{xN}}} \right]^{\mathrm{T}}}. \\ \end{gathered} \right.$

(1)

忽略系统内阻和磁悬浮轴承的阻尼，依据有限元建模理论，得到系统的运动方程为

$\left\{ \begin{gathered} {{\boldsymbol{M}}_1}{{{\boldsymbol{\ddot U}}}_1} + \Omega {{\boldsymbol{G}}_1}{{{\boldsymbol{\dot U}}}_2} + {{\boldsymbol{K}}_1}{{\boldsymbol{U}}_1} = {{\boldsymbol{Q}}_1} \\ {{\boldsymbol{M}}_1}{{{\boldsymbol{\ddot U}}}_2} - \Omega {{\boldsymbol{G}}_1}{{{\boldsymbol{\dot U}}}_1} + {{\boldsymbol{K}}_1}{{\boldsymbol{U}}_2} = {{\boldsymbol{Q}}_2} \\ \end{gathered} \right.$

(2)

式中： ${{\boldsymbol{M}}_1}$ 为质量矩阵，由于切屑质量时变导致质量矩阵 ${{\boldsymbol{M}}_1}$ 是时变的； ${{\boldsymbol{G}}_1}$ 为陀螺矩阵； ${{\boldsymbol{K}}_1}$ 为刚度矩阵，是 $2N \times 2N$ 阶对称矩阵，； $\varOmega$ 为“主轴-刀具”系统的自转角速度， ${{\boldsymbol{Q}}_1}$ 和 ${{\boldsymbol{Q}}_2}$ 均为 $2N \times 1$ 维广义力向量，包括初始不平衡力、磁悬浮轴承的电磁力、切屑旋转产生的惯性力和惯性力矩以及铣削力.

式（2）中的质量矩阵、陀螺矩阵和刚度矩阵可通过每个轴段的质量矩阵、陀螺矩阵和刚度矩阵组装起来. 每个轴段的移动惯性矩阵 ${\boldsymbol{M}}_{{\mathrm{sT}}}$ 、转动惯性矩阵 ${\boldsymbol{M}}_{{\mathrm{sR}}}$ 、陀螺矩阵 ${\boldsymbol{J}}_{{\mathrm{s}}}$ 和刚度矩阵 ${\boldsymbol{K}}_{{\mathrm{s}}}$ 表示^[18]为

$\left\{\begin{aligned} & \boldsymbol{M}_{\mathrm{sT}}=\frac{\mu l}{420}\left[\begin{array}{cccc} 156 & 22 l & 54 & -13 l \\ 22 l & 4 l^2 & 13 l & -3 l \\ 54 & -3 l & 156 & -22 l \\ -13 l & -3 l & -22 l & 4 l^2 \end{array}\right], \quad & \boldsymbol{M}_{\mathrm{sR}}=\frac{\mu r^2}{120 l}\left[\begin{array}{cccc} 36 & 3 l & -36 & 3 l \\ 3 l & 4 l^2 & -3 l & -l^2 \\ -36 & -3 l & 36 & -3 l \\ 3 l & -l^2 & -3 l & 4 l^2 \end{array}\right], \\ & \boldsymbol{J}_{\mathrm{s}}=\frac{\mu r^2}{60 l}\left[\begin{array}{cccc} 36 & 3 l & -36 & 3 l \\ 3 l & 4 l^2 & -3 l & -l^2 \\ -36 & -3 l & 36 & -3 l \\ 3 l & -l^2 & -3 l & 4 l^2 \end{array}\right], \quad & \boldsymbol{K}_{\mathrm{s}}=\frac{E I}{60 l}\left[\begin{array}{cccc} 12 & 6 l & -12 & 6 l \\ 6 l & 4 l^2 & -6 l & 2 l^2 \\ -12 & -6 l & 12 & -6 l \\ 6 l & 2 l^2 & -6 l & 4 l^2 \end{array}\right], \end{aligned}\right.$

(3)

式中： $\mu$ 为轴段单位长度的质量，l为轴段的长度；r为轴段的半径，E为轴段弹性模量，I为轴段截面的惯性矩.

以组装系统的整体质量矩阵为例进行分析. 首先将轴段的质量矩阵写成分部矩阵的形式，即

${\boldsymbol{M}}_{{\mathrm{s}}}^{(i)} = {\boldsymbol{M}}_{{{\mathrm{sT}}}}^{(i)} + {\boldsymbol{M}}_{{{\mathrm{sR}}}}^{(i)} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{m}}_{{\mathrm{11}}}^{({\mathrm{s}}i)}&{\boldsymbol{m}}_{{\mathrm{12}}}^{({\mathrm{s}}i)} \\ {\boldsymbol{m}}_{{\mathrm{21}}}^{({\mathrm{s}}i)}&{\boldsymbol{m}}_{{\mathrm{22}}}^{({\mathrm{s}}i)} \end{array}} \right].$

(4)

则磁悬浮铣削电主轴时变质量系统的整体质量矩阵M₁可表示为

${{{{\boldsymbol{M}}}}_1} = \left[ {\begin{array}{*{20}{c}} {{m}}_{{\mathrm{11}}}^{({\mathrm{s}}1)}&{{m}}_{{\mathrm{12}}}^{({\mathrm{s}}1)}&0& \cdots &0&0 \\ {{m}}_{{\mathrm{21}}}^{({\mathrm{s}}1)}&{{{m}}_{{\mathrm{22}}}^{({\mathrm{s}}1)} + {{m}}_{{\mathrm{11}}}^{({\mathrm{s}}1)}}&{{m}}_{{\mathrm{12}}}^{({\mathrm{s}}2)}& \cdots &0&0 \\ 0&{{m}}_{{\mathrm{21}}}^{({\mathrm{s}}2)}&{{{m}}_{{\mathrm{22}}}^{({\mathrm{s}}2)} + {{m}}_{{\mathrm{11}}}^{({\mathrm{s}}3)}}& \cdots &0&0 \\ \vdots & \vdots & \vdots & & \vdots & \vdots \\ 0&0&0& \cdots &{\left[ {{{{m}}_{22}}} \right]_s^{N - 2} + \left[ {{{{m}}_{{{11}}}}} \right]_s^{N - 1}}&{\left[ {{{{m}}_{12}}} \right]_s^{N - 1}} \\ 0&0&0& \cdots &{\left[ {{{{m}}_{21}}} \right]_s^{N - 1}}&{\left[ {{{{m}}_{22}}} \right]_s^{N - 1} + {{{M}}_{\mathrm{d}}}} \end{array}} \right],$

(5)

式中： ${{M}}_{{\mathrm{d}}}=\left[\begin{array}{cc}m\left(t\right)& 0\\ 0& {J}_{{\mathrm{d}}}\end{array}\right]$ ， $m\left(t\right)$ 为随时间变化的切屑质量， ${J}_{{\mathrm{d}}}$ 为时变切屑质量引起的直径转动惯量的变化量.

整体陀螺矩阵J₁和整体刚度矩阵K₁也可用类似方法形成.

1.2 铣削时电主轴变质量模型的建立

根据（a），立铣刀圆柱面上分布的切削刃呈螺旋线型，在铣削过程中，螺旋切削刃逐渐进入或退出工件，导致切削刃中切屑的厚度不断发生变化,即在切削过程中的任一时刻，沿切削刃方向分布的切屑厚度各不相同. 因此，当切屑不断进入容屑槽时，其瞬时切屑质量由切屑的瞬时切削厚度和几何边界确定；而切屑的瞬时体积为从切削刃开始接触工件的时刻 ${t_0}$ 到当前时刻 $t$ 的所有瞬时切削截面面积的积分，由此可推出单个切屑的任意时刻的质量 $\Delta m$ . 具体计算过程如下：

引用文献[19]的瞬时切削厚度模型：

$h\left(\theta \right)=\left\{\begin{array}{l}{f}_{{\mathrm{z}}}\mathrm{sin}\theta ,\quad0 < \theta < {\phi }_{{\mathrm{e}}},\\ 0,\quad 其他.\end{array}\right.$

(6)

式中： ${f_{\mathrm{z}}}$ 为每齿进给量； ${\varphi _j}\left( t \right)$ 为第 $j$ 条刀齿接触工件表面至某一瞬时时对 $t$ 时的转角，如式（7）； ${\varphi _{\mathrm{e}}}$ 为一条切削刃完成切削时的转角. 假设铣刀完全轴对称，在（b）中刀具末端单元的质心 ${o_1}$ 点建立固定坐标系 ${o_1}{x_1}{y_1}{{\textit{z}}_1}$ ，铣刀端面坐标系及相关参数如所示. 图中， ${a_{\mathrm{e}}}$ 为径向切削深度.

图 2 铣削过程示意

Figure 2. Milling process

下载: 全尺寸图片幻灯片

根据图2可得

${\varphi _{\mathrm{e}}} = {\cos ^{ - 1}}\left(\frac{{r_{\mathrm{a}} - {a_{\mathrm{e}}}}}{r_{\mathrm{a}}}\right)$

(7)

${\varphi _j}(t) = \varOmega t - (j - 1)\frac{{2{\text{π}} }}{{\textit{z}}}$

(8)

式中： $r_{\mathrm{a}}$ 为铣刀半径.

根据所示，四刃铣刀加工时，通过选择合适的铣刀规格和切削参数，可以确保每次只有一条切削刃参与切削^[20]，如所示，任一切削刃从开始切削到切削完成的时间 $\tau {\text{ = }}{{{\varphi _{\mathrm{e}}}} /\varOmega }$ ，相邻两切屑的质量变化规律在时间上相差 $\Delta \tau {\text{ = }}{ {T /k}}$ ，其中， $T$ 为主轴旋转周期， $k$ 为铣刀齿数.

图 3 切屑质量变化示意

Figure 3. Chip quality change

下载: 全尺寸图片幻灯片

由于相邻切削刃之间存在 $\Delta \tau$ 的时间间隔，任意一条切屑的质量随时间 $t$ 的变化函数为

${m}_{j}(t)=\left\{\begin{array}{l}\rho {a}_{{\mathrm{p}}}{\displaystyle {\int }_{{\phi }_{j}({t}_{0})}^{{\phi }_{j}(t)}h\left(\theta \right){\mathrm{d}}\theta },\quad{t}_{0} < t\leqslant {t}_{0} + \tau, \\ 0,\quad 其他,\end{array} \right.$

(9)

式中： $j=1、2、3、4$ ， $\rho$ 为切屑密度， ${a_{\mathrm{p}}}$ 为轴向切削深度， ${t_0} = KT + \left( {j - 1} \right)\Delta \tau$ ， $K=0、1、2\cdots$ .

当切屑 $\Delta m$ 进入容屑槽，其质心会产生一个从 ${o_1}$ 到切屑进入系统后新的质心位置 $G$ 的微小偏移量 $e$ ，以 $G$ 为坐标原点建立平行于坐标轴 ${O_1}\text{-}{x_1}{y_1}{{\textit{z}}_1}$ 的质心坐标系 $G\text{-}{x'_1}{y'_1}{{\textit{z}}'_1}$ ；此外，由于切屑的进入，原本与几何对称轴相一致的惯性主轴也会相应的产生角度为 $\varepsilon$ 的偏移，进而建立过质心的惯性主轴坐标系 $G\text{-}{x_2}{y_2}{{\textit{z}}_2}$ .

由（a）中切削区域可知，每条切削刃都是从点 $a$ 开始切削，切屑开始形成，到点 $c$ 结束切削，切屑质量达到最大. 假设切削完成时切屑即脱离容屑槽，此时切削过程中的切屑质心随着切削的进行，从点 $a$ 逐渐移动到点 $c$ . 而（a）中 $\Delta m$ 即表示切削过程中某一时刻切屑的位置；因此，切屑质心在坐标系 ${O_1}\text{-}{x_1}{y_1}{{\textit{z}}_1}$ 下的位置坐标可近似表示为

图 4 带有切屑的转动单元

Figure 4. Rotational unit with chips

下载: 全尺寸图片幻灯片

$\left\{ \begin{gathered} {x_{\mathrm{q}}} = r\cos\;\; \varOmega t \\ {y_{\mathrm{q}}} = r\sin\;\; \varOmega t \\ {{\textit{z}}_{\mathrm{q}}} = \frac{l_{\mathrm{d}}}{2} - \frac{{{a_{\mathrm{p}}}}}{\tau }t, \\ \end{gathered} \right.$

(10)

式中： $l_{\mathrm{d}}$ 为铣刀最后一个单元的长度.

由此可得到包含单个切屑的转动单元，在坐标系 ${O_1}\text{-}{x_1}{y_1}{{\textit{z}}_1}$ 下的惯性矩阵为

$\begin{split} &\boldsymbol{I}_{O_1}=\left[\begin{array}{ccc} I_{x 1} & 0 & 0 \\ 0 & I_{y 1} & 0 \\ 0 & 0 & I_{{\textit{z}} 1} \end{array}\right]+ \\ &\quad m_j\left[\begin{array}{ccc} y_{\mathrm{q}}^2+{\textit{z}}_{\mathrm{q}}^2 & -x_{\mathrm{q}} y_{\mathrm{q}} & -{\textit{z}}_{\mathrm{q}} x_{\mathrm{q}} \\ -x_{\mathrm{q}} y_{\mathrm{q}} & {\textit{z}}_{\mathrm{q}}^2+x_{\mathrm{q}}^2 & -y_{\mathrm{q}} {\textit{z}}_{\mathrm{q}} \\ -{\textit{z}}_{\mathrm{q}} x_{\mathrm{q}} & -y_{\mathrm{q}} {\textit{z}}_{\mathrm{q}} & x_{\mathrm{q}}^2+y_{\mathrm{q}}^2 \end{array}\right] \end{split},$

(11)

式中： ${I}_{x_1}、{I}_{y_1}$ 和 ${I_{{\textit{z}}_1}}$ 为未考虑切屑质量时，该单元在坐标系 ${o_1}\text{-}{x_1}{y_1}{{\textit{z}}_1}$ 下绕 $x_1、y_1、{\textit{z}}_1$ 的转动惯量， ${m_j}$ 为第 $j$ 条切削刃中的切屑质量.

由于切屑的进入，系统质心会产生一个从 ${o_1}$ 到 $G$ 的微小偏移量 $e$ ，如式（12）.

$\begin{split} &{\boldsymbol{e}} = {\left[ {{x_G}}\quad{{y_G}}\quad{{\textit{z}_G}} \right]^T} =\\ &\quad \left[ {\frac{{{m_j}}}{{{M_{\mathrm{a}}} + {m_j}}}{x_{\mathrm{q}}}}\quad{\frac{{{m_j}}}{{{M_{\mathrm{a}}} + {m_j}}}{y_{\mathrm{q}}}}\quad{\frac{{{m_j}}}{{{M_{\mathrm{a}}} + {m_j}}}{{\textit{z}}_{\mathrm{q}}}} \right] \end{split}$

(12)

式中： ${x_G}、{{y_G}}、{{\textit{z}_G}}$ 为点G坐标值， $M_{\mathrm{a}}$ 为转动单元的质量.

又因为坐标系 $G\text{-}{x'_1}{y'_1}{{\textit{z}}'_1}$ 与坐标系 ${O_1}\text{-}{x_1}{y_1}{{\textit{z}}_1}$ 平行，可根据平行轴定理，得到包含单个切屑的转动单元在坐标系 $G\text{-}{x'_1}{y'_1}{{\textit{z}}'_1}$ 下的惯性矩阵为

$\begin{split}&{{\boldsymbol{I}}_G} = {{\boldsymbol{I}}_{o_1}} - (m + {m_j}) \times \\ &\quad \left[\begin{array}{ccc} y_G^2+{\textit{z}}_G^2 & -x_G y_G & -{\textit{z}}_G x_G \\ -x_G y_G & {\textit{z}}_G^2+x_G^2 & -y_G {\textit{z}}_G \\ -{\textit{z}}_G x_G & -y_G {\textit{z}}_G & x_G^2+y_G^2 \end{array}\right]\end{split}.$

(13)

此外，由于切屑的进入，原本与几何对称轴相一致的惯性主轴也会产生倾斜，如图4（b）所示. 依据惯性矩阵的定义，总能找到一个特殊的变换矩阵 ${\boldsymbol{T}}$ 使式（13）变换为对角阵，从而获得以系统质心为原点的惯性主轴坐标系 $G\text{-}{x_2}\text{-}{y_2}{{\textit{z}}_2}$ 下的惯性矩阵：

${{\boldsymbol{T}}^{\mathrm{T}}}{{\boldsymbol{I}}_G}{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{I_x}}&0&0 \\ 0&{{I_y}}&0 \\ 0&0&{{I_{\textit{z}}}} \end{array}} \right],$

(14)

式中： ${I_x}$ 和 ${I_y}$ 为铣刀末端单元-切屑系统的x、y轴直径转动惯量， ${I_{\textit{z}}}$ 为铣刀末端单元-切屑系统的极转动惯量.

切屑随铣刀同频旋转所引起的旋转惯性力和惯性力矩可分别表示^[21]为

$\left\{ \begin{aligned} & F_{{\mathrm{c}} x}=m r \varOmega^2 \cos\;\; \varOmega t \\ & F_{{\mathrm{c}} y}=m r \varOmega^2 \sin\;\; \varOmega t \end{aligned}\right.$

(15)

$\left\{ \begin{aligned} & M_{{\mathrm{c}} x}=\left(I_x-I_{\textit{z}}\right) \varepsilon\varOmega ^2 \cos\;\; \varOmega t \\ & M_{{\mathrm{c}} y}=\left(I_y-I_{\textit{z}}\right) \varepsilon\varOmega ^2 \sin\;\; \varOmega t \end{aligned}\right.$

(16)

式中： ${F_{{\mathrm{c}}x}}$ 和 ${F_{{\mathrm{c}}y}}$ 分别为切屑运动所产生的旋转惯性力在 $xO{\textit{z}}$ 平面和 $yO{\textit{z}}$ 平面内的投影， ${M_{{\mathrm{c}}x}}$ 和 ${M_{{\mathrm{c}}y}}$ 分别为切屑运动所产生的旋转惯性力矩在 $xO{\textit{z}}$ 平面和 $yO{\textit{z}}$ 平面内的投影； $\varepsilon$ 其值可根据惯性矩阵 ${{\mathbf{I}}_G}$ 求得^[22].

1.3 铣削力模型

磁悬浮电主轴在铣削加工中会受到铣削力载荷的作用，在此引用文献[]的铣削力经验公式，可得到 $x$ 、 $y$ 方向上的铣削力均为

${F_0} = 0.85{C_{\mathrm{F}}}a_{\mathrm{e}}^{0.88}f_{\mathrm{z}}^{0.72}{a_{\mathrm{p}}}{d^{ - 0.88}}Z,$

(17)

式中： ${C_{\mathrm{F}}}$ 为铣削力系数，根据机械加工工艺设计实用手册^[24]取 ${C_{\mathrm{F}}} = 68.2$ ； $d$ 为铣刀直径.

另外，由于主轴旋转速度极快，主轴旋转一周所经历的时间极少，为简化运算，在小周期内将铣削力 ${F_0}$ 的大小视为恒定的常量，其作用时间即刀具切削刃与工件的接触时间，即产生切屑的时间，由此可建立第 $j$ 条切削刃切削时所受铣削力的模型为

${F}_{{\mathrm{q}}j}=\left\{\begin{array}{l}{F}_{0},\quad{t}_{0} < t < {t}_{0} + \tau , \\ 0,\quad 其他.\end{array}\right.$

(18)

1.4 磁悬浮轴承电磁力模型

根据磁悬浮轴承理论，并假设磁悬浮轴承各向同性，（a）中上、下两个径向磁悬浮轴承A、B在 $x$ 、 $y$ 方向产生的线性电磁力^[16]为

$\left\{ \begin{gathered} {F_{{\mathrm{A}}x}} = {k}_1{i_{ax}}{\text{ + }}{k_{\textit{z}}}{x_a} \\ {F_{{\mathrm{B}}x}} = {k}_1{i_{bx}}{\text{ + }}{k_{\textit{z}}}{x_b} \\ {F_{{\mathrm{A}}y}} = {k}_1{i_{ay}}{\text{ + }}{k_y}{y_a} \\ {F_{{\mathrm{B}}y}} = {k}_1{i_{by}}{\text{ + }}{k_y}{y_b} \\ \end{gathered} \right.$

(19)

式中： ${k_i} = \dfrac{{{\mu _0}{B^2}i_0^2A\cos {\alpha }/{2}}}{{g_0^2}}$ ， ${k_x} =k_y - \dfrac{{{\mu _0}{B^2}i_0^2A\cos {\alpha }/{2}}}{{g_0^3}}$ ，为x、y向刚度， ${i}_{{\mathrm{A}}x} 、{i}_{{\mathrm{B}}x}$ 和 ${i}_{{\mathrm{A}}y}、{i_{{\mathrm{B}}y}}$ 为磁悬浮轴承A（B） x、y的控制电流， ${\mu _0}$ 为磁导率， $B$ 为线圈匝数， ${i_0}$ 为偏置电流， $A$ 为磁路有效横截面积， ${g_0}$ 为气隙长度， $\alpha$ 为两相邻磁极之间的夹角.

2. 动态响应的计算

2.1 “主轴-刀具-切屑”质量时变系统的固有特性求解

为求解系统的固有特性，根据式（2）系统的运动微分方程，可得其齐次表达式如下：

$\left\{ \begin{gathered} {{\boldsymbol{M}}_1}{{{\boldsymbol{\ddot U}}}_1} + \varOmega {{\boldsymbol{G}}_1}{{{\boldsymbol{\dot U}}}_2} + {{\boldsymbol{K}}_1}{{\boldsymbol{U}}_1} = {\boldsymbol{0}}, \\ {{\boldsymbol{M}}_1}{{{\boldsymbol{\ddot U}}}_2} - \varOmega {{\boldsymbol{G}}_1}{{{\boldsymbol{\dot U}}}_1} + {{\boldsymbol{K}}_1}{{\boldsymbol{U}}_2} = {\boldsymbol{0}}. \\ \end{gathered} \right.$

(20)

式（19）中，用复数向量表示系统各节点的位移，即令 ${\boldsymbol{z}} = {{\boldsymbol{U}}_1} + i{{\boldsymbol{U}}_2}$ ，则式（19）可写为

${{\boldsymbol{M}}_1}{\boldsymbol{\ddot z}}{\text{ - }}{\mathrm{i}}\varOmega {{\boldsymbol{G}}_1}{\boldsymbol{\dot z}} + {{\boldsymbol{K}}_1}{\boldsymbol{z}} = {\boldsymbol{0}}$

(21)

式（20）是 $2N$ 个具有复系数的二阶微分方程组. 设其解为 ${\boldsymbol{z}} = {{\boldsymbol{z}}_0}{{\mathrm{e}}^{{\mathrm{i}}\omega t}}$ ，代入式（20）可得

$\left( { - {{\boldsymbol{M}}_1}{\omega ^2} + {{\boldsymbol{G}}_1}\varOmega \omega + {{\boldsymbol{K}}_1}} \right){{\boldsymbol{z}}_0} = {\boldsymbol{0}} ,$

(22)

式中： $\omega$ 为电主轴涡动角速度.

因此可以得到考虑陀螺力矩的频率方程为

${\text{|}} - {{\boldsymbol{M}}_1}{\omega ^2} + {{\boldsymbol{G}}_1}\varOmega \omega + {{\boldsymbol{K}}_1}{\text{|}} = 0.$

(23)

求解其特征值和特征向量，即可求出在给定自转角速度 $\varOmega$ 时，系统的涡动角速度. 为简化计算，可将式（22）改写为

${\text{|}} - \left( {{{\mathbf{M}}_1} - \frac{\varOmega }{\omega }{{\mathbf{G}}_1}} \right){\omega ^2} + {{\mathbf{K}}_1}{\text{|}} = 0.$

(24)

此时，在给定比值 $\varOmega/\omega$ 的情况下，通过求解式（22）的特征值以及特征向量就可以得到系统的模态频率和振型.

2.2 运动微分方程的求解

为方便描述，采用广义变量将式（2）合并为

${\boldsymbol{M\ddot U}} + \varOmega {\boldsymbol{G\dot U}} + {\boldsymbol{KU}} = {\boldsymbol{Q}},$

(25)

式中：质量矩阵 ${\mathbf{M}}$ 、陀螺矩阵 ${\mathbf{G}}$ 及刚度矩阵 ${\mathbf{K}}$ 为 $4N \times 4N$ 阶对称矩阵； ${\mathbf{U}}$ 为 $4N \times 1$ 维位移向量； $\boldsymbol{Q}$ 为 $4N \times 1$ 维广义力向量，其中磁轴承节点处分别为磁轴承电磁力F_Ax、F_Ay、F_Bx、F_By，末端节点处为铣削力F_q和切屑引起的旋转惯性载荷F_cx、F_cy、M_cx、M_cy，此外，其他元素为0.

由于式（24）为二阶非齐次微分方程组，求解时，首先进行降阶，然后采用四阶龙格库塔法求解该二阶微分方程组.

令 ${\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{S}}_{\mathrm{a}}}} \\ {{{\boldsymbol{S}}_{{{\mathrm{b}}}}}} \end{array}} \right]$ ，代入式（26）整理后可得

${\boldsymbol{\dot S}} = \left[ {\begin{array}{*{20}{c}} {{{{\boldsymbol{\dot S}}}_{\mathrm{a}}}} \\ {{{{\boldsymbol{\dot S}}}_{\mathrm{b}}}} \end{array}} \right] = \left[ \begin{gathered} {{\boldsymbol{S}}_{\mathrm{b}}} \\ {{\boldsymbol{M}}^{ - 1}}\left[ { - \left( {\varOmega {\boldsymbol{G}}{{\boldsymbol{S}}_{\mathrm{b}}} + {\boldsymbol{K}}{{\boldsymbol{S}}_{\mathrm{a}}}} \right) + {\boldsymbol{Q}}} \right] \\ \end{gathered} \right],$

(26)

式中： ${{\boldsymbol{S}}_{\mathrm{a}}} = {\boldsymbol{U}}$ ， ${{\boldsymbol{S}}_{\mathrm{b}}} = {\boldsymbol{\dot U}}$ .

四阶龙格库塔法的计算式为

$\left\{ \begin{gathered} {{\boldsymbol{K}}_1} = F\left( {{t_n},{{\boldsymbol{S}}_n}} \right), \\ {{\boldsymbol{K}}_2} = F\left( {{t_n} + \frac{1}{2}h,{{\boldsymbol{S}}_n} + \frac{1}{2}h{{\boldsymbol{K}}_1}} \right), \\ {{\boldsymbol{K}}_3} = F\left( {{t_n} + \frac{1}{2}h,{{\boldsymbol{S}}_n} + \frac{1}{2}h{{\boldsymbol{K}}_2}} \right), \\ {{\boldsymbol{K}}_4} = F\left( {{t_n} + h,{{\boldsymbol{S}}_n} + h{{\boldsymbol{K}}_3}} \right), \\ {{\boldsymbol{S}}_{n + 1}} = {{\boldsymbol{S}}_n} + \frac{h}{6}\left( {{{\boldsymbol{K}}_1} + 2{{\boldsymbol{K}}_2} + 2{{\boldsymbol{K}}_3} + {{\boldsymbol{K}}_4}} \right). \\ \end{gathered} \right.$

(27)

式中：h为时间步长.

由式（25）可知，当已知时刻 ${t_n}$ 的 ${{\boldsymbol{S}}_n}$ 值时，给定时间步长 $h$ ，则可求出下一时刻 ${t_{n{\text{ + }}1}}$ 时的 ${{\boldsymbol{S}}_{n{\text{ + }}1}}$ 值. 因此，计算时，给定时间变量 $t$ 的范围、时间步长 $h$ 以及 ${\boldsymbol{S}}$ 的初始值，代入式（25）和式（26），即可逐步求出每个节点任意时刻的位移、转角以及速度、角速度等.

3. 动态特性分析

为分析磁悬浮铣削电主轴系统在质量非线性变化下的动态特性，根据前述磁悬浮铣削电主轴变质量系统的动力学模型，并设在额定工作转速下铣刀每齿进给量为0.06 mm ，径向切削深度为0.04 mm，轴向切削深度为1 mm，工件材料为45钢. 同时取0时刻的位移初始值 ${{\boldsymbol{S}}_0} = {\boldsymbol{0}}$ ，计算总时间设为0.5 s，仿真时利用Maltab中的ode45求解器进行，且系统具体的结构计算参数如表1所示

表 1 磁悬浮电主轴-刀具系统的物理几何参数

Table 1. Physical geometric parameters for motorized spindle of magnetic suspension–tool system

参数	数值
转子总长/mm	500
转子质量/kg	6.427
转子材料	30CrNiMo8
转子弹性模量/Pa	2 × 10¹¹
刀具总长/mm	80
刀具直径/mm	16
刀具材料	W6Mo5Cr4V2Co8
工作转速/（r•min⁻¹）	15000
磁轴承等效刚度/（N•m⁻¹）	−2 × 10⁷

下载: 导出CSV

| 显示表格

3.1 “主轴-刀具-切屑”变质量系统的固有特性分析

根据式（24）的分析和转子动力学理论，令 $\varOmega/\omega$ 为定值时，求解式（24）的特征值和特征向量，即可获得系统的模态频率和振型. 同时，为了分析系统质量变化时，转子涡动频率变化导致系统固有频率的变化趋势，以 $\varOmega/\omega$ 为横坐标，系统模态频率为纵坐标，绘制磁悬浮电主轴-刀具系统的坎贝尔图，以得到整个转速范围内系统模态频率的变化特征，如图5所示.

图 5 “主轴-刀具-切屑”变质量系统的坎贝尔图

Figure 5. Campbell diagram of “spindle–tool–chip” time-varying mass system

下载: 全尺寸图片幻灯片

由图5知，系统各阶模态频率随转子自转速度的增加而升高. 这是因为系统在切削过程中，由于切屑不断进入刀具容屑槽，不仅改变了刀具系统的质量大小和分布，同时，因切屑质量偏心所引起的陀螺力矩在正进动状态下，将对转轴的横向变形起到抑制作用，从而增强了转轴的弯、曲刚度，使得转子的正进动模态频率升高.

以图5为基础做进一步分析可知，当系统自转速度不变时，随着切屑不断进入刀具容屑槽，即系统质量增加时，系统任意阶的模态频率呈下降趋势，如图6所示. 但阶数越高，质量对系统模态频率的影响越小. 综合对比图5和图6，可以得到高转速下陀螺力矩对系统固有频率的影响要大于系统质量对固有频率的影响.

图 6 切屑质量对“主轴-刀具-切屑”变质量系统临界转速的影响

Figure 6. Influence of chip quality on critical speed of “spindle–tool–chip” time-varying mass system

下载: 全尺寸图片幻灯片

在获得“主轴-刀具-切屑”变质量系统在不同自转速度下的固有频率和变化趋势的前提下，以 $\Delta m = 2.08 \times {10^{ - 5}}\;{\text{kg}}$ 时为计算依据，求得该状态下转速比为1时系统前三阶的模态振型如图7所示.

图 7 前三阶模态振型图

Figure 7. The first three mode shapes

下载: 全尺寸图片幻灯片

由图7可知：系统前三阶振型都为弯曲振型；再结合图1（b），在磁悬浮轴承处，即节点8和节点18处，由于位移刚度的影响，系统振幅最小；在前两阶振型下，由于电机定/转子之间电磁力和电磁力矩的影响，系统振幅均接近于0；在磁悬浮轴承的两端，即系统的悬伸部分，系统不受到任何约束，类似于两悬臂梁，因此振动振幅较大，且距离轴承越远，振幅越大；在第三阶振型下，磁悬浮轴承的支承处的振幅较前两阶振型稍有增大，且两磁悬浮轴承之间的电机转子部分，出现非常明显的弯曲振动特征，容易让电机定/转子之间产生碰摩；同时，刀具部分（节点22～26）的振幅较前两阶更大. 因此，磁悬浮电主轴高速运行和进行切削加工时应当避开临界转速，防止系统失稳.

3.2 振动响应分析

在获得“磁悬浮电主轴-刀具-切屑”变质量系统固有频率、振型等固有特征随系统质量变化趋势的基础上，为进一步分析系统在运行和切削过程中的受迫振动响应特性，以系统在切削时的初始不平衡离心力、磁轴承电磁力、切削力为激励和切削过程中切屑进入容屑槽后由切屑引起的旋转惯性载荷为激励，对系统的强迫振动响应特性进行详细的仿真分析.

仿真时，令转子初始偏心量为0.2 g•mm；依据上述切削参数，获得系统的单个切屑质量 $m_j$ = 0～2.08×10⁻⁵ kg，进而可得到旋转惯性力和力矩的变化范围依次为 ${F_{{\mathrm{c}}x}} =$ 0～0.40 N， ${F_{{\mathrm{c}}y}} =$ 0～0.12 N， ${M_{{\mathrm{c}}x}} =$ 0～3.6×10⁻³ N•m， ${M_{{\mathrm{c}}y}} =$ 0～1.1×10⁻³ N•m. 最后，在Matlab中运用ode45求解器，对式（24）进行求解，得到系统的受迫振动响应如图8所示

图 8 磁悬浮电主轴-刀具-切屑系统振动响应

Figure 8. Vibration response of motorized spindle of magnetic suspension–tool–chip system

下载: 全尺寸图片幻灯片

图8（a）和图8（b）分别表示磁悬浮铣削电主轴系统各节点x、y向的振动响应；图8（c）和图8（d）分别表示系统各节点x、y向的角向振动响应. 当沿时间轴方向进行分析时，在0～0.1 s内，表示电主轴启动并旋转至工作转速. 在此期间，电主轴处于空载状态，系统只受到由初始不平衡质量引起的离心力和磁悬浮轴承电磁力的作用；从0.1 s开始，系统进入切削状态，此时由切削所引起的周期性恒定切削力和因切屑进入容屑槽产生质量偏心所引起的惯性力和惯性力矩，将使系统各节点的振动幅值迅速增大，并导致各节点平衡位置相对于中心轴有不同程度的偏移，但最后各节点的振动逐步稳定在一定范围，且呈周期性变化趋势.

当沿电主轴轴向（即节点序号）方向分析时，两磁悬浮轴承位置（节点8～18）处的振动幅值最小，其振动平衡位置基本在中心轴附近. 而在磁悬浮轴承的两端，即从节点8～1，以及从节点18～26，振动幅值越来越大；其中，节点8～1的振动平衡位置基本与中心轴一致，但节点18～26的振动平衡位置偏离中心轴的距离也越来越大，并与图7一阶模态振型的振动趋势相符. 因此，图8中系统振动的趋势与图7相同，且振动的幅值与式（15）一致，呈正弦规律周期性变化. 又因切削力施加在节点26处，故该节点及其周边处的振动幅值最大，如图8所示.

3.3 切屑引起的旋转惯性载荷对系统振动响应的影响

为进一步直观分析系统在切屑持续进入和流出容屑槽所造成的旋转惯性载荷的作用下，其振动随时间的变化规律. 选择切削加工点处以沿 $x$ 方向的径向位移和绕 $x$ 方向的角向位移为例进行分析，然后分别计算不计及旋转惯性载荷和计及旋转惯性载荷时的系统振动响应，所得到的仿真结果如图9所示.

图 9 磁悬浮电主轴-刀具-切屑系统切削加工点的振动响应

Figure 9. Vibration response of motorized spindle of magnetic suspension–tool–chip system at cutting point

下载: 全尺寸图片幻灯片

对比图9（a）、（b）可知，旋转惯性载荷的引入基本不会改变切削点处径向振动和角向振动的振动形式，但是会使径向振动响应的幅值出现0～9.7×10⁻⁷ m不等的增大；使角向振动响应的幅值出现0～2.5×10⁻⁵ rad不等的增大. 此外，旋转惯性载荷还会使加工点处径向振动和角向振动平衡位置的偏移距离分别增加约5.1～×10⁻⁷ m和9.3×10⁻⁶ rad. 因此，尽管高速铣削时由切屑引起的旋转惯性载荷不会改变系统的振动形式，但会增大系统振动的幅值，进而影响系统运行的稳定性，并降低系统切削加工的精度.

4. 结　论

1）针对磁悬浮铣削电主轴在切削过程中，因切屑不断进入容屑槽而导致“磁悬浮轴承-主轴-刀具-切屑”系统质量不断变化的情况，基于金属切削原理，建立了时变切屑质量引起的旋转惯性载荷模型，并基于转子动力学知识和有限元思想建立了磁悬浮铣削电主轴时变质量系统的动力学模型，利用Matlab软件进行求解，得到了系统固有频率的变化趋势、振型和动态响应.

2）由于陀螺力矩的影响会使系统的模态频率随着自转角速度的增大而增大；另外，切屑的进入会导致系统临界转速的下降，且对临界转速的影响随阶数增大而降低；并且，高转速下陀螺力矩对系统固有频率的影响要大于系统质量对固有频率的影响.

3）在高速切削阶段，在初始不平衡离心力、磁悬浮轴承电磁力、切削力以及切屑引起的旋转惯性载荷的共同影响下，系统振动呈现周期性；并且切屑引起的旋转惯性载荷对系统的动态特性有一定影响，特别是对刀具部分的振动影响较大，会严重影响系统的切削精度.

致谢：湘潭市科技局科技攻关项目（GX-YB20221004）的支持.

图 1 因素自变量与造价因变量间的拟合关系

Figure 1. Fitting relationship between independent variable of factor and dependent variable of cost

下载: 全尺寸图片幻灯片

图 2 模型建构与优化流程

Figure 2. Model construction and optimization process

下载: 全尺寸图片幻灯片

图 3 训练集对比

Figure 3. Comparison of training sets

下载: 全尺寸图片幻灯片

图 4 检验集对比

Figure 4. Comparison of test sets

下载: 全尺寸图片幻灯片

图 5 不同模型相同环境下性能对比

Figure 5. Performance comparison of different models in the same environment

下载: 全尺寸图片幻灯片

图 6 相同模型不同环境下性能对比

Figure 6. Performance comparison of same model in different environments

下载: 全尺寸图片幻灯片

表 1 全局敏感性分析结果

Table 1. Global sensitivity analysis results

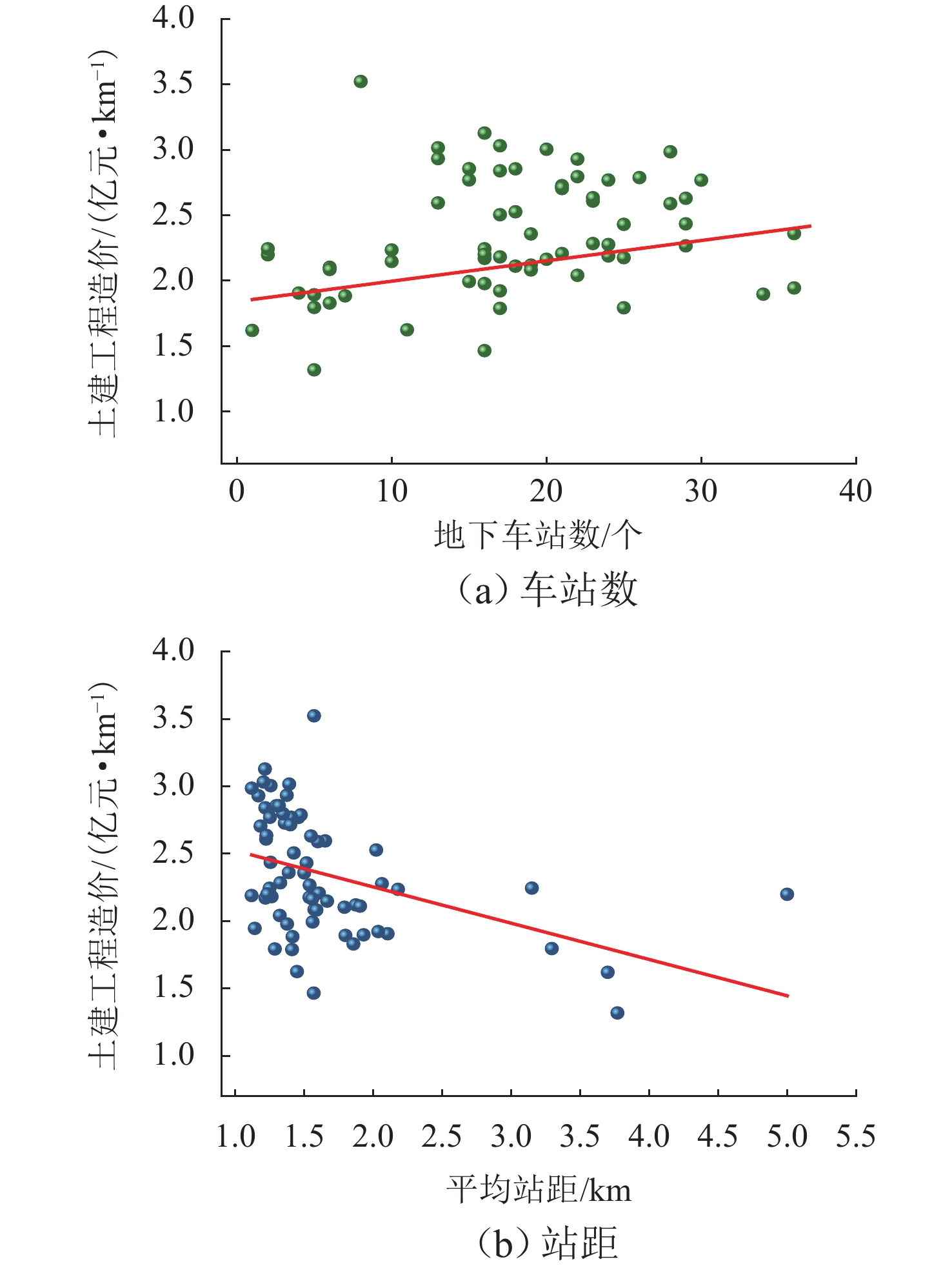
影响因素	地下线长度	高架线长度	地下车站数	地上车站数	平均站距	编组	工程环境及地质条件	国内生产总值	居民消费价格指数
总敏感度	0.653 6	0.060 3	0.223 6	0.012 4	0.008 3	0.019 3	0.000 8	0.003 1	0.018 2

下载: 导出CSV

表 2 线性拟合函数式及其对比

Table 2. Linear fitting functions and their comparison

影响因素	拟合函数式	拟合函数式影响因素与土建造价相关性	原始数据中影响因素与土建造价相关性	对比结果
地下线长度	f(x)=0.007 1x + 2.179 0	正相关	0.203 1 （正相关）	一致
高架线长度	f(x)=−0.059 2x + 2.467 0	负相关	−0.498 8 （负相关）	一致
地下车站数	f(x)=0.014 0x + 2.114 0	正相关	0.255 4 （正相关）	一致
地上车站数	f(x)=−0.101 4x + 2.455 0	负相关	−0.443 6 （负相关）	一致
平均站距	f(x)=−0.073 3x + 2.491 0	负相关	−0.167 1 （负相关）	一致
编组	f(x)=0.080 2x + 1.781 0	正相关	0.266 0 （正相关）	一致
工程环境及地质条件	f(x)=0.065 4x + 2.205 0	正相关	0.127 0 （正相关）	一致
国内生产总值	f(x)=0.000 1x + 2.202 0	正相关	0.253 5 （正相关）	一致
居民消费价格指数	f(x)=0.039 1x − 1.636 0	正相关	0.138 8 （正相关）	一致

下载: 导出CSV

表 3 各因素最优拟合函数式

Table 3. Optimal fitting functions of different factors

影响因素	拟合函数式	R²
地下线长度	f(x)=2.317 0 − 0.216 0cos 0.142 6x − 0.113 9sin 0.142 6x + 0.153 4cos 0.285 2x + 0.048 5 × sin 0.285 2x + 0.247 2cos 0.427 8x + 0.125 4sin 0.427 8x + 0.007 9cos 0.570 4x − 0.085 2 × sin 0.570 4x + 0.214 8cos 0.713 0x + 0.007 5sin 0.713 0x − 0.042 0cos 0.855 6x + 0.009 1 × sin 0.855 6x + 0.025 3cos 0.998 2x − 0.164 8sin 0.998 2x − 0.089 6cos 1.140 8x + 0.066 4sin 1.140 8x	0.645 2
高架线长度	f(x)=− 6 409 + 10⁴cos 0.998 9x + 8 473sin 0.998 9x − 2 120cos 1.997 8x − 12 500sin 1.997 8x − 5 779cos 2.996 7x + 8 477sin 2.996 7x + 7 112cos 3.995 6x − 720.100 0sin 3.995 6x − 3 340cos 4.994 5x − 2 932sin 4.994 5x + 463.200 0cos 5.993 4x + 1 899sin 5.993 4x + 74.800 0cos 6.992 3x − 395.100 0sin 6.992 3x	0.488 5
地下车站数	f(x)=− 3.368 0 10⁹ + 5.946 0 10⁹cos 0.046 2x + 2.665 0 10⁹sin 0.046 2x − 3.327 0 10⁹cos 0.092 4x − 4.480 0 10⁹sin 0.092 4x + 1.306 0 10⁸cos 0.138 6x + 3.879 0 10⁹sin 0.138 6x + 1.234 0 10⁹cos 0.184 8x − 1.667 0 10⁹sin 0.184 8x − 7.959 0 10⁸cos 0.231 0x + 1.796 0 10⁸sin 0.231 0x + 1.940 0 10⁸cos 0.277 2x + 1.099 0 10⁸sin 0.277 2x − 1.126 0 10⁷cos 0.323 4x − 3.620 0 10⁷sin 0.323 4x − 1.356 0 10⁶cos 0.369 6x + 2.710 0 10⁶sin 0.369 6x	0.486 8
地上车站数	f(x)=0.007 9x⁵ − 0.139 2x⁴ + 0.823 5x³ − 1.875 0x² + 1.143 0x + 2.530 0	0.337 0
平均站距	f(x)=3.088 0 10¹¹ + 1.954 0 10¹⁰cos 0.811 8x − 5.568 0 10¹¹sin 0.811 8x − 4.067 0 10¹¹cos 1.623 6x − 2.742 0 10¹⁰sin 1.623 6x − 2.242 0 10¹⁰cos 2.435 4x + 2.381 0 10¹¹sin 2.435 4x + 1.096 0 10¹¹cos 3.247 2x + 1.231 0 10¹⁰sin 3.247 2x + 4.558 0 10⁹cos 4.059 0x − 3.827 0 10¹⁰sin 4.059 0x − 9.559 0 10⁹cos 4.870 8x − 1.067 0 10⁹sin 4.870 8x − 1.333 0 10⁸cos 5.682 6x + 1.521 0 10⁹sin 5.682 6x + 1.157 0 10⁸cos 6.494 4x + 5.302 0 10⁶sin 6.494 4x	0.579 1
编组	f(x)=− 0.008 9x⁴ + 0.226 1x³ − 2.071 0x² + 8.206 0x-9.692 0	0.089 3
工程环境及地质条件	f(x)=2.320 0 − 0.266 6cos 1.571 0x − 0.118 8sin 1.571 0x	0.068 9
国内生产总值	f(x)=1.751 0 + 0.189 1cos 2.361 0x − 1.345 0sin 2.361 0x + 1.109 0cos 4.722 0x + 0.535 3sin 4.722 0x − 1.252 0cos 7.083 0x + 0.429 1sin 7.083 0x + 1.131 0cos 9.444 0x − 0.997 2sin 9.444 0x − 0.349 1cos 11.805 0x + 1.747 0sin 11.805 0x − 0.817 2cos 14.166 0x − 1.829 0sin 14.166 0x + 1.257 0cos 16.527 0x + 0.705 4sin 16.527 0x − 0.434 9cos 18.888 0x + 0.305 6sin 18.888 0x	0.526 1
居民消费价格指数	f(x)=2.185 0 + 0.058 3cos 5.835 0x − 0.145 6sin 5.835 0x − 0.203 1cos 11.670 0x + 0.237 2sin 11.670 0x + 0.050 6cos 17.505 0x + 0.138 8sin 17.505 0x + 0.106 0cos 23.340 0x − 0.051 0sin 23.340 0x + 0.179 2cos 29.175 0x − 0.239 2sin 29.175 0x − 0.027 0cos 35.010 0x + 0.246 6sin 35.010 0x + 0.021 3cos 40.845 0x − 0.346 3sin 40.845 0x + 0.231 5cos 46.680 0x − 0.089 9sin 46.680 0x	0.486 7

下载: 导出CSV

参考文献(25)

[1]	张飞涟,梁秀峰. 基于GA-ELM的城市轨道交通工程投资估算方法研究[J]. 铁道科学与工程学报,2019,16(7): 1842-1848. ZHANG Feilian, LIANG Xiufeng. Research on investment estimation method of urban rail transit project based on GA-ELM[J]. Journal of Railway Science and Engineering, 2019, 16(7): 1842-1848.
[2]	段晓晨,孟春成,施振东,等. 地铁车站建设投资智能预测与控制方法研究[J]. 铁道工程学报,2021,38(9): 106-111. doi: 10.3969/j.issn.1006-2106.2021.09.018 DUAN Xiaochen, MENG Chuncheng, SHI Zhendong, et al. Research on the intelligent forecast and control method of metro station construction investment[J]. Journal of Railway Engineering Society, 2021, 38(9): 106-111. doi: 10.3969/j.issn.1006-2106.2021.09.018
[3]	巫玲玲. 城市轨道交通经济指标统计及其影响因素分析[J]. 施工技术,2020,49(增1): 1432-1436. WU Lingling. Economic index statistics of urban rail transit and its influencing factors[J]. Construction Technology, 2020, 49(S1): 1432-1436.
[4]	中华人民共和国住房和城乡建设部办公厅. 工程造价改革工作方案[EB/OL]. (2020-07-24) [2023-01-11]. https://www. mohurd. gov. cn/gongkai/fdzdgknr/tzgg/ 202007/20200729_246578. html.
[5]	段晓晨,陈雨欣,施振东,等. 地铁工程建设投资智能估算方法研究[J]. 铁道工程学报,2021,38(11): 109-114. doi: 10.3969/j.issn.1006-2106.2021.11.018 DUAN Xiaochen, CHEN Yuxin, SHI Zhendong, et al. Research on the intelligent estimation method of metro construction investment[J]. Journal of Railway Engineering Society, 2021, 38(11): 109-114. doi: 10.3969/j.issn.1006-2106.2021.11.018
[6]	赵欣. 基于BP神经网络的地铁土建工程造价估算方法研究[D]. 北京:北京交通大学,2008.
[7]	陈进杰. 城市轨道交通项目广义全寿命周期成本理论与应用研究[D]. 北京:北京交通大学,2011.
[8]	杨文成,王圆圆,孙军先. 基于KR-SVM的城市轨道交通建设成本估算评价模型研究[J]. 交通工程,2017,17(3): 40-46. YANG Wencheng, WANG Yuanyuan, SUN Junxian. The research on evaluation model of urban rail transit construction cost based on KR-SVM[J]. Journal of Transportation Engineering, 2017, 17(3): 40-46.
[9]	ELMOUSALAMI H H. Artificial intelligence and parametric construction cost estimate modeling: state-of-the-art review[J]. Journal of Construction Engineering and Management, 2020, 146(1): 03119008.1-03119008.30.
[10]	陈政,郭春,谌桂舟,等. 基于MEC-BP高海拔隧道供氧浓度与劳动强度规律[J]. 西南交通大学学报,2023,58(3): 622-629. CHEN Zheng, GUO Chun, CHEN Guizhou, et al. Oxygen supply concentration and labor intensity of high altitude tunnel based on MEC-BP[J]. Journal of Southwest Jiaotong University, 2023, 58(3): 622-629.
[11]	杨飞,郝晓莉,杨建,等. 基于多车型CNN-GRU性能预测模型的轨道状态评价[J]. 西南交通大学学报,2023,58(2): 322-331. YANG Fei, HAO Xiaoli, YANG Jian, et al. Track condition evaluation for multi-vehicle performance prediction model based on convolutional neural network and gated recurrent unit[J]. Journal of Southwest Jiaotong University, 2023, 58(2): 322-331.
[12]	王彪,秦勇,贾利民,等. 监测数据驱动的城轨列车轴箱轴承剩余寿命预测[J]. 西南交通大学学报,2024,59(1):229-238. WANG Biao, QIN Yong, JIA Limin, et al. Monitoring data-driven prediction of remaining useful life of axle-box bearings for urban rail transit trains[J]. Journal of Southwest Jiaotong University, 2024, 59(1):229-238.
[13]	HUANG G B, ZHOU H M, DING X J, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics Part B (Cybernetics), 2012, 42(2): 513-529. doi: 10.1109/TSMCB.2011.2168604
[14]	KARACA I, GRANSBERG D D, JEONG H D. Improving the accuracy of early cost estimates on transportation infrastructure projects[J]. Journal of Management in Engineering, 2020, 36(5): 04020063.1-04020063.11.
[15]	SOBOLÁ I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1/2/3): 271-280.
[16]	赵美玲. 基于SPA—Vague集的地铁TOC反馈快速投资估算方法研究[D]. 南昌:华东交通大学,2017.
[17]	刘丹. 城市轨道交通工程造价控制分析[J]. 铁道工程学报,2014,31(6): 104-108. LIU Dan. Analysis of cost control of urban rail transportation construction[J]. Journal of Railway Engineering Society, 2014, 31(6): 104-108.
[18]	中华人民共和国住房和城乡建设部. 城市轨道交通岩土工程勘察规范:GB 50307—2012[S]. 北京: 中国计划出版社,2012.
[19]	王芳英. 地铁工程综合造价指标解析[J]. 铁路工程造价管理,2012,27(5):33-36. WANG Fangying. Analysis of subway engineering comprehensive cost index[J]. Railway Engineering Cost Management,2012,27(5):33-36.
[20]	中华人民共和国住房和城乡建设部. 地铁设计规范:GB 50157—2013[S]. 北京:中国建筑工业出版社,2013.
[21]	RAFIEI M H, ADELI H. Novel machine-learning model for estimating construction costs considering economic variables and indexes[J]. Journal of Construction Engineering and Management, 2018, 144(12): 04018106.1-04018106.9.
[22]	ROBNIK-ŠIKONJA M, KONONENKO I. Theoretical and empirical analysis of ReliefF and RReliefF[J]. Machine Learning, 2003, 53(1): 23-69.
[23]	段晓晨,孟春成,吴曼茜,等. 地铁车站土建工程施工进度三维动态优化控制[J]. 地下空间与工程学报,2022,18(5): 1678-1688. DUAN Xiaochen, MENG Chuncheng, WU Manxi, et al. 3D dynamic optimal control of civil engineering construction schedule of metro station[J]. Chinese Journal of Underground Space and Engineering, 2022, 18(5): 1678-1688.
[24]	夏英,刘敏. 基于时空注意力卷积神经网络的交通流量预测[J]. 西南交通大学学报,2023,58(2): 340-347. XIA Ying, LIU Min. Traffic flow prediction based on spatial-temporal attention convolutional neural network[J]. Journal of Southwest Jiaotong University, 2023, 58(2): 340-347.
[25]	梅瀚雨,王骑,廖海黎,等. 基于集成式神经网络的扁平箱梁颤振导数预测[J]. 西南交通大学学报,2022,57(4): 894-902. MEI Hanyu, WANG Qi, LIAO Haili, et al. Flutter derivative prediction of flat box girder based on ensembled neural network[J]. Journal of Southwest Jiaotong University, 2022, 57(4): 894-902.