Fast Simulation Method for Pantograph and Overhead Conductor Rail System
-
摘要:
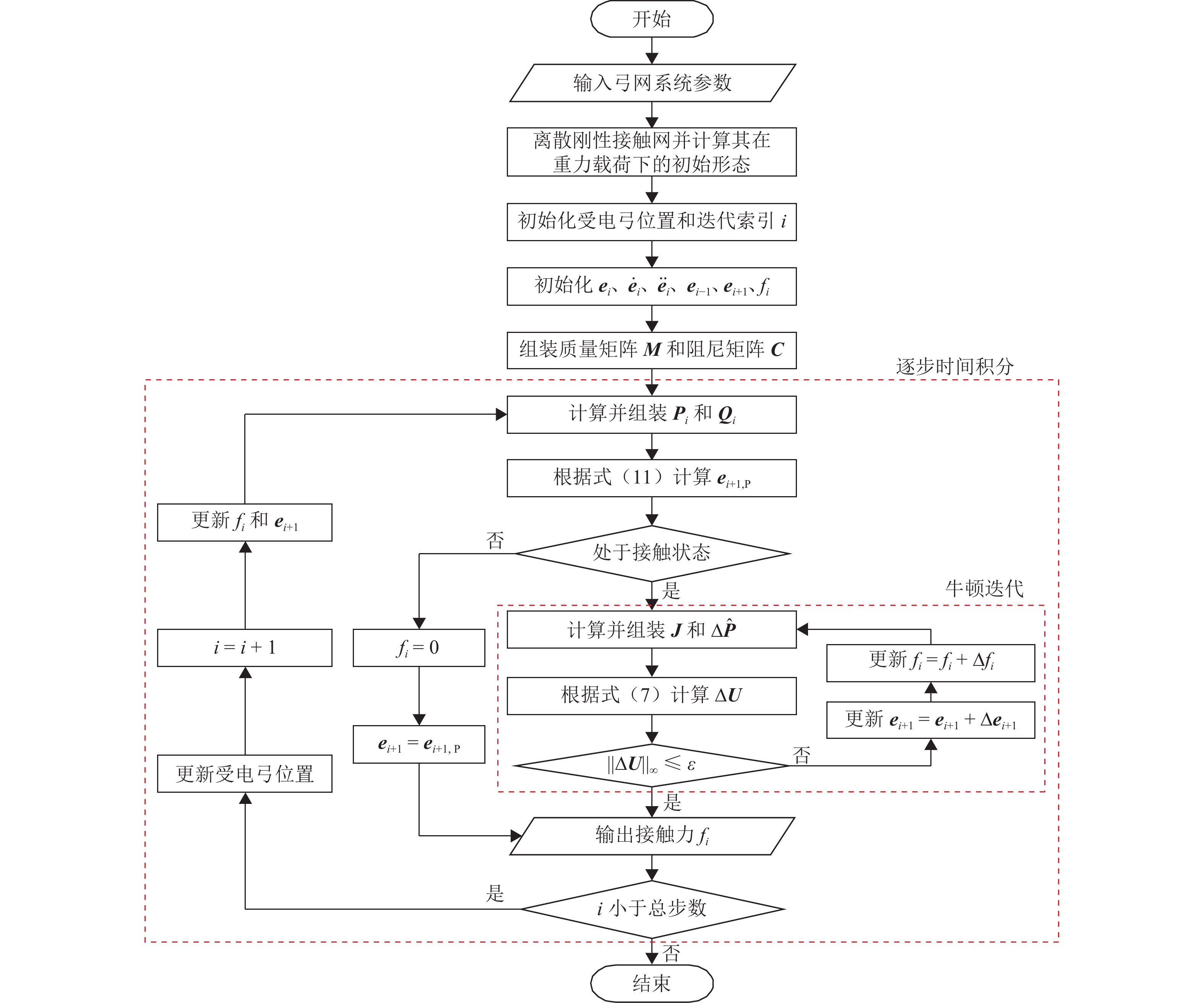
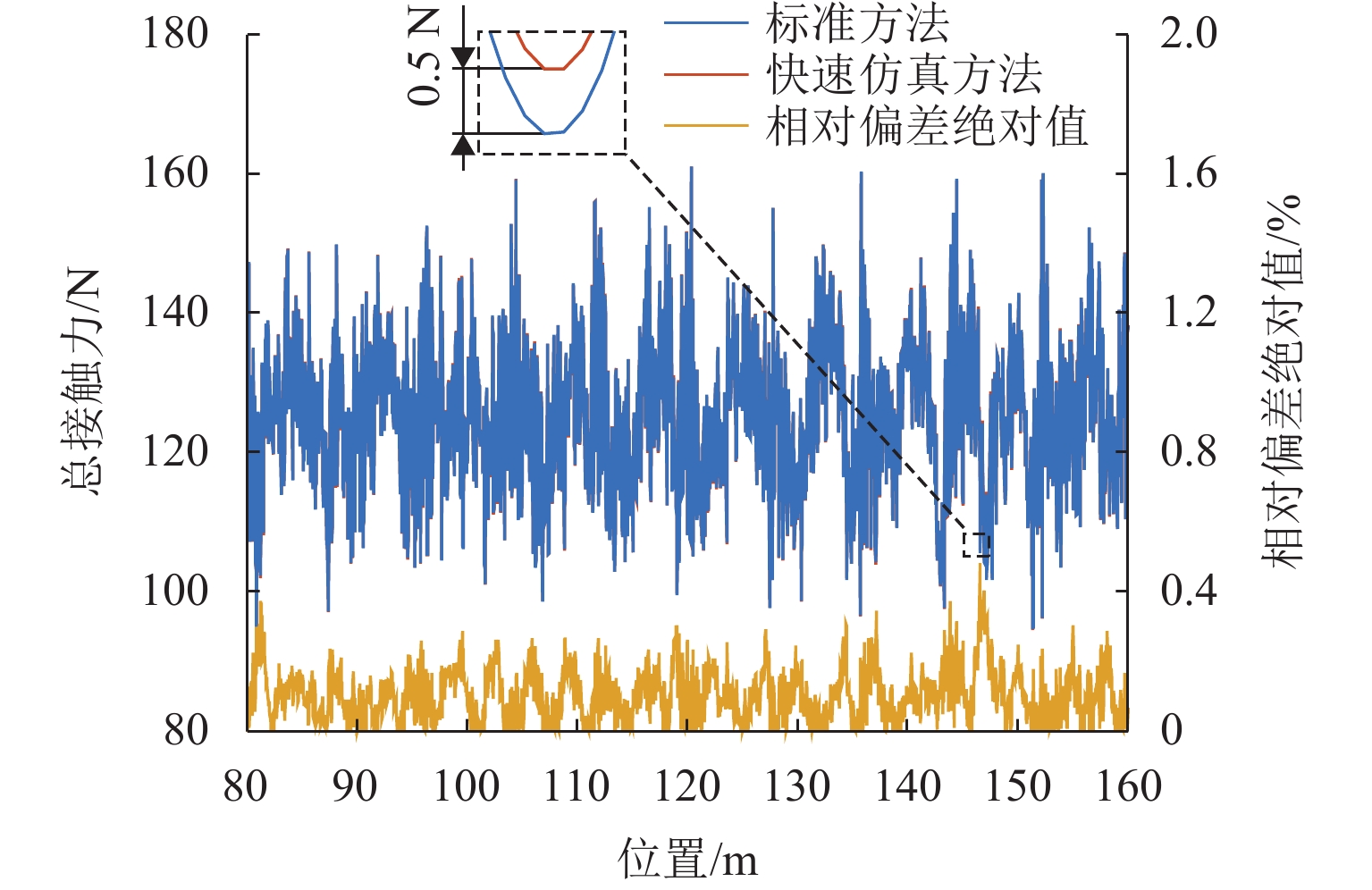
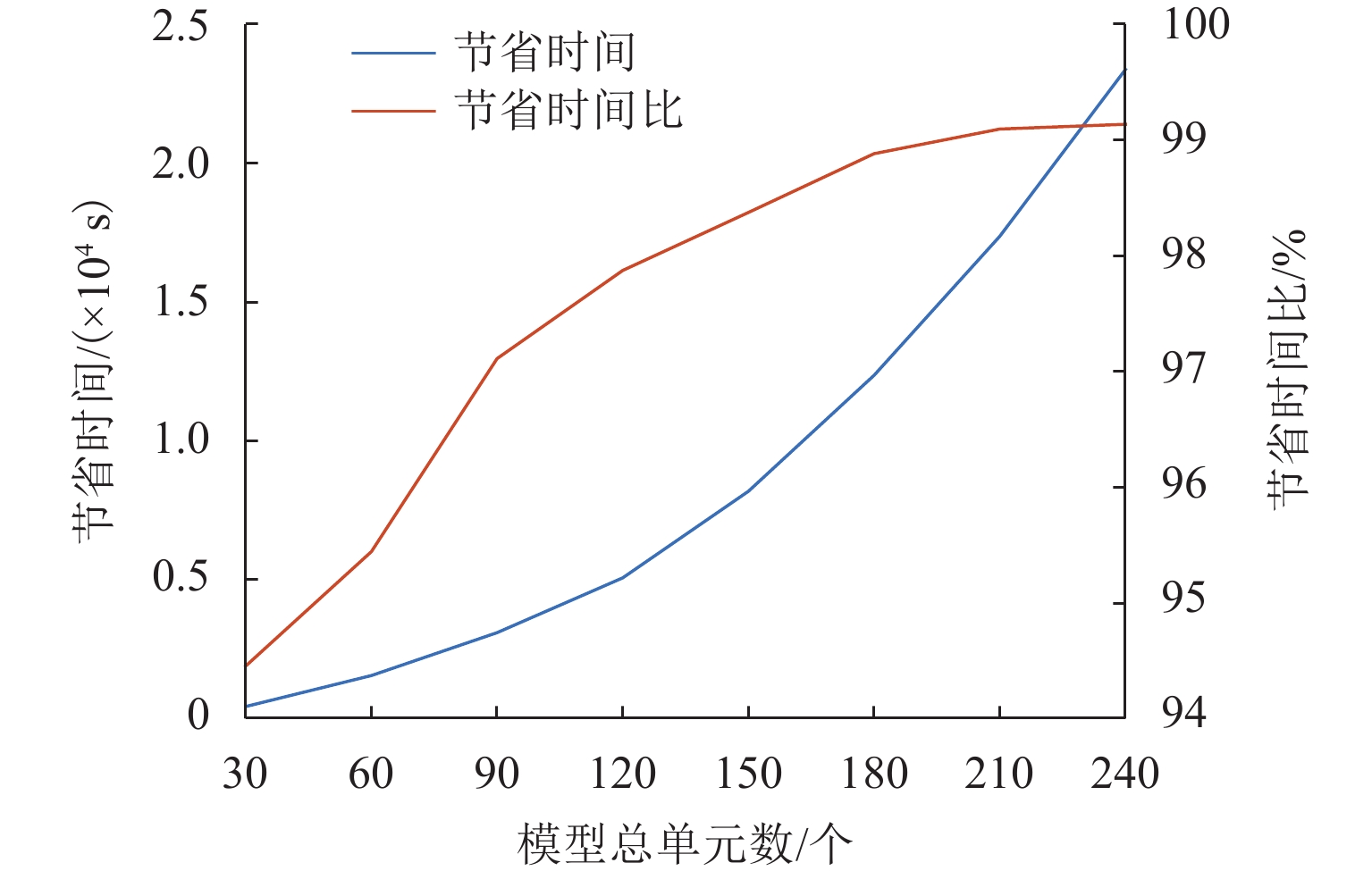
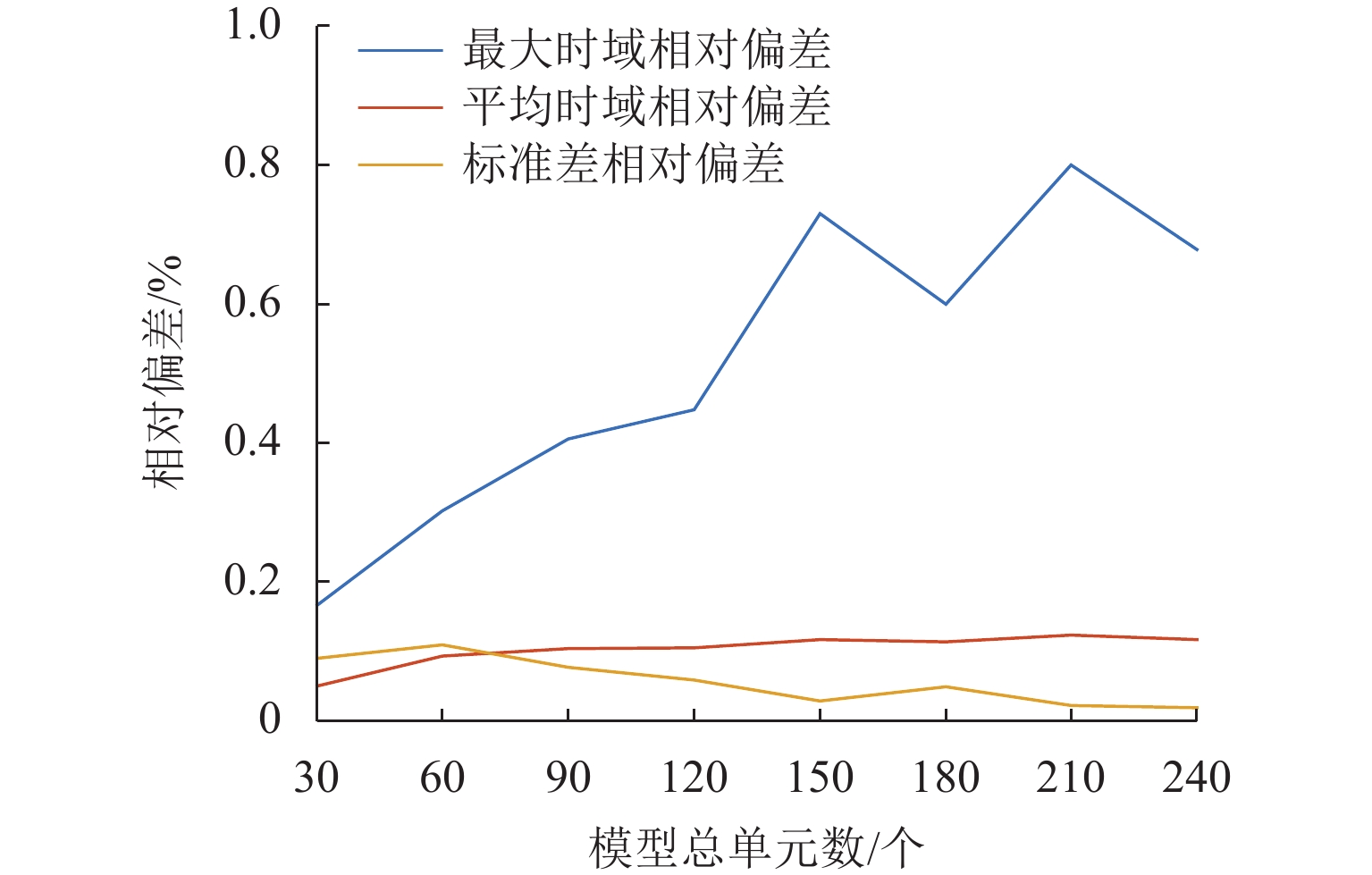
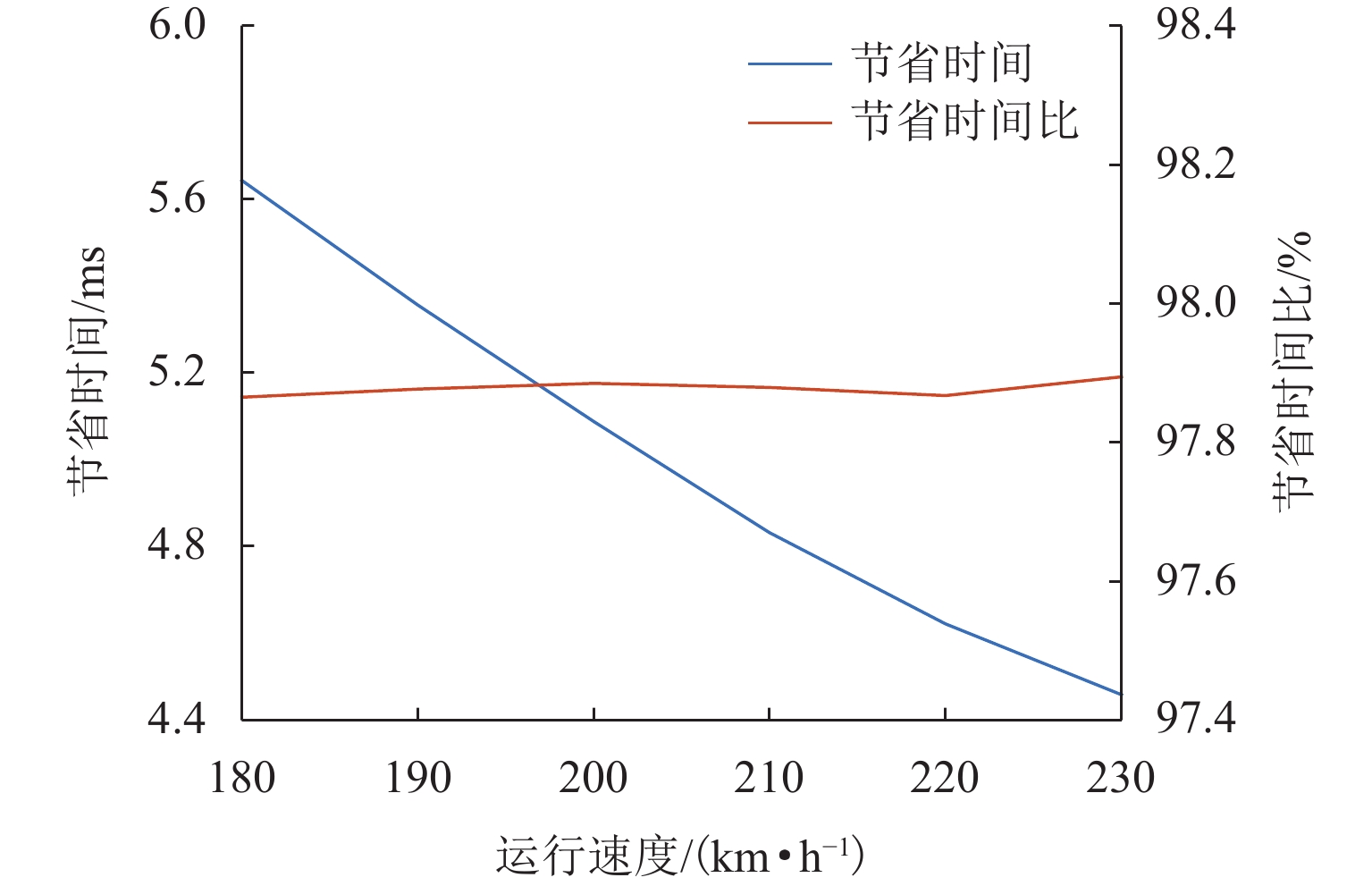
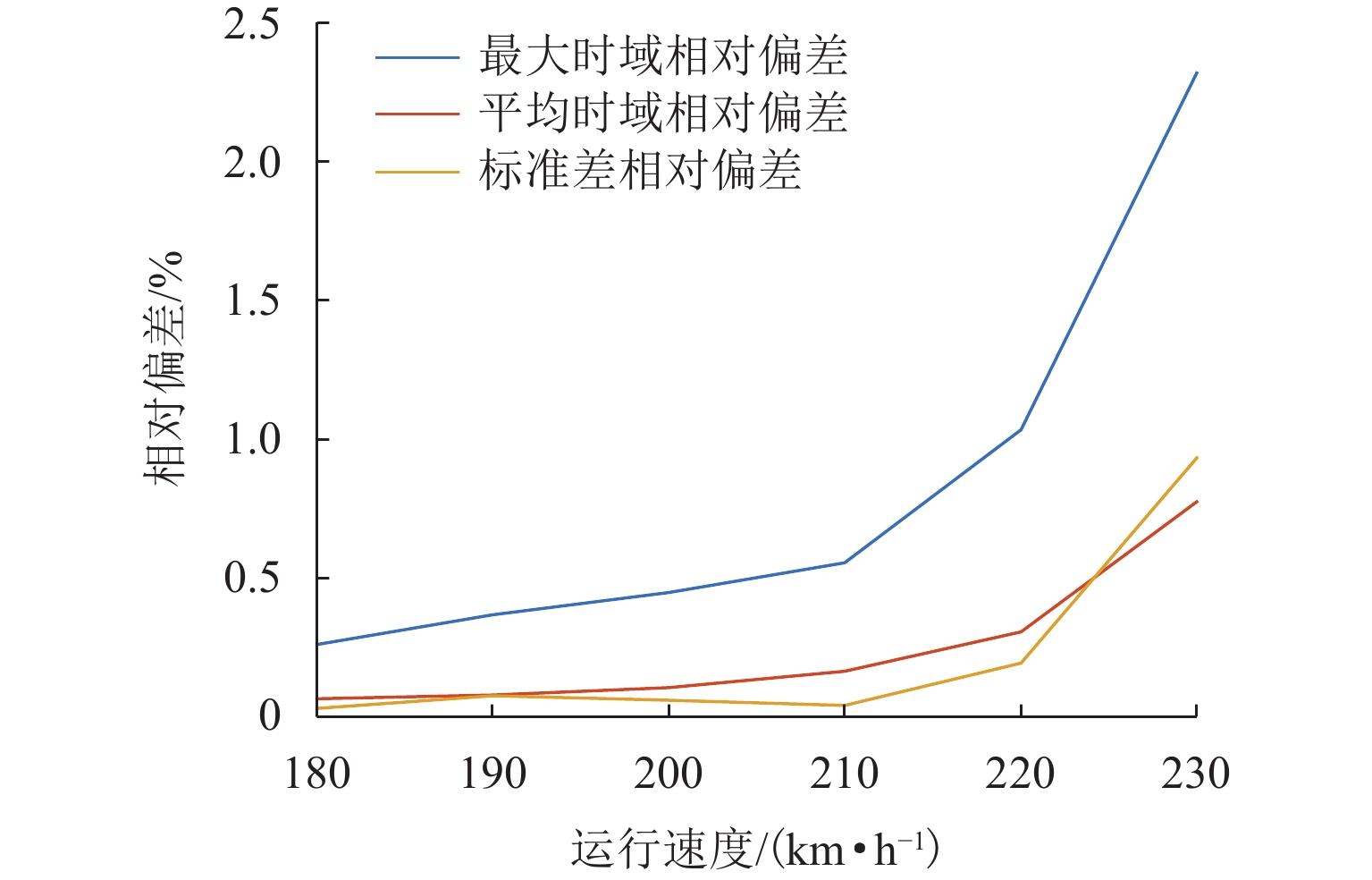
针对当前刚性接触网-受电弓系统有限元模型仿真速度慢、计算时间成本高的问题，对采用三维接触算法的弓网仿真方法与流程进行改进. 首先，采用中心差分思想，将求解弓网接触副相对运动速度时需迭代计算的方程转换为可直接计算的显式方程；然后，将刚性接触网在静平衡处进行线性化处理，以避免刚度矩阵组装耗时，并加快刚性网内力计算；其次，对弓网接触状态进行惰性判断以减少计算量；最后，对本文所提快速仿真方法在不同情况下的计算效率与精度进行分析. 研究结果表明：在30跨8 m跨距的刚性接触网-受电弓仿真算例中，快速仿真方法相比标准仿真方法节省97.67%的仿真时间，且接触力结果最大偏差仅为0.48%；随着模型规模的增大，其节省的时间迅速增加，计算效率优势愈发显著，同时接触力结果偏差均小于1.00%；随着运行速度的提高，所节省的时间占比基本不变，接触力结果偏差略有增大趋势，在230 km/h以下的速度工况中，接触力标准差偏差均小于1.00%.
Abstract:Finite element model simulation of the pantograph and overhead conductor rail (OCR) system is slow, and the time cost of calculation is high. Therefore, the simulation method and process of the pantograph and OCR system using three-dimensional contact formulation were improved. Firstly, the equation that needs to be calculated iteratively when solving the relative velocity of the contact pair between the pantograph and the OCR was replaced with an explicit equation that can be calculated directly based on the central difference method. Then, the OCR model was linearized at the static equilibrium state to avoid the time-consuming stiffness matrix assembly procedure and increase the efficiency when calculating the internal force of the OCR. Next, a lazy judgment strategy was used to estimate the contact state of the pantograph and the OCR to reduce the computational load. Finally, the computational efficiency and accuracy of the fast simulation method in different cases were analyzed. The results show that compared with the standard simulation method, the proposed fast simulation method can save 97.67% of computational time in the example of pantograph and OCR with 30 spans of 8 m, and the maximum error of contact force results is only 0.48%. With the increase in the model scale, the time saved by the fast simulation method increases sharply, and its computational efficiency advantage becomes more and more significant. Meanwhile, the errors of contact force results are all less than 1.00%. With the increase in the operation speed, the proportion of time saved by the fast simulation method remains stable, and the errors of contact force results increase slightly. At speeds under 230 km/h, the standard deviation errors of contact force are all less than 1.00%.
-
图 4 替换后仿真方法各环节耗时占比
Figure 4. Time proportion of each procedure in simulation method after replacing
图 6 刚性接触网-受电弓系统快速仿真流程
Figure 6. Fast simulation flowchart of pantograph and overhead conductor rail system
图 7 快速仿真方法与标准方法结果对比
Figure 7. Comparison of results from fast simulation method and standard method
图 8 快速仿真方法环节耗时占比
Figure 8. Time proportion of each procedure in fast simulation method
图 9 不同规模模型中快速仿真方法节省时间对比
Figure 9. Time saved for models in different scales by fast simulation method
图 11 不同速度下快速仿真方法节省时间对比
Figure 11. Time saved for models at different speeds by fast simulation method
图 12 不同速度下快速仿真方法结果偏差对比
Figure 12. Result error comparison for models at different speeds by fast simulation method
表 1 受电弓参数
Table 1. Parameters of pantograph
自由度 质量/kg 刚度/（N·m−1） 阻尼/（N·s·m−1） 自由度 1 7.12 9430.00 20 自由度 2 6.00 14100.00 20 自由度 3 5.80 0.01 70 
下载: 导出CSV
表 2 各改进措施效果
Table 2. Effect of different improvement measures
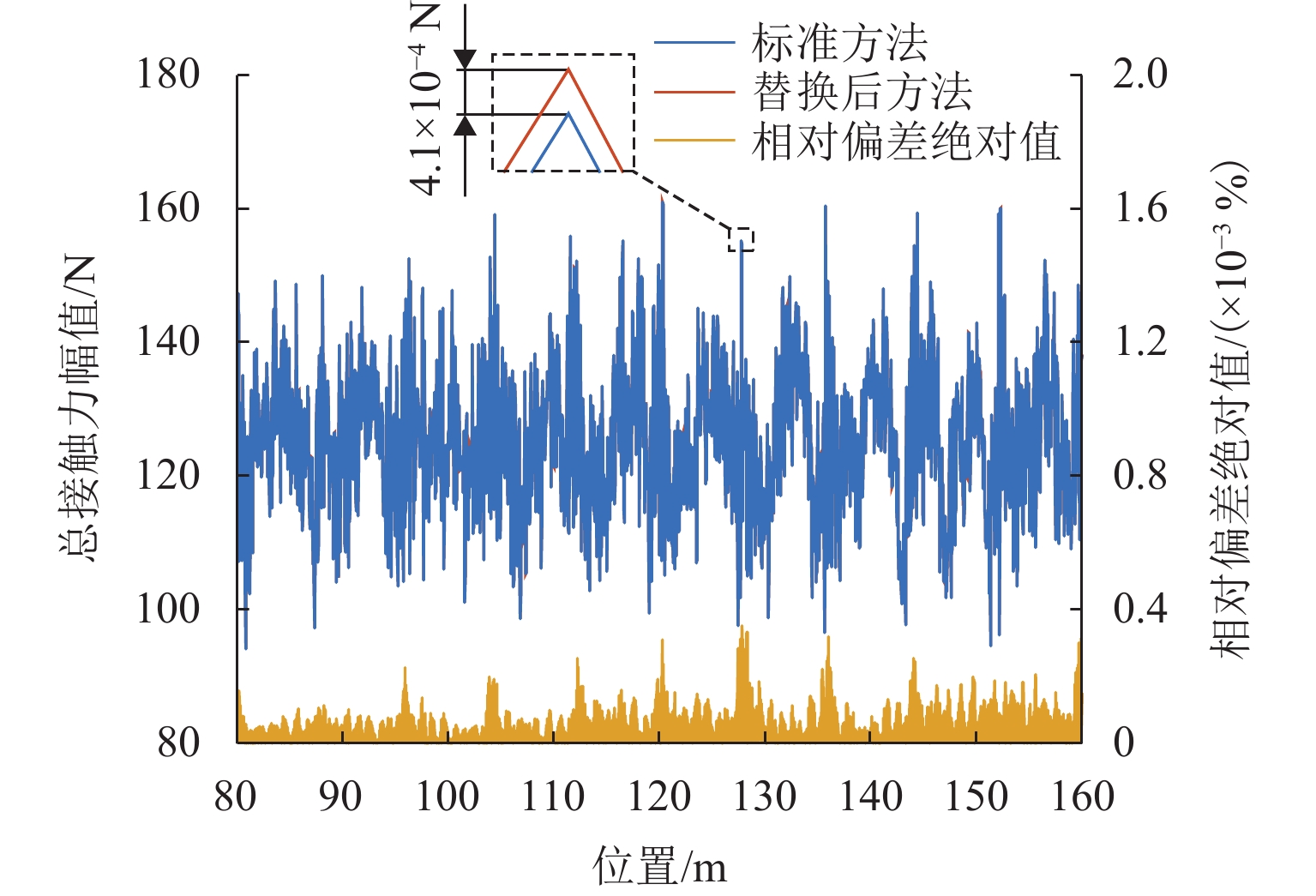
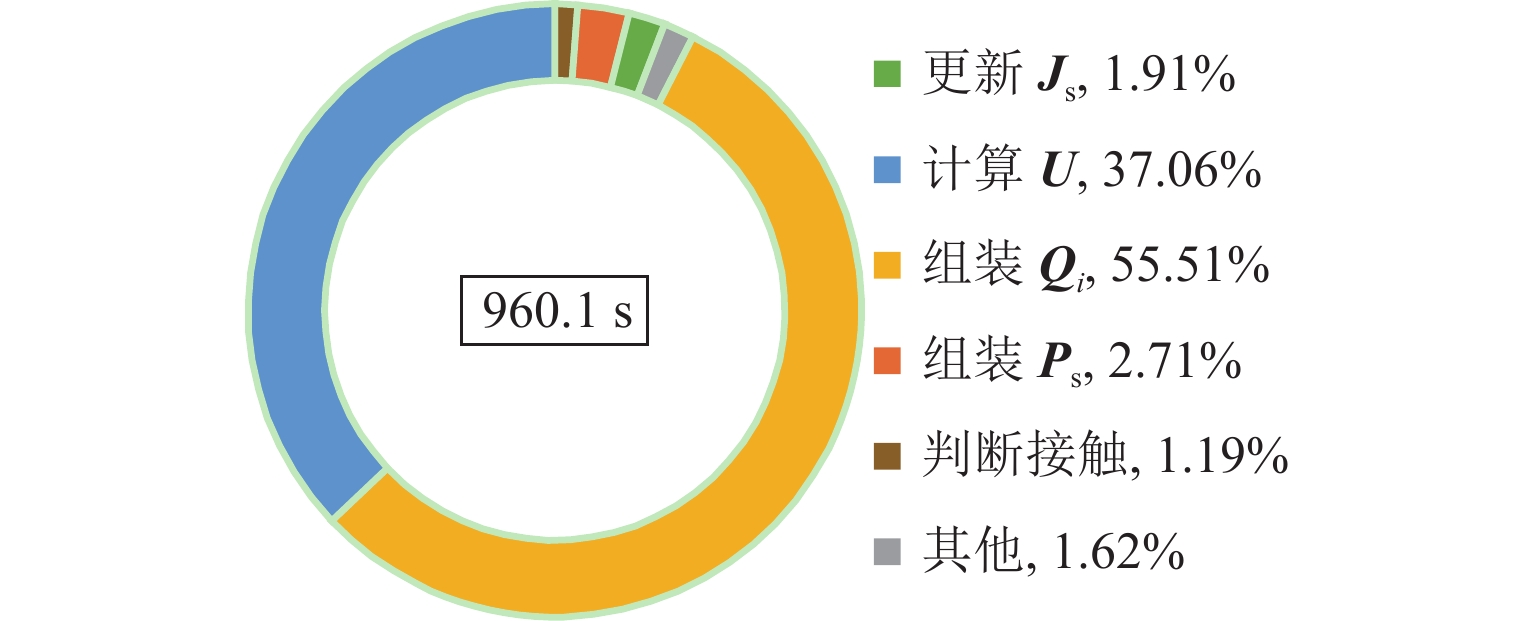
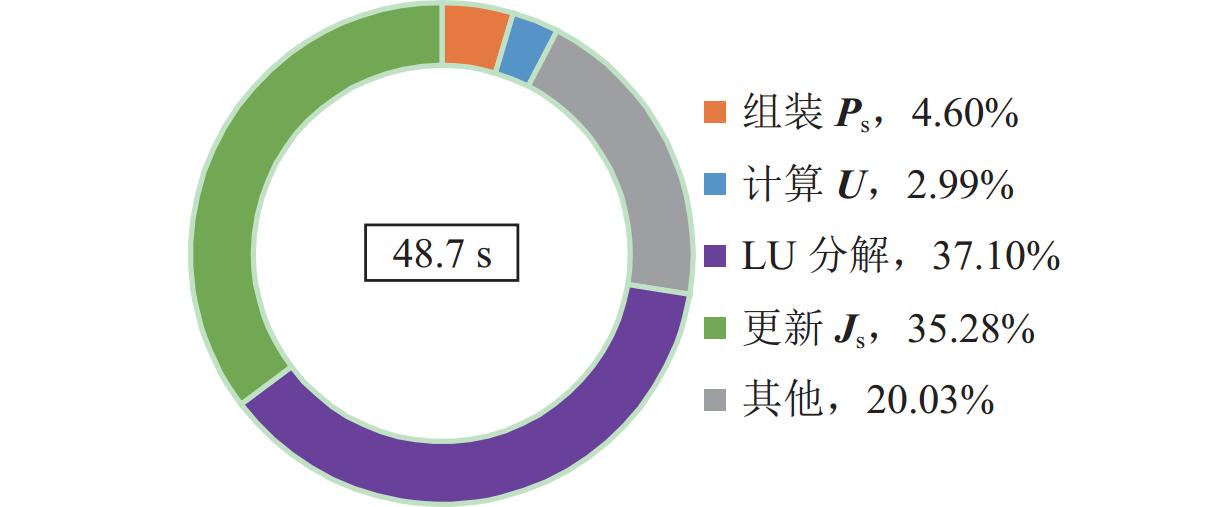
改进方法 总接触力 仿真时间 最大相对偏差/% 平均相对偏差/% 标准差相对偏差/% 耗时/s 节省时间比/% 标准方法 2092.89 ① 3.50 × 10−4 4.80 × 10−5 5.90 × 10−5 960.13 54.12 ① + ② 0.48 0.10 0.06 496.64 76.27 ① + ② + ③ 0.48 0.10 0.06 116.83 94.42 ① + ② + ③ + ④ 0.48 0.10 0.06 56.53 97.30 ① + ② + ③ + ④ + ⑤ 0.48 0.10 0.06 48.75 97.67
下载: 导出CSV
-
[1] 杜智恒. 北京大兴国际机场线160 km/h刚性接触网系统弓网耦合受流质量分析[J]. 城市轨道交通研究,2019,22(12): 157-160.DU Zhiheng. Current collection quality of pantograph-catenary coupling for 160 km/h rigid catenary system on Beijing Daxing international airport express[J]. Urban Mass Transit, 2019, 22(12): 157-160. [2] 何国军. 160 km/h架空刚性接触网技术研究进展及展望[J]. 工程建设与设计,2022,19:131-134.HE Guojun. Research progress and prospect of 160 km/h overhead rigid catenary[J]. Construction & Design for Engineering, 2022, 19: 131-134. [3] 梅桂明,张卫华. 刚性悬挂接触网动力学研究[J]. 铁道学报,2003,25(2): 24-29. doi: 10.3321/j.issn:1001-8360.2003.02.006MEI Guiming, ZHANG Weihua. Study on dynamics of rigid suspension catenary[J]. Journal of the China Railway Society, 2003, 25(2): 24-29. doi: 10.3321/j.issn:1001-8360.2003.02.006 [4] 关金发,田志军,吴积钦. 基于弓网动力学仿真的160 km/h刚柔过渡系统方案研究[J]. 铁道学报,2018,40(9): 48-56. doi: 10.3969/j.issn.1001-8360.2018.09.007GUAN Jinfa, TIAN Zhijun, WU Jiqin. Research of 160 km/h transition structure proposal between overhead conductor rail and contact line based on dynamic simulation[J]. Journal of the China Railway Society, 2018, 40(9): 48-56. doi: 10.3969/j.issn.1001-8360.2018.09.007 [5] SONG Y, ANTUNES P, POMBO J, et al. A methodology to study high-speed pantograph-catenary interaction with realistic contact wire irregularities[J]. Mechanism and Machine Theory, 2020, 152: 103940.1-103940.18. [6] GREGORI S, GIL J, TUR M, et al. Analysis of the overlap section in a high-speed railway catenary by means of numerical simulations[J]. Engineering Structures, 2020, 221: 110963.1-110963.14. [7] 周宁,邹欢,邹栋,等. 城市轨道交通弓网系统仿真模型适应性研究[J]. 西南交通大学学报,2017,52(2): 408-415,423. doi: 10.3969/j.issn.0258-2724.2017.02.026ZHOU Ning, ZOU Huan, ZOU Dong, et al. Investigation on the applicability of pantograph and catenary model urban railway system[J]. Journal of Southwest Jiaotong University, 2017, 52(2): 408-415,423. doi: 10.3969/j.issn.0258-2724.2017.02.026 [8] SONG Y, ZHANG M J, ØISETH O, et al. Wind deflection analysis of railway catenary under crosswind based on nonlinear finite element model and wind tunnel test[J]. Mechanism and Machine Theory, 2022, 168: 104608.1-104608.22. [9] 吴凡平,徐钊,刘志刚,等. 山区峡谷地形风场下柔性接触网风振特性研究[J]. 铁道学报,2021,43(5): 47-61. doi: 10.3969/j.issn.1001-8360.2021.05.006WU Fanping, XU Zhao, LIU Zhigang, et al. Research on wind-induced vibration of flexible catenary under canyon terrain wind[J]. Journal of the China Railway Society, 2021, 43(5): 47-61. doi: 10.3969/j.issn.1001-8360.2021.05.006 [10] 熊嘉铭,徐钊,鲁小兵,等. 曲线区段受电弓-接触网系统建模及动态性能分析[J]. 铁道学报,2022,44(8): 25-35. doi: 10.3969/j.issn.1001-8360.2022.08.003XIONG Jiaming, XU Zhao, LU Xiaobing, et al. Modeling and dynamic performance analysis of pantograph-catenary system in curved railway track[J]. Journal of the China Railway Society, 2022, 44(8): 25-35. doi: 10.3969/j.issn.1001-8360.2022.08.003 [11] BAUTISTA A, MONTESINOS J, PINTADO P. Dynamic interaction between pantograph and rigid overhead lines using a coupled FEM—multibody procedure[J]. Mechanism and Machine Theory, 2016, 97: 100-111. doi: 10.1016/j.mechmachtheory.2015.10.009 [12] VERA C, SUAREZ B, PAULIN J, et al. Simulation model for the study of overhead rail current collector systems dynamics, focused on the design of a new conductor rail[J]. Vehicle System Dynamics, 2006, 44(8): 595-614. doi: 10.1080/00423110500165499 [13] CHOVER J A, SUAREZ B, RODRIGUEZ P. Simulation techniques for design of overhead conductor rail lines for speeds over 140 km/h[C]//Proceedings of the 22nd International Symposium on Dynamics of Vehicles on Roads and Tracks (IAVSD 2011). Manchester: [s.n.], 2011: 14-19. [14] CHEN L, DUAN F C, SONG Y, et al. Assessment of dynamic interaction performance of high-speed pantograph and overhead conductor rail system[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 71: 9001914.1-9001914.14. [15] 周宁,王俊东,刘跃平,等. 基于图像处理技术检测弓网接触力的新方法[J]. 西南交通大学学报,2023,58(1): 1-8,57. doi: 10.3969/j.issn.0258-2724.20210509ZHOU Ning, WANG Jundong, LIU Yueping, et al. Image processing based method for measuring contact force in pantograph-catenary system[J]. Journal of Southwest Jiaotong University, 2023, 58(1): 1-8,57. doi: 10.3969/j.issn.0258-2724.20210509 [16] 关金发. 受电弓与刚性接触网动力相互作用研究[D]. 成都: 西南交通大学,2016. [17] 唐浩. AC25kV刚性接触网若干关键技术研究[D]. 成都: 西南交通大学,2018. [18] 田珂,高仕斌,于金鑫. 基于ADAMS的地铁弓网耦合仿真分析[J]. 电气化铁道,2018,29(5): 51-54. [19] 代洪宇. 200 km/h交流刚性接触网方案研究[D]. 成都: 西南交通大学,2019. [20] MASSAT J P, LAINE J P, BOBILLOT A. Pantograph-catenary dynamics simulation[J]. Vehicle System Dynamics, 2006, 44(S1): 551-559. [21] KULKARNI S, PAPPALARDO C M, SHABANA A A. Pantograph/catenary contact formulations[J]. Journal of Vibration and Acoustics, 2017, 139(1): 011010.1-011010.12. [22] CHEN L, DUAN F C, SONG Y, et al. Three-dimensional contact formulation for assessment of dynamic interaction of pantograph and overhead conductor rail system[J]. Vehicle System Dynamics, 2023, 61(9): 2432-2455. doi: 10.1080/00423114.2022.2112607 [23] PAPPALARDO C M, PATEL M D, TINSLEY B, et al. Contact force control in multibody pantograph/catenary systems[J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-Body Dynamics, 2016, 230(4): 307-328. doi: 10.1177/1464419315604756 [24] SONG Y, LIU Z G, WANG H R, et al. Nonlinear modelling of high-speed catenary based on analytical expressions of cable and truss elements[J]. Vehicle System Dynamics, 2015, 53(10): 1455-1479. doi: 10.1080/00423114.2015.1051548 [25] COLLINA A, BRUNI S. Numerical simulation of pantograph-overhead equipment interaction[J]. Vehicle System Dynamics, 2002, 38(4): 261-291. doi: 10.1076/vesd.38.4.261.8286 [26] CARPENTER N J, TAYLOR R L, KATONA M G. Lagrange constraints for transient finite element surface contact[J]. International Journal for Numerical Methods in Engineering, 1991, 32(1): 103-128. doi: 10.1002/nme.1620320107 [27] ZHANG W H, MEI G M, WU X J, et al. Hybrid simulation of dynamics for the pantograph-catenary system[J]. Vehicle System Dynamics, 2002, 38(6): 393-414. doi: 10.1076/vesd.38.6.393.8347 [28] FACCHINETTI A, GASPARETTO L, BRUNI S. Real-time catenary models for the hardware-in-the-loop simulation of the pantograph-catenary interaction[J]. Vehicle System Dynamics, 2013, 51(4): 499-516. doi: 10.1080/00423114.2012.748920 [29] GIL J, TUR M, CORRECHER A, et al. Hardware-in-the-loop pantograph tests using analytical catenary models[J]. Vehicle System Dynamics, 2022, 60(10): 3504-3518. doi: 10.1080/00423114.2021.1962538 [30] JIMENEZ-OCTAVIO J R, CARNICERO A, SANCHEZ-REBOLLO C, et al. A moving mesh method to deal with cable structures subjected to moving loads and its application to the catenary-pantograph dynamic interaction[J]. Journal of Sound and Vibration, 2015, 349: 216-229. doi: 10.1016/j.jsv.2015.03.051 [31] SONG Y, LIU Z G, XU Z, et al. Developed moving mesh method for high-speed railway pantograph-catenary interaction based on nonlinear finite element procedure[J]. International Journal of Rail Transportation, 2019, 7(3): 173-190. doi: 10.1080/23248378.2018.1532330 [32] GREGORI S, TUR M, NADAL E, et al. Fast simulation of the pantograph-catenary dynamic interaction[J]. Finite Elements in Analysis and Design, 2017, 129: 1-13. doi: 10.1016/j.finel.2017.01.007 [33] MEI G M. Tribological performance of rigid overhead lines against pantograph sliders under DC passage[J]. Tribology International, 2020, 151: 106538.1-106538.9. [34] BERZERI M, SHABANA A A. Development of simple models for the elastic forces in the absolute nodal co-ordinate formulation[J]. Journal of Sound and Vibration, 2000, 235(4): 539-565. doi: 10.1006/jsvi.1999.2935 -
下载:
点击查看大图
计量
- 文章访问数: 121
- HTML全文浏览量: 101
- PDF下载量: 23
- 被引次数: 0