Shape Analysis of Main Cable of Single Tower Suspension Bridge with Unilateral Spatial Cable Plane and Curved Beam
-
摘要:
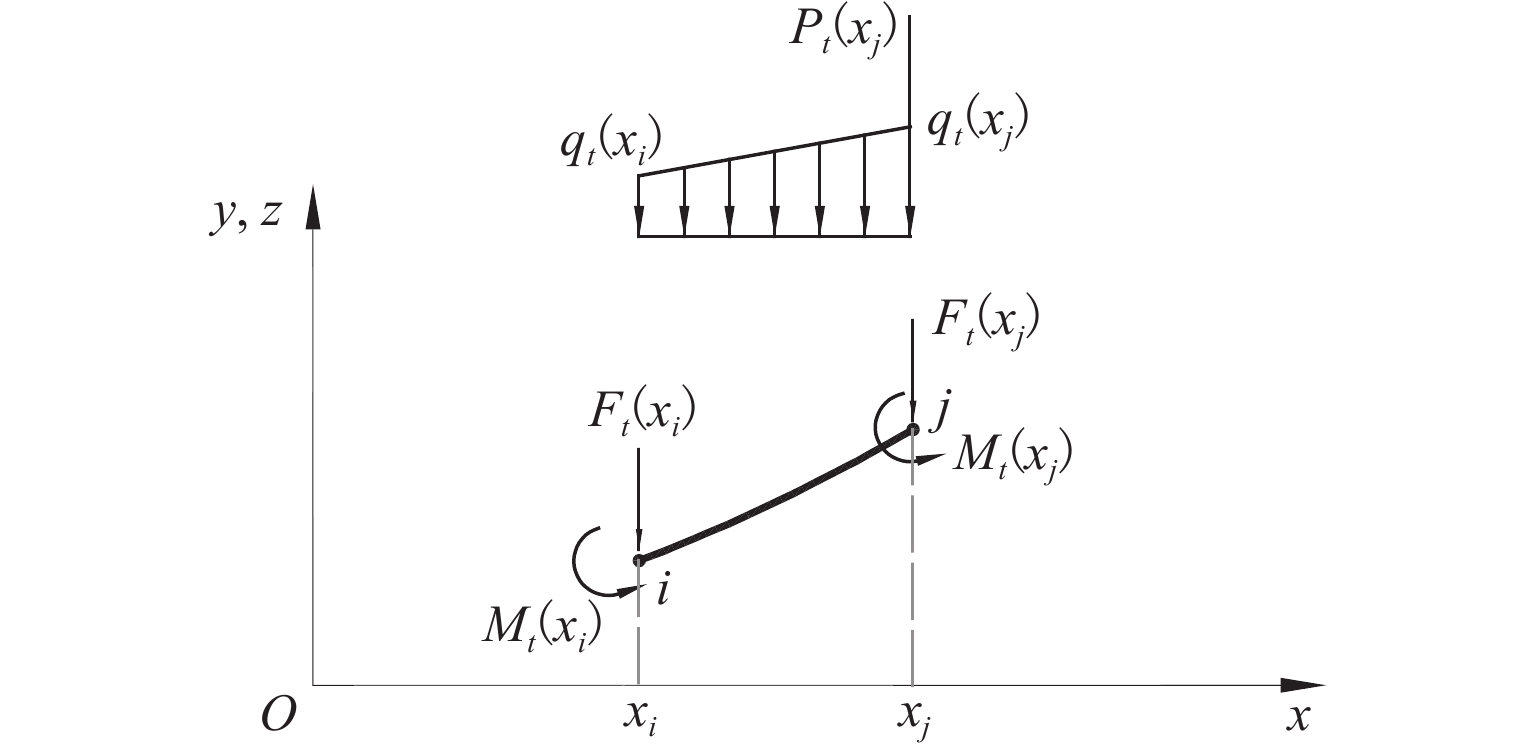
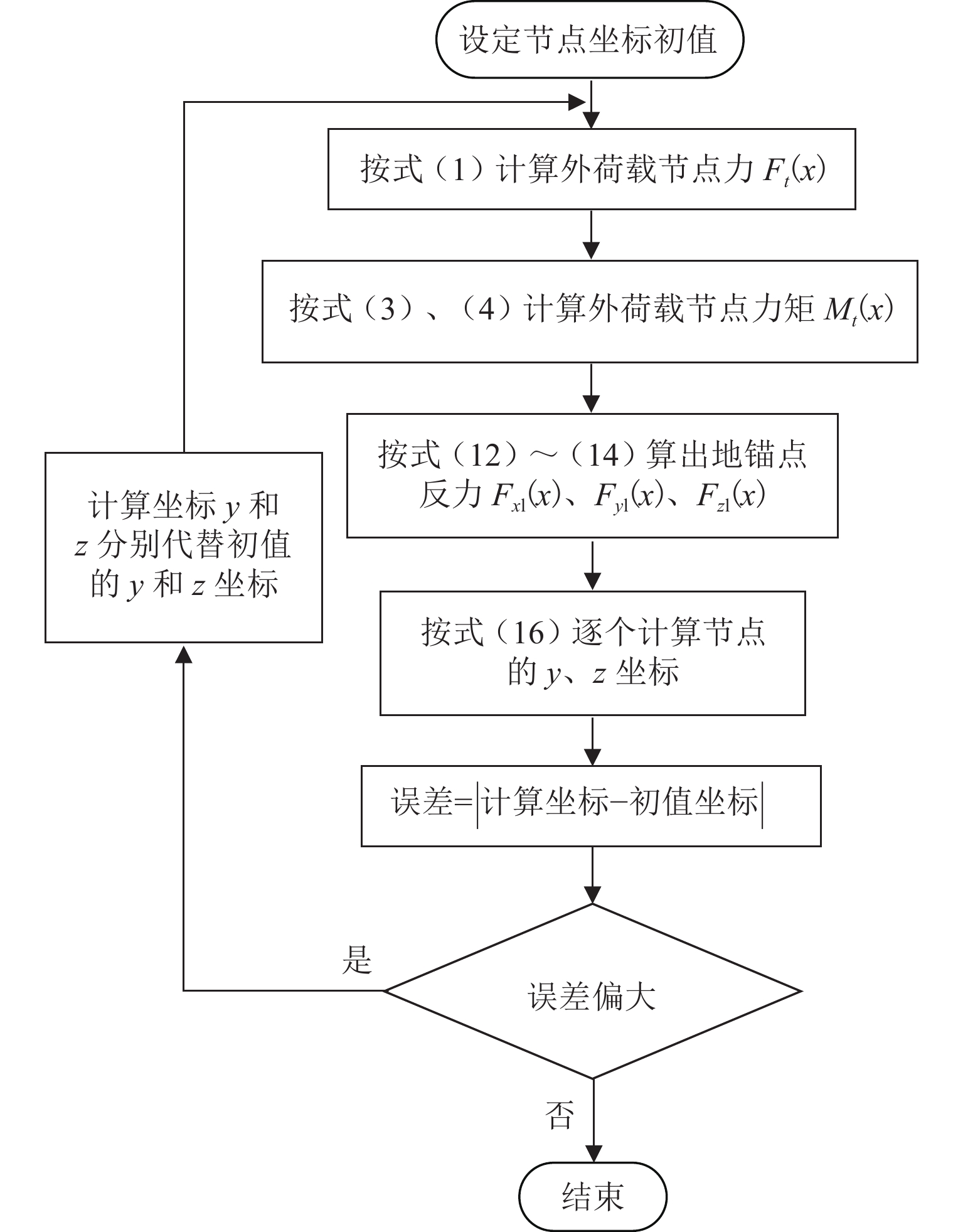
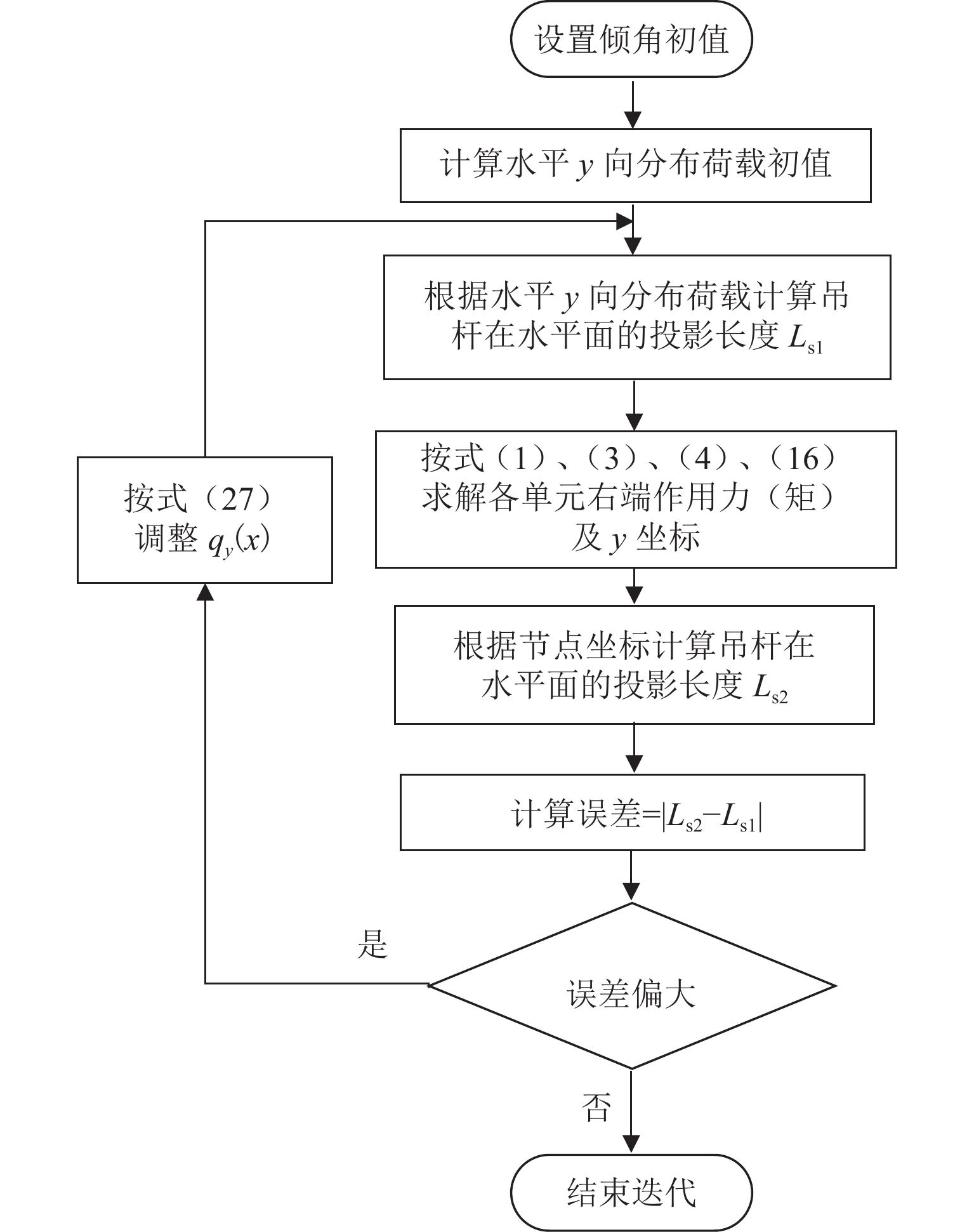
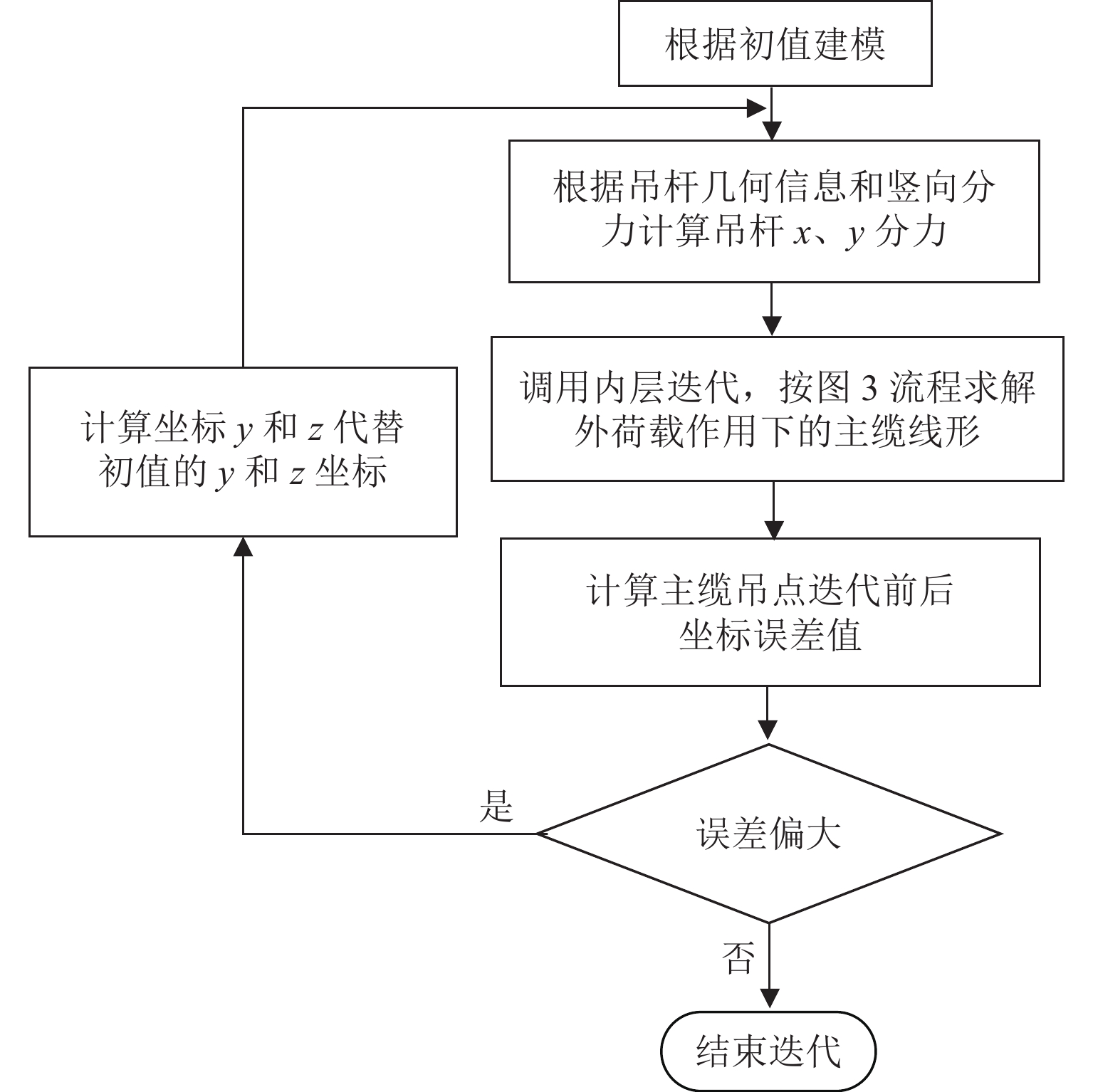
目前空间索面悬索桥主缆成桥线形分析方法需要进行复杂的主缆微分方程求解,具有约束方程形式复杂、迭代收敛性受初值影响大等不足. 为解决主缆线形求解过程收敛性问题,本文借鉴等代梁法思路,推导得到外荷载与主缆线形的几何关联方程,并进一步构造出求解空间主缆线形的两阶段分析方法:在粗算阶段,通过解耦处理将初值要求降到最低,得到“具有足够精度且确保收敛”的结果,作为精算阶段初值;在精算阶段,采用迭代计算得到空间主缆线形精确解. 通过人行悬索桥算例验证两阶段分析方法的可行性和有效性,并使用有限元软件验证计算成果精度. 研究成果表明:本文所提出的方法对初值要求低,无需专门构造初值,迭代循环剔除了变形相容条件及无应力长度计算,求解效率更高,并且能快速收敛得到主缆线形精确解,适用于单边空间索面曲梁独塔悬索桥主缆成桥线形分析.
Abstract:The current analysis method for the main cable shape of a suspension bridge with a spatial cable plane involves solving complex differential equations for the main cable. However, this approach has certain drawbacks, such as the complicated form of constraint equations and the significant influence of initial values on iterative convergence. To address these issues and improve convergence in determining the main cable shape, the equivalent beam method was used, and geometric correlation equations between external loads and the main cable shape were derived. Subsequently, a two-stage analysis method was developed to solve the spatial main cable shape: During the rough calculation stage, decoupling processing minimized initial value requirements while obtaining accurate results with sufficient convergence. These results were then used as initial values in the precise calculation stage to iteratively calculate an exact solution for the spatial main cable shape. The feasibility and effectiveness of this two-stage analysis method were demonstrated through an example involving a pedestrian suspension bridge, and finite element software was used to verify the accuracy of calculation results. The research results demonstrate that the proposed method exhibits lower requirements for initial values and does not require the setting of initial values. The iterative process eliminates deformation compatibility conditions and stress-free length calculation, resulting in enhanced solving efficiency and rapid convergence towards obtaining an accurate solution for the main cable shape. This approach is suitable for analyzing the main cable shape of a single tower suspension bridge with a unilateral spatial cable plane.
-
表 1 精算阶段迭代计算情况
Table 1. Calculation iteration in precise calculation stage
轮次 坐标偏差
组合值/mm吊杆 x 轴向
分力差值/kN吊杆 y 轴向
分力差值/kN1 62.0 0.0197 1.1095 2 1.0 0.0194 1.1095 3 0.1 0 0.0935 4 7.1×10−3 9.7000×10−8 0.0263 5 1.6×10−3 2.6000×10−8 0.0073 -
[1] 花炳灿. 悬浮在湖面上的飘带: 迪斯尼湖畔公园景观人行桥项目设计[J]. 建筑技艺,2014(5):84-86. [2] 李立斌,王立彬,李建慧. 单索面曲梁悬索人行桥主缆线形分析[J]. 铁道科学与工程学报,2017,14(10):2162-2169. doi: 10.3969/j.issn.1672-7029.2017.10.018LI Libin, WANG Libin, LI Jianhui. Cable shape analysis of curved suspension footbridge with single cable plane[J]. Journal of Railway Science and Engineering,2017,14(10):2162-2169. doi: 10.3969/j.issn.1672-7029.2017.10.018 [3] 屈红伟. 和美桥独斜塔单索面曲线悬索步道桥体系转换[J]. 福建建设科技,2022(6):108-112. doi: 10.3969/j.issn.1006-3943.2022.06.026QU Hongwei. Hemei bridge single leaning tower single cable plane curve suspension trail bridge system conversion[J]. Fujian Construction Science & Technology,2022(6):108-112. doi: 10.3969/j.issn.1006-3943.2022.06.026 [4] 唐茂林. 大跨度悬索桥空间几何非线性分析与软件开发[D]. 成都: 西南交通大学, 2003. [5] 罗喜恒,肖汝诚,项海帆. 空间缆索悬索桥的主缆线形分析[J]. 同济大学学报(自然科学版),2004,32(10):1349-1354. doi: 10.3321/j.issn:0253-374X.2004.10.017LUO Xiheng, XIAO Rucheng, XIANG Haifan. Cable shape analysis of suspension bridge with spatial cables[J]. Journal of Tongji University (Natural Science),2004,32(10):1349-1354. doi: 10.3321/j.issn:0253-374X.2004.10.017 [6] 彭苗. 自锚式悬索桥空间缆索系统的求解方法[J]. 土木工程与管理学报,2011,28(1):24-27. doi: 10.3969/j.issn.2095-0985.2011.01.006PENG Miao. Solution strategy for special spatial-cable self-anchored suspension bridge[J]. Journal of Civil Engineering and Management,2011,28(1):24-27. doi: 10.3969/j.issn.2095-0985.2011.01.006 [7] 齐东春,沈锐利. 悬索桥空间缆索主缆线形的计算方法[J]. 铁道建筑,2013(4):13-16 doi: 10.3969/j.issn.1003-1995.2013.11.05QI Dongchun, SHEN Ruili. Calculation method of main cable shape-finding of suspension bridge with spatial cables[J]. Railway Engineering,2013(4):13-16. doi: 10.3969/j.issn.1003-1995.2013.11.05 [8] 吴月星,周建庭,孙马,等. 空间异形索面悬索桥主缆成桥线形计算方法[J]. 桥梁建设,2020,50(5):37-43. doi: 10.3969/j.issn.1003-4722.2020.05.006WU Yuexing, ZHOU Jianting, SUN Ma, et al. Geometry calculation method for main cables of completed suspension bridge with irregular spatial cable planes[J]. Bridge Construction,2020,50(5):37-43. doi: 10.3969/j.issn.1003-4722.2020.05.006 [9] 邢德华,刘化涤. 基于MATLAB空间索面自锚式悬索桥主缆成桥线形精确计算[J]. 公路,2019,64(6):131-135. [10] 李传习. 现代悬索桥静力非线性理论与实践[M]. 北京: 人民交通出版社,2014: 49-67. [11] 李传习,柯红军,刘海波,等. 空间主缆自锚式悬索桥成桥状态的确定方法[J]. 工程力学,2010,27(5):137-146.LI Chuanxi, KE Hongjun, LIU Haibo, et al. Determination of finished bridge state of self-anchored suspension bridge with spatial cables[J]. Engineering Mechanics,2010,27(5):137-146. [12] 张文明,常佳琦,田根民,等. 不等主跨三塔空间缆索悬索桥主缆线形解析计算方法[J]. 桥梁建设,2022,52(1):109-115. doi: 10.3969/j.issn.1003-4722.2022.01.015ZHANG Wenming, CHANG Jiaqi, TIAN Genmin, et al. An analytical method for main cable shape of three-tower suspension bridge with asymmetrical two main spans and spatial cables[J]. Bridge Construction,2022,52(1):109-115. doi: 10.3969/j.issn.1003-4722.2022.01.015 [13] ZHANG W M, CHANG J Q, TIAN G M. FEM-based shape-finding and force-assessment of suspension bridges via completed loop adjustment[J]. Journal of Bridge Engineering,2022,27(1):4021098.1-4021098.15. [14] 马召宇,许福友,檀永刚. 悬索桥空间缆索实用找形方法[J]. 计算力学学报,2021,38(5):651-657. doi: 10.7511/jslx20200812002MA Zhaoyu, XU Fuyou, TAN Yonggang. A practical method for shape finding of spatial cable curves of suspension bridges[J]. Chinese Journal of Computational Mechanics,2021,38(5): 651-657. doi: 10.7511/jslx20200812002 [15] SONG C L, XIAO R C, SUN B. Improved method for shape finding of long-span suspension bridges[J]. International Journal of Steel Structures,2020,20(1):247-258. doi: 10.1007/s13296-019-00283-7 [16] 李保俊. 柔性人行悬索桥空间索面抗风缆索系统的找形计算方法[J]. 石家庄铁道大学学报(自然科学版),2020,33(1):25-30,81.LI Baojun. Calculation method for the shape-finding of spatial wind cable system on flexible pedestrian suspension bridge[J]. Journal of Shijiazhuang Tiedao University (Natural Science Edition),2020,33(1): 25-30,81. [17] 孙远,罗文孝,刘梅. 基于有限元列式的悬索桥主缆找形算法[J]. 土木工程与管理学报,2018,35(2):116-123. doi: 10.3969/j.issn.2095-0985.2018.02.018SUN Yuan, LUO Wenxiao, LIU Mei. Shape-finding algorithm of the main cable system of suspension bridges based on finite element formulation[J]. Journal of Civil Engineering and Management,2018,35(2):116-123. doi: 10.3969/j.issn.2095-0985.2018.02.018 [18] 刘超,高展. 基于整体力学分析的自锚式悬索桥主缆找形法[J]. 同济大学学报(自然科学版),2020,48(1):1-6. doi: 10.11908/j.issn.0253-374x.19131LIU Chao, GAO Zhan. A method for determining cable shape of a self-anchored suspension bridge based on an overall mechanical analysis[J]. Journal of Tongji University (Natural Science),2020,48(1): 1-6. doi: 10.11908/j.issn.0253-374x.19131 [19] 项海帆. 高等桥梁结构理论[M]. 2版. 北京: 人民交通出版社,2013: 419-421. [20] 李传习,刘光栋,柯红军. 悬索桥主缆系统数值解析法计算的一种收敛算法[J]. 工程力学,2008,25(7):66-73.LI Chuanxi, LIU Guangdong, KE Hongjun. A convergent algorithm for numerical-analytic method of calculating main cable system of suspension bridge[J]. Engineering Mechanics,2008,25(7): 66-73. -





 下载:
下载: