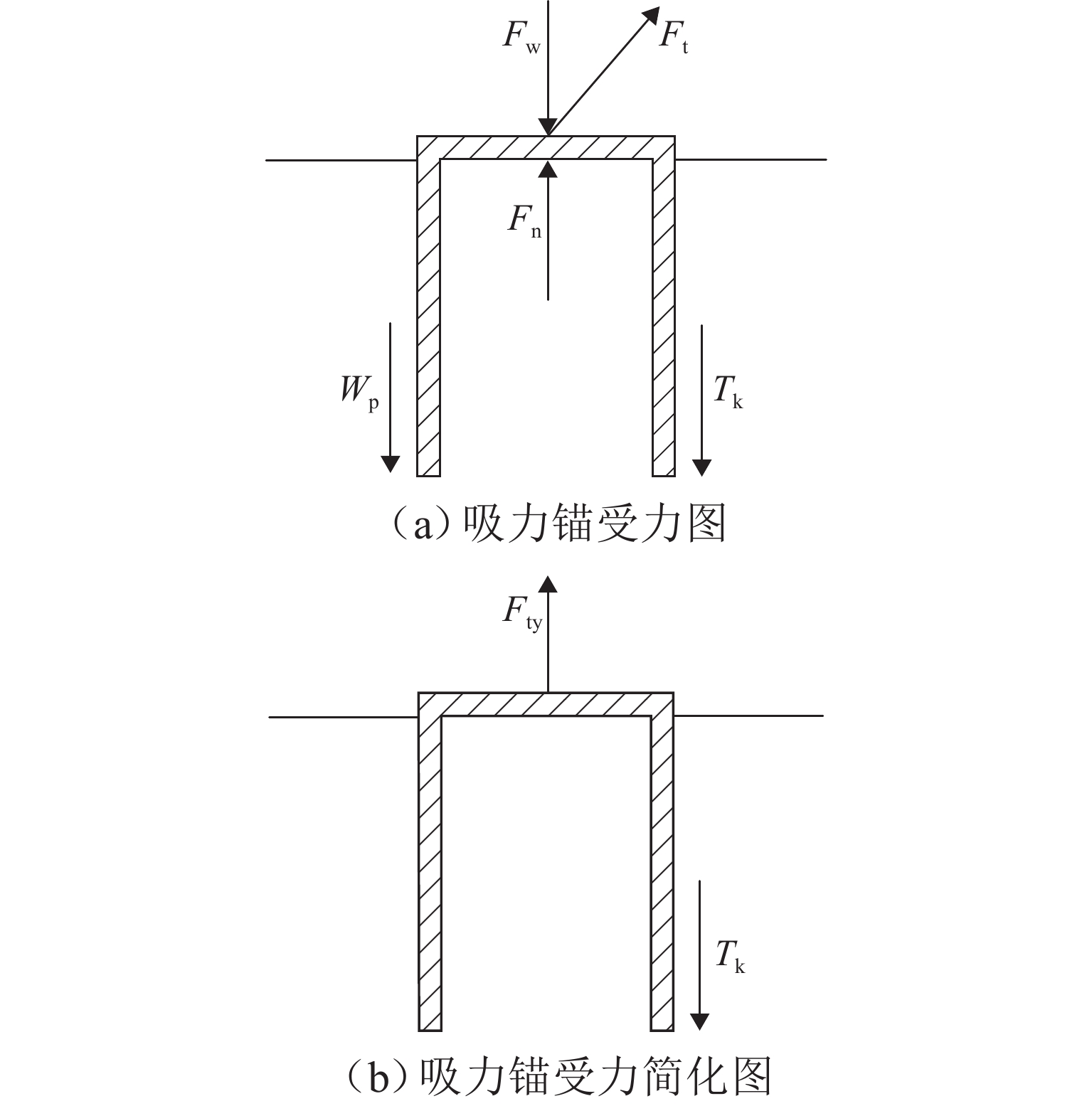
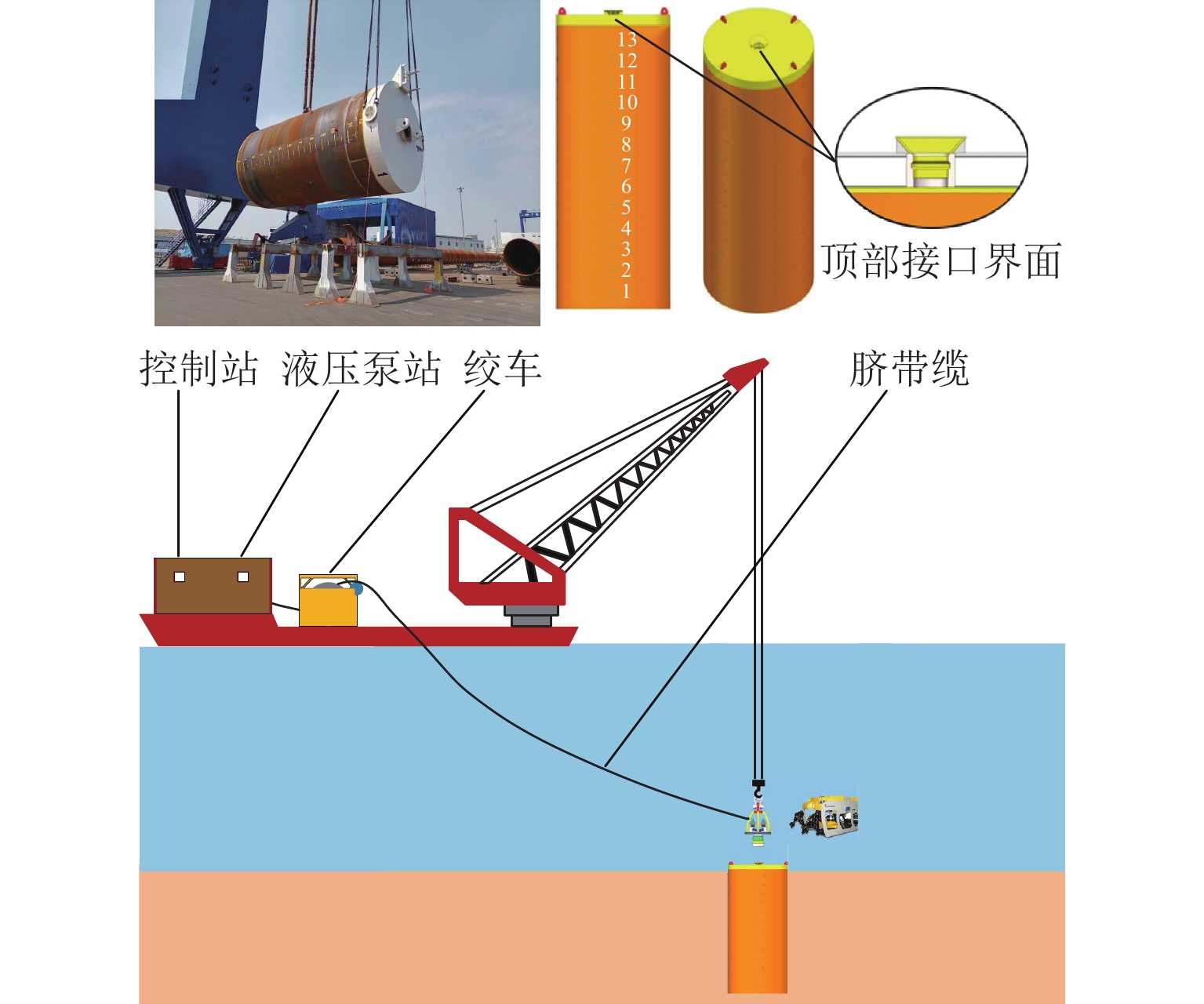
Time-Dependent Reliability Analysis of LS-FA-211001 Suction Anchor Under Cyclic Load
-
摘要:
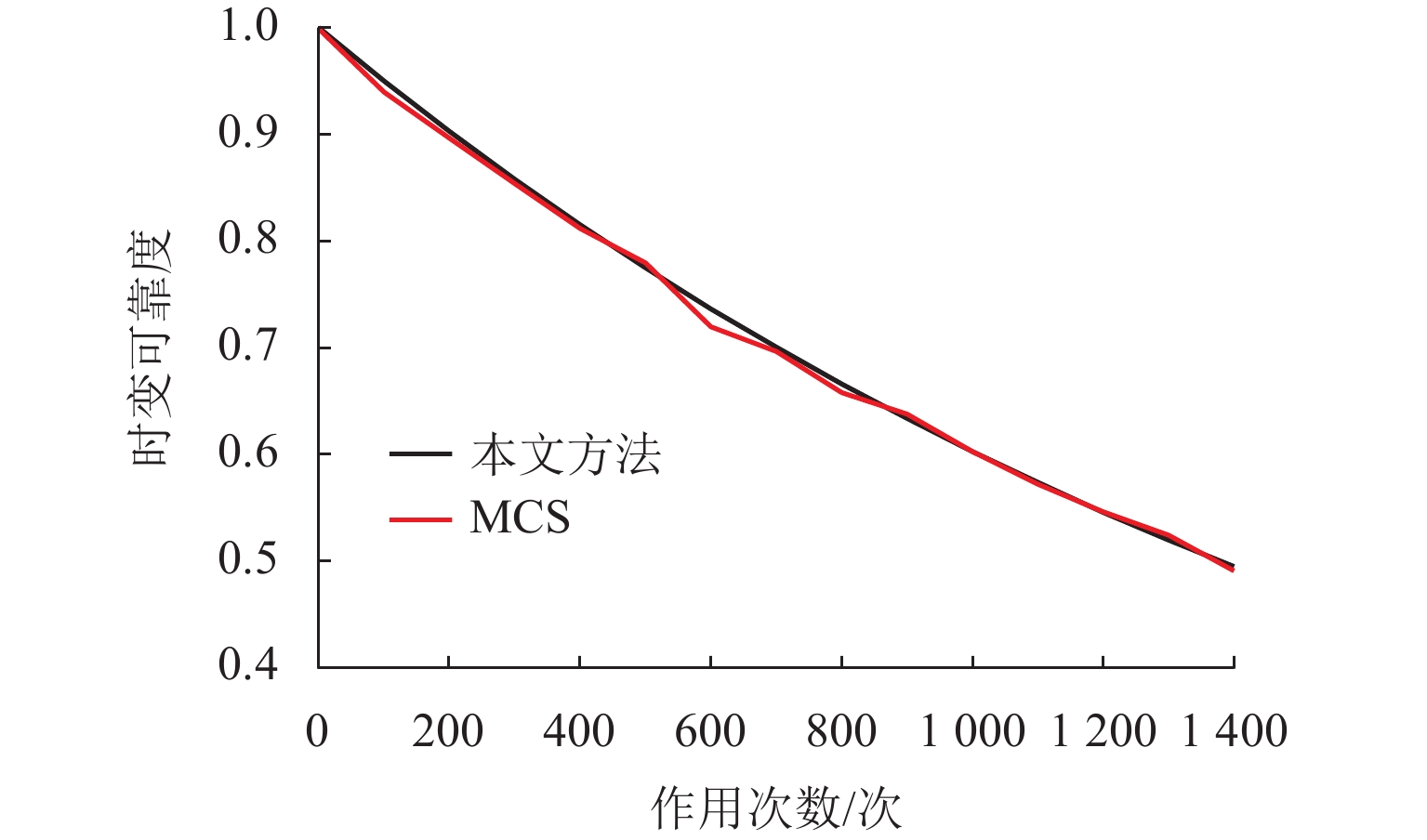
为有效评估在使用过程中LS-FA-211001吸力锚的可靠性水平，考虑外部载荷的累积效应，建立循环载荷作用下的时变可靠性模型；结合LS-FA-211001吸力锚的不确定性量化数据，对其展开时变可靠性分析；利用蒙特卡罗模拟（MCS）方法对吸力锚可靠度进行验证. 结果表明：在可靠度要求95%以上的条件下，LS-FA-211001吸力锚的寿命即使在恶劣勘探点也能达到100次；同时，在循环载荷不同作用次数下，本文建立的吸力锚时变可靠性模型与MCS方法评估出的可靠度结果相比，误差不超过2.15%，验证了本文方法的有效性.
Abstract:To effectively evaluate the reliability level of the LS-FA-211001 suction anchor during application, the cumulative effect of external loads was considered, and a time-dependent reliability model was established under cyclic loads. The time-dependent reliability analysis of the suction anchor was carried out based on the quantified uncertainty data. The Monte Carlo simulation (MCS) method was adopted to verify the reliability of the suction anchor. The results show that the life of LS-FA-211001 suction anchor can reach 100 times even in harsh exploratory points under the reliability of being over 95%. At the same time, under different cycles of load, the error of the time-dependent reliability model of the suction anchor established in this paper is less than 2.15% compared with the reliability results evaluated by the MCS method, which verifies the effectiveness of the proposed method.
-
数字孪生铁路是智能化铁路发展的新途径和信息化发展的前沿标志[1]，在勘察设计、建设施工、运营维护一直到报废处置的全生命周期管理中发挥关键作用[2]. 铁路地理地质知识库作为数字孪生铁路的重要内容[3]，是孪生应用服务过程中数据与模型不完备条件下的重要补充[3]. 现有铁路地理地质知识所描述的要素，专业的经验知识常以专题方式在铁路沿线不同区段分布式知识建库和管理[4]. 随着数字孪生铁路智能应用逐渐从单一尺度应用向“区域-工程-施工面”多尺度协同应用发展[5]，现有分区段、分主题的知识管理方式忽略了地理地质知识的内部耦合关系，易产生冗余存储[6]，导致知识检索任务效率低且关联检索结果不完整等问题. 因此，本文面向数字孪生铁路地理地质知识多尺度应用需求，设计一种适用于关联检索的知识库分布式关联管理方法. 现有分布式知识库管理方式分为云计算、图划分和联邦式三类[7]. 云计算管理方式依赖于现有的云计算系统进行知识管理，有较好的可扩展性与容错性，但是现有云计算框架大多面向离线知识，难以满足数字孪生铁路知识库实时检索需求[8]；图划分方法将知识图划分为多个子图存储到各机器中[9]，支撑海量知识高效动态管理，然而由于铁路知识一般由权属单位分类分级分散自治，该方法难以满足在长线性铁路工程的实际管理需求[10]；联邦式管理将独立知识库集成实现知识库的统一管理，具备较为灵活的存储和访问模式，可以适用于独立单位或区段专注知识管理[11]，有助于各单位各专业围绕特定领域结构化管理专业知识，是铁路地理地质知识库分布式管理的主要方法[12]，但是在进度质量安全风险管控等数字孪生铁路的专业知识应用中，需要对铁路知识库进行独立知识检索和多层次知识检索[13]，现有联邦式铁路知识库通常直接通过既有知识图谱这一特定知识类型进行检索，多层次知识检索任务也只从语义角度考虑了知识的层次性[14]，没有考虑分布在不同知识库里知识的耦合关联关系及完整性，导致知识碎片化[15]. 当知识分布在不同领域时，难以保持知识凝聚和相互关联，导致知识库规模逐渐庞大后处理多尺度检索任务检索难、耦合性低[16]，同时可能会导致知识的冗余和矛盾[17]. 因此需要特别考虑联邦式铁路地理地质知识库的分布优化方法.
传统知识库分布优化方法通常只考虑了单一的分布影响因素[18]（如知识库的用户、单位等），没有考虑多种分布影响因素及其关联关系[19]. 元网络分析方法充分考虑了多种分布影响因素及其交互[20]，是分布式管理方法研究的重要手段，通过对元网络理论构建的元网络模型在打击扰动下的表现，进行知识库分布优化分析[21]. 从元网络方法可以抽象出各种类型的实体及其关联，在可视化分析异构实体[22]及复杂关系方面具有显著优势[23]. 元网络方法已在灾害风险管理[24]和基础设施规划研究中得到广泛使用[25]，将动态元网络模型引入数字孪生铁路研究可以评估多种分布影响因素对铁路地理地质知识库应用的影响，进而优化知识库分布，提高知识库性能.
本文围绕数字孪生铁路地理地质知识库（以下简称知识库）高效关联检索需求，设计一种能够提高知识检索完整性的分布优化方法，形式化定义多尺度检索任务流，设计铁路地理地质知识分布动态元网络模型，充分考虑知识库分布影响因素并利用总度中心度和分布影响力指标评估结果. 最后，在典型的铁路特大桥工程地理地质场景中对本文方法进行示范应用. 结果表明，本文方法能够有效提高铁路地理地质知识关联检索完整性，支撑数字孪生铁路多尺度应用高性能查询检索相应地理地质知识.
1. 铁路地理地质知识多尺度检索需求
铁路地理地质知识检索任务目标是依据检索条件在分布式知识库的铁路地理地质要素中检索到服务于多尺度应用的知识结果，如图1所示，其中检索过程是知识库多尺度检索结果完整性的最重要影响因素. 本节围绕数字孪生铁路知识内部耦合关联关系和数字孪生铁路知识多尺度检索任务特点，设计了适用于铁路分布式知识库检索的任务流程.
铁路地理地质领域知识涵盖专家经验知识、领域知识图谱、工程实践知识和科研成果4类，采用集中式备份和分布式管理相结合的管理方式，如图2所示. 专家经验知识通过专家的经验描述和解决地理地质场景面临的实际问题；领域知识图谱将各领域的知识结构化成图谱，有助于相关人员快速获取所需的领域知识；工程实践知识是对铁路工程中的实践类知识进行总结和归纳；科学研究成果包含地理地质领域的前沿研究成果. 不同类型知识相互关联，共同构成了知识库的内容体系，因此这4类知识检索结果的耦合是支撑铁路地理地质工程应用和科学研究的关键.
图 2 铁路地理地质知识分布特点Figure 2. Distribution characteristics of geographic and geological knowledge of railway同时，实际部署在不同地域的铁路知识库之间存在内部耦合关联关系，包括同义关系、空间关系、上下位关系、更新关系. 同义关系指知识中的语义的相似或者等价关系；空间关系包括知识库的距离、区域范围的关系；上下位关系指知识的包含关系与被包含关系；更新关系指知识变化时产生的关联关系.
1.1 多尺度检索任务定义
将知识库多尺度检索任务定义为函数f，知识库检索工作流Q映射到知识库内容D中得到的结果集合R=f{Q, D}，工作流Q为一组检索条件集合，Q={q1, q2, ⋯, qx}，x为集合中的检索总数；D为知识库内容集合，D={d1, d2, ⋯, dy}，y为检索目标知识库中内容总数. 当函数f执行检索任务时根据Q中的检索条件，从D中检索生成结果R. 实际应用中，数字孪生铁路多尺度检索分为区域尺度检索、工程尺度检索和施工面尺度检索3类.
1） 区域尺度检索任务是指检索某一工程段落及其沿线100 km空间范围内（如成都—兰州段落）的指定知识，如通过知识库检索相关知识引导显隐结合的区域地质环境几何建模的构建与更新.
2） 工程尺度检索任务是指检索某一工程项目及其沿线10 km空间范围内（如康定隧道工程）的指定知识，如通过知识库检索相关知识驱动多源异质数据融合的特征智能提取、工程地质环境特征联合解算和多场耦合的工程精细三维地质环境数字孪生模型构建等.
3） 施工面尺度检索任务是指检索某一工点周围500 m空间范围内（如康定隧道进口工点）的指定知识，如通过知识库检索相关知识引导隧道洞内地质环境集成建模.
除了相同尺度的检索任务，在使用过程中还存在需要跨尺度知识应用. 例如，在隧道三维地质环境数字孪生建模知识检索任务中需要检索工程尺度的先期工程勘探知识和施工面尺度的掌子面相关知识，再将结果整合后输出，最后完成跨尺度知识检索.
1.2 多尺度检索任务流
本文设计的知识库多尺度检索任务流程包含任务流生成、检索任务分解、任务流映射、检索任务分发、结果返回5个步骤.
1） 任务流生成. 在处理检索任务时，知识库会先根据任务内容生成任务流，任务流抽象化描述了检索任务的参与内容集合及其执行关系. 通过任务流，知识库可以优化检索过程，确保检索任务高效有序地执行，减少整体检索时间.
2） 检索任务分解. 知识库应用常面临复杂检索任务，生成任务流后需要对检索任务进行提取关键词、解析语法和识别语义处理，将复杂的检索任务拆分为细粒度的子任务.
3） 任务流映射. 将子任务映射到知识库检索任务流中的特定节点，知识库将每个子任务与任务流节点相匹配，确保了每个子任务以合理的顺序处理，保证检索的高效执行.
4） 检索任务分发. 将每个拆解后的子任务分发到铁路沿线分布的知识库进行独立检索，获取子任务检索结果，如图3所示. 不同的知识库分布方法通过影响检索任务分发环节造成检索结果完整性的不同.
5） 结果返回. 将得到的结果进行去重、排序、合并，生成最终的检索集合R，完成检索.
2. 铁路地理地质知识分布元网络模型
地理地质知识分布元网络模型分为3个部分. 首先将影响地理地质知识分布的重要因素作为节点；其次，根据元网络节点间的关联关系，基于知识库分布会产生不同影响，设计关联关系网络；最后，设计元网络评价指标，定量计算元网络性能，如图4所示，N为网络中的节点总数.
2.1 地理地质知识分布元网络
将影响知识分布的知识使用人员、知识分布单位、知识应用场景、知识类型和知识关联关系5种要素抽象为网络节点. 用户包括铁路全生命周期中知识库用户，不同层级人员有不同的知识库使用权限. 单位代表在沿线分布管理知识库的各单位，包括业主单位、施工单位、勘察设计单位、科研单位，不同类型单位管理的不同内容知识. 知识应用场景包括施工面、工程和区域尺度3种场景的知识检索任务，不同尺度应用场景需调用不同的知识. 知识类型代表知识库中的专家经验知识、领域知识图谱、工程实践知识和科研成果. 知识关联关系表示知识库内部耦合关联，包括同义关系、上下位关系、空间关系和更新关系. 知识的关联关系会影响知识库分布，例如存在“邻近”的空间关系的知识，在分布时应将这2种知识放在一起便于调用.
元网络模型中，节点及其关联关系被抽象为11种子网络连接形成的网络图. 元网络的形成基于以下假设：1）每个检索任务都有特定的用户在特定的分布式知识库中检索；2）每个检索任务都有对应的应用场景. 例如知识用户内部构成了知识库用户子网络（AA），代表用户间的沟通与协作；知识应用场景内部构成了知识库应用子网络（EE），代表跨尺度的知识应用；知识库应用场景和知识类型的关联形成了知识应用子网络（EK），代表不同知识类型在相同尺度的应用；知识类型和知识关联之间构成了知识关联关系子网络（KR），代表不同知识类型之间的关联. 同样对其他类型网络进行建模，得到元网络关联关系如图5所示.
2.2 分布优化的元网络打击算法
元网络打击算法是元网络分析的重要部分，分布优化的元网络重点打击算法根据度中心度指标，得到节点重要性排序，通过扰动分布关系网络，计算分布影响力，得到各种影响因素对知识库分布的影响程度，进行下一步分布分析，对于不同尺度的知识应用，在检索时将尺度作为知识的一个属性存入知识库中.
2.2.1 打击算法度量指标
元网络模型中独立的关联关系子网络由若干个共享节点连接，动态分析时对一个节点或子网络的打击会引起整个网络的变化，根据变化时的评价指标测度可以计算影响知识库分布关键节点和关联关系. 本文提出网络分布效率、网络分布密度和分布网络度中心度3个评价指标来分析打击算法下的动态元网络模型.
网络分布效率EG由路径长度和网络节点总数表示，节点间的距离越长表示网络越复杂，如式（1）所示.
EG=n∑i=1(N−1)Di， (1) Di=n∑j=1,j≠i,d(i,j)>01d(i,j)， (2) 式中：n为网络中实际参与计算的节点数量；Di为节点i到网络中其他节点的“效率”总和；d（i,j）为从节点i到节点j的最短路径长度（若路径存在）.
网络分布密度DG通过网络中的实际连接数除以最大可能连接数来计算，网络密度越大，说明知识间关系越紧密，如式（3）所示.
DG=∑RKN(N−1)， (3) 式中：N为网络中的节点总数；K为实际连接数，表示网络中实际存在边的数量（网络的稠密程度）；R为子网络数，每个子网络有其对应的连接数和节点数.
分布网络度中心度指标用以描述网络的中心性程度，分为点入中心度、点出中心度和总度中心度3个子度量. 点入中心度指传入关系的总和，点入中心度高的节点表示在网络中对其他节点有较强影响力；点出中心度指传出关系的总和，点出中心度高的节点表示在网络中得到的信息多；总度中心度是点入中心度和点出中心度的总和，用以全面描述节点对其一阶邻近节点的影响. 总度中心度测度指标越大，说明这个节点在网络中重要性越高，某节点Ni的总度中心度为：
Cd(i)=n∑i=1di， (4) 式中：di为节点i与其他节点的关联关系.
为检测与评估节点打击对元网络的影响，提出一种分布影响力测度IG，如式（5）所示.
IG=αEG+βDG， (5) α+β=1, (6) 式中：α和β为加权系数.
将EG和DG进行整合，便于调整这2个指标在元网络节点打击算法的全局计算中贡献权重. 非负系数α和β的值由对应评价指标的重要性决定，由于本次实验网络分布效率和分布要素网络密度效率同样重要，因此，加权系数均设置为0.5.
2.2.2 打击实验流程
打击实验首先按照计算出的节点总度中心度对节点的重要性按由高到低排序，并按排列顺序打击节点，通过分析打击后网络的变化来评价其对知识库分布的重要程度. 若有可以代替的同类型节点，则通过随机恢复的方式进行节点替代并生成新的网络；否则，不执行网络恢复. 一直重复上述步骤直到打击完成所有节点.
3. 原型系统及案例分析
3.1 铁路特大桥工程场景案例分析
以典型的数字孪生铁路特大桥工程数字孪生铁路知识库管理及应用场景为例，通过动态元网络方法分析检索结果完整性的影响因素并对地理地质知识库分布进行优化. 根据知识库应用场景实际情况，设计影响知识库分布的节点，包括13个用户节点、8个单位、11个应用场景节点、4个知识类型节点和7个知识关联节点，如表1所示.
表 1 元网络节点的要素及代码Table 1. Meta-network node elements and codes要素 分类 内容及代码 用户
Agent业主人员 业主代表A01、项目经理A02、安全管理员A03 施工人员 项目经理A04、工程师A05、施工员A06 设计人员 项目经理A07、设计师A08、制图员A09 勘察人员 项目经理A10、勘察工程师A11 科研人员 教职工A12、研究生A13 单位
Organization业主单位 国铁集团O01、工程局O02、大桥局O03 施工单位 总承包商O04、桥梁公司O05、通信公司O06 其他单位 勘察设计单位O07、科研单位O08 应用场景
Event施工面尺度 表面形变E01、桩基钻孔E02、箱梁浇筑E03、护栏浇筑E04 工程尺度 桥面施工E05、隧道锚施工E06、重力锚施工E07、桥台施工E08 区域尺度 地质环境E09、灾害防控E10、污染治理E11 知识类型
Knowledge专家经验知识K01、领域知识图谱K02、工程实践知识K03、科研成果K04 知识关联
Relation空间关系 同义关系R01、上下位关系R02、更新关系R03 远R04、中R05、近R06、相同R07 深入分析元网络中各要素间的关系，建立15种关联关系的二元子网络，结合已有的网络节点，最终生成元网络关系图（图7）.
3.2 分布优化的元网络打击分析
通过计算各类型节点总度中心度可以得到用户、单位、应用场景、知识类型和知识关联5类所有节点的排序，如图8所示. 按照降序排列次序对地理地质知识库分布网络模型进行重点打击以减弱网络节点间的关联关系，直到网络完全瓦解，得出哪些节点对知识库检索结果完整性有较大影响，从而在地理地质知识库分布时，应特别考虑这些影响较大的节点.
场景案例网络总共559条关联关系，从总度中心度指标最高的“地质环境”节点开始打击，节点间的关联关系随着打击节点的增加而减少.
节点影响范围指各节点对分布网络的重要程度，重要程度越高则连接数越多，并非总度中心度高的节点被打击后关联关系数量下降更快，某些对整个网络影响力大的节点被打击会使关联关系数量快速下降，对所有节点完成打击后，整个分布网络完全瓦解. 分布影响力打击变化如图9所示.
分析打击结果表明：用户和应用场景是影响知识库检索结果完整性的关键节点类型. 23.0%的用户在打击实验中对分布影响力指标的影响较大，这些用户是知识库的核心使用者. 38.4%的应用场景在打击实验中对分布影响力指标的影响较大，这些应用场景对知识库的使用最为频繁.
“业主代表”“国铁集团”“专家经验知识”“空间-相同”和“地质环境”分别为各类型要素中影响范围最广的要素，说明在分布时应着重考虑管理权限较高的人员，如“业主代表”和各单位的项目经理，他们对网络的影响范围更大，占总网络关联关系的25%. 知识库分布地点应重点考虑国铁集团等高层用户单位的宏观决策和复杂调用需求，同时还要兼顾现场的施工单位的频繁使用和更新知识库需求. 知识库中专家经验知识和领域知识图谱是占比最大的2种知识类型，两者占比超70%，在分布时应增加这2种知识之间的联系，相同类型的专家经验知识和领域知识图谱尽量分布在同一单位，便于扩展检索. 在考虑知识关联关系的影响时，空间关系的远近是最重要的影响因素，空间关系为“相同”即知识所应用的对象属于同一区域. 同时，有“同义关系”的知识在打击分析中也有较大的影响范围，将有相同含义的知识分布在邻近区域可以提高知识库检索结果丰富程度. “地质环境”相关知识检索是知识库的重要应用内容，知识库应着重考虑地质环境应用内容的检索结果完整性. 次序打击对关联关系的影响如图10所示.
图 10 原型系统中展示分布优化前后检索结果展示Figure 10. Display of retrieval results before and after distribution optimization in prototype system总结起来，为提高知识库检索结果的完整性和协同耦合分析能力，在分布时应优先部署在影响范围广的单位中，同时考虑地理位置因素，将描述内容、作用范围、作用区域相似的知识分布在一起才能得到更完整的检索结果.
3.3 原型系统设计与实现
在铁路特大桥工程地理地质场景案例中使用知识库分布元网络进行分析，面向知识库多尺度检索应用，验证本文方法的有效性.
对于一个检索结果图G，用顶点的元素有限集合V={a,b,c,⋯}和不同顶点对（称为边）的有限集合E表示，G=（V,E）. 途径x是由w个边组成的边序列. 将w个边的序列称为长度为w的1个途径，则途径x表示为{x0,x1},{x1,x2},⋯{x（w-1）,xw}. 若途径中边都不相同，则称为1条迹. 在铁路特大桥工程地理地质场景案例滚石知识检索结果中，由于优化前各单位知识共享性不同导致只能检索到“滚石运动”-“接触/离开系数”-“滚石位置参数”-“摩擦系数”和“大渡河桥”-“滚石”-“烈度/方向”两个一步检索结果，如图11（a）所示. 根据元网络分布结果对知识库进行分布优化后，由于充分考虑知识库用户、地理位置、作用范围和作用区域的影响，提高了知识库的耦合关联关系检索能力，在知识库控制台中输入相同的检索内容，得到更丰富的检索结果，如图11（b）所示，能够满足多尺度应用需求. 该检索案例中优化前检索结果的迹为3，优化后的迹为8，说明优化后比优化前的检索范围更广.
本文设置3种典型知识库检索场景，以区域尺度、工程尺度和施工面尺度的知识库检索需求进行实验，以查询检索结果数目、查询检索时间和结果匹配度3个指标与优化前分布方法进行定性对比，以优化前相同应用尺度的相同检索内容为基准依据对优化后的结果进行分析，以某施工面任务的检索结果为基础衡量优化前的检索任务指标如表2所示.
表 2 优化前后多尺度检索性能表Table 2. Multi-scale retrieval performance before and after optimization任务内容 检索数目 检索时间 结果匹配度 优化前 优化后 优化前 优化后 优化前 优化后 施工面1 少 中 快 快 高 高 施工面2 少 中 快 快 高 高 施工面3 中 中 中 快 高 高 工程1 中 多 中 中 高 高 工程2 中 多 中 中 高 高 工程3 多 多 慢 中 中 高 区域1 中 多 中 中 中 高 区域2 多 多 慢 中 中 高 区域3 多 多 慢 中 中 高 分析结果表明，知识库多尺度检索性能在分布优化后明显提升，特别是在处理工程尺度和区域尺度的知识检索任务时，因为涉及知识库跨尺度耦合关联关系和共享性问题较多，分布优化能提高查询检索结果数目、查询检索时间和结果匹配度，能够满足知识库高效精确检索和协同耦合分析需求.
4. 结 语
本文面向长大带状铁路工程地理地质知识分散独立管理手段普遍忽略知识内部耦合关联关系的实际情况，针对数字孪生铁路“区域-工程-施工面”多尺度知识应用中高效完备检索知识进而协同耦合分析需求，描述并定义铁路地理地质知识多尺度检索任务并建立分布元网络模型，实现了分布优化的元网络打击算法，并依据度中心度指标计算节点重要性，通过扰动分布关系网络分析分布影响力，进而计算节点影响范围并分析得到知识库分布优化结构. 结果表明，在知识权限在不同单位具有共享能力的条件下，本文方法在处理铁路地理地质知识库多尺度检索任务时，较优化前分布方式检索结果更完整，协同耦合分析更准确，提升了数字孪生铁路地理地质知识库高效管理能力. 后续研究将进一步完善地理地质知识库在复杂场景高效应用，提升知识应用中查询检索和实时耦合分析效率.
-
图 5 不同勘探点处吸力锚抗拔力的不确定性量化结果
Figure 5. Uncertainty quantification results of pulling resistance of suction anchor at different exploratory points
图 6 锚链拉力竖直分量Fty的不确定性量化结果
Figure 6. Uncertainty quantification results of vertical componentFtyof anchor chain tension
图 7 不同作用次数下各勘探点处的时变可靠度结果
Figure 7. Time-dependent reliability results of each exploratory point under different frequency of action
图 8 勘探点A处的时变可靠度验证结果
Figure 8. Results of time-dependent reliability verification at exploratory point A
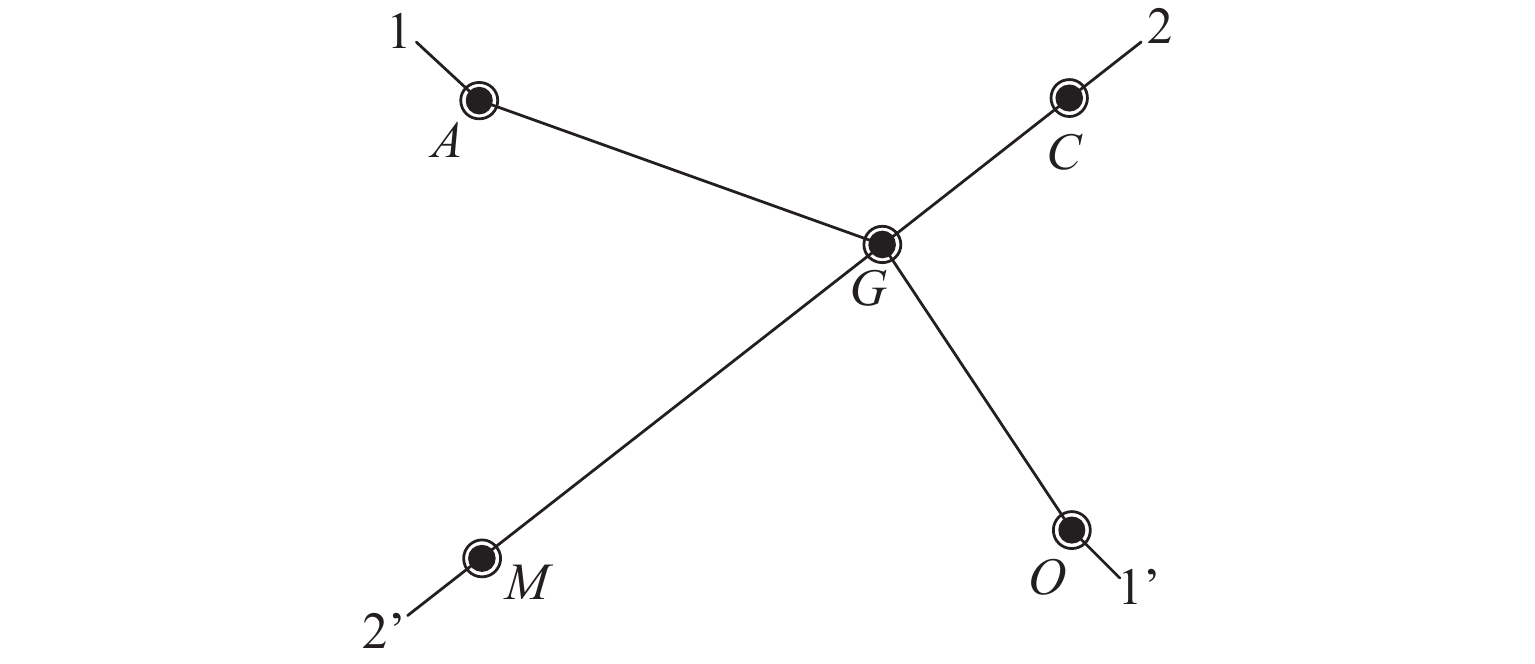
表 1 各勘探点附近的抗拔力值
Table 1. Pulling resistance values near each exploratory point
kN 组号 点A 点C 点G 点M 点O 1 1330.9777 2007.6882 2247.3961 1826.8866 1835.3776 2 1339.7254 1998.8052 2261.1515 1820.1196 1840.0185 3 1336.7282 1982.7419 2274.1373 1814.4576 1843.6222 4 1330.8861 1964.7617 2286.1875 1809.4007 1846.4546 5 1323.8135 1947.6050 2297.1344 1804.6813 1848.9262 6 1319.7456 1954.0500 2191.5069 1800.0756 1851.5450 7 1319.9079 1970.4304 2187.9786 1795.7828 1854.8203 8 1322.8437 1987.0357 2182.8988 1792.0530 1859.1009 9 1328.1747 2003.6953 2176.1155 1791.3837 1864.3240 10 1338.2259 2020.2961 2167.4843 1791.0338 1869.6512 
下载: 导出CSV
表 2 各勘探点附近抗拔力分布参数
Table 2. Parameters of pulling resistance distribution near each exploratory point
勘探点 u σ A 1329.1029 7.4612 C 1983.7110 24.2016 G 2227.1991 48.0464 M 1804.5875 12.7894 O 1851.3841 10.7934
下载: 导出CSV
-
[1] 王胤,朱兴运,杨庆. 考虑砂土渗透性变化的吸力锚沉贯及土塞特性研究[J]. 岩土工程学报,2019,41(1): 184-190.WANG Yin, ZHU Xingyun, YANG Qing. Installation of suction caissons and formation of soil plug considering variation of permeability of sand[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(1): 184-190. [2] 霍知亮. 黏土地基中桶形基础模型试验及工作机理研究[D]. 天津:天津大学,2015. [3] 王胤,杨涵,庞子毅,等. 基于CFD-DEM流固耦合方法的吸力锚基础负压沉贯数值模拟[J]. 岩土工程学报,2023,45(2): 384-393,444. doi: 10.11779/CJGE20211512WANG Yin, YANG Han, PANG Ziyi, et al. Numerical simulation of negative pressure penetration of suction anchor foundation based on CFD-DEM fluid solid coupling method[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(2): 384-393,444. doi: 10.11779/CJGE20211512 [4] 闫宏生,苑恒,李怀亮,等. 大抓力锚和吸力锚在CALM型单点系泊系统中的应用[J]. 中国海洋平台,2022,37(4): 31-36,42.YAN Hongsheng, YUAN Heng, LI Huailiang, et al. Application of fluke anchor and suction anchor in CALM single-point mooring system[J]. China Offshore Platform, 2022, 37(4): 31-36,42. [5] RICE S O. Mathematical analysis of random noise[J]. The Bell System Technical Journal, 1944, 23(3): 282-332. doi: 10.1002/j.1538-7305.1944.tb00874.x [6] CRANDALL S H, CHANDIRAMANI K L, COOK R G. Some first-passage problems in random vibration[J]. Journal of Applied Mechanics, 1966, 33(3): 532-538. doi: 10.1115/1.3625118 [7] ANDRIEU-RENAUD C, SUDRET B, LEMAIRE M. The PHI2 method: a way to compute time-variant reliability[J]. Reliability Engineering & System Safety, 2004, 84(1): 75-86. [8] SINGH A, MOURELATOS Z P. On the time-dependent reliability of non-monotonic, non-repairable systems[J]. SAE International Journal of Materials and Manufacturing, 2010, 3(1): 425-444. doi: 10.4271/2010-01-0696 [9] HU Z, DU X P. A sampling approach to extreme value distribution for time-dependent reliability analysis[J]. Journal of Mechanical Design, 2013, 135(7): 071003.1-071003.8. [10] HU Z, DU X P. Time-dependent reliability analysis with joint upcrossing rates[J]. Structural and Multidisciplinary Optimization, 2013, 48(5): 893-907. doi: 10.1007/s00158-013-0937-2 [11] JIANG C, HUANG X P, HAN X, et al. A time-variant reliability analysis method based on stochastic process discretization[J]. Journal of Mechanical Design, 2014, 136(9): 091009.1-091009.11. [12] LI C Y, ZHANG Y M. Time-variant reliability assessment and its sensitivity analysis of cutting tool under invariant machining condition based on gamma process[J]. Mathematical Problems in Engineering, 2012, 2012: 676923.1-676923.19. [13] CAZUGUEL M, RENAUD C, COGNARD J Y. Time-variant reliability of nonlinear structures: application to a representative part of a plate floor[J]. Quality and Reliability Engineering International, 2006, 22(1): 101-118. doi: 10.1002/qre.750 [14] KOPUSTINSKAS V, AUGUTIS J, RIMKEVIČIUS S. Dynamic reliability and risk assessment of the accident localization system of the Ignalina NPP RBMK-1500 reactor[J]. Reliability Engineering & System Safety, 2005, 87(1): 77-87. [15] 张德权,韩旭,姜潮,等. 时变可靠性的区间PHI2分析方法[J]. 中国科学:物理学 力学 天文学,2015,45(5):41-53.ZHANG D Q, HAN X, JIANG C, et al. The interval PHI2 analysis method for time-dependent reliability[J]. Sci Sin-Phys Mech Astron, 2015, 45(5):41-53. [16] TIAN L, NOORE A. Dynamic software reliability prediction: an approach based on support vector machines[J]. International Journal of Reliability, Quality and Safety Engineering, 2005, 12: 309-321. doi: 10.1142/S0218539305001847 [17] BECKER G, CAMARINOPOULOS L, KABRANIS D. Dynamic reliability under random shocks[J]. Reliability Engineering & System Safety, 2002, 77(3): 239-251. [18] STREICHER H, RACKWITZ R. Time-variant reliability-oriented structural optimization and a renewal model for life-cycle costing[J]. Probabilistic Engineering Mechanics, 2004, 19(1/2): 171-183. [19] SUDRET B. Analytical derivation of the outcrossing rate in time-variant reliability problems[J]. Structure and Infrastructure Engineering, 2008, 4(5): 353-362. doi: 10.1080/15732470701270058 [20] 茆诗松,王静龙,濮晓龙. 高等数理统计[M]. 2版. 北京:高等教育出版社,2006:34-35. [21] 钟泽棋. 基于FMECA的吸力锚系统可靠性评估[D]. 成都:电子科技大学,2023. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 165
- HTML全文浏览量: 104
- PDF下载量: 15
- 被引次数: 0