Optimization of JM3 Wheel Profile Considering Equivalent Conicity Dispersion
-
摘要:
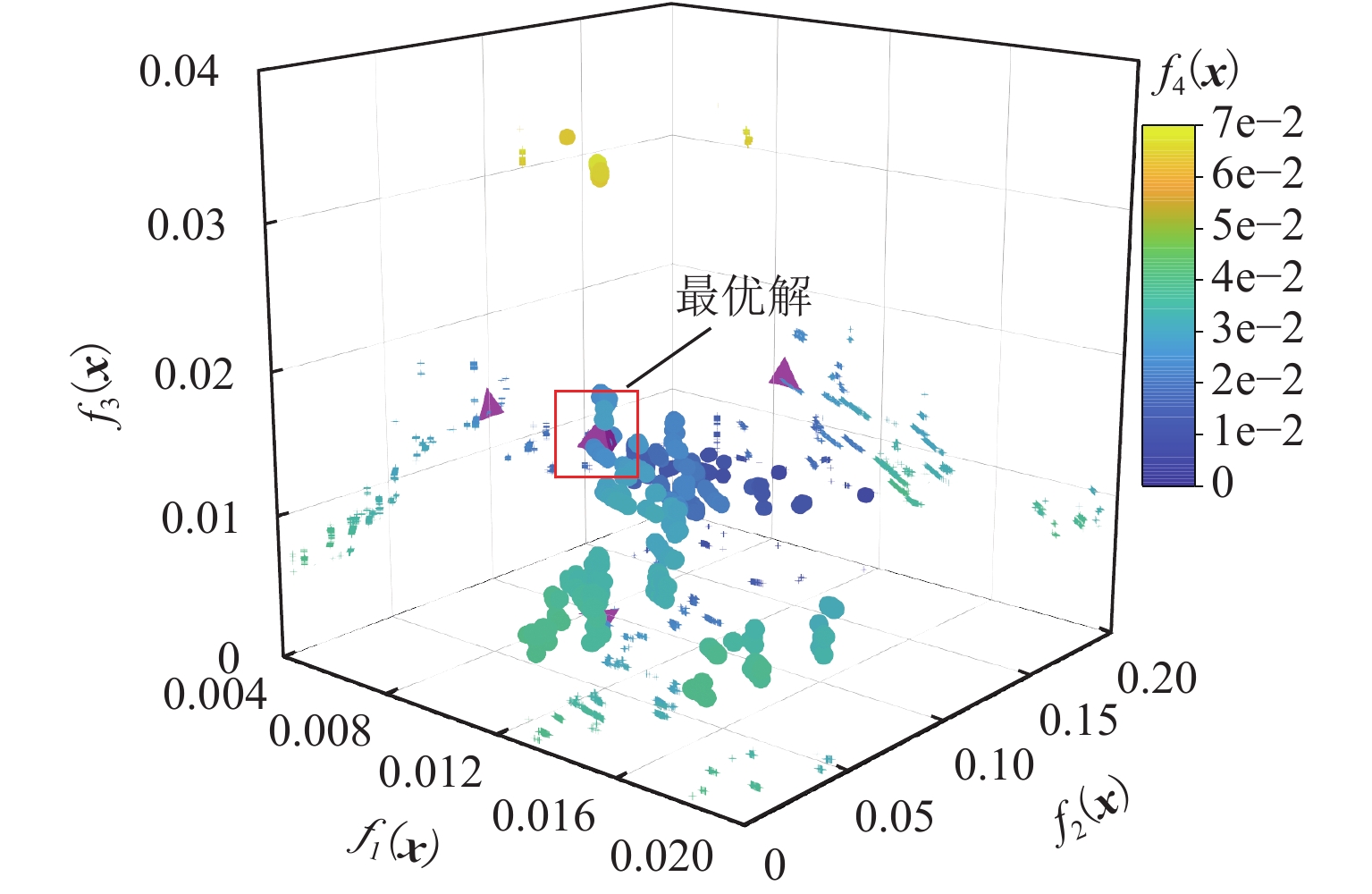
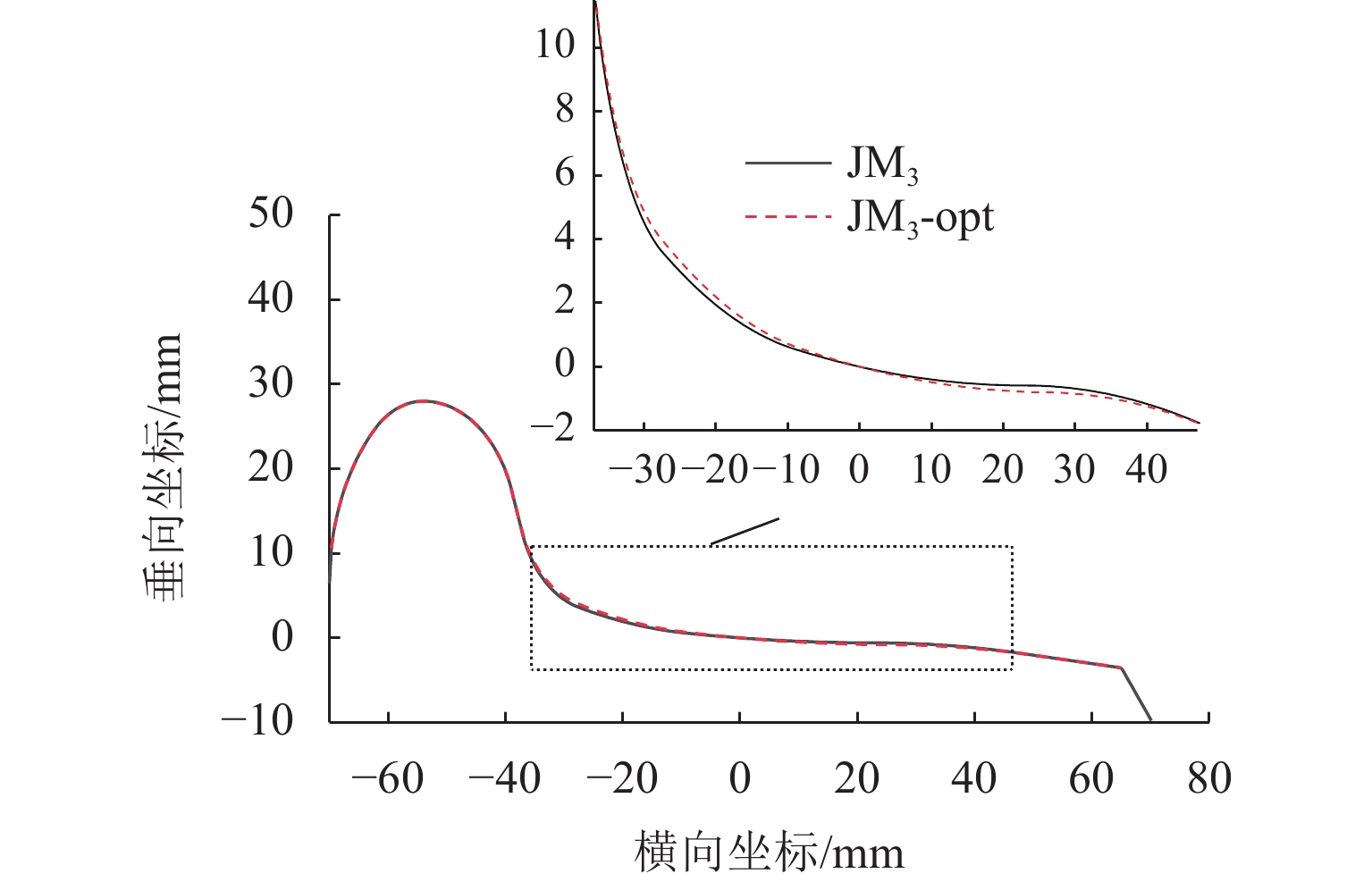
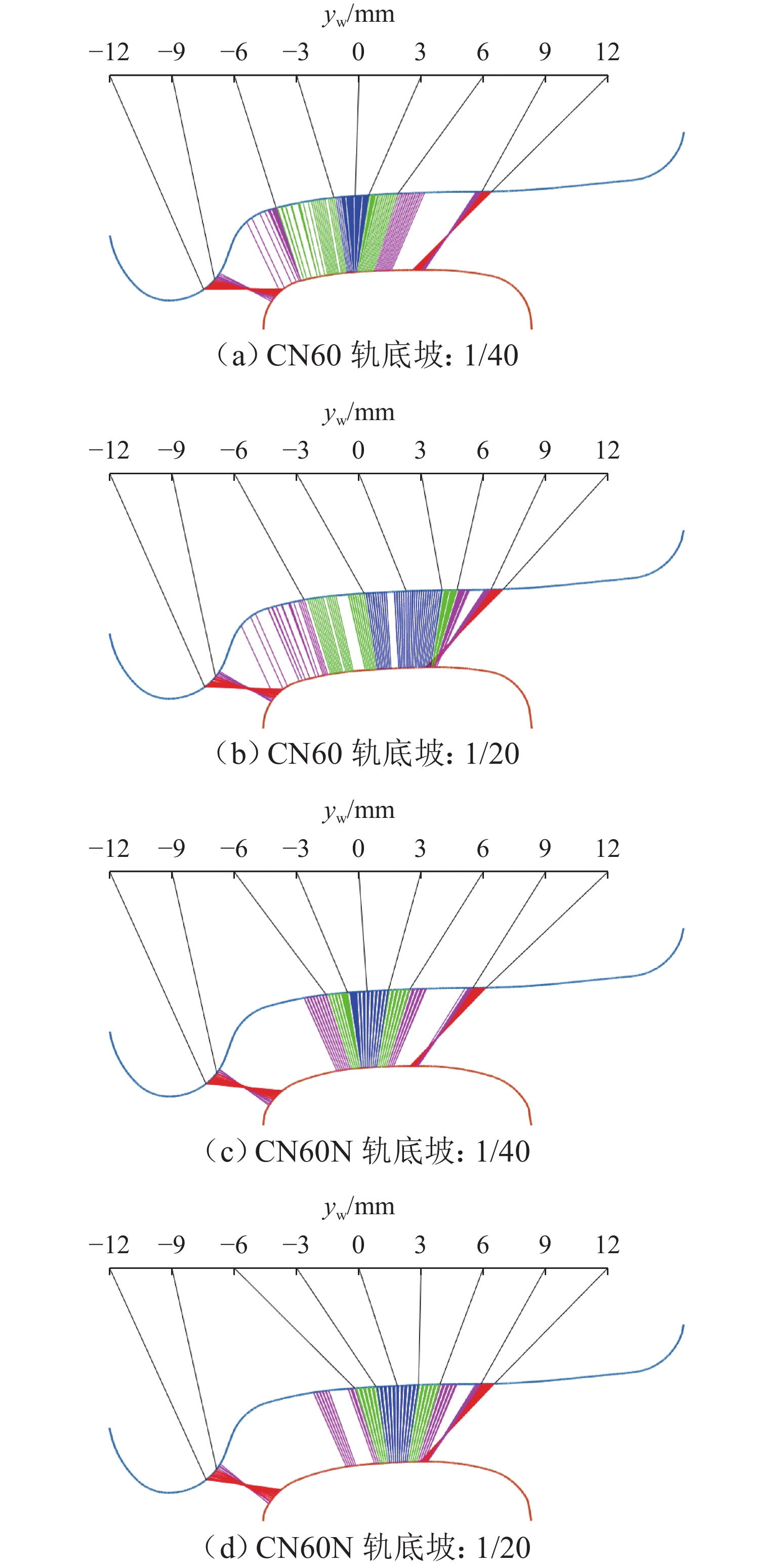
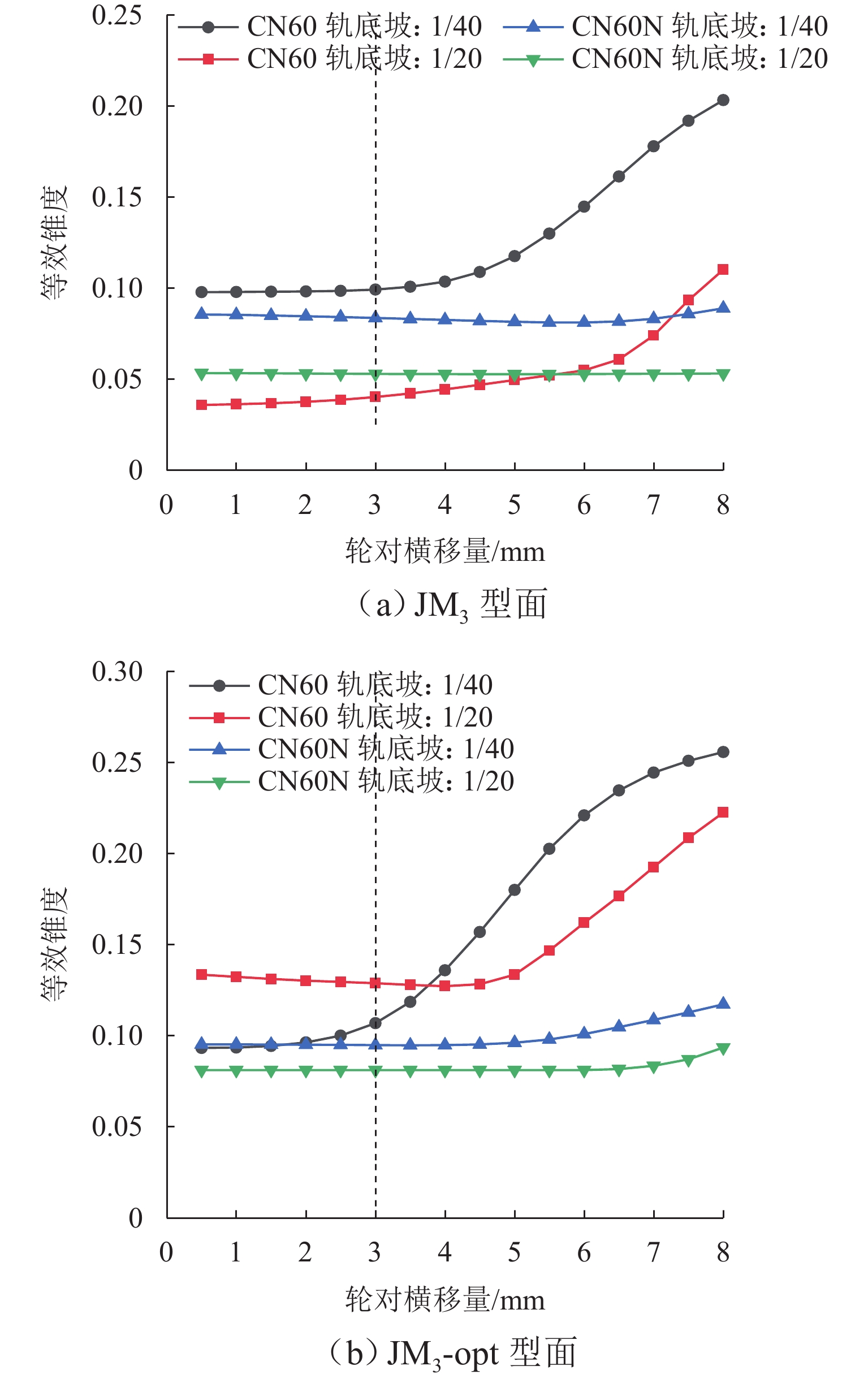
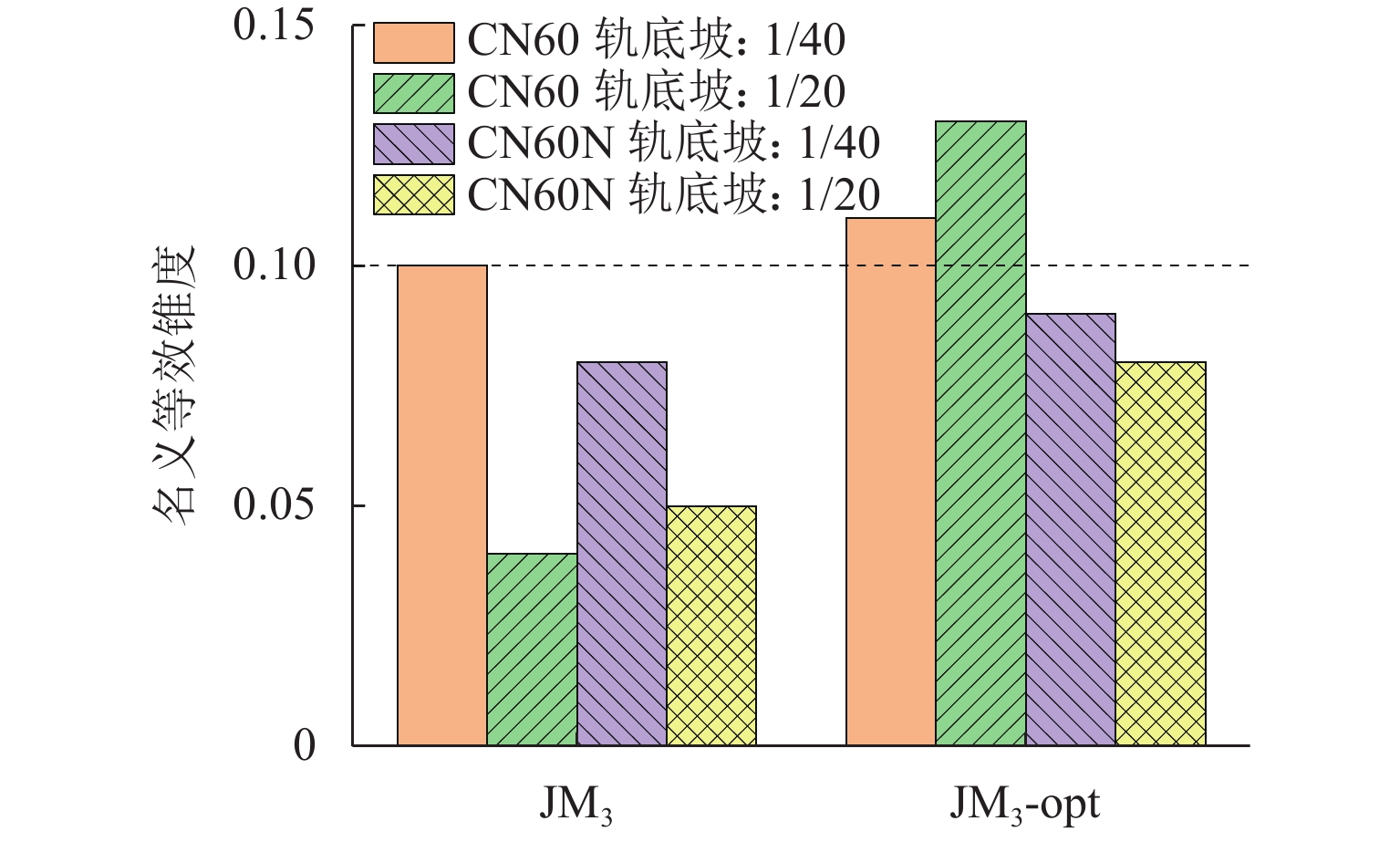
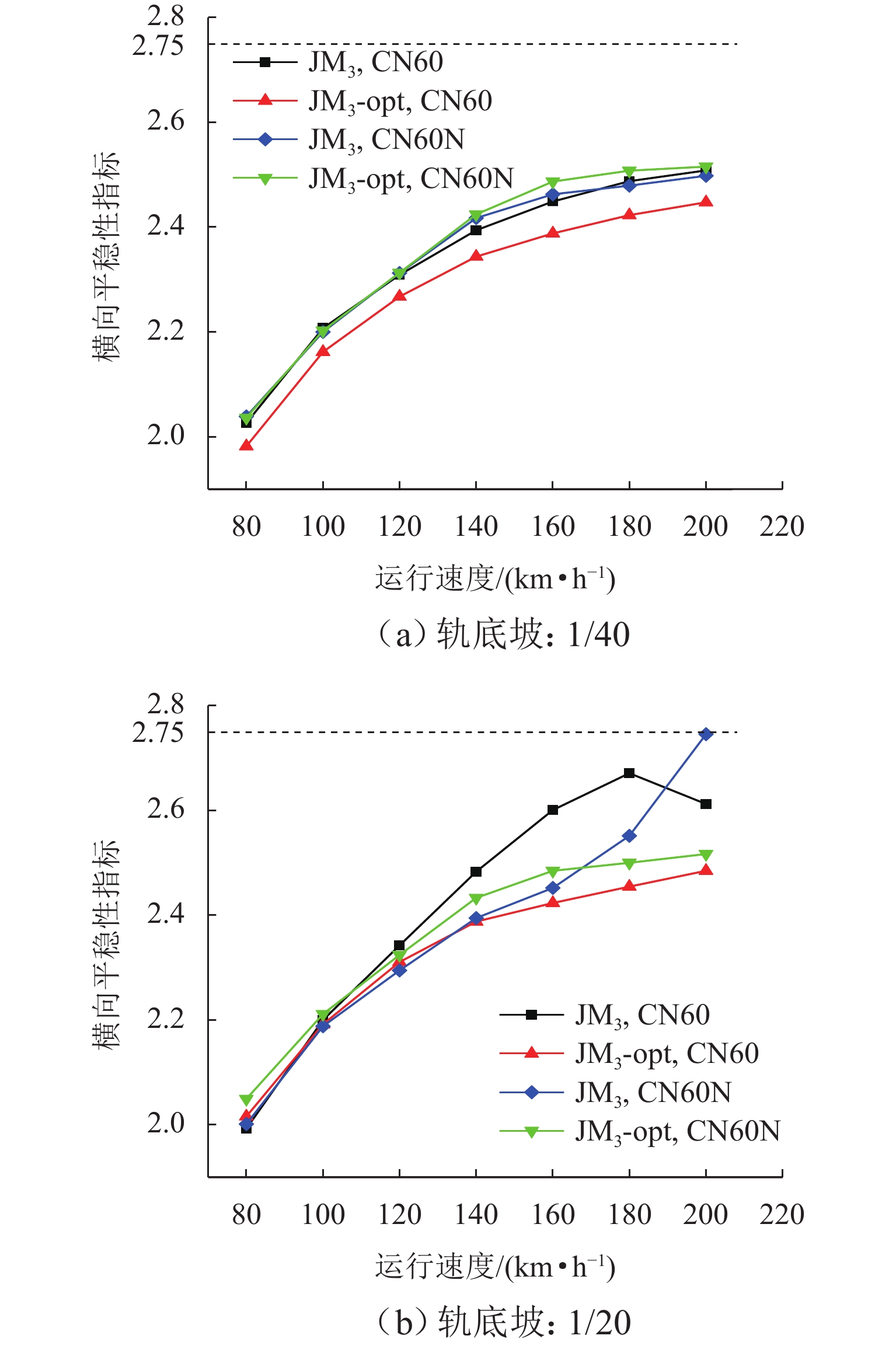
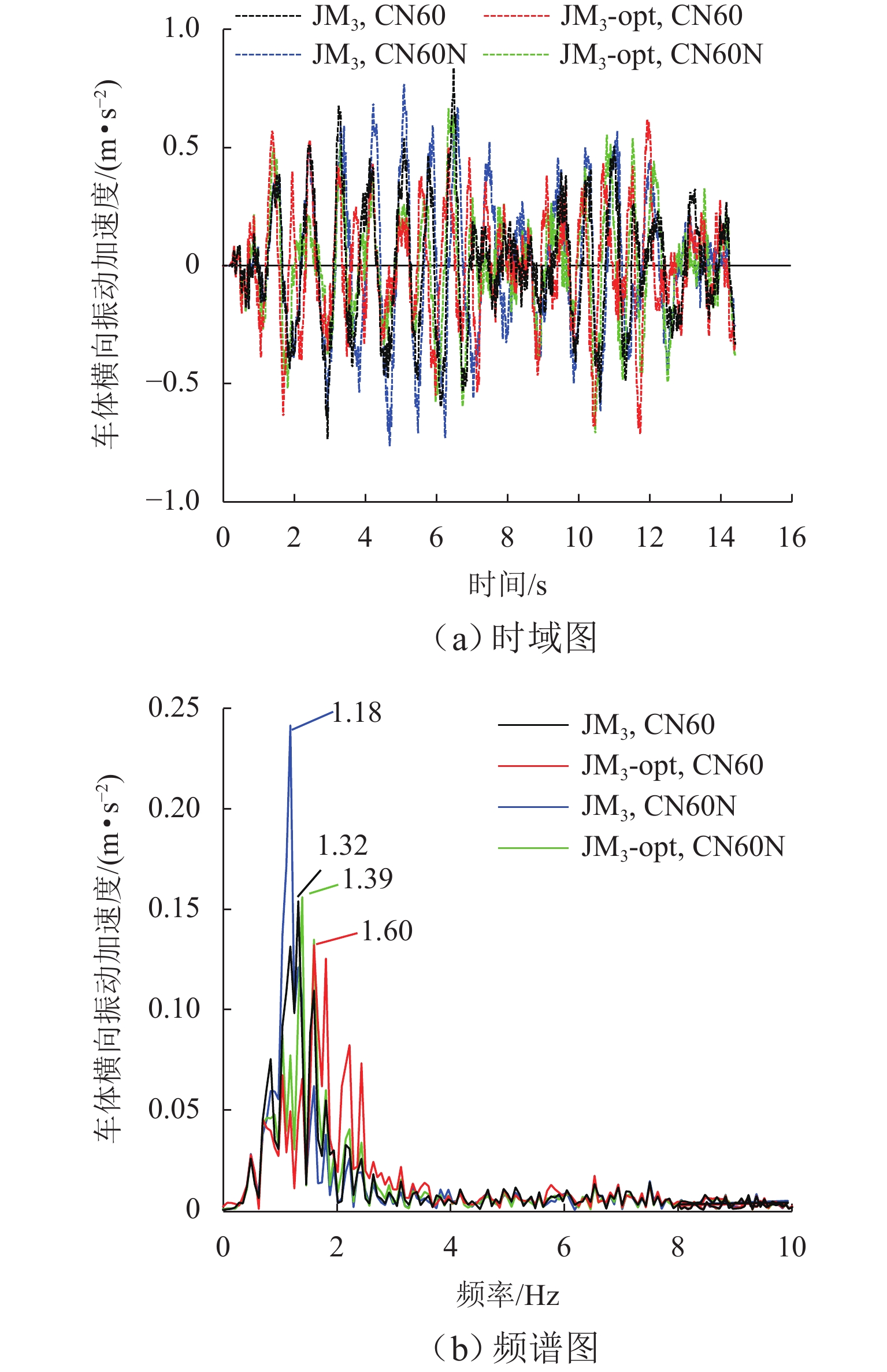
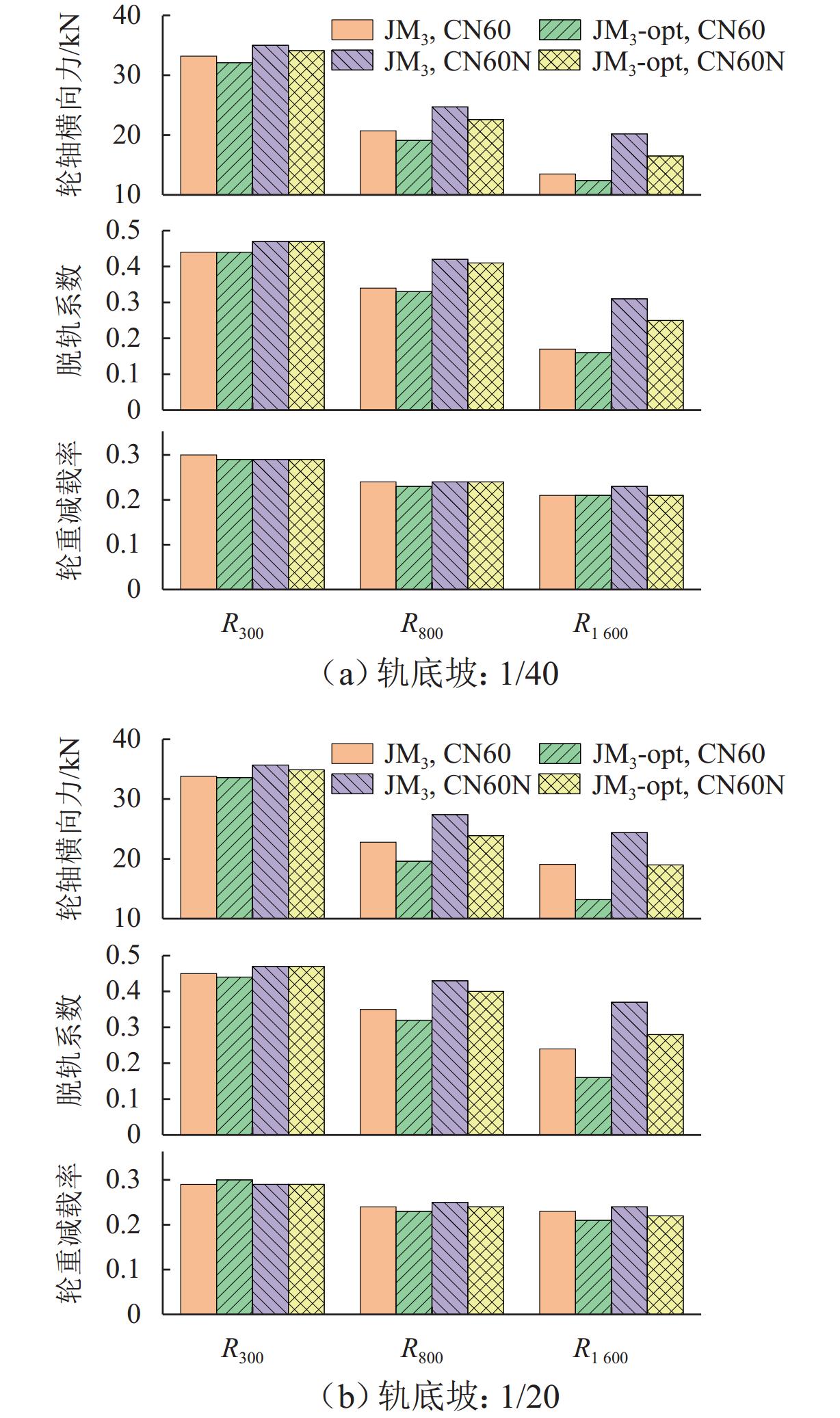
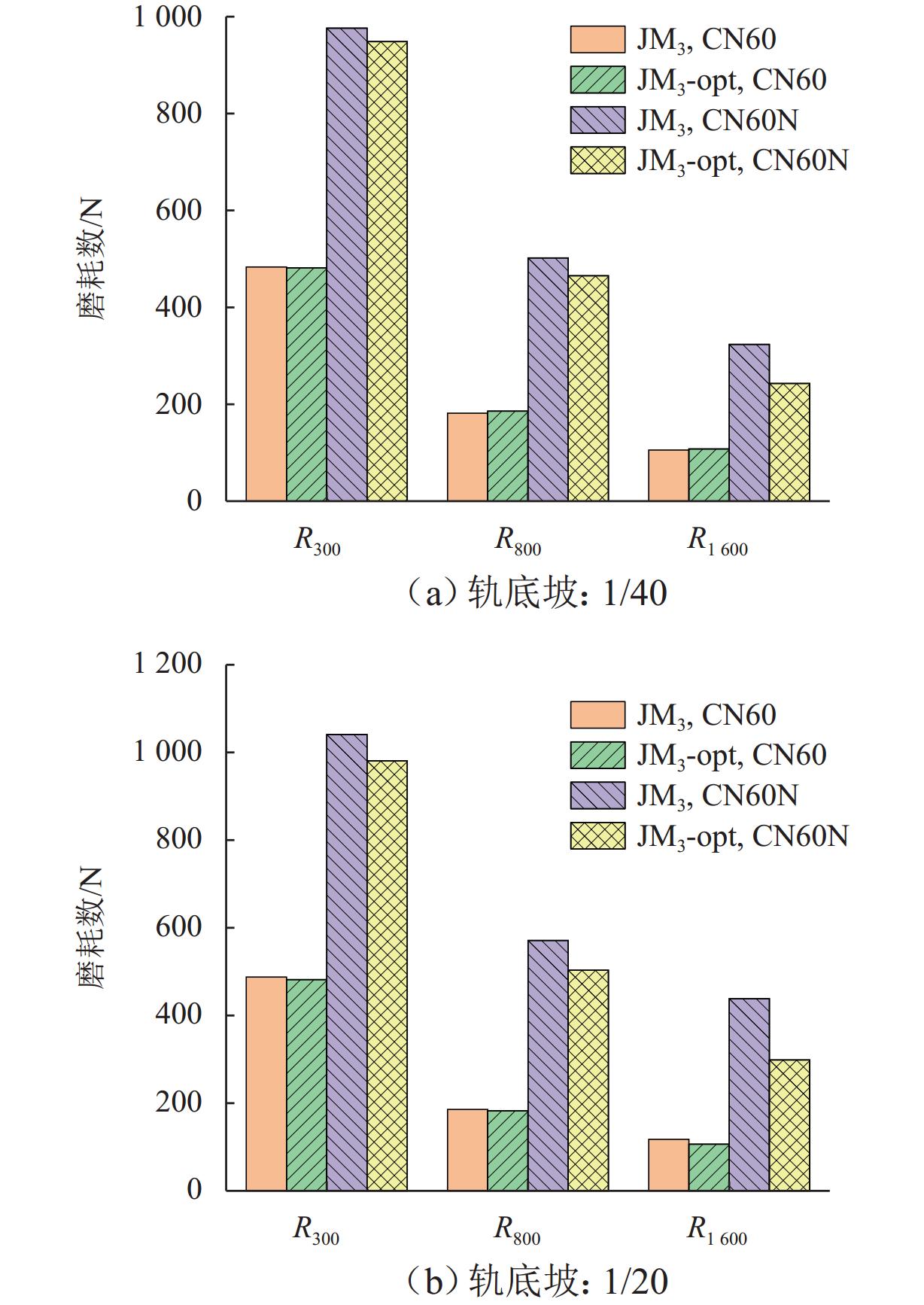
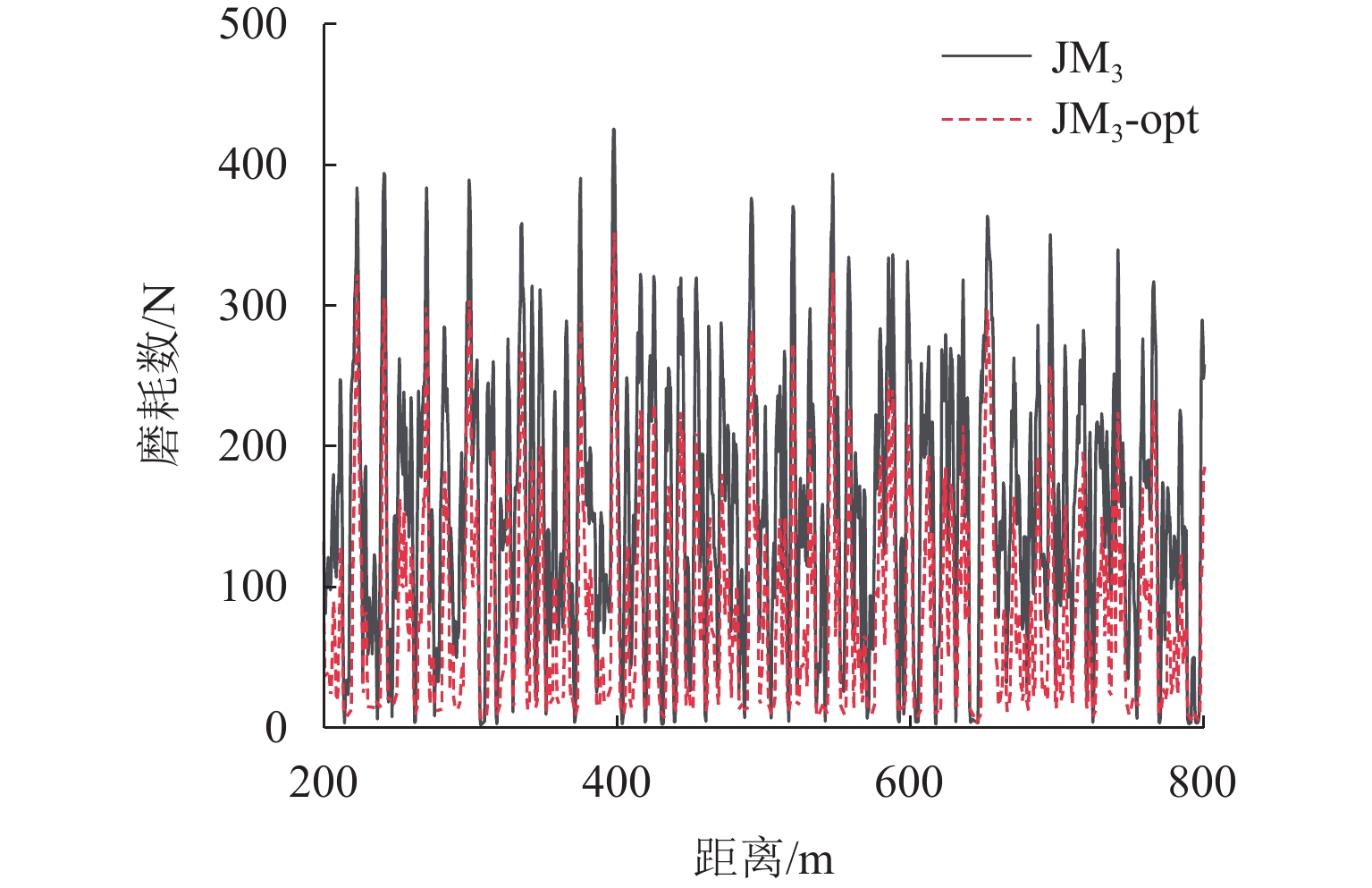
轮轨匹配对轨道车辆动力学性能有着重要影响，针对现行标准JM3车轮型面与国内不同类型钢轨廓形匹配时等效锥度差异过大，以及在大轨底坡条件下匹配打磨钢轨时因等效锥度过低而引发机车晃车的问题，本文以减小车轮型面在不同轨底坡条件下与CN60型和CN60N型2种钢轨匹配对应的等效锥度离散度为优化目标，采用圆弧、直线组合的车轮型面描述方法，应用NSGA-Ⅱ遗传算法优化滚动圆附近两段圆弧圆心横向位置参数，对JM3型面进行优化，并对优化前后的车轮型面进行轮轨接触特性和机车动力学性能仿真对比分析. 结果表明：优化型面在与上述钢轨匹配时，轮对3 mm横移量处的名义等效锥度均在0.1左右，显著降低原JM3踏面等效锥度离散度，提高了车轮型面对不同钢轨廓形和线路条件的适应性；同时，优化后的型面对应机车蛇行稳定性、横向平稳性、曲线通过性能和磨耗性能指标较原型面均得到提升，消除了特定线路机车的低频晃车现象.
Abstract:Wheel-rail profile compatibility has an important influence on the dynamic performance of rail vehicles. The present standard JM3 wheel profile has a large difference in equivalent conicity when it is matched with different types of rail profiles in China. It has the problem of locomotive swaying caused by too low equivalent conicity when the profile is matched with the grinding rail with large rail cant. To address these issues, the optimization objective of reducing the equivalent conicity dispersion of the wheel profile matched with CN60 and CN60N rail profiles under different rail cants was set. The wheel profile was described by a method combining arcs and straight lines. The JM3 wheel profile was optimized by utilizing NSGA-II genetic algorithm to improve the lateral position parameters of the two arc centers near the rolling circle. The wheel-rail contact characteristics and the locomotive dynamic simulation of the wheel profile before and after optimization were compared. The results show that when the optimized wheel profile is matched with the rails above, the nominal equivalent conicities at the 3 mm transverse displacement of the wheelset are all about 0.1, which reduces the equivalent conicity dispersion of the original JM3 wheel profile and improves the adaptability of the wheel profile to different rail profiles and line conditions. At the same time, the locomotive hunting stability, lateral stability, curving performance, and wear performance index of the optimized profile are all improved compared with the original wheel profile. In addition, the phenomenon of low-frequency swaying of locomotives on specific lines is eliminated.
-
在高速列车制动过程中，列车的动能通过闸片与制动盘摩擦面之间的剧烈摩擦转化为热能，使制动盘在制动过程中承受着巨大的热负荷，此时制动盘上产生很大的温度梯度，从而产生较大的热应力[1-2]. 若高速列车在运行过程中发生高速下的紧急制动或持续坡道制动等恶劣制动，所产生的热应力超过了材料的屈服强度，盘面进入塑性状态，并在制动结束后在制动盘内留下残余应力[3-4].
残余应力的存在会影响材料的疲劳强度和构件的稳定性[5]，长期使用后制动盘摩擦面会产生微裂纹，甚至会引起制动盘的断裂、热变形并影响接触压力的稳定性，尤其在严苛地域条件下，导致制动盘热弹性不稳定，降低制动效能与制动盘的使用寿命[6-8]. 为提高高速列车的制动性能，国内外诸多学者针对制动盘材料[9-10]、疲劳寿命预测[11]展开研究：王东伟等[12]采用ABAQUS/Explicit热-位移瞬态分析法，探究热机耦合对高速列车制动系统动力学行为的影响；Wu等[13]采用扩展有限元法和虚拟节点多边形有限元法模拟热疲劳裂纹，并利用损伤容限法评估疲劳裂纹扩展寿命；石晓玲等[14]针对高速列车锻钢制动盘在实际运用中出现的多裂纹问题，通过1∶1制动动力试验与有限元计算相结合的方法研究了制动盘多裂纹间的作用机制；Xie等[15]对铁路制动盘深层裂纹的形成与扩展进行了研究，探讨了制动工况和服役历程对动车组制动盘裂纹快速扩展行为的影响；Belhocine等[16]使用ANSYS软件对不同材料的制动盘进行热-机耦合分析发现，制动盘在热应力作用下发生“伞状”变形，导致制动盘在制动过程中产生红热带迁移，从而影响制动盘的性能；日本Saga等[17]设计了测量制动盘动态变形的方法，研究了制动过程盘体的热变形规律. 前期研究表明，制动盘摩擦面附近的周向残余应力是驱动制动盘热疲劳裂纹扩展的主要原因[4, 18].
残余应力导致轮装制动盘变形的机理已有一定的研究，但基于动车组轮装制动盘拆解维修以及后续重复利用的工程需求，服役后轮装制动盘残余应力以及翘曲变形的仿真和预测方法仍鲜见报道. 因此，制动盘服役后的残余应力分布与翘曲变形之间的关系亟待深入研究.
本文通过试验构建了铸钢制动盘材料在不同温度下的本构模型，使用弹塑性有限元法研究了不同制动工况下制动盘的残余应力分布规律与翘曲变形量的变化规律，结合残余应力测试及制动盘变形测试，验证了仿真结果的有效性. 本文研究工作可为预测动车组制动盘长期服役后的残余应力分布及翘曲变形量变化提供方法借鉴，为动车组轮装制动盘拆解检修、后续重复利用提供参考.
1. 有限元模型的建立
1.1 材料力学性能及本构模型
从高速动车组制动盘本体取样，加工为标准拉伸试样进行单调拉伸试验,拉伸试样尺寸如图1所示. 在高速列车紧急制动过程中，制动盘摩擦面的瞬时温度可高达800 ℃，因此，试验温度为25～800 ℃. 试验设备为CMT5105型电子万能试验机，测得不同温度下的拉伸应力-应变曲线如图2所示.
参考GB/T 22315—2008标准，拟合得到不同温度下的杨氏模量、屈服强度等力学性能参数. 由应力-应变曲线能够看出，铸钢制动盘材料无明显屈服平台，对于此类非线性材料，Ramberg-Osgood模型[19]可用来描述其应力-应变（σ-ε）关系，其理论表达式为
ε=σE0+0.002(σσ0.2)n， (1) 式中：E0为材料的杨氏模量，σ0.2为残余应变0.002时所对应的应力，n为材料的应变硬化指数.
使用最小二乘法对试验所得应力-应变数据进行拟合，可得到制动盘材料在不同温度下的应变硬化指数n. 材料的弹性模量、强度等力学性能参数如表1所示，σb为抗拉强度. 从表1中可以看出，随着试验温度的升高，材料的弹性模量和屈服强度不断降低，当试验温度超过400 ℃时发生明显下降.
表 1 制动盘材料不同温度下的力学性能参数Table 1. Mechanical properties of brake disc material at different temperatures温度/（℃） σ0.2/MPa σb/MPa E /GPa n 25 1055 1142 214 37.893 100 1007 1095 202 33.306 400 843 948 191 19.766 600 547 568 159 13.252 800 77 102 59 12.593 
图 2 制动盘材料不同温度下的单调拉伸应力-应变Figure 2. Monotonic tensile stress-strain curves of brake disc materials at different temperatures1.2 有限元模型的建立
制动过程的仿真模型包括制动盘、车轮与紧固件三部分，为兼顾计算精度与效率，简化了对仿真分析影响较小的圆角和倒角特征. 考虑到制动盘结构的对称性，取其1/6进行三维建模，如图3（a）所示. 利用有限元仿真软件ABAQUS开展热机耦合仿真分析，模型网格划分的结果如图3（b）所示，其中热分析部分使用三维实体单元C3D8，应力分析部分使用三维实体单元C3D8R.
高速列车在制动过程中，列车的动能会转化为摩擦面吸收的热能，假设制动盘和闸片之间理想接触，摩擦热量均匀输入，则施加在摩擦表面接触区域的热流可使用能量折算法计算，如式（2）.
q(t)=Mηa2cA(v0+at)， (2) 式中：M为单个轴重，η为制动盘的热吸收系数，a为列车制动平均减速度，A为制动摩擦面积，c为每轴制动盘数，v0为制动初速度，q(t)为制动期间随时间变化的热流密度.
对流换热系数hf是随列车速度变化的函数，制动盘摩擦面和散热筋表面与空气间换热条件不同，可分别按照式（3）计算[20].
hf={0.332λRe0.5Pr1/3/l，摩擦面，0.4Pr0.33kv0.556¯v0.556d0.444，散热筋表面， (3) 式中：λ为材料热导率，Re为雷诺数，Pr为普朗特数，l为厚度，k为热导率，v为运动黏度系数，ˉv为散热筋之间的平均风速，d为散热筋的内外径差.
在制动过程中，对流换热系数随列车速度减小而减小，假设环境恒定不变且列车进行匀减速，根据式（3），即可得到与时间相关的对流换热系数.
根据列车运行速度与1∶1制动动力试验中的试验速度等级，确定4种仿真工况的初速度（200、250、300、350 km/h），减速度恒定为1.0 m/s2，根据式（2）、（3）计算出不同工况下的热流密度与对流换热系数并施加到制动盘上，在制动盘盘体上的热流输入面、对流换热面的位置如图4所示.
本文使用间接耦合法计算制动盘热应力，将温度分析结果作为应力分析的输入载荷. 制动盘与车轮通过紧固件连接，在有限元模型中通过施加螺栓轴向载荷模拟紧固件预紧力；轮装制动盘与车轮共同压装于车轴上，运行过程中与车轴相对静止，故在轮毂孔上施加全约束；由于所使用的仿真模型为整体模型的1/6，还需在模型的分割面上施加对称约束. 应力分析的边界条件设置如图5所示. 在热应力计算完成后，移除螺栓的预紧力作用，使制动盘在不受结构约束的情形完全释放应力，以模拟制动盘从车轮拆卸后的残余变形情况.
2. 模拟结果分析及验证
2.1 不同工况下制动盘残余应力
图6为不同初速度下，制动结束并冷却至室温同时将制动盘紧固件拆除后的等效应力分布云图. 可见：4种工况制动后，制动盘螺栓孔上下侧都出现明显的应力集中现象，最大应力值均位于螺栓孔的靠近制动盘内沿侧；随着制动初速度的增加，摩擦面的残余应力值越来越大，高应力区域也越来越大，但残余应力的分布规律类似；制动盘摩擦面上的最大应力位于螺栓孔靠近制动盘内沿侧，故选择该位置处的节点分析制动过程中摩擦面的应力变化情况，所选择节点的位置及编号如图7所示.
图 6 不同制动初速度下制动结束拆除螺栓后等效应力分布Figure 6. Equivalent stress distribution after bolt removal at the end of braking with different initial braking speeds
图 7 制动盘螺栓孔边应力分析节点位置及编号Figure 7. Node position and number of bolt hole in brake disc for stress analysis当减速度恒定为1.0 m/s2，制动初速度不同时，输出摩擦面上应力最大节点的周向应力、径向应力、轴向应力以及温度瞬态变化曲线如图8所示.
图 8 不同制动初速度下摩擦面不同方向应力-时间曲线Figure 8. Stress-time curves in different directions on friction surface under different initial braking speeds由图8可见：整个过程中制动盘摩擦面的周向应力远大于径向与轴向应力，且制动初速度越高，最高温度值越大，产生的应力值就越大；在制动初期，制动盘摩擦面主要受到较大的周向压缩应力，径向与轴向应力较小，且此阶段摩擦面温度快速上升，材料屈服强度下降，所承受压应力会超过材料屈服强度，在摩擦面表层产生压缩塑性应变；制动过程中周向压缩应力逐渐减小，在制动结束前转变为周向拉伸应力，而制动盘最高温度也出现在制动后期；制动结束后随着制动盘的冷却，周向拉伸应力逐渐减小并趋于稳定；待制动盘完全冷却至室温并卸载螺栓载荷后，摩擦面会存在一定的残余拉应力，该残余拉应力的形成是由于在制动温升和热应力的共同作用下使表面形成了压缩塑性应变；在制动结束、冷却收缩的过程中，摩擦面附近的塑性应变在结构约束下无法完全恢复，从而在摩擦面表层形成残余拉应力，盘体内则形成残余压应力以达到应力平衡.
沿制动盘盘体轴向选择5个位置（距摩擦面的距离分别为0、5.5、11.0、16.5、22.0 mm）研究残余应力沿摩擦面轴向的梯度分布情况，距摩擦面不同深度取点位置以及距摩擦面不同深度的周向残余应力变化曲线如图9所示：由图9 （b）可见：在不同的制动初速度下，制动盘内的残余应力分布规律相似，摩擦面上的残余应力最大，并随着距摩擦面深度的增加而减小；在深度达到10 mm后残余应力由拉应力转变为压应力，在10～15 mm深度上应力有小幅增加，在15～20 mm深度上压应力开始逐渐减小且趋近于0；从制动盘摩擦面到制动盘心部，周向残余应力的大小与方向都有转变，不均匀的梯度型应力分布会使制动盘在失去外部结构约束后以翘曲变形的形式释放应力.
图 9 距摩擦面不同深度取点位置及周向应力变化曲线Figure 9. Circumferential stress changes at different depths from friction surface2.2 制动工况对变形量的影响
制动初速度与平均减速度是列车制动的2个重要因素，为了更好地描述制动盘翘曲变形规律，分别考虑这2个因素对制动盘翘曲变形的影响.
2.2.1 制动初速度对变形量的影响
制动盘在制动减速度恒为1.0 m/s2时，列车在初速度为200、250、300、350 km/h 4种工况下摩擦面上的周向塑性应变如图10所示. 由图可见，制动结束后摩擦面上形成压缩塑性应变，随着制动初速度的增加，塑性应变的区域和塑性应变量都随之增大.
图 10 不同制动初速度下摩擦面周向塑性应变Figure 10. Circumferential plastic strain of friction surface at different initial braking speeds对1∶1制动动力试验中常用的制动试验初速度为225、275、330、385 km/h，制动减速度恒为1.0 m/s2的4种制动工况进行分析，如图11所示. 由图可见：翘曲变形量随制动能量的升高而增加，当制动能量在26.2～59.0 MJ时，翘曲变形量随制动能量线性增加，当制动能量超过59.0 MJ后，翘曲变形量与制动能量呈二次函数关系.
因此，可以采用分段函数对翘曲变形量Y和制动能量W之间的关系进行拟合，如式（4）.
Y={0.024 64W−0.414 47，W=26.2～59.0MJ，3.29392×10−4W2−0.01425W+0.73364，W=59.0～80.3MJ. (4) 从图11还可看出：当制动能量超过59.0 MJ后，制动盘翘曲变形量增速逐渐变大；制动能量59.0 MJ所对应制动初速度为300 km/h，此初速度下制动盘最高温度达到了598 ℃. 拉伸试验结果表明，在温度达到600 ℃或更高时，制动盘材料的强度显著下降、塑性显著增大，当制动峰值温度达到对应水平时，摩擦面表层材料在制动时的压缩塑性应变也越大，冷却后形成的残余应力梯度和翘曲变形量也更大.
2.2.2 制动平均减速度对变形量的影响
列车制动时，制动盘与闸片的剧烈摩擦会使列车的动能转化为热能，当制动初速度一定时，制动平均减速度越大，摩擦副的制动热输入功率越大. 为探究不同制动热输入功率对制动盘翘曲变形的影响，在制动初速度均为300 km/h时，参照TL/CL 342—2014《中国标准动车组暂行技术条件》[21]中的减速度曲线，选择3、5、7级常用制动与紧急制动，将列车的减速过程等效为匀减速，对应的平均减速度分别为0.2、0.4、0.6、1.0 m/s2. 为保证曲线的连续性，额外选择0.8、1.2 m/s2的平均减速度，即在制动初速度均为300 km/h，平均减速度分别为0.2、0.4、0.6、0.8、1.0、1.2 m/s2的6种不同制动工况下对制动盘进行仿真分析，如图12所示，其中，制动盘的最大温度差为摩擦面上最高温度点与散热筋上最低温度点之差.
图 12 翘曲变形随制动减速度变化Figure 12. Variation of warping deformation with braking deceleration从图12可以看出：当平均减速度为0.2 m/s2时，制动盘翘曲变形量极小，在该工况下，制动盘摩擦面最高温度仅为324 ℃，摩擦面表层材料在该温度下仍有很高的强度，制动盘最大温度差仅为63 ℃，极低的温度梯度引起的热应力不足以产生大的塑性变形；当平均减速度从0.4 m/s2逐渐增大至1.2 m/s2时，制动盘的翘曲变形量也由0.02 mm逐渐增加到1.3 mm. 可见，当制动总能量恒定时，制动热输入功率需达到一定阈值才会使制动盘出现翘曲变形. 由图12还可看出：制动盘上的最高温度与最大温差都随制动平均减速度的增大而增大，但增幅逐渐降低；当制动热输入功率较高时，制动盘摩擦面产生的高温使表层材料强度降低，更大的温度梯度使制动盘内产生更高水平的热应力，因此平均减速度增大时，制动盘产生的翘曲变形量增加. 可以使用二次函数拟合得到翘曲变形量Y与平均减速度a间的关系，如式（5）.
Y=0.410 71a2+0.967 86a−0.432. (5) 3. 试验验证
3.1 翘曲变形与残余应力测试
从运行速度为300～350 km/h的动车组上选取一个经长期服役后的轮装制动盘，在拆卸前、后分别对制动盘的翘曲变形量进行测试，翘曲变形量的测试位置如图13所示. 在轮装制动盘拆卸前，采用塞尺对制动盘散热筋外环与车轮辐板之间的贴合间隙进行测量；在拆卸后，散热筋内环与散热筋外环间的产生明显高度差，测量变形量时，将平尺放置于螺栓安装孔所在散热筋的内环上，使用塞尺测量平尺与散热筋外环间的间隙大小. 在12个螺栓安装孔对应的散热筋外环重复进行上述测量步骤，记录测量数值并取平均值作为制动盘的翘曲变形量.
由于X射线法可以实现对工件残余应力的无损测试[22]，本文采用μ-360s型X射线残余应力分析仪对翘曲变形的制动盘进行表面残余应力测试，如图14（a）所示,在制动盘螺栓安装孔部位沿径向选取9个摩擦表面测点，测点位置如图14（b）所示.
图 14 X射线法测试摩擦面残余应力Figure 14. Residual stress of friction surface measured by X-ray method3.2 试验验证
对所选取的运行速度为300～350 km/h动车组上长期服役后的轮装制动盘的翘曲变形量进行测试发现：在轮装制动盘拆卸前，制动盘散热筋外环与车轮辐板之间的贴合间隙均小于0.1 mm；将轮装制动盘从车轮拆下后，制动盘的残余应力通过变形释放，翘曲变形量平均值为1.18 mm，如表2所示.
表 2 制动盘翘曲变形量测试结果Table 2. Test results of warping deformation of brake disc螺栓孔编号 1 2 3 4 5 6 7 8 9 10 11 12 平均 变形量/mm 1.20 1.24 1.18 1.20 1.16 1.20 1.16 1.20 1.16 1.20 1.18 1.18 1.18 X射线残余应力测试结果如图15所示. 可见：制动盘摩擦面中部的螺栓孔附近残余应力值较高，可达到260～280 MPa；残余应力的最大值均位于螺栓孔靠近制动盘内沿的一侧，摩擦面残余应力由摩擦面中部向边沿逐渐降低.
图 15 测试与仿真残余应力值对比Figure 15. Comparison of tested and simulated residual stress values2.2.1节的仿真分析可知：制动初速度为300 km/h的制动工况对应的残余翘曲变形量为1.04 mm，初速度为330 km/h的制动工况对应的残余翘曲变形量为1.39 mm，2种工况下的仿真翘曲变形量最接近实测翘曲变形量1.18 mm，故选取制动盘在制动初速度为300、330 km/h工况下的仿真结果与试验结果进行对比，如图15所示. 可见：仿真与实测制动盘残余应力分布规律和变化趋势具有很高的吻合度，且制动盘翘曲变形量与残余应力水平间呈现明显正相关关系. 从对比分析结果可知，有限元仿真结果能够较为准确地反映制动盘摩擦面的残余应力分布和翘曲变形量变化规律. 故式（4）、（5）可对动车组制动盘长期服役后形成的残余应力分布及翘曲变形量进行有效预测.
4. 结 论
1） 在高能量制动工况下，制动盘摩擦面热应力变化剧烈，冷却后形成残余应力. 在制动过程中，摩擦面先后受到的周向压缩应力和周向拉伸应力作用，待制动盘完全冷却后摩擦面会产生残余拉应力. 在解除紧固件对制动盘的结构约束后，制动盘形成翘曲变形以释放残余应力.
2） 制动减速度相同时，制动初速度越高、制动热输入的总能量越大；制动初速度相同时，制动减速度越大、制动热输入功率越高. 通过拟合制动能量、制动减速度与制动盘翘曲变形量的关系式发现，制动盘翘曲变形量与制动能量、制动减速度呈正相关关系，不同制动工况下的制动峰值温度与温度梯度会显著影响翘曲变形量的大小.
3） 对服役后的制动盘进行翘曲变形量与残余应力测试发现，制动盘在拆卸后通过翘曲变形释放应力，制动盘摩擦面中部螺栓孔附近的残余应力水平最高. 通过与对应工况下翘曲变形量相近的仿真结果进行对比表明，本文的仿真分析可有效反映制动盘残余应力分布及翘曲变形量变化规律.
-
图 2 4个目标函数对应Pareto优化前沿
Figure 2. Four objective functions corresponding to Pareto optimization frontier
图 4 JM3不同匹配条件的轮轨接触点分布
Figure 4. Distribution of wheel-rail contact points under different matching conditions of JM3
图 5 JM3-opt不同匹配条件的轮轨接触点分布
Figure 5. Distribution of wheel-rail contact points under different matching conditions of JM3-opt
图 6 车轮型面优化前后等效锥度对比
Figure 6. Comparison of equivalent conicities before and after wheel profile optimization
图 7 不同匹配条件对应的名义等效锥度值
Figure 7. Nominal equivalent conicity values corresponding to different matching conditions
图 9 轨底坡1/20对应的非线性临界速度对比
Figure 9. Comparison of nonlinear critical speeds corresponding to 1/20 rail cant
图 10 车轮型面优化前后横向平稳性指标对比
Figure 10. Comparison of lateral stability indexes before and after wheel profile optimization
图 11 车体横向振动加速度对比
Figure 11. Comparison of lateral vibration acceleration of vehicle body
图 12 车轮型面优化前后曲线通过性能指标对比
Figure 12. Comparison of curving performance indexes before and after wheel profile optimization
图 13 车轮型面优化前后不同曲线工况磨耗数对比
Figure 13. Comparison of wear number under different curve conditions before and after wheel profile optimization
图 14 车轮型面优化前后R1600曲线工况磨耗数对比
Figure 14. Comparison of wear number of R1600 curve before and after wheel profile optimization
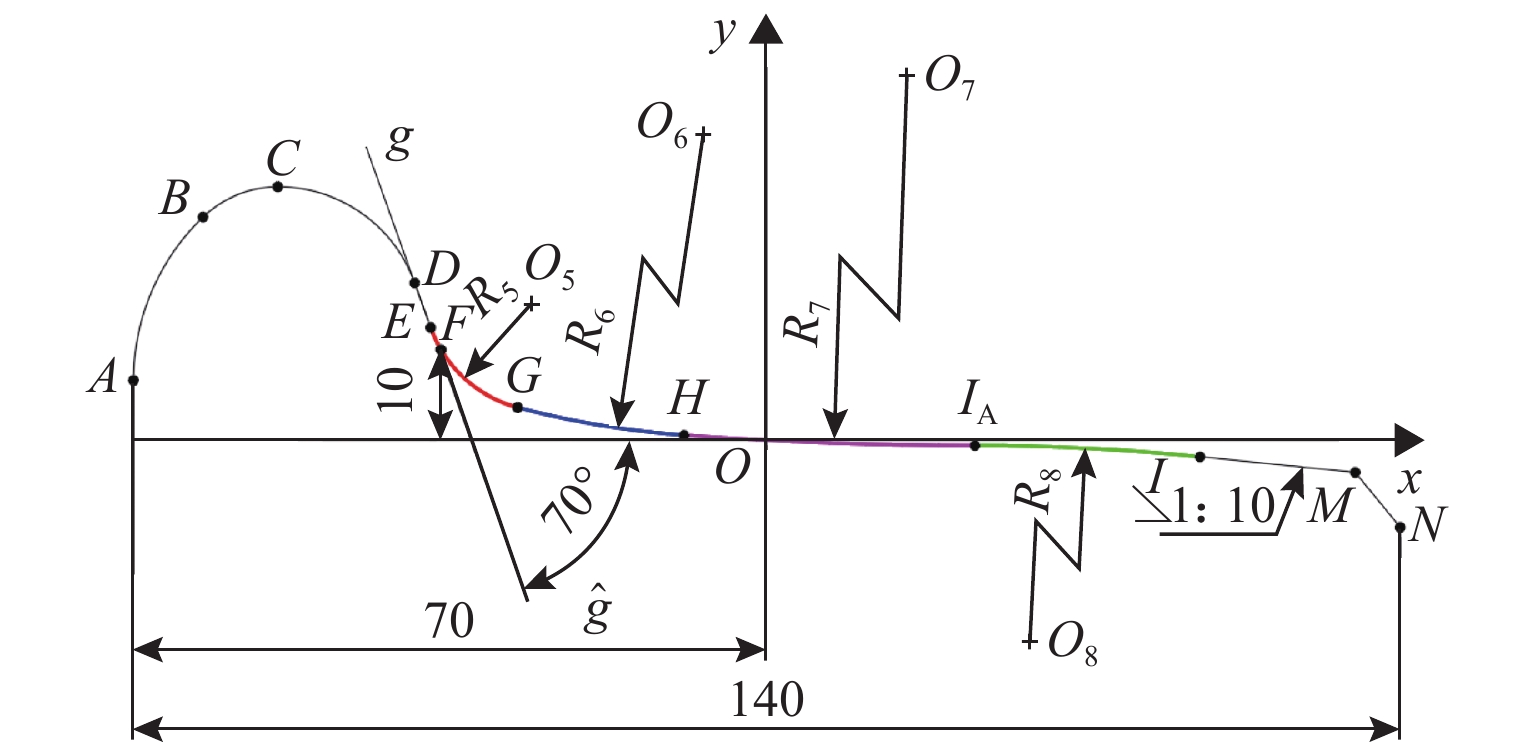
表 1 设计变量上下限
Table 1. Upper and lower limits of design variables
mm 圆弧参数 下限 上限 xO6 −9.0 −0.5 xO7 10.0 30.0 
下载: 导出CSV
表 2 计算等效锥度的匹配条件
Table 2. Matching conditions for calculating equivalent conicity
序号 钢轨 轨底坡 λi 1 CN60 1/40 λ1 2 1/20 λ2 3 CN60N 1/40 λ3 4 1/20 λ4
下载: 导出CSV
表 3 不同匹配条件的非线性临界速度
Table 3. Nonlinear critical speeds under different matching conditions
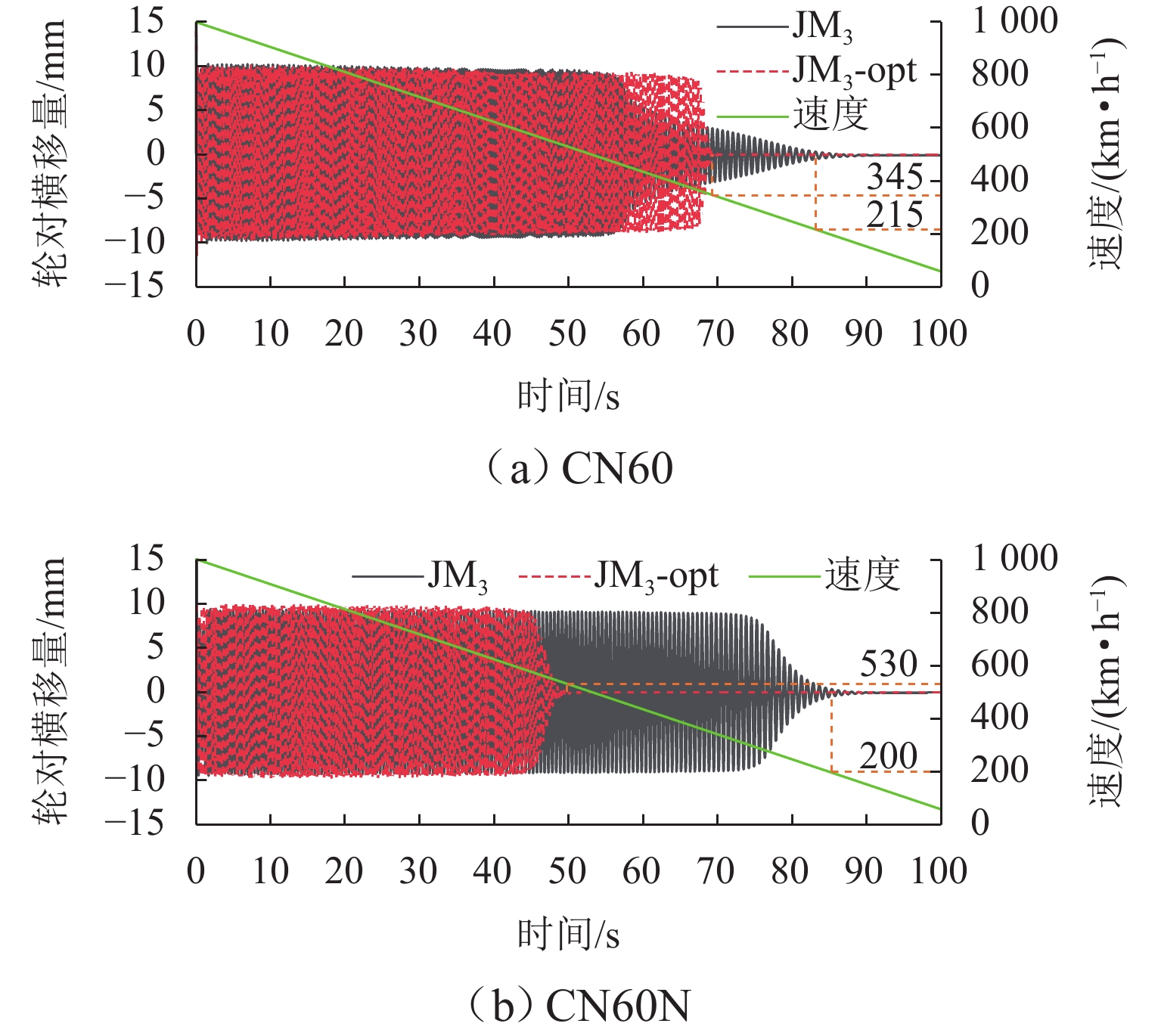
km/h 钢轨 轨底坡 JM3 JM3-opt CN60 1/40 395 390 1/20 215 345 CN60N 1/40 660 670 1/20 200 530
下载: 导出CSV
-
[1] PERSSON I, IWNICKI S. Optimisation of railway wheel profiles using a genetic algorithm[J]. Vehicle System Dynamics, 2004, 41: 517-526. [2] 李立,崔大宾,金学松. 车轮型面优化的研究进展[J]. 西南交通大学学报,2009,44(1): 13-19.LI Li, CUI Dabin, JIN Xuesong. State of arts of research on railway wheel profile optimization[J]. Journal of Southwest Jiaotong University, 2009, 44(1): 13-19. [3] 吴磊,康彦兵,董勇,等. 考虑打磨量的重载钢轨打磨廓形优化设计[J]. 西南交通大学学报,2022,57(4): 805-812.WU Lei, KANG Yanbing, DONG Yong, et al. Optimal design of heavy-haul rail grinding profile considering grinding amount[J]. Journal of Southwest Jiaotong University, 2022, 57(4): 805-812. [4] SHEVTSOV I Y, MARKINE V L, ESVELD C. Optimal design of wheel profile for railway vehicles[J]. Wear, 2005, 258(7/8): 1022-1030. [5] 成棣,王成国,刘金朝,等. 以圆弧参数为设计变量的车轮型面优化数学模型研究[J]. 中国铁道科学,2011,32(6): 107-113.CHENG Di, WANG Chengguo, LIU Jinzhao, et al. Research on the mathematical model for wheel profile optimization with arc parameters as design variables[J]. China Railway Science, 2011, 32(6): 107-113. [6] YE Y G, QI Y Y, SHI D C, et al. Rotary-scaling fine-tuning (RSFT) method for optimizing railway wheel profiles and its application to a locomotive[J]. Railway Engineering Science, 2020, 28(2): 160-183. doi: 10.1007/s40534-020-00212-z [7] SHEN G, AYASSE J B, CHOLLET H, et al. A unique design method for wheel profiles by considering the contact angle function[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2003, 217(1): 25-30. doi: 10.1243/095440903762727320 [8] JAHED H, FARSHI B, ESHRAGHI M A, et al. A numerical optimization technique for design of wheel profiles[J]. Wear, 2008, 264(1/2): 1-10. [9] POLACH O. Wheel profile design for target conicity and wide tread wear spreading[J]. Wear, 2011, 271(1/2): 195-202. [10] CUI D B, LI L, JIN X S, et al. Optimal design of wheel profiles based on weighed wheel/rail gap[J]. Wear, 2011, 271(1/2): 218-226. [11] SANTAMARIA J, HERREROS J, VADILLO E G, et al. Design of an optimised wheel profile for rail vehicles operating on two-track gauges[J]. Vehicle System Dynamics, 2013, 51(1): 54-73. doi: 10.1080/00423114.2012.711478 [12] 干锋,戴焕云,池茂儒,等. 铁道车辆车轮踏面反向优化设计方法[J]. 铁道学报,2015,37(9): 17-24.GAN Feng, DAI Huanyun, CHI Maoru, et al. A reverse optimal design method for wheel tread of railway vehicle[J]. Journal of the China Railway Society, 2015, 37(9): 17-24. [13] 成棣,孙琛,胡晓依,等. 面向低锥度晃车的CRH3平台动车组车轮型面优化[J]. 中国铁道科学,2020,41(6): 135-144.CHENG Di, SUN Chen, HU Xiaoyi, et al. Wheel profile optimization of CRH3 EMU oriented to carbody shaking caused by low equivalent conicity[J]. China Railway Science, 2020, 41(6): 135-144. [14] 祁亚运,戴焕云,干锋,等. 基于车轮磨耗和舒适度的CRH3型动车组型面优化研究[J]. 振动与冲击,2021,40(18): 148-155.QI Yayun, DAI Huanyun, GAN Feng, et al. Wheel profile optimization of CRH3 type of EMU based on wheel wear and passenger comfort[J]. Journal of Vibration and Shock, 2021, 40(18): 148-155. [15] 杜星,陶功权,杨城,等. 轨底坡变化对高速车辆运行行为的影响[J]. 西南交通大学学报,2022,57(2): 286-294.DU Xing, TAO Gongquan, YANG Cheng, et al. Influence of different rail cants on dynamical characteristics of high-speed railway vehicles[J]. Journal of Southwest Jiaotong University, 2022, 57(2): 286-294. [16] SUN J F, CHI M R, JIN X S, et al. Experimental and numerical study on carbody hunting of electric locomotive induced by low wheel–rail contact conicity[J]. Vehicle System Dynamics, 2021, 59(2): 203-223. doi: 10.1080/00423114.2019.1674344 [17] 宋志坤,孙琛,成棣,等. 车轮型面圆弧参数及其对轮轨接触和车辆动力学影响研究[J]. 中国铁道科学,2019,40(6):104-113.SONG Zhikun, SUN Chen, CHENG Di, et al. Research on arc parameters of wheel profile and its influence on wheel-rail contact and vehicle dynamics[J]. China Railway Science, 2019, 40(6):104-113. [18] 国家铁路局. 机车车辆车轮轮缘踏面外形:TB/T 449—2016[S]. 北京:中国铁道出版社,2016. [19] 孙琛. CRH3型平台高速动车组车轮型面多目标优化研究[D]. 北京:北京交通大学,2020. [20] 张维煜,李凯,杨鑫. 基于参数优先级划分的飞轮电机多目标优化[J]. 西南交通大学学报,2023,58(4): 922-932.ZHANG Weiyu, LI Kai, YANG Xin. Multi-objective optimization for flywheel motors based on parameter priority division[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 922-932. [21] 石怀龙,罗仁,曾京. 国内外高速列车动力学评价标准综述[J]. 交通运输工程学报,2021,21(1): 36-58.SHI Huailong, LUO Ren, ZENG Jing. Review on domestic and foreign dynamics evaluation criteria of high-speed train[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 36-58. [22] BRACCIALI A, MEGNA G. Contact mechanics issues of a vehicle equipped with partially independently rotating wheelsets[J]. Wear, 2016, 366/367: 233-240. doi: 10.1016/j.wear.2016.03.037 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 109
- HTML全文浏览量: 31
- PDF下载量: 21
- 被引次数: 0