Crew Rostering Schedule Optimization for Urban Rail Transit Through Resource Sharing
-
摘要:
在城市轨道交通网络化运营条件下，实现乘务资源共享对优化资源配置、降低运营成本、提高网络运输效率具有重要意义. 首先，针对城市轨道交通系统既有固定班制轮班模式，将多线乘务资源共享引入乘务轮班计划编制，在传统单一线路轮班基础上考虑乘务员的跨线值乘和出退勤偏好需求，建立面向线网乘务轮班优化模型以实现区域线网乘务计划的协同优化；其次，根据乘务员对出退勤地点的偏好进行分组，在各组内进行独立的轮班优化，均衡所有乘务员轮班计划工作量；然后，基于班次工作时间、班次间衔接时间和早晚时段工作时间，提出定量化的“辛苦”指标衡量不同班次的工作负荷；最后，根据固定班制和乘务资源共享的特点设计改进的蜂群算法，通过改进初始解生成和迭代搜索机制以完成模型的高效求解。研究表明：引入乘务资源共享可促进乘务员工作量的均衡性，同时满足乘务员对出退勤地点的偏好需求，在既有城市轨道交通乘务轮班模式下提高乘务计划效率和乘务员满意度.
Abstract:Given the context of network-level operation conditions of urban rail transit, crew resource sharing is significant for resource allocation optimization, operation cost reduction, and transport efficiency improvement. Firstly, targeted at existing fixed rostering patterns in urban rail transit systems, crew resource sharing among various lines was applied to crew rostering schedules. By considering cross-line duty and attendance and departure preferences of the crew based on traditional single line rostering, a crew rostering optimization model was proposed to achieve coordinated optimization of crew schedules for regional line networks. Secondly, the crew was grouped according to preferences for attendance and departure locations, and crew rostering in the groups was optimized separately, so as to balance the workload for crew rostering schedules. A quantified index was brought up to evaluate the workload of different crew shifts according to the shift working time, connecting time between shifts, and working time in morning and evening hours. Finally, through an improved swarm algorithm based on the characteristics of fixed crew rostering patterns and crew resource sharing, the model was solved efficiently by improving initial solution generation and iterative search methods. The results show that crew resource sharing can improve the balance of the crew workload, accommodate the crew preferences for attendance and departure locations, and enhance crew schedule efficiency and crew satisfaction under the existing crew rostering patterns of urban rail transit.
-
Key words:
- urban rail transit /
- crew rostering schedule /
- fixed rostering pattern /
- resource sharing /
- balance
-
在交通强国战略加快推进、交通运输领域基础设施建设逐步完善的背景下，隧道施工技术日趋成熟，长大隧道（长度超过1.00 km）不断涌现. 目前，我国已建成了世界最长的双洞高速公路隧道—秦岭终南山隧道（18.02 km）[1]，海拔
3000 m以上的世界最长隧道—新关角隧道（32.70 km）[2]，以及亚洲最长的单孔双线高速铁路隧道—秦岭天华山隧道（16.00 km）[3]. 面对隧道建设技术的持续革新和隧道需求的井喷式增长，我国隧道建设的规模和难度已位居世界第一，超长、超深隧道建设迎来新的发展机遇.在隧道建设过程中，地质条件复杂，视觉环境不良，施工作业难度大，具有一定的风险[4]. 因此，隧道施工期间的组织管理成为规避事故风险、保证施工效率的重要途径. Sousa等[5]研究了隧道施工过程中的事故案例，强调隧道组织管理在降低施工风险，减少施工事故方面的重要性. Zhu等[6]调查统计了我国2010年～2020年发生的重大隧道施工事故发现，低下的组织管理水平会导致施工过程中事故频发. 值得注意的是，施工车辆的运输组织管理已成为严重制约施工安全和施工效率的重点环节，隧道内的渣土运输、人员输送、交通物流配送等成为限制施工效率的瓶颈问题. 施工车辆在路况恶劣、能见度低的长大隧道内交通组织紊乱，不仅严重影响施工进度，还会增加运输安全隐患.
考虑到隧道内错综复杂的交通线路，科学的运输组织管理势在必行. 特别是长大隧道施工过程中对于施工交通流的合理组织和有效管控有利于提高施工效率，保障施工安全. 目前，国内外已有一些学者对隧道的运输组织管理进行了相关研究. Jiang等[7]通过VISSIM对隧道出入口车辆的运行情况进行仿真模拟，提出隧道施工期间隧道出入口及其周边的交通流组织优化方案. Liu等[8]在权衡施工车辆运输效率和安全性的基础上，建立了包含限高、限重、限速等约束条件的双目标车辆运输路径优化模型. 林杉等[9]提出了一种高速公路隧道交通瓶颈元胞自动机模型，为制定隧道内的交通流组织方案提供依据. 高壮[10]基于重载铁路的线路条件研究设计出 2 种隧道内无砟轨道施工物流组织方案，极大地提高了施工组织效率. 然而，现有的大多数研究都是从宏观的角度提出广泛的、借鉴性较强的交通物流组织方案，尚未有着眼于隧道内部交通冲突疏解的多工种施工车辆时刻表和运行路径的优化研究.
车辆时刻表和路径规划的协同优化问题在铁路开行方案和列车时刻表制定，公交循环计划，集装箱码头智能转运车路径、时刻规划以及智能机器人路径规划（避撞）等领域具有广泛的应用[11-14]. Zhang等[11]从宏观层面提出了一种基于扩展时空网络的列车运行周期表模型来得到最佳列车循环方案. 王志建等[12]根据公交车IC刷卡数据构建了多模式公交路网模型来设计满足乘客多种需求的路径规划方案. Cherif等[13]基于Peri网对自动化智能转运车在码头的时间调度和路径规划问题进行了研究. 徐翔斌等[14]将多自动引导车（AGV）的路径转化为离散时空网络下的路径，建立基于离散时空网络的路径优化模型. 由此可见，虽然车辆时刻表和路径的协同优化问题近年来受到了广泛关注，但是少有研究关注到隧道内部施工车辆的时刻表与运行路径的协同优化问题. 与一般隧道相比，长大隧道内道路线形差，施工车辆需求大，面临比上述领域更为棘手的难题. 如果不规定施工车辆的发车频率和路径时刻表，那么混乱、不均匀、不规律的发车会使车辆间产生过多的交通冲突，迫使车辆停止运行，进行掉头、避让、后退等操作，将严重影响施工效率.
在疏解冲突方面，Zhang等[15]针对自动导引车的离线路径规划问题，提出了一种无冲突路径规划方法. 李珣等[16]建立了基于元胞自动机的精细化车道模型，研究新的交通流模型在减少车辆堵塞方面的作用. 李英帅等[17]建立交通冲突预测模型，对直线式单泊位公交停靠站设置进行优化. 本文考虑到长大隧道内部的恶劣路况和复杂交通流促使多工种施工车辆间形成交通冲突的实际情况，对施工车辆的发车时刻表和运行路径的进行协同优化，实现交通冲突的有效消除，保证施工安全.
为解决上述难题，本文立足于施工车辆作业过程，构建路网层面的车辆时刻表和运行路径协同优化模型，并将模型重构为整数线性规划模型，利用GUROBI进行求解，制定施工车辆总运行时间最短的运输组织方案. 该优化方案能够有效疏解车辆间的交通冲突，协助调度员实施决策调度，使施工车辆在保证安全的前提下高效完成运输任务.
1. 问题描述
一般隧道的路况简单，施工过程中需求单一，多数研究侧重于其微观层面的组织管理. 而长大隧道内部道路狭长，路况复杂，需要从宏观层面对施工车辆的运输组织进行规划与管理. 在长大隧道施工作业的过程中，不同工种的施工车辆要求在指定需求点完成运渣、运材料、运人等任务.
1.1 隧道交通网络拓扑建模
长大隧道内的施工道路交通网络由正线、平导线、横洞等交错构成的复杂方格状道路网络，包含节点和路段2种基本要素. 其中，节点为路段间的交叉点，代表路段的交叉口. 交叉口按照交叉方式可分为“十字型交叉”和“T字型交叉”. 路段是连接节点的线段，代表供车辆行驶的道路，按照可供车辆行驶的方向数量分为单向路段和双向路段. 其拓扑结构如图1 所示.
图 1 隧道内部基本交通单元拓扑Figure 1. Topological diagram of basic traffic units inside the tunnel本文考虑了长大隧道内部的多样运输需求，包括运渣需求、运材料需求和运人需求. 因此，施工车辆由运渣车辆、运材料车辆和运人车辆组成，对应于不同类型的需求点. 施工车辆的作业流程包括：驶入隧道、到达需求点并完成指定运输任务、驶出隧道. 根据隧道内节点及路段间的物理连接关系，图2展示出了隧道内部的交通网络及其拓扑图.
由于隧道内部单、双向路段混合共存，行驶环境恶劣，且施工车辆本身体积大、运载质量大，其在运输过程中容易在交叉口和单向路段发生交通冲突，形成通行瓶颈，妨碍其他车辆正常通行. 根据产生原因可将交通冲突分为交叉冲突、相向冲突和赶超冲突，如图3所示. 交叉冲突是指车辆在很短的时间范围内到达同一交叉点而产生的冲突；相向冲突是指对向行驶的车辆在单向路段上相遇而产生的冲突；赶超冲突是指不同的速度的车辆在单向路段上同向行驶而产生的冲突.
2. 模型构建
在模型中，车辆时刻表的决策变量属于整数变量，车辆的运行路径由表示车辆是否经过某路段的一系列0-1变量决定.
2.1 模型假设
为了简化问题，方便后续模型的建立和求解，本文做出以下假设：
假设1. 施工车辆的运行路径分为去程和返程方向. 另外，为简化求解过程，指定车辆在去程和返程期间任意路段上的唯一可行方向，即简化车辆去程和返程方向上的有向弧集合.
假设2. 施工车辆的限速条件预先给定，其在路段上的运行时间范围由最高和最低限速确定.
假设3. 隧道内，同向行驶的车辆遵循先到先服务（FIFO）原则，即同向行驶的车辆中，先到达某路段的车辆先从该路段离开.
2.2 数学描述
隧道内的拓扑网络由有向网络${\mathcal{G}}=({\mathcal{N}}, {\mathcal{A}}) $表示，$ \mathcal{N} $为节点集合，$ \mathcal{A} $为路段集合，节点$ i, j \in \mathcal{N} $，有向弧$ (i, j) \in \mathcal{A} $，$ i \neq j $. $ \mathcal{U}=\{1,2\} $表示车辆的行驶方向集合，用$ t, u_{\mathrm{a}} \in \mathcal{U} $进行索引. 当$ u=1 $或$ u_{\mathrm{a}}=1 $时，车辆从隧道入口向需求点行驶，当$ t=2 $或$ u_{\mathrm{a}}={2} $时，车辆从需求点向隧道出口行驶. $ \mathcal{A}_{u} $表示$ u $方向上的路段集合，$ \mathcal{A}_{{\mathrm{s}}} $表示单向路段集合，$ \mathcal{K} $表示车辆集合，用$ k, k_{\mathrm{a}} \in \mathcal{K} $进行索引.
1） 车辆行驶路径的0-1决策变量：
xk,ui,j={1,若车辆k在u方向上经过路段(i,j)0,其他. 2） 车辆时刻表的决策变量：
$ h^{k} $为车辆$ k $的发车间隔.
3） 车辆到达和离开路段事件的相关变量：
$ a_{i,j}^{k,u} $为车辆$ k $在$ {u} $方向上到达路段$ (i, j) $的时刻，
$ d_{i,j}^{k,u} $为车辆$ k $在$ {u} $方向上离开路段$ (i, j) $的时刻.
2.3 目标函数和约束条件
隧道内多工种施工车辆的运输组织方案在保证系统安全的基础上，设计施工车辆的发车时刻表，合理安排运行路径，尽可能高效率地完成各项运输任务. 因此，模型以最小化所有车辆的运行（行驶）总时间为目标建立目标函数. 每辆车的行驶时长为$ \displaystyle\sum\limits_{\left( i,{{d}_{{\mathrm{s}}}} \right)\in \mathcal{A}}{d_{i,{{d}_{{\mathrm{s}}}}}^{k,2}}-\displaystyle\sum\limits_{\left( {{o}_{{\mathrm{s}}}},j \right)\in \mathcal{A}}{a_{{{o}_{{\mathrm{s}}}},j}^{k,1}}$，目标函数表示如式（1）所示.
minZ=∑k∈K(∑(i,ds)∈Adk,2i,ds−∑(os,j)∈Aak,1os,j), (1) 式中：$ o_{{\mathrm{s}}} $为隧道入口，即车辆去程方向上的起点$ o_{k, 1} $；$ d_{{\mathrm{s}}} $为隧道出口，即车辆返程方向上的终点$ d_{k, 2} $.
1） 车辆路径约束
车辆$ k $在$ {u} $方向上从起点$ o_{k, {u}} $出发，沿着路段驶过中间节点后到达终点$ d_{k,u} $，需满足所有车辆的路径均被规划（式（2）～（3））. 对于去程，车辆的起点为隧道入口，终点为相应需求点. 对于返程，车辆的起点为需求点，终点为隧道出口.
∑(ok,u,j)∈Auxk,uok,u,j=1,∀k∈K,u∈U, (2) ∑(i,dk,u)∈Auxk,ui,dk,u=1. (3) 2） 流量守恒约束
中间节点必须满足流量守恒约束，即节点流入等于节点流出，如式（4）所示.
∑(ia,i)∈Auxk,uia,i=∑(i,j)∈Auxk,ui,j,∀i∈N∖{ok,u,dk,u},k∈K,u∈U. (4) 3） 路径和时刻联系约束
只有车辆经过某一路段，才能得到其在该路段上的到达时刻和离开时刻，满足式（5）～（6）. 其中，$ M $是一个非常大的正数. 式（5）中，当车辆$ k $在方向$ {u} $上经过路段$ (i, j) $，即$ x_{i,j}^{k,u}=1 $时，$ 0 \leqslant a_{i, j}^{k, u} \leqslant M $，规定了$ a_{i, j}^{k, u} $的取值范围，强调了其非负特性，使$ a_{i, j}^{k,u} $具有实际意义. 而当车辆$ k $在$ {u} $方向上不经过路段$ (i, j) $，即$ x_{i, j}^{k, u}=0 $时，$ -M \leqslant a_{i, j}^{k,u} \leqslant 0 $，$ a_{i, j}^{k,u} $不具有实际意义. 式（6）中的$ d_{i,j}^{k,u} $同理.
(xk,ui,j−1)M⩽ak,ui,j⩽xk,ui,jM,∀(i,j)∈A,k∈K,u∈U, (5) (xk,ui,j−1)M⩽dk,ui,j⩽xk,ui,jM,∀(i,j)∈A,k∈K,u∈U. (6) 4） 发车间隔约束
在隧道中，受到技术条件和安全性能的限制，施工车辆需要满足一定的发车间隔要求，即满足式（7）.
hmin⩽hk⩽hmax,∀k∈K, (7) 式中：$ h_{\text {min }} $、$ h_{\max } $分别为给定的最小和最大发车间隔.
5） 路网进入时间约束
为保证车辆有序运行，车辆$ k $进入路网的时间由已出发车辆的发车间隔决定，满足式（8）.
∑(os,j)∈A1ak,1os,j=k∑ka=1hka,∀k∈K, (8) 式中：${\mathcal{A}_1} $为去程方向上的路段集合.
6） 路网运行时间约束
路网运行时间是指从第一辆车驶入路网开始直到最后一辆车驶出路网的总时间，即施工车队对于路网的使用周期. 路网存在一个最大的运行时间，在现实情况中可能是隧道内路段的最大工作时长或施工队的最长工时. 最后执行运输任务的车辆$ K $必须在到达路网的最大运行时间$ t_{\text{max}} $之前离开路网，即满足式（9）.
∑(i,ds)∈A2dK,2i,ds⩽tmax (9) 7） 路段运行时间约束
车辆在路段上的行驶时间范围取决于路段的长度和限速条件，满足式（10）.
τ(r)i,j,k⩾li,jvmaxk,∀(i,j)∈A,k∈K, (10) 式中：$ l_{i j} $为路段$ (i, j) $的长度，$ v_{\max {\mathrm{k}}} $为车辆$ k $的最大行驶速度，$ \tau_{i j, k}^{({\mathrm{r}})} $表示车辆$ k $在路段$ (i, j) $上的运行时间.
8） 路段到达和离开时刻约束
车辆离开某一路段的时刻等于到达该路段的时刻与路段上的行驶时间之和，即满足式（11）. 除了起始路段外，车辆到达某一路段的时刻等于离开上一路段的时刻，即满足约束条件（12）.
dk,ui,j=ak,ui,j+τ(r)i,j,k,∀(i,j)∈A,k∈K,u∈U (11) ak,ui,j=∑(ia,i)∈Audk,uia,i,∀(i,j)∈Au,i≠ok,u,i≠j,k∈K,u∈U. (12) 9） 去程和返程联系约束
对于车辆$ k $，其去程的终点和返程的起点相同，都为执行任务的需求点. 另外，车辆从返程起点出发的时刻等于离开去程终点的时刻与需求点服务时间之和，满足式（13）.
∑(ok,2,j)∈A2ak,2ok,2,j=∑(ia,dk,1)∈A1dk,1ia,dk,1+τ(w)dk,1,∀k∈K, (13) 式中：$ \boldsymbol{\tau}_{d_{k, 1}}^{({\mathrm{w}})} $表示需求点的服务时间.
10） 冲突疏解约束
为避免施工车辆间的碰撞、追尾事故，保障隧道内的运输安全，需要对车辆间的交叉冲突、相向冲突和赶超冲突进行疏解.
11） 交叉冲突疏解
若2辆车在短时间内到达同一交叉点，则会形成交叉冲突. 所以要求到达同一交叉口车流的时间间隔必须满足可保障安全的最低时间限制，满足式（14）.
|ak,uj,i−dka,uaia,j|+(1−xk,uj,i)M+(1−xka,uaia,j)M⩾τ(m)min,∀j∈N,(j,i)∈A,(ia,j)∈A,k,ka∈K,k≠ka,u,ua∈U, (14) 式中：$ \tau_{\mathrm{mim}}^{(\mathrm{m})} $表示最小会车时间间隔.
12） 相向冲突疏解约束
若2辆车在单向路段上相向而行，则会发生相向冲突. 为了避免这类情况的发生，需要保证先到达的车辆对于路段的优先使用权，满足式（15）.
(ak,ui,j−aka,uaj,i)(ak,ui,j−dka,uaj,i)+(1−xk,ui,j)M+(1−xka,uaj,i)M⩾1,∀(i,j)∈As,k,ka∈K,k≠ka,u,ua∈U. (15) 13） 赶超冲突疏解约束
若2辆车在单向路段上同向而行，由于速度不同，可能会发生赶超冲突. 在现实情况中，车辆一般遵守先到先服务的原则，满足式（16）.
(ak,ui,j−aka,uai,j)(dk,ui,j−dka,uai,j)⩾0,∀(i,j)∈As,k,ka∈K,k≠ka,u,ua∈U. (16) 14） 路段瓶颈约束
隧道内的每一路段都有通行能力限制. 当行驶车辆大于路段通行能力时，该路段成为瓶颈路段，路网安全性大幅度降低，所以需要满足式（17）.
∑k∈K∑u∈Uxk,ui,j⩽Ci,j,∀(i,j)∈A, (17) 式中：$ C_{i, j} $表示路段$ (i, j) $的最大通行能力.
15） 变量约束
车辆运行路径和时刻表的决策变量以及车辆到达和离开路段事件的相关变量满足式（18）.
{xk,ui,j∈{0,1},∀(i,j)∈A,k∈K,u∈U,ak,ui,j,dk,ui,j,hk⩾0且为整数,∀(i,j)∈A,k∈K,u∈U, (18) 3. 模型重构
本文建立的模型为整数非线性规划模型，为方便求解，结合假设1的简化条件对模型进行线性化处理，为接下来使用GUROBI求解模型做准备.
首先，通过引入$ M $，对式（11）和式（12）进行了线性化处理，得到式（19）和式（20）.
dk,ui,j⩾ak,ui,j+τ(r)i,j,k−M(1−xk,ui,j),∀(i,j)∈A,k∈K,u∈U (19) ak,ui,j⩾∑(ia,i)∈Audk,uia,i−M(1−xk,ui,j),∀(i,j)∈Au,i≠ok,u,i≠j,k∈K,u∈U (20) 根据假设1，简化后模型中去程和返程上的有向弧均为单向弧，则式（14）可简化为式（21）. 另外，由于GUROBI可对绝对值进行运算，不对式（14）进行线性化处理.
|∑u∈Uak,uj,i−∑u∈Udka,uia,j|+(1−∑u∈Uxk,uj,i)M+(1−∑u∈Uxka,uia,j)M⩾τ(m)min,∀j∈N,(i,j)∈A,(ia,j)∈A,k,ka∈K,k≠ka (21) 类似地，式（15）可简化为式（22）. 式（22）的线性化处理的结果如式（23）～（26）所示. 需要注意：$ \delta_{i, j, k, k_{\mathrm{a}}} $为0-1变量，用于辅助式（22）的线性化处理. 当$ \delta_{i, j, k, k_{\mathrm{a}}}=1 $时，式（23）和（25）的约束条件成立，式（24）和（26）的约束条件被放松，表明此时车$ k_{\mathrm{a}} $先进入路段，且在车$ k $进入路段之前就离开路段，保证不发生相向冲突. 同理，当$ \delta_{i, j, k, k_{\mathrm{a}}}=0 $时，式（24）和（26）的约束条件成立，式（23）和（25）的约束条件被放松，表明此时车$ k $先进入路段，且在车$ k_{\mathrm{a}} $进入路段之前就离开路段，保证不发生相向冲突.
(∑u∈Uak,ui,j−∑u∈Uaka,uj,i)(∑u∈Uak,ui,j−∑u∈Udka,uj,i)+(1−∑u∈Uxk,ui,j)M+(1−∑u∈Uxka,uia,j)M⩾1,∀(i,j)∈As,k,ka∈K,k≠ka, (22) ∑u∈Uak,ui,j−∑u∈Uaka,uj,i⩾1−(1−δi,j,k,ka)M−(2−∑u∈Uxk,ui,j−∑u∈Uxka,uj,i)M,∀(i,j)∈As,k,ka∈K,k≠ka (23) ∑u∈Uaka,uj,i−∑u∈Uak,ui,j⩾1−δi,j,k,kaM−(2−∑u∈Uxk,ui,j−∑u∈Uxka,uj,i)M,∀(i,j)∈As,k,ka∈K,k≠ka, (24) ∑u∈Uak,ui,j−∑u∈Udka,uj,i⩾1−(1−δi,j,k,ka)M−(2−∑u∈Uxk,ui,j−∑u∈Uxka,uj,i)M,∀(i,j)∈As,k,ka∈K,k≠ka, (25) ∑u∈Uaka,uj,i−∑u∈Udk,ui,j⩾1−δi,j,k,kaM−(2−∑u∈Uxk,ui,j−∑u∈Uxka,uj,i)M,∀(i,j)∈As,k,ka∈K,k≠ka. (26) 与式（15）的处理方式相同，式（16）可简化为式（27），线性化处理结果如式（28）、（29）所示. $ \xi_{i, j, k, k_{\mathrm{a}}} $为0-1变量. 当$ \xi_{i, j, k, k_{\mathrm{a}}}=1 $时，$ k $车先进入路段，先离开路段，保证不发生赶超冲突；当$ \xi_{i, j, k, k_{\mathrm{a}}}=0 $时，车$ k_{\mathrm{a}} $先进入路段，先离开路段，保证不发生赶超冲突.
(∑u∈Uak,ui,j−∑u∈Uaka,ui,j)(∑u∈Udk,ui,j−∑u∈Udka,ui,j)⩾0,∀(i,j)∈As,k,ka∈K, (27) −Mξi,j,k,ka⩽∑u∈Uak,ui,j−∑u∈Uaka,ui,j⩽(1−ξi,j,k,ka)M,∀(i,j)∈As,k,ka∈K, (28) −Mξi,j,k,ka⩽∑u∈Udk,ui,j−∑u∈Udka,ui,j⩽(1−ξi,j,k,ka)M,∀(i,j)∈As,k,ka∈K, (29) δi,j,k,ka,ξi,j,k,ka∈{0,1},∀(i,j)∈As,k2,ka∈K (30) 4. 案例分析
某长大隧道项目共有20辆施工车辆执行运渣、运材料、运人任务，包括12辆运渣车、4辆运材料车和4辆运人车. 隧道只有一个出入口，所有施工车辆均从该口驶入驶出隧道.
4.1 隧道网络拓扑
与一般隧道不同，长大隧道内部道路狭长，单双向路段混合，路网呈现纵横交错的结构. 本文将隧道抽象为近似3 × 5的网格结构，并对各节点进行编号，如图4所示. 其中，黄色节点为隧道出入口，绿色节点为运渣需求点，紫色节点为运材料需求点，红色节点为运人需求点，蓝色节点为中间节点. 可以看出，紫色节点，即运材料需求点也是隧道施工过程中的断点. 节点之间通过路段连接，有向双线箭头代表双向路段，有向单线箭头代表单向路段，路段上的数值代表节点间的距离. 根据假设1，对去程和返程方向上的有向弧进行简化，在去程方向上规定右行和下行有向弧，在返程方向上规定左行和上行的有向弧，如图5所示. 令Vq为图5中对应的节点. $q \in \{0,1,\cdots,16\} $.
图 5 去返程方向的隧道网络拓扑图Figure 5. Tunnel network topology diagram in inbound and outbound directions4.2 编制隧道交通组织方案
模型求解时，运行计算机硬件环境为Intel （R） Core （TM） i5-6200U CPU，主频2.40 GHz，内存8 GB；软件环境为Windows10系统，使用Python调用GUROBI求解器. 在该案例中，基于铁路隧道工程施工技术指南[18]，通过调查成兰铁路跃龙门隧道施工组织实际案例[19]，对各参数进行了规定和限制. 参考成兰铁路龙门隧道案例中车队的施工周期要求，规定路网的最大运行时间为100 min. 考虑到铁路隧道工程施工技术指南中提出的安全规范，结合成兰铁路跃龙门隧道案例涉及的车速限制，我们令运渣车（KM）和运材料车（KC）的最高限速为30 km/h，运人车（KP）的最高限速为40 km/h，车辆的最小和最大发车间隔分别为1 min和4 min，最小会车时间间隔和安全时间间隔均为1 min，单向路段和双向路段的最大通行能力分别为10辆和20辆车. 案例中20辆施工车辆根据最短行驶路径和最高行驶速度得到的施工运输组织初始方案，见表1. 然后本文使用GUROBI求解器，经过
1661 s后求解得到基于重构的整数线性规划模型的施工运输组织优化方案，见表2.表 1 施工运输组织初始方案Table 1. Initial construction organization scheme编号 车辆进入隧道运行方案 车辆离开隧道运行方案 始发时刻 运行路径 始发时刻 运行路径 KP1 0 0-1-2-5-8-11-14 13 14-11-8-5-4-1-0 KP2 1 0-1-4-5-8-11-14 14 14-11-8-5-2-1-0 KP3 2 0-1-4-5-8-11-14 15 14-11-8-5-2-1-0 KP4 3 0-1-4-5-8-11-14 16 14-11-8-5-2-1-0 KC1 4 0-1-2-3-6-9 15 9-6-3-2-1-0 KC2 5 0-1-2-3-6-9 16 9-6-3-2-1-0 KC3 6 0-1-2-3-6-9 17 9-6-3-2-1-0 KC4 7 0-1-2-3-6-9 18 9-6-3-2-1-0 KM1 8 0-1-4-7-10-13 23 13-10-7-4-1-0 KM2 9 0-1-4-7-10-13-14-16 27 16-14-13-10-7-4-1-0 KM3 10 0-1-4-5-8-11-14-15 27 15-14-11-8-5-2 1-0 KM4 11 0-1-4-7-10-13 26 13-10-7-4-1-0 KM5 12 0-1-4-7-10-13-14-16 30 16-14-13-10-7-4-1-0 KM6 13 0-1-4-5-8-11-14-15 30 15-14-11-8-5-2-1-0 KM7 14 0-1-4-7-10-13 29 10-7-4-1-0 KM8 15 0-1-4-7-10-13-14-16 33 16-14-13-10-7-4-1-0 KM9 16 0-1-4-5-8-11-14-15 33 15-14-11-8-5-2-1-0 KM10 17 0-1-4-7-10-13 32 13-10-7-4-1-0 KM11 18 0-1-4-7-10-13-14-16 36 16-14-13-10-7-4-1-0 KM12 19 0-1-4-5-8-11-14-15 36 15-14-11-8-5-2-1-0 表 2 施工运输组织优化方案Table 2. Optimization construction organization scheme编号 车辆进入隧道运行方案 车辆离开隧道运行方案 始发时刻 运行路径 始发时刻 运行路径 KP1 0 0-1-2-5-8-11-14 13 14-11-8-5-4-1-0 KP2 1 0-1-4-7-8-11-14 14 14-13-10-7-4-1-0 KP3 5 0-1-4-7-8-11-14 18 14-13-10-7-4-1-0 KP4 9 0-1-4-7-8-11-14 22 14-11-8-5-4-1-0 KC1 13 0-1-4-5-6-9 24 9-6-5-4-1-0 KC2 17 0-1-2-5-6-9 28 9-6-5-2-1-0 KC3 18 0-1-4-5-6-9 29 9-6-3-2-1-0 KC4 22 0-1-2-3-6-9 33 9-6-5-4-1-0 KM1 23 0-1-4-7-10-13 38 13-10-7-4-1-0 KM2 27 0-1-4-7-10-13-14-16 45 16-14-11-8-5-2-1-0 KM3 31 0-1-4-7-8-11-14-15 48 15-14-13-10-7-4-1-0 KM4 34 0-1-4-7-10-13 49 13-10-7-4-1-0 KM5 35 0-1-4-7-8-11-14-16 53 16-14-11-8-5-2-1-0 KM6 39 0-1-2-5-8-11-14-15 56 15-12-11-8-5-2-1-0 KM7 42 0-1-4-7-10-13 57 13-10-7-4-1-0 KM8 46 0-1-4-7-8-11-14-16 64 16-14-11-8-5-2-1-0 KM9 47 0-1-2-5-8-11-14-15 64 15-14-11-8-5-4-1-0 KM10 49 0-1-4-7-10-13 64 13-10-7-4-1-0 KM11 53 0-1-4-7-10-13-14-16 71 16-14-11-8-7-4-1-0 KM12 57 0-1-2-5-8-11-12-15 74 15-14-11-8-5-4-1-0 表1中加粗划线的节点表示车辆在该节点与其他车辆发生了交叉冲突. 易看出，优化前车辆KP1与KM3、KM9、KC2，KP2与KC3，KP3与KM9、KC4，KP4与KM6，KC1与KM12，KM1与KM10，KM2与KM11，KM3与KM7，KM6与KM10间发生了交叉冲突，甚至车辆KP2与KC3间存在3个交叉冲突点. 车辆KM3与KM9，车辆KM6与KM12在V14与V15间的路段发生了相向冲突. 对比表1和表2可以发现，优化前后施工车辆的时刻表发生了很大的变化. 车辆KP2、KC3、KM1、KM5、KM9与前车的发车间隔保持1 min没有变化，车辆KM10与前车的发车间隔从1 min增至2 min，车辆KM4、KM7与前车的发车间隔从1 min增加至3 min，剩下车辆与前车的发车间隔从1 min增加至4 min. 另外，优化前，对于需求点相同的车辆，其运行路径大多相同. 例如：需求点为V14的车辆KP2、KP3、KP4的运行路径
多数为V0→V1→V4→V5→V8→V11→V14→V11→V8→V5→V4→V1→V0；需求点为V9的车辆KC1、KC2、KC3、KC4的运行路径都为V0→V1→V2→V3→V6→V9→V6→V3→V2→V1→V0→V1. 这容易导致车辆对某路段的使用频率过高，从而产生冲突，例如：V1与V2间路段的高使用率导致V1与V2的交叉冲突点过多. 而优化后，对于需求点相同的车辆，其运行路径大多不同. 这是因为各个车辆需要尽量避免沿着相同路径行驶，减少某个路段的使用压力，规避交通冲突，保证安全行驶. 事实上，优化方案还可以在限速范围内改变车辆的行驶速度来调整车辆在路段上的运行时间，间接改变车辆的路径时刻表，达到延缓或提前到达某一节点的时刻来规避交通冲突，保证运行安全. 综上分析，本文所提出的优化方案主要从调整发车时刻表、改变车辆运行路径、调节路段行驶时间3个途径来减少交通冲突.
初始方案、优化方案的目标函数值和交通冲突数量如表3所示. 优化前后，目标函数值，即车辆的总运行（行驶）时间均为512 min，没有发生变化，交通冲突数量从21个减到0个. 因此，可以得出，对多工种施工车辆的时刻表和路径进行规划，可以在不增加车辆总运行（行驶）时间，即目标函数值（512 min）的基础上有效规避交通冲突，保证隧道内部施工期间车辆的行驶安全. 实际上，不同于理论计算结果，当隧道内部车辆间发生交通冲突时，车辆总运行时间不仅会大幅度增加，还可能引发严重的交通事故. 本案例的优化方案在不牺牲车辆理想运行（行驶）时间的条件下完全避免了交通冲突，保证了隧道内部施工车辆的畅通运行. 为进一步清晰直观地对比初始方案与优化方案的优劣，刻画2种方案优化前后的效果，我们绘制隧道运输组织初始方案和优化方案的时空轨迹图，如图6和图7所示. 图中的黑色五角星代表交叉冲突点，红色直线的交点代表相向冲突点. 优化后，图中的交通冲突点得以消除，各个车辆的路径时刻表从紧张危险、交错纵横的状态转变为疏散安全、平衡有序的状态. 另外，观察交通冲突的涉及对象和发生时刻可发现，车辆容易在去程方向上与其他返程方向上的车辆发生冲突. 这是因为去程方向和返程方向的目标方向不一致，车辆运行路径容易产生交叉相错. 初始方案的路径时刻表只能先保证去程方向上车辆的有序规律发车，难以进一步确保返程方向上车辆对于冲突的规避，而优化方案可以通过进一步调整路径时刻表来继续保证返程方向上车辆的有序安全运行. 由此可知，考虑交通冲突的长大隧道内部多工种施工车辆时刻表和运行路径的协同优化，使得隧道内部交通网络的安全性得到提高，车辆间的交通冲突得以疏解，施工任务能够高效安全完成，减少了意外事故发生的可能性.
表 3 初始和优化方案的目标函数值和交通冲突数量Table 3. Objective function values and number of traffic conflicts for initial and optimization schemes方案 目标函数值/min 交通冲突数量/个 交叉 相向 赶超 初始方案 512 19 2 0 优化方案 512 0 0 0 
图 6 隧道运输组织初始方案时空轨迹图Figure 6. Space-time trajectory map of initial scheme of tunnel transportation organization
图 7 隧道运输组织优化方案时空轨迹图Figure 7. Space-time trajectory map of optimization scheme of tunnel transportation organization综上分析，本文提出的考虑交通冲突的长大隧道内部多工种施工车辆的时刻表和运行路径系统优化模型及GUROBI求解方法具备可行性，能够在短时间内得到效果较好的优化方案，应用于隧道内部运输组织方案编制，可操作性强.
5. 结论与展望
1） 在隧道施工任务执行过程中，需求点相同的施工车辆容易发生交通冲突，不同目标方向（去程和返程）的车辆容易发生交通冲突. 本文所提出的优化方案主要从调整发车时刻表、改变车辆运行路径、调节路段行驶时间3个途径来减少交通冲突. 在案例中优化得到的多工种施工车辆运输组织方案不增加车辆的总运行（行驶）时间，即目标函数值（512 min），使车辆间的交通冲突数量从21个减为0个，提高了施工效率，保证了运输安全.
2） 本文提出的隧道内部多工种施工车辆的时刻表和运行路径协同优化模型可应用于各种隧道施工项目，也可以通过设置时间窗，考虑车辆装配过程，考虑车辆的循环运输计划等来进一步完善模型，扩大其应用场景，同时也是后续的重要研究方向.
-
图 1 基于四班三运转的轮班计划
Figure 1. Crew rostering schedule based on four-team and three-shift pattern
图 2 乘务资源共享下排班和轮班的关系
Figure 2. Relationship between crew scheduling and rostering through resource sharing
图 6 场景1四班三运转下不同算法的收敛过程
Figure 6. Convergence process of different algorithms regarding four-team and three-shift pattern in scenario 1
图 7 不同轮班模式下轮班计划“辛苦”程度对比
Figure 7. Comparison of workload degrees of rostering schedules regarding different rostering patterns
表 1 四班三运转下4个乘务组的轮班计划
Table 1. Crew rostering schedule for four crew groups regarding four-team and three-shift pattern
乘务组 第1天 第2天 第3天 第4天 第5天 第6天 … 1 E M R D E M … 2 M R D E M R 3 R D E M R D 4 D E M R D E 
下载: 导出CSV
表 2 符号定义
Table 2. Symbol definition
符号 含义 xj,i 决策变量，当且仅当班次 j 位于班次循环中第 i 个位置时取值为 1 H 优化目标，所有轮班单位“辛苦”程度的均衡性 i 班次循环中的位置序号，i∈I，I 为班次位置集合 j 班次序号，j∈J，J 为班次集合 ts, j、te, j 班次 j 的开始和结束时间 td, j、tde, j、ti, j 班次 j 的驾驶时间、特殊时段附加值、非驾驶工作时间 JM, JE 早、晚班的班次集合 IE 班次循环中应分配晚班的位置集合 Tmins 晚班和早班的最小夜间休息（接续）时间 pi,k 0-1变量，第 i 个位置的班次类型为 k 时，取值为1 lk, j 0-1变量，班次 j 属于班次类型 k 时取值为1 $t^* $ 轮班单位长度，天 r 轮班单位序号，r∈R，R 为轮班单位集合 Hr 轮班单位 r 的“辛苦”程度 h1,r、h2,r 轮班单位 r 由班次直接产生和接续产生的“辛苦”程度 qi,r 0-1变量，轮班单位 r 包含位置 i 时取值为 1 ir,m 轮班单位 r 的第 m 个班次（m=1,2,$\cdots $,$t^* $）在班次循环中的位置 Tt,i,i* 班次循环中第 i 和第 i* 个位置对应班次类型之间的接续时间阈值 v1、v2、v3、v4 驾驶时间、特殊时段附加值、非驾驶工作时间、班次接续时间转化为“辛苦”程度的折算比例
下载: 导出CSV
表 3 3个案例场景的参数
Table 3. Parameters of three scenarios in case studies
场景编号 涉及线路 乘务区段数/个 连续值乘区段数/个 场景1 线路1、3 1332 > 4567 场景2 线路1、2 1689 > 6563 场景3 线路1、2、3 1915 > 7144
下载: 导出CSV
表 4 考虑乘务员出退勤偏好的轮班输入构成
Table 4. Composition of crew rostering considering crew attendance and departure preferences
班次类型 班次数量 四班三运转 六班五运转 场景1 场景2 场景3 场景1 场景2 场景3 早班 排班数 41 43 54 56 68 78 备班数 5 5 6 6 8 8 白班 排班数 41 43 54 28 34 39 备班数 5 5 6 3 4 4 晚班 排班数 41 43 54 56 68 78 备班数 5 5 6 6 8 8 总乘务员数/人 368 384 480 372 456 516
下载: 导出CSV
表 5 不同场景和班制下乘务轮班计划优化结果
Table 5. Optimization results of crew rostering schedules in different scenarios and rostering patterns
场景 班制 A组“辛苦”程度 B组“辛苦”程度 总“辛苦”程度 计算时间/s 均值 标准差 均值 标准差 均值 标准差 场景1 四班三运转 883.6 42.2 854.3 46.2 869.0 46.5 8763 六班五运转 1311.6 58.1 1279.6 51.8 1295.6 57.3 11821 场景2 四班三运转 902.6 44.0 883.2 44.9 892.9 45.5 9138 六班五运转 1327.9 62.8 1269.1 61.0 1298.5 68.5 15033 场景3 四班三运转 902.1 48.6 869.8 46.5 886.0 50.2 11410 六班五运转 1310.6 69.7 1261.1 72.9 1285.8 75.4 16693
下载: 导出CSV
表 6 四班三运转下ABC与GA算法求解结果对比
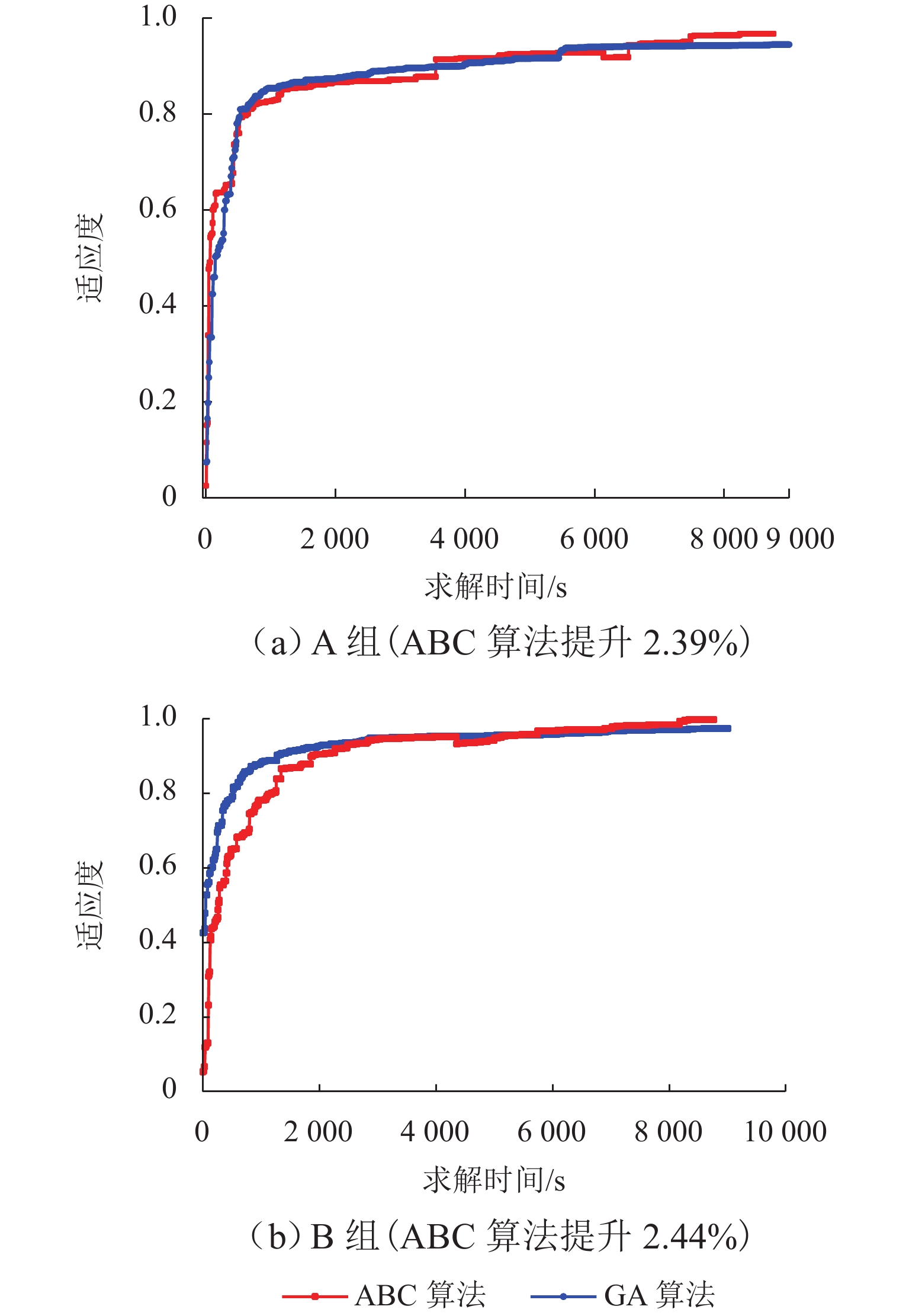
Table 6. Comparison of ABC and GA results regarding four-team and three-shift pattern
场景 总“辛苦”程度 计算时间/s ABC GA ABC GA 场景1 868.95 ± 46.53 868.96 ± 49.76 8763 9053 场景2 892.91 ± 45.45 892.90 ± 52.82 9138 9385 场景3 885.97 ± 50.20 885.98 ± 53.18 11410 11639 注：u ± v中u为各个乘务组对应统计指标的均值，v为标准差.
下载: 导出CSV
表 7 场景3轮班计划对比
Table 7. Comparison of crew rostering schedules for scenario 3
指标 四班三运转 六班五运转 分线优化 乘务共享1 乘务共享2 分线优化 乘务共享1 乘务共享2 乘务员数/人 488 480↓ 468↓ 528 504↓ 504↓ 日均额外通勤时间/h 225.7 0 216.5↓ 236.2 0 248.4↑ 工作效率/% 73.7 73.9↑ 74.9↑ 69.5 70.0↑ 70.7↑ 人均日工作时间/min 244.5 241.4↓ 244.5↓ 242.9 246.6↑ 244.3↑ “辛苦”程度均值/min 885.2 886.0↑ 890.3↑ 1287.3 1285.8 ↓1291.9 ↑“辛苦”程度标准差/min 54.9 50.2↓ 52.6↓ 89.0 75.4↓ 70.9↓ 注：“↑”表示相较分线优化情形数值上增加；“↓”表示相较分线优化情形数值上减少.
下载: 导出CSV
-
[1] 薛锋,梁鹏,李海,等. 地铁乘务排班计划优化的最短路快速算法[J]. 铁道科学与工程学报,2022,19(9): 2532-2540.XUE Feng, LIANG Peng, LI Hai, et al. Optimization of subway crew scheduling based on shortest path faster algorithm[J]. Journal of Railway Science and Engineering, 2022, 19(9): 2532-2540. [2] 潘寒川,戚博洋,胡华,等.考虑司机偏好的城市轨道交通混合乘务轮转模型[J].交通运输系统工程与信息,2023,23(1):258-267.PAN Hanchuan, QI Boyang, HU Hua, et al. Preference-oriented task-type-mixed crew rostering optimization model for urban railway transit[J]. Journal of Transportation Systems Engineering and Information Technology,2023,23(1):258-267. [3] 杨子涵,刘葛辉,李明,等. 考虑资源共享的城市轨道交通架修基地选址优化模型[J]. 铁道科学与工程学报,2023,20(1): 74-83.YANG Zihan, LIU Gehui, LI Ming, et al. Optimum location selection of heavy repair depots for urban rail transit considering resource sharing[J]. Journal of Railway Science and Engineering, 2023, 20(1): 74-83. [4] 石俊刚,杨静,王凤丽. 多线乘务员共享条件下城市轨道交通乘务计划均衡编制探讨[J]. 铁道运输与经济,2016,38(3): 84-87.SHI Jungang, YANG Jing, WANG Fengli. Discussing on balanced crew scheduling of urban rail transit based on multi-line crews sharing[J]. Railway Transport and Economy, 2016, 38(3): 84-87. [5] 金华,陈绍宽,王志美,等. 基于地铁乘务资源共享的排班计划优化方法[J]. 交通运输系统工程与信息,2021,21(2): 126-132.JIN Hua, CHEN Shaokuan, WANG Zhimei, et al. Crew schedule optimization for urban rail transit with crew resources sharing[J]. Journal of Transportation Systems Engineering and Information Technology, 2021, 21(2): 126-132. [6] JIN H, CHEN S K, RAN X C, et al. Column generation-based optimum crew scheduling incorporating network representation for urban rail transit systems[J]. Computers & Industrial Engineering, 2022, 169: 108155.1-108155.12. [7] IBARRA-ROJAS O J, DELGADO F, GIESEN R, et al. Planning, operation, and control of bus transport systems: a literature review[J]. Transportation Research Part B: Methodological, 2015, 77: 38-75. [8] 褚飞跃,田志强,倪少权. 高速铁路单循环乘务排班计划编制模型与算法[J]. 铁道学报,2012,34(7): 1-9. doi: 10.3969/j.issn.1001-8360.2012.07.001CHU Feiyue, TIAN Zhiqiang, NI Shaoquan. Model and algorithm for formulation of the single cycle crew rostering plans of high-speed railways[J]. Journal of the China Railway Society, 2012, 34(7): 1-9. doi: 10.3969/j.issn.1001-8360.2012.07.001 [9] XIE L, SUHL L. Cyclic and non-cyclic crew rostering problems in public bus transit[J]. OR Spectrum, 2015, 37(1): 99-136. doi: 10.1007/s00291-014-0364-9 [10] QUESNEL F, DESAULNIERS G, SOUMIS F. Improving air crew rostering by considering crew preferences in the crew pairing problem[J]. Transportation Science, 2020, 54(1): 97-114. [11] MAENHOUT B, VANHOUCKE M. A hybrid scatter search heuristic for personalized crew rostering in the airline industry[J]. European Journal of Operational Research, 2010, 206(1): 155-167. [12] XIE L, MERSCHFORMANN M, KLIEWER N, et al. Metaheuristics approach for solving personalized crew rostering problem in public bus transit[J]. Journal of Heuristics, 2017, 23(5): 321-347. doi: 10.1007/s10732-017-9348-7 [13] 王骁. 高速铁路客运乘务排班优化研究[D]. 兰州:兰州交通大学,2021. [14] 金华,陈绍宽,冯旭杰,等. 考虑乘务员值乘需求的地铁乘务轮班优化方法[J]. 铁道学报,2023,45(7): 29-37. doi: 10.3969/j.issn.1001-8360.2023.07.004JIN Hua, CHEN Shaokuan, FENG Xujie, et al. A crew rostering optimization method for urban rail transit considering crew preference[J]. Journal of the China Railway Society, 2023, 45(7): 29-37. doi: 10.3969/j.issn.1001-8360.2023.07.004 [15] 张增勇. 城市轨道交通乘务计划编制方法研究[D]. 北京:北京交通大学,2014. [16] 罗红双. 网络化条件下城市轨道交通乘务计划编制方法研究[D]. 成都:西南交通大学,2019. [17] 金华,陈绍宽,刘爽,等. 基于固定班制的地铁乘务计划一体化优化方法[J]. 西南交通大学学报,2020,55(5): 955-962. doi: 10.3969/j.issn.0258-2724.20190952JIN Hua, CHEN Shaokuan, LIU Shuang, et al. Integrated optimum crew planning in fixed shift system for subways[J]. Journal of Southwest Jiaotong University, 2020, 55(5): 955-962. doi: 10.3969/j.issn.0258-2724.20190952 [18] LAI D S W, LEUNG J M Y, DULLAERT W, et al. A graph-based formulation for the shift rostering problem[J]. European Journal of Operational Research, 2020, 284(1): 285-300. doi: 10.1016/j.ejor.2019.12.019 [19] 石俊刚,杨静,周峰,等. 基于任务均衡的城市轨道交通乘务任务轮转模型及算法[J]. 铁道学报,2017,39(9): 17-24. doi: 10.3969/j.issn.1001-8360.2017.09.003SHI Jungang, YANG Jing, ZHOU Feng, et al. Crew rostering model and algorithm based on balanced workload in urban rail transit[J]. Journal of the China Railway Society, 2017, 39(9): 17-24. doi: 10.3969/j.issn.1001-8360.2017.09.003 [20] 汤希峰,何杰,张浩. 考虑碳排放的两阶段选址-路径问题及其算法[J]. 西南交通大学学报,2023,58(5): 1110-1116,1125. doi: 10.3969/j.issn.0258-2724.20210773TANG Xifeng, HE Jie, ZHANG Hao. Two-echelon location routing problem considering carbon emissions and its algorithm[J]. Journal of the Southwest Jiaotong University, 2023, 58(5): 1110-1116,1125. doi: 10.3969/j.issn.0258-2724.20210773 [21] 李冰,任泽强,轩华. 考虑多编组站专场作业的铁路枢纽车流组织优化[J]. 西南交通大学学报,2023,58(3): 489-498,545. doi: 10.3969/j.issn.0258-2724.20210796LI Bing, REN Zeqiang, XUAN Hua. Optimization of wagon flow assignment with transship work for multiple marshaling stations at railroad terminals[J]. Journal of the Southwest Jiaotong University, 2023, 58(3): 489-498,545. doi: 10.3969/j.issn.0258-2724.20210796 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 35
- HTML全文浏览量: 14
- PDF下载量: 13
- 被引次数: 0